Parametric Amplification of a Superconducting Plasma Wave

Abstract

Many applications in photonics require all-optical manipulation of plasma waves¹, which can concentrate electromagnetic energy on sub-wavelength length scales. This is difficult in metallic plasmas because of their small optical nonlinearities. Some layered superconductors support Josephson plasma waves (JPWs)^2,3, involving oscillatory tunneling of the superfluid between capacitively coupled planes. Josephson plasma waves are also highly nonlinear⁴, and exhibit striking phenomena like cooperative emission of coherent terahertz radiation^5,6, superconductor-metal oscillations⁷ and soliton formation⁸. We show here that terahertz JPWs can be parametrically amplified through the cubic tunneling nonlinearity in a cuprate superconductor. Parametric amplification is sensitive to the relative phase between pump and seed waves and may be optimized to achieve squeezing of the order parameter phase fluctuations⁹ or single terahertz-photon devices.

Cuprates are strongly anisotropic superconductors in which transport is made three-dimensional by Josephson tunneling between the Cu-O planes. Tunneling reduces the superfluid density in the direction perpendicular to the planes and hence the frequency of the plasmon to below the average pair breaking gap. Weakly damped oscillations of the superfluid sustain transverse Josephson Plasma Waves (JPWs) that propagate along the planes.

Consider a complex superconducting order parameter in the i^th Cu-O plane ψ_i(x, y, t) = |ψ_i(x, y, t)|expiθ_i(x, y, t) , which depends on two in-plane spatial coordinates x and y and on time t. For a THz-frequency optical field polarized perpendicular to the planes, excitations above the superconducting gap are negligible and the modulus of the order parameter |ψ|² (number of Cooper pairs) is nearly constant in space and time. Hence, the electrodyamics is dominated by the order-parameter phase θ_i (x, y, t). Ignoring at first the spatial dependence of the phase, the local tunneling strength can, from the Josephson equations¹⁰, be expressed in terms of an equivalent inductance, L, which depends on the local interlayer phase difference ${\theta }_{i,i+1}\left(t\right)={\theta }_i\left(t\right)-{\theta }_{i+1}\left(t\right)$ as $L\left({\theta }_{i,i+1}\left(t\right)\right)\sim L_0/\text{c}os\left({\theta }_{i,i+1}\left(t\right)\right)$ (i and i+1 are the indices for two neighboring layers). Here $L_0=\frac{\hslash }{2e{I}_c}$ is the inductance at equilibrium, ћ the reduced Planck’s constant, 2e the Cooper pair charge and I_c the critical current. Denoting the capacitance of the Cu-O planes with a constant C, we express the Josephson Plasma Resonance (JPR) frequency as ${\omega }_{JP}{}^2=\frac{1}{L\left({\theta }_{i,i+1}\left(t\right)\right)C}={\omega }_{JP0}{}^2\text{cos}\left[{\theta }_{i,i+1}\left(t\right)\right]$, where ${\omega }_{JP0}{}^2=\frac{1}{L_{0}C}$ is the equilibrium value. Correspondingly, the oscillator strength f for the plasma oscillations¹¹ is also a function of the interlayer phase and scales as f = f₀ cos[θ_i,i+1(t)]. The dependence of the oscillator strength f on the cosine of the superconducting phase corresponds to a third order optical nonlinearity.

According to the second Josephson equation¹⁰, the interlayer phase difference θ_i,i+1(t) advances in time with the time integral of the interlayer voltage drop, as $\frac{\partial \left[{\theta }_{i,i+1}\left(t\right)\right]}{\partial t}=\frac{2eV}{\hslash }$. For an optical field made resonant with the Josephson plasma frequency E(t) = E₀ sin(ω_JP0t), the interlayer phase oscillates as θ_i,i+1(t) = θ₀ cos(ω_JP0t), where E₀ is the field amplitude and ${\theta }_0=\frac{2ed}{\hslash {\omega }_{JP0}}{E}_0$ (d ∼ 1 nm is the interlayer distance). This implies that the oscillator strength $f_{i,i+1}\left(t\right)=f_0\hspace{0.17em}\text{cos}\left({\theta }_0\text{cos}\left({\omega }_{JP0}t\right)\right)\approx f_0\left(1-\frac{{\theta }_0^2+{\theta }_0^2\hspace{0.17em}\text{cos}\left(2{\omega }_{JP0}t\right)}{4}\right)$ is modulated at a frequency 2ω_JP0, whenever the field E₀ is large enough to make the phase excursion θ₀ sizeable.

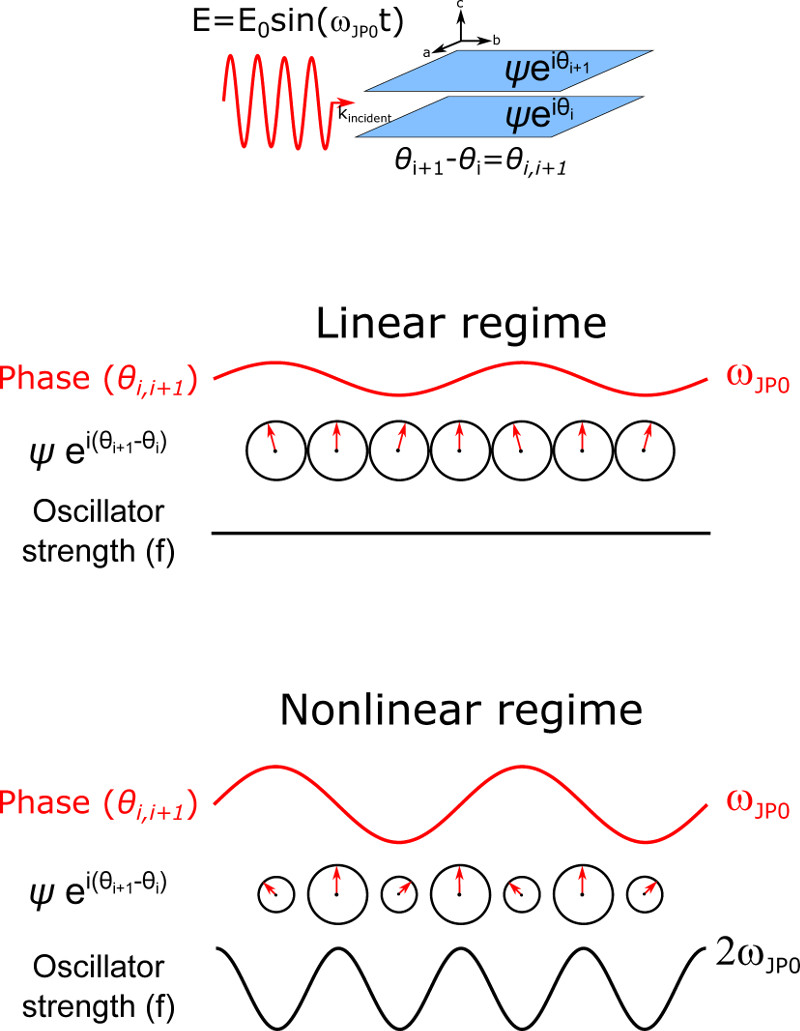
Figure 1 provides a pictorial representation of this physics. We plot a vector that represents both the phase difference θ_i,i+1(t) (vector angle) and the oscillator strength f_i,i+1(t) (vector length). This picture shows how, for small driving fields, only θ_i,i+1(t) oscillates at the driving frequency ω_JP0, whereas for larger fields these oscillations are accompanied by a 2ω_JP0 modulation of the oscillator strength f_i,i+1(t).

Figure 1. Schematic representation of Josephson plasma waves.

Schematic time-dependent representation of JPWs in linear and nonlinear regime, in presence of a driving field E(t) = E₀ sin(ω_JP0t) polarized along the out-of-plane direction of a layered superconductor. Red arrows indicate the Josephson phase while the corresponding oscillator strength f is represented by the black circle area. A JPW in linear regime consists of small amplitude modulations of θ_i,i+1 at constant oscillator strength $f\sim {\omega }_{JP0}^2$. In nonlinear regime, the Josephson phase oscillates at ω_JP0, whereas f is modulated at 2ω_JP0.

Note also that the phenomena discussed above can be casted in terms of a Mathieu equation (see Supplementary Information 2). Thus, a 2ω_Jp0 modulation of the oscillator strength can serve as a pump for the parametric amplification of a second, weak plasma wave at frequency ω_JP0. In this paper we demonstrate experimentally this effect in La_1.905Ba_0.095CuO₄ (LBCO_9.5), a cuprate superconductor with the equilibrium JPR at ω_JP0 ≅ 0.5 THz.

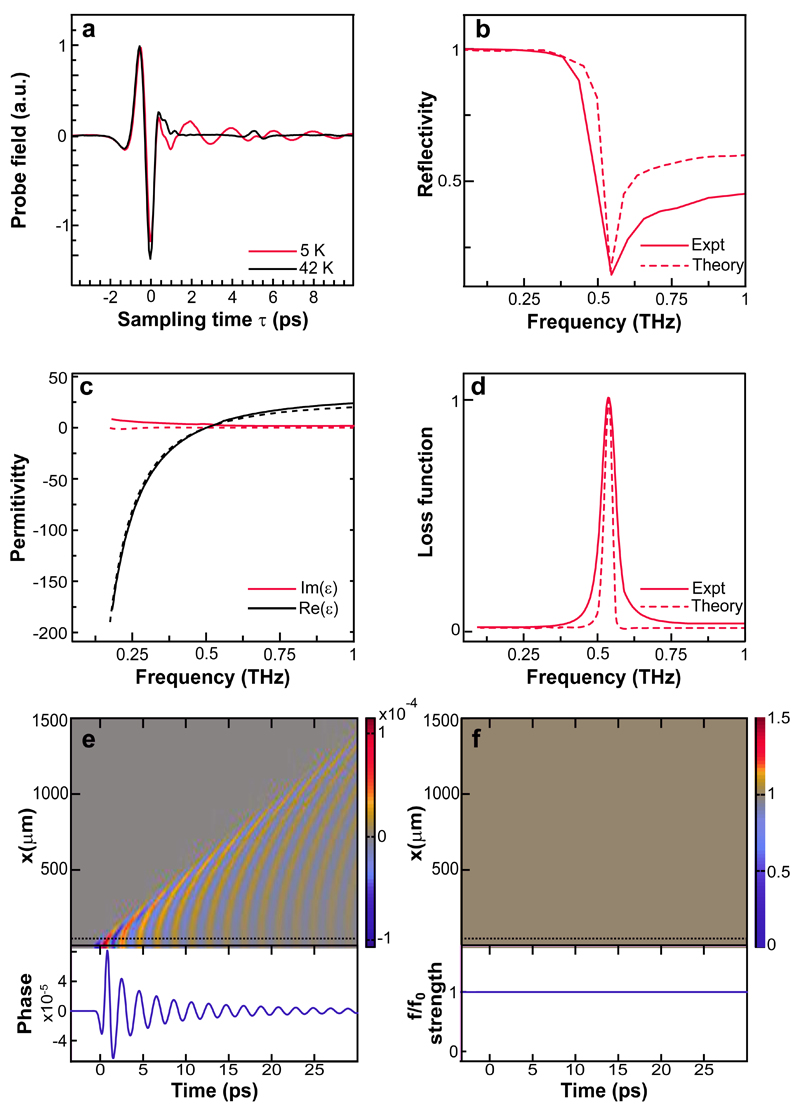
Terahertz pulses, generated with a photoconductive antenna¹², were used as a weak probe of JPWs (a schematic drawing of the measurement geometry is reported in Supplementary Information 1). A typical THz-field trace¹³ reflected by the sample is shown in Fig. 2A. Two different measurements are displayed: one taken below (red line) and the other one above (black line) the superconducting transition temperature T_c = 32 K. In the superconducting state, long-lived oscillations with ~ 2 ps period were observed on the trailing edge of the pulse, indicative of the JPR at ω_JP0 ≅ 0.5 THz. Figure 2B (solid red line) displays the corresponding reflectivity edge in frequency domain. The solid lines in Fig. 2C -2D are the complex dielectric permittivity ε(ω) and the loss function $L\left(\omega \right)=-\text{Im}\left(\frac{1}{\epsilon \left(\omega \right)}\right)=\frac{{\epsilon }_2\left(\omega \right)}{{\left({\epsilon }_1\left(\omega \right)+{\epsilon }_2\left(\omega \right)\right)}^2}\cdot L\left(\omega \right)$ peaks at ω_JP0, where the real part of the dielectric permittivity, ε₁(ω), crosses zero. These optical properties could be well reproduced by solving the wave equation in the superconductor in one dimension⁸ (see Supplementary Information 3), which yields the space and time dependent order parameter phase θ_i,i+1(x,t) (Fig. 2E) and the corresponding changes (negligible in linear response regime) of the oscillator strength f = f₀ cos[θ_i,i+1(x, t)] (Fig. 2F). The reflectivity, complex permittivity, and loss function (dashed lines in Fig. 2B, 2C, and 2D, respectively), calculated from these simulations by solving the electromagnetic field at the sample surface⁸, are in good agreement with the experimental data.

Figure 2. Linear JPWs in LBCO_9.5.

a, E_probe (τ) measured in absence of pump field both above and below T_c = 32 K. b, Frequency-dependent, c-axis reflectivity at T = 5 K (solid line), extracted from the E_probe (τ) trace of panel a. c, Corresponding real and imaginary part of the complex permittivity and (d) energy loss function (solid lines). Dashed lines in b-d were calculated by numerically solving the sine-Gordon equation in linear regime. e, Simulated phase θ_i,i+1(x,t) and (f) corresponding oscillator strength f (no change) induced by a weak probe THz field. Horizontal dotted lines indicate the spatial coordinate x at which the line cuts are displayed (lower panels).

Amplification of a weak JPW like the one above (probe field) was achieved by mixing it with a second, intense pump field, which resonantly drove the Josephson phase to large amplitudes. Quasi-single cycle THz pulses, generated in LiNbO₃ with the tilted pulse front method¹⁴ (yielding field strengths up to ~100 kV/cm), were used to excite these waves in nonlinear regime. The spectral content of these pulses extended between 0.2 and 0.7 THz, centered at the JPR frequency (see Supplementary Information 4). Note that the pump field strength used in this experiment exceeds the expected threshold to access the nonlinear regime, defined by ${\theta }_0=\frac{2e{E}_{0}d}{\hslash {\omega }_{JP0}}\sim 1$ and corresponding in this material to field amplitudes $E_0=\frac{\hslash {\omega }_{JP0}}{2ed}$ ~ 20 kV/cm.

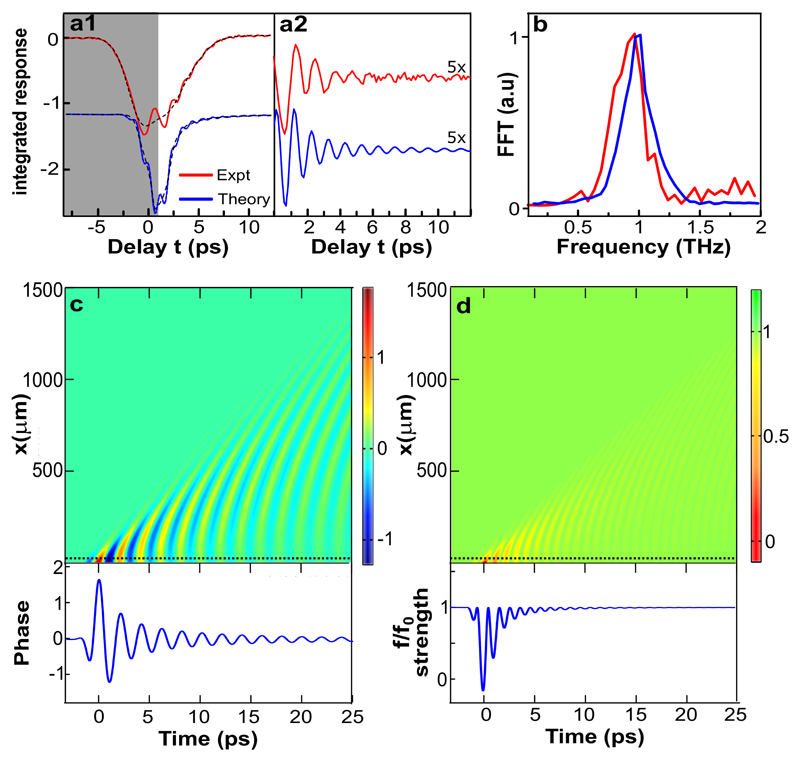
In Fig. 3, we report the time-delay dependent, spectrally integrated pump-probe response of LBCO_9.5. Changes in the reflected probe field were measured at one specific probe sampling time (τ = τ₀), as a function of pump-probe time delay (t). For a system in which the optical properties are dominated by a single plasma resonance, the spectrally integrated response is proportional to the plasma oscillator strength f.

Figure 3. Nonlinear JPWs in LBCO_9.5.

a1, Normalized spectrally integrated pump-probe response $\frac{\text{Δ}{E}_{\text{probe}}}{E_{\text{probe}}}\left(t,{\tau }_0=2\text{ ps}\right)$. Experimental data are shown along with calculations based on the sine-Gordon equation in nonlinear regime (displayed with a vertical offset). Dashed lines indicate an average reduction that accompanies the oscillations (see model). The reduction was subtracted through Fourier filtering (>0.2 THz) to obtain the oscillations shown in a2. The signal buildup region affected by perturbed free induction decay is shaded in grey. b, Fourier transform of the extracted oscillations, showing a peak at ~1 THz. c, Phase θ_i,i+1(x,t) and (d) corresponding oscillator strength f induced by a strong THz pump field, as determined by numerically solving the sine-Gordon equation in nonlinear regime. Horizontal dotted lines indicate the spatial coordinate x at which the line cuts are displayed (lower panels).

As shown in Fig. 3A-3B, this integrated response exhibits a reduction of the signal and oscillations at a frequency ~ 2ω_JP0. Note that the oscillation frequency did not depend on the pump electric field strength E₀, while the frequency reduced when the base temperature of the experiment was increased, consistent with the reduction of the equilibrium ω_JP0 (see Supplementary Information 5 and 6). The effect completely disappeared at T > T_c.

Hence, the theoretically predicted 2ω_JP0 modulation of the total oscillator strength f (see above) is well reproduced by the data in Fig. 3. This response could also be simulated using the space- and time-dependent sine-Gordon equation (see Fig. 3C-3D), yielding good agreement between experiment and theory (see dashed lines in Fig. 3A-3B).

Note that here we only analyze pump-probe delays t ≳ 0 ps, because the response at the earliest times suffers from perturbed free induction decay¹⁵. This effect consists in the deformation of a coherent signal, which occurs when the pump strikes the sample during the oscillatory relaxation of the probe (for t ≲ 0 ps in our case). Perturbations of the response are particularly evident in case of long momentum relaxation times, as in superconductors.

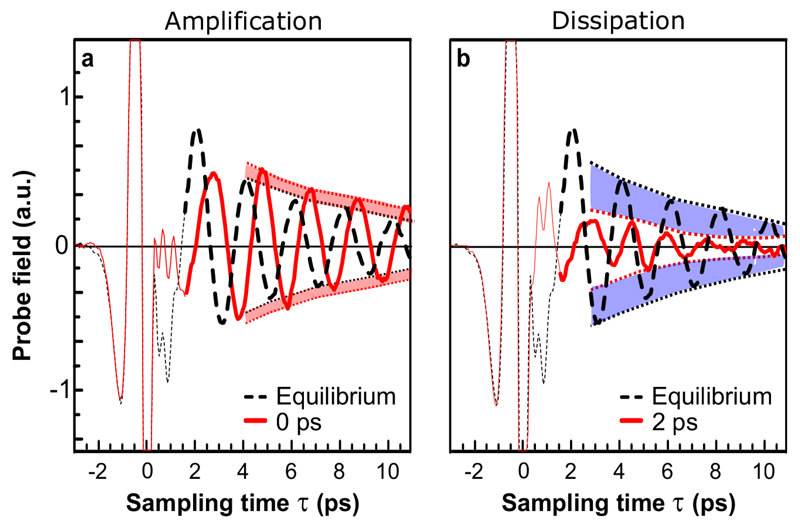
Selected time-domain probe traces measured before and after excitation are displayed in Fig. 4. Crucially, at specific time delays the probe field is amplified (Fig. 4A), whereas at other delays it is suppressed (Fig. 4B) with respect to that measured at equilibrium.

Figure 4. Amplification and suppression of plasma oscillations.

E_probe (t, τ) traces measured by scanning the electro-optic sampling time τ at selected pump-probe delays t = 0 ps and t = 2 ps. Data are shown along with the same quantity measured at equilibrium (pump off). Plasma oscillations on the trailing edge of the pulses (τ ≳ 2 ps) are highlighted by thicker lines. Colored shadings in a and b indicate amplification and suppression of the JPW amplitude, respectively.

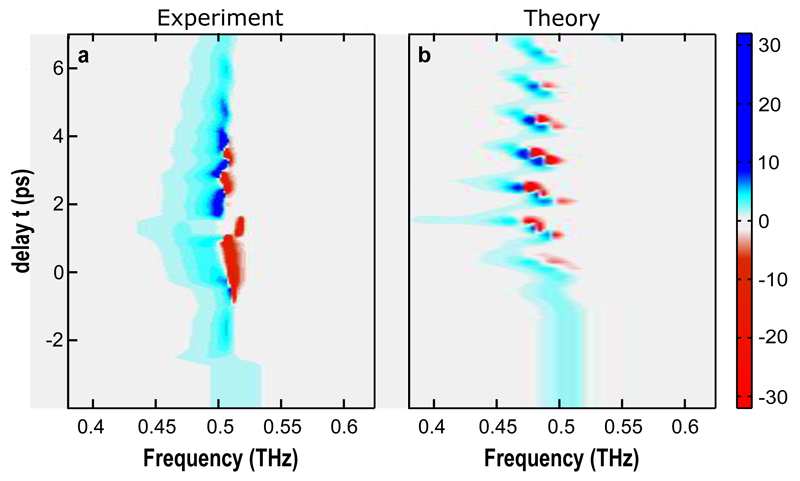
In Fig. 5 we report the time-delay and frequency dependent loss function $L(t,\omega )=-\text{Im}\left(\frac{1}{\epsilon (t,\omega )}\right)=\frac{{\epsilon }_2(t,\omega )}{{({\epsilon }_1(t,\omega )+{\epsilon }_2(t,\omega ))}^2}$, a quantity that peaks at the zero crossing of ε₁(t,ω) and is always positive for a dissipative medium (i.e., a medium with ε₂(t,ω) > 0). The experimental data of Fig. 5A show that after excitation L(ω) acquires negative values around ω_JP0 (red regions). This is indicative of a negative ε₂(t,ω) and hence amplification. The effect is strong near zero pump-probe time delay, then disappears after ~1 ps and is observed again periodically with a repetition frequency of ~ 2ω_JP0. The same effect appears also in the simulations (Fig. 5B), yielding periodic amplification at a repetition frequency of 2ω_JP0.

Figure 5. Time-delay and frequency dependent loss function.

Time-delay and frequency dependent loss function L(t,ω) determined (a) experimentally and (b) by numerically solving the sine-Gordon equation in nonlinear regime. Note that experimental and simulated L(ω) in the region between t=-4 ps and t=-2 ps have been multiplied by a factor of 5 to be better visualized with the other data.

In Supplementary Information 7 we report additional quantitative estimates of the degree of amplification. We include a negative absorption coefficient and a reflectivity larger than 1 at ω ≃ ω_p. The extracted values are α = (−0.090 ± 0.003)μm⁻¹ and R = (1.042 ± 0.008), respectively.

The data and theoretical analysis reported here demonstrate that terahertz JPWs can be parametrically amplified, exhibiting the expected sensitivity to the relative phase of strong and weak fields mixed in this process and the oscillatory dependence at twice the frequency of the drive.

Parametric amplification of THz light based on nonlinear optical techniques has already been shown in the past¹⁶. However, the physics demonstrated here extend beyond potential applications in photonics, directly leading to coherent parametric control of the superfluid in layered superconductors, and providing a means to manipulate the properties of the material or to probe them in new ways¹⁷.

Moreover, the ability to amplify a plasma wave could lead to single-THz photon manipulation devices that may operate above 1 K temperatures. These would exploit concepts that to date have been developed only at microwave frequencies and in the milli-Kelvin regime^18–21. Finally, the parametric phenomena discussed here can also potentially be used to squeeze^{9,22, 23} the superfluid phase, and may lead to control of fluctuating superconductivity²⁴, perhaps even over a range of temperatures above T_c ^25,26.

Methods

Laser pulses with 100 fs duration and ~5 mJ energy from a commercial Ti:Sa amplifier were split into 3 parts (92%, 7%, 1%). The most intense beam was used to generate strong-field THz pulses with energies up to ~3 μJ via optical rectification in LiNbO₃ with the tilted pulse front technique. These were collimated and then focused at normal incidence onto the sample (with polarization perpendicular to the Cu-O planes, i.e. along the c axis) using a Teflon lens and a parabolic mirror, with focal lengths of 150 mm and 75 mm, respectively. The pump spot diameter at the sample position was ~2.5 mm. The pump field strength was calibrated with electro-optic sampling in a 0.2-mm-thick GaP crystal, yielding a maximum value of ~100 kV/cm (see Supplementary Information 4).

The 7% beam was used to generate the THz probe pulses with a photoconductive antenna. These had a dynamic bandwidth of 0.1-3 THz, corresponding to a time resolution of ~250 fs. The c-axis optical properties of the superconductor (both at equilibrium and throughout the pump-induced dynamics) were probed in reflection geometry, with a probe incidence angle of 45° and a spot diameter at the sample position of ~2 mm). The reflected probe pulses were electro-optically sampled in a 1-mm-thick ZnTe crystal, using the remaining 1% of the 800 nm beam. This measurement procedure returned the quantity E_probe (t, τ), with t being the pump-probe delay and τ being the electro-optic sampling time coordinate.

The sample used in our experiment was a single crystal of La_1.905Ba_0.095CuO₄ cut and polished along an ac oriented surface of ~3x3 mm size. Its equilibrium optical response in the superconducting state was determined by measuring the complex-valued E_probe(ω) (pump off) both at T < T_c and T > T_c and by referencing it to the normal-state reflectivity measured in another crystal coming from the same batch of samples²⁷.

The spectrally integrated pump-probe traces of Fig. 3 were measured by scanning the pump-probe delay t at a fixed sampling time τ= τ₀. This was chosen to be on the trailing edge of the pulse, where the JPR oscillations are present. Note that the observed dynamics, and in particular the 2ω_JP0 oscillations, did not depend significantly on the specific τ₀ value at which the scan was performed.

The frequency and time-delay dependent loss function of Fig. 5 (as well as all complex optical properties of the perturbed material) was determined by applying Fresnel equations¹¹ to the pump-induced changes in the reflected electric field. These were normalized by independently recording E_probe (t, τ) in presence and absence of the THz pump field. Note that there was no need to take into account any pump-probe penetration depth mismatch in the calculation.

In the simulations, the Josephson phase evolution θ_i,i+1(x,t) was determined through the one-dimensional sine-Gordon equation⁶:

$$\frac{{\partial }^2{\theta }_{i,i+1}\left(x,t\right)}{\partial x^{{}_2}}-\frac{1}{\gamma }\frac{\partial {\theta }_{i,i+1}\left(x,t\right)}{\partial t}-\frac{{\epsilon }_r}{c^2}\frac{{\partial }^2{\theta }_{i,i+1}\left(x,t\right)}{\partial t^{{}_2}}=\frac{{\omega }_{JP0}^2{\epsilon }_r}{c^2}\sin {\theta }_{i,i+1}\left(x,t\right)$$

being γ a damping constant, c the speed of light, ε_r the dielectric permittivity, and ω_JP0 the equilibrium JPR frequency. This equation was solved numerically, with the THz pump and probe fields overlapping at the vacuum-superconductor interface. For more details on this topic, we refer the reader to Supplementary Information 3.