Summary
Presence-only records may provide data on the distributions of rare species, but commonly suffer from large, unknown biases due to their typically haphazard collection schemes. Presence–absence or count data collected in systematic, planned surveys are more reliable but typically less abundant.
We proposed a probabilistic model to allow for joint analysis of presence-only and survey data to exploit their complementary strengths. Our method pools presence-only and presence–absence data for many species and maximizes a joint likelihood, simultaneously estimating and adjusting for the sampling bias affecting the presence-only data. By assuming that the sampling bias is the same for all species, we can borrow strength across species to efficiently estimate the bias and improve our inference from presence-only data.
We evaluate our model’s performance on data for 36 eucalypt species in south-eastern Australia. We find that presence-only records exhibit a strong sampling bias towards the coast and towards Sydney, the largest city. Our data-pooling technique substantially improves the out-of-sample predictive performance of our model when the amount of available presence–absence data for a given species is scarce
If we have only presence-only data and no presence–absence data for a given species, but both types of data for several other species that suffer from the same spatial sampling bias, then our method can obtain an unbiased estimate of the first species’ geographic range.
Keywords: presence-absence, presence-only, sampling bias, spatial point processes, species distribution models
Introduction
Presence-only data sets (Pearce & Boyce 2006) are key sources of information about factors that influence the habitat relationships and distributions of plants and animals, and analysing them accurately is crucial for successful wildlife management policy. Examples include specimen collection data from museums and herbaria, and atlas records maintained by government agencies and non-government organizations. Often, these are the most abundant and freely available data on species occurrence. However, sampling bias often confounds efforts to reconstruct species distributions.
Recent work has shown that several of the most popular methods for species distribution modelling with presence-only data are equivalent or nearly equivalent to each other, and may be motivated by an underlying inhomogeneous Poisson process (IPP) model (Warton & Shepherd 2010; Aarts, Fieberg & Matthiopoulos 2012; Fithian & Hastie 2013; Renner & Warton 2013). In effect, all of these methods estimate the distribution of species sightings (i.e. of presence-only records) under an exponential family model for the species distribution (Fithian & Hastie 2013). Because presence-only data are commonly collected opportunistically, the sightings distribution is typically biased towards regions more frequented by whoever is collecting the data. Thus, it may be a poor proxy for the distribution of all organisms of that species, sighted or unsighted.
Presence–absence and other data sets collected via systematic surveys do not typically suffer from such bias. Even if (say) survey sites cluster near a major city, the data will contain more presences and more absences there. Unfortunately, if the species under study is rare, presence–absence data may carry little information about its species distribution. In this article, we consider a large presence–absence data set on eucalypts in south-eastern Australia. Although there are over 32 000 sites, four of the 36 species we consider are present in fewer than 20 of the survey sites. Presence-only data for rare species, suitably adjusted for bias, can supplement survey data.
We propose a natural extension of the IPP model for single-species presence-only data, with a view towards estimating and adjusting for sampling bias. In particular, our method brings other sources of data – presence-only and presence–absence data for multiple species – to bear on the problem, by incorporating them into a single joint probabilistic model to estimate and adjust for the bias. Some of the most popular approaches to analysis of presence–absence or presence-only data for one species are special cases of our joint approach. We evaluate our model using both presence-only and presence–absence data for a set of eucalypt species from south-eastern Australia. An R package implementing our method, multi-speciesPP, is available in the public github repository wfithian/multispeciesPP.
THE INHOMOGENEOUS POISSON PROCESS MODEL
The starting point for our model is the random set 𝒮 of point locations of all individuals of a given species in some geographic domain 𝒟. In spatial statistics, such a random set is called a point process, and we will call the set 𝒮 the species process. Typically, 𝒟 is a bounded two-dimensional region.
The IPP model is a probabilistic model for the random set 𝒮 = {si} ⊆ 𝒟. It is characterized by an intensity function λ(s), which maps sites in 𝒟 to non-negative real numbers. Informally, λ(s) quantifies how many si are likely to occur near s.
For any subregion A within 𝒟, let N𝒮 (A) denote the number of points si ∈ 𝒮 falling into A. If 𝒮 is an IPP with intensity λ, then N𝒮 (A) is a Poisson random variable with mean
| eqn 1 |
For non-overlapping subregions A and B, N𝒮 (A) and N𝒮 (B) are independent.
If A is a quadrat centred at s, small enough that λ is nearly constant over A, then Λ(A) ≈ λ(s)|A|, where |A| represents the area of subregion A. Therefore, the intensity λ(s) represents the expected species count per unit area near s. The integral Λ (𝒟) over the entire study region is the expectation of N𝒮 (𝒟), the population size.
We can normalize λ(s) to obtain the function , which integrates to one and represents the probability distribution of individuals. An IPP may be defined equivalently as an independent random sample from pλ(s) whose size N𝒮 (𝒟) is itself a Poisson random variable with mean Λ (𝒟). Conditional on the number N𝒮 (𝒟) of points, their locations s1, …, sN𝒮(𝒟) are independent and identically distributed (i.i.d.) draws from pλ(s). We call the intensity λ(s) of 𝒮 the species intensity and the density function pλ(s) the species distribution. See Cressie (1993) for a more in-depth discussion of Poisson processes and other point process models.
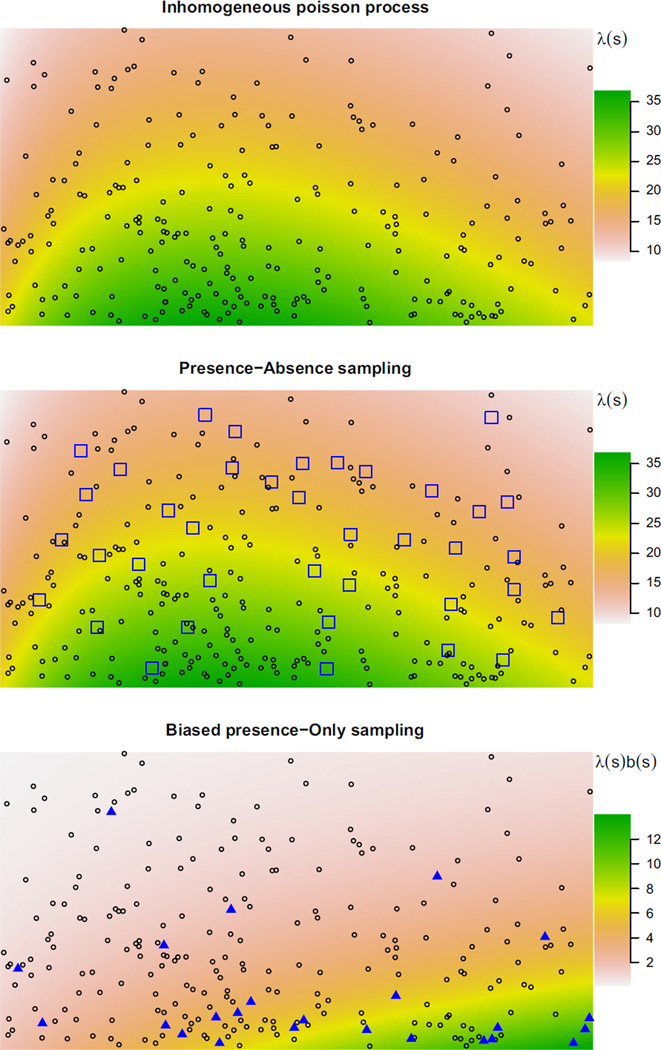
The first panel of Fig. 1 shows a realization of a simulated IPP on a rectangular domain. The background colouring shows the intensity, and the black circles denote the si ∈ 𝒮. Relatively more of the black circles occur in the green region where the intensity is highest.
Fig. 1.
A Poisson process with two different sampling schemes representing our models for presence–absence and presence-only data. The top panel represents the species process against a heat map of the species intensity λ(s). The second panel depicts presence–absence or other systematic survey methods: quadrats (blue squares) are surveyed and organisms counted in each one. The third panel depicts biased presence-only sampling, with the blue triangles indicating the presence-only process, a small and unrepresentative subset of the species process. The heat map shows the presence-only intensity λ(s) · b(s).
In modern ecological data sets each site in the domain has associated environmental covariates x(s) measured in the field, by satellite, or on biophysical maps. These are assumed to drive the intensity λ(s). It is convenient to model the intensity using a loglinear form for its dependence on the features:
| eqn 2 |
The linear assumption in (2) is not nearly as restrictive as it might at first seem. The feature vector x(s) could contain basis expansions such as interactions or spline terms allowing us to fit highly nonlinear functions of the raw features [see, e.g. Hastie, Tibshirani & Friedman (2009)].
Unfortunately, we cannot observe the entire species process 𝒮, but we can glimpse it incompletely in various ways. The most straightforward and reliable way to learn about 𝒮 is with presence–absence or count sampling via systematic surveys, as depicted in the second panel of Fig. 1. In survey data, an ecologist visits numerous quadrats Ai throughout 𝒟 (the blue squares) and records the species’ occurrence or count N𝒮 (Ai) at each one.
Presence-only data is a less reliable but often more abundant source of information about 𝒮. We discuss our model for presence-only data in the next section.
THINNED POISSON PROCESSES
The presence-only process 𝒯 comprises the set of all individuals observed by opportunistic presence-only sampling. Assuming they are identified correctly (not always a given), 𝒯 is the subset of 𝒮 that remains after the unobserved individuals are removed – or thinned, in statistical language.
We propose a simple model for how 𝒯 arises given 𝒮: an individual at location si ∈ 𝒮 is included in 𝒯 (is observed) with probability b(si) ∈ [0,1], independently of all other individuals. The function b(s), which we call the sampling bias, represents the expected fraction (typically small) of all organisms near location s that are counted in the presence-only data. As a result of the biased thinning, individuals in areas with relatively large b(s) will tend to be over-represented relative to areas with small b(s).
It can be shown that marginally
| eqn 3 |
For a formal proof, see Cressie (1993) section 8.5.6, p. 689. Informally, a small subregion A centred at s contains on average |A|λ(s) individuals, of which on average |A|λ(s) b(s) are observed. If two sites s1 and s2 have the same intensity λ(s1) = λ(s2), but b(s1) = 2b(s2), then (3) means the presence-only data will have about twice as many records near s1 as s2.
The third panel of Fig. 1 displays a thinning of the Poisson process shown in the first two panels. The thinned process 𝒯, consisting of the solid blue triangles, is shown against a heat map of the biased intensity λ(s) b(s).
Sampling bias in presence-only data is not a subtle phenomenon. By our estimates in Eucalypt data, b(s) ranges from about 3 × 10−3 near Sydney to about 3 × 10−7 in the more rugged inland areas of south-eastern Australia – a dynamic range of 10 000.
Some of the most popular methods for analysing presence-only data are based explicitly or implicitly on fitting a loglinear IPP model for the process 𝒯. It is clear from (3) that this approach effectively yields an estimate of the presence-only intensity λ(s) b(s) and not the species intensity λ(s). These estimates may be dramatically inaccurate if treated as estimates of the species intensity or species distribution.
In the case of presence-only data, b(s) typically depends on the behaviour of whoever is collecting the presence-only data. When sampling bias is thought to depend mainly on a few measured covariates z(s) (such as distance from a road network or a large city), several authors have proposed modelling presence-only data directly as a thinned Poisson process (Chakraborty et al. 2011; Fithian & Hastie 2013; Hefley et al. 2013b; Warton, Renner & Ramp 2013). A similar method was proposed in Dudık, Schapire & Phillips (2005) in the context of the Maxent method, and Zaniewski, Lehmann & McC Overton (2002) similarly propose weighting background points in presence-background GAMs according to a model for their likelihood of appearing as absences in presence–absence data.
If both λ and b are modelled as loglinear in their respective covariates, then we have
| eqn 4 |
Modelling the bias as above amounts to estimating the effects of the variables x(s) in a generalized linear model (GLM) for the Poisson process 𝒯, while adjusting for control variables z(s). We will refer to it as the ‘regression adjustment’ strategy.1
IDENTIFIABILITY, ABUNDANCE AND THE ROLE OF γ
Modelling presence-only data as a thinned Poisson process as in (4) sheds light on why it is so difficult to obtain useful estimates of presence probabilities: at best, presence-only data reflect relative intensities and not properly calibrated probabilities of occurrence. If the covariates comprising x and z are distinct and have no perfect linear dependencies on one another, then β, δ, and the sum α + γ are identifiable, but individually α and γ are not.
To see why, consider
A presence-only process governed by species process parameters (α, β) and thinning parameters (γ, δ) and
An alternative process with α replaced by α̃ = α + log 2 (trees are twice as abundant overall) and γ replaced by γ̃ = γ − log 2 (the chance of observing any given tree is halved overall).
(4) means that the probability distribution of the thinned process 𝒯 is identical in these two cases. Therefore, no matter how much data we collect, we can never distinguish parameters (α, β, γ, δ) from (α̃, β, γ̃, δ) on the basis of presence-only data alone.
Because β is identifiable, we can use presence-only data alone to obtain an estimate for λ(s) up to the unknown proportionality constant eα; in other words, we can estimate the species distribution pλ but not the species intensity λ. If the model is correctly specified, then likelihood estimation gives an asymptotically unbiased estimate of the model’s parameters (see e.g. Lehmann & Casella 1998).
The species intensity λ(s) is the product of the species distribution pλ(s) and the overall abundance Λ (𝒟). Predicting the probability that a species is present in some new quadrat A requires information about both. Considerable attention has focused on whether or not we can obtain plausible estimates of abundance or of presence probabilities based on presence-only data alone. Methods like Maxent and presence-background logistic regression explicitly estimate pλ(s), but require an externally given specification of the overall abundance if presence probabilities are required (for example, Maxent’s ‘logistic output’, see Elith et al. 2011). Other methods attempt to estimate presence probabilities (Lele & Keim 2006; Royle et al. 2012), but estimates can be highly variable and non-robust to minor misspecifications of the modelling assumptions (Ward et al. 2009; Hastie & Fithian 2013).
One of the purported advantages of the IPP as a model for presence-only data is that it does yield an estimate of overall abundance because its intercept term is identifiable (Renner & Warton 2013). However, Fithian & Hastie (2013) show that the maximum-likelihood estimate of Λ̂ (𝒟) obtained from that model is exactly the number of presence-only records in the data set, so it should not be regarded as an estimate of the overall abundance.
CHALLENGES FOR REGRESSION ADJUSTMENT USING PRESENCE-ONLY DATA
Regression adjustment works best when the control variables z(s) are not too correlated with x(s), the covariates of interest. If, for example, x1(s) and z2(s) are highly correlated, then we can increase β1 and decrease δ2 without altering the model’s predictions much. As a result, we may need a great deal of data to distinguish the effects of β1 and δ2 and hence to tease apart λ and b.
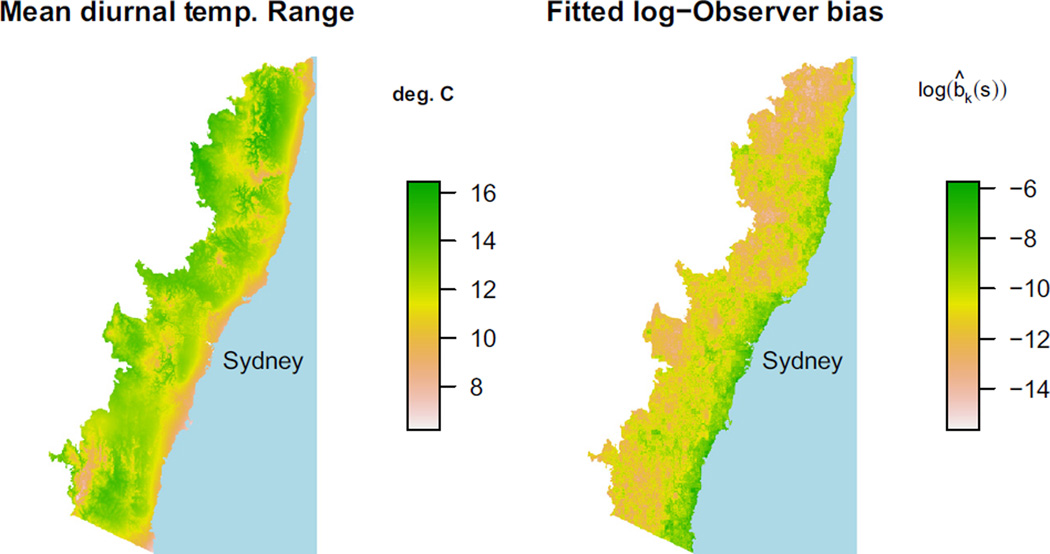
Unfortunately, correlation between x and z is all too common, in part because humans respond to many of the same covariates as other species do. For example, in south-eastern Australia, major population centres lie along the eastern coastline, but many important climatic variables are also correlated with distance from the coast. Figure 2 plots the mean diurnal temperature range over a region of south-eastern Australia, juxtaposed against our fitted bias from the model we will fit in the section Eucalypt data. The bias is almost perfectly confounded with temperature range, making estimation highly variable even if the model is correctly specified.
Fig. 2.
Mean diurnal temperature range in a coastal region of south-eastern Australia, juxtaposed against our model’s fitted sampling bias. Because most people live near the coast, sampling bias is highly correlated with distance from the coastline. Unfortunately, so are many important climatic variables. Because these variables are almost perfectly confounded with bias, it is very difficult to correct for sampling bias using presence-only data alone.
Another difficulty of regression adjustment in real-world settings is that our functional form is always misspecified. In particular, it may be difficult to obtain good features in modelling the bias. Suppose, for example, that x1(s) is highly correlated with z2(s)2, which (unbeknown to us) is an important bias covariate. If we fit our model without including z2(s)2, then the β1x1(s) term may serve as a proxy for the missing quadratic effect, biasing our estimate β̂1.
In practice we expect there to be missing variables as well as unaccounted for nonlinearities and interactions in our models for both the species intensities and the bias alike. We can mitigate this sort of problem by adding more basis functions to z(s), but as the dimension of the model increases, the standard errors of our estimates will tend to increase along with it.
If any bias covariates coincide with x variables – for example, if rugged terrain is undersampled due to inaccessibility and has an effect on a species’ abundance – then, the corresponding coordinates of β and δ are unidentifiable no matter how much presence-only data we collect.
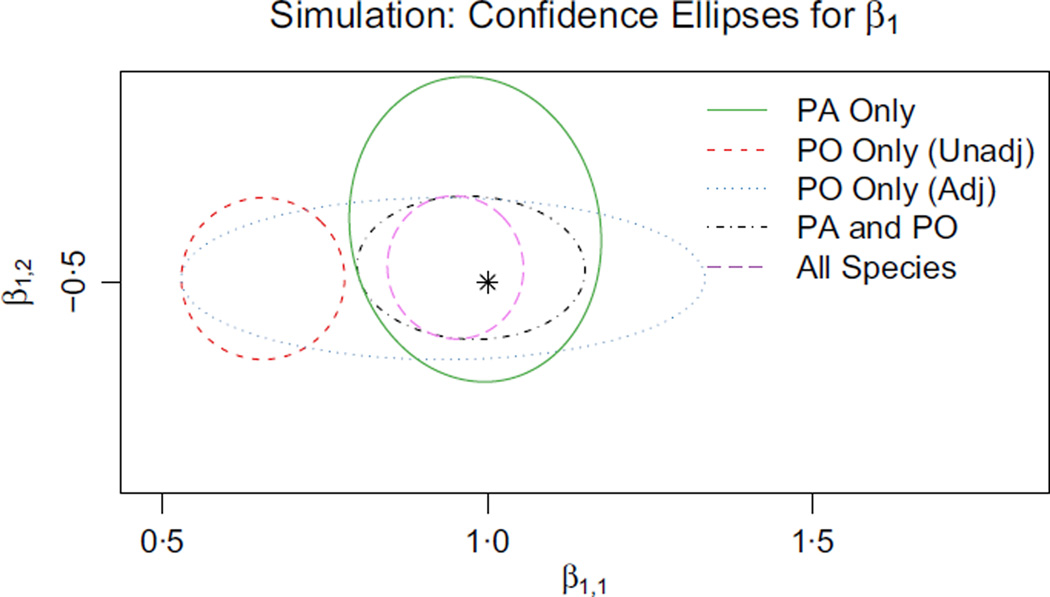
For all its difficulties, regression adjustment on presence-only data is often preferable to no adjustment and may be the best option when unbiased survey data is unavailable. Still, when some components of x are nearly or completely confounded by z, a small quantity of unbiased data can go a long way, because it may provide the only solid information to distinguish true effects from bias effects (see, e.g. Fig. 3). This motivates a method that can combine both biased and unbiased data to exploit the strengths of each.
Fig. 3.
Ninety-five percent Wald confidence regions for β1, the species distribution coefficients for species 1, obtained by using five different methods. The plot illustrates the precision and accuracy with which the coefficients are estimated by each method. The black star denotes the true values of the parameters of interest. The different model types are described below: PA data alone (Green): The most straightforward method when PA data for species 1 is to maximize likelihood for it alone. Our estimates of both coefficients are unbiased but less precise than they could be. z plays no role in the PA data or our model for it, so the precisions for the two coordinates of β1 are about the same;PO data alone, no regression adjustment (Red): The most common use of presence-only data is to maximize likelihood using only the presence-only data for species 1, making no adjustment for sampling bias. In that case, we are effectively estimating the presence-only intensity instead of the species intensity. Here, x1 proxies for the confounding variable z and β̂1,1 is severely biased, whereas β̂1,2 is unaffected; PO data alone, with regression adjustment (Blue): We can address sampling bias by attempting to estimate the effect of the confounder z. Our estimates are now unbiased, but β̂1,1 is noisy and its interval is very wide. It is quite hard to tease apart the effects of x1 and z given only PO data; PA and PO data for species 1 (Black): The PO data carry solid information about β1,2, whereas the PA data carry the only usable information about β1,1. When we combine both data sources for species 1, the precision of β̂1,2 roughly matches the methods using PO alone (blue and red), and the precision of β̂1,1 matches the method using PA alone (green); Pooled data for all species (Purple): We obtain the best results by pooling both presence–absence and presence-only data sets for many different species. Species 2,3,…,m all contribute to estimating δ to high precision. As a result, the presence-only data for species 1 becomes much more useful for estimating β1,1, because we know how to correct for the sampling bias.
A unifying model for presence–absence and presence-only data
The above discussion motivates a natural unifying model to explain both presence–absence and presence-only data for many species at once, which we discuss in detail here.
Assume we are equipped with a real-valued environmental covariate function x(s), which takes values in ℝp, and bias covariate function z(s), which takes values inℝr. x(s) and z(s) represent features thought respectively to influence habitat suitably and heterogeneity in sampling effort. In general, some variables may appear in both x and z.
Let m denote the total number of species for which we have data. Let 𝒮k and 𝒯k denote the species and presence-only processes for species k = 1,…,m. Our data set consists of two distinct types of observations for each species, presence–absence or count survey sites and presence-only sites. By modelling each of the two sampling schemes in terms of the latent species processes, we can use likelihood methods to pool data from each. We adopt the convention of indexing observations by the letter i, variables by the letter j and species by the letter k.
Each observation i is associated with a site si ∈ 𝒟, as well as covariates xi = x(si) and zi = z(si). For survey sites, si represents the centroid of a quadrat Ai. At survey site i we observe counts Nik = N𝒮k (Ai) or binary presence/absence indicators yik, with yik = 1 if Nik > 0 and yik = 0 otherwise.
JOINT LOGLINEAR IPP MODEL FOR MULTISPECIES DATA
For species k, we propose to model 𝒮k ~ IPP(λk (s)), with 𝒯k ~ IPP(λk (s) bk (s)) obtained by thinning 𝒮k via bk(s). Both 𝒮k and 𝒯k are assumed to be independent across species with loglinear intensity λk and bias bk:
| eqn 5 |
| eqn 6 |
Note that δ is the only model parameter not allowed to vary across species – in other words, the functions b1(s),…,bm(s) are all assumed to be proportional to one another. We call this the proportional-bias assumption, and it lets us pool information across all m species to jointly estimate the selection bias affecting the presence-only data. When m is large, this affords us the option of working with a more expansive model for the bias term, reducing the resulting bias in our estimates for the αk and βk, which are typically of greater scientific interest.
Scientifically, the proportional-bias assumption corresponds to a belief that the biasing process has more to do with the behaviour of observers than of plants and animals. Put simply, if one species is oversampled near Sydney by a factor of five relative to another region with similar features, the most likely explanation is that observers spend one fifth as much time in the second region as they do in Sydney. In that case, we should expect other species to be undersampled in the second region by roughly the same factor relative to Sydney.
The proportional-bias assumption could well be violated if, for example, most of the observers collecting samples for species 1 reside in Sydney and those collecting samples for species 2 reside in Newcastle. Even under the best of circumstances, this modelling assumption (like the other assumptions we have made) is an idealization of the truth, but it can be a very useful one if it is not too badly wrong. In Eucalypt data we provide evidence that the proportional-bias model improves out-of-sample reconstruction of the species intensity.
We allow γk, the proportionality constant of the sampling bias, to vary by species, representing a species-dependent effect on overall sampling effort. This allows us to account for observers systematically oversampling some species relative to others. For example, if an ecologist is collecting samples in a forest, she may preferentially collect samples from rarer species. In the section Eucalypt data we give some evidence that sampling effort does indeed vary significantly by species in just this way. The cost of letting γk vary by species is that αk is unidentifiable unless we have some presence– absence data for species k. Consequently, we can estimate the species distribution pλ(s), but not the overall abundance Λ (𝒟), unless we have some presence–absence or count data for species k.
While this paper was in press we learned of concurrent and independent work by Giraud (2014) and Dorazio (2014) which use similar Poisson thinning models to combine survey and collection data.
INDUCED MODEL FOR SURVEY DATA
Survey data provides information about the species process 𝒮k restricted to the survey quadrats. If the point locations of each individual within quadrat Ai are recorded, we can directly model those locations as a loglinear IPP over the entire surveyed domain ∪i Ai. Often, we do not have access to such granular data, and only the count Nik = NSk (Ai) or presence/absence yik is recorded. In such cases, the IPP model still induces a GLM likelihood for the available summary statistics Nik or yik, so that we can maximize likelihood for the available data.
If the features are continuous, then for a small quadrat Ai the species count at the site is
| eqn 7 |
Thus, our joint IPP model induces a Poisson loglinear model for survey count data. The probability of yik=1 is
| eqn 8 |
a Bernoulli GLM with complementary log-log link (McCullagh & Nelder 1989; Baddeley et al. 2010). The complementary log-log link has been used before to study presence–absence data in ecology (e.g. Yee & Mitchell 1991; Royle & Dorazio 2008; Lindenmayer et al. 2009). If the expected count η = |Ai|λk (si) is very small, then there is not much difference between the complementary log-log link, the logistic link and the log link, since
| eqn 9 |
For simplicity assume quadrat sizes are constant and work in units where |Ai| = 1. When this is not the case, log |Ai| enters as an offset in the GLM for observation i.
Importantly, we make no assumption that the survey quadrats Ai are distributed evenly across 𝒟 in any sense. However, our model does assume that, given the locations of Ai, the responses yik for the presence–absence data are in no way impacted by b(s), the sampling bias of the presence-only data.
Informally, if the Ai tend to cluster near some population centre, then we will see many presences yik = 1 and absences yik = 0 there, so we will not be fooled into believing the species is more prevalent there. Because we are only modelling the distribution of yik, the presence–absence data do not suffer from selection bias even if the geographic distribution of quadrats is very uneven.
TARGET-GROUP BACKGROUND METHOD
Phillips et al. (2009) suggested another method of using many species’ presence-only data to account for sampling bias. Using a discretization of 𝒟 into grid cells, they propose sampling background points only from grid cells where at least one species was sighted, guaranteeing that completely inaccessible areas play no role in estimation. This method, dubbed the ‘target-group background’ (TGB) method, can tackle sampling bias with only presence-only data, and without requiring specification of its functional form.
However, the TGB method does not distinguish between inaccessible regions and regions in which all the species are not very prevalent. Moreover, because it samples background points equally from all accessible grid cells, the TGB method does not adjust for biased sampling from one accessible region relative to another. Our method can leverage presence–absence data to directly estimate sampling bias and predict absolute prevalence. We will empirically compare our method’s out-of-sample predictive performance to several competitors including the TGB method.
MAXIMUM-LIKELIHOOD ESTIMATION
In this section, we discuss estimation of our joint model. As we will see, maximum-likelihood estimation amounts to fitting a very large generalized linear model to all of the data. Moreover, several familiar methods for single-species distribution modelling amount to exactly or approximately maximizing our model’s likelihood for a specific subset of our joint data set.
Because we have various sorts of observation sites si we introduce notation to allow for summing over relevant subsets of them. Let IPA denote the set of indices i for which si are presence–absence survey quadrats, and let IPOk denote the indices for presence-only sites si ∈ 𝒮k. Let nPA be the total number of survey quadrats.
For species k, the log-likelihood for the presence–absence data is
| eqn 10 |
If ℙ(yi = 1) is small for each quadrat, then ℓk,PA is very close to the log-likelihood for logistic regression on presence–absence data. In other words, applying our method to a single presence–absence data set with no other data reduces to something very close to presence–absence logistic regression for that species.
The log-likelihood for the presence-only data is
| eqn 11 |
| eqn 12 |
In general, we cannot evaluate the integral in (12) exactly. As usual, we replace the integral with a weighted sum over nBG background sites si ∈ 𝒟. For weights wi, we obtain the numerical approximation
| eqn 13 |
where IBG are the indices corresponding to background sites. In the simplest case, the background sites are sampled uniformly from 𝒟 and all the , but other sampling schemes are possible (for a review of techniques see Renner et al. 2014). Popular procedures like Maxent and presence-background logistic regression approximately maximize (13).
Maximizing (13) for a single species k with the γk + δ′zi terms included reduces to the regression adjustment strategy discussed the section in Challenges for regression adjustment using presence-only data. If we do not include γk + δ′zi terms (i.e. if we assume there is no bias) we obtain the unadjusted fit (i.e. the usual fit) to the biased presence-only intensity λk(s) bk(s).
The presence–absence and presence-only data sets for all m species together represent 2m independent data sets.2 Maximizing likelihood for all the data means maximizing the sum
| eqn 14 |
where θ represents the full complement of coefficients
| eqn 15 |
With a bit of work, we can massage the form of (14) into one large GLM in terms of a common set of m(p + 2) + r predictors corresponding to the entries of θ. We do so by introducing auxiliary predictor variables uk, a binary indicator that we are predicting for species k, and v, an indicator that we are predicting for presence-only instead of presence–absence data. In terms of these variables, αk is the coefficient for uk, βk,j for ukxj, γk for ukv and δj for vzj. More details are given in Appendix S1.
The result is a very large GLM with m(p + 2) + r total parameters and m(nBG + nPA) total observations (one per species for each survey site and background site). Because both the number of observations and number of parameters scale linearly with m, the computational cost of standard approaches to estimation scales as m3p2(nBG + nPA).
For our eucalypt example, we have m = 36 species, nBG = 40 000 background sites, nPA = 32,612 survey quadrats and p = 38 predictors (including interactions and nonlinear terms), so m3p2(nBG + nPA) ≈ 5 × 1012. This is a very high computational load even for modern computers.
Fortunately, there is a great deal of structure in the design matrix, and if we exploit it properly, our computations need only scale linearly with m, cutting the cost by a factor of roughly 362 ≈1000. Appendix S1 also details our efficient computing scheme.
FITTING PROPORTIONAL-BIAS MODELS INR
As a companion to this article, we have released an R package, multispeciesPP, that can efficiently fit the models described here. The method requires formulae for the species intensity and the sampling bias and carries out maximum likelihood as described in Maximum-likelihood estimation. For example, the code
would fit a multispecies Poisson process model with presence–absence data set PA, list of presence-only data sets PO and background data BG. The R function maximizes likelihood under the model
| eqn 16 |
| eqn 17 |
and returns fitted coefficients and predictions.
Simulation
Thus far, we have discussed several distinct data sources we can bring to bear on estimating λk(s), the intensity for the kth species process. A simple simulation illustrates the interplay of the different data types.
We simulate from the model (4) with covariates (x1, x2, z) following a trivariate normal distribution with mean zero and covariance
| eqn 18 |
and the coefficients for species 1 equal to:
| eqn 19 |
Presence–absence data for species 1 are the most reliable reflection of λ1(s), but are available only in small quantities. Presence-only data for species 1 are abundant, but biased, as they are sampled from the intensity
| eqn 20 |
Because z is independent of x1 but highly correlated with x2, a presence-only data point is mainly informative about β1,1 and β1,2 + δ. Without supplementary data, it carries almost no information about β1,2 itself.
If presence-only and presence–absence data are available for many other species, then they all contribute information helping us to precisely estimate δ. This makes species 1’s presence-only data much more useful: given a precise estimate of δ from other species’ data, information about β1,2 + δ is equivalent to information about β1,2.
Figure 3 and the accompanying commentary show what each data set contributes to estimating β1,1 and β1,2 by plotting the 95% Wald confidence ellipse for each of several models.
Eucalypt data
We have just seen how the various sources of data can work in concert to give far more precise estimates than we could obtain from any one data set by itself. Additionally, we evaluate our model’s performance on a data set of 36 species of genera Eucalyptus, Corymbia and Angophora in south-eastern Australia.
The presence–absence data consist of 32 612 sites where all the species were surveyed, with an average of 547 presences per species. The species exhibit a great deal of variability with respect to their overall abundance, with four species having fewer than 20 total observations, and eight having more than 1000.
The presence-only data consist of 764 observations on average per species, supplemented with 40 000 background points sampled uniformly at random from the study region. More information on data sources may be found in Appendix S3. The rarest species in the presence-only data, Eucalyptus stenostoma, has 90 observations.
We use 15 environmental covariates in our model for the species process, allowing for nonlinear effects in four of them: temperature seasonality, rainfall seasonality, precipitation in June/July/August, moisture index in the lowest quarter and annual precipitation overall. Our model for the bias includes nonlinear effects for predictors including distance to road, distance to the nearest town, distance to the coast, ruggedness, whether the locale has extant vegetation and the number of presence–absence sites nearby. Appendix S2 discusses the model form in more detail.
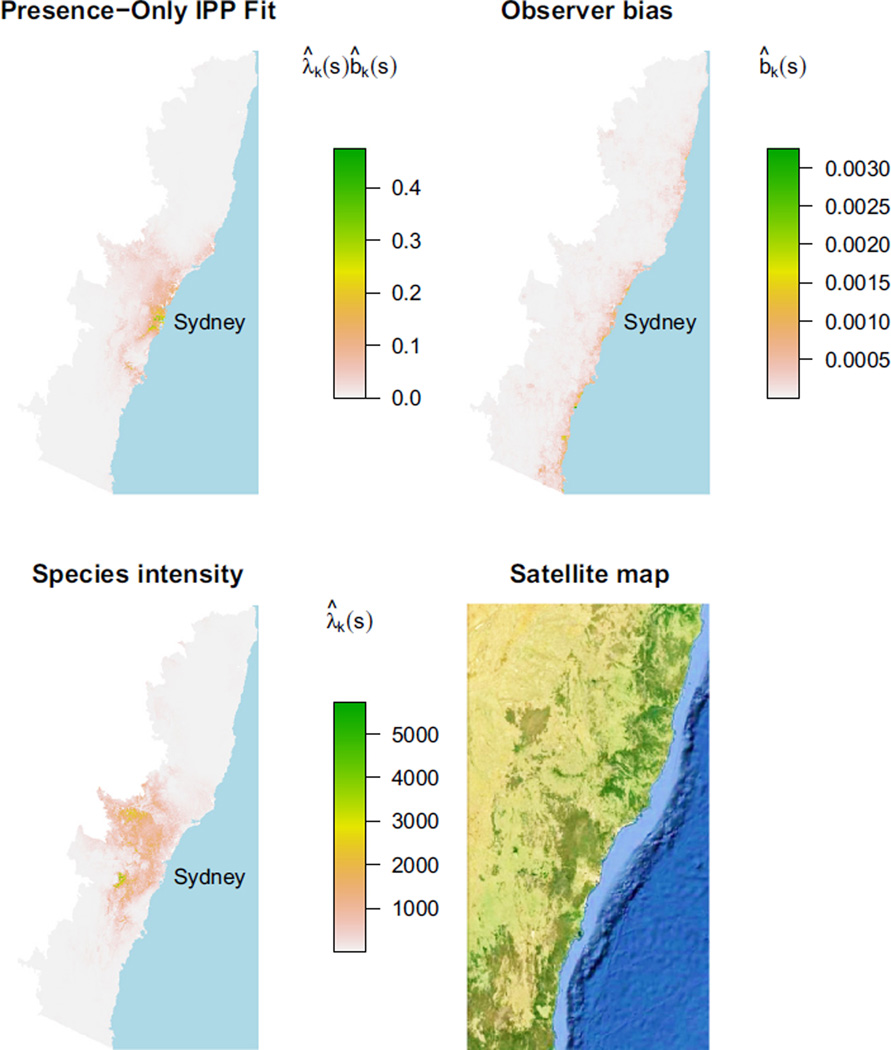
The four panels of Fig. 4 contrast our model’s fit for a single species, Eucalyptus punctata, with the fit that we would obtain by using presence-only data alone with no bias adjustment. A satellite image of the same region is provided for comparison and orientation. The top left panel displays the fitted intensity we obtain by modelling E. punctata’s presence-only data as an IPP whose intensity is driven by environmental variables. We obtain an estimate of the presence-only intensity, which in this case is concentrated mostly near Sydney and the coast.
Fig. 4.
Model fits for Eucalyptus punctata in south-eastern Australia. Top left panel: estimate of presence-only intensity in units of 1/km2, using presence-only data alone and making no adjustment for bias. Top right: fitted sampling bias b̂k (s) in our proportional sampling bias model. Lower left: fitted species intensity λ̂k (s) for our model, in units of 1/km2. Lower right: satellite image from Google Earth. In the presence-only data, many more trees were observed in near Sydney than in the western hinterland, but our model infers a higher intensity in the undersampled western region.
The top right and lower left panels show our model’s estimates b̂k (s) of the bias and λ̂k (s) of the species intensity. Unsurprisingly, distance from the coast, and from Sydney, is strong driver of our model’s fitted sampling bias. In the lower left panel, the intensity is shifted significantly towards the western hinterland.
To evaluate our model quantitatively, we ask two questions: first, how well do the data agree with the assumption of proportional sampling bias? Secondly, do we obtain better predictions when pooling multiple data sets across multiple species?
CHECKING THE PROPORTIONAL-BIAS ASSUMPTION
We can check the proportional-bias assumption within the context of our GLM. To check whether the bias coefficient corresponding to some zj should vary by species, we can estimate the same model as before, but now allowing that coordinate of δ to vary by species.
In terms of the large GLM described in the section Maximum-likelihood estimation, we can estimate our model as before by augmenting the design matrix with interactions between the species identifiers uk and the bias variable zj. These variables then have coefficients δk,j. In this model, the proportional-bias assumption corresponds to the null hypothesis of no interaction effects, which we can test using standard likelihood-based methods.
As usual, it is rather unlikely that the proportional-bias assumption – or any other aspect of our model – holds exactly. Even if the assumption holds for some true functions λk(s) and bk(s), we may still see spurious correlations when we fit a complex model using a misspecified loglinear functional form. Nevertheless, it is of interest to identify whether some interactions stand out strongly compared to the noise level, and if so how large they are.
Because of spatial autocorrelation in both the presence–absence and presence-only data, traditional likelihood-based confidence intervals for the interaction effects δk,j are likely to be anticonservative, as are bootstrap intervals based on i.i.d. resampling. To account properly for the spatial autocorrelation, we use the block bootstrap to compute confidence intervals for the coefficients (Efron & Tibshirani 1993). We separate the landscape into a checkerboard pattern with 261 rectangular regions with sides of length 1/3-degree of longitude and latitude (approximately 31 km × 37 km at latitude 33° South). In each of 400 bootstrap replicates, we resample 261 whole regions with replacement.
Dependence of δ on species
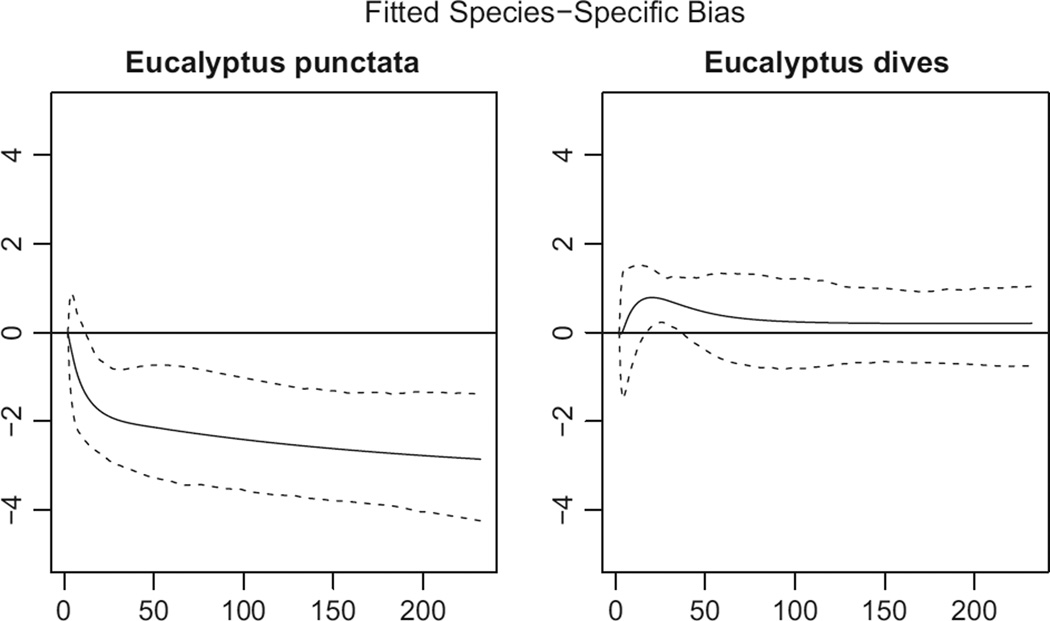
We test our assumption explicitly for the variable ‘distance to coast’, which is the most important predictor of bias. The evidence in the data regarding our assumption is somewhat mixed, but on the whole, it does not appear that the proportional-bias model fits the data perfectly. For some species, there is sufficient evidence to reject H0.
Figure 5 shows the 95% bootstrap confidence interval for the idiosyncratic sampling bias of Eucalyptus punctata, as a function of distance to coast. We see that, even after accounting for the overall bias that affects the other 35 species, we still have too many coastal presence-only observations of punctata. This could be linked to the fact that the punctata data are concentrated near Sydney, which is more heavily populated than other coastal regions, but with many confounding factors at play it is hard to know. Appendix S2 has more detailed results for more species.
Fig. 5.
Idiosyncratic sampling bias for E. punctata and E. dives as a function of distance to coast in km. The dashed lines show 95% block-bootstrap confidence intervals. It appears that after adjusting for the bias δ′z(s) that is shared across all species, there is some residual bias left over for punctata. By contrast, for E. dives, there is no significant interaction. Even though the proportional sampling bias model is misspecified for E. punctata, it still substantially improves out-of-sample predictive accuracy, as we will see in Predictive evaluation of the model. The corresponding curves for all the species can be found in Appendix S2.
If interactions like these are strong, we can allow some of the coordinates of δ to vary by k and others not. There is a bias-variance trade-off, however, as the proportional-bias assumption is what allows us to share information across species. We will see in the section Predictive evaluation of the model that even when the model is an imperfect fit, it can nevertheless sub-stantially improve predictive performance on held-out presence–absence data.
Dependence of γ on species
By default, our model allows γ to vary by species, but we need not always do so. In fact, if we assumed γ does not vary by species, then we would only need joint presence–absence and presence-only data for one species to obtain an estimate for γ. Therefore, we could estimate abundance (and therefore presence probabilities) for every species given presence–absence and presence-only data for a single species and presence-only data for every other species.
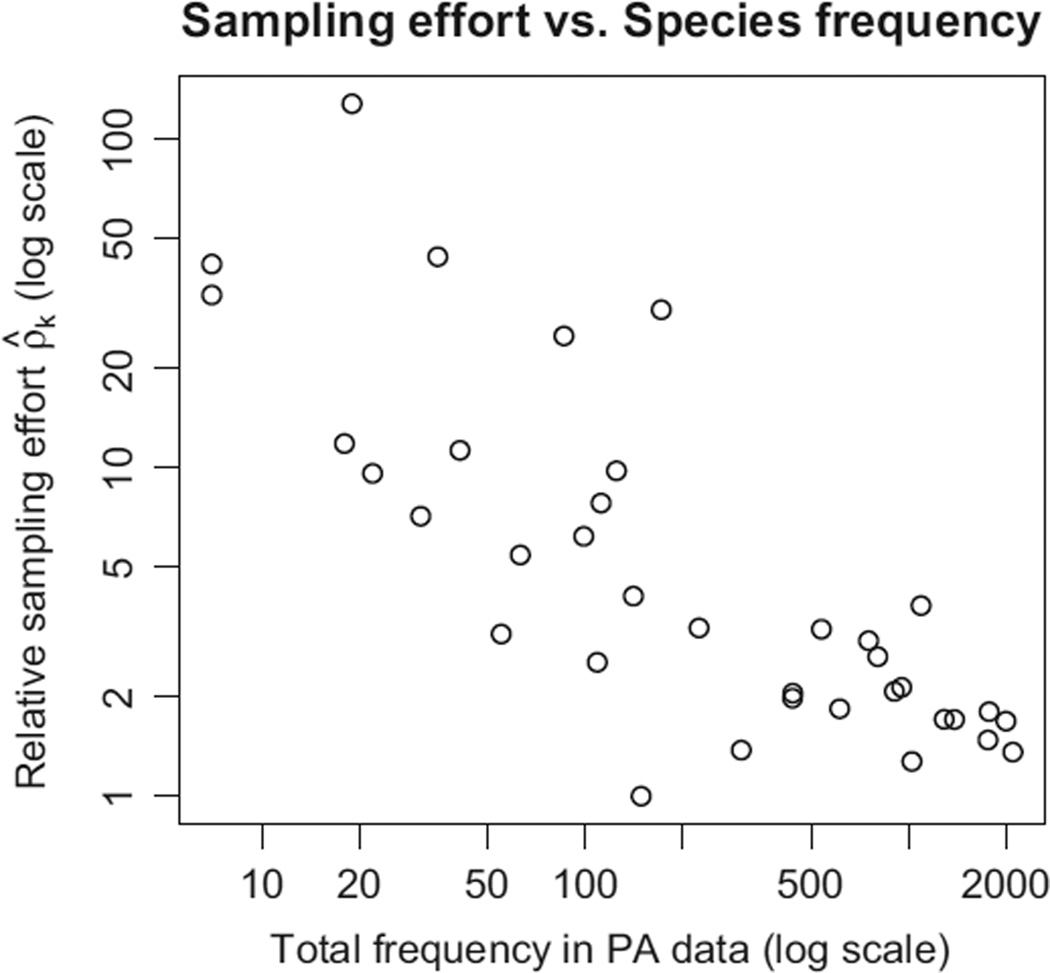
Define relative sampling effort as the ratio
| eqn 21 |
so that ρk = 1 for all k if and only if the γk are all equal.
Figure 6 shows our model’s estimates ρ̂k, plotted against the total number of presence–absence observations. For the eucalypt data, it appears that the assumption of a common γ for every species is probably not reasonable. It appears the presence-only intercept γ varies systematically by species, with effort being substantially higher for the rarer species. Thus, the data appear to support our decision to allow γ to vary by species.
Fig. 6.
Our model’s estimate of relative sampling effort ρk, plotted vs. the total abundance of each species, with each variable plotted on a log scale. It appears that more effort is made to sample rare species.
PREDICTIVE EVALUATION OF THE MODEL
Our goal in pooling data was to supplement the presence–absence data for a given species with multiple other more abundant sources of data, to allow for more efficient estimation of the species intensity λk(s) and its coefficients. One measure of our success is whether this data pooling actually improves predictive performance on held-out presence–absence data.
For comparison, we also estimate our joint model using (i) both the presence-only and presence–absence data for species k and (ii) presence-only and presence–absence data for all 36 species combined.
Note that in all three cases, we are estimating the exact same joint model with three nested data sets:
PA data alone for species k. The most natural competitor to our method is to fit the Bernoulli complementary log-log GLM model with the same predictors, but only on species k’s presence–absence data. This is a special case of the joint method, for which only presence–absence data are available for species k.
PA and PO data for species k. Augmenting the presence–absence data with presence-only data for the same species improves our coefficient estimates for environmental variables that are independent of sampling bias. When there is no presence–absence data, we are fitting the thinned Poisson process model to PO data alone. This is regression-adjusted analysis of PO data, discussed in the section Challenges for regression adjustment using presence-only data.
Pooled data for all species. Using data for all species gives better estimates of the predictors that are badly confounded by sampling bias.
In addition, we introduce two more competitors that use presence-only data alone:
PO data alone for species k, unadjusted for bias: Using species k’s presence-only data alone, and ignoring sampling bias, is the most common method for analysing presence-only data. It estimates the presence-only intensity and then makes predictions as though that were the same as the species intensity. This method can suffer dramatically from bias.
PO data for all species, using the TGB method: We implement the TGB method with pixel size 9 arc seconds (the resolution level of our covariates).
Our evaluation method effectively treats the presence–absence data as a ‘gold standard’, unaffected by bias. This point of view may not always be reasonable, but eucalypts are relatively large and hard for surveyors to miss, so the presence–absence data probably do reflect the true presence or absence of trees in their respective quadrats, notwithstanding identification errors.
We emphasize that we are comparing the different methods with respect to their performance on held-out presence–absence data and not on held-out presence-only data. This distinction is important, because our goal is to reconstruct the species intensity and not the presence-only intensity. All three methods train on the same amount of presence–absence data for species k. The data-pooling methods can only beat the simpler method if the other data sets carry useful information about the species intensity of species k, and if our joint model effectively processes that information without biasing our estimate too badly.
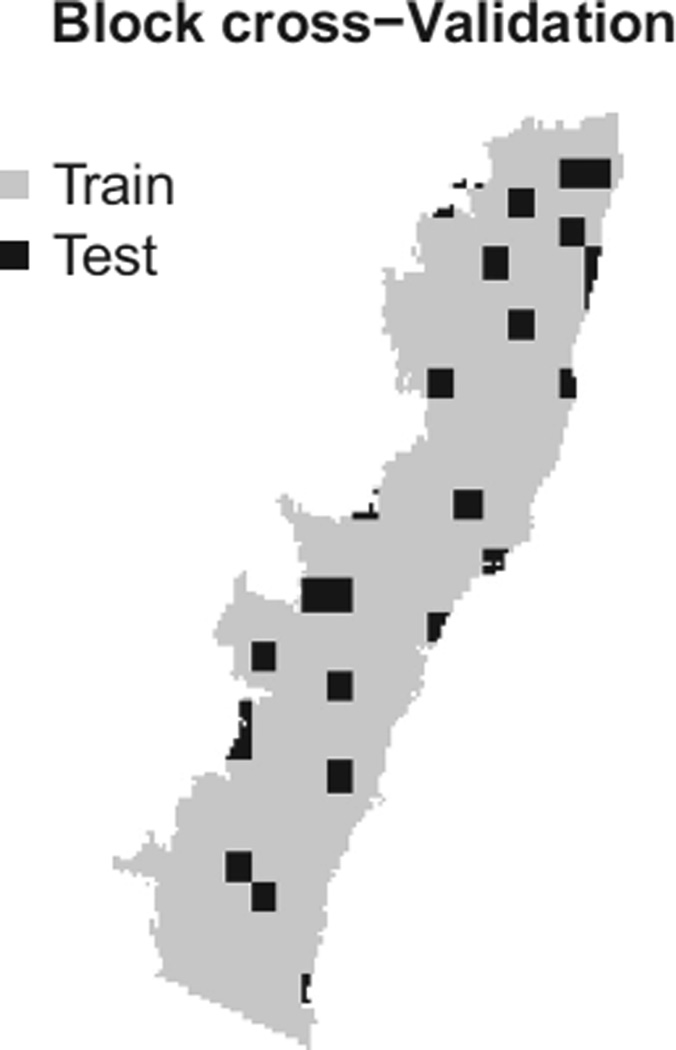
We then use ten-fold block cross-validation to evaluate each method with respect to its predictive log-likelihood. Using the same rectangular regions as in Checking the proportional-bias assumption, we randomly assign the 261 whole regions to ten-folds, with each fold containing 26 random regions and the one left-over region excluded. Figure 7 shows one training-test split used for our procedure. Importantly, all data taken from the test region – presence–absence, presence-only and background – is held out of the training set.
Fig. 7.
Depiction of our block cross-validation scheme for the eucalypt data. Entire rectangular blocks are sampled together to help account for spatial autocorrelation.
The gains from data pooling are greatest when the presence–absence data for a species of particular interest (say, species k) are either scarce or non-existent. To emulate estimation with presence–absence data sets ranging from scarce to abundant, we further downsampled the presence–absence training data for species k.
We fit all the models with a ridge penalty on all of the coefficients except the intercepts α and γ. That is, we minimize
| eqn 22 |
with penalty multiplier ν = 100. Penalizing the coefficients in this way is known as regularization, and it allows for efficient estimation of parameters in complex models. For more details, see for example Hastie, Tibshirani & Friedman (2009).
Figures 8 and 9 show the results of block cross-validation for two species in the data set: Eucalyptus punctata and Eucalyptus dives. Results for the other species are qualitatively similar and can be found in Appendix S2. We evaluate the various methods according to two metrics of predictive performance: predictive log-likelihood (left panel) and area under the predictive ROC curve, averaged over the ten test folds (AUC, right panel). Lawson et al. (2014) contrast prevalence-dependent metrics like log-likelihood, which measure the accuracy of absolute out-of-sample presence probabilities, with prevalence-independent metrics like AUC, which depend only on the ordering of predictions.
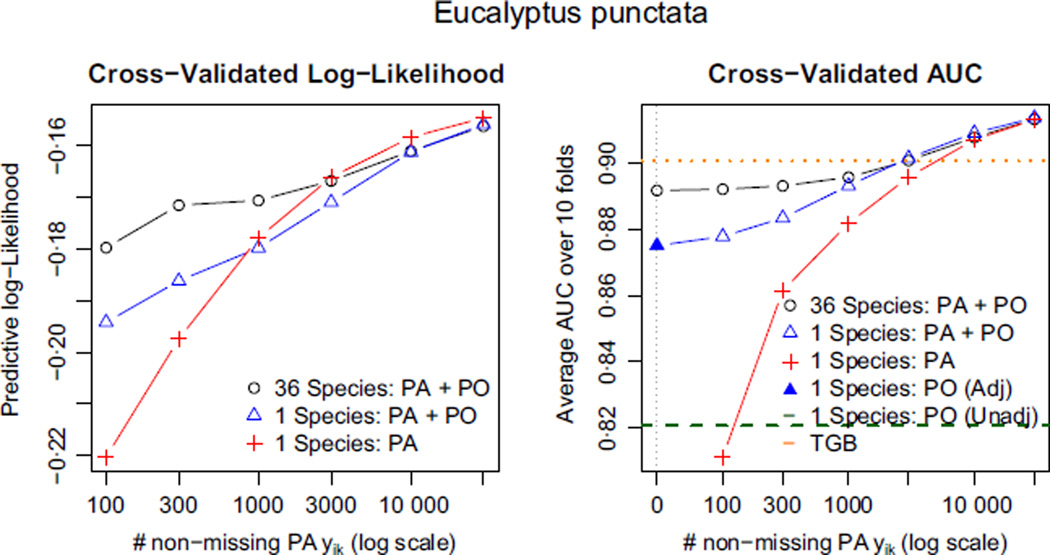
Fig. 8.
Block cross-validated log-likelihood and AUC for E. punctata (higher is better). Pooling data from other sources gives a substantial boost to predictive performance when the presence–absence data set is small, but only when we make an adjustment for the bias. In the right panel, the leftmost blue triangle (‘1 species: PA + PO’ with no PA data), we are fitting the thinned IPP model to PO data alone. This is the regression adjustment strategy discussed in the section Challenges for regression adjustment using presence-only data. Note that using presence-only data without any adjustment for bias performs quite poorly compared to the other methods. Because the habitable zone for E. punctata includes Sydney as well as more inaccessible regions to its west, ignoring the sampling bias can wreak havoc on our estimates.
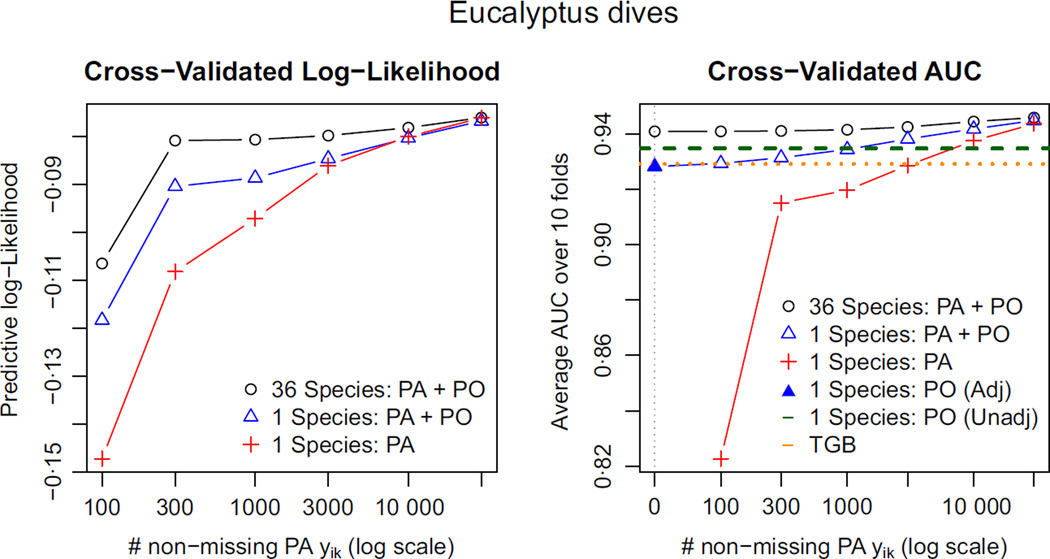
Fig. 9.
Block cross-validated log-likelihood and cross-valid AUC for the species E. dives (higher is better). Pooling data from other sources gives a substantial boost to predictive performance when the presence–absence data set is small. Because E. dives occurs in the southwestern part of the study region, where the bias function has a relatively gentle gradient, the sampling bias plays a less vital role. In the right panel, the leftmost blue triangle (‘1 species: PA + PO’ with no PA data), we are fitting the thinned IPP model to PO data alone. This is the regression adjustment strategy discussed in the section Challenges for regression adjustment using presence-only data.
Doing well in predictive log-likelihood requires a good estimate of the intercept αk – that is, of the absolute intensity λk(s). Because αk is confounded with γk in presence-only data, and because γk varies by species, the two data-pooling methods cannot estimate absolute intensities without a little presence–absence data from species k. By contrast, AUC only depends on estimates of relative intensity , which is invariant to α̂k and can be estimated with no presence–absence data for species k. Estimates without any presence–absence data for species k are shown above the label ‘0’ on the horizontal axis.
As we have seen in Fig. 4, E. punctata suffers dramatically from sampling bias because Sydney, the largest city, lies on the eastern edge of its habitable zone. As a result, the unadjusted presence-only method performs very poorly compared to the methods that account for bias. By contrast, the habitable zone of E. dives lies mainly in the western part of the study region where the sampling bias function log bk has a much gentler gradient. As a result, the unadjusted presence-only analysis does relatively well. The method that pools across all 36 species does even better: its AUC using none of E. punctata’s presence–absence data (and only the presence–absence data for the other 35 species) is indistinguishable from its AUC using all of the presence–absence data. See Appendix S2 for the corresponding plots for all species.
Table 1 compares the four best methods using a moderate value, 1000, for the number of non-missing presence–absence sites. Our method pooling presence–absence and presence-only data for all species performs well consistently, coming within 0·01 of the best method for all but one species. Interestingly, the TGB method performs second best despite its having no access to the presence–absence data.
Table 1.
AUC cross-validation results for all species with at least 100 presence–absence data points. The first three methods are evaluated with 1000 non-missing presence– absence data points for the species under study. In each row, numbers are bolded for methods coming within 0·01 of the best method. Our method pooling presence–absence and presence-only data for all species performs well consistently, coming within 0·01 of the best method for all but one species
| PA Only 1 Species |
PA + PO 1 Species |
PA + PO 36 Species |
TGB 36 Species |
|
|---|---|---|---|---|
| A. bakeri | 0·893 | 0·915 | 0·932 | 0·933 |
| C. eximia | 0·921 | 0·947 | 0·952 | 0·952 |
| C. maculata | 0·783 | 0·778 | 0·785 | 0·742 |
| E. agglomerata | 0·801 | 0·834 | 0·820 | 0·808 |
| E. blaxlandii | 0·904 | 0·934 | 0·944 | 0·934 |
| E. cypellocarpa | 0·861 | 0·852 | 0·867 | 0·825 |
| E. dalrympleana (S) | 0·873 | 0·910 | 0·926 | 0·931 |
| E. deanei | 0·811 | 0·855 | 0·906 | 0·894 |
| E. delegatensis | 0·971 | 0·971 | 0·981 | 0·982 |
| E. dives | 0·920 | 0·934 | 0·941 | 0·929 |
| E. fastigata | 0·905 | 0·900 | 0·916 | 0·907 |
| E. fraxinoides | 0·920 | 0·935 | 0·963 | 0·963 |
| E. moluccana | 0·881 | 0·909 | 0·911 | 0·881 |
| E. obliqua | 0·870 | 0·914 | 0·918 | 0·906 |
| E. pauciflora | 0·874 | 0·897 | 0·928 | 0·928 |
| E. pilularis | 0·807 | 0·807 | 0·805 | 0·811 |
| E. piperita | 0·889 | 0·844 | 0·886 | 0·871 |
| E. punctata | 0·882 | 0·893 | 0·896 | 0·901 |
| E. quadrangulata | 0·835 | 0·843 | 0·840 | 0·823 |
| E. robusta | 0·878 | 0·883 | 0·892 | 0·894 |
| E. rossii | 0·957 | 0·966 | 0·965 | 0·962 |
| E. sieberi | 0·857 | 0·813 | 0·881 | 0·875 |
| E. tricarpa | 0·969 | 0·970 | 0·971 | 0·965 |
Discussion
We have proposed a unifying Poisson process model that allows for joint analysis of presence–absence and presence-only data from many species. By sharing information, we can obtain more precise and reliable estimates of the species intensity than we could obtain from either data set by itself.
Moreover, we have seen in Eucalypt data that the proportional bias can be a reasonable fit for some real ecological data sets. In this data set, and we suspect in many others, sampling bias can have a major effect on fitted intensities if not appropriately accounted for.
BENEFITS OF DATA POOLING
Throughout we have focused mainly on the way that pooling presence–absence and presence-only data from many species can help address selection bias. Even when selection bias is not a major concern, data pooling can still be beneficial.
In the simplest case, presence–absence data can be fruitfully supplemented by more abundant presence-only data from the same species. In Fig. 9, we see that the presence-only data for E. dives is not very biased, as evidenced by the good performance of the unadjusted fit. In this case, combining the presence–absence data with presence-only data still led to a substantial improvement in predictive performance, and combining with data from other species helped even more. In other cases, we may have presence-only data for many species but no presence–absence data. In that case, our method still provides a means for pooling data to estimate δ more efficiently.
COMMON MISSPECIFICATIONS OF THE IPP MODEL
Aside from the proportional-bias assumption, we should be mindful of several other sources of misspecification. The most obvious is that our loglinear functional form is almost certainly incorrect in any given case. Three others that merit special consideration are spatial autocorrelation in the data, biased detection of presence–absence data and spatial errors in environmental covariates and point observations.
Spatial autocorrelation
The Poisson process model assumes that, given the covariates for a given site, an individual is no more or less likely to occur simply because there is another individual nearby. In ecological data, this assumption is rather tenuous; for example, trees of the same species often occur together in stands; or different species may compete with each other for resources. Renner & Warton (2013) discuss goodness-of-fit checks and present empirical evidence against the Poisson assumption. For a more general discussion of alternatives to the Poisson process model, see Cressie (1993); Gaetan & Guyon (2009).
Similarly, for systematic survey data, we should proceed with caution in modelling count data as Poisson, because actual counts may be overdispersed due to autocorrelation within a quadrat, or correlated with counts for nearby sites because of longer-range autocorrelation. When autocorrelation is present, nominal standard errors computed under the Poisson assumption can be much too small, as can i.i.d. cross-validation estimates of prediction error or i.i.d. bootstrap standard errors. Resampling methods such as the bootstrap or cross-validation can be made much more robust to autocorrelation if they resample whole blocks at a time (Efron & Tibshirani 1993), and in the section Eucalypt data, we use the block bootstrap and block cross-validation to analyse our eucalypt data set. Discussion of alternative block bootstrap procedures and choosing block size may be found in Hall, Horowitz & Jing (1995); Nordman, Lahiri & Fridley (2007); Guan & Loh (2007).
Imperfect detection
Even in presence–absence and other systematic survey data, surveyors may not have the time or resources to exhaustively survey a given quadrat, and thus, some organisms may be missed in the surveys.
Suppose, for example, that an organism at s is detected by surveyors with probability q(s). Then, the count y in quadrat A centred at s is not distributed as Pois(λ(s)|A|), but rather as Pois(q(s)λ(s)|A|). If q(s) is constant, all our estimates of αk will be biased downward by exactly log q. This would bias estimates of abundance but not the estimated species distribution, which depends only on β̂k.
If q(s) is a non-constant function of s – for example, if non-detection is a bigger problem in heavily forested sites – then we may incur bias for both αk and βk. If sites are visited repeatedly, then under some assumptions an estimate of non-detection may be obtained, by methods discussed in, for example, Royle & Nichols (2003); Dorazio (2012). Estimates of detection probability can sometimes be obtained without repeat observations under stronger modelling assumptions (Lele, Moreno & Bayne 2012; Sólymos, Lele & Bayne 2012)
Non-detection in presence–absence data is largely analogous to the sampling bias problem for presence-only data, and we could in principle model and adjust for it using similar methods to the ones we propose for addressing biased presence-only data.
Spatial errors
Opportunistic presence-only data may also suffer from errors in the recorded locations of point observations. Similarly, environmental covariates are often measured at a relatively coarse scale, in which case the covariates attributed to point si may be inaccurate. If important environmental covariates fluctuate on a fine scale compared to the scale of these errors, the errors may lead to attenuated effect size estimates (see e.g. Graham et al. 2008). Hefley et al. (2013a) propose methods to correct for spatial errors in presence-only records.
A similar issue can arise in the analysis of presence–absence or count data, when we use the centroid of a presence–absence quadrat as a proxy for the integral ∫Ai λ(s)ds, which may not be appropriate if the variables fluctuate on a fine scale relative to quadrat size. In such cases, it is especially helpful to record point locations within quadrats rather than recording only presence–absence or count data summarized at the quadrat level.
EXTENSIONS
As discussed elsewhere, there are many useful ways to extend GLM fitting procedures. GAMs, gradient-boosted trees and other forms of regularization on model parameters are all immediate extensions of the approach we have outlined here. Like other methods, our method’s results on a given data set will depend on making good choices regarding featurization and regularization.
Finally, in our approach, we are forced to assume a functional form for the sampling bias, and if our model is wrong, we will not account correctly for the sampling bias. Studies quantifying patterns of sampling bias in relation to spatial covariates are currently scarce, but could help to justify a more accurate model of sampling bias than one based on intuitive selection of covariates, as applied here. Nonetheless, in future work, we plan to investigate models that treat the sampling bias nonparametrically, imposing no assumptions on its functional form.
Supplementary Material
Acknowledgments
Survey data were sourced from the NSW Office of Environment and Heritages (OEH) Atlas of NSW Wildlife, which holds data from a number of custodians. Data obtained July 2013. Many thanks to Philip Gleeson, OEH, for help with understanding the database and for checking quarantined records for us. And to Christopher Simpson, OEH, for making the distance to roads layer. William Fithian was supported by National Science Foundation VIGRE grant DMS-0502385. Jane Elith was funded by Australian Research Council grant FT0991640. Trevor Hastie was partially supported by grantDMS-1007719 from the National Science Foundation, and grant RO1-EB001988-15 from the National Institutes of Health. Finally, we are very grateful to Trevor Hefley, Geert Aarts and our editors, for their very thorough and helpful comments which greatly improved our manuscript.
Footnotes
Because b(s) is a probability, readers familiar with logistic regression may wonder why we model b(s)= eγ+δ′z(s) instead of . When b(s) is close to zero, the denominator 1 + eγ+δ′z(s) ≈ 1 and the two models roughly coincide. We use the loglinear form because it leads to the convenient loglinear form for the presence-only intensity in (4).
Technically, the portion of 𝒯k that coincides with survey quadrats Ai is not independent of the presence–absence data for species k. We could repair this by discarding all presence-only and background sites occurring in survey quadrats, but in practice this is unnecessary because the Ai represent a miniscule fraction of the domain.
Data accessibility
The data and R code necessary to reproduce our model fit for the eucalypt data can be found on Stanford’s online research data repository: http://purl.stanford.edu/vt558xk1600. The data provided in this archive are described in Appendix S3. The presence-only species data are sourced from Atlas of Living Australia and Atlas of NSW Wildlife, Office of Environment and Heritage (OEH), both publicly available. The presence–absence data were downloaded from the Flora Survey Module of the Atlas of NSW Wildlife, Office of Environment and Heritage (OEH), and we thank them for permission to archive the data here.
Supporting Information
Additional Supporting Information may be found in the online version of this article.
Appendix S1.
A maximum likelihood estimation as a joint GLM.
Appendix S2.
Results of eucalypt study in more detail.
Appendix S3.
Description of data.
Figure S1.
Bootstrap confidence intervals for the species-specific effect of distance-to-coast on log-sampling bias.
Figure S2.
Cross-validation results for all species that were observed in at least 110 different presence-absence sites.
Figure S3.
Cross-validation results for all species that were observed in at least 110 different presence-absence sites.
References
- Aarts G, Fieberg J, Matthiopoulos J. Comparative interpretation of count, presence-absence and point methods for species distribution models. Methods in Ecology and Evolution. 2012;3:177–187. [Google Scholar]
- Baddeley A, Berman M, Fisher NI, Hardegen A, Milne RK, Schuhmacher D, Shah R, Turner R. Spatial logistic regression and change-of-support in poisson point processes. Electronic Journal of Statistics. 2010;4:1151–1201. [Google Scholar]
- Chakraborty A, Gelfand AE, Wilson AM, Latimer AM, Silander JA. Point pattern modelling for degraded presence-only data over large regions. Journal of the Royal Statistical Society: Series C (Applied Statistics) 2011;60:757–776. [Google Scholar]
- Cressie NAC. Statistics for Spatial Data. Vol. 928. New York: Wiley; 1993. revised edition. [Google Scholar]
- Dorazio RM. Predicting the geographic distribution of a species from presence-only data subject to detection errors. Biometrics. 2012;68:1303–1312. doi: 10.1111/j.1541-0420.2012.01779.x. [DOI] [PubMed] [Google Scholar]
- Dorazio RM. Accounting for imperfect detection and survey bias in statistical analysis of presence-only data. Global Ecology and Biogeography. 2014 [Google Scholar]
- Dudık M, Schapire RE, Phillips SJ. Correcting sample selection bias in maximum entropy density estimation. Advances in Neural Information Processing Systems. 2005;17:323–330. [Google Scholar]
- Efron B, Tibshirani R. An Introduction to the Bootstrap. Vol. 57. Boca Raton, Florida, USA: CRC press; 1993. [Google Scholar]
- Elith J, Phillips SJ, Hastie T, Dudík M, Chee YE, Yates CJ. A statistical explanation of maxent for ecologists. Diversity and Distributions. 2011;17:43–57. [Google Scholar]
- Fithian W, Hastie T. Finite-sample equivalence in statistical models for presence-only data. The Annals of Applied Statistics. 2013;7:1917–1939. doi: 10.1214/13-AOAS667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gaetan C, Guyon X. Spatial Statistics and Modeling. New York, USA: Springer Verlag; 2009. [Google Scholar]
- Giraud C, Calenge C, Julliard R. Capitalising on opportunistic data for monitoring biodiversity. 2014 doi: 10.1111/biom.12431. airXiv preprint arXiv:1407.2432. [DOI] [PubMed] [Google Scholar]
- Graham CH, Elith J, Hijmans RJ, Guisan A, Peterson AT, Loiselle BA. The influence of spatial errors in species occurrence data used in distribution models. Journal of Applied Ecology. 2008;45:239–247. [Google Scholar]
- Guan Y, Loh JM. A thinned block bootstrap variance estimation procedure for inhomogeneous spatial point patterns. Journal of the American Statistical Association. 2007;102:1377–1386. [Google Scholar]
- Hall P, Horowitz JL, Jing B-Y. On blocking rules for the boot-strap with dependent data. Biometrika. 1995;82:561–574. [Google Scholar]
- Hastie T, Fithian W. Inference from presence-only data; the ongoing controversy. Ecography. 2013;36:864–867. doi: 10.1111/j.1600-0587.2013.00321.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning. New York, USA: Springer Series in Statistics; 2009. [Google Scholar]
- Hefley TJ, Baasch DM, Tyre AJ, Blankenship EE. Correction of location errors for presence-only species distribution models. Methods in Ecology and Evolution. 2013a;5:207–214. [Google Scholar]
- Hefley TJ, Tyre AJ, Baasch DM, Blankenship EE. Nondetection sampling bias in marked presence-only data. Ecology and Evolution. 2013b;3:5225–5236. doi: 10.1002/ece3.887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lawson CR, Hodgson JA, Wilson RJ, Richards SA. Prevalence, thresholds and the performance of presence–absencemodels. Methods in Ecology and Evolution. 2014;5:54–64. [Google Scholar]
- Lehmann EL, Casella G. Theory of Point Estimation. Vol. 31. New York, USA: Springer; 1998. [Google Scholar]
- Lele SR, Keim JL. Weighted distributions and estimation of resource selection probability functions. Ecology. 2006;87:3021–3028. doi: 10.1890/0012-9658(2006)87[3021:wdaeor]2.0.co;2. [DOI] [PubMed] [Google Scholar]
- Lele SR, Moreno M, Bayne E. Dealing with detection error in site occupancy surveys: what can we do with a single survey? Journal of Plant Ecology. 2012;5:22–31. [Google Scholar]
- Lindenmayer DB, Welsh A, Donnelly C, Crane M, Michael D, Macgregor C, McBurney L, Montague-Drake R, Gibbons P. Are nest boxes a viable alternative source of cavities for hollow-dependent animals? Long-term monitoring of nest box occupancy, pest use and attrition. Biological Conservation. 2009;142:33–42. [Google Scholar]
- McCullagh P, Nelder JA. Generalized Linear Models. Vol. 37. Boca Raton, Florida, USA: CRC Press; 1989. [Google Scholar]
- Nordman DJ, Lahiri SN, Fridley BL. Optimal block size for variance estimation by a spatial block bootstrap method. Sankhyā: The Indian Journal of Statistics. 2007;69(part 3):468–493. [Google Scholar]
- Pearce JL, Boyce MS. Modelling distribution and abundance with presence-only data. Journal of Applied Ecology. 2006;43:405–412. [Google Scholar]
- Phillips SJ, Dudík M, Elith J, Graham CH, Lehmann A, Leathwick J, Ferrier S. Sample selection bias and presence-only distribution models: implications for background and pseudo absence data. Ecological Applications. 2009;19:181–197. doi: 10.1890/07-2153.1. [DOI] [PubMed] [Google Scholar]
- Renner IW, Warton DI. Equivalence of maxent and poisson point process models for species distribution modeling in ecology. Biometrics. 2013;69:274–281. doi: 10.1111/j.1541-0420.2012.01824.x. [DOI] [PubMed] [Google Scholar]
- Renner IW, Baddeley A, Elith J, Fithian W, Hastie T, Phillips S, Popovic G, Warton DI. Point process models for presence-only analysis – a review. Methods in Ecology and Evolution. 2014 [Epub ahead of print] [Google Scholar]
- Royle JA, Dorazio RM. Hierarchical Modeling and Inference in Ecology: The Analysis of Data from Populations, Metapopulations and Communities. London: Academic Press; 2008. [Google Scholar]
- Royle JA, Nichols JD. Estimating abundance from repeated presence– absence data or point counts. Ecology. 2003;84:777–790. [Google Scholar]
- Royle JA, Chandler RB, Yackulic C, Nichols JD. Likelihood analysis of species occurrence probability from presence-only data for modelling species distributions. Methods in Ecology and Evolution. 2012;3:545–554. [Google Scholar]
- Sólymos P, Lele S, Bayne E. Conditional likelihood approach for analyzing single visit abundance survey data in the presence of zero inflation and detection error. Environmetrics. 2012;23:197–205. [Google Scholar]
- Ward G, Hastie T, Barry S, Elith J, Leathwick JR. Presence-only data and the em algorithm. Biometrics. 2009;65:554–563. doi: 10.1111/j.1541-0420.2008.01116.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warton DI, Shepherd LC. Poisson point process models solve the “pseudoabsence problem" for presence-only data in ecology. The Annals of Applied Statistics. 2010;4:1383–1402. [Google Scholar]
- Warton DI, Renner IW, Ramp D. Model-based control of observer bias for the analysis of presence-only data in ecology. PLoS ONE. 2013;8:e79168. doi: 10.1371/journal.pone.0079168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yee TW, Mitchell ND. Generalized additive models in plant ecology. Journal of vegetation science. 1991;2:587–602. [Google Scholar]
- Zaniewski AE, Lehmann A, McC Overton J. Predicting species spatial distributions using presence-only data: a case study of native new zealand ferns. Ecological modelling. 2002;157:261–280. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.