An Integrated Stochastic Model of Matrix-Stiffness-Dependent Filopodial Dynamics

Abstract

The ways that living cells regulate their behavior in response to their local mechanical environment underlie growth, development, and healing and are important to critical pathologies such as metastasis and fibrosis. Although extensive experimental evidence supports the hypothesis that this regulation is governed by the dependence of filopodial dynamics upon extracellular matrix stiffness, the pathways for this dependence are unclear. We therefore developed a model to relate filopodial focal adhesion dynamics to integrin-mediated Rho signaling kinetics. Results showed that focal adhesion maturation, i.e., focal adhesion links reinforcement and integrin clustering, dominates over filopodial dynamics. Downregulated focal adhesion maturation leads to the biphasic relationship between extracellular matrix stiffness and retrograde flow that has been observed in embryonic chick forebrain neurons, whereas upregulated maturation leads to the monotonically decreasing relationship that has been observed in mouse embryonic fibroblasts. When integrin-mediated Rho activation and stress-dependent focal adhesion maturation are combined, the model shows how filopodial dynamics endows cells with exquisite mechanosensing. Taken together, the results support the hypothesis that mechanical and structural factors combine with signaling kinetics to enable cells to probe their environments via filopodial dynamics.

Introduction

Extracellular matrix (ECM) sensing by filopodia is important to the regulation of neuronal growth, wound healing, and cancer metastasis (1, 2, 3). This sensing is tied to the dynamics of filopodial extensions, which are highly dependent upon matrix stiffness. For instance, nerve cells guide axons via ECM-stiffness-dependent tractions within the growth cone that are regulated by filopodia (4), and fibroblasts migrate in directions chosen by ECM stiffness probing by filopodia (5). Pathological changes to the relationship between ECM stiffness and mean filopodium length are thought to underlie the metastatic potential of cancer cells (6, 7, 8, 9), for example, the mean length of lung cancer cell filopodia decreases with substrate stiffness (10). Clearly, mechanics and signaling factors interact, and these observations motivate a hypothesis that mechanical and structural factors combine with signaling kinetics to enable cells to probe their environments via filopodial dynamics.

Although the spectrum of factors that contribute to filopodial dynamics is enormous, experiments in idealized cellular microenvironments point to special roles for cytoskeletal, adhesion, and signaling dynamics (2). From the cytoskeletal perspective, growth and retraction of a filopodium are dominated by actin polymerization at the tip and retrograde actin flow away from the tip due to the action of myosin motors at the base (11, 12, 13). From the perspective of adhesions, substrate-stiffness-dependent filopodial dynamics are dominated by molecular clutches connecting actin filaments to the substrate (14) through adhesion proteins including integrins, talin, and vinculin (15, 16, 17). From the perspective of signaling, these interactions with substrate are dominated by adhesion-driven kinetics of the small GTPases of the Rho family (18, 19, 20), which we refer to collectively as Rho. These three factors are obviously coupled, with tension in engaged molecular clutches due to retrograde flow needing to be balanced by tractions from substrate deformation (14). Our aim was therefore to test our hypothesis by developing a model integrating actin cytoskeletal and molecular clutch biophysics with integrin-based Rho signaling and then determining whether these factors are capable of capturing key features of substrate-stiffness-dependent filopodial dynamics.

The strategy for verifying our model was to attempt to predict radically different behaviors observed in three different cell types. Whereas retrograde flow in embryonic chick forebrain neurons (ECFNs) and talin 2 short-hairpin RNA (shRNA) mouse embryonic fibroblasts (MEFs) varies with ECM stiffness in a biphasic fashion, retrograde flow in normal MEFs decreases monotonically with ECM stiffness (14, 21). By verifying against observations in these two cell types, we were able to identify what factors are important controls in stiffness-dependent filopodial dynamics in various cells.

Our model builds upon a wealth of models that provide insight into the mechanisms underlying filopodial dynamics. The Chan-Odde “motor-clutch model” is the starting point for explaining the effect of substrate stiffness on filopodial dynamics. The Chan-Odde model explained traction dynamics of filopodia in a nerve growth cone on compliant substrates, where the mechanical coupling between substrate and actin cytoskeleton forms a force transmission system (14, 22, 23). However, they found that filopodia generate a biphasic relationship between retrograde flow and substrate stiffness (lower retrograde flow on the soft substrate than on the stiff substrate) in ECFNs, which is contradicted with a monotonic relationship (retrograde flow decreases with increasing substrate stiffness) in MEFs (21, 23). Recently, Roca-Cusachs and co-authors proposed an improved molecular clutch model to validate the distinct relationship between retrograde flow and substrate stiffness (21). They found that talin-mediated mechanosensing could lead to a monotonic relationship in normal MEFs but a biphasic relationship in talin 2 shRNA MEFs. All of the above molecular clutch models have offered evidence that filopodial focal adhesions could strongly influence retrograde flow rate on different substrates. Increasing retrograde flow rate would effectively diminish filopodial growth in the Lan-Papoian stochastic model (24), suggesting that regulating the retrograde flow would be a highly efficient way to control filopodial extension dynamics. The Lan-Papoian stochastic filopodial model identifies the key physical and chemical parameters that control filopodial growth, including retrograde flow, membrane fluctuations, actin monomer diffusion, and polymerization and depolymerization of actin filaments, in filopodial dynamics, but their model has not yet been extended to include effects of substrate stiffness. The deterministic model of Welf and co-workers considers coupling between integrin-mediated signaling, motor proteins, and fibronectin (FN) density (25), but not substrate stiffness. Therefore, there is still an unmet need to develop a model of filopodial dynamics that is capable of capturing the distinct key features for various cell types.

Toward this end, we have improved and analyzed an integrated filopodial stochastic model with the following main features. First, our integrated model combined the dynamics of the actin cytoskeleton, molecular clutches, and integrin-based Rho signaling to reflect more realistic and necessary processes in filopodial dynamics. Second, there are two different ways for focal adhesions to mature; one is by actin-talin bond reinforcement by vinculin (the weakest link shifts from a talin-actin bond to an integrin-FN bond), and the other is by integrin clustering, probably by PIP2 signaling (integrin density is a function of substrate stiffness) (26). We find that clutch reinforcement and integrin clustering both can effectively influence the relationship between retrograde flow and stiffness. More interestingly, the model suggests that an α-actinin-mediated clutch shows a different biphasic relationship in talin 2 shRNA MEFs compared with the talin-mediated clutch in ECFNs. Finally, we explored the effect of the key biophysical and biochemical parameters (e.g., membrane force, concentration of talin, and characteristic force of talin unfolding and Rho signaling activation) on filopodial dynamics.

Materials and Methods

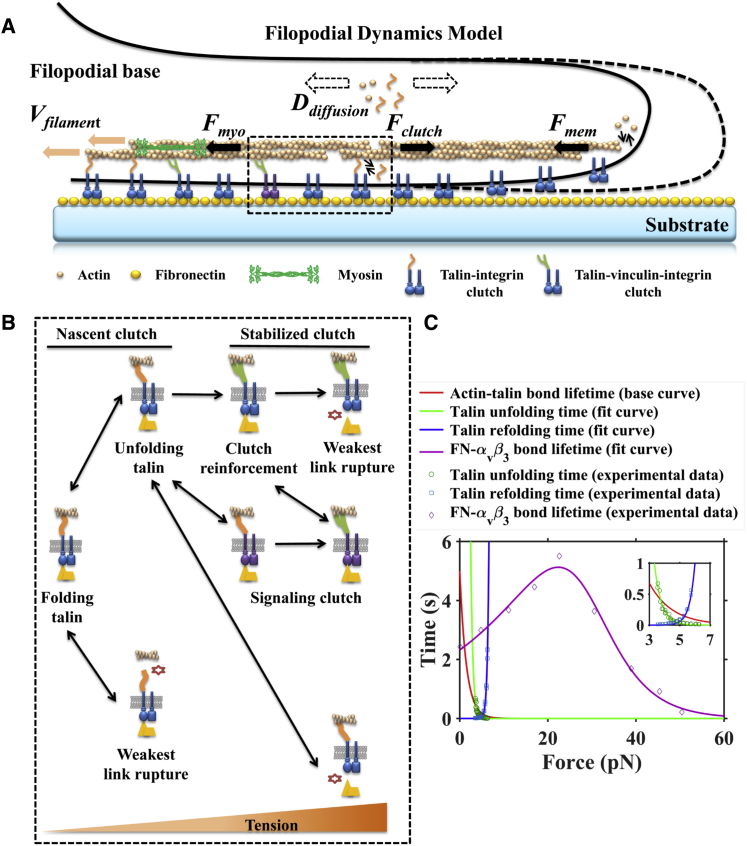
The integrated filopodial model (Fig. 1; Fig. S1 in the Supporting Material) approximated filopodia as an assemblage of actin filaments, adhesive molecular clutches, myosin motors, and a substrate and employed a stochastic reaction-diffusion algorithm via the Gillespie (kinetic Monte Carlo) method to simulate the complex interaction of various dynamic components in filopodia (27, 28). The key processes were 1) talin binding with inactive integrin with rate k_1f, talin-integrin complex dissociation with rate k_1r; 2) talin-integrin complex binding with FN or actin with rates k_2f and k_3f, respectively; 3) actin-talin-integrin complex or talin-integrin-FN complex dissociation with rates k_2r and k_3r, respectively; 4) actin-talin-integrin complex or talin-integrin-FN complex binding with FN or actin resulting in actin-talin-integrin-FN complex (nascent clutch), with rates k_4f and k_5f, respectively; 5) nascent clutch rupture at the talin/actin interface or integrin/FN interface with rates k_4r and k_5r, respectively; 6) talin unfolding and refolding with rates k_6f and k_6r; 7) vinculin binding with unfolding talin and actin with rate k_vin, resulting in actn-talin-vinculin-integrin-FN complex (stabilized clutch); 8) stabilized clutch rupture at integrin/FN surface with rate k_7r; 9) activation and deactivation of myosin motors with the corresponding rates k_am and k_dm; 10) actin polymerization and depolymerization at the barbed end of actin filaments with the corresponding rates k_ona and k_offa; 11) activation of Rho signaling above the characteristic force F_R; 12) and stretching of nascent and stabilized clutches under retrograde flow at rate V_u. As depicted in Fig. 1 A, the red solid arrows represent the actin retrograde flow caused by the contraction force of active myosin in the filopodial base and the solid black arrows represent the force applied by the active myosin, the molecular clutch, and the membrane on the actin filament. The dotted arrows represent actin and talin diffusion in filopodia, i.e., actin and talin can hop between adjacent compartments with a rate constant k_D. The detailed simulation algorithm is provided in the Supporting Material, as are the variables and parameters of the model (Table S1).

Figure 1.

Integrated stochastic model of substrate-stiffness-dependent filopodial dynamics. (A) Schematic depicting the model of filopodial dynamics on substrate. Actin polymerization and depolymerization at the tips of filopodia are coupled to the substrate through molecular clutches, and these molecular clutches resist the retrograde flow driven by myosin motors and membrane fluctuations. (B) Role of mechanosensing for molecular clutches. With increasing tension, the following transformation of molecular clutches could happen: talin unfolding and refolding, clutch reinforcement by vinculin binding, clutch configuration change for signaling activation, and weakest-link rupture. (C) The measured average lifetime of fibronectin (FN)-α_vβ₃ bonds (purple diamonds) (21) and measured average unfolding and refolding time of talin (green circles and blue squares, respectively) (41) as a function of force. Lines are the fitted curves of experiments for talin unfolding (green line) and refolding (blue line) and FN-α_vβ₃ bonds (purple line). The red line indicates the base curve of talin-actin bond lifetime. The inset shows the force-dependent unfolding and refolding time of the talin R3 domain (41). To see this figure in color, go online.

Filopodial focal complex maturation and rupture

Previous work suggests that filopodia could form small but fully assembled filopodial focal complexes that connect filopodia to the substrate along the filopodium axis (29). We modeled these focal complexes as groupings of idealized molecular clutches consisting of integrin, talin, and vinculin (29, 30).

Talin enables tension-mediated strengthening of adhesions to the substrate via its 11 cryptic vinculin binding sites (VBSs) that may be exposed under mechanical force (i.e., 5 pN for the VBS in the R3 domain) for further association with vinculin (31). Through binding with vinculin, a nascent clutch becomes stabilized, reducing the likelihood of dissociation of a linkage between the actin cytoskeleton and the integrin. With increased tension on a stabilized clutch, the integrin-FN bond will rupture according to the Bell model. In our model, we set the force necessary to remove a nascent clutch from the actin cytoskeleton (actin-talin bond rupture) to be F_tb ∼2 pN as a base value (32). A series of force-dependent processes at the molecular level constitute the foundation of mechanosensing behavior for filopodia (Fig. 1, B and C).

Integrin molecules commonly exhibit two states, the inactive and active states (33). Active talin binds with inactive integrin, which results in integrin activation and substrate binding (26). Active integrin in a molecular clutch could undergo configurational changes that reveal a site for protein (PIPKIγ) docking on the integrin cytoplasm. PIPKIγ could activate PIP2 signaling, resulting in more active integrins forming clutch links. We term this “integrin clustering” (26). In our model, we used different functions to differentiate distinct integrin clustering behaviors in different cell types according to previous experimental observations. We use a linear function to model integrin clustering in normal MEFs (21),

$$C_{\text{ti}}=0.02E+0.098,$$ (1)

where C_ti represents the integrin density and E is the substrate stiffness (0.1∼100 kPa). On the other hand, a Gaussian function,

$$C_{\text{ti}}=\frac{0.1}{\sqrt{2\pi }}{e}^{\frac{-{\left(E-1\right)}^2}{2}},$$ (2)

is used to model integrin clustering in ECFNs (4). No integrin clustering happens when the level of talin 2 is knocked down $\left(C_{\text{ti}}=0.1\right)$ in talin 2 shRNA MEFs.

Four noncovalent interactions in series contribute to the transmission of force from filopodia to substrate: 1) interaction of myosin motors and actin filaments, 2) binding of talin molecules to actin filaments, 3) binding of integrin molecules to talin molecules, and 4) binding of integrin molecules to the substrate (34). It has been reported that catch bonds between myosin and actin have a characteristic rupture force of ∼10 pN (35). The bond strength of talin-actin and talin-integrin is ∼2 pN (we used the characteristic rupture force of 2 pN for the talin-actin bond in our model, because there is no exact experimental description of the difference between these two interfaces) (32) and that of integrin-FN is ∼25 pN (21). We assumed that the weakest links in our model were the actin-talin bonds in nascent clutches and integrin-FN bonds in stabilized clutches; note that debate persists about whether or not the weakest link is in the interior of the cell (36).

In our model, nascent and stabilized clutches could dissociate between the actin cytoskeleton and integrins stochastically with the corresponding rates k_4r/5r and k_7r. Talin could unfold and refold with the corresponding rates k_6f and k_6r. Following the work of others, k_4r/5r and k_6f/6r were modeled as a slip bond and k_7r were modeled as a catch-slip bond (Fig. 1 C) (21). We transformed the Hookean spring constant to a Young’s modulus to compare the simulated results with those of experiments, according to

$$E=\frac{9K_{\text{ecm}}}{4\pi a},$$ (3)

where a is the radius of a nominally circular adhesion site, taken from experimental measurements (16).

Integrin-mediated Rho signaling dynamics

Focal adhesion complexes are stretch-sensitive and can trigger mechanochemical signaling in response to tension (19, 21). Integrin has sufficient energy to participate in the activation of the RhoA/Rho kinase (ROCK)/myosin II pathway when subjected to a tension larger than a characteristic force of F_R according to the Bell model (37). Following earlier models, we used a phenomenological equation to relate the myosin binding (i.e., attachment to actin filaments) rate, k_am, to the number of signaling integrins, N_ai, that participate in the Rho pathway and also defined k_dm as the myosin unbinding (i.e., detachment from actin filaments) rate (25). In our model,

$$k_{\text{am}}=k_{\text{am0}}\left(\frac{1+\alpha \lambda N_{\text{ai}}}{1+\lambda N_{\text{ai}}}\right),$$ (4)

where k_am0 is the myosin binding rate without the influence of Rho signaling, αk_am0 is the maximum myosin binding rate with the influence of Rho signaling, and λ is a saturation constant that represents the effect of Rho signaling on the myosin binding rate.

Filopodial growth dynamics

Actin filaments were modeled as bundled by cross-linking proteins including fascin, and as residing in the center of a filopodium. For modeling actin and talin diffusion in filopodia, we used the stochastic reaction-diffusion algorithm in the Lan-Papoian stochastic filopodial model (24). Actin and talin monomers can diffuse from the (proximal) filopodial base to the (distal) filopodial tip. Actin molecules at the filopodial tip can attach to actin filaments through a mechanism mediated by formins with a rate constant k_ona and can dissociate with a rate constant k_offa. Because the action of fascin is fast compared to these other factors, the kinetics of fascin was omitted, enabling the treatment of actin filaments as residing within a single bundle in the center of a filopodium without the need to differentiate individual filaments within the bundle (28). Cytosolic molecules such as actin and talin can diffuse in filopodia with a diffusion constant of approximately k_D = 5/16 μm²/s (28). At the filopodial base, the concentration of actin and talin was kept at constant values C_A and C_T (38). Our stochastic model began with a short, mature filopodium with an initial length of 81 nm. This was divided into two compartments, each of length 50 nm (24). The integrin density on the membrane in filopodia was also kept at the constant value, C_ti, for the same stiffness. We neglected integrin diffusion but plan to add this in future versions of the model if experimental data justify it.

Results

Stronger actin-talin bond strength can shift the optimum stiffness toward higher stiffness

Inactive integrin can be activated by talin and then bind with FN and actin, which results in a nascent clutch (26). Nascent-clutch formation occurs at the beginning of adhesion maturation. A nascent clutch has two possible dissociation loci (Fig. S1 B), the actin-talin bond and the integrin-FN bond. It has been shown that the actin-talin bond strength is ∼2 pN and the integrin-FN bond strength is ∼25 pN. It seems that actin-talin bonds are the weakest points in nascent clutches, so the actin-talin bond strength would have an important role in rigidity sensing for filopodia.

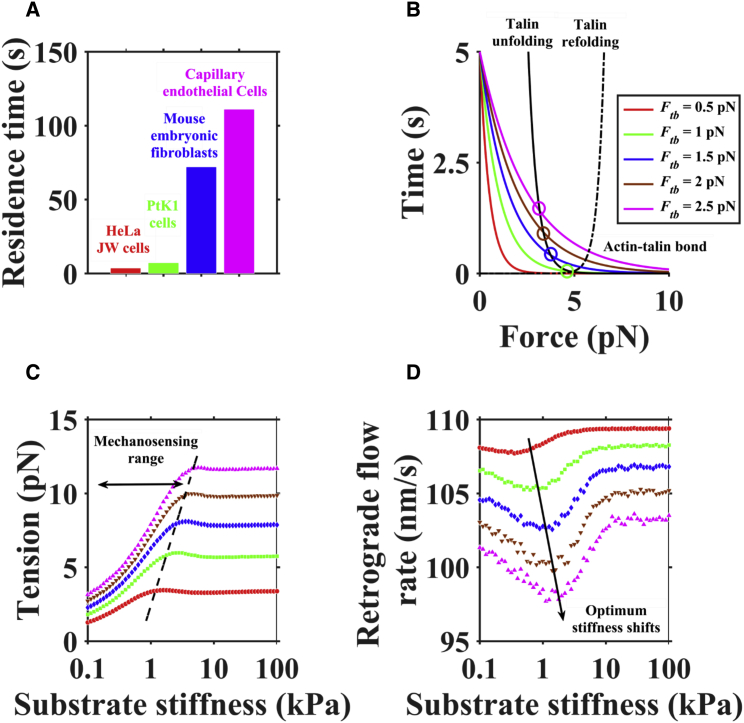
The residence time of talin is significantly different in different cell types (Fig. 2 A); for example, the talin residence time values in MEFs and capillary endothelial cells are nearly two orders of magnitudes greater than those in Hela JW cells and PtK1 cells. Talin-mediated clutch links between the actin cytoskeleton and integrin may exhibit distinct structures in different cell types, leading to different actin-talin bond strengths (39). To investigate the effect of distinct actin-talin bond strengths on clutch dynamics and rigidity sensing for different substrate stiffnesses ranging from 0.01 kPa to 100 kPa, covering a wide range of biological tissue stiffnesses (40), we increased F_tb from 0.5 pN to 2.5 pN to model stronger actin-talin bond strengths (as well as longer lifetimes) in our model (Fig. 2 B). Increasing F_tb increases the probability of talin unfolding before actin-talin bond rupture. For the same F_tb, we observed that the clutch tension significantly increased with increasing substrate stiffness from 0.1 kPa to 10 kPa, but there was no significant difference with further increase of substrate stiffness (Fig. 1 C). Increasing F_tb allows the actin-talin bond to bear greater tension and sense a larger stiffness range. The stronger actin-talin links lead to a smaller retrograde flow rate and shift the optimum stiffness to higher stiffness (Fig. 1 D). However, distinct actin-talin bond strengths would not change the biphasic relationship between retrograde flow and stiffness; a similar result is reported in the literature (22). Taken together, stronger actin-talin bond strength can make filopodia have a larger stiffness range.

Figure 2.

Distinct optimal stiffnesses in different cell types. (A) The residence time of talin in different cell types (43). (B) Increasing F_tb causes a larger actin-talin bond lifetime (a stronger actin-talin link). (C) Increasing F_tb causes an increase in clutch tension, which results in a larger mechanosensing range. (D) The stronger actin-talin bond strength can shift the optimum stiffness toward a higher value. To see this figure in color, go online.

Clutch reinforcement by vinculin binding and integrin clustering can explain the biphasic and monotonic relationship between retrograde flow and stiffness

Although the preceding analysis explains that the actin-talin bonds alone could serve as the rigidity sensor, some experimental observations, such as the monotonic relationship between retrograde flow and stiffness, still cannot be explained well. To address this, we added the process of clutch reinforcement by vinculin binding into our integrated clutch model. Vinculin could bind with the unfolding talin’s VBS site before talin refolding or unbinding. Increasing the vinculin binding rate could effectively increase the probability of stabilized clutch formation. Thus, the vinculin binding rate is also an important factor for mechanosensing.

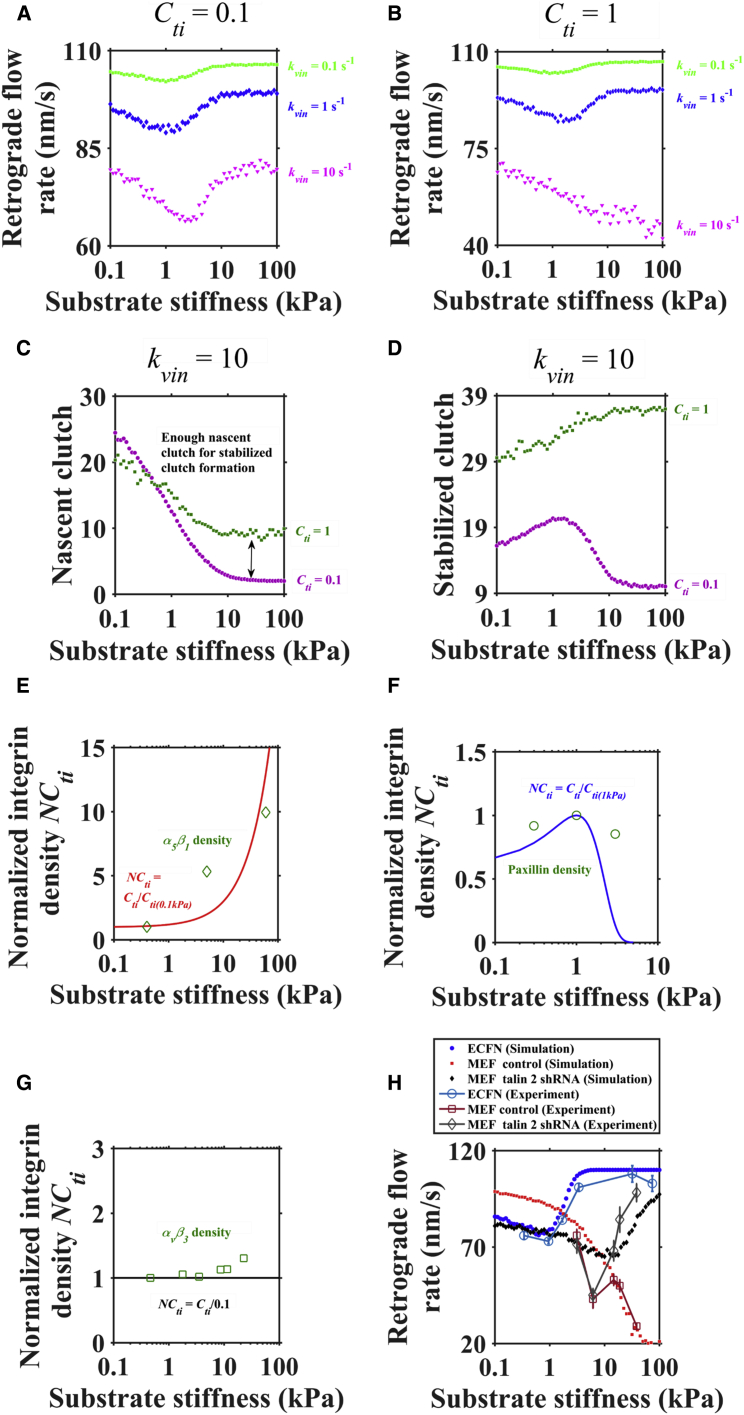
To investigate the effect of vinculin binding on filopodial rigidity sensing, we set different vinculin binding rates, k_vin (0.1 s⁻¹, 1 s⁻¹, and 10 s⁻¹), in our model. When the vinculin binding rate is large (k_vin = 10 s⁻¹), a monotonic relationship between retrograde flow and stiffness happens at the high integrin density (C_ti = 1) and a biphasic relationship is observed at the low integrin density (C_ti = 0.1) (Fig. 3, A and B). Obviously, integrin density is also a key factor influencing mechanosensing behavior. Higher integrin density causes more nascent-clutch formation on stiff substrates, so that there are enough nascent clutches to further form stabilized clutches (Fig. 3, C and D). As a result, stabilized clutches could inhibit retrograde flow on stiff substrates, which results in a monotonic relationship.

Figure 3.

Vinculin binding and integrin clustering both can explain the distinct relationship between retrograde flow and stiffness. (A and B) Increasing the vinculin binding rate (k_vin) caused a monotonic relationship with high integrin density (C_ti = 1). (C and D) Enough nascent clutches can promote stabilized clutch formation. (E–G) Distinct integrin clustering behaviors in different cell types, i.e., a linear function for MEFs, a Gaussian function for ECFNs, and a constant for talin 2 shRNA MEFs. (H) The distinct relationship between retrograde flow and stiffness in response to rigidity for various cell types. Shown are the biphasic relationship in ECFNs and talin 2 shRNA MEFs, experimental data from Odde et al. (14) and Roca-Cusachs et al. (21), the monotonic relationship in normal MEFs, and experimental data from Roca-Cusachs et al. (21). Parameter values are given in Table S2. To see this figure in color, go online.

Although clutch reinforcement by vinculin could reproduce a monotonic relationship, the change of retrograde flow rate is only ∼20∼30 nm from 0.1 kPa to 100 kPa, which is smaller than experimental values (∼50 nm). To address this, we have added integrin clustering into our integrated clutch model. Very recently, Elosegui-Ertola and co-authors proposed an improved molecular clutch model that also includes the integrin clustering process (integrin density increases upon vinculin binding and decreases when the clutch link ruptures). To model the process of integrin clustering on substrates with different stiffness, we directly set different functions of integrin density and stiffness (i.e., integrin density varies with substrate stiffness) dependent on experimental observations. It has been shown that integrin has distinct clustering behaviors in different cell types; for example, it increases with increasing stiffness for normal MEFs, increases first and then decreases with stiffness for ECFNs, and shows nearly no change for talin 2 shRNA MEFs (4, 21). Thus, we used a linear function, a Gaussian function, and a constant, respectively, to model these integrin clustering processes in different cell types (Fig. 3, E–G). As shown in Fig. 3 H, our simulation results are consistent with experimental data. More interestingly, we obtained the biphasic relationship in talin 2 shRNA MEFs by α-actinin-mediated clutches rather than talin-mediated clutches. Taken together, clutch reinforcement by vinculin could influence the types of rigidity sensing by filopodia (biphasic or monotonic relationship) and distinct integrin clustering behaviors in different cell types can expand the change of retrograde flow rate.

Integrin-mediated Rho signaling can promote actin cytoskeleton backward movement in filopodia

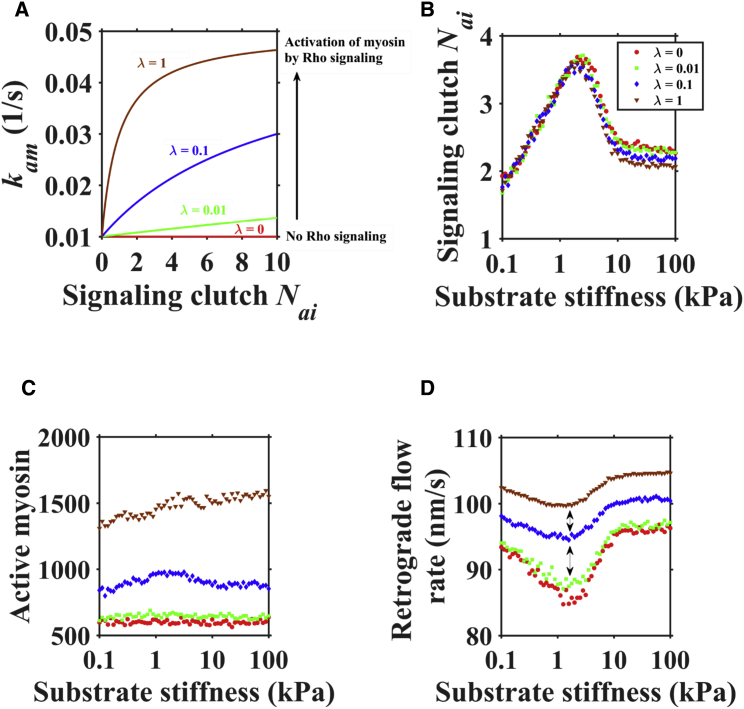
Tension in integrins can activate Rho signaling, which upregulates the myosin motor binding rate (20). To investigate the effect of Rho signaling on filopodial dynamics, we set a parameter λ to represent the Rho effect on the myosin activation rate for the same signaling clutch (Rho signaling would be turned off at λ = 0) (Fig. 4 A). We found that the number of signaling clutches stays in the range 2∼4 with different values of λ (Fig. 4 B). Increasing λ increases the active myosin number (Fig. 4 C) and the retrograde flow rate at the same stiffness (Fig. 4 D). We then studied how the function and disposition of myosin motors are affected by clutch dynamics for different substrate stiffnesses (Fig. S3). On compliant substrate (0.01 kPa), active myosin showed a random fluctuation at a value of 600, mainly because of Rho signaling of clutch formation is rare at this stiffness (Fig. S3 A), whereas on intermediate (0.1 kPa and 1 kPa) and stiff (10 kPa and 100 kPa) substrates, active myosin tended to fluctuate between 600 and 700 (Fig. S3, B–E), since, obviously, myosin activation is more frequent at these stiffnesses. The distribution of active myosin motors calculated from Fig. S3, A–E, displayed a characteristic unimodal shape (Fig. S3 F). More myosin motors attached to actin fibers on stiffer substrates, increasing the contraction force and thereby increasing the tension in engaged molecular clutches and retrograde flow rate. Taken together, Rho signaling would increase the retrograde flow rate but not change the optimum stiffness.

Figure 4.

Activation of integrin-mediated Rho signaling can increase retrograde flow rate by enhancing myosin activity. (A) λ represents the Rho signaling effect on myosin activation rate for different numbers of signaling clutches. (B) The effect of substrate stiffness on the number of signaling clutches. (C) Active myosin number increases with increasing λ. (D) Retrograde flow rate, but not optimum stiffness, increases with increasing λ. To see this figure in color, go online.

Filopodia exhibit distinct growth dynamics on substrates with different stiffness

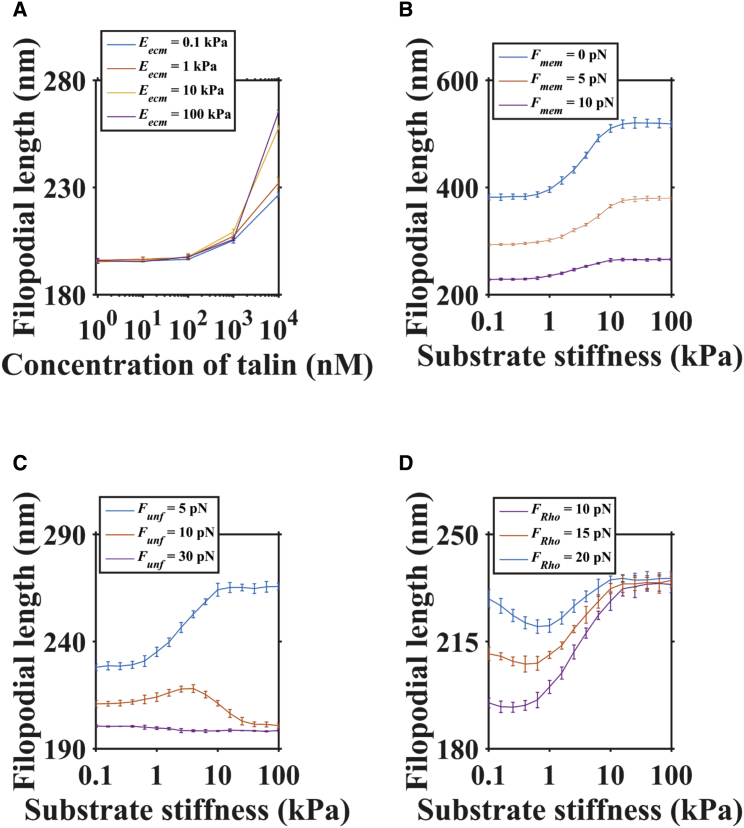
Generally, the concentration of actin-binding proteins (such as formin and talin) is less than that of actin and constantly varies in filopodia (15, 29, 38). To investigate the effect of talin concentration on filopodial dynamics, we changed the talin concentration from 0 μM to 10 μM in our model. When the concentration of talin is large (e.g., 10 μM), the filopodial length shows an obviously substantial increase other than random fluctuation around the equilibrium position of ∼200 nm (Fig. S4 A). There are enough stabilized clutches formed between actin and the substrate to inhibit the retrograde flow when talin concentration is >100 nM (Fig. 5 A; Fig. S4 B). When the talin concentration is small (<100 nM), stabilized clutches rarely form, resulting in a faster retrograde flow and a shorter filopodial length.

Figure 5.

Distinct filopodial length on substrate with different stiffness. (A) The effect of talin concentration on filopodial length for different substrate stiffnesses (0.1 kPa, 1 kPa, 10 kPa, and 100 kPa). (B) The effect of membrane force on filopodial length for different substrate stiffnesses (0.1∼100 kPa). (C) The effect of talin unfolding on filopodial length for different substrate stiffnesses (0.1∼100 kPa). (D) The effect of characteristic force of Rho activation on filopodial length for different substrate stiffnesses (0.1∼100 kPa). To see this figure in color, go online.

In a previous model, filopodial length decreased with increasing membrane force without the influence of substrate (24). We also investigated the effect of the membrane force on filopodial length with different substrate stiffnesses. We found that the mean filopodial length decreases with increasing membrane force (e.g., by ∼100 nm when the membrane force increases from 0 pN to 10 pN in our model) at different substrate stiffnesses ranging from 0.1 kPa to 100 kPa (Fig. 5 B). In our model, membrane force inhibits filopodial growth by perturbing the filament polymerization rate, and the perturbation would not significantly change the variation of filopodial length with substrate stiffness (such as the optimal stiffness change).

It has been shown that talin is a “force buffer,” which means that all VBSs in talin can be unfolded within a relatively small force range (5∼10 pN), indicating the important role of rigidity sensing under physiological conditions in vivo (41). More interestingly, it has been shown that cells exhibit distinct behaviors for rigidity sensing because of the slight difference in the talin unfolding threshold between talin isoforms (talin 1 and talin 2) (42). To investigate the effect of talin unfolding on filopodial growth, we increased F_unf to represent the larger force needed to unfold talin. Increasing F_unf causes a decrease in stabilized clutches, which results in a faster retrograde flow rate, and then causes shorter filopodial length on the same substrate stiffness (Fig. 5 C). When F_unf is ∼30 pN, there is nearly no link formation between actin and the substrate, which makes filopodia lose their mechanosensing function (there is almost no change in retrograde flow rate). When F_unf is ∼10 pN, there would be more stabilized clutches to inhibit retrograde flow, resulting in longer filopodial length. Because a stabilized clutch has a maximum value at intermediate substrate stiffness, as shown in our previous analysis (Fig. 3 D), filopodial length also has a maximum value at intermediate substrate stiffness. When F_unf is ∼5 pN, the probability of talin unfolding is much larger than in the unbound case. When nascent clutches form, they translate into stabilized clutches, resulting in an increase in filopodial length.

Finally, we investigated the effect of characteristic force of Rho activation on filopodial dynamics. Although the value of F_R remains to be determined (20), we used the range 10–20 pN based on published data (25). Increasing F_R represented the larger tension needed to activate Rho signaling. Increasing F_R causes an increase in filopodial length on soft stiffness (0.1∼1 kPa) (Fig. 5 D). In contrast to F_tb, the effect of F_R would not change the optimum stiffness at different substrate stiffnesses. Taken together, these findings demonstrate the potential to control filopodial dynamics by regulation of a few key parameters, several of which are accessible through both physiological regulation and experimental manipulation. Examples include modulating treatment with blebbistatin to decrease F_R (22) and expression of different talin isoforms for different values of F_unf (42).

Discussion

In this work, we proposed an integrated stochastic model of filopodial dynamics to explore the mechanisms by which substrate stiffness regulates filopodial dynamics and also to reconcile previous experimental observations. Recently, it was shown that substrate stiffness can significantly influence filopodial dynamics, also leading to a distinct response in different types of cells (4). With our model, we show that the major reasons for this are the distinct molecular clutch dynamics and Rho signaling dynamics in different types of cells. For example, talin has a different residence time in different cells, as do other important adhesion proteins, such as vinculin, α-actinin, paxillin, and FAK (Fig. 2 A) (43). Integrin clustering also exhibits distinct behaviors, showing almost linear clustering in MEFs (21), maximum clustering at ∼1 kPa in DRG neurons (4), and nearly no change in hippocampal neurons (4) and talin 2 shRNA MEFs (21) (Fig. 3, E–G). Also, there is a different vinculin binding rate in different regions of cells, which is important for stabilized maturation, such as a higher vinculin exchange rate (enhancing the level of phosphorylated vinculin) in the leading edge of migrating cells compared to stationary cells. Although it remains unclear how much tension, F_R, is needed to activate Rho signaling, this value may be different, since various integrins (e.g., α₅β₁ integrins and α_vβ₃ integrins) have been found in various cells with distinct functions (44). Therefore, the different molecular clutch dynamics (e.g., F_tb, C_ti, and k_vin) and Rho signaling dynamics (e.g., F_R) in different cell types could explain their distinct filopodial dynamics. Finally, there are four factors related to adhesion maturation that result in increased filopodial length, including an increased actin-talin bond lifetime (Fig. 2 D), increased vinculin binding rate (Fig. 3, A and B), increased integrin density on the membrane (Fig. 3, E–H), and increased talin concentration in the filopodia (Fig. 5 A). In this sense, our model is important, because it provides a bridge between filopodial dynamics, adhesion dynamics, and signaling dynamics.

Our simulations revealed a trade-off between strain localization and nascent clutch rupture as a key phenomenon underlying filopodial mechanosensing of substrate stiffness by molecular clutches. On stiffer substrates, strains associated with retrograde flow localized in talin due to talin’s relatively low stiffness. This strain localization exposed more cryptic VBSs in filopodia on stiff substrates, increasing the probability of stabilization through vinculin binding before nascent clutch rupture. However, increased tension on a clutch also increased the probability of nascent clutch rupture, and indeed, most nascent clutches ruptured quickly before stabilization by vinculin. The trade-off between these two factors led to a maximum number of stabilized clutches at an intermediate substrate stiffness of 1∼10 kPa.

Here, we first investigated the molecular clutch dynamics and contraction dynamics on substrates with different stiffness and found that clutch adhesion maturation and contraction force are significantly enhanced on stiff substrates. When the actin flow pulls back the engaged clutches, the stiffness of the substrate will determine to what extent the molecular clutches will be displaced in a given time period before clutches rupture. On soft substrates, actin flow could induce high substrate deformation and low tension in engaged molecular clutches. The clutch adhesion layer would then be less deformed, resulting in a weak filopodial response. On stiff substrates (i.e., less deformable), actin flow could lead to increasing stretch of molecular clutches that would activate Rho signaling pathways and enhance contraction force. Increasing tension in molecular clutches would expose the VBSs of talin for binding to vinculin, leading to clutch adhesion maturation. Recent experiments have shown that nascent adhesion decreases while stabilized adhesion increases with increasing substrate stiffness (45). Our model also captures these substrate-stiffness-dependent changes of cell adhesions.

There are two main kinds of molecular clutch models, that of the Odde group (14, 22), and that of the Roca-Cusachs group (16, 21). The Chan-Odde model explained traction dynamics of filopodia in nerve growth cones on compliant substrates, where the mechanical coupling between substrate and actin cytoskeleton forms a force transmission system (14, 22). However, they found that filopodial adhesion generates higher traction force (i.e., lower retrograde flow) on the soft substrate than on the stiff substrate, which is contradicted by reported experimental observations for fibroblasts, where traction force (retrograde flow) increases (decreases) with increasing substrate stiffness (21, 23). To address this question, the Bangasser-Odde group proposed the concept of “optimum stiffness,” where the actin cytoskeleton exhibits a minimal value in retrograde flow rate (22). The Bangasser-Odde motor-clutch model suggests that a monotonic relationship between retrograde flow and stiffness would appear for experimentally accessible values mainly because of the shift of optimal stiffness, but the relationship essentially remains a biphasic curve over a wide range of stiffnesses. Recently, Roca-Cusachs and co-authors proposed an improved molecular clutch model to validate the effect of talin mechanosensing on the relationship between retrograde flow and stiffness (21). They found that talin-mediated mechanosensing (integrin density increases with the combination of vinculin and unfolding talin and decreases with talin refolding or unbinding of clutches) could lead to a monotonic relationship in normal MEFs but a biphasic relationship in talin 2 shRNA MEFs. Although Roca-Cusachs’s simulations are in good agreement with experimental observations, the roles of some key factors in focal adhesion maturation are simplified in their model; for instance, talin turnover and actin-talin-integrin bond rupture occurs at a very small force (∼2 pN).

There are three new features in our integrated model with respect to previous work. 1) Our integrated stochastic model combines the dynamics of the actin cytoskeleton, molecular clutches, and integrin-based Rho signaling to reflect realistic, fundamental processes in filopodial dynamics. To date, the dynamics of the actin cytoskeleton and signaling pathways have not been incorporated into any other clutch model. Thus, the filopodial dynamics (such as the statistics of filopodial length) is only validated indirectly by retrograde flow rate in other models. Filopodia also contain many signaling molecules (such as paxillin and FAK) to regulate their dynamics, and our integrated model offers a direct platform to test the function of these signaling molecules (especially integrin-mediated signaling). 2) Our model is, to our knowledge, the first to contain two molecular “weak links”: the actin-talin bond and the integrin-FN bond. Both links are important in mechanosensing processes and adhesion maturation. In our model, the weakest link is the talin-actin bond in nascent clutches and the integrin-FN bond in stabilized clutches. The change of the weakest link during clutch reinforcement (from the talin/actin interface to the integrin/FN interface) is essential to determine whether a distinct relationship exists between retrograde flow and stiffness. To date, the Odde clutch model contains one weak point and yields a biphasic relationship. The Elosegui-Artola clutch model also contains one weak point and yields a (different) monotonic relationship, mainly by increasing integrin density. Clearly, the change of the weakest point also is one important factor for cell mechanosensing. 3) There are two different pathways for focal adhesion maturation in the clutch model: actin-talin bond reinforcement by vinculin (the weakest link in the molecular clutch shifts from the talin-actin bond to the integrin-fibronectin bond) and integrin clustering, probably by PIP2 signaling (integrin density is dependent upon substrate stiffness). In our model, we used different functions to model integrin clustering behaviors in different cell types. The Odde clutch model does not include integrin clustering. The Elosegui-Artola clutch model proposed that integrin density increases with vinculin binding and decreases with talin unbinding or refolding; this model combined vinculin binding with integrin clustering and was successfully validated against experimental data. In our model, integrin density is directly related to substrate stiffness and also could fit experimental data well. We believe that we offer a more fundamental approach to this problem.

Additionally, there are two features in our model that are required to provide experimental support for the model. One is the molecular-clutch mechanosensing process, including actin-talin bond rupture, integrin-FN bond rupture, and talin unfolding and refolding (Fig. 1 C). All of these kinetic parameters were obtained by fitting measured experimental data except the actin-talin bond rupture, which we studied parametrically to investigate its effect on clutch dynamics. The other feature is integrin clustering functions (the linearity function and Gaussian function) (Fig. 3, E–G). All of these functions are qualitatively consistent with experimental data to ensure that integrin clustering behaviors are realistic and effective. The validation of our simulation results is the distinct relationships between retrograde flow and substrate stiffness in different cell types. We have found that the results predicted experimental data well (Fig. 3 H).

We believe that actin flow has remarkably different behaviors due to different molecular-clutch dynamics for different types of cells. For example, frictional slippage may be dominant for ECFNs on stiff substrates because of the lack of stable adhesion on stiff substrates, whereas adhesion maturation may be more important for MEFs at the same stiffness. We can see that our model has captured the key features observed for different cell types in previous experiments. Generally, adhesion kinetics (such as the talin or vinculin exchange rate) differs among cell types (43), migration states (46), developmental stages (47), and mechanical microenvironment (16), even for genetically identical cells. These differences may relate to other complex gene regulation, signaling pathway and mechanosensing and so on. The change of molecular-clutch dynamics and signaling dynamics helps them to adapt to the surrounding microenvironment. For example, ECFNs do not generally bear a significant load in the brain, but MEFs may need strong adhesions to withstand mechanical force imposed by the ECM. Such differences in adhesion dynamics in various cells have been verified by previous experiments where the level of paxillin (another adhesion protein) is larger in dorsal root ganglion neurons than in hippocampal neurons (4). Thus, different populations of cells appear to have developed specific stiffness-response mechanisms to their local environments.

Author Contributions

F.X., T.J.L., and B.C. designed research; M.L., Y.H.L., and B.C. performed research; G.M.G., V.S.D., and B.C. analyzed data; G.M.G., G.Y. H., H.Y., and B.C. wrote the article.

Editor: Anatoly Kolomeisky.

Supporting Citation

References (48, 49) appear in the Supporting Material.