Heavy-Hole States in Germanium Hut Wires

Abstract

Hole spins have gained considerable interest in the past few years due to their potential for fast electrically controlled qubits. Here, we study holes confined in Ge hut wires, a so-far unexplored type of nanostructure. Low-temperature magnetotransport measurements reveal a large anisotropy between the in-plane and out-of-plane g-factors of up to 18. Numerical simulations verify that this large anisotropy originates from a confined wave function of heavy-hole character. A light-hole admixture of less than 1% is estimated for the states of lowest energy, leading to a surprisingly large reduction of the out-of-plane g-factors compared with those for pure heavy holes. Given this tiny light-hole contribution, the spin lifetimes are expected to be very long, even in isotopically nonpurified samples.

The interest in group IV materials for spin qubits has been continuously increasing over the past few years after the demonstration of long electron spin decay times.¹⁻⁵ Silicon (Si) not only has the advantage of being the most important element in semiconductor industry; it can also be isotopically purified, eliminating the problem of decoherence from hyperfine interactions. Indeed, the use of such isotopically purified samples allowed the observation of electron spin coherence times of almost 1 s.⁶ One limitation of Si is the difficulty in performing fast gate operations while maintaining good coherence. One way around this problem is to use the spin–orbit interaction of holes⁷ and manipulate the spin with electric fields. First steps in this direction have been recently reported.⁸ Holes in germanium (Ge) have an even stronger spin–orbit coupling.⁹⁻¹¹ This fact together with the rather weak hyperfine interaction, already in nonpurified materials, make Ge quantum dots (QDs) a promising platform for the realization of high-fidelity spin qubits.¹²

In 2002, the first Ge–Si core–shell nanowires (NWs) were grown by chemical vapor deposition,¹³ and soon after, QDs were investigated in such structures.¹⁴⁻¹⁶ The cylindrical geometry of the NWs, however, leads to a mixture of heavy holes (HH) and light holes (LH).^9,17−19 As a consequence, the hyperfine interaction is not of Ising type, which thus reduces the spin coherence times.²⁰ Still, spin relaxation times of about 600 μs²¹ and dephasing times of about 200 ns²² were reported. One way of creating Ge QDs with noncylindrical symmetry is by means of the so-called Stranski–Krastanow (SK) growth mode.²³ In 2010, the first single-hole transistors based on such SK Ge dome-like nanostructures were realized.²⁴ Electrically tunable g-factors were reported,²⁵ and Rabi frequencies as high as 100 MHz were predicted.²⁶ However, due to their very small size, it is difficult to create double-QD structures, typically used in spin-manipulation experiments.²⁷ A solution to this problem can come from a second type of SK Ge nanostructures, the hut clusters, which were observed for the first time in 1990.²⁸ Zhang et al.²⁹ showed in 2012 that under appropriate conditions, the hut clusters can expand into Ge hut wires (HWs), with lengths exceeding 1 μm. Two years later, the growth of SiGe HWs was also demonstrated.³⁰ HWs have a triangular cross-section with a height of about 2 nm above the wetting layer (WL) and are fully strained. These structural properties should lead to a very large HH–LH splitting, minimizing the mixing and, as a consequence, the non-Ising type coupling to the nuclear spins. Despite this interesting perspective, not much is known about their electronic properties.

Here, we study three-terminal devices fabricated from Ge HWs. Scanning transmission electron microscopy (STEM) images verify that during their formation via annealing, no defects are induced. From magnetotransport measurements, a strong in-plane vs out-of-plane g-factor anisotropy can be observed, and numerical simulations reveal that the low-energy states in the HWs are of HH type. The calculated results are consistent with the experimental data and confirm that confined holes in Ge are promising candidates for spin qubits.

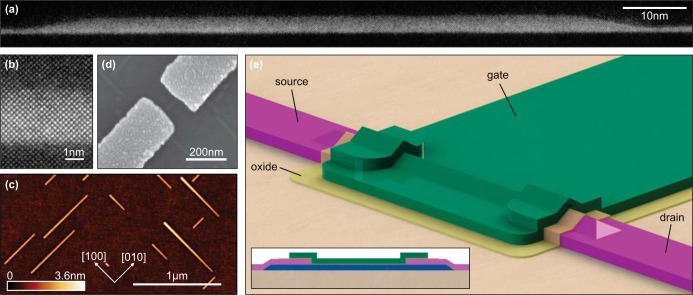
The Ge HWs used in this study were grown by means of molecular beam epitaxy on 4-inch low-miscut Si(001) wafers, as described in ref (30). Ge (6.6 Å) was deposited on a Si buffer layer, leading to the formation of hut clusters. After a subsequent annealing process of roughly 3 h, in-plane Ge HWs with lengths of up to 1 μm were achieved. In the last step of the growth process, the wires were covered with a 5 nm thick Si cap to prevent the oxidation of Ge. The deposited Si acts also as a potential barrier that enables hole confinement. Figure 1a shows a STEM image taken with an annular dark-field detector. The Ge HW and the WL (bright) are surrounded by the Si substrate below and the Si cap on top (dark). The STEM lamella containing the HW was prepared along the [100] direction by focused ion beam milling and thinned to a final thickness of about 60 nm. The STEM images show no signs of dislocations or defects, indicating perfect heteroepitaxy (see also Figure 1b). The height of the encapsulated wires is about 20 monolayers (2.8 nm), including the WL. Besides having well-defined triangular cross-sections, the HWs are oriented solely along the [100] and the [010] directions, as can be seen in the atomic force micrograph of uncapped Ge HWs in Figure 1c.

Figure 1.

(a) Scanning transmission electron microscope image along a HW embedded in epitaxial Si. (b) Wire cross-section at higher resolution showing the defect-free growth of the wires. (c) Atomic force microscopy image of uncapped Ge HWs. (d) Scanning electron micrograph of a HW contacted by Pd source and drain electrodes. (e) Schematic representation of a processed three-terminal device studied in this work. The Ge HW, which is grown on a Si substrate, and its source and drain electrodes are covered by a thin hafnium oxide layer. The top gate covers the HW and partly the source and drain contacts. Correspondingly, the cross-section of the device along the HW (blue) is shown in the inset.

For the fabrication of three-terminal devices, metal electrodes were defined by electron beam lithography. After a short oxide removal step with buffered hydrofluoric acid, 30 nm thick palladium (Pd) contacts were evaporated. The gap between source and drain electrodes ranges from 70 to 100 nm and is illustrated in Figure 1d. The sample was then covered by a 10 nm thick hafnium oxide insulating layer. As a last step, top gates consisting of Ti/Pd (3/20 nm) were fabricated. A schematic representation of a processed HW device is depicted in Figure 1e.

The devices were cooled in a liquid He-3 refrigerator with a base temperature of about 250 mK equipped with a vector magnet. The sample characterization was performed using low-noise electronics and standard lock-in techniques.

In the following, the results of two similar devices are presented that only differ slightly in the gap size between source and drain; the two devices have channel lengths of 95 and 70 nm, respectively. A stability diagram of the first device is shown in Figure 2a. Closing Coulomb diamonds prove that a single QD formed in the HW. Typical charging energies lie between 5 and 10 meV, and excited states can be clearly observed. The corresponding level spacing between the ground states and the first excited states is up to 1 meV. Because at more positive gate voltages, the current signal becomes too small to be measured, we cannot define the absolute number of holes confined in the QD. At least 10 more charge transitions after the 2N state can be observed for more positive gate voltages. To get additional information, the device was cooled down a second time and measured at 4 K by radio frequency dispersive reflectometry.³¹ The reflectometry signal did not reveal the existence of additional holes beyond the regime in which the current signal vanished, which, however, could be also due to the slow tunnel rates. We can thus just estimate that in the discussed crossings, the number of holes is about 10 to 20, i.e., the QD states most likely form from the first sub-band.

Figure 2.

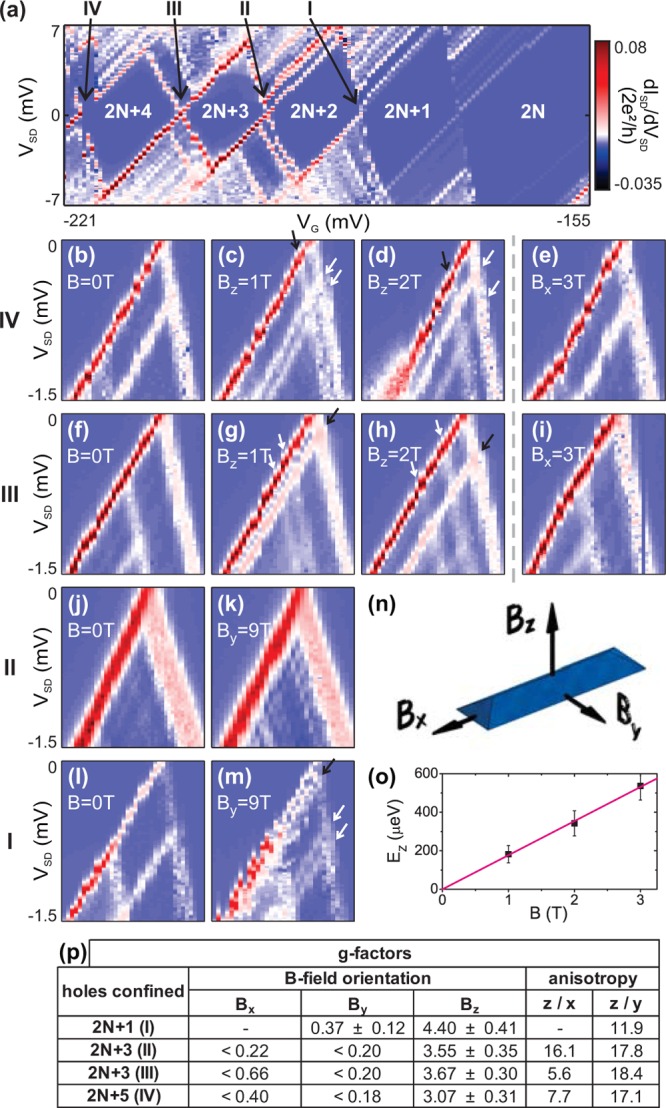
(a) Stability diagram of a HW device taken at ∼250 mK and zero magnetic field. The number of confined holes is indicated in white and the relevant crossings are labeled with roman numerals. The shown color scale is also valid for panels b–m. (b–e) Differential conductance measurements vs V_G (x-axis) and V_SD (y-axis) for crossing IV for B_z = 0, 1, and 2 Tesla (T) and B_x = 3 T, respectively. Similarly, panels f–h show the differential conductance of the lower half of crossing III vs V_G and V_SD for B_z = 0, 1, and 2 T and (i) for B_x = 3 T. Measurements of crossing II are shown in panel j for 0 T and in panel k for B_y = 9 T. Likewise, panels l and m show the lower part of crossing I at 0 T and B_y = 9 T, respectively. For all measurements shown in panels b–m, the gate range is roughly 6 mV. In panel n, the used nomenclature for the magnetic field orientations is illustrated. (o) Dependence of the Zeeman energy E_Z of the ground state in crossing IV vs B_z. The g-factors are extracted from the linear fit (red line). The measured g-factors for the three different magnetic field orientations, as well as the resulting anisotropies z/x and z/y, are listed in (p) for crossings I to IV.

For holes, the band structure is more complex than for electrons. At the Γ point, the HH and LH bands are degenerate. This degeneracy can be lifted by strain and confinement.³² In two-dimensional hole gases of semiconductors with compressive, biaxial in-plane strain, the HH states lie lower in energy than the LH states, i.e., it would cost less energy to excite an electron to the conduction band from the HH than the LH band.³³ However, further carrier confinement can induce a strong mixture of HH and LH states.³⁴

To investigate the nature of the HW hole states, their g-factors were determined via magnetotransport measurements. In the presence of an external magnetic field B, the doubly degenerate QD energy levels split. For more than 15 diamond crossings, the Zeeman splitting was measured for the three orientations illustrated in Figure 2n. In Figure 2a–m, measurements of four representative crossings showing the differential conductance (dI_SD/dV_SD) vs gate (V_G) and source-drain voltage (V_SD) at various magnetic fields are presented. The signature of a singly occupied doubly degenerate level is the appearance of an additional line ending at both sides of the diamond once a magnetic field is applied. These extra lines are indicated by black arrows in panels c and d of Figure 2 for crossing IV, in panels g and h for crossing III, and in panel m for crossing I. They allow us to identify the diamonds between crossing II and III and on the right side of crossing I as diamonds with an odd number of confined holes.

In addition, from the position of these extra lines, the Zeeman energy E_Z= gμ_BB can be extracted with μ_B the Bohr magneton, B = |B|, and g standing for the absolute value of the g-factor. By the plotting of the Zeeman energies vs the magnetic field and the application of a linear fit to the data, forced through the origin, the hole g-factor can be determined (see Figure 2o). For crossing IV and an out-of-plane magnetic field B_z we determine that g_⊥ = 3.07 ± 0.31. The same type of measurements result in a slightly higher value of the g_⊥-factor for the diamonds with a smaller amount of holes. Compared to the out-of-plane magnetic field, the in-plane directions have an almost negligible effect on the hole state splitting, as shown in Figure 2e for crossing IV and in (i) for crossing III, both at B_x = 3 T. Due to the thermal broadening, the split lines can be barely resolved. Therefore, an upper limit of the g-factor is given for these cases. The lower parts of crossings II and I at B_y = 9 T are shown in panels k and m of Figure 2, respectively, where only the latter shows an observable splitting. The small g-factors for both in-plane magnetic fields lead to large g-factor anisotropies z/x and z/y, ranging from 5 to about 20, as shown in the table in Figure 2p. A similar anisotropy was observed in crossing IV (III) for the triplet-like splitting indicated by white arrows in Figure 2c and d (g and h), resulting in g_⊥ = 2.61 ± 0.56; the corresponding in-plane splitting is too small to be resolved at 250 mK. When the measured g-factors are compared with those reported for dome-like Ge QDs,^24,26 it is observed that HWs have larger g_⊥ and much larger anisotropies, which are both characteristics of HH states.^33,34

To validate whether our findings are general characteristics of HW devices, a second device was also measured. Figure 3a shows the overview stability diagram with a focus on crossing i and ii. Due to reasons of visibility, the corresponding magnetic field spectroscopy measurements are partly shown in current representation. In Figure 3b–e and f–i, the dependence on the three different B-field orientations is illustrated for crossing ii and i, respectively. Inelastic cotunneling measurements for 2N + 5 holes are shown in Figure 3j–l as a function of B_x, B_y, and B_z, respectively. The obtained g-factors are listed in the table in Figure 3m, with the highest out-of-plane g-factor being 4.3, similar to the first device. For the in-plane g-factors, g_x or g_y, slightly increased values can be observed (because g_x and g_y show comparable values, they will be referred to as g_∥ in the following). However, the g-factors in out-of-plane direction are still 10 times larger than for the in-plane orientation.

Figure 3.

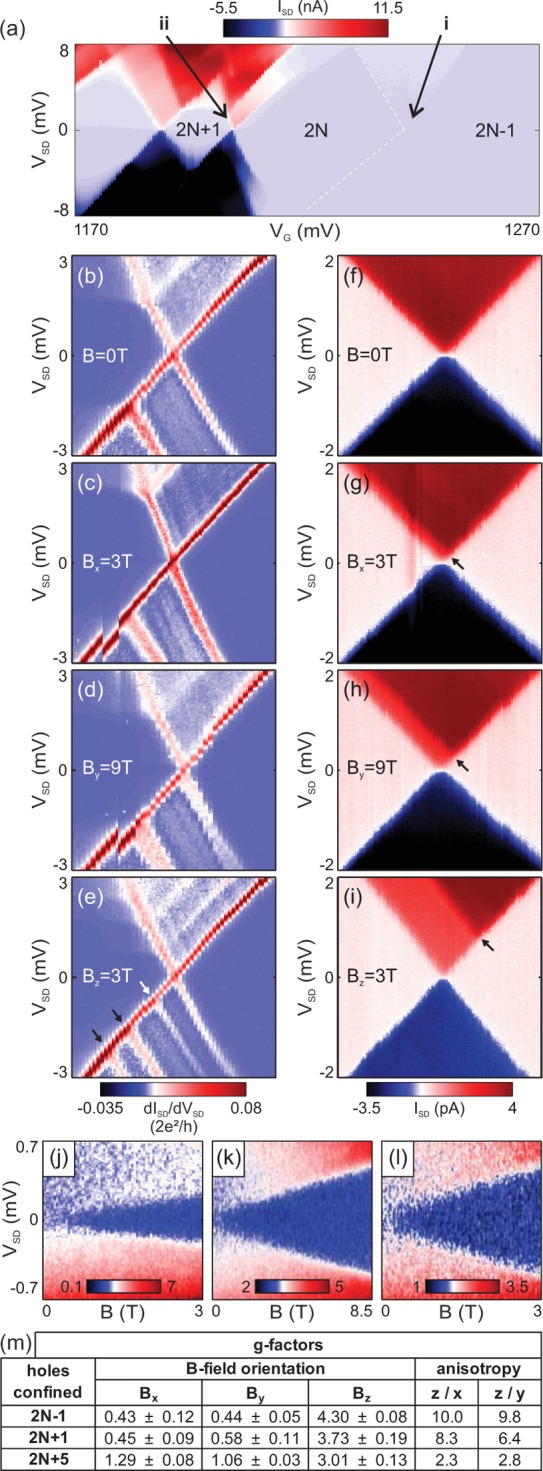
(a) Stability diagram of the second device with a focus on the crossings denoted as i and ii. The magnetic field dependence is shown in panels b–e for crossing ii and in panels f–i for crossing i. For crossing ii, the splitting of the excited state can also be observed, as indicated in panel e by black arrows. The corresponding g-factors were extracted as g_⊥ = 3.79 ± 0.45, g_x < 1.30, g_y < 0.68. Panels j–l show differential conductance plots of inelastic cotunneling measurements for the 2N + 5 hole state vs V_SD and B for B_x, B_y, and B_z, from left to right, respectively. The color scale insets indicate the differential conductance in units of 2e²/h · 10^–4. In panel m, the determined g-factor values and the corresponding anisotropy factors for the ground state of the discussed crossings are listed. The g-factors were determined from direct tunneling except the values for 2N + 1 holes at B_x = 3 T and for 2N + 5 holes, which were obtained from inelastic cotunneling measurements.

From the listed g-factor values, two interesting observations can be made. First, as for the first device, the g_⊥-factor is decreasing for a higher number of holes, and second, the g_∥-factors have clearly increased for a larger number of holes. As a consequence, a decrease of the anisotropies to less than 3 was observed for the 2N + 5 hole state, indicating an increased LH contribution.^33,34

To get a better understanding of the measured g-factor values and their anisotropies, we consider a simple model for hole states in HWs. Taking into account the HH and LH bands of Ge and assuming that the HWs are free of shear strain, our model Hamiltonian in the presence of a magnetic field is

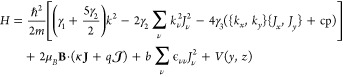1

It comprises the Luttinger–Kohn Hamiltonian,³⁵ the Bir–Pikus Hamiltonian,³⁷ and the confinement in the transverse directions V(y,z), for which we take a rectangular hard-wall potential of width L_y and height L_z for simplicity, i.e., V(y,z) = 0 if both |y|<L_y/2 and |z|<L_z/2 and V(y,z) = ∞ otherwise. In eq 1, we omitted the term −(a + 5 b/4)(ϵ_xx + ϵ_yy + ϵ_zz) from the Bir–Pikus Hamiltonian, where a is the hydrostatic deformation potential. This term corresponds to a global energy shift in our model and therefore cannot affect the results. In an extended model, where the energy of the valence band edge matters, this term should be included. We note that −H refers to the valence band electrons, and a global minus was applied for our description of holes (which are unfilled valence band states). In eq 1, {A,B}= (AB + BA)/2, “cp” are cyclic permutations, m is the bare electron mass, and J_ν are dimensionless spin-3/2 operators. The subscript ν stands for the three axes x, y, z, which are oriented along the length, width, and height, respectively, of the HW (see Figures 2n and 4a) and coincide with the main crystallographic axes. With the listed vector components referring to the unit vectors along these three directions, the magnetic field is B = (B_x, B_y, B_z) and, furthermore, J = (J_x, J_y, J_z), 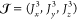. The operators k_ν are components of the kinetic electron momentum ℏk = −i ℏ∇+ eA, where e is the elementary positive charge, ∇ is the Nabla operator, and B = ∇ × A. For the vector potential, we choose a convenient gauge A = (B_yz – B_zy, − B_xz/2, B_xy/2), and we note that k² = k·k.

Figure 4.

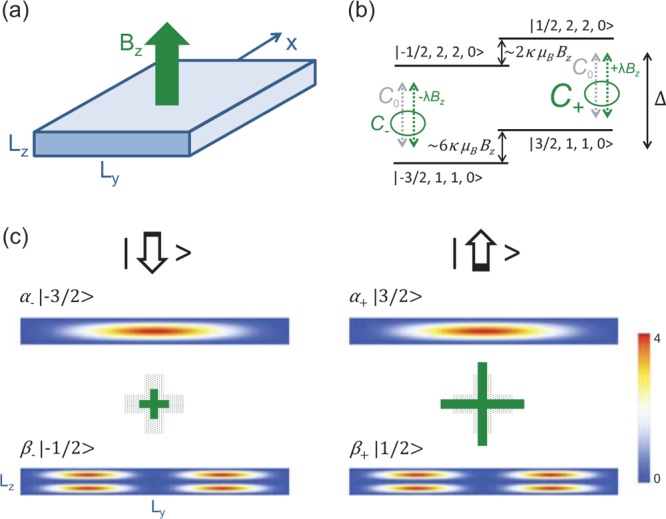
(a) Sketch of the HW model in the theoretical analysis. The cross-section is approximated by a rectangle of width L_y and small thickness L_z. The green arrow represents an out-of-plane magnetic field B_z. (b) Effective four-level system used to derive the dominant correction g_C (eq 5) in the out-of-plane g-factor g_⊥ ≃ 6 κ + 27 q/2 + g_C. The LH states |±1/2, 2, 2, 0⟩ and the HH states |±3/2, 1, 1, 0⟩ (see eqs 2 and 3 for details) differ by an energy of order Δ. In the presence of B_z, the couplings between these states have the form C_±= C₀ ± λB_z. That is, zero-field couplings of equal strength (C₀, gray dotted arrows) are enhanced and reduced, respectively (±λB_z with a proportionality factor of λ, green dotted arrows), which results in |C_–|<|C₊| for B_z > 0 as sketched in the diagram. (c) The Zeeman split eigenstates of lowest energy after diagonalization of the system in panel b. The ground state α_– |−3/2, 1, 1, 0⟩+ β_– |−1/2, 2, 2, 0⟩ (left, pseudospin down) consists of a HH state with spin |−3/2⟩ with a probability density that has a peak at the center of the HW cross-section and a LH state with spin |−1/2⟩ and four peaks near the corners (analogous for the excited state shown on the right, pseudospin up). The plots for the probability densities are dimensionless and correspond to L_zL_y |φ_1, 1, 0|² and L_zL_y |φ_2, 2, 0|², respectively (eq 3). We find |α_±|² > 0.99 for typical parameters, so the LH admixtures are very small. However, due to |C_–|<|C₊| caused by B_z, the LH admixtures |β_–|² < |β₊|² differ slightly, as illustrated by the different plus signs (green) and the different LH contributions (black, not to scale) in the arrows for the pseudospin. This difference is associated with a substantial reduction of g_⊥; see g_C. The gray plus signs of equal size in the background refer to the initial couplings, which are reduced or enhanced, respectively, in the presence of B_z.

The Hamiltonian H of eq 1 may be written in matrix form by projection onto a suitable set of basis states. In agreement with the boundary conditions, we use the basis states¹⁸

2

with orbital part

3

where the n_z ≥ 1 and n_y ≥ 1 are integer quantum numbers for the transverse sub-bands, and k̃_x is a wavenumber. Eq 3 applies when both |y|<L_y/2 and |z|<L_z/2, otherwise φ_{nz, ny, k̃x} = 0. The spin states |j_z⟩ are eigenstates of J_z and satisfy J_z |j_z⟩= j_z |j_z⟩, where j_z ∈{3/2, 1/2, –1/2, –3/2}. Because of the very strong confinement along z in our system, basis states with j_z = ± 3/2 (j_z = ± 1/2) correspond to HH (LH) states. To analyze the low-energy properties of H, we project it onto the 36 dimensional subspace with n_z ≤ 3 and n_y ≤ 3. This range of sub-bands is large enough to account for the most important couplings and small enough to enable fast numerical diagonalization.

The band structure parameters of (bulk) Ge are γ₁ = 13.35, γ₂ = 4.25, γ₃ = 5.69, κ = 3.41, and q = 0.07;^38,39 the deformation potential is b = −2.5 eV.³⁷ The values for the strain tensor elements ϵ_xx = −0.033 = ϵ_yy and ϵ_zz = 0.020 are obtained from finite element simulations, as described in the Supporting Information. That is, the Ge lattice in the HW has almost completely adopted the lattice constant of Si along the x and y directions and experiences tensile strain along the out-of-plane direction z. Using moderate magnetic fields (of the order of Tesla) as in the experiment, L_y = 20 nm, L_z ≤ 3 nm, and the above-mentioned parameters, we diagonalize the resulting 36 × 36 matrix numerically and find that the eigenstates of lowest energy are close-to-ideal HH states. They feature spin expectation values ⟨J_z ⟩ above 1.49 and below −1.49, respectively, when B is along z, and ⟨J_ν ⟩ ≃ 0 for all ν ∈{x, y, z} when B is in-plane. This corresponds to a LH admixture of less than 1%. (An upper bound for the LH probability p_LH is given by (1–p_LH) 3/2 + p_LH 1/2 > 1.49, which results in p_LH < 0.01.) Furthermore, the admixture remains very small even when electric fields that may have been present in the experiment are added to the theory (see the Supporting Information).

The numerically observed HH character of the low-energy states in our model can easily be understood. First, with ϵ_xx = ϵ_yy = ϵ_∥, the spin-dependent part of the strain-induced Hamiltonian can be written in the form b(ϵ_zz – ϵ_∥) J_z², and so basis states with j_z = ± 1/2 are shifted up in energy by more than 250 meV compared to those with j_z = ± 3/2. Second, the strong confinement along z leads to an additional HH–LH splitting of the order of ℏ² π² (m_LH – m_HH^–1)/(2 L_z), where m_LH = m/(γ₁ + 2 γ₂) and m_HH = m/(γ₁ – 2 γ₂). This results in a large splitting of 2 γ₂ ℏ² π²/(m L_z²) ≥ 710 meV for L_z ≤ 3 nm.

The result that hole states with j_z = ± 1/2 are so much higher in energy than those with j_z = ± 3/2 suggests that one may simplify the Hamiltonian of eq 1 by projection onto the HH subspace, which is described in detail in the Supporting Information. If the LH states are ignored, one expects small in-plane g-factors g_∥ ≃3q ≃0.2 and very large out-of-plane g-factors g_⊥ ≃ 6 κ + 27q/2 ≃ 21.4 (see the Supporting Information).⁴¹ While g_∥ is indeed small in our experiment and g_⊥ ≫g_∥ is indeed observed, the measured value of g_⊥ is significantly smaller than the one obtained from the pure-HH approximation.

When we diagonalize the 36 × 36 matrix, we find that the in-plane g-factors are close to 3q, as also expected, e.g., from studies of the in-plane g-factors in narrow [001]-grown quantum wells.^39,41,42 Our results for g_∥ agree well with the experiment and are consistent with the HH character of the low-energy states. Rather surprisingly, however, even though the low-energy eigenstates consist almost exclusively of either |3/2⟩ or |−3/2⟩ when the magnetic field is applied along z, we also find that the resulting g_⊥ ≈ 15 is indeed smaller than the value expected from the pure-HH approximation. The reason is that, in fact, the tiny admixtures from the LH bands are not negligible for the g-factors, as illustrated in Figure 4 and described in the following. When the magnetic field is applied along the z axis, the Zeeman split states of lowest energy consist mostly of |−3/2, 1, 1, 0⟩ and |3/2, 1, 1, 0⟩, respectively. It turns out that the corresponding g_⊥ is strongly affected by the couplings

4

because they satisfy |C₊| ≠ |C_–| in the presence of B_z and therefore lead to different LH admixtures in the low-energy eigenstates of the HW (see the Supporting Information). The splitting between the basis states |±1/2, 2, 2, 0⟩ and |±3/2, 1, 1, 0⟩ in our model is predominantly determined by the confinement and can be approximated by Δ = ℏ² π² (4 m_LH^–1 – m_HH)/(2 L_z²) using L_z ≪L_y. From second-order perturbation theory,³⁹ we therefore find that the couplings of eq 4 lead to a correction

5

to the out-of-plane g-factor g_⊥ ≃ 6 κ + 27q/2 + g_C. Eq 5, whose derivation is explained in detail in the Supporting Information, contains the factor 2¹⁷/(81 π⁴) ≃16.6 and, remarkably, depends solely on the three Luttinger parameters γ_1,2,3. With the parameters of Ge, this formula yields g_C ≃ −6.5, which is a substantial reduction of g_⊥ due to orbital effects.^18,43 Of course, H couples |±3/2, 1, 1, 0⟩ not only with |±1/2, 2, 2, 0⟩ but also with other states. However, even when we take a large number of 10⁴ basis states into account (n_y, n_z ≤ 50) and calculate the admixtures to |±3/2, 1, 1, 0⟩ via perturbation theory, we find that the sum of all corrections to g_⊥ is still close to g_C, i.e., eqs 4 and 5 describe the dominant part.

We note that if the HH–LH splitting in our model were dominated by the strain, such that Δ in eq 5 were much greater than the splitting caused by the confinement, the correction to g_⊥ from LH states would be suppressed, and the model Hamiltonian would indeed approach the pure-HH approximation for the low-energy states (see the Supporting Information). Moreover, we found in our calculations that magnetic-field-dependent corrections to the g-factors are negligible given our HW parameters. This is consistent with 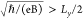for B ≤ 6.5 T, where 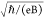is the magnetic length, and agrees well with the experiment (see, e.g., Figure 2o, where the measured Zeeman energy is proportional to the applied magnetic field).

Although the result g_⊥ ≈ 15 from our simple model is already smaller than g_⊥ ≈ 21 from the pure-HH approximation, it is still larger than the measured values. We believe that this remaining deviation is mainly due to the following three reasons. First, given the small height of the HW, the eigenenergies in our model approach or even exceed the valence band offset ∼0.5 eV between Ge and Si,¹⁵ and so the hole wave function will leak into the surrounding Si. This certainly leads to a reduction of g_⊥ because the values of κ in Ge and Si have opposite signs.^38,39 Second, we used here the parameters of bulk Ge for simplicity. However, the strong confinement and the strain change the gaps between the various bands of the semiconductor, which (among other things) may lead to a substantial rescaling of the effective band structure parameters.³⁹ Improvements can be expected from an extended model that also involves the split-off band and the conduction band.^34,43,44 Finally, although our assumption of an infinite HW with a rectangular cross-section is a reasonable approximation for the elongated HW QDs realized here, the details of the confinement (and the strain) along all spatial directions can provide additional corrections. Taking all these elements fully into account is beyond the scope of the present work and requires extensive numerics.

In summary, having analyzed our HW model in detail, we can conclude that it reproduces all the key features of our experimental data and provides useful insight. It predicts a large g-factor anisotropy with g_∥ close to zero and g_∥ ≪g_⊥ < 6κ, as seen in the experiment. The spin projections calculated with our model suggest that the low-energy states of HWs are almost pure HHs and that the tiny admixtures from energetically higher LH states lead to a substantial reduction of g_⊥, which is a consequence of the orbital part of the magnetic-field-coupling. Finally, keeping in mind the finite valence band offset between Ge and Si, a possible explanation for the increasing g_∥ and the decreasing g_⊥ observed experimentally with increasing occupation number is that the confinement caused by the Ge–Si interface becomes less efficient as the eigenenergy of the hole increases (also due to the Coulomb repulsion, which leads to an additional charging energy if more than one hole is present). Hence, a larger occupation number may change the effective aspect ratios of the HW QD experienced by the added hole and, thus, increase its HH–LH mixing.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.6b02715.

• Additional details on finite element simulations of the strain distribution in a HW, matrix representation of the spin operators, calculation with electric fields, couplings, correction g_C to the out-of-plane g-factor, and Hamiltonian for pure heavy holes. A figure showing COMSOL simulations of the out-of-plane and the in-plane strain distribution in a capped HW. (PDF)

The authors declare no competing financial interest.