Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2016 Nov 14.
Published in final edited form as: Nat Nanotechnol. 2015 May 18;10(6):554–562. doi: 10.1038/nnano.2015.88

Vertical nanopillars for in situ probing of nuclear mechanics in adherent cells

Lindsey Hanson 1, Wenting Zhao 2, Hsin-Ya Lou 1, Ziliang Carter Lin 3, Seok Woo Lee 2, Praveen Chowdary 1, Yi Cui 2,4,*, Bianxiao Cui 1,*
PMCID: PMC5108456  NIHMSID: NIHMS820357  PMID: 25984833

Abstract

The mechanical stability and deformability of the cell nucleus are crucial to many biological processes, including migration, proliferation and polarization. In vivo, the cell nucleus is frequently subjected to deformation on a variety of length and time scales, but current techniques for studying nuclear mechanics do not provide access to subnuclear deformation in live functioning cells. Here we introduce arrays of vertical nanopillars as a new method for the in situ study of nuclear deformability and the mechanical coupling between the cell membrane and the nucleus in live cells. Our measurements show that nanopillar-induced nuclear deformation is determined by nuclear stiffness, as well as opposing effects from actin and intermediate filaments. Furthermore, the depth, width and curvature of nuclear deformation can be controlled by varying the geometry of the nanopillar array. Overall, vertical nanopillar arrays constitute a novel approach for non-invasive, subcellular perturbation of nuclear mechanics and mechanotransduction in live cells.

The nucleus is the largest organelle in the cell and a major contributor to the mechanical properties of the cell as a whole1. The mechanical properties of the nucleus and its mechanical coupling to the plasma membrane are crucial to cell behaviours such as migration2, polarization3, proliferation4 and mechanically induced changes in gene expression5. In humans, alterations of nuclear mechanics are implicated in a number of diseases including dilated cardiomyopathy6, Emery–Dreifuss muscular dystrophy7–9 and Hutchinson–Gilford progeria10–12.

Although the importance of nuclear mechanics and mechano-transduction is evident, the means to investigate these properties are limited. The most common techniques for studying nuclear mechanics include micropipette aspiration13,14, atomic force microscopy15, parallel plate compression16 and induced strain on deformable substrates16,17. Although those studies have provided valuable information about nuclear mechanics, the applied forces are transient and only acute responses are measured. A few studies have shown that cell nuclei can change shape in response to confinement by arrays of microposts18–20, to geometrical constraint by micropatterned adhesion molecules5,21 and to cell constriction in microfiuidic channels22. These studies give insight into how cells sense and adapt to their environment under long-term nuclear deformation. However, these deformations are on the scale of several micrometres, and significant nuclear deformation is observed mostly in cancerous cells with large, deformable nuclei. In vivo, nuclei also exhibit deformations on a much smaller scale, even around a single collagen fibre23. Furthermore, nuclei derived from patients with Hutchinson–Gilford progeria or lamin A deficiency often show lobulation on the scale of just hundreds of nanometres11,24.

Recent advances in nanotechnology have led to the burgeoning field of nanobiotechnology. Vertical nanopillars or nanowires have been found to support long-term cell culture25 and thus have emerged as a unique platform for probing live cells. Adherent cells engulf nanopillars with a variety of aspect ratios25–29, and the tight membrane–nanopillar attachment affords highly sensitive nanopillar-based electrical30,31 and optical32 sensors. We hypothesize that the nanopillar-induced membrane deformation can be communicated by the cytoskeleton to induce nuclear deformation (Fig. 1a). In this case, the forces involved are generated by the cell itself, and highly localized deformation can be induced inside an intact cell. Indeed, as we show in the following section, vertical nanopillars induce significant nuclear deformation in a variety of cell types. The extent of deformation can be precisely controlled by the geometry of the nanopillar array. Quantitative analysis and modelling demonstrate that the forces originate from the combination of a perinuclear actin cap on top of the nucleus and local accumulation of actin around the nanopillars.

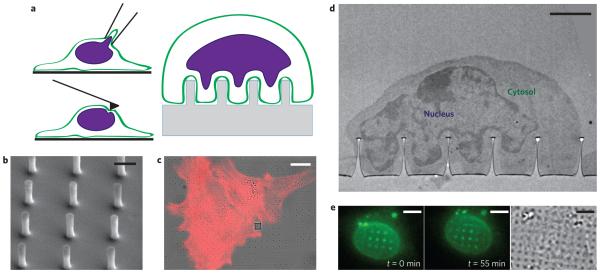
Figure 1. The nuclear envelope deforms around nanopillars, creating a non-invasive platform for studying in situ nuclear deformation.

Figure 1

Open in a new tab

a, Illustrations of techniques for studying nuclear mechanics. Anticlockwise from top left: micropipette aspiration, atomic force microscopy and nanopillar arrays. b, SEM image of nanopillar array with 75 nm radius, 2 μm pitch and 1.4 μm height. Scale bar, 1 μm. c, Overlay of differential interference contrast (DIC) and fluorescence images of 3T3 cells cultured on a nanopillar array. The red colour shows actin staining, and nanopillars are visible as dark spots in the bright-field image. The grey square in the DIC image is an alignment marker used to locate the nanopillar arrays. Scale bar, 10 μm. d, TEM image showing the nucleus deformed around a nanopillar array with the cytosol visible between the nuclear envelope and the cell membrane. Scale bar, 2 μm. e, Fluorescence (left and middle, different time points) and DIC (right) images of a live 3T3 cell transfected with GFP-Sun2. Nuclear deformation is evident as bright fluorescent spots around the nanopillars and changes as the cell migrates. See Supplementary Movies 1 and 2 for complete time lapse of nuclear deformation during cell migration. Scale bars, 5 μm.

Characterization of nanopillar-induced nuclear deformation

Our substrates consist of regular arrays of vertical quartz nanopillars, fabricated on quartz coverslips by electron-beam lithography and subsequent anisotropic reactive ion etching (see Methods for fabrication details). As such, the fabrication process affords precise control over the nanopillar radius, the centre-to-centre distance (pitch) between nanopillars, and the height of the nanopillars. The dimensions of the nanopillars were verified by scanning electron microscopy (SEM) before use in culture (Fig. 1b, see Supplementary Fig. 1 for more examples). In the following studies, the nanopillar radius was varied from 50 nm to 350 nm, the pitch from 2 μm to 10 μm and the height from 700 nm to 2 μm. Each nanopillar array covers a 100 μm × 100 μm area and consists of 100–2,500 nanopillars, all with the same geometric parameters.

In agreement with previous studies, NIH3T3 fibroblast cells spread on the nanopillar substrate (Fig. 1c). On closer examination by transmission electron microscopy (TEM), the plasma membrane is seen to have deformed to conform to the surface of each nanopillar (Fig. 1d), in agreement with previous observations26. Interestingly, not only does the cell membrane deform around the nanopillars, but the membrane deformation results in significant nuclear deformation (see Fig. 1d, where the darkly stained nucleus of a cortical neuron can be seen deformed vertically at each nanopillar).

To rule out the possibility that the observed nuclear deformation under TEM is an artefact of the fixation process, we used live-cell imaging to confirm nanopillar-induced nuclear deformation. We transfected 3T3 cells with GFP-Sun2, an inner nuclear membrane protein important for nuclear–cytoplasmic connections33, to illuminate the nuclear envelope. Nuclear deformation around the nanopillars was evident in conventional fluorescence imaging as bright spots or rings, which result from the projection of the vertically pinched nuclear envelope onto the camera. Live imaging also reveals the dynamic nature of nuclear deformation during cell migration, during which the new deformations appear or disappear as the cell moves around the substrate (Fig. 1e). The dynamic nature of the nuclear deformation can be seen more clearly in Supplementary Movies 1–4.

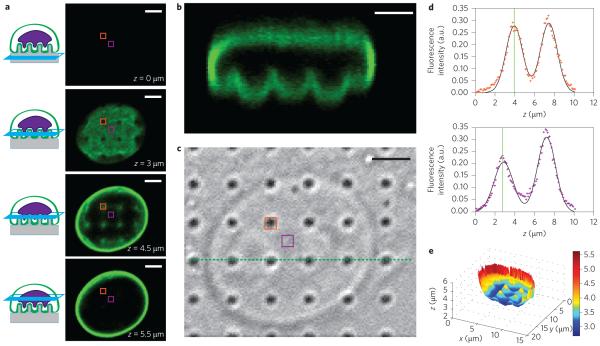
For a quantitative analysis of the nuclear deformation around nanopillars we reconstructed the topology of the nucleus using confocal fluorescence microscopy. NIH3T3 cells cultured on nanopillars were fixed and immunolabelled with anti-lamin A (Fig. 2) to reveal the shape of the nuclear envelope. In a three-dimensional confocal scan, the nuclear envelope does not appear in a single optical section (Fig. 2a). Rather, the nuclear envelope above each nanopillar is further from the surface than in neighbouring pixels. The deformation of the nucleus at the nanopillar locations is clearly visible in a side-view reconstruction (Fig. 2b), in which the deformed locations align precisely with the nanopillar locations (as shown in a differential interference contrast (DIC) image of the same field, Fig. 2c). Most cells exhibit well-resolved pinches in the nucleus over each nanopillar, and a few exhibit trenches in the nucleus along a row or column of nanopillars (Supplementary Fig. 3).

Figure 2. Quantitative analysis of nanopillar-induced nuclear deformation.

Figure 2

Open in a new tab

a, Immunostaining of lamin A reveals nuclear deformation in confocal microscopy. Four optical z slices are shown, beginning from the basal surface of the cell. b, Reconstructed side view of the confocal scan from a. The pinches above each nanopillar in a row are visible (corresponding to the green dotted line in c). c, Corresponding DIC image showing the locations of the nanopillars. d, The z position of the nuclear envelope can be localized precisely by fitting two Gaussian functions to the confocal z scan of the fluorescence signal at each pixel. Top panel: Confocal z scan of the fluorescence signal for a pixel on top of a nanopillar (location indicated by orange boxes in a and c). Bottom panel: Confocal z scan of the fluorescence signal for a pixel between nanopillars (location indicated by purple boxes in a and c). The fitted z positions of the basal nuclear envelope are illustrated by vertical green lines and the difference between the two z positions of the two pixels is evident. e, Nanopillar-induced nuclear deformation is clear in a reconstructed surface of the basal nuclear envelope. The value at each pixel is the height of the nuclear envelope, calculated as the centre of a Gaussian fit to the confocal z scan at that pixel. The nanopillars in this example have the following dimensions: 300 nm radius, 3 μm pitch and 2 μm height. Scale bars, 3 μm.

To overcome the intrinsic axial diffraction limit of confocal microscopy, we calculated the height of the nuclear envelope at each pixel, with 60 nm accuracy. For each pixel, a one-dimensional scan through z shows two peaks in the fluorescence intensity (Fig. 2d), which correspond to the nuclear envelope at the bottom and top of the nucleus, respectively. Each of the two peaks was fitted with a Gaussian function to determine the centre location with much higher accuracy34. The localization accuracy was determined to be ~60 nm by calculating the z position of a fluorescently labelled supported lipid bilayer (Supplementary Methods and Supplementary Fig. 4). After fitting the z location for every pixel of the image, a three-dimensional surface of the nuclear envelope was then reconstructed. The topology clearly shows the deformation of the nuclear envelope at the locations of the pillars (Fig. 2e). Reconstruction of the three-dimensional surface of the nuclear envelope could also be achieved in live cells transfected with GFP-lamin A or GFP-Sun2 (Supplementary Fig. 2). While nuclear deformation is evident in live cells, overexpression of lamin A alters the mechanical properties of the nucleus, as we show in the next section, and fluorescent proteins also create a higher fluorescent background. As a result, for the remainder of this work we use fixed and immunostained cells to fully characterize and quantify nanopillar-induced nuclear deformation.

Nuclear stiffness affects deformation depth

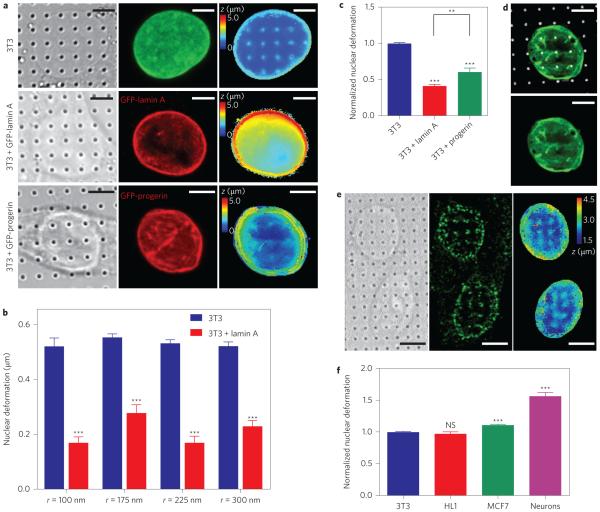
We expect that nanopillar-induced nuclear deformation depends on the mechanical properties of the nucleus. To test this hypothesis we quantitatively measured nanopillar-induced nuclear deformation in nuclei of different stiffnesses. First, the nuclear stiffness was increased by transfecting 3T3 cells with a plasmid encoding GFP-lamin A under a high-expression promoter, which caused a 50–90% increase in the total lamin A level compared with non-transfected cells (Supplementary Fig. 5). Lamins make up the filamentous network underlying the inner nuclear membrane, and recent studies have shown that the levels of expression of lamin A scale with tissue and nuclear stiffness35. Figure 3a presents examples of a non-transfected 3T3 cell, as well as a 3T3 cell transfected with GFP-lamin A (revealed by anti-lamin A and anti-GFP immunostaining; middle column in Fig. 3a). The calculated surface of the nuclear envelope (right column in Fig. 3a) reveals much less nuclear deformation in the transfected cell. This behaviour was also confirmed by a population analysis of 168 nanopillars with four different radii, all of which showed a significant decrease in nanopillar-induced nuclear deformation in transfected versus non-transfected 3T3 cells (Fig. 3b). This result confirms that nanopillar-induced nuclear deformation decreases in stiffer nuclei. Note that there is no statistical difference in the size of the nuclei of 3T3 cells and 3T3 cells transfected with lamin A (Supplementary Fig. 5). Statistics regarding the number of nanopillars and the number of nuclei used for these and subsequent analyses are listed in Supplementary Table 1.

Figure 3. Nanopillar-induced nuclear deformation shows a strong dependence on nuclear stiffness.

Figure 3

Open in a new tab

a, Reconstructed surfaces of the nuclear envelope reveal differences in the deformability of an untransfected 3T3 cell (top), a GFP-lamin A-transfected 3T3 cell (middle) and a GFP-progerin-transfected 3T3 cell (bottom). The locations of the nanopillars were identified by DIC imaging (left column) and the nuclear envelope was visualized by fixing the cells and immunostaining with anti-lamin A (untransfected cells, green) or anti-GFP (transfected cells, red) antibodies (middle column). The surface of the nuclear envelope (right column, false-coloured in z position) is visibly deformed at nanopillars in the untransfected cell but less so in GFP-progerin-transfected and GFP-lamin A-transfected cells. b, Average nuclear deformation, consistently showing less deformation for lamin A-transfected cells than for untransfected 3T3 cells for all nanopillar geometries tested. Nanopillars with four different radii are shown, but with the same pitch of 3 μm and height of 1.4 μm. c, When normalized to untransfected 3T3 cells on the same geometry, 3T3 cells transfected with lamin A and progerin cells show much less deformation than untransfected cells. Interestingly, progerin-transfected cells show more deformation than lamin A-transfected cells. d, GFP-progerin-transfected 3T3 cell shows characteristic folds in the nuclear lamina (green). These folds align with nanopillar locations (false-coloured white) at the basal nuclear envelope. e, Representative images of hippocampal neurons show significant nuclear deformation on nanopillars. Left: DIC image showing pillar locations. Middle: Immunostaining image with anti-nuclear pore complex illustrating nuclear envelope. Right: Reconstructed z surface of nuclear envelope (false coloured in z) showing that the nuclear envelope is deformed at nanopillar locations. f, Average nuclear deformation in different cell types, normalized to 3T3 cells on the same geometry. HL1 and 3T3 cells are equally deformable, while MCF7 cells show more deformation. Neurons show significantly more deformation than any of the other cell types. All measurements were performed in triplicate. The numbers of nanopillars and nuclei included in each sample are provided in Supplementary Table 1. Comparisons were analysed with two-tailed, unequal variance student t-tests, corrected for multiple comparisons where necessary (c). **P < 0.01, ***P < 0.001. NS, no significant difference. Error bars indicate standard error of the mean. Scale bars, 5 μm.

We also measured nanopillar-induced nuclear deformation in 3T3 cells transfected with a mutant form of lamin A called progerin36. Progerin causes the rapid-ageing disease Hutchinson– Gilford progeria37–39, and cells expressing progerin exhibit misshapen nuclei. Previous measurements with micropipette aspiration report stiffer nuclei in cells expressing progerin40, which suggests there will be less nanopillar-induced nuclear deformation in progerin-transfected cells than in wild-type lamin A-transfected cells. As we show in later sections, nanopillar-induced nuclear deformation depends on the dimension of the nanopillars. To compare the average behaviour, the nuclear deformation in each population (untransfected 3T3 cells, 3T3 cells transfected with GFP-lamin A, and 3T3 cells transfected with GFP-progerin) was normalized to the average deformation of untransfected 3T3 cells on the same nanopillar geometry. Surprisingly, although progerin-transfected cells exhibited significantly less deformation than untransfected cells, they deformed significantly more (P = 0.002) than cells transfected with wild-type lamin A (60% versus 40% of untransfected cells) (Fig. 3a). This is in spite of a slight reduction in nuclear size after transfection with GFP-progerin (Supplementary Fig. 5).

In our observations, the nuclear grooves common to progerin-expressing nuclei40 are often aligned to the locations of the nanopillars (Fig. 3d). Supported by a recent report that progerin-expressing nuclei more easily distorted during migration41, our results imply that some compensatory mechanisms unique to intact cells can result in more nuclear deformation despite the more rigid nuclei. This measurement both highlights the advantages of the nanopillar platform for studying nuclear deformation in the context of intact cells and warrants further investigation into the precise nature of the compensation.

In addition to the ability to test different proteins in the same cellular contexts, nanopillars enable us to quantify nuclear deformation in a variety of cell types, both primary and immortalized. This was first tested using primary hippocampal neurons, which were expected to be soft given that brain is one of the softest tissues in the mammalian anatomy35. Statistical analysis shows that neurons indeed exhibit significantly larger nuclear deformation, an increase of over 50% compared to untransfected 3T3 cells (Fig. 3f). We also tested nanopillar-induced nuclear deformation in other cell types, including HL1 cardiomyocytes42 and MCF7 cancer cells. Although HL1 cells exhibit similar deformation to 3T3 cells, MCF7 cells show about 10% more deformation (Fig. 3f). These tests establish the versatility of nanopillar-induced nuclear deformation as a method for studying nuclear deformability in a variety of cell types.

Cytoskeletal filaments distinctly affect nuclear deformation

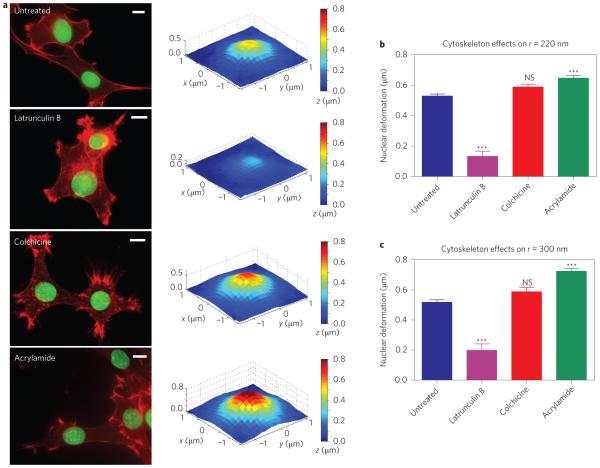
The nanopillar platform affords a unique way to investigate the roles of different cytoskeletal components in the mechanical coupling between the nuclear envelope and the cell membrane. For this purpose, we measured the extent of nuclear deformation in 3T3 cells treated with small molecular drugs to depolymerize actin filaments, microtubules or intermediate filaments. In the following experiments, nanopillars were used that had a pitch of 3 μm, height of 1.4 μm and radius of 220 nm or 300 nm. These geometries induce an intermediate amount of nuclear deformation, so either an increase or decrease in deformation can be observed. Compared with untreated cells, actin depolymerization with low-dose latrunculin B (LatB) drastically decreased the extent of nuclear deformation, while the cell membrane remained spread on the substrate (Fig. 4a). Statistical analysis showed a drastic reduction in nuclear deformation for latrunculin B-treated versus untreated cells for nanopillars with radii of either 220 nm (Fig. 4b) or 300 nm (Fig. 4c). This result was corroborated by treatment with another actin inhibitor, cytochalasin D (Supplementary Fig. 6). Taken together, these measurements confirm the central role of actin in mechanical coupling between the nuclear envelope and the cell membrane43,44.

Figure 4. Nanopillar-induced nuclear deformation depends on the integrity of cytoskeletal components.

Figure 4

Open in a new tab

a, Latrunculin B treatment results in decreased nuclear deformation, whereas acrylamide treatment shows increased nuclear deformation compared with untreated cells. Colchicine did not alter the extent of nuclear deformation. Left column: Fluorescence images showing cell morphology without treatment and under treatment with different cytoskeletal inhibitors: latrunculin B for actin filaments, colchicine for microtubules, and acrylamide for intermediate filaments. Actin was stained with phalloidin-Alexa568 (red) and the nuclear envelope was immunostained for lamin A (green). Scale bars, 10 μm. Right column: Surface plots showing average deformed nuclear surfaces under the different inhibitor treatments. b,c, The change in the depth of nuclear deformation showed the same response to inhibitor treatments on nanopillars with radii of 220 nm (b) and 300 nm (c). All measurements were performed in triplicate. The numbers of nanopillars and nuclei included in each sample are provided in Supplementary Table 1. One-way analysis of variance (ANOVA) was performed on the results in b and c, comparing each group to the untreated cells. NS, no significant difference. ***P < 0.001. Error bars indicate standard error of the mean.

The role of microtubules in mechanical relay between the nucleus and cell membrane is more complex. When cells were treated with 1 μM colchicine for 10 min to depolymerize the microtubules45, the extent of nuclear deformation was not significantly different from that in untreated cells on nanopillars with radii of 220 nm (Fig. 4b) or 300 nm (Fig. 4c). On the other hand, when the duration of colchicine treatment was increased to 1 h, the extent of nuclear deformation was significantly decreased. High-dose colchicine treatment also disrupted actin filaments, as shown by immunostaining (Supplementary Fig. 7). As such, the decrease in nuclear deformation by longer colchicine treatment may be mediated by the loss of actin rather than directly by microtubule depolymerization.

Interestingly, depolymerization of intermediate filaments with acrylamide caused an increase in nuclear deformation around the nanopillars. Following 1 h treatment with 4 mM acrylamide to depolymerize intermediate filaments, nanopillar-induced nuclear deformation increased significantly when measured on nanopillars with radii of 220 nm (Fig. 4b) and 300 nm (Fig. 4c). The actin structure after acrylamide treatment was unchanged compared to wildtype cells (Fig. 4a). Our results suggest that the actomyosin network provides the contractile force pulling the nucleus towards the cell membrane, and intermediate filaments serve to balance it. This result agrees with previous tensegrity models, in which intermediate filaments serve as tension-bearing cables that stabilize the nucleus46–48; that is, intermediate filaments provide mechanical resistance against the deformation arising from actin. This picture is also in line with previous studies on the lateral forces on the nucleus in micropatterned substrates21, but has not been previously shown in the normal direction.

Nuclear deformation depends on nanopillar array geometry

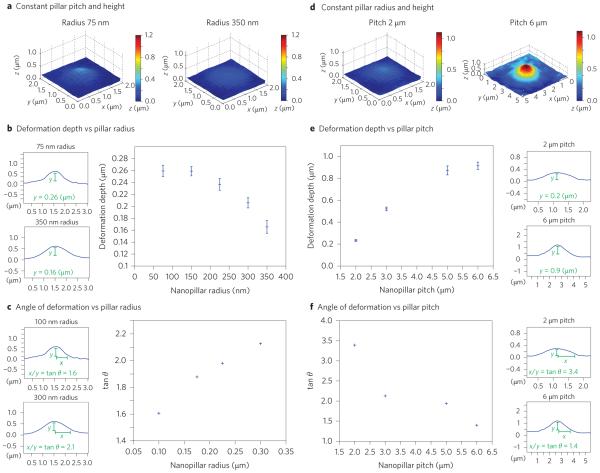
In addition to probing nuclear and cytoskeletal stiffness, nanopillar-induced nuclear deformation affords precise control over the depth, width and angle of indentations in the nucleus. We investigated this control by systematically varying the radius, pitch and height of the nanopillar array. We first quantified how the depth, width and angle of nanopillar-induced nuclear deformation depend on the nanopillar radius. In a series of experiments, nanopillar radius was varied from 75 nm to 150 nm, 230 nm, 300 nm and 350 nm, with the height of 1.4 μm and pitch of 2 μm held constant. Figure 5a shows that the average nuclear deformation decreased from 0.26 μm with a 75 nm radius to 0.16 μm with 350 nm radius. The trend that a larger-radius nanopillar induces smaller deformation depth is clearly evident in the plot of deformation depth versus radius in Fig. 5b. (For representative confocal fluorescence images see Supplementary Fig. 8.) Furthermore, we observed that the width of the induced nuclear deformation increased with the nanopillar radius (Supplementary Fig. 9). This resulted in an increase in the deformation angle (defined as tan θ = deformation width/deformation depth) with increasing nanopillar radius (Fig. 5c).

Figure 5. Nanopillar geometry determines the depth and shape of nuclear deformation.

Figure 5

Open in a new tab

a, At constant pitch, larger radii induce shallower, broader deformation. Reconstructed surfaces show the average deformation on nanopillar arrays with constant height (1.4 μm) and pitch (2 μm) but different radii: 75 nm (left) and 350 nm (right). b, The depth of deformation decreases with increasing nanopillar radius. The large plot shows the average depth of nuclear deformation versus nanopillar radius. The two small plots to the left show the profile through the centre of the indentation on 75 nm (top) and 350 nm (bottom) nanopillars, with the depth indicated. Height (1.4 μm) and pitch (2 μm) were held constant for all data points. c, The angle of deformation increases with nanopillar radius. The large plot shows the average angle of nuclear deformation versus nanopillar radius. The two small plots show the nuclear profile on 100 nm (top) and 300 nm (bottom) nanopillars, with the angle measurement indicated. Height (1.4 μm) and pitch (3 μm) were held constant for all data points. d, With the same radius, nanopillar arrays with larger pitch induce deeper, narrower deformation. Reconstructed surface showing average deformation on nanopillar arrays with constant height (1.4 μm) and radius (300 nm) but different pitch: 2 μm (left) and 6 μm (right). e, The depth of deformation increases with increasing pitch. The large plot shows average depth of nuclear deformation versus nanopillar pitch. The two small plots to the right show the nuclear profile for 2 μm (top) and 6 μm (bottom) pitch. f, The angle of deformation decreases with increasing pitch. The large plot shows the average angle of nuclear deformation versus nanopillar pitch. The two small plots show the nuclear profile for 2 μm (top) and 6 μm (bottom) pitch. Height (1.4 μm) and radius (300 nm) were held constant for all data points in e and f. The numbers of nanopillars and nuclei included in each sample are provided in Supplementary Table 1. Error bars indicate standard error of the mean.

Surprisingly, we found that the pitch of the nanopillar array has a much stronger effect on nuclear deformation than the nanopillar radius. In another series of experiments, the distance between nanopillars was varied from 2 μm to 3 μm, 5 μm and 6 μm, while keeping the nanopillar radius at 300 nm and the nanopillar height at 1.4 μm. The averaged nuclear deformation profiles shown in Fig. 5d show that the deformation is drastically increased four times from 0.23 μm to 0.95 μm as the pitch is increased from 2 μm to 6 μm (Fig. 5d,e). On the other hand, the deformation angle decreased significantly with pitch (Fig. 5f). The smaller plots in Fig. 5b,c,e,f are experimental measurements of the deformation profile in the z direction with various nanopillar dimensions.

Finally, we found that the height of the nanopillars has a moderate effect on nuclear deformation. The depth of nuclear deformation increased from 0.26 μm on 1.4-μm-tall nanopillars to 0.29 μm on 2-μm-tall nanopillars, while keeping the nanopillar radius at 150 nm and the pitch at 2 μm (Supplementary Fig. 10). Similarly, an increase in nanopillar height from 1.4 μm to 2 μm caused a slight increase in nuclear deformation from 0.52 μm to 0.53 μm for nanopillars with 100 nm radius at 3 μm pitch.

Model of nanopillar-induced nuclear deformation

To gain deeper insight into nanopillar-induced nuclear deformation, we performed finite-element analysis of nuclear deformation when pressed onto nanopillar arrays. The nucleus was treated as a soft nucleoplasm surrounded by a stiffer nuclear envelope and lamina using previously reported values49 for the Young’s modulus of the nucleoplasm and the bending stiffness of the nuclear envelope and nuclear lamina (values are shown in Supplementary Table 2). Details of the modelling can be found in the Supplementary Information.

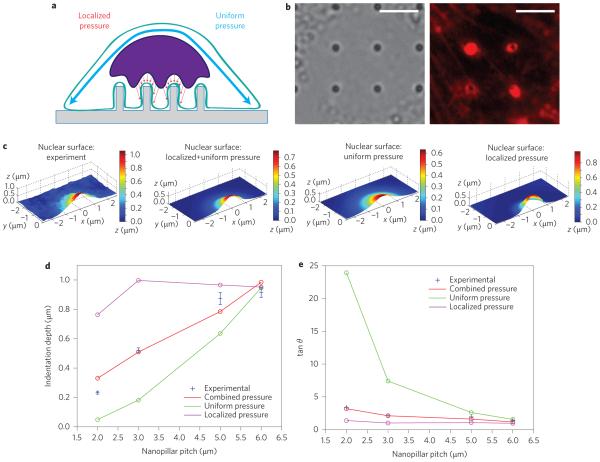
The force acting on the nucleus could come from the perinuclear actin cap or the actin underneath the nucleus. The actin cap, a subset of actin stress fibres that pass over the top of the nucleus44,50, results in a uniform pressure pushing the nucleus towards the substrate (Fig. 6a). On the other hand, the actin underneath the nucleus is observed to accumulate around the nanopillars (Fig. 6b), yielding a localized pressure on the nucleus nearest each nanopillar (Fig. 6a). To model localized pressure, we applied pressure with a Gaussian profile centred at the nanopillar, the width of which was chosen to match that observed in fluorescence actin staining around the nanopillars (Supplementary Fig. 11). In our simulation, the nucleus was subjected to either uniform pressure (from the actin cap alone), localized pressure (from the actin accumulated around the nanopillar alone) or a combination of the two. (See Methods for simulation details.)

Figure 6. Finite-element analysis suggests that nanopillar-induced deformation is a cumulative result of both the actin cap above the nucleus and actin accumulated around the nanopillar.

Figure 6

Open in a new tab

a, Illustration of the mechanical model, in which the force pulling the nucleus toward the nanopillars can either be uniformly applied to the apical surface of the nucleus, locally applied around the nanopillar, or a combination of the two. b, Local actin accumulation around nanopillars. Left: Bright-field image showing nanopillar locations. Right: Fluorescence image of actin staining showing bright rings around nanopillars with 300 nm radii. Scale bars, 5 μm. c, Nuclear deformation surfaces display the differential effects of applied pressure profiles. From left to right: experimental surface; simulated surface under combined uniform and localized pressure; simulated surface under uniform pressure only; simulated surface under localized pressure only. d, Of the simulated pressure profiles, the combined uniform and localized pressure most closely reproduces the experimental dependence of nuclear deformation depth on nanopillar pitch. e, Experimental measurements of the deformation angle, shown in blue, match the results from combined pressure more closely than those from either localized or uniform pressure alone.

In response to either uniform pressure, localized pressure or the combination of the two, an indentation was formed around the nanopillar. The general shape of the deformations is similar to the experimental deformation. However, at the same pitch, uniform pressure results in a wider indentation and localized pressure in a narrower indentation than the experimental observation (Fig. 6c). More importantly, the depth of nuclear deformation under uniform pressure scales with the projected area of the nucleus over each nanopillar, which results in a quadratic dependence on nanopillar pitch (green line in Fig. 6d). This dependence is much stronger than that observed in the experiments (blue dots in Fig. 6d). In addition, the angle of the deformation from uniform pressure is much larger than observed in the experiments, especially at smaller pitch (Fig. 6e). On the other hand, the nuclear deformation under localized pressure around nanopillars is, as expected, relatively independent of nanopillar pitch greater than 3 μm (purple line in Fig. 6d). The angle of deformation is also smaller than observed in the experiments at every pitch tested (Fig. 6e).

In the final approach we applied a combination of uniform pressure and localized pressure. The combined uniform and localized pressure recapitulated both the dependence of the deformation depth (Fig. 6d) and the deformation angle (Fig. 6e) on nanopillar pitch. With this combination, the force due to localized pressure is independent of the pitch, while the force due to the uniform pressure increases with the square of the pitch. Thus, while at the smallest pitch (2 μm) the force is dominated by localized pressure, the relative contribution of the uniform pressure increases at larger pitches. These results strongly support the model in which nanopillar-induced deformation is a cumulative result of both a uniform pressure from the actin cap above the nucleus and a localized pressure from the actin accumulated around the nanopillar.

Discussion

Nanopillar arrays provide a new and exciting opportunity to probe cellular mechanics through the lens of the forces that cells apply on themselves. In this work we have shown that nanopillars impose drastic subcellular nuclear deformation, the extent of which is dependent on the stiffness of the nucleus, the geometry of the nanopillars, and the strength of the cytoskeleton. Specifically, we have shown that actin provides most of the force pulling the nucleus onto the nanopillars, while intermediate filaments resist deformation of the nucleus. Furthermore, our results indicate that the depth, width and curvature of nuclear deformation can be finely tuned by varying the geometry of the nanopillar array. As a result of this tight, subcellular control, nanopillar arrays comprise a unique platform for future studies in nuclear mechanotransduction and the effect of local nuclear deformation on cell behaviour and gene expression.

Methods

Nanopillar fabrication

The nanopillars were fabricated on square quartz coverslips by reactive ion etching with an electron-beam patterned mask. The coverslips were first spin-coated with 300 nm of polymethylmethacrylate (PMMA), followed by a thin conductive layer of Espacer. The PMMA was patterned by electron-beam lithography (Raith) and developed in 3:1 isopropanol:methylisobutylketone. The mask was then formed by sputter deposition of 100 nm Cr, followed by lift-off with acetone. Afterwards, the quartz chip with patterned Cr mask was subjected to reactive ion etching with O2 and CHF3 chemistry. The substrate was then cleaned in O2 plasma for 5 min and sputter coated with 3 nm Cr for SEM imaging to measure the dimensions of the nanopillar array. Before cell culture, the Cr was removed by wet etching in 9% acetic acid plus 22% ceric ammonium nitrate in water. The substrate was cleaned again in O2 plasma, sterilized in ethanol and coated overnight in 0.2 mg ml−1 poly-l-lysine.

Calculation of nucleus deformation

Custom-written Matlab software was used to find the height of the nuclear envelope with 60 nm accuracy. For this purpose we scanned the nucleus with a small aperture (100 μm) in closely spaced z slices (0.1 μm/slice) to give 101 images per nucleus. Confocal stacks of fluorescence images of the nuclear envelope were parsed into individual z-vectors at each pixel. Each vector was then fit to the sum of two Gaussian functions, one corresponding to the basal side of the nuclear envelope (closer to the substrate) and the other to the apical side. The centre locations of the basal peaks were plotted to represent the surface of the nucleus closest to the nanopillar substrate. The nanopillar locations were established using DIC, and a square window was defined centred at each nanopillar, the width of which was the pitch of that nanopillar array. For the average nuclear deformation, the depth of the indentation was calculated for each nanopillar as the difference in z between the centre pixel above each nanopillar and the pixels at the border of the window. To see the shape of the deformation, the nuclear surface was averaged over the windows of all nanopillars of a given geometry. The angle of deformation θ was calculated by measuring the depth and width of the average indentation profile.

For a comparison of different populations (cell types, transfection and cytoskeletal inhibitors), statistical analysis was performed in GraphPad Prism 6.04 for Windows. Individual t-tests were used to compare each pair in Fig. 3b. One-way ANOVA with Tukey’s post test to correct for multiple comparisons was used to compare the transfected wild-type lamin A and progerin populations with the untransfected cells, as well as with each other. All other reported P values were assessed with one-way ANOVA with Dunnett’s post test to compare each test individually with untreated 3T3 cells.

Because of the low levels of lamin A, neurons were immunostained with antinuclear pore complex to label the nuclear envelope. The signal intensity of the nuclear pore complex staining was highly heterogeneous due to the punctate nature of the label. Thus, each confocal stack was thresholded at 200 photons and the pixels below the threshold in each z-slice were replaced with the median value of the surrounding 9 × 9 pixel window. The resulting smoothed stack was then analysed as above.

Cytoskeleton inhibitors

NIH 3T3 cells were cultured on the nanopillar substrates for 2 days before treatment with cytoskeletal inhibitors. Actin was depolymerized by treatment with 100 nM Latrunculin B for 1 h at 37 °C. Microtubules were depolymerized with 1 μM colchicine (from 10 mM stock solution in water) in culture medium for 10 min at 37 °C. Intermediate filaments were depolymerized with 4 mM acrylamide (from 4 M stock solution in water) in culture medium for 1 h at 37 °C, as previously reported21. Following drug treatments, cells were washed three times with PBS at 37 °C, fixed, and immunostained for imaging as noted above.

Mechanical simulations

Finite-element analysis of the mechanical models was performed in COMSOL Multiphysics. The basic structure was the cell nucleus on top of a single cylindrical nanopillar, with periodic boundary conditions at the edges of a square centred at the nanopillar. The size of the square was determined by the pitch of the array being simulated and the boundary conditions required that the nuclear envelope remain parallel to the substrate at the edge of the square. The cytoplasm between the nucleus and the nanopillar was added as a soft cap atop the nanopillar. The nucleus was modeled as a soft nucleoplasm, 5 μm thick, bordered by the stiffer nuclear envelope, the mechanical properties of which were calculated to include both the inner and outer nuclear envelope and the nuclear lamina, as previously reported49. See Supplementary Table 2 for the mechanical properties used for each component.

Supplementary Material

Movie1
Download video file (140.4KB, avi)
Movie2
Download video file (508.1KB, avi)
Movie3
Download video file (2.8MB, avi)
Movie4
Download video file (324.7KB, avi)
SupplFigure

Acknowledgements

This work was supported by the National Science Foundation (award no. 1055112 and 1344302), the National Institutes of Health (grant no. DP2NS082125), a Searle Scholar award, a Packard Science and Engineering Fellowship (to B.C.) and a National Defense Science and Engineering Graduate Fellowship (to Z.L.). The authors thank H. Worman at Columbia University for providing the GFP-Sun2 plasmid. The authors thank M. Lin at Stanford University for helping with the confocol microscope.

Footnotes

Author contributions

L.H., B.C. and Y.C. designed experiments. L.H., W.Z., H.L. and Z.L. carried out the experiments. L.H. and S.W.L. designed and carried out the simulations. L.H. and P.C. designed and carried out the data analysis. All authors contributed to scientific planning, discussions and writing of the manuscript.

Additional information

Supplementary information is available in the online version of the paper. Reprints and permissions information is available online at www.nature.com/reprints. Correspondence and requests for materials should be addressed to Y.C. and B.C.

Competing financial interests

The authors declare no competing financial interests.

References

  • 1.Caille N, Thoumine O, Tardy Y, Meister J-J. Contribution of the nucleus to the mechanical properties of endothelial cells. J. Biomech. 2002;35:177–187. doi: 10.1016/s0021-9290(01)00201-9. [DOI] [PubMed] [Google Scholar]
  • 2.Khatau SB, et al. The distinct roles of the nucleus and nucleus–cytoskeleton connections in three-dimensional cell migration. Sci. Rep. 2012;2:488. doi: 10.1038/srep00488. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Lee JSH, et al. Nuclear lamin A/C deficiency induces defects in cell mechanics, polarization, and migration. Biophys. J. 2007;93:2542–2552. doi: 10.1529/biophysj.106.102426. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Roca-Cusachs P, et al. Micropatterning of single endothelial cell shape reveals a tight coupling between nuclear volume in G1 and proliferation. Biophys. J. 2008;94:4984–4995. doi: 10.1529/biophysj.107.116863. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Jain N, Iyer KV, Kumar A, Shivashankar GV. Cell geometric constraints induce modular gene-expression patterns via redistribution of HDAC3 regulated by actomyosin contractility. Proc. Natl Acad. Sci. USA. 2013;110:11349–11354. doi: 10.1073/pnas.1300801110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Taylor MR, et al. Natural history of dilated cardiomyopathy due to lamin A/C gene mutations. J. Am. Coll. Cardiol. 2003;41:771–780. doi: 10.1016/s0735-1097(02)02954-6. [DOI] [PubMed] [Google Scholar]
  • 7.Méjat A, et al. Lamin A/C-mediated neuromuscular junction defects in Emery– Dreifuss muscular dystrophy. J. Cell Biol. 2009;184:31–44. doi: 10.1083/jcb.200811035. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Rowat AC, Lammerding J, Ipsen JH. Mechanical properties of the cell nucleus and the effect of emerin deficiency. Biophys. J. 2006;91:4649–4664. doi: 10.1529/biophysj.106.086454. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Lammerding J, et al. Abnormal nuclear shape and impaired mechanotransduction in emerin-deficient cells. J. Cell Biol. 2005;170:781–791. doi: 10.1083/jcb.200502148. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Hale CM, et al. Dysfunctional connections between the nucleus and the actin and microtubule networks in laminopathic models. Biophys. J. 2008;95:5462–5475. doi: 10.1529/biophysj.108.139428. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Goldman RD, et al. Accumulation of mutant lamin A causes progressive changes in nuclear architecture in Hutchinson–Gilford progeria syndrome. Proc. Natl Acad. Sci. USA. 2004;101:8963–8968. doi: 10.1073/pnas.0402943101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Yang SH, et al. Eliminating the synthesis of mature lamin A reduces disease phenotypes in mice carrying a Hutchinson–Gilford progeria syndrome allele. J. Biol. Chem. 2008;283:7094–7099. doi: 10.1074/jbc.M708138200. [DOI] [PubMed] [Google Scholar]
  • 13.Ivanovska I, Swift J, Harada T, Pajerowski JD, Discher DE. Physical plasticity of the nucleus and its manipulation. Methods Cell Biol. 2010;98:207–220. doi: 10.1016/S0091-679X(10)98009-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Guilak F, Tedrow JR, Burgkart R. Viscoelastic properties of the cell nucleus. Biochem. Biophys. Res. Commun. 2000;269:781–786. doi: 10.1006/bbrc.2000.2360. [DOI] [PubMed] [Google Scholar]
  • 15.Dahl KN, Engler AJ, Pajerowski JD, Discher DE. Power-law rheology of isolated nuclei with deformation mapping of nuclear substructures. Biophys. J. 2005;89:2855–2864. doi: 10.1529/biophysj.105.062554. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Lombardi ML, Lammerding J. Altered mechanical properties of the nucleus in disease. Methods Cell Biol. 2010;98:121–141. doi: 10.1016/S0091-679X(10)98006-0. [DOI] [PubMed] [Google Scholar]
  • 17.Lammerding J, Lee RT. Mechanical properties of interphase nuclei probed by cellular strain application. Methods Mol. Biol. 2009;464:13–26. doi: 10.1007/978-1-60327-461-6_2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Davidson PM, Özçelik H, Hasirci V, Reiter G, Anselme K. Microstructured surfaces cause severe but non-detrimental deformation of the cell nucleus. Adv. Mater. 2009;21:3586–3590. [Google Scholar]
  • 19.Badique F, et al. Directing nuclear deformation on micropillared surfaces by substrate geometry and cytoskeleton organization. Biomaterials. 2013;34:2991–3001. doi: 10.1016/j.biomaterials.2013.01.018. [DOI] [PubMed] [Google Scholar]
  • 20.Pan Z, et al. Control of cell nucleus shapes via micropillar patterns. Biomaterials. 2012;33:1730–1735. doi: 10.1016/j.biomaterials.2011.11.023. [DOI] [PubMed] [Google Scholar]
  • 21.Versaevel M, Grevesse T, Gabriele S. Spatial coordination between cell and nuclear shape within micropatterned endothelial cells. Nature Commun. 2012;3:671. doi: 10.1038/ncomms1668. [DOI] [PubMed] [Google Scholar]
  • 22.Fu Y, Chin LK, Bourouina T, Liu AQ, VanDongen AMJ. Nuclear deformation during breast cancer cell transmigration. Lab Chip. 2012;12:3774–3778. doi: 10.1039/c2lc40477j. [DOI] [PubMed] [Google Scholar]
  • 23.Wolf K, Friedl P. Mapping proteolytic cancer cell–extracellular matrix interfaces. Clin. Exp. Metastasis. 2009;26:289–298. doi: 10.1007/s10585-008-9190-2. [DOI] [PubMed] [Google Scholar]
  • 24.Fidziañska A, Walczak E, Glinka Z, Religa G. Nuclear architecture remodelling in cardiomyocytes with lamin A deficiency. Folia Neuropathologica. 2008;46:196–203. [PubMed] [Google Scholar]
  • 25.Kim W, Ng JK, Kunitake ME, Conklin BR, Yang P. Interfacing silicon nanowires with mammalian cells. J. Am. Chem. Soc. 2007;129:7228–7229. doi: 10.1021/ja071456k. [DOI] [PubMed] [Google Scholar]
  • 26.Hanson L, Lin ZC, Xie C, Cui Y, Cui B. Characterization of the cell–nanopillar interface by transmission electron microscopy. Nano Lett. 2012;12:5815–5820. doi: 10.1021/nl303163y. [DOI] [PubMed] [Google Scholar]
  • 27.Bucaro MA, Vasquez Y, Hatton BD, Aizenberg J. Fine-tuning the degree of stem cell polarization and alignment on ordered arrays of high-aspect-ratio nanopillars. ACS Nano. 2012;6:6222–6230. doi: 10.1021/nn301654e. [DOI] [PubMed] [Google Scholar]
  • 28.Shalek AK, et al. Vertical silicon nanowires as a universal platform for delivering biomolecules into living cells. Proc. Natl Acad. Sci. USA. 2010;107:1870–1875. doi: 10.1073/pnas.0909350107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Curtis ASG, Dalby MJ, Gadegaard N. Nanoprinting onto cells. J. R. Soc. Interface. 2006;3:393–398. doi: 10.1098/rsif.2005.0104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Xie C, Lin Z, Hanson L, Cui Y, Cui B. Intracellular recording of action potentials by nanopillar electroporation. Nature Nanotech. 2012;7:185–190. doi: 10.1038/nnano.2012.8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Robinson JT, et al. Vertical nanowire electrode arrays as a scalable platform for intracellular interfacing to neuronal circuits. Nature Nanotech. 2012;7:180–184. doi: 10.1038/nnano.2011.249. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Xie C, Hanson L, Cui Y, Cui B. Vertical nanopillars for highly localized fluorescence imaging. Proc. Natl Acad. Sci. USA. 2011;108:3894–3899. doi: 10.1073/pnas.1015589108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Ostlund C, et al. Dynamics and molecular interactions of linker of nucleoskeleton and cytoskeleton (LINC) complex proteins. J. Cell Sci. 2009;122:4099–4108. doi: 10.1242/jcs.057075. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 34.Huang B, Wang W, Bates M, Zhuang X. Three-dimensional super-resolution imaging by stochastic optical reconstruction microscopy. Science. 2008;319:810–813. doi: 10.1126/science.1153529. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35.Swift J, et al. Nuclear lamin-A scales with tissue stiffness and enhances matrix-directed differentiation. Science. 2013;341:1240104. doi: 10.1126/science.1240104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 36.McClintock D, Gordon LB, Djabali K. Hutchinson–Gilford progeria mutant lamin A primarily targets human vascular cells as detected by an anti-lamin A G608G antibody. Proc. Natl Acad. Sci. USA. 2006;103:2154–2159. doi: 10.1073/pnas.0511133103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 37.Eriksson M, et al. Recurrent de novo point mutations in lamin A cause Hutchinson–Gilford progeria syndrome. Nature. 2003;423:293–298. doi: 10.1038/nature01629. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38.De Sandre-Giovannoli A, et al. Lamin A truncation in Hutchinson–Gilford progeria. Science. 2003;300:2055. doi: 10.1126/science.1084125. [DOI] [PubMed] [Google Scholar]
  • 39.Cao H, Hegele RA. LMNA is mutated in Hutchinson–Gilford progeria (MIM 176670) but not in Wiedemann–Rautenstrauch progeroid syndrome (MIM 264090) J. Hum. Genet. 2003;48:271–274. doi: 10.1007/s10038-003-0025-3. [DOI] [PubMed] [Google Scholar]
  • 40.Dahl KN, et al. Distinct structural and mechanical properties of the nuclear lamina in Hutchinson–Gilford progeria syndrome. Proc. Natl Acad. Sci. USA. 2006;103:10271–10276. doi: 10.1073/pnas.0601058103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 41.Booth-Gauthier EA, et al. Hutchinson–Gilford progeria syndrome alters nuclear shape and reduces cell motility in three dimensional model substrates. Integr. Biol. 2013;5:569–577. doi: 10.1039/c3ib20231c. [DOI] [PubMed] [Google Scholar]
  • 42.Claycomb WC, et al. HL-1 cells: a cardiac muscle cell line that contracts and retains phenotypic characteristics of the adult cardiomyocyte. Proc. Natl Acad. Sci. USA. 1998;95:2979–2984. doi: 10.1073/pnas.95.6.2979. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 43.Geiger B, Spatz JP, Bershadsky AD. Environmental sensing through focal adhesions. Nature Rev. Mol. Cell Biol. 2009;10:21–33. doi: 10.1038/nrm2593. [DOI] [PubMed] [Google Scholar]
  • 44.Khatau SB, et al. A perinuclear actin cap regulates nuclear shape. Proc. Natl Acad. Sci. USA. 2009;106:19017–19022. doi: 10.1073/pnas.0908686106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 45.Stamenović D, Mijailovich SM, Tolić-Nørrelykke IM, Chen J, Wang N. Cell prestress. II. Contribution of microtubules. Am. J. Physiol. Cell Physiol. 2002;282:C617–C624. doi: 10.1152/ajpcell.00271.2001. [DOI] [PubMed] [Google Scholar]
  • 46.Maniotis AJ, Chen CS, Ingber DE. Demonstration of mechanical connections between integrins, cytoskeletal filaments, and nucleoplasm that stabilize nuclear structure. Proc. Natl Acad. Sci. USA. 1997;94:849–854. doi: 10.1073/pnas.94.3.849. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 47.Ingber DE, Tensegrity I. Cell structure and hierarchical systems biology. J. Cell Sci. 2003;116:1157–1173. doi: 10.1242/jcs.00359. [DOI] [PubMed] [Google Scholar]
  • 48.Wang N, Stamenovic D. Contribution of intermediate filaments to cell stiffness, stiffening, and growth. Am. J. Physiol. Cell Physiol. 2000;279:C188–C194. doi: 10.1152/ajpcell.2000.279.1.C188. [DOI] [PubMed] [Google Scholar]
  • 49.Vaziri A, Lee H, Mofrad MRK. Deformation of the cell nucleus under indentation: mechanics and mechanisms. J. Mater. Res. 2006;21:2126–2135. [Google Scholar]
  • 50.Kim D-H, et al. Actin cap associated focal adhesions and their distinct role in cellular mechanosensing. Sci. Rep. 2012;2:555. doi: 10.1038/srep00555. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Movie1
Download video file (140.4KB, avi)
Movie2
Download video file (508.1KB, avi)
Movie3
Download video file (2.8MB, avi)
Movie4
Download video file (324.7KB, avi)
SupplFigure
NIHMS820357-supplement-SupplFigure.pdf (1.7MB, pdf)

RESOURCES