How environment and self‐motion combine in neural representations of space

Abstract

Estimates of location or orientation can be constructed solely from sensory information representing environmental cues. In unfamiliar or sensory‐poor environments, these estimates can also be maintained and updated by integrating self‐motion information. However, the accumulation of error dictates that updated representations of heading direction and location become progressively less reliable over time, and must be corrected by environmental sensory inputs when available. Anatomical, electrophysiological and behavioural evidence indicates that angular and translational path integration contributes to the firing of head direction cells and grid cells. We discuss how sensory inputs may be combined with self‐motion information in the firing patterns of these cells. For head direction cells, direct projections from egocentric sensory representations of distal cues can help to correct cumulative errors. Grid cells may benefit from sensory inputs via boundary vector cells and place cells. However, the allocentric code of boundary vector cells and place cells requires consistent head‐direction information in order to translate the sensory signal of egocentric boundary distance into allocentric boundary vector cell firing, suggesting that the different spatial representations found in and around the hippocampal formation are interdependent. We conclude that, rather than representing pure path integration, the firing of head‐direction cells and grid cells reflects the interface between self‐motion and environmental sensory information. Together with place cells and boundary vector cells they can support a coherent unitary representation of space based on both environmental sensory inputs and path integration signals.

Abbreviations

BVC

boundary vector cell

GC

grid cell

HDC

head direction cell

lEC

lateral entorhinal cortex

mEC

medial entorhinal cortex

PC

place cell

Introduction

Knowing one's location relative to the environment is crucial to the survival of most mobile creatures, and explicitly relies on environmental sensory input. Many organisms also use their own self‐motion to maintain an estimate of location and orientation in the absence of sensory input, a process referred to as ‘spatial updating’ or ‘path integration’ (e.g. Mittelstaedt & Mittelstaedt, 1980; for reviews see Etienne & Jeffrey 2004; Barry & Burgess, 2014). Self‐motion can be estimated from vestibular, proprioceptive and visual (e.g. optic flow) information and integrated over time to update an estimate of location (Etienne et al. 1996). However, the cumulative nature of this path integration process dictates that the underlying representations will also integrate error, making the estimate of location and orientation less reliable over time. These location and orientation estimates therefore need to be corrected by environmental sensory information whenever possible, rectifying any misalignment between the internally derived representation and the current perceptual estimate.

The hippocampal formation contains several well described classes of neuron whose activity correlates with an animal's location or orientation. These include place cells (PCs) in the hippocampus proper, which fire in specific locations (O'Keefe and Dostrovsky, 1971); head direction cells (HDCs), found along Papez's circuit, which signal the orientation of an animal's head with respect to the environment (Ranck, 1984; Taube et al. 1990 a, b ); grid cells (GCs) in the medial entorhinal cortex (mEC) and pre‐ and parasubiculum, which exhibit multiple firing fields arranged on a hexagonal grid (Hafting et al. 2005; Boccara et al. 2010); and border or boundary vector cells (BVCs) in the mEC and subiculum, which fire due to the presence of an extended boundary in a fixed allocentric direction (Barry et al. 2006; Savelli et al. 2008; Solstad et al. 2008; Lever et al. 2009).

In particular, the firing patterns of HDCs and GCs are thought to reflect angular and translational path integration, respectively (McNaughton et al. 2006; Taube, 2007). If this is the case, then these cells must receive both environmental and self‐motion‐related sensory information, allowing them to update their activity according to path integration and eliminate accumulated error according to perceptual information. Here we review current knowledge about how environmental sensory inputs interact with spatial representations of location and orientation to reduce accumulated error.

Sensory reset of angular path integration

The firing rates of individual HDCs are strongly tuned to the direction that an animal's head is facing relative to the environment, and specifically to landmarks placed at or beyond the edge of the environment (Taube et al. 1990 a). The resultant Gaussian tuning curves are centred on a distinct direction for each cell (the so‐called preferred direction, see Fig. 1 A and B). HDCs are found along Papez's circuit, e.g. in the dorsal tegmental nucleus, lateral mammillary nucleus, anterior dorsal thalamus, lateral dorsal thalamus and dorsal presubiculum (also called postsubiculum; for review see, Taube, 2007), as well as in the mEC (Sargolini, 2006) and retrosplenial cortex (Chen et al. 1994). Lesion studies suggest that the generative circuitry is restricted to the dorsal tegmental nucleus and the mammillary bodies (Blair et al. 1998; Bassett et al. 2007), while little is known about the computations carried out by the downstream structures.

Figure 1. Properties of head direction cells .

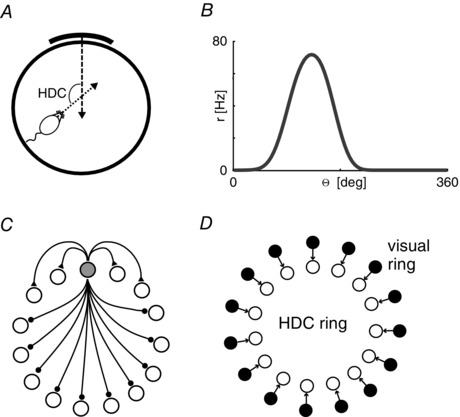
A, head direction cells (HDC) code for the allocentric direction of an animal's head with reference to the normal vector of a salient landmark. B, a prototypical head direction tuning curve (head direction Θ, firing rate r). C, the topology of a canonical ring attractor circuit. Only connections from one cell (filled circle) are shown. Short range excitatory connections (ending in filled triangles) and long range inhibitory connections (ending in filled circles) assure a local self‐sustaining ‘packet of activity’. D, the standard model of visual feedback in the head direction system. Each head direction is associated with a unique visual activity profile. Topographic connections (black arrows) excite the correct portion of the head direction ring to prevent drift.

Several findings support the hypothesis that HDC firing patterns reflect angular path integration. First, differences in preferred direction between cells are conserved after environmental manipulations (i.e. displacement of a salient landmark), suggesting that the entire ensemble of HDCs forms a coherent unit (Taube et al. 1990 b). Second, HDCs maintain coherent firing patterns after the removal of prominent visual cues and in darkness (Taube et al. 1990 b; Mizumori & Williams, 1993; Goodridge et al. 1998), demonstrating that their activity can be sustained internally. However, cumulative drift of HDC preferred directions is observed during this period, presumably due to the accumulation of error expected of a path integration system. Third, shifts in the preferred firing direction of HDCs correlate with angular error in the homing trajectory (Valerio & Taube, 2012). Fourth, HDC firing patterns are strongly dependent on self‐motion inputs from the vestibular system (Stackman & Taube, 1997; Stackman et al. 2002; Muir et al. 2009). Finally, angular head velocity cells, which would be required to update HDC firing patterns in accordance with the animal's head movements, have been identified throughout the HDC network (Sharp, 1996; Stackman & Taube, 1998; Bassett & Taube, 2001; Sharp et al. 2001).

There is strong evidence that a continuous ring attractor circuit generates the head direction signal (see e.g. Zhang, 1996; Peyrache et al. 2015). Attractor networks can sustain persistent activity (the so‐called activity packet or activity bump on topographically organized cells) by virtue of translation invariant recurrent connectivity, most often local excitation in combination with long‐range inhibition (Fig. 1 C). Unlike discrete attractor networks, which can occupy a finite set of stable states, the variable encoded by a continuous attractor circuit can in principle assume any value within its range (e.g. 1 to 360 deg for the head direction system), constraining patterns of activity to a continuous subspace corresponding to these values.

The sensitivity of continuous attractor networks to noise (in external drive, network topology and neuronal parameters) explains the observation that HDCs’ preferred directions begin to drift in darkness (corresponding to drift of the activity packet in the attractor network), rendering the angular path integration system unreliable over time. Despite the fact that rodents have poor vision, drift of the head direction signal in darkness is a well‐established experimental finding (Mizumori & Williams, 1993; Goodridge et al. 1998) underlining the strong influence of visual information. A small amount of drift can even be observed in light (Yoder et al. 2015).

Correcting for drift in the head direction circuit is closely tied to the notion of cue control, where a salient landmark in the environment gains control over the head direction ensemble (Taube et al. 1990 a, b ). Shifting the landmark in the absence of the animal leads to corresponding shifts in the head direction representation (measured in the laboratory reference frame) when the animal is reintroduced into the arena. Cue control can be established within the first few minutes of exploration in a novel environment (Goodridge et al. 1998), implying a fast‐acting plasticity mechanism. Similarly, gradually shifting the angular position of the reference landmark in the presence of the animal leads to a corresponding shift in head direction. Interestingly, however, the shift in HDC firing lags behind the movement of the cue, suggesting that plasticity may also act during the shift, leading to a stabilization of head direction activity offset towards the previously learned value (Knight et al. 2013).

Learning the correct mapping between visual representations and head direction is a dynamic process, which takes several minutes, and will most likely be refined with prolonged exposure to the same environment. Associating the head direction representation with environmental input will also rely on the spatiotemporal stability of external cues, with animals preferring to use stable landmarks as reference points (Knierim et al. 1995). While environmental boundaries can anchor head direction, ensembles of distal landmarks, which are more stable in the visual field, appear to exert the strongest influence (Jeffery, 1998; Zugaro et al. 2001; Clark et al. 2012). It has also been demonstrated that the preferred firing directions of HDCs are reset by visits to familiar locations (Valerio & Taube, 2012).

In models of head direction, both cue control and sensory reset of the activity packet in the ring attractor circuit rely on a separate sensory representation, usually in the form of a ring of visual cells (or an equivalent implementation) that represent the angular bearing of a distal reference landmark (Skaggs et al. 1995). Topographic connections between this visual ring and corresponding cells in the head direction attractor ensure stability and cue control (cf. Fig. 1 D). Suppose, for example, that facing magnetic North corresponds to a head direction of 90 deg. When the animal is facing North, visual cells firing in response to a distal landmark located straight ahead will drive the 90 deg head direction cells in the ring attractor, shifting the activity bump to that position if it was misaligned. In the absence of this visual input (i.e. in darkness), drift of the activity bump is no longer overridden by the comparatively strong visual signal and will re‐emerge due to the inherent noise‐accumulating properties of attractor networks.

It is not entirely clear where such a visual representation may reside. Anatomical considerations suggest that retrosplenial cortex and postsubiculum are the main gateways for visual information onto the head direction circuit (Taube, 2007; Vann et al. 2009). Neurons in the postsubiculum receive direct input from visual area 17, which may represent salient visual landmarks. Retrosplenial cortex is reciprocally connected to two main downstream loci of HDCs (the anterior dorsal thalamic nucleus and postsubiculum, i.e. dorsal presubiculum; Vann & Aggleton, 2005), and appears to be crucial for spatial orientation in rodents. Lesions to the dysgranular area of retrosplenial cortex lead rats to switch to a motor turn strategy instead of relying on visual landmarks (Vann & Aggleton, 2005), suggesting landmark‐based navigation is impaired after retrosplenial cortex lesions. More recently, Yoder et al. (2015) have shown that an intact postsubiculum is crucial for stable head direction tuning in the lateral mammillary nucleus. In all likelihood, both retrosplenial cortex and postsubiculum are necessary processing stages for visual feedback to reach the generative head direction circuitry in upstream structures (for a review, see Yoder et al. 2011).

Sensory reset of translational path integration

Whereas the head direction system appears to reflect the angular component of path integration, GCs, which exhibit a unique hexagonal pattern of firing fields that tile any given environment, are thought to reflect the translational component (Hafting et al. 2005). These grid patterns are characterized by their spatial scale (distance between grid fields) and orientation relative to the environment (Fig. 2 A). Moving dorsoventrally along the mEC, GCs increase their scale in discrete steps (Barry et al. 2007; Stensola et al. 2012, 2015). GCs with similar scales share the same orientation relative to their environment but have offset firing fields, providing uniform spatial coverage (Hafting et al. 2005; Fig. 2 B).

Figure 2. The grid cell path integration system .

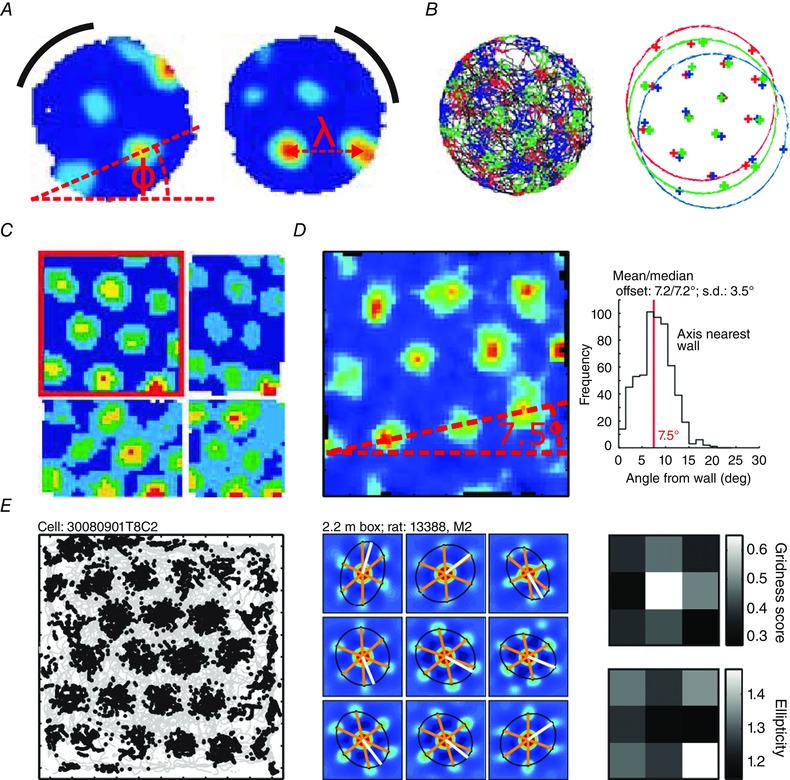
A, rotation of a black cue card causes rotation of the grid pattern. Φ shows the grid orientation, λ the grid scale (adapted with permission from Hafting et al. 2005). B, topologically neighbouring grid cells (red, green, blue) have different spatial phases, but equal scale and orientation (adapted with permission from Hafting et al. 2005). C, animals were placed in an environment with moveable walls (adapted with permission from Barry et al. 2007). Grid cell firing patterns responded to uniaxial (top right, bottom left) and biaxial (bottom right) contraction and returned to their original configuration (top left). D, grids have three measures of orientation corresponding to their three axes. In a square environment, the angle from the wall is defined as the smallest of the three axis angles from their nearest wall. The smallest of these three angle clusters bi‐modally about 7.5 deg (adapted with permission from Stensola et al. 2015). E, left, an example binned spike map in a 2.2 m² box. Middle, ellipses fitted to the innermost six peaks of the local autocorrelogram (different to right). Right, ellipticity and gridness scores in different sections of a 2.2 m² box, showing greater distortion near the edges (adapted with permission from Stensola et al. 2015).

Multiple mechanisms have been suggested for the means by which GC firing patterns might track the movement of the animal. These include spatially asymmetric network interactions modulated by the animal's direction and speed of movement, analogous to those proposed for head‐direction circuits (Skaggs et al. 1995; Zhang, 1996). These asymmetries, which may be mediated by ‘directional’ or ‘conjunctive’ GCs (Fuhs & Touretzky, 2006; McNaughton et al. 2006; Sargolini, 2006) and by ‘speed cells’ (O'Keefe et al. 1998; Sharp & Turner‐Williams, 2005; Sharp et al. 2006; Kropff et al. 2015), generate depolarization in GCs whose firing fields lie along the movement trajectory adjacent to the current location, causing a shift of the grid firing pattern in that direction. Alternatively, this depolarization might be driven by interference between a global oscillation and velocity‐controlled oscillators in the theta frequency band that have non‐collinear preferred firing directions (Burgess et al. 2007; Bush & Burgess, 2014). This oscillatory interference model is consistent with the theta‐phase precession effect observed in GC (Hafting et al. 2008) and PC firing (O'Keefe & Recce, 1993). Interestingly, it has also been demonstrated that impairing the theta rhythm, either by inactivating medial septum or by the passive transport of animals, disrupts periodic grid firing without affecting head direction or place cell firing patterns (Brandon et al. 2011; Koenig et al. 2011; Winter et al. 2015 b). In either case, translation of GC activity patterns according to self‐motion information requires accurate heading information and, accordingly, it has been demonstrated that inactivation of HDCs in the anterior thalamic nuclei also leads to a loss of periodic grid field firing (Winter et al. 2015 a).

What evidence is there that the firing patterns of GCs reflect translational path integration? Firstly, while PCs undergo re‐mapping between different environments (Muller & Kubie, 1987), GCs preserve their firing patterns across all environments visited by the animal (Hafting et al. 2005). Importantly, the relative spatial offset of firing fields recorded from cells in the same module is also maintained across different environments (Hafting et al. 2005; Yoon et al. 2013). These properties suggest that GCs whose firing fields share a similar scale and orientation form cohesive functional modules (Stensola et al. 2012). Moreover, in situations where the grids are unlikely to be directly driven by common environmental cues (Barry et al. 2012), this invariance in spatial offset between grid firing fields within the same module also points to a shared path integration mechanism (Yoon et al. 2013). Secondly, the spatial stability of grid firing fields decreases over time in darkness, in the supposed absence of ‘corrective’ sensory inputs (Hafting et al. 2005). Finally, lesion studies suggest that navigation tasks that rely specifically on path integration mechanisms can be impaired after lesions of mEC (van Cauter et al. 2013).

The fact that the location of GC firing fields is stable between visits to an environment, and that grid orientation rotates (along with the tuning curves of HDCs) with a prominent visual cue (Fig. 2 A; Hafting et al. 2005; Sargolini, 2006) indicates that GCs also receive environmental sensory inputs. More dramatically, reshaping a familiar rectangular environment along one axis can cause the parametric deformation of previously stable GC firing patterns along the same axis, resulting in both elliptical firing fields and grid patterns (Barry et al. 2007; Stensola et al. 2012; Fig. 2 C). This suggests that, in familiar environments, sensory inputs can shift and deform the intrinsic metric generated by self‐motion information. Interestingly, with repeated reshaping of the environment the expansion and contraction of GC firing patterns is diminished, suggesting that sensory inputs that are known to be unstable are eventually ignored, mirroring similar results for orientation, described above (Knierim et al. 1995).

How might environmental sensory inputs be used to correct drift in GC firing? Hebbian associations from PCs to GCs have been proposed as a likely route, given the convenient overlap between the PC firing fields and single nodes of a grid (O'Keefe & Burgess, 2005), with PCs mediating the effect of boundary manipulations via their proposed BVC inputs (Hartley et al. 2000). However, it is equally possible that BVCs directly stabilize GC firing (Solstad et al. 2008). Several theoretical studies have demonstrated that input from either PCs or BVCs is sufficient to ameliorate the effects of noisy self‐motion input to the GC network (e.g. Fuhs & Touretzky, 2006; Guanella et al. 2007; Pastoll et al. 2013; Bush & Burgess, 2014; Hardcastle et al. 2015). The spatial stability and parametric deformation of grid firing fields described above, for example, could be mediated by direct excitatory input from BVCs or PCs with firing fields either along the borders or distributed evenly throughout the environment, ‘correcting’ the uniform hexagonal firing produced by self‐motion inputs (Bush & Burgess, 2014).

Exploring the hypothesis that boundary input acts to stabilize path integration, Hardcastle et al. (2015) analysed the stability of GC firing patterns recorded in vivo with respect to rats’ encounters with boundaries. They showed that ‘error’ in the grid fields (the distance between spikes and the centre‐of‐mass of their nearest firing field, measured across the whole recording session) increases with both time and distance since the last boundary encounter. Interestingly, both the magnitude and the direction of the error were also consistent across all recorded GCs, suggesting a coherent drift of the grid pattern relative to the environment, as opposed to an increase in the size of individual grid fields. Moreover, error correction was greater in the direction perpendicular to the last boundary encounter, as might be expected if the grid were responding to BVCs that provide information about distance perpendicular to that boundary. These findings suggest that positional uncertainty may manifest itself as environmental misalignment of an intrinsically stable GC firing pattern, rather than a breakdown of GC firing patterns altogether. Furthermore, the hypothesis that GC firing patterns are stabilized by environmental boundaries predicts that time‐averaged grid fields should be smaller and more elliptical near to the boundary, and that this effect would be more pronounced in larger environments.

Not with standing the possibility of direct boundary‐related input to GCs, there is also evidence that input from PCs contributes to stable GC firing. For example, inactivation of the hippocampus rapidly disrupts the spatial periodicity of GC firing patterns, decreases the mean firing rate of GCs and increases their directional tuning (Bonnevie et al. 2013). Moreover, stable PC, BVC and HDC firing patterns are known to precede stable GC firing patterns in the developmental timeline, suggesting that input from each of these cell types might be required for the generation of stable GC firing patterns (Langston et al. 2010; Wills et al. 2010). Interestingly, it has recently been shown that the stability of PC firing fields is inversely correlated with distance to the nearest environmental boundary in pre‐weanling rats, but that this relationship disappears in adult animals (Muessig et al. 2015). This suggests that, prior to the development of GCs, inputs from BVCs active around the boundaries of an environment also serve to stabilize PC firing (O'Keefe & Burgess, 1996; Hartley et al. 2000). Later in development, the appearance of stable place fields in the centre of an environment coincides with the establishment of stable GC firing (Muessig et al. 2015). However, whether path integration input from GCs is required to stabilize place fields, or environmental sensory input from PCs is required to eliminate grid field drift away from environmental boundaries is yet to be determined.

Adaptation over multiple time scales

The discussion so far has concerned interactions between place or boundary vector and grid cell populations according to pre‐established neural connections. However, in new environments these connections must develop through synaptic plasticity over longer time scales, and may be associated with gradual changes observed in GC firing patterns with increasing experience of an environment. Notably, the spatial scale of grid firing patterns reduces and their spatial regularity increases with experience of a novel environment (Barry et al. 2012). At the same time, the orientation of the grid firing patterns relative to the boundaries of a square environment changes from an initially parallel alignment to develop a small (∼7.5–8.8 deg) angular offset (Krupic et al. 2015; Stensola et al. 2015; Fig. 2 D). In larger square environments, local 7.5 deg orientation to multiple boundaries is observed, and is associated with a departure from the globally regular hexagonal firing pattern, resulting in local ellipticity (the skew of an ellipse tracing the innermost six peaks of a grid; see Fig. 2 E).

In smaller square environments, both the angular offset of the grid firing pattern to local boundaries and its ellipticity can be modelled as a uniaxial shearing transformation – where grid fields are shifted away from one boundary by an amount proportional to location along that boundary – suggesting that both are the result of a common underlying process (Stensola et al. 2015). In larger square environments, the effects can only be fully removed by a biaxial shearing centred about ‘anchoring’ points in opposite corners. Whether or not the observed angular offsets and distortions of the grid fields that develop with experience, as well as the initial decrease in grid scale, serve to distort the perception of space, or offer some functional advantage, are questions for future empirical studies. In either case, the influence of environmental boundaries on GC firing patterns seems likely to arise as a consequence of functional BVC inputs to GCs, possibly mediated by PCs (O'Keefe & Burgess, 2005), and which could counteract error accumulation (Hardcastle et al. 2015; Stensola et al. 2015).

In addition to changes in GC firing patterns that may reflect their association to environmental sensory inputs, both PC and GC firing patterns are known to exhibit more gradual changes that reflect the slow disambiguation of perceptually similar environments. For example, on initial exposure to square and circular environments, place fields share preferred firing locations, measured relative to both a cue card and environmental boundaries, consistent with an important role of BVC inputs (Lever et al. 2002). However, over a period of days, firing locations in each environment diverge, either as a result of the gradual shifting of firing fields, or through the disappearance and emergence of the original and new fields, respectively.

Similarly, when rats are allowed to commute freely between two perceptually identical environments, GC firing patterns that are initially identical in both boxes gradually shift to form a unified, globally consistent representation with experience (Carpenter et al. 2015). The alignment and spatial phase of the initially local GC firing patterns are consistent with conserved boundary‐related inputs, and the subsequent shift suggests that, during navigation between the two environments, path integration input slowly forces the sensory associations to be relearned. Interestingly, global (i.e. path integration consistent) tuning of HDCs in connected environments emerges on similar time scales (Dudchenko & Zinkyuk, 2005). Thus, longer‐term adaptation may be important both in disambiguating perceptually similar environments, and in embedding these localized representations within a consistent global framework.

Origins of the sensory inputs to grid cells and place cells

The firing patterns of place cells in CA1 are robust to the lesioning of many different input streams, including CA3 (Brun et al. 2002), mEC (Miller & Best, 1980; Brun et al. 2008), lateral entorhinal cortex (lEC) (Lu et al. 2013), pre‐ and parasubiculum (Liu et al. 2004), and subcortical structures (Miller & Best, 1980). Thus, it seems likely that PC firing patterns are supported by a wide range of multi‐modal inputs that converge on the hippocampus from a variety of different cortical structures. Accordingly, PC firing fields are modulated by contextual inputs such as wall colour and odour (Bostock et al. 1991; Anderson & Jeffery, 2003; Lu et al. 2013), manifested in PC ‘remapping’. It has been hypothesized that BVCs are a potential source for the environmental determination of the spatial firing locations of PCs, but it is important to note that BVC firing patterns are allocentric representations, e.g. responding to a boundary to the North independent of the orientation of the animal. By contrast, sensory representations are necessarily egocentric in nature. Hence, environmental sensory inputs to BVCs will at some stage require an egocentric–allocentric coordinate transformation.

One such mechanism for transformation between population codes in different frames of reference has been proposed, involving an expanded ‘gain field’ representation formed by the product of both individual sets of basis functions (Salinas & Abbott, 1996; Pouget & Sejnowski, 1997; Burgess et al. 2001; Byrne et al. 2007). To account for the allocentric firing patterns of BVCs, it has been hypothesized that BVCs in the hippocampal formation have an egocentric analogue in medial parietal areas (Burgess et al. 2001; Byrne et al. 2007). These putative cells would signal the presence of boundaries at given distances in an egocentric frame of reference via receptive fields in peripersonal space. This egocentric representation could be driven directly by sensory input and transformed to an allocentric representation via a ‘gain field’ circuit in posterior parietal or retrosplenial cortex. This egocentric–allocentric transformation depends on the head direction system to correctly map egocentric into allocentric direction (e.g. North corresponds to left when facing East).

Thus, boundary‐related input would arrive at the hippocampal formation from the dorsal processing stream (Ungerlieder & Mishkin, 1982; Goodale & Milner, 1992) via the parietal, retrosplenial, parahippocampal and medial entorhinal cortices. By contrast, contextual and object‐related inputs (Deshmukh & Knierim, 2011; Lu et al. 2013; Tsao et al. 2013) likely arrive from the ventral processing stream via perirhinal and lateral entorhinal cortices. Hence, these pathways carry complementary sensory signals (see colour code in Fig. 3), which provide input to PCs and GCs independently, increasing the robustness of the global path‐integration system.

Figure 3. Main pathways for sensory signals necessary to reset path integration systems .

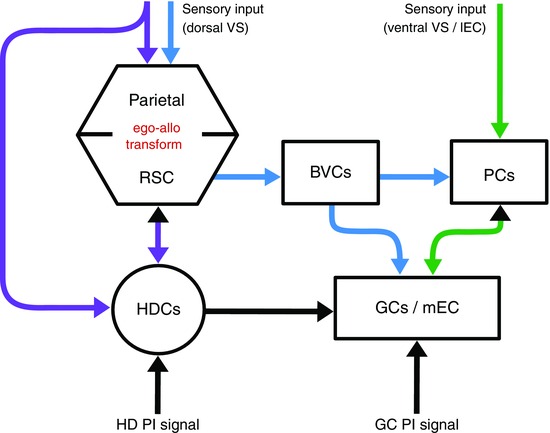
Coloured arrows: known/hypothesized pathways for sensory information. Purple: the head direction system receives projections from visual area 17 and from retrosplenial cortex (RSC). Head direction potentially gates an egocentric–allocentric transformation (red) between parietal and retrosplenial cortices, necessary to transform egocentric boundary distance (sensory input) to allocentric boundary distance (BVCs). Blue and green: complementary pathways conveying sensory information to grid cells, sources attributed to the dorsal and ventral visual streams (VS), respectively. Black arrows/arrowheads: pathways for idiothetic information, i.e. path integration signals. Abbreviations: BVCs, boundary vector cells; GCs, grid cells; HDCs, head direction cells; lEC, lateral entorhinal cortex; mEC; medial entorhinal cortex; PCs, place cells. Note, some known projections are omitted for clarity, e.g. from retrosplenial cortex to mEC.

Discussion

We have discussed how an effective spatial navigation system requires complementary information from both self‐motion and environmental sensory inputs, and reviewed evidence that the firing patterns of HDCs and GCs reflect angular and translational path integration, respectively, and receive the environmental sensory inputs needed to reduce errors in estimates of self‐location that accumulate during path integration. Thus, rather than representing pure path integration, HDC and GC firing reflect the interface between self‐motion and environmental sensory information. This distinction is particularly obvious in GCs, whose firing patterns are significantly more complex than required by the simple accumulation of displacement for translational path integration, and provide a modular, high capacity code for location that, in combination with PCs, may support efficient navigation within large‐scale space (Fiete et al. 2008; Bush et al. 2015).

In this review, we have focused primarily on unidirectional processing pathways, i.e. the transmission of environmental information directly to HDCs, or via BVCs and PCs to GCs. However, it is important to note that GCs are also likely to project to PCs in the hippocampus (van Strien et al. 2009), and it has been suggested that GCs can partially support and update PC firing when sensory inputs are reduced (e.g. in darkness). Accordingly, evidence indicates that when visual and path integration information are dissociated, the resulting PC firing is best described by a balanced combination of these inputs (Gothard et al. 1996; Chen et al. 2013).

More generally, it makes sense that our perception of spatial location and orientation combines both types of input. Behavioural evidence in humans further suggests that the two input streams are integrated into a single representation (Tcheang et al. 2011), and are possibly weighted to reflect the relative reliability of the available sources of information (Nardini et al. 2008). Thus, reciprocal connectivity between PCs and GCs is likely to underlie the concurrent development of stable PC and GC firing fields away from the boundaries of an environment (Muessig et al. 2015), in order to form a single multimodal representation of location. Similarly, HDC input is critical for the transformation of egocentric sensory input to allocentric BVC and PC firing patterns, all of which rotate coherently with HDC firing patterns when a single prominent cue is shifted in a circular arena (O'Keefe & Conway, 1978; Muller & Kubie, 1987; Knierim et al. 1995; Sargolini, 2006). Conversely, spatial information from PCs and GCs is likely to be involved in the development of coherent HD representations across connected environments (Dudchenko & Zinyuk, 2005). To summarize, these data suggest that the different spatial representations found in and around the hippocampal formation are mutually interdependent and support a coherent unitary representation of space based on both environmental sensory and path integration inputs.

Additional information

Competing interests

The authors declare no conflicts of interest.

Author contributions

All authors have approved the final version of the manuscript and agree to be accountable for all aspects of the work. All persons designated as authors qualify for authorship, and all those who qualify for authorship are listed.

Funding

This work was supported by the EPSRC, Wellcome Trust, Medical Research Council UK and the EU FP7 FET project SpaceCog.

Biographies

Talfan Evans studied Engineering at the University of Oxford and is a CoMPLEX doctoral student at the Space and Memory Group within the Institute of Cognitive Neuroscience, University College London.

Andrej Bicanski studied Physics at the University of Heidelberg, and did his PhD in the Biorobotics lab at the École polytechnique fédérale de Lausanne. He joined the Space and Memory group in 2013.

Daniel Bush studied Chemical Engineering at Imperial College, London, and completed his PhD at the University of Sussex before joining the Space and Memory group in 2011.

Neil Burgess received a PhD in Theoretical Physics from Manchester University, is a Professor of Cognitive and Computational Neuroscience, head of the Space and Memory group and Director of the Institute of Cognitive Neuroscience at University College London.