Skip to main content
PMC home page
The Journal of Physiology logoLink to The Journal of Physiology
. 2016 Oct 5;594(22):6527–6534. doi: 10.1113/JP272945

Optimal cue combination and landmark‐stability learning in the head direction system

Kate J Jeffery 1,✉, Hector J I Page 1, Simon M Stringer 2
PMCID: PMC5108898  PMID: 27479741

Abstract

Maintaining a sense of direction requires combining information from static environmental landmarks with dynamic information about self‐motion. This is accomplished by the head direction system, whose neurons – head direction cells – encode specific head directions. When the brain integrates information in sensory domains, this process is almost always ‘optimal’ – that is, inputs are weighted according to their reliability. Evidence suggests cue combination by head direction cells may also be optimal. The simplicity of the head direction signal, together with the detailed knowledge we have about the anatomy and physiology of the underlying circuit, therefore makes this system a tractable model with which to discover how optimal cue combination occurs at a neural level. In the head direction system, cue interactions are thought to occur on an attractor network of interacting head direction neurons, but attractor dynamics predict a winner‐take‐all decision between cues, rather than optimal combination. However, optimal cue combination in an attractor could be achieved via plasticity in the feedforward connections from external sensory cues (i.e. the landmarks) onto the ring attractor. Short‐term plasticity would allow rapid re‐weighting that adjusts the final state of the network in accordance with cue reliability (reflected in the connection strengths), while longer term plasticity would allow long‐term learning about this reliability. Although these principles were derived to model the head direction system, they could potentially serve to explain optimal cue combination in other sensory systems more generally.

graphic file with name TJP-594-6527-g007.jpg

Keywords: attractor networks, cue combination, sensory integration

Abbreviations

MEC

medial entorhinal cortex

PoS

postsubiculum

RSC

retrosplenial cortex

Introduction

Self‐localisation and navigation benefit from maintenance of a stable sense of direction so that a navigator knows which way he or she is facing, and therefore how to interpret the field of view and plan movements through the surrounding space. In the mammalian brain, this sense is constructed and maintained by a network of structures known collectively as the head direction system (Taube et al. 1990; Taube, 2007). Cells in these areas, called head direction cells, fire when an animal's head faces in a particular direction; they do this by combining external, environment‐based information with internally generated, dynamic information about self‐motion (Blair & Sharp, 1996).

When an animal enters a new environment, the head direction system first has to learn about the local landmarks, which it uses to establish a frame of reference relative to which head directions can thereafter be specified (Taube & Burton, 1995). To do this, the animal has to identify those environmental features that are directionally useful, namely, features that are stable, and are thus part of the static background (or allocentric) frame of reference. Instability can take two forms – it can occur because the objects themselves move, or it can occur because small and nearby fixed objects, which can be walked around, also change their apparent direction relative to the background and so are less useful as directional landmarks. Deciding which objects are distant and stable vs. nearby and/or unstable poses something of a chicken‐and‐egg problem because the purpose of stable landmark identification is to establish the directional reference frame, but the reference frame itself is used to decide whether a given landmark is stable or not. Landmark‐learning thus involves a process of continual cue conflict resolution as the system constantly judges, on balance of probabilities, whether its own signal has accrued an error or whether a given landmark is uninformative.

The question addressed by this article, then, is how – at a neural level – the head direction system resolves conflicts between sets of incoming signals. Cue integration and conflict resolution is an area that has had extensive theoretical treatment in other domains, but the neural basis of this process remains unknown. Understanding cue combination by head direction cells, which form a relatively simple sensory system, may shed light not just on navigation computations but also on more general principles of optimal cue combination.

Optimal sensory integration

Sensory integration in the nervous system is often optimised (Ernst & Banks, 2002), such that better or more reliable information is given a stronger role in the final sensory decision. Several experiments have shown that subjects are able to combine sensory information in a way that gives more weight to the more reliable cue: for example, Ernst and Banks found that subjects judging the texture of a surface using both vision and touch benefitted from use of both senses, and tended to weight the lower‐variance visual stimulus more strongly. Similar findings have arisen from studies investigating the combining of stereo cues and texture cues to estimate surface slant (Knill & Saunders, 2003), and combining of vision and sound to estimate speaking direction (the so‐called ‘ventriloquist effect’: Alais & Burr, 2004) or temporal order (Shams et al. 2005).

Cue combination has been well described by maximum likelihood estimation (Ernst & Banks, 2002), in which each parameter (e.g. a visual stimulus and a tactile stimulus) is modelled by a Gaussian curve, which depicts the probability of the stimulus location in parameter space (for example, the probability that a surface has a given texture, given its visual appearance). The height of these Gaussian curves is proportional, and width inversely proportional, to the reliability of the estimate (Fig. 1), so that a tall narrow curve reflects a more accurate estimate, and a lower broader one a more diffuse or uncertain estimate. The process has been formulated in Bayesian terms (Knill & Pouget, 2004), in which the height and width of the Gaussian probability density estimates reflect the prior information present in the system about each cue. For example, if a subject has learned that tactile cues are less reliable (let's say they are wearing gloves, and have learned from experience that gloves reduce tactile accuracy), then the shape of the tactile Gaussian probability distribution will change to reflect the lower informativeness, and so tactile cues should have less impact on the final decision. Given two such distributions, corresponding to two sets of cues, cue combination in theory simply involves multiplication of these probabilities. It is a property of Gaussians that the product of two curves is itself a Gaussian curve, located between the originals and closer to the taller narrower one, producing optimal cue combination exactly as required.

Figure 1. Cue conflict by combination of Gaussian activations .

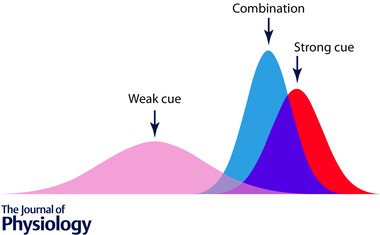
Figure 1

Open in a new tab

The x‐axis refers to some quantifiable parameter distributed across a sensory network such as size, optical slant, spatial location, heading direction, etc., and the y‐axis reflects intensity of the sensory drive. The Gaussian curves depict the distribution of drive across the parameter space: the red curve denotes a strong (tall) and reliable (narrow) cue, and the pink curve a weaker and less reliable one. The blue curve reflects the outcome of a decision process that has taken both cues into account and derived a weighted average, in which the more reliable cue has exerted a stronger positioning effect.

Cue combination and prior‐informed sensory processing are highly relevant to spatial processing (Cheng et al. 2007), including directional estimation. Cue combination could occur when head direction cells are faced with more than one indicator of direction and have to decide how best to exploit these. Examples of multiple directional cues include self‐motion cues from the vestibular and motor systems vs. static landmarks in the environment, both of which can vary in reliability: animals can become internally disoriented, or landmarks can be unstable. Studies in which landmark stability and/or internal cues have been manipulated have found a re‐weighting of the relative influence of these cues, both in behavioural and physiological observations. Behaviourally, one of the first experiments, by Biegler and Morris, found that rats would only use landmarks as a guide to food location if the landmarks were spatially stable (Biegler & Morris, 1993). Physiologically, Knierim et al. found that place and head direction cells of rats would not use landmarks to reset their firing directions if the landmarks were not consistently aligned with the rats’ sense of direction (Knierim et al. 1997). Similarly, hippocampal place cells would not use landmarks to orient their firing if the landmarks had been experienced by the rats as spatially unstable (Jeffery & O'Keefe, 1999; Fig. 2 A). This latter experiment also found that weighting could shift progressively from one cue to another: if rats were deprived of vision for only short periods of time, so that the internal sense of direction had had less time to drift and lose accuracy, cells followed the internal cues more and the cue card less: with longer periods of visual deprivation the balance reversed, and cells were more likely to be ‘reset’ by the landmark (Fig. 2 B). Thus, it seems that the weighting of cues can be adjusted by experience of their relative reliability.

Figure 2. Re‐weighting of internal vs. external directional cue use by hippocampal place cells .

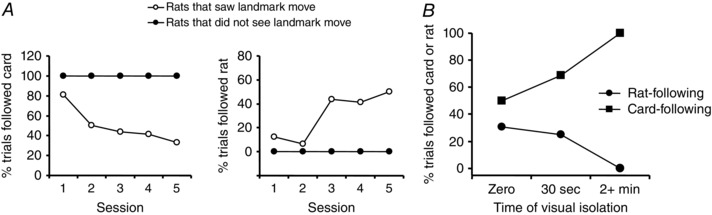
Figure 2

Open in a new tab

Place field rotation was assessed in rats exposed to a combination of landmark cue‐card rotation and self‐rotation: rats either saw the cue card move, or did not. A, for those that saw the cue card move, cells stopped rotating with (‘following’) it (left) and started rotating with the rat's internal direction sense (right). B, the longer the rats were deprived of visual cues, the less likely they were to rotate with the rat and the more likely they were to rotate with the cue card. This suggests that the propensity to follow one or other cue type was a function of its reliability (longer visual deprivation = less reliability of internal direction sense). Adapted from Jeffery & O'Keefe (1999).

If optimal cue combination involves reliability‐weighted integration, then how might this occur at a neural level? As yet, there currently exists no generally accepted neural‐level model of how these Gaussian likelihood estimations might be accomplished by real neurons, although some investigators have started to tackle this issue (Ma et al. 2006; Fetsch et al. 2012). The head direction system may offer some new insights: it could be that the same mechanism that head direction cells use for optimal landmark use might be employed for optimal cue combination in other sensory systems too.

The head direction ring attractor

To begin with we will examine the basic principles of landmark processing by the head direction system, before turning to the question of how the network might achieve cue combination. The basis of the head direction signal, generated in the brainstem (Clark & Taube, 2012), is thought to comprise a ring attractor (Skaggs et al. 1995; Zhang, 1996), in which excitatory interconnections between neurons of similar preferred directions (e.g. two ‘north’ neurons both firing when the animal faces north) cooperate with inhibitory interconnections between neurons with dissimilar preferences (‘north’ vs. ‘south’, etc.) to restrict activity to just one part of the imaginary ring of neurons (Fig. 3 A). Activity can be moved from one part of the ring to another, either by the animal's own movements or by detection of familiar landmarks which adjust the signal to correct errors (Fig. 3 B). Note that in mammals, these neurons are not arranged in an actual physical ring (Fig. 3 C), although recent evidence suggests that in insects they might be (Seelig & Jayaraman, 2015). While the generative and updating parts of this process are intrinsic and may even operate in the absence of visual landmark information (in the dark, or – in infant rats – pre‐eye‐opening (Bjerknes et al. 2015; Tan et al. 2015), the landmark‐based setting and resetting depend on learned information about the environment and about which elements of it are stable and thus useful as directional indicators. Since excitatory interconnections have not been observed in the known head direction areas, variants of the basic attractor model have been proposed that use inhibitory interconnections to achieve the same result (Song & Wang, 2005). The lack of excitatory interconnections may be due to the deleterious effect these are predicted to have on the speed of updating during movement (Page et al. 2015).

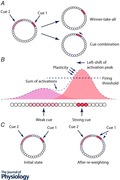
Figure 3. Hypothetical ring attractor structure for neurons in the rodent head direction system .

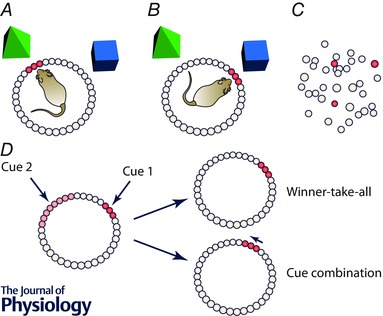
Figure 3

Open in a new tab

The diagram shows neurons arranged according to their preferred firing direction. A, when the animal faces a landmark, neurons corresponding to that facing direction become activated (shown in red). B, when the animal turns to face a new landmark, the combination of internally generated self‐motion information together with the sight of the new landmark now drives activity in the part of the network corresponding to the animal's new facing direction. C, the physical arrangement of the neurons is thought to be random in mammals. D, when two cues simultaneously try to drive activity in different parts of the network (for example, due to conflict between the rat's current directional estimate and the relevant landmark), theory makes one of two predictions. In a winner‐take‐all scenario, the strongest cue dominates, and activity moves to the appropriate part of the network. In cue combination, both cues influence the final outcome to a degree proportional to their intensity and/or reliability, with the final result being a compromise.

The attractor model in its simplest form predicts that sensory cue integration should be not Bayesian but rather ‘winner take all’, with the strongest cue dominating over all the others, because the sensory cue with the strongest inputs to the attractor would continue to preferentially drive activity in that part of the ring until the activity moves there (Touretzky, 2005). Thus, when there are conflicting information sources onto head direction cells (Fig. 3 D), one source should always win out. However, numerous experiments over many years show that when there is a conflict between a landmark and the current state of the network (‘current state’ being the animal's current estimate of its directional heading) then the landmark's correction of the error is incomplete (see Knight et al. (2014) for a compilation of these studies). This incomplete correction is manifested as an under‐rotation of the head direction cell's firing direction relative to the cue rotation, and indicates that the strongest cues – the landmarks – do not always capture the network completely. The degree to which the system compromises between the two cue sets – the cues that supported the initial firing direction, and the now‐rotated landmarks that drive the new one – can be a function of experience (Knight et al. 2014) suggesting that head direction cells can also perform weighted cue integration.

How could a ring attractor perform weighted cue integration, in light of the capture dynamics discussed above? Given the two basic premises, (i) that weighted cue integration requires the resulting final activation on the ring attractor to be located between the two initial external (cue‐driven) inputs, but closer to the stronger one, and (ii) that activation of a ring attractor will always settle to a stable state centred at the location of the strongest drive onto the ring attractor, then logically, there is only one solution, which is to dynamically rewire the connections so that the incoming afferents shift their drive onto the ring to the desired intermediate location. In other words, for cue integration, inputs should be adjusted so that the strongest drive onto the attractor is the location corresponding to the integrated decision. For this shift to occur, there needs to be plasticity that alters the pattern of incoming synaptic weights. This plasticity would have to occur rapidly and dynamically as the attractor is processing the cues, so that the strongest cue comes to drive activation at a new location predicted by a weighted combination of the two original contributing cues.

In a recent modelling study we have found that Hebbian long‐term potentiation (LTP) based on co‐activation of pre‐ and postsynaptic neurons, combined with long‐term depression (LTD) due to synaptic weight vector renormalisation, can in principle accomplish this re‐weighting, in the direction and by the amount required (Page et al. 2013). To see how this could occur, this re‐weighting process is shown using a linearised attractor in Fig. 4. The pattern of drive from the two cue sets, one broad/weak (corresponding to the activation of the network from self‐motion – ‘idiothetic’ – cues, and corresponding to current head direction estimate) and one narrow/strong (corresponding to a landmark), is shown by the two Gaussian curves, whose ‘reach’ far exceeds the zone of actual cell spiking (shown as red cells in the figure). Because of an additive co‐activation effect in the overlap zone between the weak and strong cues, plasticity occurs in the connections onto those cells within reach of both of the activations. This has the effect of selectively strengthening those connections only, such that the distribution of synaptic weights now becomes shifted in the direction of the weaker cue, although still remaining close to the strong one. As this process iterates, activation eventually comes to settle in in the intermediate portion of the ring, between the two cues but closer to the stronger one, exactly as required.

Figure 4. Shift of activation in a ring attractor network from a strong cue towards a weaker one .

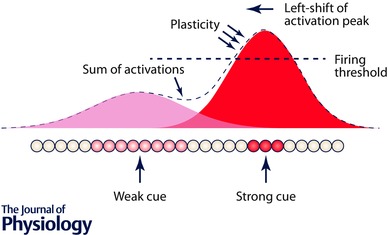
Figure 4

Open in a new tab

The attractor is shown linearised for convenience; the Gaussian curves depict the external drive (from sensory cues; idiothetic for the weak cue and landmark‐based for the strong one) onto the network. Because of the overlap of this drive, an asymmetry of activation occurs, with greater activation in the zone between the two cues. For the stronger cue, which is able to drive neurons to their activation threshold, this asymmetry results in asymmetric synaptic strengthening (dashed line), which will result in a shift of the activation peak in the direction of overlap, with the final result as shown in Fig. 1.

Landmark‐learning and dynamic re‐weighting

Dynamic re‐weighting can in principle explain within‐trial cue integration; it can account for the online adjustment of the head direction signal when there is a transient mismatch. However, a second important function of cue conflict resolution is to produce long‐term learning about relevant and irrelevant landmarks. If a landmark is unstable, for example, then it may fail to acquire the ability to influence, or ‘reset’, the head direction network (Knierim et al. 1997; Jeffery, 1998). Even if a landmark is spatially stable, its proximal location relative to an exploring animal may mean that it is located at many different directions relative to the animal and hence is not useful as a directional cue (Zugaro et al. 2001). In such cases, it is necessary to disconnect the irrelevant (i.e. unstable) landmarks from the network so that they can no longer drive head direction cell activity (Fig. 5 A), and also necessary to strengthen the relevant ones so that they can reorient the head direction network in future. How does this occur?

Figure 5. Disconnection (‘re‐weighting’) of spatially unstable sensory cues from the head direction cell attractor network .

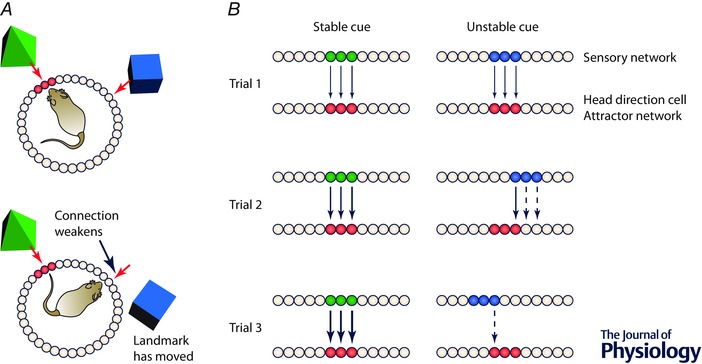
Figure 5

Open in a new tab

A, top, landmarks become associated with activation of the HD ring attractor by Hebbian re‐weighting, forming strong connections (red arrows). Bottom, when a landmark moves, the existing connection with the ring attractor weakens (dotted arrow). B, how unstable landmarks could become disconnected by Hebbian re‐weighting. When a given set of sensory neurons has activity reliably associated with the same set of head direction neurons (left‐hand panels), connections become stronger by Hebbian associativity. If the cues are spatially unstable (right‐hand panels) and are associated with different parts of the attractor network on different trials, the connections will weaken by an anti‐Hebbian mechanism (Hebb–Stent rule) and connections will lose strength.

For this, we need to recruit longer term plasticity, that lasting days or more. Using a Hebb–Stent rule in which connections become stronger with repeated agreement, while with repeated conflicts then the connections become weaker (Fig. 5 B), the system could become strongly attached to stable landmarks (those that constantly agree with the attractor state) while disconnecting from unstable ones. In this way the system is able to assimilate long‐term learning about landmark reliability, and in so doing establish a stable reference frame which can be used in short‐term correction of a drifted ring attractor network.

Future directions

How could cue combination in the head direction system be investigated further? The first task is to identify where, in the head direction network, such plasticity (both short‐ and long‐term) between landmarks and the ring attractor might occur. Likely candidate areas are the cortical head direction areas, including retrosplenial cortex (RSC), postsubiculum (PoS) and medial entorhinal cortex (MEC; Yoder et al. 2011), because of their proximity to the incoming sensory signals pertaining to landmarks. RSC and PoS cortices both have direct connections with primary visual areas (Vogt & Miller, 1983), and it seems likely that these two areas perform different functions that may be related to visual landmark processing, although what these might be remains a mystery. Interestingly, evidence from human neuroimaging suggests a function for RSC in learning about landmark stability, both in processing familiar landmarks (Auger et al. 2012) and in learning about novel ones (Auger et al. 2015). Humans also show RSC activation guided by local environmental cues rather than by global directional ones (Marchette et al. 2014). In further support of a role for RSC in landmark processing, we have recently found neurons in dysgranular RSC that respond to environmental directional cues in preference to the main head direction signal (Jacob et al. 2016), suggesting that this region might indeed be the interface between landmarks and the head direction ring attractor. The cortical head direction areas also show plasticity (Garden et al. 2009; Dumont et al. 2012; Shires et al. 2013). Little is yet known about the interactions between these three cortical structures, nor of how such interactions may adapt with experience, but it seems likely that this would be the place to start looking for such cue combination processes.

Having identified the locus of plasticity, the next step is to determine what happens when a cue is moved. The first prediction of our model is that blocking synaptic plasticity should abolish the undershoot of head direction cells in response to a shifted landmark. Although the mechanisms of synaptic plasticity in this system have not yet been identified, a good place to start would be the NMDA receptor, since these receptors have been widely implicated in plasticity in a wide range of brain systems (Sweatt, 2016). Ultimately, however, imaging of dendritic networks will be necessary to determine how the pattern of incoming landmark projections alters with learning.

The third task is to find out where in the system the putative attractor dynamics occur. The attractor hypothesis, well established though it is, still lacks strong experimental support (Knierim & Zhang, 2012) but it remains a compelling idea, and one that has applicability to other brain systems (Hopfield, 1982; Lansner, 2009). If so, then perhaps the ideas about cue combination presented here have general utility: in any attractor system we can apply the notion of short‐term dynamic plasticity acting to ‘drag’ the network state as it tries to move towards one cue and away from another, together with long‐term plasticity acting to re‐weight the cues, and in doing so yield a potential mechanism for cue combination in these other domains too.

Conclusion

This review has examined optimal cue combination, a widely studied form of perceptual decision‐making and learning, in the context of landmark learning by the head direction network. Understanding this network is important in understanding spatial cognition, but more than that, it is a simple perceptual/cognitive system that provides a useful model system with which to study the neural basis of sensory processing. We have reviewed the proposal that the head direction system might undertake optimal cue combination by re‐weighting the incoming inputs from landmarks, as a function of experience of their stability. This re‐weighting achieves, in practical terms, the same reliability‐weighted cue combination that has been seen experimentally in a variety of settings, and modelled mathematically by maximum likelihood estimation. We suggest that such synaptic plasticity might subserve cue combination in other sensory domains too.

Additional information

Competing interests

The authors declare no competing interests.

Author contributions

K.J. wrote the paper, K.J., H.P. and S.S. contributed ideas and discussion. All authors approved the final version of the manuscript and confirm that all persons designated as authors qualify for authorship, and all those who qualify for authorship are listed.

Funding

This work was supported by grants to K.J. from the Medical Research Council (G1100669), Biotechnology and Biological Sciences Research Council (BB/J009792/1) and the Wellcome Trust (WT103896AIA), and to S.S. from The Hintze Family Foundation.

Acknowledgements

The authors would like to thank Daniel Walters for useful discussion.

Biographies

Kate Jeffery is Professor of behavioural Neuroscience at University College London, and Director of the Institute of Behavioural Neuroscience (IBN) in the department of Experimental Psychology. She currently holds a Wellcome Investigator Award with which she is investigating the neural basis of the brain's representation of complex space.

graphic file with name TJP-594-6527-g001.gif

Hector Page is a postdoctoral researcher working with Jeffery at the IBN; he was formerly a DPhil student with Stringer at the Oxford Foundation for Theoretical Neuroscience and Artificial Intelligence (OFTNAI).

Simon Stringer has been a research mathematician at Oxford University for about 25 years. He has worked across various areas of applied mathematics such as control systems, computational aerodynamics and epidemiology. For the last decade, he has led OFTNAI.

References

  1. Alais D & Burr D (2004). The ventriloquist effect results from near‐optimal bimodal integration. Curr Biol 14, 257–262. [DOI] [PubMed] [Google Scholar]
  2. Auger SD, Mullally SL & Maguire EA (2012). Retrosplenial cortex codes for permanent landmarks. PLoS One 7, e43620. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Auger SD, Zeidman P & Maguire EA (2015). A central role for the retrosplenial cortex in de novo environmental learning. Elife 4, DOI: 10.7554/eLife.09031. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Biegler R & Morris RG (1993). Landmark stability is a prerequisite for spatial but not discrimination learning. Nature 361, 631–633. [DOI] [PubMed] [Google Scholar]
  5. Bjerknes TL, Langston RF, Kruge IU, Moser EI & Moser MB (2015). Coherence among head direction cells before eye opening in rat pups. Curr Biol 25, 103–108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Blair HT & Sharp PE (1996). Visual and vestibular influences on head‐direction cells in the anterior thalamus of the rat. Behav Neurosci 110, 643–660. [DOI] [PubMed] [Google Scholar]
  7. Cheng K, Shettleworth SJ, Huttenlocher J & Rieser JJ (2007). Bayesian integration of spatial information. Psychol Bull 133, 625–637. [DOI] [PubMed] [Google Scholar]
  8. Clark BJ & Taube JS (2012). Vestibular and attractor network basis of the head direction cell signal in subcortical circuits. Front Neural Circuits 6, 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Dumont JR, Amin E, Poirier GL, Albasser MM & Aggleton JP (2012). Anterior thalamic nuclei lesions in rats disrupt markers of neural plasticity in distal limbic brain regions. Neuroscience 224, 81–101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Ernst MO & Banks MS (2002). Humans integrate visual and haptic information in a statistically optimal fashion. Nature 415, 429–433. [DOI] [PubMed] [Google Scholar]
  11. Fetsch CR, Pouget A, DeAngelis GC & Angelaki DE (2012). Neural correlates of reliability‐based cue weighting during multisensory integration. Nat Neurosci 15, 146–154. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Garden DLF, Massey PV, Caruana DA, Johnson B, Warburton EC, Aggleton JP & Bashir ZI (2009). Anterior thalamic lesions stop synaptic plasticity in retrosplenial cortex slices: expanding the pathology of diencephalic amnesia. Brain 132, 1847–1857. [DOI] [PubMed] [Google Scholar]
  13. Hopfield JJ (1982). Neural networks and physical systems with emergent collective computational abilities. Proc Natl Acad Sci USA 79, 2554–2558. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Jacob P, Casali G, Spieser L & Page H (2016). Uncoupling of dysgranular retrosplenial “head direction” cells from the global head direction network. bioRxiv, doi: 10.1101/062042. [Google Scholar]
  15. Jeffery KJ (1998). Learning of landmark stability and instability by hippocampal place cells. Neuropharmacology 37, 677–687. [DOI] [PubMed] [Google Scholar]
  16. Jeffery KJ & O'Keefe J (1999). Learned interaction of visual and idiothetic cues in the control of place field orientation. Exp Brain Res 127, 151–161. [DOI] [PubMed] [Google Scholar]
  17. Knierim JJ, Kudrimoti HS & McNaughton BL (1997). Place cells, head direction cells, and the learning of landmark stability. J Neurosci 15, 1648–1659. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Knierim JJ & Zhang K (2012). Attractor dynamics of spatially correlated neural activity in the limbic system. Annu Rev Neurosci 35, 267–285. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Knight R, Piette CE, Page H, Walters D, Marozzi E, Nardini M, Stringer S & Jeffery KJ (2014). Weighted cue integration in the rodent head direction system. Philos Trans R Soc Lond B Biol Sci 369, 20120512. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Knill DC & Pouget A (2004). The Bayesian brain: The role of uncertainty in neural coding and computation. Trends Neurosci 27, 712–719. [DOI] [PubMed] [Google Scholar]
  21. Knill DC & Saunders JA (2003). Do humans optimally integrate stereo and texture information for judgments of surface slant? Vision Res 43, 2539–2558. [DOI] [PubMed] [Google Scholar]
  22. Lansner A (2009). Associative memory models: from the cell‐assembly theory to biophysically detailed cortex simulations. Trends Neurosci 32, 178–186. [DOI] [PubMed] [Google Scholar]
  23. Ma WJ, Beck JM, Latham PE & Pouget A (2006). Bayesian inference with probabilistic population codes. Nat Neurosci 9, 1432–1438. [DOI] [PubMed] [Google Scholar]
  24. Marchette SA, Vass LK, Ryan J & Epstein RA (2014). Anchoring the neural compass: coding of local spatial reference frames in human medial parietal lobe. Nat Neurosci 17, 1598–1606. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Page HJ, Walters DM, Knight R, Piette CE, Jeffery KJ & Stringer SM (2013). A theoretical account of cue averaging in the rodent head direction system. Philos Trans R Soc Lond B Biol Sci 369, 20130283. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Page HJI, Walters D & Stringer SM (2015). Architectural constraints are a major factor reducing path integration accuracy in the rat head direction cell system. Front Comput Neurosci 9, 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Seelig JD & Jayaraman V (2015). Neural dynamics for landmark orientation and angular path integration. Nature 521, 186–191. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Shams L, Ma WJ & Beierholm U (2005). Sound‐induced flash illusion as an optimal percept. Neuroreport 16, 1923–1927. [DOI] [PubMed] [Google Scholar]
  29. Shires KL, Hawthorne JP, Hope AMJ, Dudchenko PA, Wood ER & Martin SJ (2013). Functional connectivity between the thalamus and postsubiculum: Analysis of evoked responses elicited by stimulation of the laterodoursal thalamic nucleus in anaesthetized rats. Hippocampus 23, 559–569. [DOI] [PubMed] [Google Scholar]
  30. Skaggs WE, Knierim JJ, Kudrimoti HS & McNaughton BL (1995). A model of the neural basis of the rat's sense of direction. Adv Neural Inf Process Syst 7, 173–180. [PubMed] [Google Scholar]
  31. Song P & Wang X‐J (2005). Angular path integration by moving “hill of activity”: a spiking neuron model without recurrent excitation of the head‐direction system. J Neurosci 25, 1002–1014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Sweatt JD (2016). Neural plasticity and behaviour – sixty years of conceptual advances. J Neurochem 139, 179–199. [DOI] [PubMed] [Google Scholar]
  33. Tan HM, Bassett JP, O'Keefe J, Cacucci F & Wills TJ (2015). The development of the head direction system before eye opening in the rat. Curr Biol 25, 479–483. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Taube JS (2007). The head direction signal: origins and sensory‐motor integration. Annu Rev Neurosci 30, 181–207. [DOI] [PubMed] [Google Scholar]
  35. Taube JS & Burton HL (1995). Head direction cell activity monitored in a novel environment and during a cue conflict situation. J Neurophysiol 74, 1953–1971. [DOI] [PubMed] [Google Scholar]
  36. Taube JS, Muller RU & Ranck JB (1990). Head‐direction cells recorded from the postsubiculum in freely moving rats. 1. Description and quantitative analysis. J Neurosci 10, 420–435. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Touretzky DS (2005). Attractor network models of head direction cells. In Head Direction Cells and the Neural Mechanisms Underlying Directional Orientation, ed. Wiener SI. & Taube JS, pp. 411–432. MIT Press, Cambridge, MA. [Google Scholar]
  38. Vogt BA & Miller MW (1983). Cortical connections between rat cingulate cortex and visual, motor, and postsubicular cortices. J Comp Neurol 216, 192–210. [DOI] [PubMed] [Google Scholar]
  39. Yoder RM, Clark BJ & Taube JS (2011). Origins of landmark encoding in the brain. Trends Neurosci 34, 561–571. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Zhang K (1996). Representation of spatial orientation by the intrinsic dynamics of the head‐direction cell ensemble: a theory. J Neurosci 16, 2112–2126. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Zugaro MB, Berthoz A & Wiener SI (2001). Background, but not foreground, spatial cues are taken as references for head direction responses by rat anterodorsal thalamus neurons. J Neurosci 21, RC154. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from The Journal of Physiology are provided here courtesy of The Physiological Society

RESOURCES