Significance
As datasets get larger and more complex, there is a growing interest in using machine-learning methods to enhance scientific analysis. In many settings, considerable work is required to make standard machine-learning methods useful for specific scientific applications. We find, however, that in the case of treatment effect estimation with randomized experiments, regression adjustments via machine-learning methods designed to minimize test set error directly induce efficient estimates of the average treatment effect. Thus, machine-learning methods can be used out of the box for this task, without any special-case adjustments.
Keywords: high-dimensional confounders, randomized trials, regression adjustment
Abstract
We study the problem of treatment effect estimation in randomized experiments with high-dimensional covariate information and show that essentially any risk-consistent regression adjustment can be used to obtain efficient estimates of the average treatment effect. Our results considerably extend the range of settings where high-dimensional regression adjustments are guaranteed to provide valid inference about the population average treatment effect. We then propose cross-estimation, a simple method for obtaining finite-sample–unbiased treatment effect estimates that leverages high-dimensional regression adjustments. Our method can be used when the regression model is estimated using the lasso, the elastic net, subset selection, etc. Finally, we extend our analysis to allow for adaptive specification search via cross-validation and flexible nonparametric regression adjustments with machine-learning methods such as random forests or neural networks.
Randomized controlled trials are often considered the gold standard for estimating the effect of an intervention, as they allow for simple model-free inference about the average treatment effect on the sampled population. Under mild conditions, the mean observed outcome in the treated sample minus the mean observed outcome in the control sample is a consistent and unbiased estimator for the population average treatment effect.
However, the fact that model-free inference is possible in randomized controlled trials does not mean that it is always optimal: As argued by Fisher (1), if we have access to auxiliary features that are related to our outcome of interest via a linear model, then controlling for these features using ordinary least squares will reduce the variance of the estimated average treatment effect without inducing any bias. This line of research has been thoroughly explored: Under low-dimensional asymptotics where the problem specification remains fixed while the number of samples grows to infinity, it is now well established that regression adjustments are always asymptotically helpful—even in misspecified models—provided we add full treatment-by-covariate interactions to the regression design and use robust standard errors (2–10).
The characteristics of high-dimensional regression adjustments are less well understood. In a recent advance, Bloniarz et al. (11) show that regression adjustments are at least sometimes helpful in high dimensions: Given an “ultrasparsity” assumption from the high-dimensional inference literature, they establish that regression adjustments using the lasso (12, 13) are more efficient than model-free inference. This result, however, leaves a substantial gap between the low-dimensional regime—where regression adjustments are always asymptotically helpful—and the high-dimensional regime where we have only special-case results.
In this paper, we show that high-dimensional regression adjustments to randomized controlled trials work under much greater generality than previously known. We find that any regression adjustment with a free intercept yields unbiased estimates of the treatment effect. This result is agnostic as to whether the regression model was obtained using the lasso, the elastic net (14), subset selection, or any other method that satisfies this criterion. We also propose a simple procedure for building practical confidence intervals for the average treatment effect.
Furthermore, we show that the precision of the treatment effect estimates obtained by such regression adjustments depends only on the prediction risk of the fitted regression adjustment. In particular, any risk-consistent regression adjustment can be made to yield efficient estimates of the average treatment effect in the sense of refs. 15–18. Thus, when choosing which regression adjustment to use, practitioners are justified in using standard model selection tools that aim to control prediction error, e.g., Mallow’s Cp or cross-validation.
This finding presents a striking contrast to the theory of high-dimensional regression adjustments in observational studies. In a setting where treatment propensity may depend on covariates, simply fitting low-risk regression models to the treatment and control samples via cross-validation is not advised, as there exist regression adjustments that have low predictive error but yield severely biased estimates of the average treatment effect (19–22). Instead, special-case procedures are needed: For example, Belloni et al. (21) advocate a form of augmented model selection that protects against bias at the cost of worsening the predictive performance of the regression model. The tasks of fitting good high-dimensional regression adjustments to randomized vs. observational data thus present qualitatively different challenges.
The first half of this paper develops a theory of regularized regression adjustments with high-dimensional Gaussian designs. This analysis enables us to highlight the connection between the predictive accuracy of the regression adjustment and the precision of the resulting treatment effect estimate and also to considerably improve on theoretical guarantees available in prior work. In the second half of the paper, we build on these insights to develop cross-estimation, a practical method for inference about average treatment effects that can be paired with either high-dimensional regularized regression or nonparametric machine-learning methods.
1. Setting and Notation
We frame our analysis in terms of the Neyman–Rubin potential outcomes model (23, 24). Given n i.i.d. observations we posit potential outcomes and then, the outcome that we actually observe is We focus on randomized controlled trials, where is independent of all pretreatment characteristics,
| [1] |
We take the predictors to be generated as and assume a homoskedastic linear model in each arm,
| [2] |
for where is mean-zero noise with variance more general models are considered later. We use the notation and We study inference about the average treatment effect In our analysis, it is sometimes also convenient to study estimation of the conditional average treatment effect
| [3] |
As discussed by ref. 17, good estimators for are generally good estimators for τ and vice versa. In the homogeneous treatment effects model τ and coincide.
All technical derivations can be found in the Supporting Information, A. Proofs.
2. Regression Adjustments with Gaussian Designs
Suppose that we have obtained parameter estimates for the linear model Eq. 2 via the lasso, the elastic net, or any other method. We then get a natural estimator for the average treatment effect:
| [4] |
In the case where is the ordinary least-squares estimator for the behavior of this estimator has been carefully studied by refs. 8 and 10. Our goal is to characterize its behavior for generic regression adjustments all while allowing the number of predictors p to be much larger than the sample size n.
The only assumption that we make on the estimation scheme is that it be centered: For
| [5] |
i.e., the mean of the predicted outcomes matches that of the observed outcomes; and is translation invariant and depends only on
| [6] |
Here, and denote the mean of the outcomes and features over all observations with Algorithmically, a simple way to enforce this constraint is to first center the training samples run any regression method on these centered data, and then set the intercept using Eq. 5; this is done by default in standard software for regularized regression, such as glmnet (25). We also note that ordinary least-squares regression is always centered in this sense, even after common forms of model selection.
Now, if our regression adjustment has a well-calibrated intercept as in Eq. 5, then we can write Eq. 4 as
| [7] |
To move forward, we focus on the case where the data-generating model for is Gaussian; i.e., for some and positive-semidefinite matrix and For our purpose, the key fact about Gaussian data is that the mean of independent samples is independent of the within-sample spread; i.e.,
| [8] |
conditionally on the treatment assignments Thus, because depends only on the centered data and we can derive a simple expression for the distribution of The following is an exact finite sample result and holds no matter how large p is relative to n; a key observation is that is mean zero by randomization of the treatment assignment, for
Proposition 1.
Suppose that our regression scheme for and is centered and that our data-generating model is Gaussian as above. Then, writing for
| [9] |
If the errors in and are roughly orthogonal, then
| [10] |
and, in any case, twice the right-hand side is always an upper bound for the left-hand side. Thus, the distribution of effectively depends on the regression adjustments only through the excess predictive error
| [11] |
where the above expectation is taken over a test set example X. This implies that, in the setting of Proposition 1, the main practical concern in choosing which regression adjustment to use is to ensure that has low predictive error.
The above result is conceptually related to recent work by Berk et al. (3) (also ref. 26), who showed that the accuracy of low-dimensional covariate adjustments using ordinary least-squares regression depends on the mean-squared error of the regression fit; they also advocate using this connection to provide simple asymptotic inference about τ. Here, we showed that a similar result holds for any regression adjustment on Gaussian designs, even in high dimensions; and in the second half of this paper we discuss how to move beyond the Gaussian case.
Risk Consistency and the Lasso.
As stated, Proposition 1 provides the distribution of conditionally on and so is not directly comparable to related results in the literature. However, whenever is risk consistent in the sense that
| [12] |
for we can asymptotically omit the conditioning.
Theorem 2.
Suppose that, under the conditions of Proposition 1, we have a sequence of problems where is risk consistent (Eq. 12), and Then,
| [13] |
or, in other words, is efficient for estimating (15–18).
In the case of the lasso, Theorem 2 lets us substantially improve over the best existing guarantees in the literature (11). The lasso estimates as the minimizer over β of
| [14] |
for some penalty parameter Typically, the lasso is used when we believe a sparse regression adjustment to be appropriate. In our setting, it is well known that the lasso satisfies provided the penalty parameter λ is well chosen and does not allow for too much correlation between features (27, 28).
Thus, whenever we have a sequence of problems as in Theorem 2 where is k-sparse, i.e., has at most k nonzero entries, and we find that is efficient in the sense of Eq. 13. Note that this result is much stronger than the related result of ref. 11, which shows that lasso regression adjustments yield efficient estimators in an ultrasparse regime with
To illustrate the difference between these two results, it is well known that if then it is possible to do efficient inference about the coefficients of the underlying parameter vector β (29–31), and so the result of ref. 11 is roughly in line with the rest of the literature on high-dimensional inference. Conversely, if we have only accurate inference about the coefficients of β is in general impossible without further conditions on the covariance of X (32, 33). However, we have shown that we can still carry out efficient inference about τ. In other words, the special structure present in randomized trials means that much more is possible than in the generic high-dimensional regression setting.
Inconsistent Regression Adjustments.
Even if our regression adjustment is not risk consistent, we can still use Proposition 1 to derive unconditional results about whenever
| [15] |
We illustrate this phenomenon in the case of ridge regression, where regression adjustments generally reduce—but do not eliminate—excess test-set risk. Recall that ridge regression estimates as the minimizer over β of
| [16] |
The following result relies on random-matrix theoretic tools for analyzing the predictive risk of ridge regression (34).
Theorem 3.
Suppose we have a sequence of problems in the setting of Proposition 1 with and such that the spectrum of the covariance has a weak limit. Following ref. 34, suppose moreover that the true parameters and are independently and randomly drawn from a random-effects model with
| [17] |
Then, selecting in Eq. 4 via ridge regression tuned to minimize prediction error, and with we get
| [18] |
where the are the companion Stieltjes transforms of the limiting empirical spectral distributions for the treated and control samples, as defined in the proof.
To interpret this result, we note that the quantity can also be induced via the limit (35, 36)
Finally, we note that the limiting variance of obtained via ridge regression above is strictly smaller than the corresponding variance of the unadjusted estimator, which converges to this is because optimally tuned ridge regression strictly improves over the “null” model in terms of its predictive accuracy.
3. Practical Inference with Cross-Estimation
In the previous section, we found that—given Gaussianity assumptions—generic regression adjustments yield unbiased estimates of the average treatment effect and also that low-risk regression adjustments lead to high-precision estimators. Here, we seek to build on this insight and to develop simple inferential procedures about τ and that attain the above efficiency guarantees, all while remaining robust to deviations from Gaussianity or homoskedasticity.
Our approach is built around cross-estimation, a procedure inspired by data splitting and the work of refs. 37 and 38. We first split our data into K equally sized folds (e.g., ) and then, for each fold we compute
| [19] |
Here, etc., are moments taken over the kth fold, whereas and are centered regression estimators computed over the other folds. We then obtain an aggregate estimate where is the number of observations in the kth fold. An advantage of this construction is that an analog to the relation Eq. 8 now automatically holds, and thus our treatment effect estimator is unbiased without assumptions. Note that the result below references both the average treatment effect τ and the conditional average treatment effect
Theorem 4.
Suppose that we have n independent and identically distributed samples satisfying Eq. 1, drawn from a linear model Eq. 2, where has finite first moments and the conditional variance of given may vary. Then, If, moreover, the are all risk consistent in the sense of Eq. 12 for and both the signals and residuals are asymptotically Gaussian when averaged, then writing we have
| [20] |
In the homoskedastic case, i.e., when the variance of conditionally on X does not depend on X, then the above is efficient. With heteroskedasticity, the above is no longer efficient because we are in a linear setting and so inverse-variance weighting could improve precision; however, Eq. 20 can still be used as the basis for valid inference about τ.
Confidence Intervals via Cross-Estimation.
Another advantage of cross-estimation is that it allows for moment-based variance estimates for Here, we discuss practical methods for building confidence intervals that cover the average treatment effect τ. We can verify that the variance of is after conditioning on the and with
| [21] |
Now, the above moments correspond to observable quantities on the kth data fold, so we immediately obtain a moment-based plug-in estimator for Finally, we build α-level confidence intervals for τ as
| [22] |
where is the appropriate standard Gaussian quantile. In the setting of Theorem 4, i.e., with risk consistency and bounded second moments, we can verify that the are asymptotically uncorrelated and so the above confidence intervals are asymptotically exact.
Cross-Validated Cross-Estimation.
High-dimensional regression adjustments usually rely on a tuning parameter that controls the amount of regularization, e.g., the parameter λ for the lasso and ridge regression. Although theory provides some guidance on how to select λ, practitioners often prefer to use computationally intensive methods such as cross-validation.
Now, our procedure in principle already allows for cross-validation: If we estimate in Eq. 19 via any cross-validated regression adjustment that relies only on all but the kth data folds, then will be unbiased for τ. However, this requires running the full cross-validated algorithm K times, which can be very expensive computationally.
Here, we show how to obtain good estimates of using only a single round of cross-validation. First, we specify K regression folds, and for each and we compute and as the mean of all observations in the kth fold with Next, we center the data such that and for all observations in the kth fold. Finally, we estimate by running a standard out-of-the-box cross-validated algorithm (e.g., cv. glmnet for R) on the triples with the same K folds as specified before and then use Eq. 19 to compute
The actual estimator that we use to estimate and in our experiments is inspired by the procedure of Imai and Ratkovic (39). Our goal is to let the lasso learn shared “main effects” for the treatment and control groups. To accomplish this, we first run a -dimensional lasso problem,
| [23] |
and then set and We simultaneously tune λ and estimate τ by cross-validated cross-estimation as discussed above. When all our data are Gaussian, this procedure is exactly unbiased by the same argument as used in Proposition 1; and even when X is not Gaussian, it appears to work well in our experiments.
4. Nonparametric Machine-Learning Methods
In our discussion so far, we have focused on treatment effect estimation using high-dimensional, linear regression adjustments and showed how to provide unbiased inference about τ under general conditions. Here, we show how to extend our results about cross-estimation to general nonparametric regression adjustments obtained using, e.g., neural networks or random forests (40). We assume a setting where
for some unknown regression functions and our goal is to leverage estimates obtained using any machine-learning method to improve the precision of as*,†
| [24] |
where is any estimator that does not depend on the ith training example; for random forests, we set to be the “out-of-bag” prediction at To motivate Eq. 24, we start from Eq. 7 and expand out terms using the relation
| [25] |
where etc. The remaining differences between Eq. 24 and Eq. 7 are due to the use of out-of-bag estimation to preserve randomization of the treatment assignment conditionally on the corresponding regression adjustment. We estimate the variance of using the formula
| [26] |
Formal Results.
The following result characterizes the behavior of this estimator, under the assumption that the estimator is “jackknife compatible,” meaning that the expected jackknife estimate of variance for converges to 0. We define this condition in Supporting Information, A. Proofs and verify that it holds for random forests.
Theorem 5.
Suppose that is jackknife compatible. Then, the estimator in Eq. 24 is asymptotically unbiased, Moreover, if the regression adjustments are risk consistent in the sense that‡ and the potential outcomes have finite second moments, then is efficient and is asymptotically standard Gaussian.
We note that there has been considerable recent interest in using machine-learning methods to estimate heterogeneous treatment effects (42–45). In relation to this literature, our present goal is more modest: We simply seek to use machine learning to reduce the variance of treatment effect estimates in randomized experiments. This is why we obtain more general results than the papers on treatment heterogeneity.
5. Experiments
In our experiments, we focus on two specific variants of treatment effect estimation via cross-estimation. For high-dimensional linear estimation, we use the lasso-based method Eq. 23 tuned by cross-validated cross-estimation. For nonparametric estimation, we use Eq. 24 with random forest adjustments. We implement our method as an open-source R package, crossEstimation, built on top of glmnet (25) and randomForest (46) for R. Supporting Information, B. Additional Simulation Results and Table S1 have additional simulation results.
Table S1.
Coverage rates for 95% nominal confidence intervals obtained by cross-validated cross-estimation with the joint lasso procedure, Eq. 23
| p | |||||||
| 60 | 500 | ||||||
| n | |||||||
| Signal | Noise | Correlation | Design | 80 | 200 | 80 | 200 |
| Dense | Gauss. X | 0.94 | 0.96 | 0.95 | 0.95 | ||
| Bern. X | 0.95 | 0.95 | 0.94 | 0.95 | |||
| Gauss. X | 0.94 | 0.94 | 0.94 | 0.95 | |||
| Bern. X | 0.93 | 0.95 | 0.93 | 0.92 | |||
| Gauss. X | 0.95 | 0.95 | 0.92 | 0.94 | |||
| Bern. X | 0.93 | 0.95 | 0.94 | 0.93 | |||
| Gauss. X | 0.93 | 0.94 | 0.93 | 0.94 | |||
| Bern. X | 0.95 | 0.96 | 0.92 | 0.94 | |||
| Geometric | Gauss. X | 0.94 | 0.95 | 0.93 | 0.94 | ||
| Bern. X | 0.92 | 0.95 | 0.94 | 0.96 | |||
| Gauss. X | 0.95 | 0.94 | 0.95 | 0.95 | |||
| Bern. X | 0.94 | 0.93 | 0.95 | 0.94 | |||
| Gauss. X | 0.94 | 0.94 | 0.94 | 0.94 | |||
| Bern. X | 0.95 | 0.94 | 0.95 | 0.95 | |||
| Gauss. X | 0.91 | 0.96 | 0.94 | 0.95 | |||
| Bern. X | 0.95 | 0.97 | 0.94 | 0.95 | |||
| Sparse | Gauss. X | 0.94 | 0.96 | 0.94 | 0.95 | ||
| Bern. X | 0.95 | 0.95 | 0.92 | 0.94 | |||
| Gauss. X | 0.92 | 0.95 | 0.93 | 0.96 | |||
| Bern. X | 0.93 | 0.95 | 0.92 | 0.97 | |||
| Gauss. X | 0.94 | 0.93 | 0.94 | 0.95 | |||
| Bern. X | 0.94 | 0.93 | 0.93 | 0.95 | |||
| Gauss. X | 0.95 | 0.94 | 0.93 | 0.95 | |||
| Bern. X | 0.94 | 0.94 | 0.94 | 0.94 | |||
All numbers are aggregated over 500 simulation runs; the above numbers thus have a standard sampling error of roughly 0.01. Bern., Bernoulli; Gauss., Gaussian.
Simulations.
We begin by validating our method in a simple simulation setting with where In all simulations, we set the features X to be Gaussian with autoregressive AR-ρ covariance. We compare our lasso-based cross-estimation with both the simple difference-in-means estimate and the proposal of Bloniarz et al. (11) that uses lasso regression adjustments tuned by cross-validation. Our method differs from that of Bloniarz et al. (11) in that we use a different algorithm for confidence intervals and also that we use the joint lasso algorithm Eq. 23 instead of computing separate lassos in both treatment arms.
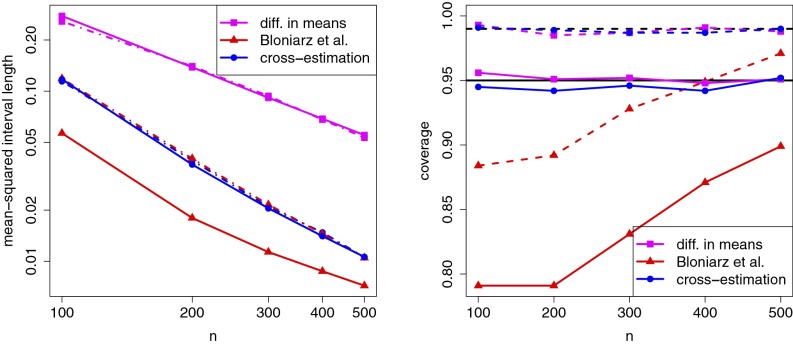
Figs. 1 and 2 display results for different choices of β, ρ, etc., while varying n. In both cases, we see that the confidence intervals produced by our cross-estimation algorithm and the method of Bloniarz et al. (11) are substantially shorter than those produced by the difference-in-means estimator. Moreover, our confidence intervals accurately represent the variance of our estimator (compare solid and dashed-dotted lines in Figs. 1 and 2, Left) and achieve nominal coverage at both the 95% and 99% levels. Conversely, especially in small samples, the method of Bloniarz et al. (11) underestimates the variance of the method and does not achieve target coverage.
Fig. 1.
Simulation results with and All numbers are based on 1,000 simulation replications. Left panel shows both the average variance estimate produced by each estimator (solid lines) and the actual variance Var[] of the estimator (dashed-dotted lines); note that is directly proportional to the squared length of the confidence interval. Right panel depicts realized coverage for both 95% confidence intervals (solid lines) and 99% confidence intervals (dashed lines).
Fig. 2.
Simulation results with β proportional to a permutation of and All numbers are based on 1,000 simulation replications. The plots are produced the same way as in Fig. 1.
Understanding Attitudes Toward Welfare.
We also consider an experimental dataset collected as a part of the General Social Survey.§ The dataset is large ( after preprocessing), so we know the true treatment effect essentially without error: The fraction of respondents who say we spend too much on assistance to the poor is smaller than the fraction of respondents who say we spend too much on welfare by 0.35. To test our method, we repeatedly drew subsamples of size from the full dataset and examined the ability of both lasso-based and random-forest–based cross-estimation to recover the correct answer. We had regressors.
First, we note that both variants of cross-estimation achieved excellent coverage. Given a nominal coverage rate of 95%, the simple difference-in-means estimator, lasso-based cross-estimation, and random-forest cross-estimation had realized coverage rates of 96.3%, 96.5%, and 95.3%, respectively, over 1,000 replications. Meanwhile, given a nominal target of 99%, the realized numbers became 99.0%, 99.0%, and 99.3%. We note that this dataset has non-Gaussian features and exhibits considerable treatment effect heterogeneity.
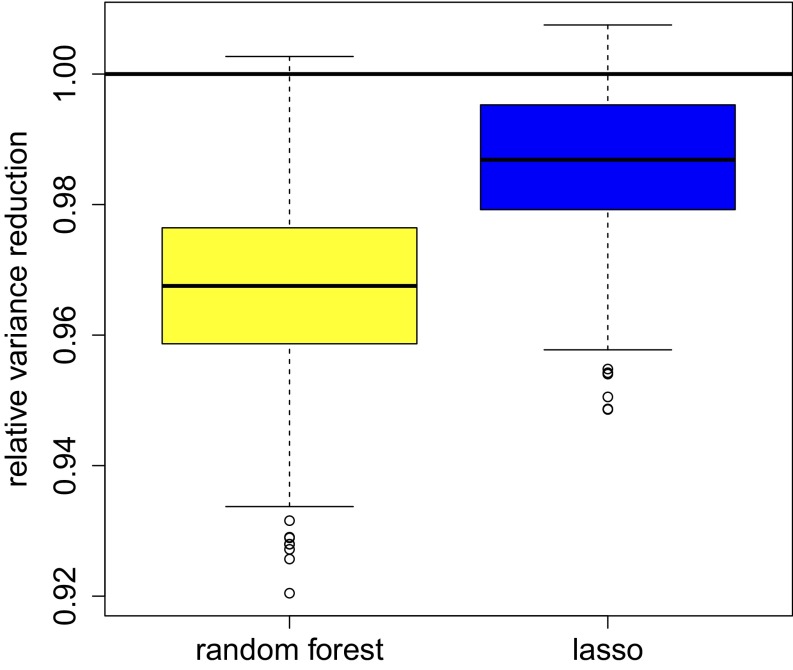
Second, Fig. 3 depicts the reduction in squared confidence interval length for individual realizations of each method. More formally, we show boxplots of where is the variance estimate used to build confidence intervals. Here, we see that although cross-estimation may not improve the precision of the simple method by a large amount, it consistently improves performance by a small amount. Moreover, in this example, random forests result in a larger improvement in precision than lasso-based cross-estimation.
Fig. 3.
Reduction in squared confidence interval length achieved by random forests and a lasso-based method, relative to the simple difference-in-means estimator. Confidence intervals rely on cross-estimation. The plot was generated using 1,000 simulation replications.
6. Discussion
In many applications of machine-learning methods to causal inference, there is a concern that the risk of specification search, i.e., trying out many candidate methods and choosing the one that gives us a significant result, may reduce the credibility of empirical findings. This has led to considerable interest in methodologies that allow for complex model-fitting strategies that do not compromise statistical inference.
One prominent example is the design-based paradigm to causal inference in observational studies, whereby we first seek to build an “observational design” by looking only at the features and the treatment assignments and reveal the outcomes only once the observational design has been set (48, 49). The observational design may rely on matching, inverse-propensity weighting, or other techniques. As the observational design is fixed before the outcomes are revealed, practitioners can devote considerable time and creativity to fine-tuning the design without compromising their analysis.
From this perspective, we have shown that regression adjustments to high-dimensional randomized controlled trials exhibit a similar opportunity for safe specification search. Concretely, imagine that once we have collected data from a randomized experiment, we provide our analyst only with class-wise centered data: and The analyst can then use these data to obtain any regression adjustment they want, which we will then plug into Eq. 4. Our results guarantee that—at least with a random Gaussian design—the resulting treatment effect estimates will be unbiased regardless of the specification search the analyst may have done using only the class-wise centered data. Cross-estimation enables us to mimic this phenomenon with non-Gaussian data.
A. Proofs
Proof of Proposition 1.
Beginning from Eq. 3, we see that
where and are as defined in the statement of Proposition 1, and Now, because of Eq. 8, we can verify that that the three summands above are independent conditionally on and with
and
Proof of Theorem 2.
Given our hypotheses, we immediately see that and The conclusion follows from Proposition 1 via Slutsky’s theorem.
Proof of Theorem 3.
For a covariance matrix we define its spectral distribution as the empirical distribution of its eigenvalues. We assume that, in our sequence of problems, converges weakly to some limiting population spectral distribution Given this assumption, it is well known that the spectra of the sample covariance matrices also converge weakly to a limiting empirical spectral distribution with probability 1 (35, 36). In this notation, the companion Stieltjes transform is defined as
Given these preliminaries and under the listed hypotheses, ref. 34 shows that the risk of optimally tuned ridge regression converges in probability,
where is the asymptotically optimal choice for λ.
Now, in our setting, we need to apply this result to the treatment and control samples separately. The asymptotically optimal regularization parameters for and are and respectively. Moreover, by spherical symmetry,
Thus, together with the above risk bounds, we find that
where and are the companion Stieltjes transforms for the control and treatment samples, respectively. The desired conclusion then follows from Proposition 1.
Proof of Theorem 4.
By randomization of the treatment assignment we have, within the kth fold and for
and
Thus, we see that
Meanwhile, writing for the set of observations in the kth fold and for the number of those observations with we can write
Now, by consistency of the regression adjustment, the third summand decays faster than and so can asymptotically be ignored. Rearranging the first two summands, we get
which has the desired asymptotic variance and is asymptotically Gaussian under the stated regularity conditions.
Proof of Theorem 5.
We begin with a definition. The estimator is jackknife compatible if, for any and a new independently drawn test point X,
| [S1] |
for some sequence The quantity inside the left-hand expectation is the popular jackknife estimate of variance for the condition requires that this variance estimate converge to 0 in expectation. We note that this condition is very weak: Most classical statistical estimators will satisfy this condition with whereas subsampled random forests of the type studied in ref. 44 satisfy it with where s is the subsample size.
Now, as in the proof of Theorem 4, we write as
where R is a residual term
The main component of is an unbiased, efficient estimator for τ. It remains to show that R is asymptotically unbiased given jackknife compatibility and is moreover asymptotically negligible if is risk consistent.
For the remainder of the proof, we focus on the setting where the regression adjustments and are computed separately on samples with and respectively. The reason R may not be exactly unbiased is that is a function of observations if whereas it is a function of observations if and this effect can create biases. Our goal is to show, however, that these biases are small for any jackknife-compatible estimator. To do so, we first define a “leave-two-out” approximation to R,
where the are predictions obtained without either the ith or the jth training examples. We see that is always computed on observations and, moreover, is independent of conditionally on Thus, we see that by randomization and moreover that under risk consistency.
To establish our desired result, it remains to show that In the case where and are computed separately on samples with and respectively, we can write
The jackknife-compatibility condition implies that
for any j with etc., and so we find that
which converges to 0 in probability at a rate faster than as desired. In the case where and are not computed separately, we attain the same result by applying the jackknife-compatibility condition on the leave-one-out estimators.
B. Additional Simulation Results
We now present additional simulation results for coverage rates of cross-validated cross-estimation, with a focus on settings with treatment heterogeneity and potentially non-Gaussian designs. In an effort to challenge our method, we used signals with very high signal-to-noise ratio. We estimate and jointly, using the procedure described in ref. 22.
In these simulations, we always used an autoregressive covariance structure with where we interpret The design matrices X were generated as where Z was either Gaussian or Bernoulli uniformly at random. The treatment assignment was random with Conditionally on and we generated Finally, we considered three different settings for the signal,
for Results are presented in Table S1. Overall, the coverage rates appear quite promising, especially noting the wide variety of simulation settings.
Footnotes
*We note that Eq. 24 depends on and implicitly only through It may thus also be interesting to estimate directly using, e.g., the “tyranny of the minority” scheme of Lin (8).
†A related estimator is studied by Rothe in the context of classical nonparametric regression adjustments, e.g., local regression, for observational studies with known treatment propensities. [Rothe C (2016) The value of knowing the propensity score for estimating average treatment effects, (IZA), discussion paper 9989.]
‡With random forests, ref. 41 provides such a risk-consistency result.
§Subjects were asked whether we, as a society, spend too much money either on “welfare” or on “assistance to the poor.” The questions were randomly assigned and the treatment effect corresponds to the change in the proportion of people who answer “yes” to the question. This dataset is discussed in detail in ref. 43; we preprocess the data as in ref. 47.
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1614732113/-/DCSupplemental.
References
- 1.Fisher R. Statistical Methods for Research Workers. Oliver and Boyd; Edinburgh, UK: 1925. [Google Scholar]
- 2.Athey S, Imbens G. 2016. The econometrics of randomized experiments. arXiv:1607.00698. [DOI] [PMC free article] [PubMed]
- 3.Berk R, et al. Covariance adjustments for the analysis of randomized field experiments. Eval Rev. 2013;37(3–4):170–196. doi: 10.1177/0193841X13513025. [DOI] [PubMed] [Google Scholar]
- 4.Ding P, Feller A, Miratrix L. 2016. Decomposing treatment effect variation. arXiv:1605.06566.
- 5.Freedman D. On regression adjustments in experiments with several treatments. Ann Appl Stat. 2008;2(1):176–196. [Google Scholar]
- 6.Freedman DA. On regression adjustments to experimental data. Adv Appl Math. 2008;40(2):180–193. [Google Scholar]
- 7.Imbens GW, Wooldridge JM. Recent developments in the econometrics of program evaluation. J Econ Lit. 2009;47(1):5–86. [Google Scholar]
- 8.Lin W. Agnostic notes on regression adjustments to experimental data: Reexamining Freedman’s critique. Ann Appl Stat. 2013;7(1):295–318. [Google Scholar]
- 9.Rosenbaum PR. Covariance adjustment in randomized experiments and observational studies. Stat Sci. 2002;17(3):286–327. [Google Scholar]
- 10.Cochran W. Sampling Techniques. 3rd Ed Wiley; New York: 1977. [Google Scholar]
- 11.Bloniarz A, Liu H, Zhang CH, Sekhon JS, Yu B. Lasso adjustments of treatment effect estimates in randomized experiments. Proc Natl Acad Sci USA. 2016;113(27):7383–7390. doi: 10.1073/pnas.1510506113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Chen S, Donoho D, Saunders M. Atomic decomposition for basis pursuit. SIAM J Sci Comput. 1998;20(1):33–61. [Google Scholar]
- 13.Tibshirani R. Regression shrinkage and selection via the lasso. J R Stat Soc B. 1996;58:267–288. [Google Scholar]
- 14.Zou H, Hastie T. Regularization and variable selection via the elastic net. J R Stat Soc B. 2005;67(2):301–320. [Google Scholar]
- 15.Bickel P, Klaassen C, Ritov Y, Wellner J. Efficient and Adaptive Estimation for Semiparametric Models. Springer; New York: 1998. [Google Scholar]
- 16.Hahn J. On the role of the propensity score in efficient semiparametric estimation of average treatment effects. Econometrica. 1998;66(2):315–331. [Google Scholar]
- 17.Imbens GW. Nonparametric estimation of average treatment effects under exogeneity: A review. Rev Econ Stat. 2004;86(1):4–29. [Google Scholar]
- 18.Robins JM, Rotnitzky A. Semiparametric efficiency in multivariate regression models with missing data. J Am Stat Assoc. 1995;90(429):122–129. [Google Scholar]
- 19.Athey S, Imbens GW, Wager S. 2016. Efficient inference of average treatment effects in high dimensions via approximate residual balancing. arXiv:1604.07125.
- 20.Belloni A, Chernozhukov V, Fernández-Val I, Hansen C. Program evaluation with high-dimensional data. Econometrica. 2016 in press. [Google Scholar]
- 21.Belloni A, Chernozhukov V, Hansen C. Inference on treatment effects after selection among high-dimensional controls. Rev Econ Stud. 2014;81(2):608–650. [Google Scholar]
- 22.Farrell MH. Robust inference on average treatment effects with possibly more covariates than observations. J Econom. 2015;189(1):1–23. [Google Scholar]
- 23.Neyman J. On the application of probability theory to agricultural experiments. Essay on principles, section 9. translation of original 1923 paper, which appeared in Roczniki Nauk Rolniczych. Stat Sci. 1990;5(4):465–472. [Google Scholar]
- 24.Rubin DB. Estimating causal effects of treatments in randomized and nonrandomized studies. J Educ Psychol. 1974;66(5):688–701. [Google Scholar]
- 25.Friedman J, Hastie T, Tibshirani R. Regularization paths for generalized linear models via coordinate descent. J Stat Softw. 2010;33(1):1–22. [PMC free article] [PubMed] [Google Scholar]
- 26.Pitkin E, et al. 2013. Improved precision in estimating average treatment effects. arXiv:1311.0291.
- 27.Bickel PJ, Ritov Y, Tsybakov AB. Simultaneous analysis of lasso and Dantzig selector. Ann Stat. 2009;37(4):1705–1732. [Google Scholar]
- 28.Meinshausen N, Yu B. Lasso-type recovery of sparse representations for high-dimensional data. Ann Stat. 2009;37(1):246–270. [Google Scholar]
- 29.Javanmard A, Montanari A. Confidence intervals and hypothesis testing for high-dimensional regression. J Mach Learn Res. 2014;15(1):2869–2909. [Google Scholar]
- 30.Van de Geer S, Bühlmann P, Ritov Y, Dezeure R. On asymptotically optimal confidence regions and tests for high-dimensional models. Ann Stat. 2014;42(3):1166–1202. [Google Scholar]
- 31.Zhang CH, Zhang SS. Confidence intervals for low dimensional parameters in high dimensional linear models. J R Stat Soc B. 2014;76(1):217–242. [Google Scholar]
- 32.Cai TT, Guo Z. 2015. Confidence intervals for high-dimensional linear regression: Minimax rates and adaptivity. arXiv:1506.05539.
- 33.Javanmard A, Montanari A. 2015. De-biasing the lasso: Optimal sample size for Gaussian designs. arXiv:1508.02757.
- 34.Dobriban E, Wager S. 2015. High-dimensional asymptotics of prediction: Ridge regression and classification. arXiv:1507.03003.
- 35.Bai Z, Silverstein JW. Spectral Analysis of Large Dimensional Random Matrices. Vol 20 Springer; New York: 2010. [Google Scholar]
- 36.Marchenko VA, Pastur LA. Distribution of eigenvalues for some sets of random matrices. Math USSR Sbornik. 1967;114(4):507–536. [Google Scholar]
- 37.Aronow PM, Middleton JA. A class of unbiased estimators of the average treatment effect in randomized experiments. J Causal Inference. 2013;1(1):135–154. [Google Scholar]
- 38.Tibshirani R, Efron B. Pre-validation and inference in microarrays. Stat Appl Genet Mol Biol. 2002;1(1):1–15. doi: 10.2202/1544-6115.1000. [DOI] [PubMed] [Google Scholar]
- 39.Imai K, Ratkovic M. Estimating treatment effect heterogeneity in randomized program evaluation. Ann Appl Stat. 2013;7(1):443–470. [Google Scholar]
- 40.Breiman L. Random forests. Mach Learn. 2001;45(1):5–32. [Google Scholar]
- 41.Scornet E, Biau G, Vert JP. Consistency of random forests. Ann Stat. 2015;43(4):1716–1741. [Google Scholar]
- 42.Athey S, Imbens G. Recursive partitioning for heterogeneous causal effects. Proc Natl Acad Sci USA. 2016;113(27):7353–7360. doi: 10.1073/pnas.1510489113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Green DP, Kern HL. Modeling heterogeneous treatment effects in survey experiments with Bayesian additive regression trees. Public Opin Q. 2012;76(3):491–511. [Google Scholar]
- 44.Hill JL. Bayesian nonparametric modeling for causal inference. J Comput Graph Stat. 2012;20(1):217–240. [Google Scholar]
- 45.Wager S, Athey S. 2015. Estimation and inference of heterogeneous treatment effects using random forests. arXiv:1510.04342.
- 46.Liaw A, Wiener M. Classification and regression by randomForest. R News. 2002;2(3):18–22. [Google Scholar]
- 47.Wager S. 2016. Causal inference with random forests. PhD thesis (Stanford University, Stanford, CA)
- 48.Rosenbaum PR. Observational Studies. Springer; New York: 2002. [Google Scholar]
- 49.Rubin DB. The design versus the analysis of observational studies for causal effects: Parallels with the design of randomized trials. Stat Med. 2007;26(1):20–36. doi: 10.1002/sim.2739. [DOI] [PubMed] [Google Scholar]