Co-clustering directed graphs to discover asymmetries and directional communities

Significance

This paper adds to the continuing and long-running interest in networks and network clustering. For directed networks, we propose the di-sim algorithm to capture asymmetries of connections and discover directional clusters. We illustrate this algorithm with three data examples: the Enron email network, the hyperlinked blog network during the 2004 US presidential election, and the chemical connections among the neurons in Caenorhabditis elegans. We identify informative and bottleneck nodes in all three networks. In particular, for the third example, di-sim finds bottleneck nodes that create a feedforward structure among clusters of nodes.

Abstract

In directed graphs, relationships are asymmetric and these asymmetries contain essential structural information about the graph. Directed relationships lead to a new type of clustering that is not feasible in undirected graphs. We propose a spectral co-clustering algorithm called di-sim for asymmetry discovery and directional clustering. A Stochastic co-Blockmodel is introduced to show favorable properties of di-sim. To account for the sparse and highly heterogeneous nature of directed networks, di-sim uses the regularized graph Laplacian and projects the rows of the eigenvector matrix onto the sphere. A nodewise asymmetry score and di-sim are used to analyze the clustering asymmetries in the networks of Enron emails, political blogs, and the Caenorhabditis elegans chemical connectome. In each example, a subset of nodes have clustering asymmetries; these nodes send edges to one cluster, but receive edges from another cluster. Such nodes yield insightful information (e.g., communication bottlenecks) about directed networks, but are missed if the analysis ignores edge direction.

Clustering is widely used to study the structure of social, biological, and technological networks because it provides an aggregated and simplified representation of the complex interactions. The difficulty of the clustering problem has inspired an extensive literature devoted to the statistical and computational issues. Spectral approximation algorithms have become popular due to their computational speed and empirical performance across domain areas.

In the clustering literature, the vast majority of the models and algorithms presumes that the interactions are symmetric or undirected. In some settings, the relationships can be well approximated as symmetric. However, asymmetric or directed relationships more fully represent the vast majority of interactions. For example, in the gene regulatory network, one gene drives the transcription of the other gene. In the power grid network, electricity flows from one node to the other. In a communication network, one node initiates the conversation. In other examples, it might be easier to observe the relationship without direction, but the direction remains of fundamental importance. For example, in a social network, a business searching for “trend leaders” wants to know the direction of influence in relationships, which is not directly observable. In a regulatory network, knockout experiments seek to estimate the direction of gene regulation. For many questions of interest, making the edges undirected does not provide an appropriate approximation. In all of these examples, the direction of the edges is essential to the function of the network. Directionality gives asymmetry to a relationship and the standard notion of clustering is insufficient to explore and appropriately aggregate asymmetric relationships in our data examples.

To extend clustering to directed networks, we use Hartigan’s notion of co-clustering, which he proposed as a way to simultaneously cluster both the rows and the columns of a two-way table (1). In the two-way data table, the rows and columns index different sets. For example, ref. 1 discusses election results with matrices that are indexed with (state $\times$ year) and ref. 2 discusses co-clusters matrices that are indexed with (document $\times$ word).

This paper carries out co-clustering on the adjacency matrix, where the rows and columns index the same set of nodes. The adjacency matrix $A\in {\left\{\mathrm{0,1}\right\}}^{n\mathrm{\times }n}$ records the pattern of edges in the network; if there is an edge starting from node $i\in \left\{1,\mathrm{\dots },n\right\}$ and ending at node $j\in \left\{1,\dots ,n\right\}$ (i.e., $i\to j$), then $A_{ij}=1$; otherwise, $A_{ij}=0$. So, the ith row of A records how node i sends edges and the ith column of A records how node i receives edges. Co-clustering this matrix yields two partitions of the same set of nodes. The row clusters contain nodes with similar sending patterns and the column clusters contain nodes with similar receiving patterns.

The proposed co-clustering algorithm di-sim is designed for sparse, heterogeneous, and directed networks. di-sim combines two basic algorithms. First, the singular value decomposition of a modified version of A generates two lower-dimensional representations, one representation for the sending relationships and the other for the receiving relationships; the outcome of this step is of independent interest for further exploratory analysis via a nodewise asymmetry score. The second basic algorithm within di-sim is the clustering step via k means. By separating the sending and receiving information, di-sim can discover the asymmetries in the relationships and describe the directional communities. Two additional steps––(i) regularization in the modification of A and (ii) projection of the lower-dimensional representations––are included in di-sim to improve the performance of the algorithm on sparse networks with heterogeneous degrees.

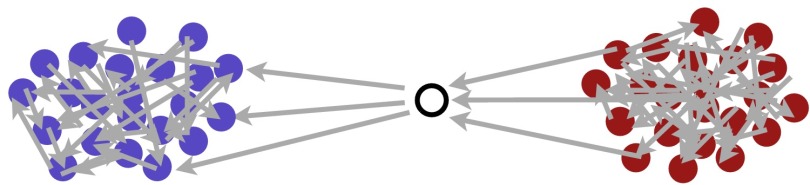
We illustrate the utility of di-sim through three data examples. In all three examples, a subset of the nodes have different sending and receiving clusters. These nodes are bottleneck communicators that receive edges from one cluster of nodes and send edges to another cluster of nodes (see Fig. 2); an analysis of Enron emails and a political blog network finds such bottleneck nodes and illustrates their unique role in the network. The final example analyzes the chemical connections between the neurons in Caenorhabditis elegans (C. elegans). In this example, 30% of the nodes have different sending and receiving clusters and in an estimated ordering of the clusters, the majority of the bottleneck nodes have a receiving cluster label that exceed their sending cluster label; we interpret this imbalance as a feedforward structure. Next, the paper introduces a directed Stochastic co-Blockmodel and shows that di-sim performs well under this model. The paper concludes with a discussion section.

Fig. 2.

In this diagram, there are two clusters and a bottleneck node between the two clusters.

Method: di-sim

To co-cluster the adjacency matrix $A\in {\left\{\mathrm{0,1}\right\}}^{n\times n}$ of a directed graph with n nodes, di-sim first normalizes the rows and columns by the row and column sums, plus a regularizer. Define the regularized graph Laplacian $L\in {\mathrm{ℝ}}^{n\times n}$ as

$$L_{ij}=\frac{A_{ij}}{\sqrt{O_{ii}^{\tau }{P}_{jj}^{\tau }}}={\left[{\left(O^{\tau }\right)}^{-1/2}A{\left(P^{\tau }\right)}^{-1/2}\right]}_{ij},$$ [1]

where $P^{\tau },O^{\tau }\in {\mathrm{ℝ}}^{n\times n}$ are diagonal matrices with $P_{jj}^{\tau }={\displaystyle {\sum }_k{A}_{kj}}+\mathit{\tau }$ and $O_{ii}^{\tau }={\displaystyle {\sum }_k{A}_{ik}}+\tau$. The regularization parameter $\tau \ge 0$ is set to the average out-degree, ${\displaystyle {\sum }_{i,k}{A}_{ik}/n}$.

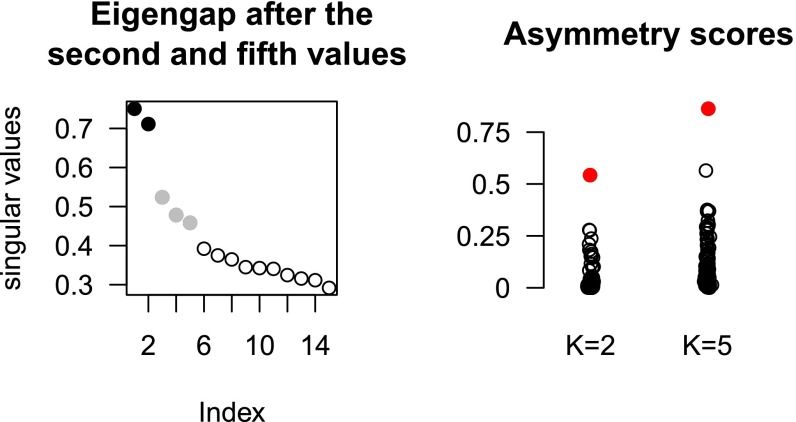
In the data examples below, the number of clusters K is selected in two different ways. In the first and third examples, K is selected by inspecting the singular values of L (Fig. 1). In the second example, prior knowledge indicates a reasonable choice of K. Should prior knowledge indicate a differing number of sending clusters $k_y$ and receiving clusters $k_z$, di-sim allows for this. If $k_y<k_z$, then SI Appendix, Theorem C.1 highlights how it is more difficult to estimate the receiving clusters (and vice versa if $k_y>k_z$).

Fig. 1.

(Left) Top 15 singular values of L. There are two eigengaps. The first eigengap suggests $K=2$ using the singular values in solid black. The second eigengap suggests $K=5$ by adding the singular values in solid gray. (Right) asymmetry scores $a_i\left(K\right)$ as defined in Eq. 2 for $K=2$ and $K=5$. For $K=2$, the outlier is Enron’s Director for Regulatory and Government Affairs, Jeff Dasovich. For $K=5$, the outlier is Bill Williams, who is discussed in the text.

As a way to explore and understand a directional network, we propose a nodewise asymmetry score that provides a preliminary diagnostic to highlight individual nodes with highly asymmetric patterns. Let the columns of $X_L,X_R\in R^{n\times K}$ contain the top K left and right singular vectors of L, respectively. In an undirected graph, $X_L=X_R$ because $A=A^T$. Deviations from equality between $X_L$ and $X_R$ can be measured for each node; denote

$$a_i\left(K\right)={\left({\displaystyle \sum _{\ell =1}^K{\left({\left[X_L\right]}_{i\ell }-{\left[X_R\right]}_{i\ell }\right)}^2}\right)}^{1/2},$$ [2]

as the asymmetry score for node i. The left singular vectors describe the sending patterns of the nodes and the right singular vectors describe the receiving patterns. As such, a node with a large asymmetry score has different sending and receiving patterns.

Our proposed di-sim algorithm is given below. The name di-sim has two meanings. First, because di-sim co-clusters the nodes, it estimates two distinct (but related) notions of stochastic equivalence. In this sense, di-sim means two similarities and two partitions. Second, di- denotes that this algorithm is specifically for directed graphs. di-sim is pronounced “dice ‘em.” The algorithm differs from other, more standard, spectral algorithms in three ways. First, the algorithm regularizes the graph Laplacian with τ. This step is essential for the convergence of L in spectral norm; this result is given in SI Appendix, Theorem E.1. Second, step 3 of the algorithm projects the rows of the singular value matrices onto the unit sphere using ${\Vert x\Vert }_2=\sqrt{{\displaystyle {\sum }_{i=1}^d{x}_i^2}}$, for $x\in {\mathrm{ℝ}}^d$. This type of projection was first proposed and studied in ref. 3. SI Appendix, Theorem F.1 extends results from ref. 4 to show that this step is essential for di-sim when there is degree heterogeneity within the co-clusters. di-sim is a generalization of previous algorithms because, if the graph is undirected, then $X_L=X_R$ and these singular vectors are also eigenvectors.

The regularization of L comes from inflating the diagonals of $O^{\tau }$ and $P^{\tau }$ by τ. This form of regularization follows the form proposed by Chaudhuri (5). An alternative regularization scheme, proposed by Amini et al. (6) and studied in refs. 7 and 8, directly adds $\tau /n$ to each element of A (call this matrix $A^{\tau }$) and replaces A with $A^{\tau }$ in Eq. 1. The Google pageRank algorithm uses a slightly different form of the regularization (9). Particularly when the graph is sparse, regularization helps the Laplacian concentrate around its mean matrix. It has been empirically observed to drastically improve clustering results, as in ref. 6.

di-sim.

Input: Adjacency matrix $A\in {\left\{\mathrm{0,1}\right\}}^{n\times n}$, regularizer $\tau \ge 0$ (Default: $\tau =$ average node degree), number of row clusters $k_y$, number of column clusters $k_z$.

• (1)Compute the regularized graph Laplacian

$$L={\left(O^{\tau }\right)}^{-1/2}A{\left(P^{\tau }\right)}^{-1/2}.$$

• (2)Compute the top K left and right singular vectors $X_L\in {\mathrm{ℝ}}^{n\times K},X_R\in {\mathrm{ℝ}}^{n\times K}$, where $K=\text{min}\left\{k_y,k_z\right\}.$
• (3)Normalize each row of $X_L$ and $X_R$ to have unit length. That is, define $X_L^{\mathrm{*}}\in {\mathrm{ℝ}}^{n\times K},X_R^{\mathrm{*}}\in {\mathrm{ℝ}}^{n\times K}$, such that

$${\left[X_L^{\mathrm{*}}\right]}_i=\frac{{\left[X_L\right]}_i}{{\Vert {\left[X_L\right]}_i\Vert }_2},{\left[X_R^{\mathrm{*}}\right]}_j=\frac{{\left[X_R\right]}_j}{{\Vert {\left[X_R\right]}_j\Vert }_2},$$

where ${\left[X_L\right]}_i$ is the ith row of $X_L$ and similarly for ${\left[X_L^{\mathrm{*}}\right]}_i,{\left[X_R\right]}_j,{\left[X_R^{\mathrm{*}}\right]}_j$.

• (4)(Optional) If $k_y=k_z=K$, run k means on the rows of

$$X^{\mathrm{*}}=\left(\begin{array}{c}{X}_L^{\mathrm{*}}\\ X_R^{\mathrm{*}}\end{array}\right)\in R^{2n\mathrm{\times }K}$$

with K centers or centroids. Using these K centers, cluster the rows of $X_L^{\mathrm{*}}$ into a partition, and similarly cluster the rows of $X_R^{\mathrm{*}}$ into another partition.

• (5)If not using step 4, run k means separately on rows of $X_L^{\mathrm{*}}$ and $X_R^{\mathrm{*}}$, using $k_y$ and $k_z$ clusters, respectively.

It is natural to ask whether a sending cluster is aligned with a specific receiving cluster in some way; perhaps it sends most of its edges to one receiving cluster, or many of its members appear together in the same receiving cluster, or both. If $k_y\ne k_z$, such an alignment can be examined in a post hoc analysis. If $k_y=k_z≔K$, then another option exists. Step 4 of the algorithm runs k means only once, on all $2n$ points at the same time, akin to techniques in correspondence analysis. Each node is mapped to two points in ${\mathrm{ℝ}}^K$. Optional step 4 ignores the labeling (i.e., sending or receiving) and runs k means on all $2n$ points, leading to a combined clustering of all $2n$ points into K clusters. After this, the sending and receiving labels are used to find both the sending and receiving clustering; this induces a one-to-one correspondence between the sending and receiving clusters that result from step 4. Let u be the label of a cluster. Step 4 implicitly encourages a clustering in which the nodes in sending cluster u send several edges to nodes in receiving cluster u. If cluster u contains only sending points or only receiving points, then this structure is not present for this cluster.

Results

This section uses asymmetry score and di-sim to find asymmetries in three networks. The first is a communication network at Enron. The data and analyses can be found at https://github.com/karlrohe/disim. The second is a hyperlinked network of political blogs. The final example is a network of chemical connections among the neurons in C. elegans.

Bottleneck Communicators at Enron.

In the popular Enron email network, di-sim finds two individuals with sending patterns which are exceedingly different from their receiving patterns. The email pattern of these “bottleneck communicators” suggests that they relay information from one part of the network to another. The defunct corporation Enron went bankrupt on 2 December 2001 because “its reported financial condition was sustained substantially by an institutionalized, systematic, and creatively planned accounting fraud” (10). This example examines a communication network formed with a portion of the corporation’s emails that were made publicly available as a result of the federal investigation into corporate misconduct.

The emails used in the following analysis form a communication network for 154 employees of Enron between 1998 and 2002 (11). The weighted adjacency matrix $A\in R^{154\times 154}$ contains elements $A_{ij}$ equal to the number of emails that i sends to j over the entire time period. Fig. 1 shows that two employees have outlying asymmetry scores. The outlier for $K=2$ is Enron’s Director for Regulatory and Government Affairs, Jeff Dasovich. Using $K=5$, the outlier is an energy trader at Enron named Bill Williams.

In addition to having large asymmetry scores, Dasovich and Williams also have large in- and out-degrees.* As such, their positions in the network allow them to relay information from one part of the network to another. For example, the diagram in Fig. 2 gives a schematic illustration of a network with a bottleneck communicator (not from Enron data). For the node in the middle of this figure, the edge directions are particularly salient. Similarly, if one ignores edge direction in the Enron data, then the bottleneck analysis in Fig. 2 would be infeasible; it is exactly the disparity between sending and receiving patterns that identifies the bottleneck nodes.

Although such network patterns do not necessarily imply criminal activity, the analysis identifies Enron employee Bill Williams as a clear outlier. Using evidence not associated with the data presented here, Williams was convicted of creating artificial energy shortages by ordering power plants to temporarily shut down. The New York Times reported on 4 February 2005 and quoted from audio recordings of Bill Williams telling a power plant to shut down. The day after that audio recording, roughly half a million Californians suffered from rolling blackouts (12).^† Williams’ communications with the power plant make him a bottleneck communicator. However, the network analyzed herein does not contain people outside of Enron. As such, Williams was identified for playing the bottleneck communicator for other activities within Enron. The data in this section have been extensively preprocessed by Zhou et al. (13) and Perry and Wolfe (14).

Asymmetric Linking Among Political Blogs.

Political blogs typically send and receive hyperlinks to and from blogs of the same political persuasion (15). However, the following analysis shows that in a network of political blogs from the 2004 US presidential election, a small number of blogs appear to have been doing opposition research, where they link to blogs that hold different political views and receive links from blogs of the same persuasion. This analysis does not find any “straw man blogs” which link to blogs of the same political persuasion, but receive a disproportionate share of edges from blogs across the political divide.

To create the network analyzed herein, Adamic and Glance (15) curated a list of the top 1,494 political blogs and, in February 2005, (i) recorded the front page of each blog and (ii) identified the hyperlinks that point to other blogs on the list. From these links, the authors (15) created a directed network.^‡ Each blog was identified as liberal or conservative. Some of these labels were manually identified and some of the labels were self-reported to one of several blog directories. Whereas these labels may be subject to various types of errors, they are generally consistent with the network connectivity and the names of the blogs (e.g., xtremerightwing.net/ vs. loveamericahatebush.com). We will refer to these labels as the reported labels. To refer to the blogs on either side of the political partition, we will use the terms {Kerry, liberal} interchangeably and the terms {Bush, conservative} interchangeably. Karrer and Newman (16) and others estimated the political partition from the network alone. This previous analysis of the network symmetrized the edge directions.

We restrict our analysis to the 1,222 blogs in the largest connected component. This contains 586 liberal blogs and 636 conservative blogs. Although this network is sparse (the average degree is 16), clustering is feasible because there are roughly 10 times as many edges between blogs of the same party than between blogs of different party affiliations.

Because there are two political parties, we set $k_y=k_z=2$ and run di-sim with the optional step 4. The resulting sending and receiving partitions are roughly similar, with both partitions roughly aligning with the political divide in the reported labels (liberal vs. conservative). Subsequent analysis is restricted to the blogs that have at least three incoming edges and at least three outgoing edges. There are 549 such blogs and here again, both partitions of these blogs (sending and receiving) broadly agree with the reported labels of Kerry vs. Bush. This suggests that most blogs send and receive edges with blogs that share the same political views.

However, 6 of the 549 blogs are clustered into different sending and receiving clusters. These bottleneck blogs send hyperlinks to conservative blogs and receive hyperlinks from liberal blogs, or vice versa. Although many of the blogs are defunct, some are still functioning. SI Appendix, Table S1 presents some information on the content of these six blogs (as of this writing). This information, along with the Bush/Kerry labeling of the blogs provided in the data set, indicates that the actual beliefs of these bottleneck blogs matches their receiving memberships (not their sending memberships). One possible reason that they send so many links to the opposition is that they are doing “opposition research,” where they link to blogs that they dislike so that they may criticize it. We found no evidence of any asymmetric blogs receiving links from the opposite party. This suggests that the incoming edges appear to be more informative for detecting the actual political persuasion of a political blog.

Of the six bottleneck blogs, only one receives links from Bush blogs and sends links to Kerry blogs. It is www.quando.net/. This blog hosts a collection of conservative/libertarian bloggers.^§ It is only feasible to find these bottleneck blogs because di-sim respects the asymmetry between incoming and outgoing edges.

The Neural Connectome of C. elegans.

This section investigates the posterior neural connectome of the male C. elegans, which was mapped by Jarrell et al. (17). To map the connectome, the authors (17) sliced the 1-mm-long worm into 5,000 serial slices and imaged each slice with an electron microscope. In each image, they identified the neurons, their chemical connections, and their electrical connections. Piecing these images back together created a 3D image of the connectome. In analyzing the connectome, the authors (17) identified several network features. The two features identified by ref. 17 that are most relevant to the analysis in this section are (i) several neurons participate in feedforward loops (see Fig. 5 for definition) and (ii) there are clusters of neurons with dense connections inside the clusters. The analysis in this section uses di-sim to rediscover these two findings using the directed network in ref. 17; our analysis shows how the di-sim clusters create a feedforward structure, revealing a hierarchical pattern in the connectome as reported in ref. 17.

Fig. 5.

The three-node graph on the left is a feedforward loop. The adjacency matrix of a feedforward loop contains ones in every element above the diagonal. All other elements are zero (displayed with dots). This structure is mimicked by the table in Fig. 4.

The chemical connectome can be represented as a directed graph, where the edges represent chemical connections among the neurons, muscles, and gonad. In the posterior chemical connectome, there are 226 nodes and they all receive at least one edge. Their average in-degree is roughly 11. Only 147 nodes (of the 226 nodes) send at least 1 edge. Of these nodes that send at least 1 edge, their average out-degree is roughly 17. Both of these degree calculations are on the unweighted graph. In fact, each edge has an edge weight that corresponds to the size of the synaptic connection; larger connections produce a more robust connection between neurons. More details can be found in ref. 17. The distribution of these edge weights has a long tail. To minimize the effect of very large weights, the edge weights were log transformed and then used to construct the weighted adjacency matrix $A\in {\mathrm{ℝ}}^{226\times 226}$. This log transformation is discussed at the end of SI Appendix, section B.

To select the number of clusters, we investigated the leading singular values of L (given in SI Appendix, Fig. S1). This figure reveals an “elbow” at the seventh singular value. Because we have no additional information to suspect that the sending or receiving partition should have more than seven clusters, we set $k_y=k_z$ and present the results for seven clusters. Using the directed spectral algorithm of ref. 18, which only provides a single partition of the nodes, Jarrell et al. (17) reported the results for five clusters. SI Appendix, section B contains the di-sim results with $k_y=k_z=5$; under this perturbation from seven to five clusters, the key findings below are qualitatively unchanged.

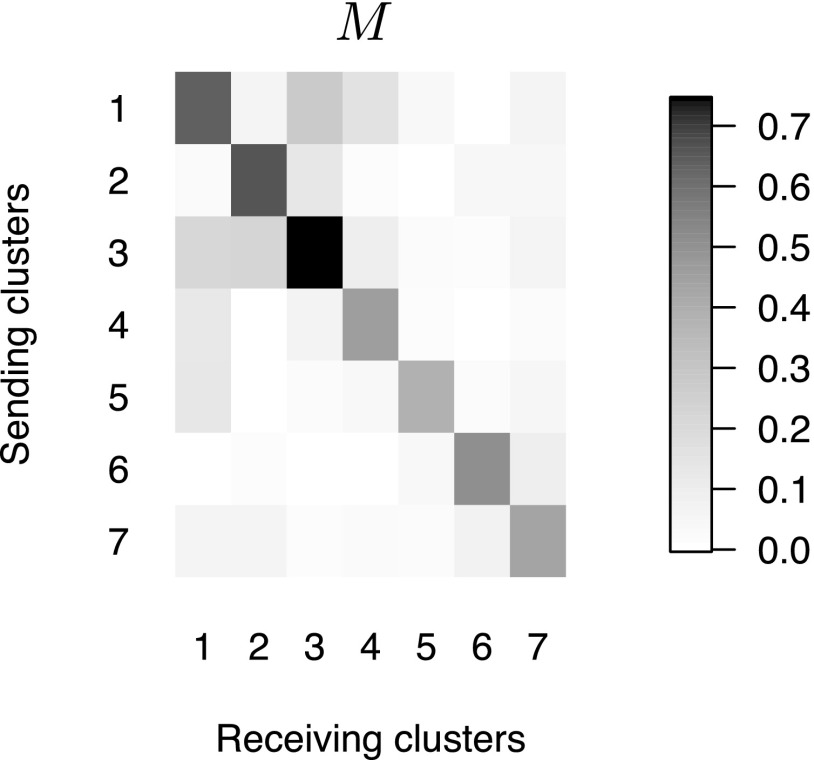
Because $k_y=k_z(≔K)$, we use di-sim with the optional step 4, where the rows of $X_L^{\mathrm{*}}$ and $X_R^{\mathrm{*}}$ are concatenated into a matrix with $2n$ rows. In the optional step 4, the k-means algorithm is run only once on the matrix with $2n$ rows. So, the partitions estimated from left and right singular vectors are both derived from the same k-means centers.^¶ For $u\in \left\{1,\dots ,K\right\}$, there is a correspondence between sending cluster u and receiving cluster u when they both correspond to the same k-means center. Refer to this as cluster u. Fig. 3 reveals the “edgewise” relationships between the seven di-sim clusters; it shows the matrix M whose $\left(u,v\right)$ th element is the average weight of edges going from sending cluster u to receiving cluster v (if there is no edge between nodes i and j, then create an edge with weight zero).^# The strong diagonal in Fig. 3 shows most edges stay within the same cluster; this means that most edges coming from nodes with sending membership u go to nodes with receiving membership u.

Fig. 3.

Element $u,v$ is darker when there are stronger connections from block u to block v. A strong diagonal in this matrix suggests that most connections stay within the same block.

The edgewise relationships revealed in Fig. 3 provide one way to assess the relationships between clusters. In addition to edgewise relationships between clusters, a sending and receiving cluster can relate to one another via the number of nodes that they have in common. Two clusters u and v have a nodewise relationship if there is a node that belongs to both sending cluster u and receiving cluster v. Both edgewise and nodewise relationships are asymmetric relationships between clusters.

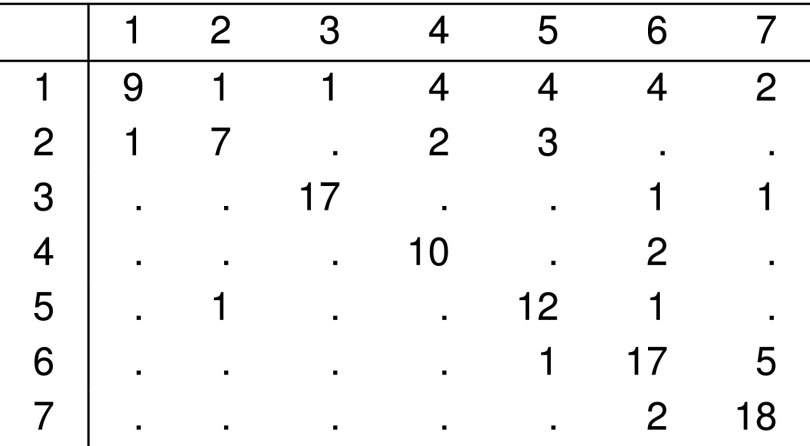
The table in Fig. 4 displays the nodewise relationships between the clusters. The $\left(u,v\right)$ th element of the table in Fig. 4 gives the number of neurons in both sending cluster u and receiving cluster v. The strong diagonal of this matrix reveals that each cluster is formed from a coherent core of nodes; the nonzero off-diagonal elements give the strength of the nodewise relationship between clusters. The order of the rows and columns in Fig. 4 was determined algorithmically; we considered the table as a weighted adjacency matrix on seven “metanodes” or clusters and ran pageRank on this graph of seven metanodes (9). pageRank returns a centrality score for each of the seven clusters. The rows/columns were ordered in ascending pageRank centrality scores.

Fig. 4.

Element $u,v$ is the number of nodes with sending cluster u and receiving cluster v. Only nodes that both send and receive edges are counted.

For each pair of clusters $u,v\in \left\{1,\dots ,7\right\}$ denote $w_{u,v}$ as the number of neurons in sending cluster u and receiving cluster v (this is the $u,v$ element in Fig. 4). In the labeling found by pageRank, the weights with $u<v$ are larger than the weights with $u>v$; the sum of the weights with $u<v$ (above the diagonal) is 39, the sum of the weights with $u<v$ (below the diagonal) is 9, and the sum of the weights with $u=v$ (on the diagonal) is 99. To examine whether this imbalance could be expected due to chance, we performed a simple permutation test. Denote the random variable corresponding to $w_{u,v}$ as $W_{u,v}$ and denote ${\stackrel{\sim }{W}}_u\in {\mathrm{ℝ}}^6$ as the uth row, excluding $W_{u,u}$. We test $H_o:$ for each u, the vector ${\stackrel{\sim }{W}}_u$ is exchangeable. This is a strong null because it assumes exchangeability of the outgoing edge weights for all clusters u. To sample from this null: take the table in Fig. 4 as a weighted adjacency matrix (on metanodes) and for each row of the table, permute the off-diagonal elements. That is, one row at a time, keep the self-loops fixed and randomly rewire the edges to the other six nodes. After sampling a permuted graph, reorder the seven metanodes via pageRank. Finally, define the balance score of this graph as the sum of the weights of the edges with $u>v$. The original data have a balance score of 9; smaller balance scores correspond to a more imbalanced structure. This permutation test was performed 1 × 10⁶ times and only $2\mathrm{\%}$ had scores less than or equal to 9, the score of the actual graph. A similar analysis using M as the weighted adjacency matrix did not reveal a statistically significant imbalance; roughly $80\mathrm{\%}$ of its permuted graphs had scores less than the score from M.

The analysis above suggests that there is an ordering of the clusters such that most nodes have a sending cluster label less than or equal to their receiving cluster label. This pattern does not appear to be replicated in the matrix M. Said another way, in the nodewise similarities between clusters (or metanodes) there is an ordering. However, in the edgewise similarity between clusters (or metanodes) the same analysis does not find an ordering.

As nonexperts, we interpret this ordering as similar to a pattern found in ref. 17. A feedforward graph, also known as a directed acyclic graph, is a graph with a labeling of the nodes $\left\{1,\dots ,n\right\}$ such that for any two nodes $u,v$, if $u\to v$ is an edge, then $u<v$. A feedforward loop is a simple example of a feedforward graph on three nodes; Fig. 5 displays this graph and its adjacency matrix. Looking at individual neurons and their connections, Jarrell et al. (17) find several feedforward loops among the neurons. See ref. 19 for more on feedforward loops. The feedforward loops found by Jarrell et al. (17) are on the microscale, looking at individual neurons and their relationships. We interpret our analysis of Fig. 4 as finding a macrolevel feedforward system on the nodewise similarities between clusters (or metanodes). Our analysis of Fig. 3 does not find an analogous feedforward ordering in the edgewise similarities between clusters.

SI Appendix, Fig. S2 presents the left and right partitions of the C. elegans connectome as estimated by di-sim with $k_y=k_z=7$. The figure compares the two di-sim partitions with the single partition estimated in the original paper (ref. 17), in which the authors used the spectral technique of ref. 18. Whereas both the sending and receiving partitions of di-sim are largely similar to the partition estimated in ref. 17, the results of di-sim emphasize that several neurons change sending and receiving clusters. With $k_y=k_z=7$, di-sim finds that roughly 30% of the neurons belong to different sending and receiving clusters. This massive disparity between sending and receiving reveals a macrolevel feature in the topology of the network and it is not feasible without separate notions of sending and receiving clusters.

The Stochastic Co-Blockmodel and Theory for di-sim.

The Stochastic Blockmodel is a classical model of clustering in social networks (20). This model assigns each node to one of K blocks and nodes in the same block are stochastically equivalent. Specifically, i and j are stochastically equivalent if

$$P\left(i\hspace{0.17em}\text{connects}\hspace{0.17em}\text{to}\hspace{0.17em}\ell \right)=P\left(j\hspace{0.17em}\text{connects}\hspace{0.17em}\text{to}\hspace{0.17em}\ell \right)$$

for every actor $\ell$ in the network. The Stochastic co-Blockmodel, proposed below, generalizes the notion of stochastic equivalence to directed graphs, where there are two separate notions of stochastic equivalence between any nodes i and j:

$$\text{Sending}:P\left(i\to \ell \right)=P\left(j\to \ell \right)\forall \ell$$ [3]

and

$$\text{Receiving}:P\left(\ell \to i\right)=P\left(\ell \to j\right)\forall \ell .$$ [4]

Each notion of stochastic equivalence provides a partition of the nodes. di-sim estimates both partitions.

Because the Stochastic co-Blockmodel naturally generalizes to bipartite graphs, this section allows for a different number of rows ($N_r$) and columns ($N_c$) in the adjacency matrix A.

Definition 1: Let $Y\in {\left\{\mathrm{0,1}\right\}}^{N_r\times k_y},Z\in {\left\{\mathrm{0,1}\right\}}^{N_c\times k_z}$ and $B\in {\left[\mathrm{0,1}\right]}^{k_y\times k_z}$. Each row of Y and each row of Z has exactly one 1 and each column has at least one 1. Under the Stochastic co-Blockmodel (ScBM), the adjacency matrix $A\in {\left\{\mathrm{0,1}\right\}}^{N_r\times N_c}$ contains independent Bernoulli random variables with

$$\mathbb{E}\left(A\right)=YB{Z}^T.$$

In the Stochastic Blockmodel, $\mathbb{E}\left(A\right)=ZB{Z}^T$. In the ScBM, $\mathbb{E}\left(A\right)=YB{Z}^T$. In this definition, Y and Z record two types of block membership which correspond to the two types of stochastic equivalence (Eqs. 3 and 4). Denote $y_i$ as the ith row of Y and $z_i$ to be the ith row of Z. Under the ScBM for a directed graph, if $y_i=y_j$, then nodes i and j are stochastically equivalent senders, Eq. 3. Similarly, if $z_i=z_j$, then nodes i and j are stochastically equivalent receivers, Eq. 4.

The degree-corrected ScBM generalizes this model to allow for highly heterogeneous node degrees within the same block (16). SI Appendix, Theorem E.2 shows that under certain assumptions, the sending and receiving partitions estimated by di-sim are a weakly consistent estimates of the partition contained in Y and Z, respectively. As such, the di-sim partitions estimate sets of stochastically equivalent senders and stochastically equivalent receivers.

Discussion

This paper aims to identify the clustering asymmetries in directed graphs by extending both spectral clustering and the Stochastic Blockmodel to a co-clustering framework.

We propose a spectral algorithm di-sim. To accommodate sparse graphs, di-sim uses the regularized graph Laplacian. To allow for heterogeneous degrees within clusters, di-sim normalizes the rows of the singular vector matrices (step 3 of the algorithm). In the data examples of this paper and in other data examples that we have encountered, spectral algorithms with these regularization and projection steps find clusters with more balanced sizes. The theoretical results in SI Appendix highlight the importance of these steps by studying di-sim under the degree-corrected ScBM.

Throughout the three examples in the paper, di-sim reveals asymmetries in the structure of the example networks. This highlights the dangers of symmetrizing the relationships. In both the Enron and political blog example, certain nodes played the role of bottleneck communicators. In the C. elegans network, di-sim finds 48 bottleneck nodes. The bottleneck nodes in C. elegans display an imbalance; under an estimated ordering of the clusters, the vast majority of bottleneck nodes have a sending cluster which is less than their receiving cluster. We interpret this imbalance as a macrolevel feedforward structure. Symmetrizing the graph conceals these directed and asymmetric patterns.