Evolutionary consequences of behavioral diversity

Significance

Access to a diversity of behavioral choices makes social dynamics rich and difficult to analyze. Individuals are rarely constrained to a binary choice between “cooperate” or “defect,” as many theoretical treatments assume. Here we use game theory to ask what social behaviors will emerge in populations as the number of behavioral choices grows. We show that simple strategies, where players do not vary their behavior much at all, can nonetheless be successful, and that access to a broader range of behavioral choices can cause a population to evolve toward lower levels of cooperation. Finally, we show that access to greater choice in rock–paper–scissors games inevitably leads to behavioral diversity, with players using strategies that make use of all possible choices.

Abstract

Iterated games provide a framework to describe social interactions among groups of individuals. This body of work has focused primarily on individuals who face a simple binary choice, such as “cooperate” or “defect.” Real individuals, however, can exhibit behavioral diversity, varying their input to a social interaction both qualitatively and quantitatively. Here we explore how access to a greater diversity of behavioral choices impacts the evolution of social dynamics in populations. We show that, in public goods games, some simple strategies that choose between only two possible actions can resist invasion by all multichoice invaders, even while engaging in relatively little punishment. More generally, access to a larger repertoire of behavioral choices results in a more ”rugged” fitness landscape, with populations able to stabilize cooperation at multiple levels of investment. As a result, increased behavioral choice facilitates cooperation when returns on investments are low, but it hinders cooperation when returns on investments are high. Finally, we analyze iterated rock–paper–scissors games, the nontransitive payoff structure of which means that unilateral control is difficult to achieve. Despite this, we find that a large proportion of multichoice strategies can invade and resist invasion by single-choice strategies—so that even well-mixed populations will tend to evolve and maintain behavioral diversity.

Diversity in social behaviors, in humans as well as across all domains of life, presents a daunting challenge to researchers who work to explain and predict individual social interactions or their evolution in populations. Iterated games provide a framework to approach this task, but determining the outcome of such games under even moderately complex, realistic assumptions—such as memory of past interactions (1–7); signaling of intentions, indirect reciprocity, or identity (9–16); or a heterogeneous network of interactions (17–25)—is exceedingly difficult.

Developing models that capture complex and diverse social behaviors is an important step toward quantitative, falsifiable predictions about a host of problems, such as the emergence and stability of cooperation, policing, and social institutions in human populations; and the de novo evolution of social hierarchies in natural populations (7, 9, 10, 26–29). Recent work has expanded the reach of game-theoretic models to describe ever more sophisticated forms of social interactions (3, 30–39). This work has begun to unravel the evolutionary and behavioral dynamics that determine the long-term stability of cooperation in a group. It has allowed researchers to explore the role of memory in social dynamics (40–44), and it has shown that, even with multiple players (33, 38) and arbitrary action spaces (36), an individual can often unilaterally influence the outcome of social interactions across a broad range of contexts.

Here we study the evolutionary dynamics of social interactions under the quite general setting of all “memory-1” strategies—that is, strategies that specify the choice a player makes in each round of a repeated game depending on the choices made in the preceding round. We study the evolutionary dynamics of memory-1 strategies in a population of players with access to multiple behavioral choices, including games where unilateral control through so-called zero-determinant (ZD) strategies (30) is impossible.

Many game-theoretic studies of social behavior, although by no means all (36, 45, 46), constrain players to a binary behavioral choice such as “cooperate” or “defect” (47, 48). Other studies, particularly those looking at social evolution, constrain players to a single type of behavioral strategy, but allow for a continuum of behavioral choices—e.g., the option to contribute an arbitrary amount of effort to an obligately cooperative interaction (45, 46). In general, and especially in the case of human interactions, individuals have access to both a wide variety of behavioral choices, and to a complex decision-making process among these choices. Here we bridge this gap and study how the diversity of behavioral choices impacts the evolution of decision making in a replicating population, focusing on the prospects for cooperation and for the maintenance of behavioral diversity.

We develop a framework for analyzing iterated two-player games in which players can access an arbitrary number of behavioral choices and use an arbitrary memory-1 strategy for choosing among them. We apply this framework to study the effect of a large behavioral repertoire on the evolution of cooperation in public goods games. We show that increasing the number of investment levels available to a player can either facilitate or hinder the evolution of cooperation in a population, depending on the ratio of individual costs to public benefits in the game. We apply the same framework to study games with nontransitive payoff structures, under which no hierarchical ordering of payoffs is possible—e.g., the game of rock–paper–scissors in which scissors cuts paper, and paper covers rock, but rock crushes scissors. We show that nontransitive payoff structures generally preclude unilateral control through ZD strategies, but that nonetheless there exist memory-1 strategies that ensure the maintenance of behavioral diversity, in which players make use of all of the choices available to them.

Methods and Results

Players in an iterated game repeatedly choose from a fixed set of possible actions. Depending on the choice she makes, and the choices her opponents make, a player receives a certain payoff each round. The process by which a player determines her choice each round is called her strategy. A strategy may in general take into account a wide variety of information about the environment, memory of prior interactions between players, an opponent’s identity, or his social signals, etc. (1–6, 11, 13–16, 20–25). Here we restrict our analysis to two-player, simultaneous iterated games in which a player chooses from among d possible actions each round using a memory-1 strategy, which takes into account only the immediately preceding interaction between her and her opponent. We consider games that are discounted at rate δ, where $0<\delta \le 1$ can be understood either as the probability each round that the game is repeated for another round, or as a factor that reduces the payoff received with each additional round in an infinitely repeated game (36, 37). Although memory-1 strategies may seem restrictive, in fact a strategy that is a Nash equilibrium against all memory-1 strategies is also robust against all longer memory strategies as well (SI Appendix; refs. 3, 30, 35, 38).

A memory-1 strategy is specified by choosing $d^2$ probabilities for each possible action i, denoted $p_{jk}^i$, which specify the chance the player executes that action in a round of play, given that she made choice j and her opponent made choice k in the preceding round. The strategy must also specify d probabilities $p_i^0$ for a player to execute action i in the first round of play. Each probability can be chosen independently, save for the constraint that the sum across actions ${\displaystyle {\sum }_{i=1}^d{p}_{jk}^i}=1$ must hold. We study the evolution of social behavior by analyzing the composition of such strategies in a replicating population over time. In an evolving population the reproductive success of a player depends on the total payoff she receives in pairwise interactions with other members of the population (49). We study how strategy evolution is affected by the number and types of behavioral choices available to individuals.

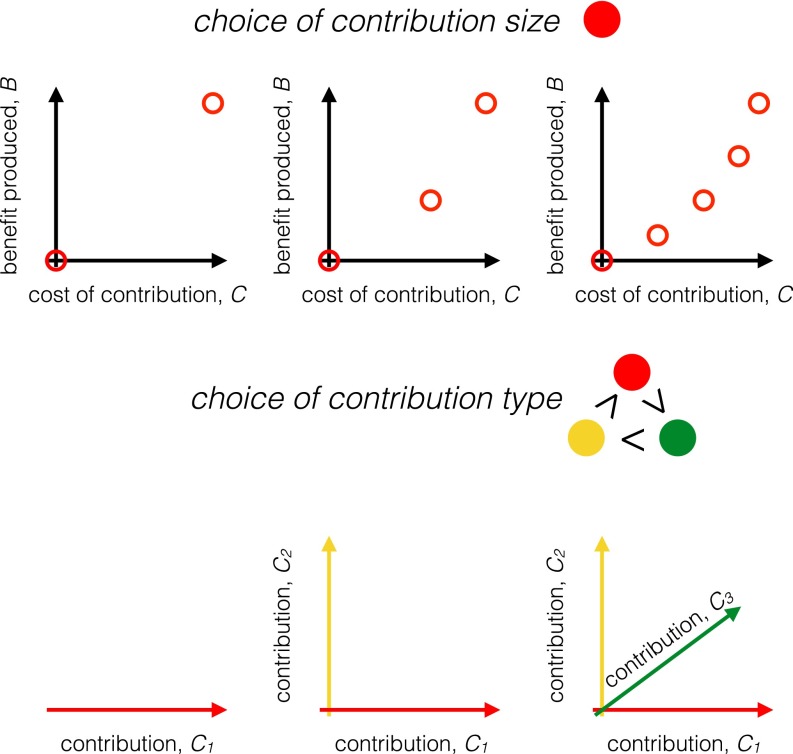
We study two qualitatively different behavioral choices that players can make: different sizes of contributions and different types of contributions to social interactions (Fig. 1). If players can vary the size of the contribution they make to a social interaction, this means that they alter the degree of their participation but not the qualitative nature of the interaction. For example, in a public goods game, a player may choose to contribute an amount C to the public good, or $2C$, or $3C$, etc. In contrast, when players can vary the type of contribution they make, this can change the qualitative nature of the social interaction. For example, unicellular organisms may produce pathogens, social signals, public goods, or all three (50–53). In a game of rock–paper–scissors the different behavioral choices result in qualitatively different social interactions—rock beats scissors, but scissors beats paper, etc. Such qualitative differences can lead to nontransitive payoffs and correspondingly complex social and evolutionary dynamics (50, 54–59).

Fig. 1.

Two ways to expand the behavioral repertoire in iterated games. (Upper) In a public goods game a player contributes to a public pool at some cost to herself, and she receives a benefit based on the contributions of all players in the game. In a simple two-choice game, such as the prisoner’s dilemma, players face a binary choice, to cooperate and contribute cost C or to defect and contribute nothing. At the other extreme, in a continuous game, players have an unlimited number of options and may contribute any amount. What happens to the evolution of social behavior as the numbers of choices increases? Is it beneficial for a population to have access to more choices in a public goods game? (Lower) Players may also choose between qualitatively different types of contributions to social interactions. Qualitatively different behavioral options produce complex payoff structures, such as the nontransitive rock–paper–scissors interactions (50, 54–56). What happens to the evolution of social behavior as the types of contributions to social interactions expand? Is it better to maintain a diversity of behavioral options, or to restrict to a single type of contribution?

Here we study both kinds of behavioral choice, differences in size and type, and their effects on the evolution of strategies in a population. We analyze well-mixed, finite populations of N players reproducing according to a copying process or pairwise comparison rule (8), in which a player X copies her opponent Y’s strategy with probability $1/\left(1+\exp \left[\sigma \left(S_x-S_y\right)\right]\right)$ where σ scales the strength of selection and $S_x$ is the average payoff received by player X from her social interactions with each of the $N-1$ other members of the population (47, 49). The average payoffs correspond to the fitnesses associated with each strategy, given the current composition of the population. For a single invader Y in a population otherwise composed of strategy X, we have the average payoffs $S_y=S_{yx}$ and $S_x=\frac{N-2}{N-1}{S}_{xx}+\frac{1}{N-1}{S}_{xy}$. Throughout we consider the case of strong selection, so that the stability of a resident strategy in a population can be determined by its ability to resist selective invasion by a rare mutant. We define a resident strategy to be evolutionary robust if it resists selective invasion by any rare mutant [2].

The Outcome of an Iterated d-Choice Game.

To analyze social evolution in multichoice iterated games we must first calculate the expected long-term payoff $S_{xy}$ of an arbitrary player X facing an arbitrary opponent Y. To do this, we will generalize an approach used for two-choice two-player games, in which a player’s memory-1 strategy $\mathbf{p}$ is represented in an alternate coordinate system (31), so that the outcome of the repeated game can be determined with relative ease. For a d-choice two-player game, the probability that a focal player chooses action i, given that she played action j and her opponent action k in the preceding round, is denoted $p_{jk}^i$. For each action $1\le i<d$ there are $d^2$ independent probabilities, corresponding to each possible outcome of the preceding round. In the alternate coordinate system we construct (SI Appendix), the probabilities $p_{jk}^i$ are written as linear combinations of the payoff $R_{jk}$ the focal player received in the preceding round, times a coefficient ${\chi }^i$; the payoff $R_{kj}$ her opponent received, times a coefficient ${\varphi }^i$; the number of times she played action i within her memory (which is 1 or 0 for a memory-1 strategy); a baseline rate of playing action i, denoted ${\kappa }^i$; and $d^2-3$ additional terms that depend on the specific outcome of the preceding round, denoted ${\lambda }_{jk}^i$. This choice of coordinate system enforces the following relationship between the long-term average payoffs received by the two players:

$${\varphi }^i{S}_{yx}-{\chi }^i{S}_{xy}-\left({\varphi }^i-{\chi }^i\right){\kappa }^i+{\displaystyle \sum _{j=1}^d{\displaystyle \sum _{k=1}^d{\lambda }_{jk}^i{v}_{jk}}}=\frac{1-\delta }{\delta }{p}_i^0,$$ [1]

where δ is the rate of discounting, $p_i^0$ is the probability of playing action i in the first round, and $v_{jk}$ denotes the equilibrium rate of action pair $jk$, and where we fix the values of three of the ${\lambda }_{jk}^i$ to ensure a system of $d^2$ coordinates (SI Appendix). Note there are d − 1 such equations, one for each behavioral choice $1\le i<d$. A ZD strategy of the type studied in ref. 36 can be recovered by setting all ${\lambda }_{jk}^i=0$. However, the constraint that $p_{jk}^i\in \left[\mathrm{0,1}\right]$ implies that the ZD condition does not always produce a viable strategy, as in the case of a rock–paper–scissors game discussed below.

Choosing How Much to Contribute to a Public Good.

We will use the relationship between two players’ scores (Eq. 1) to analyze the evolution and stability of cooperative behaviors in multichoice public goods games, played in a finite population. In the two-player public goods game each player chooses an investment level, C, which produces a corresponding amount of public benefit that is then shared equally between both players, regardless of their investment choices. In general, if a player invests $C_j$ and her opponent $C_k$ the public benefit produced is determined by a function $B\left(C_j+C_k\right)$, so that her net payoff is $B\left(C_j+C_k\right)/2-C_j$ and her opponent’s payoff is $B\left(C_j+C_k\right)/2-C_k$. Two-choice public goods games have been studied extensively, producing a clear understanding of the cooperative equilibria that exist in populations (3, 31, 32, 35, 40–42,).

A wide variety of evolutionary robust memory-1 strategies exist for two-choice public goods games. The character and evolvability of these strategies have been explored in detail (3, 35, 40, 42, 60–62). But the assumption of only two investment levels—of two behavioral choices—is unrealistic for many applications. Even if a player adopts such a two-choice strategy, there is in general no reason for her opponent to do the same. Thus, we begin our analysis by asking whether a two-choice memory-1 strategy that stabilizes investment at the maximum level when resident in a population (and is therefore considered a “cooperative” two-choice strategy) can resist invasion against players who are allowed to make arbitrary investment choices.

For simplicity, we will focus here on a linear relationship between costs and benefits of investment in the public good, so that $B=rC$ where values $1<r<2$ produce a social dilemma in which mutual cooperation is beneficial but each player has an incentive to defect. The more general case, with nonlinear functional relationships, is described in the SI Appendix.

For linear benefits, a two-choice strategy is related to our alternate coordinate system according to $p_{1i}=-\left(\left(\varphi -\chi \right)\left(r\left(C_1+C_i\right)/2-\kappa \right)-\varphi C_i+\chi C_1+{\lambda }_{1i}\right)$ and $p_{2i}=1-\left(\left(\varphi -\chi \right)\left(r\left(C_2+C_i\right)/2-\kappa \right)-\varphi C_i+\chi C_2+{\lambda }_{2i}\right)$ where the index i corresponds to an opponent who invests $C_i$, which in general can take any nonnegative value (for a detailed description of this coordinate transform, see SI Appendix, section 3). Here we choose the boundary conditions ${\lambda }_{11}={\lambda }_{22}=0$ and ${\lambda }_{12}={\lambda }_{21}$, and from Eq. 1 we obtain the following relationship between two players’ long-term payoffs

$$\varphi S_{yx}-\chi S_{xy}-\left(\varphi -\chi \right)\kappa +{\lambda }_{12}\left(v_{12}+v_{21}\right)+{\displaystyle \sum _{j=3}^d\left({\lambda }_{1j}{v}_{1j}+{\lambda }_{2j}{v}_{2j}\right)}=\frac{1-\delta }{\delta }{p}_2^0.$$

When player Y is constrained to the same two choices as player X, then this relationship reduces to the relationship for a two-player, two-choice game discussed in refs. 30, 31, 35, 42. However, we will consider the more general case when player Y has access to different, and possibly more, investment choices than player X. In general, a strategy X resident in a population of size N can resist selective invasion by a mutant Y iff

$$S_{yx}<\frac{N-2}{N-1}{S}_{xx}+\frac{1}{N-1}{S}_{xy},$$ [2]

where $S_{xx}$ is the long-term payoff of the resident strategy against itself. This condition is closely related to the ESS_N condition (47), which defines the evolutionary stability of a resident strategy in terms of its ability to resist both invasion and replacement by a mutant. In the large space of memory-1 strategies we study here, no two-choice resident is strictly ESS_N (35), because any strategy can be invaded and replaced neutrally. Thus, we look for strategies that can resist selective invasion by any rare mutant, which we call evolutionary robustness (42). A cooperative two-choice strategy by definition has $S_{xx}=\left(r-1\right)C_2$; i.e., it stabilizes cooperative behavior when resident so that both players choose to invest the maximum public good they can contribute. To produce such a strategy we must set $p_{22}=p_2^0=1$; i.e., the strategy must invest $C_2$ in the first round, and must always invest $C_2$ if both players invested $C_2$ in the preceding round.

Using the relationships above we can derive conditions for a two-choice cooperative strategy to be universally robust to invasion; that is, robust against all invaders Y, who can make an arbitrary number of different investment choices, including values above $C_2$ or below $C_1$ (SI Appendix). This in turn allows us to derive the following necessary and sufficient condition for the existence of a two-choice strategy that is universally robust:

$$\frac{C_1}{C_2}<\frac{\left(r-1\right)\left(2\delta -1\right)}{\delta \frac{r}{2}+\delta \frac{1}{N-2}-\left(1-\delta \right)\left(r-1\right)}.$$ [3]

If (and only if) 3 is satisfied, then there exists a two-choice strategy that enforces cooperation at some level $C_2$ when resident in a population, and that resists invasion by any invader, regardless of the invader’s ability to choose different investment levels or memory.

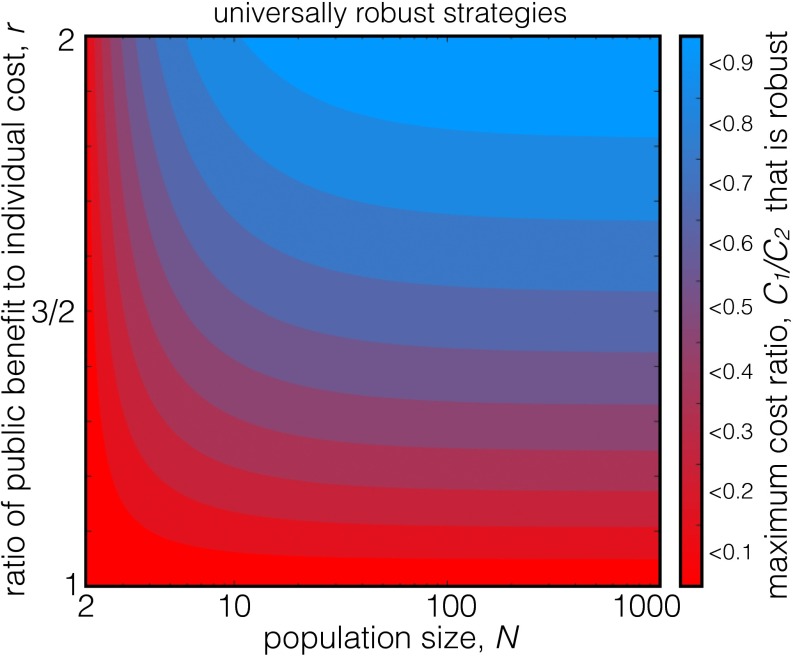
The inequality in 3 offers insight into the degree of punishment that a resident cooperative strategy must be prepared to wield, to remain robust against all invaders (Fig. 2). Setting $\delta =1$ (i.e., no discounting), a resident strategy can punish a noncooperative invader by reducing her investment in the public good from $C_2$ to $C_1$. If $C_1$ is only slightly smaller than $C_2$ then the resident strategy has a limited capacity to punish invaders. Whereas if $C_1$ is much less than $C_2$ the resident strategy has a greater capacity for punishment. The critical question is how much capacity for punishment, quantified by the ratio of $C_1$ and $C_2$, is required to ensure that the resident two-choice cooperator can be robust against all invaders, who can make arbitrary investments outside of those available to the resident. The answer to this question is shown in Fig. 2, which quantifies the minimum reduction in public investment that a cooperative two-choice strategy must make to be universally robust. As might be expected from 3, larger ratios of public benefit to individual cost r and larger population sizes N mean that smaller reductions in public investment are sufficient for universal robustness of the resident cooperator. And as Fig. 2 shows, for a wide range of parameters a population can enjoy robust cooperation using a two-choice strategy with only moderate threat of punishment, e.g., $C_1$ no less than one half of $C_2$.

Fig. 2.

When are simple two-choice strategies robust against all multichoice invaders in public goods games? We considered the evolutionary robustness of two-choice strategies, in which players iteratively choose to invest amount $C_1$ or $C_2>C_1$ to produce a public benefit B proportional to the total investment of both players, $B=rC$. Cooperative strategies limited to two investment choices can be evolutionary robust against all invaders, who may invest an arbitrary amount $C\ne C_1,C_2$, provided the strategy has sufficient opportunity to punish a defector—that is, provided $C_1$ is sufficiently smaller than $C_2$. We determined [2] the largest ratio of investment levels, $C_1/C_2$, that permits universally robust cooperative two-choice strategies, as a function of the population size, N, and the public return on individual investment, r in the absence of discounting ($\delta =1$). Colors are gradated in 10% intervals, so that the light blue region indicates a two-choice player can choose a strategy that maintains robust cooperation while engaging in relatively little punishment, by reducing her investment to only 90% of its maximum. The bright red region indicates that a two-choice player must have access to a high degree of punishment, $C_1$ much less than $C_2$, to maintain cooperation and be robust against all invaders. As described in 3, the figure can alternatively be interpreted as the proportion of pairs of investment levels used by a d-choice player that produce a robust suboptimal fitness peak, and thus represents a lower bound on the “ruggedness” of the fitness landscape experienced by a population of d-choice players.

We can also investigate whether strategies that stabilize behavior at the lower investment level, $C_1$, can be robust against invasion (SI Appendix). We find that, indeed, such strategies can also be robust, but such strategies are never of the “extortion” type (30), which is perhaps unsurprising given that extortion strategies are unstable even when invaders are limited to only two choices (39).

Perception of Novel Actions.

In our analysis so far we have considered players that use a strategy composed of probabilities $p_{1j}$ and $p_{2j}$, corresponding to a player who always invests either $C_1$ or $C_2$ faced with an opponent’s investment of any amount $C_j$. However, a player who is restricted to investment levels $C_1$ and $C_2$ may also be restricted in her ability to perceive investments $C_j\ne \left\{C_1,C_2\right\}$ by her opponent. The exact nature and extent of such a constraint will depend on the specific system of interest, but any such constraint in perception can be studied using our analytical framework. In this section we apply the general results derived above to a very natural case of limited perception: a player who uses a strategy composed of just four probabilities, $\mathbf{p}=\left\{p_{11},p_{12},p_{21},p_{22}\right\}$. We assume that such a player uses a threshold $C_T$ such that she perceives her opponents’ investment $C_j<C_T$ as an investment of $C_1$ and she perceives $C_j\ge C_T$ as an investment of $C_2$.

For a resident strategy that stabilizes investment at the higher level, $C_2$, such a strategy can always be invaded by some mutant if her threshold satisfies $C_T<C_2$. However, for thresholds $C_T\ge C_2$, such resident two-choice strategies can be universally robust (SI Appendix). Indeed, if we make the natural threshold choice $C_T=C_2$, so that any decline in investment below the norm for the resident population is treated as defection, the condition for the existence of a universally robust strategy in the absence of discounting is

$$\frac{C_1}{C_2}<\frac{r-1}{\frac{r}{2}+\frac{1}{N-2}},$$

which is precisely the same as 3 (with $\delta =1$).

We have verified the condition above by numerical simulation (SI Appendix, Fig. S1), and we find that not only do simple, universally robust strategies of this type exist, but when they exist they are typically very common.

Evolutionary Consequences of Multiple Investment Choices.

We now turn our attention to the implications of these results for an evolving population of players who can make $d>2$ choices for investment in the public good. We assume a discrete series of $d+1$ investment levels, from 0 to the maximum $C_{max}$, so that subsequent levels of investment differ by $C_{\mathit{max}}/d$. When d is large, players have more options for investment, between the fixed minimum value zero and fixed maximum value $C_{max}$.

Because all two-choice strategies form a subset of d-choice strategies, an evolving population of d-choice players has access to, at minimum, all evolutionary robust two-choice strategies. Thus, unlike in the two-choice case, where there are only three qualitatively distinct types of evolutionary robust strategies (35), a d-choice population may result in many different classes of evolutionary robust outcomes, most of which are suboptimal in the sense that they produce less public good than the global maximum, $r{C}_{max}$.

We can place a lower bound on how many such suboptimal, but evolutionary robust, outcomes are possible when players have $d+1$ choices. Any given pair of investment levels $C_i$ and $C_j$, with $i>j$, can be a robust two-choice strategy, provided $C_i$ and $C_j$ satisfy 2. Thus, when there is no discounting ($\delta =1$) all pairs of investment levels $j<\frac{r-1}{\frac{r}{2}+\frac{1}{N-2}}i$ have viable robust two-choice strategies associated with them; and for a $d+1$ -choice game the total number of such evolutionary robust but suboptimal strategies, $P_r$, satisfies

$$P_r>\left(\frac{r-1}{\frac{r}{2}+\frac{1}{N-2}}\right)\frac{d\left(d+1\right)}{2}.$$ [4]

Thus, the number of suboptimal evolutionary robust outcomes grows at least quadratically with the number of investment levels available to individuals.

Fig. 2 can now be reinterpreted as showing the proportion of pairs of investment levels that can produce a robust, suboptimal two-choice strategy for a population of $d+1$ -choice players. To put these results in perspective, if players are allowed $d=100$ investment choices, with return on investment $r=3/2$, then in a population size $N=\mathrm{1,000}$ there are at least $3.6\times {10}^3$ robust strategies that fail to maximize the total public good—resulting in an extremely “rugged” fitness landscape and a large number of suboptimal evolutionary outcomes. By contrast, with only $d=2$ choices, there are at most two suboptimal evolutionary robust outcomes (35).

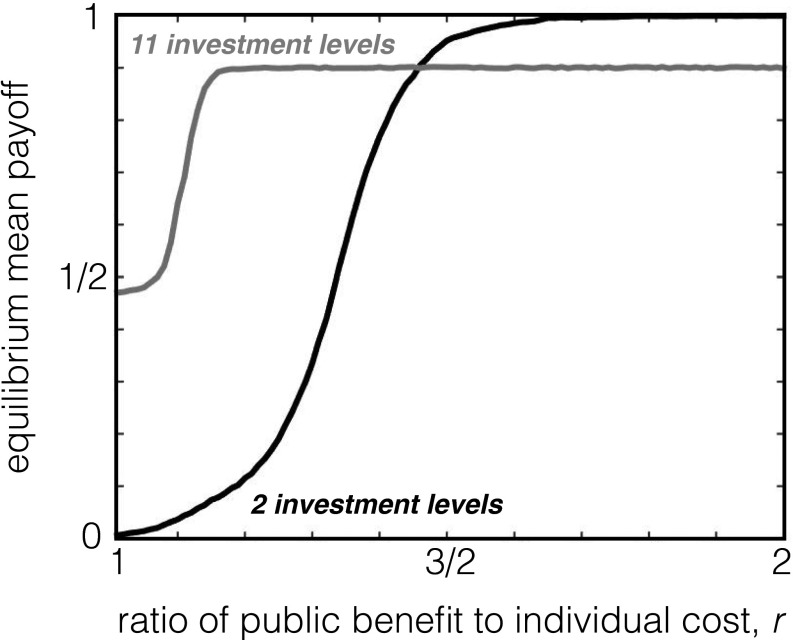
We have seen that increasing the number of available choices to players, between a fixed minimum and maximum investment level, has the potential to produce suboptimal but evolutionary robust outcomes. To test how the number of available choices impacts evolutionary dynamics in a population, we ran evolutionary simulations under weak mutation (42), with mutants drawn uniformly from all d-choice memory-1 strategies. We compared the mean payoffs received by populations constrained to $d=2$ choices, to the mean payoffs in populations with access to $d=11$ choices (Fig. 3). The results are striking: when the ratio of public benefit to individual cost are low, so that robust strategies are rare (Eqs. 3–4), the population that has $d=11$ investment choices evolves a higher mean payoff than the $d=2$ choice population, because a greater number of robust cooperative strategies provides an advantage. But when the ratio of public benefit to individual cost are higher, so that robust strategies are more common, the 11-choice population evolves a lower mean payoff than the two-choice population—because the huge number of suboptimal robust strategies causes the 11-choice population to “get stuck” and fail to maximize its evolutionary potential. Thus, increasing the number of investment options, between a fixed minimum and maximum, can either facilitate or hinder cooperative interactions in a population.

Fig. 3.

Does a larger behavioral repertoire make cooperation easier to evolve? We evolved a well-mixed population of $N=100$ haploid, asexual individuals reproducing according to the copying process (49) with an individual’s fitness determined by playing pairwise iterated public goods games with selection strength $\sigma =10$, with each game played for 1,000 rounds. We calculated ensemble mean fitness across ${10}^5$ replicate populations, each evolved under weak mutation for at least ${10}^6$ fixation events. We compared populations with only two investment choices available, $C_1=0$ and $C_2=1$, versus populations in which players could choose among 11 levels of investment, between 0 and 1 in increments of 0.1. In both cases evolution occurred on the full set of memory-1 strategies. When the ratio of public benefit to individual cost is small, two-choice populations evolve to low mean fitness and exhibit little cooperation; whereas, 11-choice populations evolve higher fitness and higher levels of investment in the public good. However, when the ratio of public benefit to individual cost is higher two-choice populations evolve strategies that maximize the public good, whereas 11-choice populations are less cooperative and receive roughly 10% payoff reduction compared with the two-choice case. Thus, a larger repertoire of behavioral options can either facilitate or impede the evolution of cooperation, depending upon the public return on individual investment.

Nontransitive Payoff Structures.

So far we have focused on multiple options for investment and its impact on the evolution of cooperative behaviors in public goods games. But the coordinate system we have introduced for studying multichoice iterated games, and the resulting relationship between two players’ scores (Eq. 1), applies generally, and so it can be applied to study many other questions in evolutionary game theory. Among the most interesting questions occur with only $d=3$ choices, but with nontransitive payoffs, where the evolutionary dynamics are complex and the impact of repeated interactions remains unclear (50, 54–59).

Games with nontransitive payoff structures, such as rock–paper–scissors, describe social dynamics without any strict hierarchy of behaviors. Individuals can invest in qualitatively different types of behavior, which dominate in some social interactions but lose out in others. Such nontransitive interactions have been observed in a range of biological systems, from communities of Escherichia coli species (50), to mating competition among male side-blotched lizards Uta stansburiana (54). Rock–paper–scissors interactions are well known in ecology as having important consequences for the maintenance of biodiversity: in well-mixed populations playing the one-shot game, diversity is often lost; whereas, in spatially distributed populations, multiple strategies can be stably maintained (55, 56). Here we analyze the equivalent problem for the maintenance of diversity in evolving populations of players who engage in iterated nontransitive interactions.

We will assess the potential for maintaining behavioral diversity in a population playing an iterated rock–paper–scissors game—that is, we look for strategies that can resist invasion by players who use a single behavioral choice (1 = rock, 2 = paper, or 3 = scissors). We assume that, in any given interaction, a fixed benefit B is at stake, and players invest a cost $C_1$, $C_2$, or $C_3$ to execute the corresponding behavioral choice. Under the rock–paper–scissors game we then have payoffs $R_{13}=B-C_1$, $R_{21}=B-C_2$, $R_{32}=B-C_3$, $R_{31}=-C_3$, $R_{12}=-C_1$, and $R_{23}=-C_2$. When two players make the same choice we assume they receive equal payoff: $R_{11}=B/2-C_1$, $R_{22}=B/2-C_2$, and $R_{33}=B/2-C_3$.

We first consider the case of a completely symmetric game of rock–paper–scissors, with $C_1=C_2=C_3=C$. In this case a given round of the game has only three distinct outcomes for a player: win (+), lose (−), or draw (o). A player’s memory-1 strategy can be thought of as the probability that she plays, for example, a move that would have won in the preceding round, given that she lost. We write this probability $p_{-}^{+}$. Similarly $p_{-}^{-}$ is the probability she plays the same move that lost the preceding round; and $p_{-}^o$ is the probability that she plays the move that would have resulted in a draw. This symmetric strategy is thus composed of nine probabilities, which are written in our alternative coordinate system in SI Appendix, section 4. From this coordinate system we see immediately that there exists no viable ZD strategy, with the sole exception of the singular “repeat” strategy (30). Despite the absence of ZD strategies, we can still analyze the outcome of iterated rock–paper–scissors games using this coordinate system.

Maintaining Behavioral Diversity in a Game of Rock–Paper–Scissors.

The symmetric, iterated rock–paper–scissors game is simple to analyze, because payoff is conserved, meaning that the sum of two interacting players’ payoffs is constant, $S_{xy}+S_{yx}=B-2C$. Thus, the expected fitness of a population is independent of the strategy that is resident, and $S_{xx}=B/2-C$ holds for all strategies X. It might seem unlikely, then, that behavioral diversity offers any advantage in this situation. After all, a player who uses a strategy that employs rock, paper, and scissors produces no higher mean fitness at the population level than a player who always uses rock. To determine whether this intuition is correct, and nontransitive payoffs lead inevitably to a loss of behavioral diversity, we evaluated the conditions for a strategy to resist selective invasion by a player who always uses the same move. Such strategies do indeed exist, and satisfy the following inequality:

$$p_o^{-}\left(1-p_{-}^{-}-p_{+}^{-}\right)>p_o^{+}\left(1-p_{+}^{+}-p_{-}^{+}\right).$$ [5]

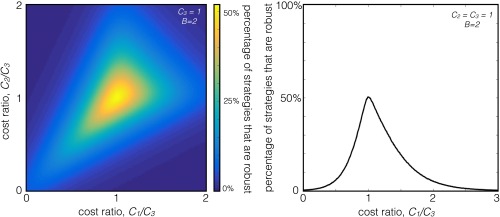
As one might hope, strategies that tend to switch to the move that would have won in the preceding round—corresponding to larger values of $p_o^{+}$, $p_{-}^{+}$, $p_{+}^{+}$ and smaller values of $p_o^{-}$, $p_{-}^{-}$, $p_{+}^{-}$ —tend to be evolutionary robust. However, 5 also provides a more valuable insight, as it allows us to calculate the overall robustness of memory-1 strategies to the loss of behavioral diversity. To do this we calculate the probability that a randomly drawn memory-1 strategy satisfies 5, which reveals that fully 50% of such strategies maintain behavioral diversity in the completely symmetric rock–paper–scissors game (Fig. 4). Furthermore, due to symmetry, the condition for a new strategy to invade a resident is simply $S_{yx}>S_{xy}$ (SI Appendix). And so if a resident can resist invasion against a particular invader, it can also invade a population in which that invader is resident. Thus, 50% of strategies can successfully invade in a population that lacks behavioral diversity—so that behavioral diversity is both highly evolvable and easy to maintain in the iterated rock–paper–scissors game, even in a well-mixed population—in sharp contrast to the one-shot game.

Fig. 4.

Can behavioral diversity be maintained under nontransitive payoff structures? We considered a rock–paper–scissors-type game in which players could use up to three different behaviors, at a cost $C_1$, $C_2$, and $C_3$, in an attempt to obtain a fixed benefit B. The payoff structure was nontransitive so that action 1 dominates action 2, action 2 dominates action 3, and action 3 dominates action 1. We determined whether a memory-1 strategy that employs all three behaviors can resist invasion by a player who uses a single action exclusively (either 1, 2, or 3). (Left) With fixed benefit $B=2$ and cost $C_3=1$ we systematically varied costs $C_1$ and $C_2$, and we calculated the percentage of memory-1 strategies that could successfully maintain behavioral diversity. Behavioral diversity can indeed be maintained for a wide range of costs. The highest level of robust diverse strategies occurs in the symmetric case, when $C_1=C_2=C_3$. But diverse behaviors are also observed across a broad range of parameters including, surprisingly, when both $C_1>B$ and $C_2>B$. This is seen more clearly on the Right, which shows the percentage of robust strategies as a function of $C_1$ with $C_2=C_3$.

We can also assess the robustness of behavioral diversity when the symmetry of the game is broken, so that $C_1\ne C_2\ne C_3$. In Fig. 4A we numerically calculate the overall robustness of randomly drawn strategies as a function of the costs $C_1/C_3$ and $C_2/C_3$ keeping B and $C_3$ fixed. We find that, for a wide range of costs, including in some cases with $B<C$, behavioral diversity can be maintained with relative ease in an evolving population (Fig. 4).

Discussion

We have studied how the repertoire of behavioral options influences the prospects for cooperation, and the maintenance of behavioral diversity, in evolving populations. Our analysis has relied on the theory of iterated games and, in particular, on a coordinate system we developed to describe strategies for multichoice games and their effects on long-term payoffs. In the context of public goods games, we have shown that simple strategies that use only two levels of investment can nonetheless stabilize cooperative behavior against arbitrarily diverse mutant invaders, provided the simple strategy has sufficient opportunity to punish defectors. More generally, a greater diversity of investment options can either facilitate or hinder the evolution of cooperation, depending on the ratio of public benefit produced to an individual’s investment cost. We have applied the same analytical framework to study more complicated multichoice iterated games with nontransitive payoffs, such as the rock–paper–scissors game. In this case, behaviorally diverse strategies that use multiple actions are often evolutionary robust, even in a well-mixed population, and they can likewise invade populations that lack diverse behaviors. Overall, the view emerges that simple behavioral interactions are sometimes surprisingly robust against diverse alternatives, and yet, in many circumstances, diverse behavior serves the mutual benefit of a population and is a likely outcome of evolution.

Our results on the impact of multiple behavioral choices should be compared with those of McAvoy and Hauert (36), who studied ZD strategies in two-player games with arbitrary action spaces. They established that ZD strategies exist even in this general setting. They focused especially on extortion strategies, whereby one player unilaterally sets the ratio of scores against her opponent. McAvoy and Hauert found, remarkably, that extortion strategies exist with support on only two actions, even against an opponent who can choose from an uncountable number of actions. Our results form an intriguing contrast to those of McAvoy and Hauert. Instead of studying ZD strategies and extortion in the classical context of two players, we have studied all memory-1 strategies and the prospects for robust cooperation in a population of $N>2$ players. We find that behaviorally depauperate strategies that rely on only two actions can nonetheless sustain cooperation in a population facing diverse invaders; and yet diversity can either hinder or facilitate cooperation, depending upon the ratio of public benefit to individual cost. These results were derived for well-mixed finite populations; the impact of behavioral diversity on evolution in structured populations, including graphs (21, 22), remains to be explored.

We have analyzed the entire space of memory-1 strategies for iterated multichoice games. Our ability to do so rests on a key mathematical result: the outcome of iterated games can be easily understood when players’ strategies, even those of startling complexity (3, 33, 38), are viewed in the right coordinate system. This coordinate system was suggested by the discovery of ZD strategies and developed fully by Akin (31) and others (3, 33, 35–37). The purview of our analysis can be put in context by comparison with the yet wider space of long-memory strategies, on the one hand, and the smaller space of ZD strategies, on the other hand. As discussed here and elsewhere, strategies that are evolutionary robust against the full space of memory-1 strategies are also robust against all longer-memory strategies (30, 38) (SI Appendix), making this a natural strategy space to consider from an evolutionary perspective. Nonetheless, memory can have an important impact on the relative success of different types of robust strategies, by making them more or less evolvable (3), or by allowing qualitatively different types of decision making via tagging or kin recognition (39, 63). Conversely, it is important to consider the full space of memory-1 strategies in the context of multichoice games because, as we have shown, such games may contain no ZD strategies at all, as in the case of iterated rock–paper–scissors.

It is unsurprising, perhaps, that games with nontransitive payoffs do not generally admit the opportunity for one player to exert unilateral control over the game’s outcome via ZD strategies. After all, a player cannot successfully extort an opponent whose behavior is so diverse that it cannot be pinned down. However, our analysis also offers perspective on the problem of diversity maintenance in evolving populations. One-shot rock–paper–scissors games have long been studied in the context of evolutionary ecology as a system that cannot easily maintain diversity without spatial structure or other exogenous population heterogeneity (50, 54–59). Here, by contrast, we have shown that behaviorally diverse strategies in the iterated game can easily emerge and resist invasion by behaviorally depauperate mutants, an observation that is relevant to behavioral interactions within a single population and also to interactions between species.

Overall we have seen that, as players gain access to more behavioral choices, either due to environmental shifts or evolutionary innovation, the dynamics of social evolution can be profoundly altered. This view is reflected by empirical studies, which have found that greater behavioral choice, via factors such as the ability to communicate or signal to others, has a significant impact on the level of cooperation in a group (9–15). Moving forward, we must connect the insights drawn from complex behavioral and evolutionary models of the type described here to empirical studies, where we can now seek quantitative predictions for the dynamics of group behavior in real populations.