Abstract
Several measurement assumptions were examined with the goal of assessing the validity of the Multidimensional Students’ Life Satisfaction Scale (MSLSS), a measure of adolescents’ satisfaction with their family, friends, living environment, school, self, and general quality of life. The data were obtained via a cross-sectional survey of 8,225 adolescents in British Columbia, Canada. Confirmatory factor and factor mixture analyses of ordinal data were used to examine the measurement assumptions. The adolescents did not respond to all the MSLSS items in a psychometrically equivalent manner. A correlated five-factor model for an abridged version of the MSLSS resulted in good fit when all negatively worded items and several positively worded items (the least invariant) were excluded. The abridged 18-item version of the MSLSS provides a promising alternative for the measurement of five life domains that are pertinent to adolescents’ quality of life.
Keywords: Quality of life, Adolescence, Measurement, Validity, Factor mixture analysis
1 Introduction
Adolescents’ quality of life is increasingly viewed as an important consideration for health researchers (Dannerbeck et al. 2004; Huebner et al. 2003, 2004; Kaplan 1998; Koot and Wallander 2001; Raphael 1996; Raphael et al. 1996; Topolski et al. 2001, 2004; Wallander et al. 2001). Instruments to measure quality of life have been developed to examine adolescents’ perceptions of the impact of various health care interventions and of supportive services designed to address mental or physical health problems (Drotar 1998; Edwards et al. 2003; Hinds and Haase 2003; Spieth and Harris 1996). Quality of life instruments also have been used in population health surveys of adolescents to examine the impact of various health policies and health promotion initiatives (Bradford et al. 2002; Huebner et al. 2004; Kaplan 1998; Raphael 1996; Raphael et al. 1996; Topolski et al. 2001, 2004). In these studies, “quality of life” is often meant to refer to adolescents’ satisfaction with life as a whole and with various life domains that are important to them. These life domains are typically defined as “the areas of experience which have significance for all or most people and which may be assumed to contribute in some degree to the general quality of life experience” (Campbell et al. 1976, p. 12). The life domains that are of particular importance to children and adolescents include the following: (a) perceptions of self (e.g., self-esteem), (b) social relationships with friends and family members, (c) school experiences, and (d) their living environment (Edwards et al. 2002; Huebner 1994).
Considering the multiple life domains that have been associated with quality of life, it is not surprising that quality of life is widely referred to as a multidimensional construct (Fayers and Machin 2007; Rapley 2003). Accordingly, most measurement instruments of quality of life consist of several subscales that correspond to the relevant life domains. “Overall” or “general” quality of life scores are often obtained by averaging the subscale scores. Huebner (1994, 2001) developed the 40-item Multidimensional Students’ Life Satisfaction Scale (MSLSS) for the measurement of five life domains of importance to children and adolescents (satisfaction with family, peers, school, self, and living environment). The life domains were based on theoretical developments and empirical studies about life satisfaction in adults and children, interviews with elementary school children, student essays, and exploratory factor analyses. The underlying measurement structure of the MSLSS was based on the theoretical premise that the life domains constitute dimensions that correspond to a common source, general quality of life, in a manner that is congruent with a second-order factor model (e.g., Huebner 1997). This measurement structure, if valid, implies that general quality of life scores could be obtained by averaging the scores of the MSLSS subscales.
Based on the results of several confirmatory factor analyses, it has been suggested that the reliability and construct validity of the MSLSS, for the measurement of satisfaction with family, friends, living environment, school and self, are supported by having confirmed the fit of a measurement structure with five correlated first-order factors (Gilman 1999; Gilman and Ashby 2003; Greenspoon and Saklofske 1998; Huebner et al. 1998; Park 2000; Park et al. 2004). The construct validity, for the measurement of general quality of life, has been examined by fitting a second-order factor that accounted for the correlations among the five-first-order factors (Gilman 1999; Gilman et al. 2000; Huebner and Gilman 2002; Huebner et al. 1998). Although these studies suggest preliminary support for the measurement validity of the MSLSS, several psychometric assumptions and theoretical premises underlying this measurement structure have not been examined explicitly.
1.1 Examining Measurement Validity
Despite the prevalent use of second-order factor models in quality of life measurement, the underlying psychometric assumptions are rarely explicitly stated and examined. The Draper-Lindley-de Finetti framework of measurement validity (Zumbo 2007a) provides a useful overview of the assumptions that must be tested to validate the use of a psychometric instrument for specific research purposes. According to this framework, measurement problems and sampling problems must both be examined when assessing measurement validity. Measurement problems include those pertaining to the psychometric equivalence (exchangeability) of the observed indicators (i.e., the items of each subscale), and sampling problems refer to the degree to which the measurement structure is appropriate for all respondents (i.e., equivalent across different sampling units in the target population). Factor analysis techniques are widely used to examine measurement problems by evaluating the extent to which the covariances of the observed indicators are accounted for by a common cause (or causes) (Nunnally and Bernstein 1994). The following assumptions must be tested when examining the psychometric equivalence of observed indicators with respect a second-order factor model: (a) the observed indicators uniquely respond to one of the first-order factors (i.e., their correlations are accounted for by one of the first-order factors) and (b) the correlations among the first-order latent factors are fully accounted for by a second-order latent factor (i.e., the residual variances of the first-order factors are uncorrelated with each other and with the second-order factor) (Edwards and Bagozzi 2000; Fayers and Machin 2007). Evidence of this pattern of covariance is a necessary (but not sufficient) condition for construct validity (Nunnally and Bernstein 1994; Viswanathan 2005).
Although measurement problems can be examined by testing the extent to which a particular factor structure fits the data of a sample as a whole, an examination of sampling problems involves determining the extent to which the factor structure is appropriate for all respondents. Zumbo (2007a) referred to this as “the exchangeability of sampled and un-sampled units (i.e., respondents) in the target population” (p. 59). This aspect of measurement validation relates to the degree to which individuals interpret and respond to items in a consistent and comparable manner. The exchangeability of sampling units is a necessary condition for the generalizability of inferences made about the measurement structure of a particular instrument. The following assumptions must be tested when examining the exchangeability of sampling units with respect to a second-order factor model: (a) respondents interpret and respond to the items in a consistent manner (i.e., the thresholds representing the probability distributions of the ordinal item responses are invariant in the sample), (b) the observed indicators of each subscale consistently reflect a single latent factor (i.e., they provide a measure of their respective first-order latent factor such that the factor loadings are invariant in the sample), and (c) the first-order latent factors consistently correlate because of a second-order latent factor (i.e., the second-order factor loadings are invariant in the sample). These assumptions relate to the degree to which a sample is homogeneous with respect to the parameters of the measurement model. If the assumptions do not hold for the respondents in a particular sample, then that sample can be said to be heterogeneous with respect to the measurement model. Conversely, a sample can be said to be homogeneous if the relationships among the corresponding indicators, as specified by the measurement model, are invariant irrespective of any differences among the respondents in a particular sample.
The notion of sample heterogeneity has not received sufficient attention with respect to the examination of measurement validity (Samuelsen 2008; Zumbo 2007a). Considering the diversity of items that compose most multidimensional quality of life instruments, it is plausible that some items are interpreted in different ways because of cultural, developmental, or personality differences, or because of contextual factors such as different living environments, employment experiences or other life circumstances. Consequently, respondents may not share a common frame of reference by which they interpret the various items. They also may adopt different response styles with respect to the rating scales of the items. For example, they may respond to some items by upward or downward comparisons of their life circumstances with those of their peers, with previous life circumstances, or to some ideal or model life circumstance. The resulting differences in “response style behaviours” can greatly distort the measurement of psychological constructs (Moors 2003, p. 278; Viswanathan 2005). These sources of sample heterogeneity with respect to a specified measurement structure, if present, threaten the internal validity of the construct that is being measured and limit the extent to which generalizable inferences pertaining to the comparison of individuals and groups within the target population can be made (Zumbo 2007a, b). Although some relevant differences in the sample may be readily recognized and observed, there also may be unrecognized or unknown differences, or unknown interactions among observed differences, that could result in inconsistent interpretations and responses to some items.
Multi-group confirmatory factor analysis (MGCFA) has been widely used to examine sample heterogeneity by comparing the measurement structure of psychological constructs among known or manifest categorical differences in a sample (e.g., Byrne 1998; Schumacker and Lomax 2004; Steenkamp and Baumgartner 1998; Vandenberg and Lance 2000; Zumbo 2007b). However, as pointed out by Samuelsen (2008), the use of MGCFA necessitates that the relevant differences in a sample are known and measured, a priori. Empirical studies have shown that sample heterogeneity with respect to the measurement structures of psychological constructs may be under detected when only relying on a priori observed differences in a sample (e.g., Cohen and Bolt 2005; De Ayala et al. 2002). Other statistical techniques must be employed to examine variation in measurement model parameters due to differences that are not known, a priori. Relevant differences in a sample that are not known can be identified by adding latent classes to a measurement model (Cohen and Bolt 2005; De Ayala et al. 2002; Lubke and Muthén 2005; Samuelsen 2008; Zumbo 2007a). The corresponding statistical technique, factor mixture analysis (FMA), can be used to: (a) examine the extent to which a sample is heterogeneous with respect to a specified measurement structure, (b) identify latent classes that represent subsamples characterized by unknown, or unrecognized, differences in the sample, and (c) evaluate the extent to which individual item parameters vary across the latent classes.
1.2 Purpose
We used the Draper-Lindley-de Finetti framework (Zumbo 2007a) to evaluate the measurement validity of Huebner’s (1994, 2001) MSLSS for the assessment of adolescents’ quality of life by examining the above stated potential measurement and sampling problems. We specifically addressed the following research questions: (a) is a second-order factor structure, or the implied measurement structure with five correlated latent factors, adequately supported in the sample? and (b) did the adolescents respond to the items in a consistent fashion (i.e., was the sample homogeneous with respect to a unidimensional measurement structure for each of the MSLSS subscales)? A second purpose was to determine whether any observed measurement or sampling problems could be addressed through modifications to the measurement structure.
2 Methods
2.1 Data Collection
The data were taken from the British Columbia Youth Survey on Smoking and Health II, a cross-sectional health survey of adolescents in grades 7–12 who attended schools in the province of British Columbia, Canada. Of the 60 school districts in the province, 19 were contacted to obtain permission for schools within their jurisdiction to participate. The 19 districts were purposely selected to maximize geographic coverage of the province while avoiding areas known to have low smoking prevalence rates and to be remote, sparsely populated, and relatively difficult to access. Fourteen school districts provided permission for a sample of 86 eligible schools (five school districts declined). Of the 86 schools, 49 (57%) agreed to participate. Sampling of the adolescents in 22 of the 49 schools was completed by inviting the entire student body or students in particular grades to participate. In the remaining 27 schools, the selection of participants primarily occurred by recruiting students in courses that enrolled most of the student body. It was anticipated that these sampling strategies would result in a sample of adolescents who were at various stages of development, who lived in diverse geographical locations and living conditions, and who reflected the diversity of cultures represented throughout the province.
Ethical approval was granted by the Behavioural Research Ethics Board of the University of British Columbia (Canada); passive parental consent was obtained by providing the parents of the adolescents with a letter that informed them of the survey. Less than 1% of the students refused to participate and the response rate within schools was 84%, on average (non-response was mostly due to student absenteeism) (Richardson et al. 2007; Tu et al. 2008). The resulting sample consisted of 8,225 adolescents who completed the survey.
2.2 Instrument and Reliability
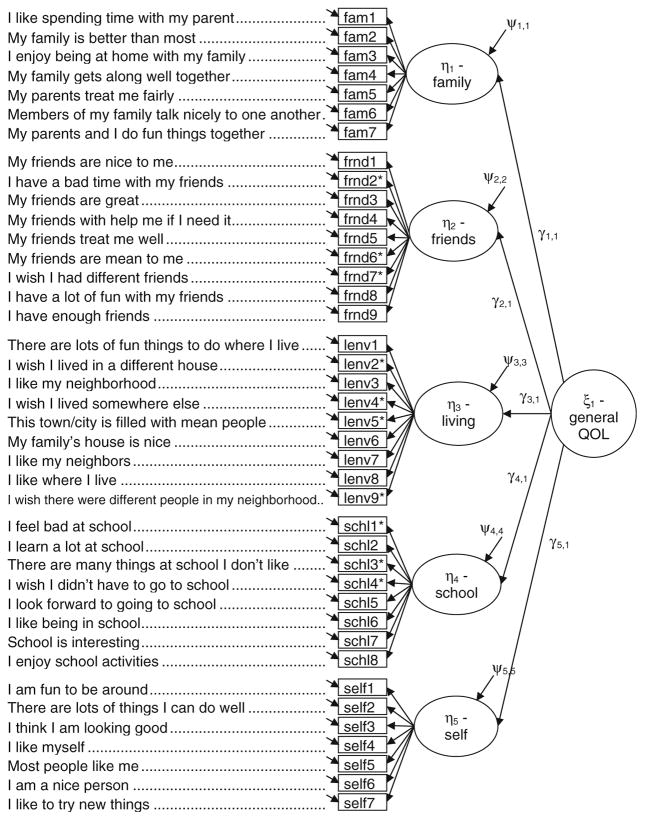
Huebner’s 2001 version of the MSLSS assesses adolescents’ satisfaction with family (7 items), friends (9 items), school (8 items), living environment (9 items), and self (7 items) (Fig. 1 provides the wording of all the items). The items were placed in the questionnaire in the order recommended in the MSLSS manual (Huebner 2001). The MSLSS includes 10 negatively worded items that were reverse-scored prior to analysis. As recommended by Huebner, a 6-point response format with options ranging from “strongly disagree” to “strongly agree” was used (Gilman et al. 2000; Huebner et al. 1998). In the sample, the reliability estimates for the subscales were comparable to those reported in the literature (Huebner and Gilman 2002) (current study coefficient alpha ≥ 0.81). To be consistent with our analyses, wherein the data are treated as ordinal rather than interval, we also computed ordinal coefficient alphas for the subscales, which were all ≥ 0.85 (Zumbo et al. 2007).
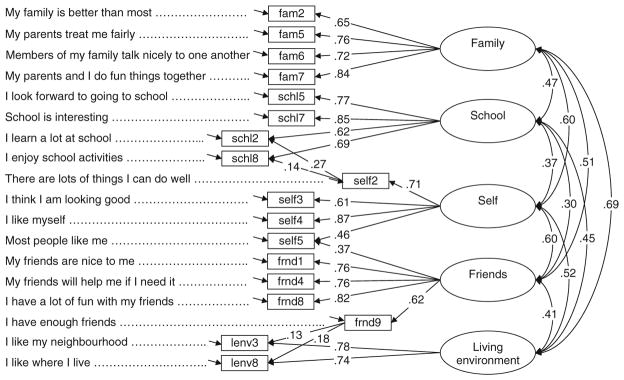
Fig. 1.
A second-order factor model specification of the MSLSS. “*” Negatively worded items
2.3 Methods of Validity Assessment
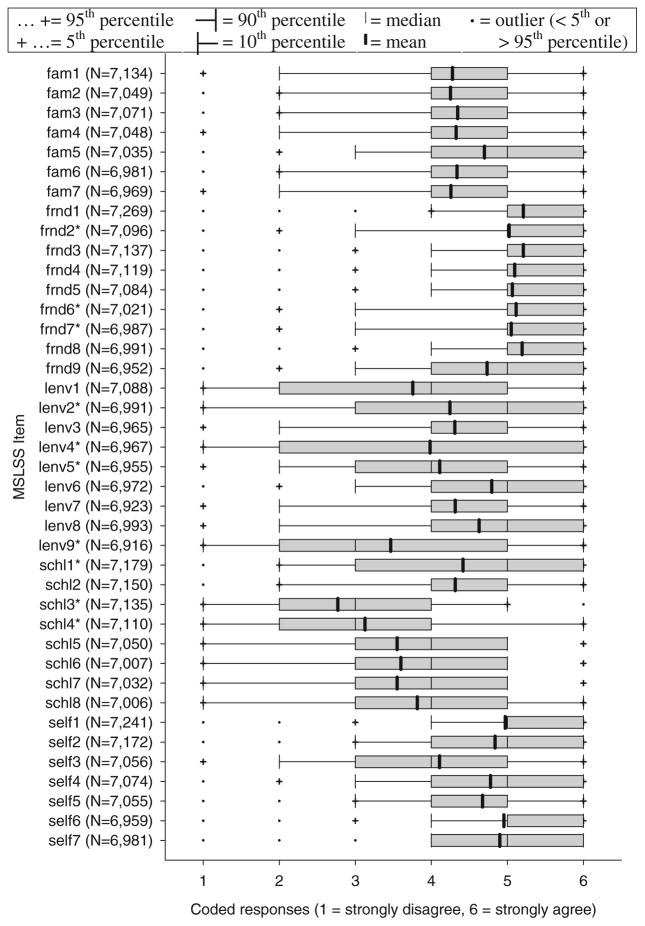
Confirmatory factor analysis (CFA) was used to test the fit of the second-order factor model. We specified that the 40 observed indicators of the MSLSS responded to one of five first-order latent factors, which in turn responded to one common second-order factor (Fig. 1). The variances for all of the latent factors were specified to equal one to avoid indeterminacy and to set the metric of the latent factors (Schumacker and Lomax 2004). The distributions of the observed indicators clearly revealed the non-normal and discrete nature of the data (Fig. 2). The resulting deviations from multivariate normality could have resulted in severely biased parameter estimates and indicators of model fit had they been treated as interval-level data (Finney and DiStefano 2006; Flora and Curran 2004; Lee et al. 2005). We followed the widely recommended approach of using polychoric correlations to model the observed indicators as ordinal-level data to avoid such bias (Finney and DiStefano 2006; Jöreskog 1990; Jöreskog and Moustaki 2001; Millsap and Yun-Tein 2004; Rigdon and Ferguson 1991).
Fig. 2.
Box plots of the distributions of the MSLSS items. “*” Negatively worded items (reverse coded)
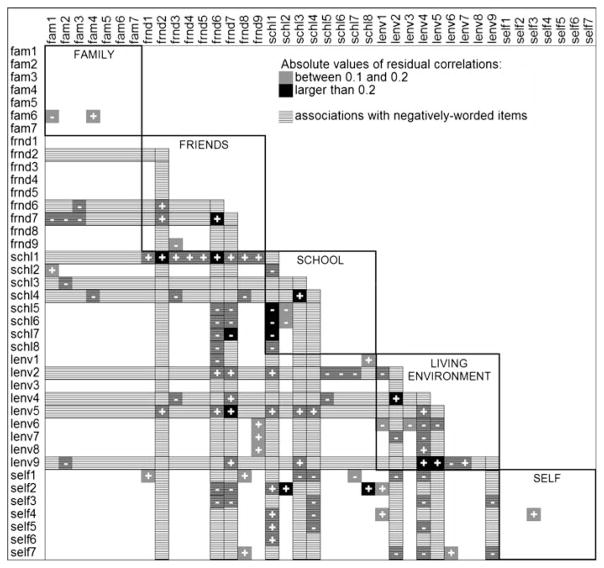
A robust mean and variance adjusted weighted-least squares estimation method (WLSMV), included in the Mplus 4.2 software, was used (Muthén and Muthén 2006). This estimation method is recommended for use with ordinal data resulting in more robust χ2 statistics, less bias in the parameter estimates, and lower Type I error rates (Beauducel and Herzberg 2006; Finney and DiStefano 2006). The following desirable criteria were used to examine model fit: (a) a root mean square error of approximation (RMSEA) <0.06, (b) a comparative fit index (CFI) >0.95, and (c) a standardized root mean residual (SRMR) ≤0.08 (e.g., Hu and Bentler 1999; Schumacker and Lomax 2004; Vandenberg and Lance 2000). Several simulation studies have shown that these criteria could be cautiously applied to the use of WLSMV estimation with ordinal variables (Beauducel and Herzberg 2006; Yu 2002). However, we concur with Marsh et al. (2004) and others (e.g., McDonald and Ho 2002) who cautioned against the overgeneralization and uncritical application of cutoff values for goodness of fit indices. Ultimately, the assessment of model fit should be based on a comparison of the observed and implied correlation matrices (McDonald and Ho 2002). We therefore mapped the residual correlations so as to locate any specific areas of misfit (Fig. 3). A summary of the residual correlations is provided by reporting the percentage of residual correlations with absolute values >0.10. We also conducted a principal component analysis on the residual correlations to ascertain whether an unspecified latent factor accounted for any observed misfit.
Fig. 3.
Residual correlations for the correlated five-factor model. Notes: Residual correlations = observed polychoric correlations minus the estimated correlations of the correlated 5-factor model (N = 6,325)
2.4 Factor Mixture Analysis
FMA was used to examine potential sample heterogeneity with respect to the measurement structure for each subscale (domain). A factor mixture model can be viewed as the combination of a latent class model and a confirmatory factor model (Lubke and Muthén 2005). In a latent class model, individuals are clustered so as to maximize local independence among the observed variables conditional upon a categorical latent class variable (Hagenaars and McCutcheon 2002; Magidson and Vermunt 2004). By combining a latent factor model with a latent class model, one obtains a clustering of individuals so as to maximize independence among the observed variables conditional on the class-specific measurement model parameters (Lubke and Muthén 2005).
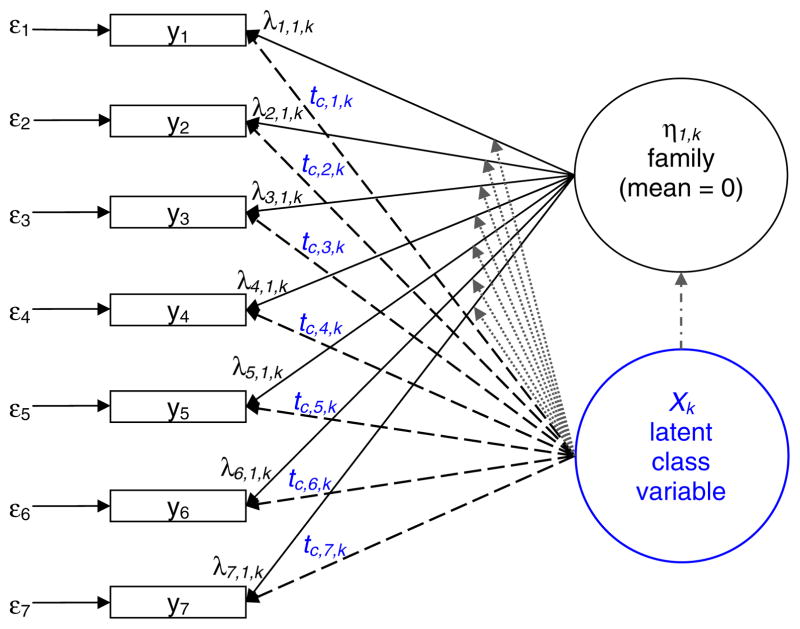
Factor mixture models were specified for each subscale by allowing the thresholds, factor loadings and factor variances to vary across two or more latent classes (Fig. 4). This approach was used to determine whether: (a) the sample was heterogeneous with respect to the unidimensional measurement structure of each MSLSS subscale and (b) the measurement model parameters (i.e., the thresholds and factor loadings) were invariant across two or more latent classes. Sample heterogeneity was examined by determining the number of latent classes needed to achieve the best model fit, and invariance of the model parameters was determined by comparing the magnitude of the obtained estimates across two or more latent classes. A comparison of the thresholds across latent classes was obtained by graphing their values (and 95% confidence intervals) within the latent classes along the Y-axis and the threshold number along the X-axis. A relative lack of invariance could be identified by assessing those items with the most discrepant threshold values across latent classes. A similar approach was used to compare the differences in factor loadings across latent classes.
Fig. 4.
The factor mixture model for the family subscale.
 λ Parameters for relationships between the latent factor and the observed variables.
λ Parameters for relationships between the latent factor and the observed variables.
 t Parameters for c−1 thresholds that are conditional on latent class variable Xk, k = 1, …, K.
t Parameters for c−1 thresholds that are conditional on latent class variable Xk, k = 1, …, K.
 Indicates that the λ parameters are conditional on latent class variable Xk, k = 1, …, K.
Indicates that the λ parameters are conditional on latent class variable Xk, k = 1, …, K.
 Indicates that the variance of the latent factor, η, is conditional on latent class variable Xk, k = 1, …, K−1. K is the number of latent classes and C is the number of ordinal categories for the observed variables
Indicates that the variance of the latent factor, η, is conditional on latent class variable Xk, k = 1, …, K−1. K is the number of latent classes and C is the number of ordinal categories for the observed variables
The model parameters were estimated using a robust maximum likelihood estimation method (MLR) available in Mplus 4.2 (Muthén and Muthén 2006). A local maximum was avoided by using a large number of randomly generated sets of parameter starting values (up to 500 sets for each model). The Bayesian information criterion (BIC) was used to compare the solution for a model with K classes to a solution for a model with K−1 classes to determine the best fitting and most parsimonious model (i.e., the model with the least number of classes) (Nylund et al. 2007).
2.5 Data Screening
The data were screened for implausible response patterns and missing responses. Data for 72 respondents that had the same value for all positively and negatively worded MSLSS items were excluded from the analyses because these responses were deemed to be untrustworthy. Of the remaining 8,153 respondents, 5,269 (64.6%) completed all the MSLSS items, 1,056 (13.0%) had a missing value for only one of the items, 980 (12.0%) had missing values for more than one of the items, and 848 (10.4%) did not complete any of the items (this latter group was not included in our analyses).
2.6 Missing Data Techniques
The expectation maximization (EM) algorithm was used to impute a single value for the 1,056 adolescents who had a missing value for one of the MSLSS items (N = 6,325; 0.42% imputed data). We sought to impute only a very small amount of data because single imputation based on the EM algorithm can result in biased standard errors and model fit indices (Enders 2006). We evaluated whether the CFA results may have been biased due to the use of single value imputation, where the data are assumed to be missing completely at random, by comparing the results to: (a) those obtained using full information maximum likelihood (FIML) with respondents with values for at least one MSLSS indicator (N = 7,305) and (b) those obtained using EM for multiple imputation (MI) of data based on all relevant available information for the respondents with values for at least one MSLSS indicator (N = 7,305). The SAS 9.2 software package (SAS Institute 2005) was used to create 10 imputed datasets for the MI analyses, following the guidelines offered by Allison (2002) and Enders (2006), to assess convergence and to incorporate auxiliary variables associated with the MSLSS indicators (i.e., demographic variables (sex, ethnicity, grade), two measures of overall quality of life, perceived mental and physical health status, symptoms of depression, and two variables pertaining to the adolescents’ experiences at school). The FIML and MI results are available upon request.
3 Results
3.1 Sample Description
The sample of adolescents who completed at least one of the MSLSS items (N = 7,305) consisted of an approximately equal percentage of boys (48.1%) and girls in grades seven through 12. The average age was 15.2 years (SD = 1.5, N = 7,261) with 7,188 adolescents being between the ages of 12 and 18 years. Although most of the adolescents described themselves as “white/Caucasian” (72.6%), the sample also included Aboriginal adolescents (14.7%), Asian adolescents (Chinese, Japanese, Korean, Filipino or South–East Asian) (5.6%), and adolescents that described themselves as belonging to one or more “other ethnic” groups (4.9%) (2.3% did not report their ethnicity). Most adolescents (94.6%) reported speaking English at home (4.7% did not speak English at home; 0.8% did not answer this question), and 16.4% of the adolescents reported regularly speaking a language other than English at home (82.3% did not regularly speak a language other than English at home; 1.3% did not answer this question).
3.2 Distribution of MSLSS Indicators
The distributions of the MSLSS items are provided in Fig. 2. The modal responses after reverse coding the negatively worded items were ‘strongly disagree’ for 1 item (schl4), ‘disagree’ for 1 item (schl3), ‘mildly disagree’ for 1 item (lenv9), ‘mildly agree’ for 6 items, ‘agree’ for 20 items, and ‘strongly agree’ for 11 items. Several discrepancies were observed in how the adolescents responded to the negatively worded items in comparison with the positively worded items. For example, 32.1% of the adolescents strongly agreed that they wished there were different people in their neighborhoods. This response seemed to contradict their responses to the other living environment items, which suggested that they were satisfied with their living environment. Similarly, 22.9% of the adolescents strongly agreed with the statement that they wished they did not have to go to school, whereas only 13.2% strongly disagreed with the statement that they liked being at school. These discrepancies suggest that the adolescents may not have responded to some of the negatively worded items in a manner congruent with their responses to other items within the corresponding subscale.
3.3 Confirmatory Factor Analyses
Neither the second-order factor model nor the measurement structure with five correlated latent factors was supported (Table 1). The fit indices for both models did not fall within the recommended ranges and the residual correlations were very large (ranging from −0.23 to 0.35 for the less restrictive correlated five-factor model) with 107 (13.7%) of the 780 residual correlations, for the correlated five-factor model, having absolute values >0.10. Principal components analysis of the residual correlations (resulting from the correlated five factor model) was conducted to identify whether the residuals could be attributed to one or more unspecified latent factors. Only 6.6% of the total variance could be attributed to the first component, which had an eigenvalue of 2.60. A methods factor, to accommodate the negatively worded items, was added to the model, which led to substantial improvement in model fit (ΔWLSMV χ2 = 2,306.39, Δdf = 5, p < 0.001); however, the model still did not fit the data very well (see third model in Table 1).
Table 1.
CFA of multidimensional measurement structures for the MSLSS
| Model | WLSMV χ2 | df | CFI | RMSEA | SRMR | Residual correlations
|
|
|---|---|---|---|---|---|---|---|
| Range | % >|0.1| | ||||||
| Second-order factor model | 17,500.98 | 195a 735b |
0.713 | 0.118 | 0.077 | −0.24 to 0.32 | 17.3% |
| Correlated five-factor model | 17,336.59 | 215a 730b |
0.716 | 0.112 | 0.070 | −0.23 to 0.35 | 13.7% |
| Correlated five-factor model with methods factor | 14,752.07 | 239a 720b |
0.759 | 0.098 | 0.060 | −0.19 to 0.25 | 8.6% |
| Correlated five-factor model excluding negatively worded items | 8,977.99 | 167a 395b |
0.813 | 0.091 | 0.049 | −0.15 to 0.20 | 4.1% |
Notes: analyses using EM imputations for those with one missing MSLSS value (N = 6,325) and mean and variance adjusted weighted least squares estimation (WLSMV). Similar findings were obtained when using MI (N = 7,325)
RMSEA = root mean square error of approximation, SRMR = standardized root mean square residual, CFI = comparative fit index
df based on WLSMV estimation
df based on number of free parameters
Further examination of the pattern of residual correlations for the correlated five-factor model, without the methods factor, revealed that 93 (87%) of the 107 residual correlations with absolute values>0.10 were associated with the negatively worded items, many of the covariate pairs being between negatively worded and positively worded items (Fig. 3). The model misfit was largely attributable to the negatively worded items. The analyses were continued by removing the negatively worded items altogether, which resulted in a better fitting model (see last model in Table 1). The magnitude of the residual correlations was substantially reduced as indicated by: (a) a smaller SRMR value of 0.05, (b) a narrower range of residual correlations (from −0.15 to 0.20), and (c) a smaller proportion of residuals with absolute values >0.10 [18 of 435 (4.1%)]. However, the magnitude of the remaining residual correlations and the values of the CFI and RMSEA suggested that some problems with model fit persisted. Similar results were obtained when the CFAs for the three subscales that included the negatively worded items were compared with results obtained when the negatively worded items were removed (Table 2) (there are no negatively worded items for the family and self subscales). The analyses using FIML and MI (not reported due to space limitations) resulted in similar findings.
Table 2.
CFA models of the MSLSS subscales
| Model | # Items | WLSMV χ2 | dfa | CFI | RMSEA | SRMR | Residual correlations
|
|
|---|---|---|---|---|---|---|---|---|
| Range | % >|0.1| | |||||||
| CFAs of the original subscales | ||||||||
| Family | 7 | 3,020.71 | 11 | 0.908 | 0.208 | 0.050 | −0.16 to 0.10 | 19.0% |
| Self | 7 | 976.17 | 13 | 0.940 | 0.108 | 0.040 | −0.09 to 0.08 | 0.0% |
| Friends | 9 | 3,334.86 | 18 | 0.902 | 0.171 | 0.055 | −0.10 to 0.19 | 5.6% |
| Living environment | 9 | 3,123.06 | 17 | 0.865 | 0.170 | 0.077 | −0.18 to 0.16 | 25.0% |
| School | 8 | 2,504.89 | 15 | 0.925 | 0.162 | 0.052 | −0.07 to 0.18 | 7.1% |
| CFAs of the subscales excluding the negative-worded items | ||||||||
| Friends | 6 | 643.48 | 8 | 0.979 | 0.112 | 0.026 | −0.05 to 0.07 | 0.0% |
| Living environment | 5 | 412.50 | 5 | 0.971 | 0.114 | 0.031 | −0.06 to 0.04 | 0.0% |
| School | 5 | 1,270. 96 | 4 | 0.958 | 0.224 | 0.042 | −0.06 to 0.07 | 0.0% |
| CFAs of the abridged subscales (including the 4 items with the most consistent responses) | ||||||||
| Family | 4 | 5.13 | 2 | 1.000 | 0.016 | 0.004 | −0.01 to 0.00 | 0.0% |
| Self | 4 | 16.97 | 2 | 0.999 | 0.034 | 0.008 | −0.02 to 0.01 | 0.0% |
| Friends | 4 | 45.07 | 2 | 0.996 | 0.058 | 0.013 | −0.02 to 0.03 | 0.0% |
| Living environment | 4 | 28.2 | 2 | 0.998 | 0.046 | 0.011 | −0.03 to 0.02 | 0.0% |
| School | 4 | 8.73 | 2 | 1.000 | 0.023 | 0.004 | −0.01 to 0.01 | 0.0% |
Notes: analyses based on EM imputations for those with one missing MSLSS value (N = 6,325). Similar findings were obtained when using FIML or MI (N = 7,325)
df based on WLSMV estimation
3.4 Examining Sample Heterogeneity
FMA techniques were used to examine potential sample heterogeneity with respect to the unidimensional measurement structure for each of the subscales (excluding the negatively worded items). Significant improvements in model fit were obtained when four latent classes for the family subscale, three latent classes for the self subscale, four latent classes for the school subscale, two latent classes for the friends subscale, and three latent classes for the living environment subscale were specified (Table 3). The smallest latent class was representative of 14% of the sample, which indicates that the latent classes were not trivial. Thus, the sample was heterogeneous with respect to a unidimensional measurement structure for each of the subscales.
Table 3.
FMA of the MSLSS subscales
| Subscale | K | P | LL | BIC | Entropy | Class proportionsa
|
|||
|---|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | ||||||
| Family | 1 | 42 | −58,211.65 | 116,790.89 | 1.000 | 1.00 | |||
| 4 | 171 | −55,899.78 | 113,296.20 | 0.607 | 0.18 | 0.36 | 0.23 | 0.29 | |
| Self | 1 | 42 | −54,173.18 | 108,713.96 | 1.000 | 1.00 | |||
| 3 | 128 | −52,758.93 | 106,638.14 | 0.517 | 0.41 | 0.46 | 0.14 | ||
| School | 1 | 30 | −44,727.06 | 89,716.70 | 1.000 | 1.00 | |||
| 4 | 123 | −42,772.53 | 86,621.59 | 0.568 | 0.36 | 0.30 | 0.19 | 0.15 | |
| Friends | 1 | 36 | −37,575.70 | 75,466.48 | 1.000 | 1.00 | |||
| 2 | 73 | −36,632.35 | 73,903.61 | 0.486 | 0.61 | 0.39 | |||
| Living environment | 1 | 30 | −45,283.93 | 90,830.43 | 1.000 | 1.00 | |||
| 3 | 92 | −43,856.87 | 88,518.95 | 0.521 | 0.46 | 0.27 | 0.27 | ||
Notes: N = 6,325. K = # of latent classes. P = # of parameters estimated LL = log likelihood, BIC = Bayesian information criterion
Predicted class proportions based on the largest posterior latent class probability
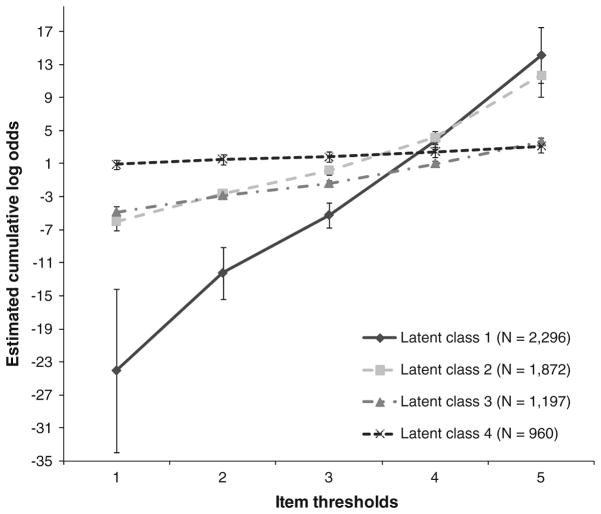
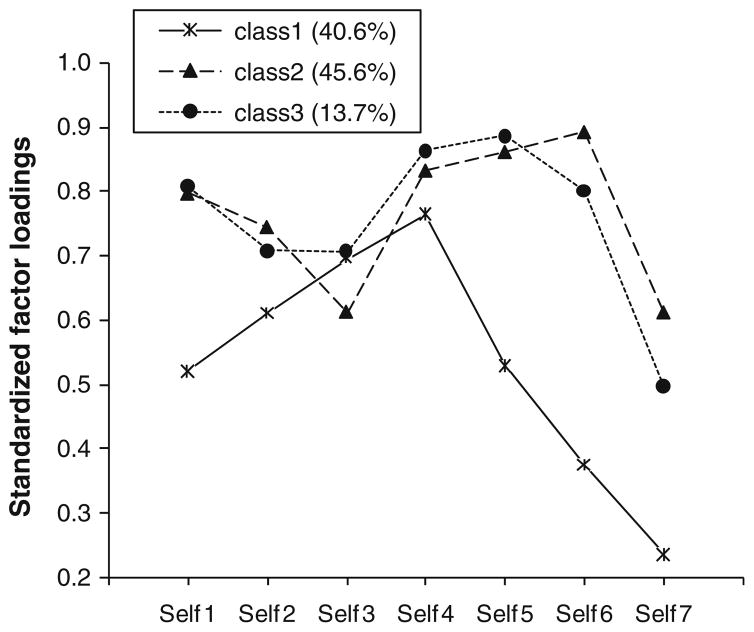
The four most invariant items for each subscale were identified by comparing the factor loadings and thresholds across the latent classes for each subscale. For example, when the thresholds of the five positively worded items in the school subscale were compared, several thresholds for the item “I like being at school” were found to be very different in some of the latent classes (Fig. 5). The adolescents in this sample did not respond to this item in a consistent manner. The standardized factor loadings across the latent classes for each subscale were also compared. For example, for the self subscale, the factor loadings were most invariant for the items: “There are lots of things I can do well” (self 2), “I think I am looking good” (self 3), and “I like myself” (self 4) (Fig. 6). With respect to the remaining four items, the thresholds were most invariant for the item, “Most people like me” (self 5). These were the four most invariant items for the self subscale. This approach to identifying and retaining the four most invariant items was used to create an abridged version of each of the five MSLSS subscales.
Fig. 5.
Thresholds of the item “I like being at school” in four latent classes. Notes: N = 6,325. The bars in each line graph represent 95% confidence intervals
Fig. 6.
Class-specific standardized factor loadings for the self subscale. Notes: N = 6,325
The CFAs of the abridged subscales revealed that model fit was substantially improved (Table 2). The reliability estimates for the abridged subscales were: coefficient alphas ≥0.75 and ordinal coefficient alphas ≥0.80 (Zumbo et al. 2007). However, although good model fit for a unidimensional factor structure of the abridged living environment subscale was obtained, the standardized factor loadings of the items, “My family’s house is nice” (lenv6) and “There are lots of fun things to do where I live” (lenv1) differed substantially across two latent classes when we re-estimated the factor mixture model. The adolescents may not have responded to these items in a consistent manner.
3.5 CFAs of the Abridged MSLSS
The CFA of the model with five correlated first-order factors for the abridged MSLSS indicated that the model did not fit the data well (Table 4). Examination of the residual correlations revealed that the model misfit could be primarily attributed to several items from the living environment subscale and several items from the self subscale. It is common practice to modify a model when relatively minor areas of misfit are found by specifying cross-loadings or correlating residuals. However, any theoretical explanations underlying the observed lack of misfit are ignored when correlating residuals. We therefore chose to revise the model by explicitly testing hypotheses pertaining to a few theoretically defensible modifications. Specifically, two living environment items (lenv1 and lenv6) were removed (based on the FMA findings that revealed that the adolescents may not have responded to these items in a consistent manner). The two remaining living environment items were regressed on one of the items of the friends subscale (frnd9)—it was hypothesized that the degree to which adolescents like where they live might be associated with the degree to which their living environment is conducive to having enough friends. With respect to the items in the self subscale, a cross-loading onto the latent factor for friends was specified for the item, “Most people like me” (self5). This was based on the rationale that adolescents’ experiences of being liked by people is associated with the relationships they have with their friends and peers. And, two of the school subscale items (schl2 and schl8) were regressed on the item, “There are lots of things I can do well” (self2). Adolescents’ responses about their learning experiences at school may be influenced by their perception of whether they can do things well, in general. The specification of the correlated five-factor model, including all of these modifications, is displayed in Fig. 7. This model resulted in good fit (WLSMV χ2 (80) = 1,368.26, RMSEA = 0.05, CFI = 0.96) and all parameter estimates were statistically significant (p < 0.05). The standardized factor loadings were smallest for the relationships between self5 and satisfaction with self (0.46) and friends (0.37), and the remaining factor loadings ranged from 0.61 to 0.87 (Fig. 7). All the polychoric correlations among the five latent factors were statistically significant with values ranging from 0.30 to 0.69.
Table 4.
CFA models of the abridged MSLSS
| Model | WLSMV χ2 | df | CFI | RMSEA | SRMR | Residual correlations
|
|
|---|---|---|---|---|---|---|---|
| Range | % >|0.1| | ||||||
| Correlated five-factor model | 4,182.79 | 102a 160b |
0.869 | 0.080 | 0.041 | −0.13 to 0.18 | 2.1% |
| Modified five-factor model of the abridged MSLSSc | 1,368.26 | 80a 120b |
0.958 | 0.050 | 0.026 | −0.07 to 0.07 | 0.0% |
| Modified 2nd order factor model of the bridged MSLSS | 1,801.15 | 72a 125b |
0.944 | 0.062 | 0.035 | −0.09 to 0.09 | 0.0% |
Notes: analyses using EM imputations for those with one missing MSLSS value (N = 6,325) and mean and variance adjusted weighted least squares estimation (WLSMV). Similar findings were obtained when using MI (N = 7,325)
RMSEA root mean square error of approximation, SRMR standardized root mean square residual, CFI comparative fit index
df based on WLSMV estimation
df based on number of free parameters
Modified correlated five-factor model with two living environment items
Fig. 7.
Correlated five-factor structure of the abridged and modified MSLSS. Notes: N = 6,325, WLSMV χ2 (80) = 1,368.26, RMSEA = 0.050, CFI = 0.958. All parameter values are standardized. Variances of the latent factors were constrained to equal 1.0 for identification. The four parameters between frnd9, lenv8 and lenv3, and between self2, schl2, and schl8, were specified by creating a latent variable corresponding to each of these variables with factor loadings fixed at 1.0, and a theta matrix was used to fix the residual variances of the corresponding observed variables at zero
The purpose of the above minor modifications was to obtain a well-fitting model with correlated first-order factors so that we could subsequently examine whether these first-order factors responded to a common second-order factor. The second-order factor model with the above modifications did not fit as well as the correlated first-order factor model (WLSMV χ2 (91) = 1,801.15, ΔWLSMV χ2 (5) = 372.19, RMSEA = 0.06, CFI = 0.94). In addition, several changes in the correlational structure of the first-order factors arose as a result of the constraints implied by the second-order factor. In particular, the correlation between friends and self (r = 0.60) based on the correlated five-factor model, was larger than the correlation implied by the second-order factor structure (r = 0.49). In contrast, the correlations between friends and living environment (r = 0.41) and friends and school (r = 0.30) were smaller than those implied by the second-order factor structure (r = 0.52 and 0.35, respectively). The correlated five-factor model provided a better representation of the dimensional structure than did the second-order factor model. The relationships between the second-order factor and the first-order factors were also examined. The second-order factor accounted for a substantial percentage of the variance in family (R2 = 0.68), living environment (R2 = 0.63) and self (R2 = 0.56). However, the explained variance in friends (R2 = 0.43) and school (R2 = 0.28) was much smaller. This indicated that the second-order factor predominantly represented satisfaction with family, self, and living environment and, to a lesser extent, satisfaction with friends and school.
3.6 Comparison with Other Published CFAs of the MSLSS
The results that we obtained are inconsistent with those of other published CFAs of all the MSLSS items, which produced acceptable model fit for a measurement structure with five correlated latent factors (Gilman 1999; Gilman et al. 2000; Greenspoon and Saklofske 1998; Huebner et al. 1998; Park 2000; Park et al. 2004), and a second-order factor (Gilman 1999; Gilman et al. 2000; Huebner et al. 1998). These differences can be partly attributed to the different methodological approaches that were employed. Most of the published CFAs were based on the analysis of item parcels (Gilman 1999; Gilman et al. 2000; Huebner et al. 1998; Park 2000; Park et al. 2004), whereas the models here were based on the observed indicator scores. When using item parcels, the model is estimated based on the correlations (or covariances) among the item parcels rather than on the observed indicators. Item parceling can therefore be used to reduce the shared systematic and random error by averaging the effects of these errors across the items that share the same parcel. Generally, the use of item parceling methods results in better fitting models (Bandalos 2002; Little et al. 2002). However, an important assumption of item parceling is that the factor structure is known to be unidimensional. Item parceling can lead to inaccurate parameter estimates and misleading conclusions about model fit, if this assumption is not met (Bandalos 2002; Little et al. 2002; Nasser 2003). A particular concern is that item parcels can hide areas of model misspecification and, thereby, lead to an increased chance of a Type II error (accepting a model that does not fit).
To examine this concern, the findings from the correlated five factor model in our study (including all items and prior to any modifications) were compared with those obtained when using item parcels so as to determine whether the different result could be attributed to the use of item parcels. Both the parceling criteria used by Gilman (1999) and by Huebner et al. (1998) were applied. As expected, the model’s fit was much improved in both cases. For example, when Gilman’s criteria were applied to create 18 parcels, acceptable overall fit for a correlated five-factor model was obtained (χ2 (125) = 2,629.37, RMSEA = 0.06, CFI = 0.95). However, the areas of misfit identified in our unparceled analyses were not revealed. In particular, our unparceled analyses revealed that a unidimensional structure for each of the subscales was not supported because the adolescents did not respond to the negatively worded items, and some of the positively worded items, in a consistent manner. The use of item parceling methods was not justifiable. We therefore conclude that the differences between our CFA results and the published CFA results can be attributed to the use of item parceling methods in previously published CFAs.
4 Discussion
The general purpose of these analyses was to test the assumptions of a second-order factor model specification of the MSLSS with the goal of assessing its reliability and validity for the measurement of adolescents’ satisfaction with their family, friends, living environment, school, self, and their general quality of life. The CFA results of the second-order model demonstrated that the model did not accurately account for the covariances among the 40 MSLSS items. Thus, the 40 items did not provide a valid measure of general quality of life. The CFA of the correlated five-factor structure revealed that the negatively worded items did not co-vary in a consistent manner with the positively worded items, although such consistency was implied by the measurement structure. Subsequent CFAs of each of the subscales also resulted in poor fit. And the FMAs of the subscales excluding the negatively worded items revealed that the adolescents did not respond to some of the positively worded items in each subscale in a consistent manner. Thus, the items for each subscale were not valid measures of satisfaction with family, friends, living environment, school, and self, respectively. However, good model fit for each of the subscales was obtained when the negatively worded items were excluded and when only the four items with the most invariant model parameters across latent classes were retained. Good model fit for a correlated five-factor model was also obtained when a few minor and theoretically defensible modifications were introduced to account for the otherwise unexplained correlations among some of the items. However, the modified second-order model did not fit the data as well.
4.1 Recommendations for the Use of the MSLSS
The adolescents did not respond to the negatively worded items in a manner that was consistent with their responses to the positively worded items. Several researchers have raised similar concerns about the use of negatively worded items for the measurement of psychological constructs in children and adolescents, such as those related to self-esteem and self-concept (Barnette 2000; Borgers et al. 2004; Marsh 1986, 1996). It has been noted that the use of negatively worded items results in bias associated with differences in age, verbal ability (Marsh 1986), and gender (Fletcher and Hattie 2005), that the responses are inconsistent with responses to positively worded items (Borgers et al. 2004), and that the combination of negatively and positively worded items results in lower internal consistency (Barnette 2000).
One approach to addressing concerns about negatively worded items is to model the effect of these items by including a methods factor. This has, for example, been recommended for the Rosenberg self-esteem scale (Rosenberg 1989) (e.g., Marsh 1996; Tomas and Oliver 1999). Although the model with a methods factor resulted in better fit, it did not sufficiently account for the patterns of misfit involving the negatively worded items. Another approach is to exclude negatively worded items altogether (e.g., Barnette 2000; Fletcher and Hattie 2005; Marsh 1996). In our analysis, the exclusion of negatively worded items resolved many patterns of misfit in the residual correlation matrix. Based on these findings, and considering other findings pertaining to the use of negatively worded items in studies involving adolescents, in general, we suggest that it is justifiable to use only the positively worded items for the measurement of adolescents’ satisfaction with the five life domains, and we therefore recommend that the negatively worded items be omitted.
A second recommendation relates to the use of the abridged version of the MSLSS. Although the abridged version of the MSLSS requires further validation in different samples, the findings provide preliminary support for its use for the measurement of adolescents’ satisfaction with the five life domains. Good fit for a unidimensional structure for the abridged four-item version of each subscale was obtained. However, the adolescents may not have responded to the four living environment items in a consistent manner. Only two of the living environment items were retained in the subsequent CFAs of the modified measurement model with five correlated latent factors. Although the findings should be replicated in another sample before drawing further conclusions, it may be necessary to develop new items for the measurement of adolescents’ satisfaction with their living environment.
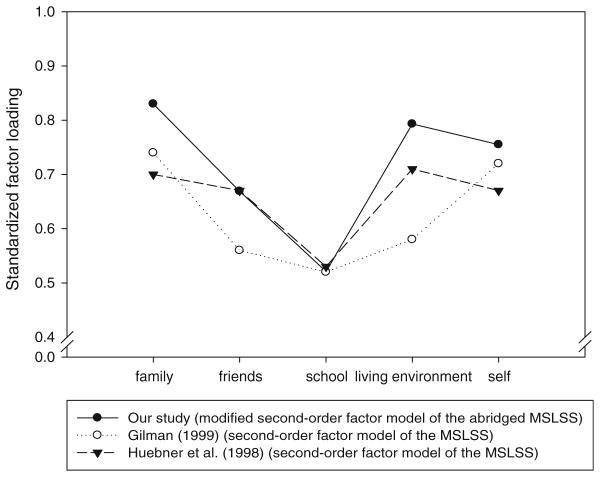
A third recommendation is that researchers ought to be cautious in the use of the abridged MSLSS as a measure of general quality of life whether they use total scores or a second-order factor. A second-order factor structure resulted in relatively poorer fit than a nested model with five correlated latent factors. Evidently, the second-order factor did not sufficiently account for the correlations among the first-order factors. In addition, the standardized second-order factor loadings differed substantially from those that were found in the CFAs reported by Gilman (1999), Gilman et al. (2000), and Huebner et al. (1998) (Fig. 8). Further studies are needed to examine whether the second-order factor loadings are indeed invariant with respect to observed and unobserved differences among adolescents before assuming that the five first-order factors reflect a single second-order factor. This caution is also theoretically warranted. Specifically, is it reasonable to expect that adolescents’ satisfaction with their families, friends, schools, living environments, and self arises from a single common source (i.e., general quality of life)? Certainly this model is incompatible with the proposition that these life domains represent experiences with aspects of life that may contribute to one’s overall quality of life (Campbell et al. 1976; Michalos 1985; Nordenfelt 1993; Veenhoven 2000). We therefore suggest that a second-order factor model may not be the best approach to combining measures of various life domains into a total score for the measurement of general quality of life. Instead, we recommend further studies to examine theoretically defensible propositions about the relationships among the life domains that contribute to adolescents’ quality of life.
Fig. 8.
Standardized second-order factor loadings for our study and published CFAs of the MSLSS.
Our last recommendation is that the modified correlated five-factor structure supported by our findings, albeit theoretically defensible, does not justify the conventional approach of developing subscale scores by averaging the responses to the relevant items. Rather, the cross loadings in our model, albeit relatively small in magnitude, suggest that some of the items do not respond to a single latent factor. In addition, adolescents’ responses to some items are not entirely independent from their responses to other items (after controlling for the latent factors). These findings suggest that conventional scoring methods are inadequate. We therefore recommend the use of more complex arithmetic approaches (most suitably supported by computerization), to account for the modifications in the measurement structure, when using this instrument to derive domain-specific scores of adolescents’ quality of life.
4.2 Explaining Adolescents’ Inconsistent Responses
We offer a few possible explanations for the adolescents’ inconsistent responses to some of the MSLSS items. We specifically observed that most of the items include words that pertain to the adolescents’ perceptions of self (e.g., I, me, or my). These items required the adolescents to reflect on how they viewed themselves in the various social contexts defined by the corresponding subscales (family, friends, school and living environment). For example, although the items, “I like spending time with my parents” and “I enjoy being at home with my family” were part of the family subscale, they may have conflated the adolescents’ perceptions of their families with how they viewed themselves. Similarly, the items, “I have a bad time with my friends” and “I wish I had different friends” in the friends subscale may reflect how the adolescents viewed themselves rather than exclusively referring to how they viewed their friends.
Based on these observations we suggest that several MSLSS items may have conflated the adolescents’ evaluations of their selves with the various other life domains measured by the MSLSS. Adolescents may describe themselves differently and inconsistently in different relational or social contexts (e.g., they may describe themselves differently in relation to their peers than in relation to their friends) (Harter 1999). It is therefore possible that the adolescents may not have been consistent in their interpretations of and responses to the items that involved a degree of self evaluation in relation to different social contexts. In addition, with respect to the living environment subscale, the term “neighborhood” may have taken on different meanings for adolescents in urban regions than for those who lived in rural regions (Greenspoon and Saklofske 1997).
Although the above considerations do not provide definitive answers, they provide some guidance for further research to determine what adolescents think about when they respond to the MSLSS items. Cognitive interviewing or talk-aloud protocols could be used to obtain qualitative data for this purpose (Drennan 2003). Further analysis is recommended to explain the obtained latent classes by, for example, regressing the latent classes on demographic, developmental, psychological, environmental or any other factors that may explain why adolescents do not respond to some questions about their quality of life in a consistent fashion.
5 Conclusions
We set out to examine the assumptions of a second-order model specification of the MSLSS with the goal of assessing its validity for the measurement of adolescents’ satisfaction with their family, friends, living environment, school, self, and their general quality of life. The results revealed several concerns pertaining to the measurement of adolescents’ satisfaction with various life domains and their general quality of life including: (a) adolescents may not respond in a consistent manner to questions about their satisfaction with various life domains and (b) combining domain satisfaction scores in a second-order factor model may not be a valid approach for the measurement of adolescents’ general quality of life. These findings reveal problems with the internal validity of the 40-item MSLSS thereby limiting the extent to which generalizable inferences about adolescents’ satisfaction with each of the life domains and their general quality of life can be made. FMA was subsequently used to develop an abridged 18-item version of the MSLSS for the measurement of adolescents’ satisfaction with their family, friends, school, living environment, and their self. However, only two of the living environment items were retained, and we therefore suggest that it may be necessary to develop additional items for this subscale. We caution that researchers who use multidimensional instruments for the measurement of quality of life in adolescents must critically examine whether adolescents respond to the items in a consistent manner.
Acknowledgments
This research was completed with support for doctoral research from the Canadian Institutes of Health Research (CIHR), the Michael Smith Foundation for Health Research (MSHFR), and the Canadian Nurses Foundation. Dr. Kopec and Dr. Ratner hold Senior Scholar Awards from the MSFHR and Dr. Johnson holds a CIHR Investigator Award. Funding for the survey research was provided by the CIHR (grant #: 62980).
Contributor Information
Richard Sawatzky, Department of Nursing, Trinity Western University, 7600 Glover Road, Langley, BC V2Y 1Y1, Canada.
Pamela A. Ratner, School of Nursing, University of British Columbia, Vancouver, BC, Canada
Joy L. Johnson, School of Nursing, University of British Columbia, Vancouver, BC, Canada
Jacek A. Kopec, School of Population and Public Health, University of British Columbia, Vancouver, BC, Canada
Bruno D. Zumbo, ECPS, Measurement, Evaluation & Research Methodology, University of British Columbia, Vancouver, BC, Canada
References
- Allison PD. Missing data. Thousand Oaks, CA: Sage; 2002. [Google Scholar]
- Bandalos DL. The effects of item parceling on goodness-of-fit and parameter estimate bias in structural equation modeling. Structural Equation Modeling. 2002;9:78–102. [Google Scholar]
- Barnette JJ. Effects of stem and Likert response option reversals on survey internal consistency: If you feel the need, there is a better alternative to using those negatively worded stems. Educational and Psychological Measurement. 2000;60:361–370. [Google Scholar]
- Beauducel A, Herzberg PY. On the performance of maximum likelihood versus means and variance adjusted weighted least squares estimation in CFA. Structural Equation Modeling. 2006;13:186–203. [Google Scholar]
- Borgers N, Hox J, Sikkel D. Response effects in surveys on children and adolescents: The effect of number of response options, negative wording, and neutral mid-point. Quality & Quantity. 2004;38:17–33. [Google Scholar]
- Bradford R, Rutherford DL, John A. Quality of life in young people: Ratings and factor structure of the Quality of Life Profile-Adolescent Version. Journal of Adolescence. 2002;25:261–274. doi: 10.1006/jado.2002.0469. [DOI] [PubMed] [Google Scholar]
- Byrne BM. Structural equation modeling with LISREL, PRELIS, and SIMPLIS: Basic concepts, applications, and programming. Mahwah, NJ: Lawrence Erlbaum; 1998. [Google Scholar]
- Campbell A, Converse P, Rodgers WL. The quality of American life. New York: Sage; 1976. [Google Scholar]
- Cohen AS, Bolt DM. A mixture model analysis of differential item functioning. Journal of Educational Measurement. 2005;42:133–148. [Google Scholar]
- Dannerbeck A, Casas F, Sadurni M, Coenders G, editors. Quality-of-life research on children and adolescents. Vol. 23. Dordrecht: Kluwer; 2004. [Google Scholar]
- De Ayala RJ, Seock H, Stapleton LM, Dayton CM. Differential item functioning: A mixture distribution conceptualization. International Journal of Testing. 2002;2:243. [Google Scholar]
- Drennan J. Cognitive interviewing: Verbal data in the design and pretesting of questionnaires. Journal of Advanced Nursing. 2003;42:57–63. doi: 10.1046/j.1365-2648.2003.02579.x. [DOI] [PubMed] [Google Scholar]
- Drotar D, editor. Measuring health-related quality of life in children and adolescents: Implications for research and practice. Mahwah, NJ: Lawrence Erlbaum; 1998. [Google Scholar]
- Edwards JR, Bagozzi RP. On the nature and direction of relationships between constructs and measures. Psychological Methods. 2000;5:155–174. doi: 10.1037/1082-989x.5.2.155. [DOI] [PubMed] [Google Scholar]
- Edwards TC, Huebner CE, Connell FA, Patrick DL. Adolescent quality of life, part I: Conceptual and measurement model. Journal of Adolescence. 2002;25:275–286. doi: 10.1006/jado.2002.0470. [DOI] [PubMed] [Google Scholar]
- Edwards TC, Patrick DL, Topolski TD. Quality of life of adolescents with perceived disabilities. Journal of Pediatric Psychology. 2003;28:233–241. doi: 10.1093/jpepsy/jsg011. [DOI] [PubMed] [Google Scholar]
- Enders CK. Analyzing structural equation models with missing data. In: Hancock GR, Mueller RO, editors. Structural equation modeling: A second course. Greenwich: Information Age Publishing; 2006. pp. 313–342. [Google Scholar]
- Fayers P, Machin D. Quality of life: The assessment, analysis and interpretation of patient-reported outcomes. Chichester, West Sussex: Wiley; 2007. [Google Scholar]
- Finney SJ, DiStefano C. Non-normal and categorical data in structural equation modeling. In: Hancock GR, Mueller RO, editors. Structural equation modeling: A second course. Greenwich: Information Age Publishing; 2006. pp. 269–314. [Google Scholar]
- Fletcher R, Hattie J. Gender differences in physical self-concept: A multidimensional differential item functioning analysis. Educational and Psychological Measurement. 2005;65:657–667. [Google Scholar]
- Flora DB, Curran PJ. An empirical evaluation of alternative methods of estimation for confirmatory factor analysis with ordinal data. Psychological Methods. 2004;9:466–491. doi: 10.1037/1082-989X.9.4.466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilman R. Validation of the Multidimensional Students’ Life Satisfaction Scale with adolescents. Dissertation Abstracts International. 1999;60(04):1901B. [Google Scholar]
- Gilman R, Ashby JS. A first study of perfectionism and multidimensional life satisfaction among adolescents. Journal of Early Adolescence. 2003;23:218–235. [Google Scholar]
- Gilman R, Huebner ES, Laughlin JE. A first study of the Multidimensional Students’ Life Satisfaction Scale with adolescents. Social Indicators Research. 2000;52:135–160. [Google Scholar]
- Greenspoon PJ, Saklofske DH. Validity and reliability of the Multidimensional Students’ Life Satisfaction Scale with Canadian children. Journal of Psychoeducational Assessment. 1997;15:138–155. [Google Scholar]
- Greenspoon PJ, Saklofske DH. Confirmatory factor analysis of the Multidimensional Students’ Life Satisfaction Scale. Personality and Individual Differences. 1998;25:965–971. [Google Scholar]
- Hagenaars JA, McCutcheon AL. Applied latent class analysis. Cambridge, NY: Cambridge University Press; 2002. [Google Scholar]
- Harter S. The construction of the self: A developmental perspective. New York: Guilford; 1999. [Google Scholar]
- Hinds PS, Haase J. Quality of life in children and adolescents with cancer. In: King CR, Hinds PS, editors. Quality of life from nursing and patient perspectives: Theory, research, practice. 2. Sudbury, MA: Jones and Bartlett; 2003. pp. 143–168. [Google Scholar]
- Hu L, Bentler PM. Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structural Equation Modeling. 1999;6:1–55. [Google Scholar]
- Huebner ES. Preliminary development and validation of a multidimensional life satisfaction scale for children. Psychological Assessment. 1994;6:149–158. [Google Scholar]
- Huebner ES. Life satisfaction and happiness. In: Bear G, Minke K, Thomas A, editors. Children’s needs-II. Silver Springs, MD: National Association of School Psychologists; 1997. pp. 271–278. [Google Scholar]
- Huebner ES. Manual for the Multidimensional Students’ Life Satisfaction Scale. 2001 Retrieved June 29, 2007, from http://www.cas.sc.edu/psyc/pdfdocs/huebslssmanual.doc.
- Huebner ES, Gilman R. An introduction to the Multidimensional Students’ Life Satisfaction Scale. Social Indicators Research. 2002;60:115–122. [Google Scholar]
- Huebner ES, Laughlin JE, Ash C, Gilman R. Further validation of the Multidimensional Students’ Life Satisfaction Scale. Journal of Psychoeducational Assessment. 1998;16:118–134. [Google Scholar]
- Huebner ES, Nagle RJ, Suldo S. Quality of life assessment in child and adolescent health care: The Multidimensional Students’ Life Satisfaction Scale (MSLSS) Social Indicators Research Series: Advances in Quality-of-Life Theory and Research. 2003;20:179–189. [Google Scholar]
- Huebner ES, Valois RF, Suldo SM, Smith LC, McKnight CG, Seligson JL, et al. Perceived quality of life: A neglected component of adolescent health assessment and intervention. Journal of Adolescent Health. 2004;34:270–278. doi: 10.1016/j.jadohealth.2003.07.007. [DOI] [PubMed] [Google Scholar]
- Jöreskog KG. New developments in LISREL: Analysis of ordinal variables using polychoric correlations and weighted least squares. Quality & Quantity. 1990;24:387. [Google Scholar]
- Jöreskog KG, Moustaki I. Factor analysis of ordinal variables: A comparison of three approaches. Multivariate Behavioral Research. 2001;36:347–387. doi: 10.1207/S15327906347-387. [DOI] [PubMed] [Google Scholar]
- Kaplan RM. Implication of quality of life assessment in public policy for adolescent health. In: Drotar D, editor. Measuring health-related quality of life in children and adolescents. Mahwah, NJ: Lawrence Erlbaum; 1998. pp. 63–84. [Google Scholar]
- Koot HM, Wallander JL. Quality of life in child and adolescent illness: Concepts, methods and findings. Hove, East Sussex: Brunner-Routledge; 2001. [Google Scholar]
- Lee SJ, Song X, Skevington S, Hao YT. Application of structural equation models to quality of life. Structural Equation Modeling. 2005;12:435–453. [Google Scholar]
- Little TD, Cunningham WA, Shahar G, Widaman KF. To parcel or not to parcel: Exploring the question, weighing the merits. Structural Equation Modeling. 2002;9:151–173. [Google Scholar]
- Lubke GH, Muthén B. Investigating population heterogeneity with factor mixture models. Psychological Methods. 2005;10:21–39. doi: 10.1037/1082-989X.10.1.21. [DOI] [PubMed] [Google Scholar]
- Magidson J, Vermunt JK. Latent class models. In: Kaplan D, editor. The Sage handbook of quantitative methodology for the social sciences. Thousand Oaks, CA: Sage; 2004. pp. 175–195. [Google Scholar]
- Marsh HW. Negative item bias in ratings scales for preadolescent children: A cognitive-developmental phenomenon. Developmental Psychology. 1986;22:37–49. [Google Scholar]
- Marsh HW. Positive and negative global self-esteem: A substantively meaningful distinction or artifactors? Journal of Personality and Social Psychology. 1996;70:810–819. doi: 10.1037//0022-3514.70.4.810. [DOI] [PubMed] [Google Scholar]
- Marsh HW, Hau KT, Wen Z. In search of golden rules: Comment on hypothesis-testing approaches to setting cutoff values for fit indexes and dangers in overgeneralizing Hu and Bentler’s (1999) findings. Structural Equation Modeling. 2004;11:320–341. [Google Scholar]
- McDonald RP, Ho MHR. Principles and practice in reporting structural equation analyses. Psychological Methods. 2002;7:64–82. doi: 10.1037/1082-989x.7.1.64. [DOI] [PubMed] [Google Scholar]
- Michalos AC. Multiple discrepancies theory (MDT) Social Indicators Research (Historical Archive) 1985;16:347–413. [Google Scholar]
- Millsap RE, Yun-Tein J. Assessing factorial invariance in ordered-categorical measures. Multivariate Behavioral Research. 2004;39:479. [Google Scholar]
- Moors G. Diagnosing response style behavior by means of a latent-class factor approach. Socio-demographic correlates of gender role attitudes and perceptions of ethnic discrimination reexamined. Quality & Quantity. 2003;37:277–302. [Google Scholar]
- Muthén B, Muthén LK. MPlus (version 4.2) Los Angeles: Statmodel; 2006. [Google Scholar]
- Nasser F. The effect of using item parcels on ad hoc goodness-of-fit indexes in confirmatory factor analysis: An example using Sarason’s reactions to tests. Applied Measurement in Education. 2003;16:75–97. [Google Scholar]
- Nordenfelt L. Quality of life, health and happiness. Aldershot: Avebury; 1993. [Google Scholar]
- Nunnally JC, Bernstein IH. Psychometric theory. 3. New York: McGraw-Hill; 1994. [Google Scholar]
- Nylund KL, Asparouhov T, Muthén B. Deciding on the number of classes in latent class analysis and growth mixture modeling: A Monte Carlo simulation study. Structural Equation Modeling. 2007;14:535–569. [Google Scholar]
- Park NS. Life satisfaction of school age children: Cross-cultural and cross-developmental comparisons. Dissertation Abstracts International. 2000;62(02):1118B. [Google Scholar]
- Park NS, Huebner ES, Laughlin JE, Valois RF, Gilman R. A cross-cultural comparison of the dimensions of child and adolescent life satisfaction reports. Social Indicators Research. 2004;66:61–79. [Google Scholar]
- Raphael D. Determinants of health of North-American adolescents: Evolving definitions, recent findings, and proposed research agenda. Journal of Adolescent Health. 1996;19:6–16. doi: 10.1016/1054-139X(95)00233-I. [DOI] [PubMed] [Google Scholar]
- Raphael D, Brown I, Rukholm E, Hill-Bailey P. Adolescent health: Moving from prevention to promotion through a quality of life approach. Canadian Journal of Public Health. 1996;87:81–83. [PubMed] [Google Scholar]
- Rapley M. Quality of life research: A critical introduction. Thousand Oaks, CA: Sage; 2003. [Google Scholar]
- Richardson CG, Johnson JL, Ratner PA, Zumbo BD, Bottorff JL, Shoveller JA, et al. Validation of the dimensions of tobacco dependence scale for adolescents. Addictive Behaviors. 2007;32(7):1498–1504. doi: 10.1016/j.addbeh.2006.11.002. [DOI] [PubMed] [Google Scholar]
- Rigdon EE, Ferguson CE., Jr The performance of the polychoric correlation coefficient and selected fitting functions in confirmatory factor analysis with ordinal data. Journal of Marketing Research. 1991;28:491–497. [Google Scholar]
- Rosenberg M. Society and the adolescent self-image. Middletown, CT: Wesleyan University Press; 1989. (Rev. ed.) [Google Scholar]
- Samuelsen KM. Examining differential item functioning from a latent mixture perspective. In: Hancock GR, Samuelsen KM, editors. Latent variable mixture models. Charlotte, NC: Information Age Publishing; 2008. pp. 177–198. [Google Scholar]
- SAS Institute. Statistical analysis software (version 9.2) Cary, NC: SAS Institute; 2005. [Google Scholar]
- Schumacker RE, Lomax RG. A beginner’s guide to structural equation modeling. 2. Mahwah, NJ: Lawrence Erlbaum; 2004. [Google Scholar]
- Spieth LE, Harris CV. Assessment of health-related quality of life in children and adolescents: An integrative review. Journal of Pediatric Psychology. 1996;21:175–193. doi: 10.1093/jpepsy/21.2.175. [DOI] [PubMed] [Google Scholar]
- Steenkamp J, Baumgartner H. Assessing measurement invariance in cross-national consumer research. Journal of Consumer Research. 1998;25:78–90. [Google Scholar]
- Tomas JM, Oliver A. Rosenberg’s Self-Esteem Scale: Two factors or method effects. Structural Equation Modeling. 1999;6:84. [Google Scholar]
- Topolski TD, Edwards TC, Patrick DL. Toward youth self-report of health and quality of life in population monitoring. Ambulatory Pediatrics. 2004;4:387–394. doi: 10.1367/A03-131R.1. [DOI] [PubMed] [Google Scholar]
- Topolski TD, Patrick DL, Edwards TC, Huebner CE, Connell FA, Mount KK. Quality of life and health-risk behaviors among adolescents. Journal of Adolescent Health. 2001;29:426–435. doi: 10.1016/s1054-139x(01)00305-6. [DOI] [PubMed] [Google Scholar]
- Tu AW, Ratner PA, Johnson JL. Gender differences in the correlates of adolescents’ cannabis use. Substance Use and Misuse. 2008;43:1438–1463. doi: 10.1080/10826080802238140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vandenberg RJ, Lance CE. A review and synthesis of the measurement invariance literature: Suggestions, practices, and recommendations for organizational research. Organizational Research Methods. 2000;3:4–69. [Google Scholar]
- Veenhoven R. The four qualities of life. Journal of Happiness Studies. 2000;1:1–39. [Google Scholar]
- Viswanathan M. Measurement error and research design. Thousand Oaks, CA: Sage; 2005. [Google Scholar]
- Wallander JL, Schmitt M, Koot HM. Quality of life measurement in children and adolescents: Issues, instruments, and applications. Journal of Clinical Psychology. 2001;57:571–585. doi: 10.1002/jclp.1029. [DOI] [PubMed] [Google Scholar]
- Yu CY. Evaluating cutoff criteria of model fit indices for latent variable models with binary and continuous outcomes. Dissertation Abstracts International. 2002;63(10):3527B. [Google Scholar]
- Zumbo BD. Validity: Foundational issues and statistical methodology. In: Rao CR, Sinharay S, editors. Handbook of statistics (Psychometrics) Vol. 26. Amsterdam: Elsevier; 2007a. pp. 45–79. [Google Scholar]
- Zumbo BD. Three generations of DIF analyses: Considering where it has been, where it is now, and where it is going. Language Assessment Quarterly. 2007b;4(2):223–233. [Google Scholar]
- Zumbo BD, Gadermann AM, Zeisser C. Ordinal versions of coefficients alpha and theta for Likert rating scales. Journal of Modern Applied Statistical Methods. 2007;6:21–29. [Google Scholar]