Tailored Near‐Infrared Photoemission in Fluoride Perovskites through Activator Aggregation and Super‐Exchange between Divalent Manganese Ions

Abstract

Biomedical imaging and labeling through luminescence microscopy requires materials that are active in the near‐infrared spectral range, i.e., within the transparency window of biological tissue. For this purpose, tailoring of Mn²⁺–Mn²⁺ activator aggregation is demonstrated within the ABF₃ fluoride perovskites. Such tailoring promotes distinct near‐infrared photoluminescence through antiferromagnetic super‐exchange across effective dimers. The crossover dopant concentrations for the occurrence of Mn²⁺ interaction within the first and second coordination shells comply well with experimental observations of concentration quenching of photoluminescence from isolated Mn²⁺ and from Mn²⁺–Mn²⁺ effective dimers, respectively. Tailoring of this procedure is achieved via adjusting the Mn–F–Mn angle and the Mn–F distance through substitution of the A⁺ and/or the B²⁺ species in the ABF₃ compound. Computational simulation and X‐ray absorption spectroscopy are employed to confirm this. The principle is applied to produce pure anti‐Stokes near‐infrared emission within the spectral range of ≈760–830 nm from codoped ABF₃:Yb³⁺,Mn²⁺ upon excitation with a 976 nm laser diode, challenging the classical viewpoint where Mn²⁺ is used only for visible photoluminescence: in the present case, intense and tunable near‐infrared emission is generated. This approach is highly promising for future applications in biomedical imaging and labeling.

1. Introduction

The transition metal ion Mn²⁺ is a vital component in the further development of lighting and display systems. There are a large variety of commercial phosphors such as Ca₅(PO₄)₃Cl:Sb³⁺,Mn²⁺ (used in fluorescent lamps), Zn₂SiO₄:Mn²⁺, BaAl₁₂O₁₉:Mn²⁺ and BaMgAl₁₀O₁₇:Eu²⁺,Mn²⁺ (used in plasma display panels), or Eu²⁺/Mn²⁺‐codoped polycrystalline powders (used in high‐power white light‐emitting diodes).1, 2, 3, 4 Usually, in a solid matrix, the Mn²⁺ ion exhibits only visible (VIS) photo­luminescence, related to the relatively large energy gap (>17 000 cm⁻¹) between the first excited level and the ground state of the 3d⁵ electronic configuration. In a situation that has been denoted as “normal photoluminescence,”5 when electrons are excited to energy levels above the emitting state, relaxation from these higher states occurs nonradiatively until the emitting state is reached. For Mn²⁺, normal photo­emission occurs from the state ⁴ T ₁(⁴ G) to the ground state ⁶ A ₁(⁶ S). This transition depends strongly on the crystal field of the ligands, what is most visible in the characteristic distinction between green luminescence that is typically associated with a tetrahedral coordination environment, ^IVMn²⁺ (i.e., lower ligand field strength), and orange or red luminescence from octahedral ^VIMn²⁺ (i.e., stronger ligand field).6, 7 Between those two species, the overall luminescence properties, in particular, emission color and quantum efficiency, can be tailored by controlling the precipitation of the Mn²⁺ activator.8, 9, 10

In addition to this “normal” VIS photoemission, a near‐infrared (NIR) emission band has recently been observed in association with Mn²⁺ doping at specifically elevated Mn²⁺ concentration.11, 12, 13 Such an additional emission band is undesirable for lighting and display applications that target the visible spectral range because it reduces the luminous efficacy of the phosphor by drawing on the excitation reservoir.14 The origin of such “anomalous” NIR emission from of Mn²⁺‐doped systems is presently not understood, which is mainly because only the one large energy gap between the ground state and the first excited state of Mn²⁺ has thus far been known to cause luminescence. The now‐observed NIR emission clearly cannot be attributed to the typically isolated Mn²⁺ ions; however, one possible explanation is given by the occurrence of Mn²⁺ ion aggregation. Interionic coupling between transition metal ions often leads to fascinating physical phenomena, such as ferromagnetism in Zn_1–xMn_xTe15 and ZnO:Mn,16 multiferroism in BiFeO₃ thin films,17 superconduction in Y/La–Ba/Sr–Cu–O ceramics,18, 19 and giant magnetoresistance in thin films of La_2/3Ba_1/3MnO_x 20 and La_0.67Ca_0.33MnO_x.21 These physical properties are primarily ascribed to the delocalization and interaction of the 3d electrons of transition metal ions. In analogy, coupling reactions between transition metal ions may result in novel luminescent centers with unusual luminescence behavior. This, in turn, can shed new light onto the nature of the underlying coupling reactions. Besides, luminescent materials that emit in the NIR (700–1100 nm) themselves are attractive for a variety of applications. Recently, the most vibrant field of interest in this context has been in the area of biomedical imaging, where cells and tissue exhibit weak autofluorescence and low transmission loss for optical signals just within the NIR.22, 23 It has hence been crucial to design (nano) materials that exhibit both emission and excitation of luminescence in the NIR region for in vitro and in vivo imaging applications.24, 25 For example, rare‐earth‐doped nanocrystals have attracted considerable interest in recent years as potential candidates for high‐resolution bioimaging because such nanocrystals may exhibit NIR upconversion (UC) emission upon excitation by a 976 nm laser diode (LD).26, 27, 28, 29 However, the accompanying intrinsically strong VIS emission that is additionally occurring in these rare‐earth‐doped materials limits the emission penetration depth in biological tissue because of the tissue's low transparency for wavelengths below 600 nm.30

In‐depth understanding and, consequently, knowledge‐based design of Mn²⁺‐activated materials that produce exclusively “anomalous” NIR emission, therefore, is of great significance from both theoretical and practical perspectives. Herein, we report the realization of anomalous and tailorable Stokes and anti‐Stokes single‐band NIR photoemission from Mn²⁺‐, and Mn²⁺/Yb³⁺‐doped perovskite‐type ABF₃ via heavy doping with Mn²⁺ ions. Upon excitation with UV light or with an NIR LD, we observe anomalous NIR emission that can be adjusted between 760 and 830 nm. The well‐defined structure of ABF₃ makes it an ideal and archetype model material for investigating the concentration‐dependent aggregation and luminescence behavior of Mn²⁺ ions. The underlying mechanism of anomalous NIR emission is consequently studied in this material by dynamic luminescence spectroscopy, analyses of the X‐ray absorption fine structure (XAFS), computational simulation through density functional theory (DFT), and through crystallographic analysis.

2. Results

The X‐ray diffraction (XRD) patterns of a series of KMgF₃:Mn²⁺ samples and the corresponding JCPDS standard cards of KMgF₃ and KMnF₃ are shown in Figure 1 a. All of the observed diffraction peaks of the KMg_(1–x)F₃:Mn²⁺ _x samples (with x ≤ 0.40) match well to those of JCPDS card no. 18‐1033 for cubic KMgF₃. KMgF₃ possesses a perovskite structure with space group Pm–3m and lattice constants a = b = c = 3.98 Å. This structure is constructed from corner‐sharing MgF₆ octahedra in which the Mg²⁺ ions are coordinated by six F⁻ ions, and the K⁺ ions are located in the tetrakaidecahedron cavity between the MgF₆ octahedra (ICSD 94089). Increasing the Mn²⁺ content results in a gradual shift of all diffraction peaks to lower angles, i.e., to larger scattering units, because the partial replacement of the Mg²⁺ ions (r = 0.72 Å) by Mn²⁺ ions (r = 0.80 Å) leads to gradual lattice expansion (Figure 1b).31 After complete substitution, the diffraction peaks are in good agreement with those of the cubic perovskite phase KMnF₃ (JCPDS card No. 17‐0116). A representative transmission electron microscopy (TEM) image is shown in Figure 1c for KMg_(1–x)F₃:Mn²⁺ _x (with dopant fraction x = 0.10). It clearly reflects the quasicubic shape of the as‐synthesized nanocrystals, with an average size of ≈200 nm. Figure 1d shows a typical high‐resolution TEM image of a single such crystal. The spacing of the lattice planes is 0.40 and 0.28 nm, which is consistent with the (100) and (110) lattice planes (d ₁₀₀ = 0.398 nm and d ₁₁₀ = 0.282 nm), respectively, of cubic KMgF₃ (JCPDS card No. 18‐1033). The slight increase in the observed d values is assumedly caused by the partial substitution of Mg²⁺ ions by Mn²⁺ ions. The Fourier transform (FT) of the high‐resolution TEM image (inset in Figure 1d) and the regular selected area electron diffraction patterns (Figure 1e) confirm that the synthesized particles are KMgF₃ single crystals.

Figure 1.

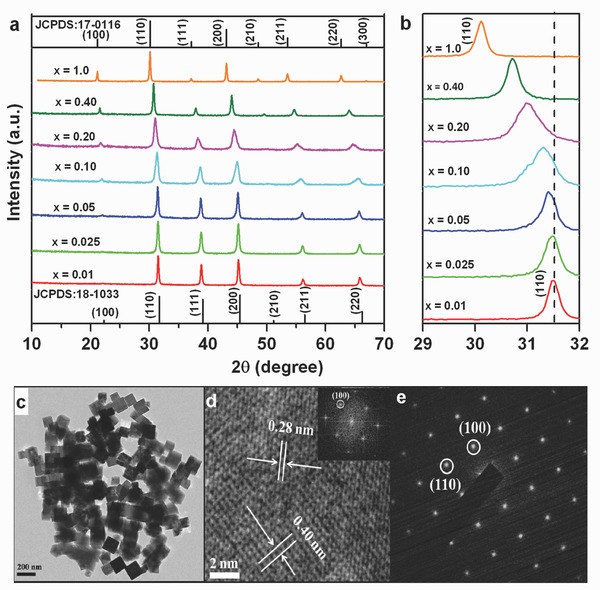
a) X‐ray diffraction patterns of KMg_(1–x)F₃:Mn²⁺ _x for various Mn²⁺ doping levels (labels). Standard patterns of KMgF₃ (JCPDS: 18‐1033) and KMnF₃ (JCPDS: 17‐0116) are shown for reference; b) zoom at the angular region of 29–32°; c) typical TEM image for the sample with x = 0.1; d) high‐resolution TEM image of a single nanocrystal and corresponding Fourier transform (inset); and e) selected‐area electron diffraction pattern of a single nanocrystal.

The emission spectra of KMg_(1–x)F₃:Mn²⁺ _x with varying Mn²⁺ content (0.01 ≤ x ≤ 1.0) are shown in Figure 2 a for an excitation wavelength of 396 nm. For x < 0.10, the emission spectra consist of a single VIS emission band that is centered at ≈600 nm. This corresponds to normal photoluminescence due to the ⁴ T ₁(G)→⁶ A ₁(S) transition in Mn²⁺. However, when the Mn²⁺ concentration reaches x = 0.10, the anomalous NIR emission band appears at ≈760 nm, together with the VIS emission. At the same time, the VIS emission band undergoes a slight blueshift, which we attribute to the gradually reducing ligand field strength. The NIR emission band, on the other side, redshifts with further increasing Mn²⁺ concentration, i.e., 0.10 ≤ x ≤ 1.0. This, in turn, indicates that the NIR and VIS emission procedures are characteristically different and do not share a single origin. Band maxima are observed for x = 0.025 (VIS) and x = 0.40 (NIR), respectively. In particular, a doping concentration of Mn²⁺ of x ≥ 0.40 produces pure NIR emission (with a band maximum at 768 nm), implying that the VIS band is quenched‐out at this dopant concentration. This is another evidence for the different origins of the VIS and NIR bands. Second, this indicates that at sufficiently high dopant concentration, the energy that is absorbed on the Mn²⁺ ions is fully converted into NIR radiation. The excitation spectra and luminescence decay curves of the two emission bands are reported in Figure 2. Both bands exhibit similar excitation spectra (Figure 2b). Moreover, there is only little change in the positions of the excitation bands with increasing Mn²⁺ content, indicating that both emission bands are directly associated with Mn²⁺ content. The excitation peaks at 302, 331, 354, 396, 438, and 541 nm are due to electronic transitions of Mn²⁺ from the ground state ⁶ A ₁(S) to the excited states ⁴ T ₁(P), ⁴ E(D), ⁴ T ₂(D), [⁴ A ₁(G), ⁴ E(G)], ⁴ T ₂(G), and ⁴ T ₁ (G), respectively. In Figure 2c, the luminescence decay curves of the VIS emission are shown for x ≤ 0.10. The VIS emission dynamics clearly deviate from a single‐exponential decay function, what points to the participation of multiple processes in the VIS radiative relaxation. The effective lifetime of the VIS emission band decreases monotonically from ≈60.3 to ≈11.1 ms as the Mn²⁺ concentration increases from x = 0.01 to x = 0.20. In contrast, the NIR emission exhibits nearly single exponential decay behavior, as shown in Figure 2d. Here, the effective decay times are approximately 0.43, 0.33, 0.27, and 0.19 ms for Mn²⁺ doping levels of x = 0.10, 0.20, 0.40, and 1.0, respectively.

Figure 2.

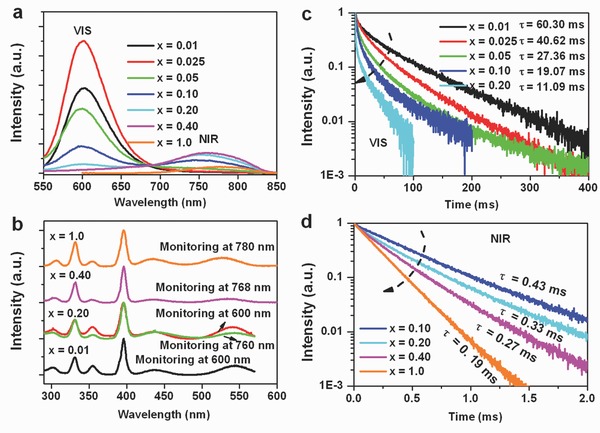
a) Room temperature emission spectra upon excitation with 396 nm UV light; b) excitation spectra, monitoring VIS and NIR emission bands; c) VIS luminescence decay curves; and d) NIR luminescence decay curves.

Since the divalent manganese ion (Mn²⁺) has a 3d⁵ electronic configuration with only one large gap between all the adjacent energy levels, luminescent materials activated by Mn²⁺ ions exhibit only one emission peak at a particular occupied site.6 As previously mentioned, the 3d electrons of Mn²⁺ ions are not fully localized. In particular, when Mn²⁺ ions are sufficiently close to each other, i.e., at lateral separations of only several angstroms,32, 33 Mn²⁺‐Mn²⁺ super‐exchange interactions occur alongside bridges that connect two Mn²⁺ cations via another anion, here F⁻. Then, the Mn²⁺‐Mn²⁺ pair may be treated as an effective dimer, which possesses a different emission band as compared to that of the isolated Mn²⁺ ion: ⁶ A ₁(⁶ S)⁶ A ₁(⁶ S) and ⁶ A ₁ ⁴ T ₁(⁴ G) have been suggested as the ground state and the first excited state (emitting state), respectively, of the effective dimer.32 In the following, we intend to exploit this behavior as a novel approach for tailoring the emission wavelength of Mn²⁺‐based phosphors, whereby the Mn²⁺ doping concentration is varied to control the distance between the Mn²⁺ ions in the crystal lattice. That is, aggregation of Mn²⁺ ions in a suitable host lattice produces a new emission band, ${}^6{A}_1{{(}^{6}S)}^4{T}_1{(}^{4}G){\to }^6{A}_1{{(}^{6}S)}^6{A}_1{(}^{6}S)$. Increasing the Mn²⁺ concentration allows for the formation of effective Mn²⁺‐Mn²⁺ dimers via super‐exchange in KMgF₃:Mn²⁺. The excitation spectra and luminescence decay lifetime data shown in Figure 2 indicate that the NIR emission in KMgF₃:Mn²⁺ (x ≤ 0.4) and KMnF₃ is of the same nature and origin.

To validate our hypothesis, we investigated the possibility of Mn²⁺ ion aggregation in KMgF₃:Mn²⁺ by using both simulations and experiments. Figure 3 a shows that the nearest Mg²⁺–Mg²⁺ distance in cubic KMgF₃ is 3.98 Å, whereas the nearest Mg²⁺—F⁻ and Mg²⁺—K⁺ distances are approximately 1.99 and 3.45 Å (ICSD 94089), respectively. For Mn²⁺‐doped KMgF₃, the Mn²⁺ ions substitute on Mg²⁺ sites that have the same charge and approximately the same ionic size (Mg²⁺: r = 0.72 Å; Mn²⁺: r = 0.80 Å). Therefore, at a sufficiently high doping concentration, Mn²⁺(Mg²⁺)‐Mn²⁺(Mg²⁺) dimers are likely to form over one F⁻ anion bridge in this system. A simple statistical consideration34 of the probability for the existence of {—Mn—F—Mn—}, {—Mn—F—Mg—F—Mn—}, and {—Mn—F—Mn—F—Mn—} entities, respectively, is done on the basis of corner‐sharing MnF₆ and/or MgF₆ octahedra where each octahedron is connected to six other octahedra. It yields a distribution as shown in Figure 3b. Here, the {—Mn—F—Mn—} entity is an effective dimer, the {—Mn—F—Mn—F—Mn—} entity represents two interacting effective dimers, and {—Mn—F—Mg—F—Mn—} stands for isolated Mn²⁺ species where no other Mn²⁺ ion is found in the first coordination shell. It can be seen from Figure 3b that the concentration of the latter species decreases continuously when the concentration of Mn²⁺ exceeds x = 0.25. This coincides with the observation of VIS luminescence, which undergoes notable concentration quenching from this concentration upward. The probability for the formation of neighboring effective clusters, {—Mn—F—Mn—F—Mn—}, is low at first, but increases strongly for x > 0.40. Here, as well, concentration quenching is observed for NIR luminescence at x > 0.40.

Figure 3.

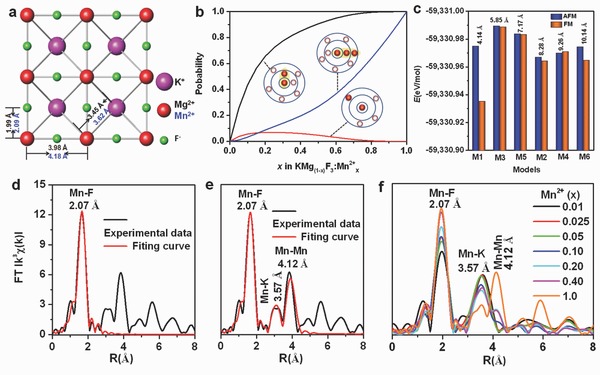
a) Crystal structure of KMg(Mn)F₃; b) probability for the occurrence of specific Mn²⁺‐Mn²⁺ coordination environments (see text for details); c) energy of formation (E) for six possible situations in a 2 × 2 × 4 supercell of KMgF₃:Mn²⁺ with two Mg²⁺ ions substituted by two AFM or FM‐coupled Mn²⁺ ions (denoted as M1, M2, M3, M4, M5, and M6 with different shortest Mn–Mn distances); d) FT k³‐weighted χ(k)‐function of EXAFS spectrum for Mn²⁺ in KMnF₃ with Mn–F fitting; e) FT k³‐weighted χ(k)‐function of EXAFS spectrum for KMnF₃ with Mn–F, Mn–K, and Mn–Mn fitting; and f) k³‐weighted χ(k)‐function of EXAFS spectra for KMgF₃:Mn²⁺ at various Mn²⁺ doping levels.

To further elaborate this hypothesis, we perform first‐principle calculations on the lattice geometry following substitution by using DFT for a 2 × 2 × 4 supercell of KMgF₃:Mn²⁺ with two Mg²⁺ ions substituted by two Mn²⁺ ions. The cell parameters of the initial supercell are listed in Table S1 (Supporting Information). There are six possible substitution models as illustrated in Figure S1 (Supporting Information). The computational results are listed in Tables S2–S4 (Supporting Information). Since the optimized cell parameters and the crystal structures of all models do not vary significantly between each other, the derived data appear convincing. Here, the energy of formation E is the energetic difference between the crystalline unit cell and the isolated constituting atoms.35 As seen in Figure 3c, the M1 model with shortest Mn²⁺‐Mn²⁺ distance and antiferromagnetic (AFM) interaction has a lower formation energy than the model M1 with ferromagnetic (FM) interaction. Other situations with Mn²⁺‐Mn²⁺ distance larger than 5 Å exhibit little energetic difference for the two types of interactions, which suggests that AFM interaction lowers the energy for the model with neighboring Mn²⁺‐Mn²⁺, and high Mn²⁺‐Mn²⁺ distance leads to the absence of any AFM or FM interaction. The situation denoted as M1 in which AFM occurs as a result of Mn²⁺ aggregation with a Mn²⁺‐Mn²⁺ distance of about 4.14 Å possesses, in this context, a relatively low energy of formation. We hence assume that this is the most probable situation which occurs when a certain Mn²⁺ doping concentration is reached. This is in line with the experimental observation of AFM in KMnF₃ and KMgF₃:Mn²⁺.36, 37

XAFS, comprising X‐ray absorption near‐edge spectroscopy (XANES) and extended X‐ray absorption fine structure (EXAFS), was used to provide complementary information on the electronic and local geometric configuration in the present KMgF₃:Mn²⁺ compound. These experiments were done on the beamline BL14W1 at the Shanghai Synchrotron Radiation Facility (SSRF). Mn K‐edge (XANES) spectra were measured for the KMgF₃:Mn²⁺ samples as shown in Figure S2 (Supporting Information). The Fourier transform (FT) k ³‐weighted χ(k)‐functions of the KMnF₃–EXAFS spectrum with Mn–F, Mn–K, and Mn–Mn shells fitting are shown in Figure 3d–e. For the Mn–F fit to the KMnF₃ sample, a coordination number (N) of 6 for the Mn²⁺ ions is obtained, clearly confirming the assumption of octahedral configuration. Fits for the Mn–F, Mn–K, and Mn–Mn shells are used to determine the respective interionic distances, 2.07, 3.57, and 4.12 Å, respectively. These values are in good agreement with the ones of cubic perovskite KMnF₃ (Figure 3a). The EXAFS spectrum of KMnF₃ was used as a reference to compare the EXAFS spectra of samples with various Mn²⁺ contents, i.e., KMg_(1–x)F₃:Mn²⁺ _x for 0.01 ≤ x ≤ 0.40 (see Figure 3f). For a Mn²⁺‐doping concentration below x = 0.10, only the Mn–F and Mn–K peaks can be observed in the fits of the EXAFS spectra, indicating that the still isolated Mn²⁺ ions are randomly and homogeneously distributed in the host lattice at such low dopant concentrations. However, when the Mn²⁺ doping concentration rises to x = 0.10, also the peak attributed to Mn–Mn appears in the spectra, which is taken as experimental evidence for Mn²⁺ ion aggregation in KMgF₃:Mn²⁺. This observation appears to be in good agreement with both the Stokes emission behavior of KMgF₃:Mn²⁺ for increasing Mn²⁺ content, and with the DFT results. Therefore, we conclude at this point that the Mn²⁺‐related NIR emission in perovskite KMgF₃:Mn²⁺ originates from Mn²⁺‐Mn²⁺ effective dimers that form by statistical aggregation of Mn²⁺ ions in the form of {—Mn—F—Mn—} bridges. It should be noted, though, that aggregation would not by itself lead to distinct luminescence38, 39 because there has to be some kind of interaction between the activators. Such interaction reactions between transition metal ions are generally dependent on orbital and ligand geometry.40 In order to obtain a deeper understanding of this, we recorded the temperature‐dependent emission spectra for Mn²⁺‐doped KMnF₃, NaMnF₃, and CsMnF₃, in which different alkali ions are used to provide different Mn²⁺—Mn²⁺ linkage geometry. The corresponding XRD patterns reveal a pure perovskite structure for all three as‐synthesized materials (Figure S3, Supporting Information). Figure 4 a shows the emission spectra of KMnF₃ at different temperatures within 10–300 K under 396 nm light excitation. The 10 K emission spectrum consists of a broad VIS band centered at 656 nm, and a NIR band at approximately 780 nm, which is quite different from the room temperature emission spectrum. For one, the NIR emission is much stronger than the VIS emission at 10 K. Monitoring the emission wavelengths at 656 and 780 nm reveals similar excitation spectra for both bands (Figure S4a, Supporting Information), indicating that both emission bands are associated with Mn²⁺ ions. The VIS emission band is ascribed to the ⁴ T ₁(G)→⁶ A ₁(S) transition in Mn²⁺ ions, as commonly reported in the literature,11, 41, 42 whereas the NIR emission band, as already argued, is assigned to the presence of effective Mn²⁺‐Mn²⁺ dimers. Increasing the temperature leads to a significant decrease in the intensity of both emission bands because of the more and more prominent interference of nonradiative relaxation (Figure 4d). As the temperature is increased to 100 K, the VIS emission is almost fully quenched, whereas the NIR emission can be observed even at room temperature. These results clearly show that thermal quenching has a much more significant effect on the normal Mn²⁺ luminescence than it has on the proposed Mn²⁺‐Mn²⁺ dimer emission. NaMnF₃ and CsMnF₃ are studied to verify the aggregation‐induced geometry‐dependent coupling of Mn²⁺ ions (see Figure 4b,c). At room temperature, the emission spectra of the two compounds exhibit solely NIR emission with band maxima at approximately 772 and 795 nm, respectively, very similar to KMnF₃. The spectra for orthorhombic NaMnF₃ and hexagonal CsMnF₃ at 10 K show dominance of the VIS emission band at ≈600 nm. Again, the excitation spectrum of this band is similar to that of the NIR emission at room temperature (Figure S4b,c, Supporting Information). For NaMnF₃, the VIS emission intensity sharply decreases as the temperature increases, whereas the NIR emission increases and reaches a maximum at 150 K before decreasing monotonically to almost its original level (Figure 4e). When the temperature reaches 200 K, the VIS emission is completely quenched. The low temperature emission spectra of hexagonal CsMnF₃ are similar to those of orthorhombic NaMnF₃. Both the VIS and NIR emission intensities gradually decline with temperature (Figure 4f), similarly as in KMnF₃ (Figure 4d). Here, VIS emission is completely quenched at 300 K. These results confirm that the nature of the NIR and VIS emission bands is the same in all three different perovskite compounds. The differences in the temperature‐dependent quenching are attributed to differences in the Mn²⁺‐Mn²⁺ linkage configurations.

Figure 4.

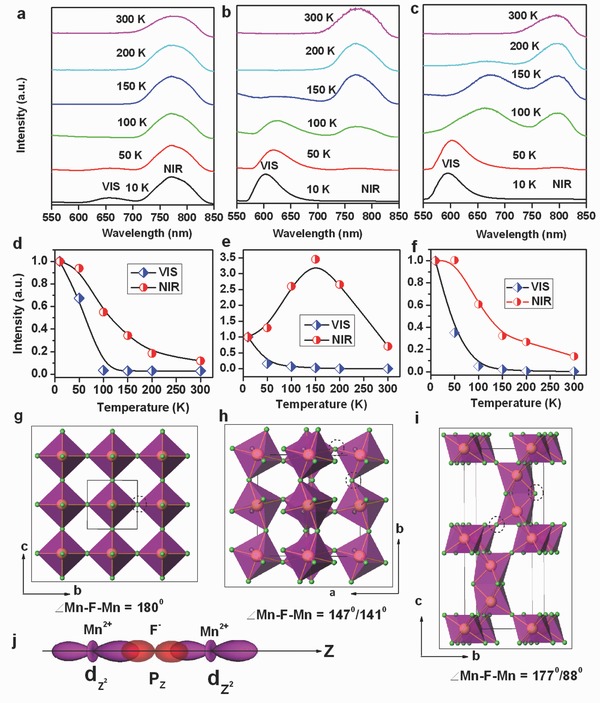
PL spectra of a) KMnF₃; b) NaMnF₃ and c) CsMnF₃ at various temperatures ranging from 10 to 300 K; d–f) show variations of temperature‐dependent emission intensities of VIS and NIR emissions for KMnF₃, NaMnF₃, and CsMnF₃, respectively; g–i) crystal structures of KMnF₃, NaMnF₃, and CsMnF₃, respectively (for clarity, the alkali cations are omitted in the structures and only the MnF₆ octahedra are shown); and j) schematic representation of the most important sigma overlaps between the d orbitals of Mn²⁺ and the p orbital of ligand F⁻ with a bridging angle of 180°.

In Figure 4g, we illustrate that the MnF₆ octahedra in the cubic perovskite KMnF₃ are connected through a common F atom at a Mn—F—Mn angle of 180°. Orthorhombic perovskite NaMnF₃ is a somewhat distorted version of the ideal perovskite structure in which the MnF₆ octahedra are tilted, and the connecting angle of Mn—F—Mn is 147°/141° because of the small radius of the Na⁺ cation, as shown in Figure 4h. For hexagonal CsMnF₃ (Figure 4i), the MnF₆ octahedra share a corner and a face with a connecting angle of 177°/88°. It has been reported that the exchange interaction between two coupling ions is primarily governed by the overlap of the orbital wavefunctions for linear configuration,40, 43 see Figure 4j. Thus, enhanced coupling between Mn²⁺ ions is expected in KMnF₃ and CsMnF₃ because these compounds have nearly linear Mn—F—Mn configuration. For the tilted linkage in NaMnF₃, only reduced coupling is expected. As a consequence, VIS emission is less prone to concentration quenching. Thermal quenching effect is responsible for the variation in the NIR emission intensity in KMnF₃ and CsMnF₃ with varying temperature. On the other side, the significant increase in the NIR emission of NaMnF₃ with temperature (Figure 4e) suggests that interionic coupling is enhanced with temperature in the tilted NaMnF₃ structure, associated with the less‐and‐less strong localization of the d electrons of the Mn²⁺ ion. This hypothesis is corroborated by the gradual shift in the VIS emission peaks to longer wavelength with increasing temperature. The decrease of the NIR emission in NaMnF₃ above 150 K is then attributed to the competing effect of thermal quenching.

To further investigate Mn²⁺ UC emission, we considered the introduction of Yb³⁺ as a codopant into the KMgF₃:Mn²⁺ lattice. Figure 5 a shows the UC emission spectra of KMg_(1–x–y)F₃:Yb³⁺ _y/Mn²⁺ _x (0.01 ≤ x ≤ 0.40; y = 0.005) after excitation with a 976 nm LD. For the sample with x = 0.01, the emission spectrum consists of a single VIS emission band centered at 595 nm, which corresponds to the $|{}^{2}F{}_{7/2}{,}^4{T}_{1\mathrm{g}}(G)\to |{}^{2}F{}_{7/2}{,}^6{A}_{1\mathrm{g}}(S)〉$ transition of the Yb³⁺—Mn²⁺ pair.44 Increasing the Mn²⁺ doping concentration to x = 0.025 results in the appearance of an anomalous NIR emission band at ≈760 nm, in addition to the VIS emission band. A sole NIR emission band is obtained at doping concentrations x ≥ 0.10. The NIR UC emission band is located within the transmission window of biological tissue. Additionally, we find a high thermal stability of the UC NIR emission band (Figure S5, Supporting Information). We hence conclude that such materials could have potential applications in high‐resolution and deep‐penetration bioimaging. Increasing the Mn²⁺ concentration causes the intensity of the VIS and NIR emission bands to increase up to their maximum values at x ≈ 0.025 and x ≈ 0.20, respectively, before monotonically decreasing because of concentration quenching. We use the pump‐power‐dependent UC emission (Figure S6, Supporting Information), the Stokes emission spectra (Figure S7, Supporting Information) and an analysis of the crystal structure to formulate a ground‐state absorption (GSA) and excited‐state absorption (ESA) UC mechanism for both the VIS and NIR emissions, which are shown in Figure 5b. In the GSA step, an electron of a pair (cluster) is excited from the $|{}^2{F}_{7/2}{,}^6{A}_1{(}^{6}S)〉\hspace{0.17em}(|{}^2{F}_{7/2}{,}^6{A}_1{(}^{6}S){}^6{A}_1{(}^{6}S)〉)$ ground state into the $|{}^2{F}_{5/2}{,}^6{A}_1{(}^{6}S)〉\hspace{0.17em}\left(|{}^2{F}_{5/2}{,}^6{A}_1{{(}^{6}S)}^6{A}_1{(}^{6}S)〉\right)$ intermediate excited state, which is mainly localized on the Yb³⁺ ion. In the ESA step, the electron is further promoted from the $|{}^2{F}_{5/2}{,}^6{A}_1{(}^{6}S)〉\hspace{0.17em}\left(|{}^2{F}_{5/2}{,}^6{A}_1{{(}^{6}S)}^6{A}_1{(}^{6}S)〉\right)$ state into the$|{}^2{F}_{7/2}{,}^4{T}_1{(}^{4}G)〉\hspace{0.17em}\left(|{}^2{F}_{7/2}{,}^6{A}_1{{(}^{6}S)}^4{T}_1{(}^{4}G)〉\right)$ emitting state, followed by the emission of a VIS (NIR) photon.

Figure 5.

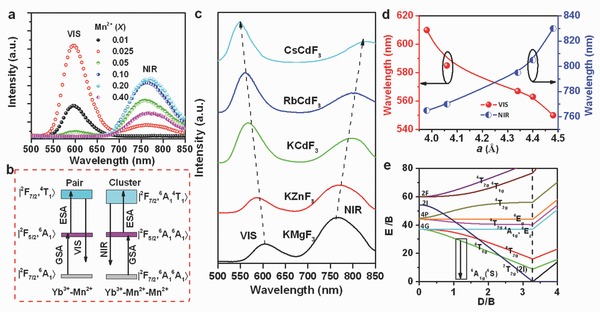
a) Room‐temperature upconversion emission spectra of KMg_(1–x–y)F₃:Yb³⁺ _y/Mn²⁺ _x (0.01 ≤ x ≤ 0.40; y = 0.005); all samples were excited with a 976 nm LD at a power density of 10 W cm⁻²; b) proposed two‐photon upconversion mechanism for KMgF₃:Yb³⁺,Mn²⁺; c) room temperature upconversion emission spectra of AB_(1–x–y)F₃:Yb³⁺ _y/Mn²⁺ _x (x = 0.20; y = 0.005; A = K, Rb, Cs; B = Mg, Zn, Cd); here, too, all samples were excited with a 976 nm LD at a power density 10 W cm⁻²; d) emission peak positions of VIS and NIR emissions from AB_(1–x–y)F₃:Yb³⁺ _y/Mn²⁺ _x (x = 0.20; y = 0.005) as a function of the lattice constant a for perovskite KMgF₃, KZnF₃, KCdF₃, RbCdF₃, and CsCdF₃; and e) Tanabe–Sugano energy diagram of a 3d⁵ system in an octahedral crystal field.

It is well known that the emission color of isolated Mn²⁺ ions can be tailored from green to deep red by changing the crystal field strength around the Mn²⁺ ion.45 Mn²⁺‐Mn²⁺ dimers are formed from two neighboring Mn²⁺ ions, and both the isolated Mn²⁺ ion and the Mn²⁺‐Mn²⁺ dimers have similar excitation spectra; thus, we speculated that the emission wavelength of the Mn²⁺‐Mn²⁺ dimers could also be tailorable by changing the host lattice (i.e., the ligand field strength). To investigate this hypothesis, further varieties of cubic perovskite AB_(1–x–y)F₃:Yb³⁺ _y/Mn²⁺ _x (x = 0.05, 0.20; y = 0.005; A = K, Rb, Cs; B = Mg, Zn, Cd) were synthesized (XRD patterns are shown in Figure S8, Supporting Information). UC emission is observed also from these Yb³⁺/Mn²⁺ codoped materials. At the lowest Mn²⁺ concentration, only a VIS UC emission band is found (Figure S9, Supporting Information), whereas NIR UC emission can be obtained at sufficiently high Mn²⁺‐doping concentration. Figure 5c shows the corresponding UC emission spectra. All spectra exhibit both VIS and NIR emission bands, with peaks of VIS UC emission at 605, 585, 567, 563, and 550 nm in KMgF₃, KZnF₃, KCdF₃, RbCdF₃, and CsCdF₃, respectively. The corresponding NIR UC emission bands are centered at 765, 770, 795, 805, and 830 nm, respectively. These results show that the UC emission centers of the Yb³⁺‐Mn²⁺ pairs and the Yb³⁺‐Mn²⁺‐Mn²⁺ clusters have different intrinsic electronic structures in these Yb³⁺/Mn²⁺ doped fluorides. More importantly, both the VIS and the NIR emission bands have good tuning capabilities, which points to the great potential of this class of materials for various applications. In Figure 5d, the emission peak positions of the two emission bands are displayed as a function of the lattice constant a. As a increases, the VIS emission band monotonically blueshifts because of the decreasing crystal field strength (Figure 5e). However, the NIR emission band gradually redshifts with increasing a. Hence, and in accordance with our previous arguments, also here, the shift of the NIR emission band cannot be explained by considering isolated Mn²⁺ ions (Figure 5e).43, 44 Instead, the NIR emission band is generated by the ${}^6{A}_1{{(}^{6}S)}^4{T}_1{(}^{4}G){\to }^6{A}_1{{(}^{6}S)}^6{A}_1{(}^{6}S)$ transitions of the coupled Mn²⁺‐Mn²⁺ entities, which could be a spin‐allowed (s = 1 to s = 1) transition33, 46 since the luminescence decay lifetime is shorter than 0.50 ms (Figure 2). In terms of excitation and emission spectra, and also in terms of the decay curve, the NIR emission behavior of ABF₃:Yb³⁺/Mn²⁺ is similar to that of a d⁸‐configuration Ni²⁺ ion.47 Therefore, the ${}^6{A}_1{{(}^{6}S)}^4{T}_1{(}^{4}G){\to }^6{A}_1{{(}^{6}S)}^6{A}_1{(}^{6}S)$ transitions of the coupled Mn²⁺‐Mn²⁺ dimers can be analogous to the ³ T ₂(³ F)→³ A ₂(³ F) transitions of Ni²⁺ ions. The Tanabe–Sugano diagram for the Ni²⁺ ion in an octahedral geometry shows that the spin‐allowed ³ T ₂(³ F)→³ A ₂(³ F) transitions can be finely tuned by changing the crystal field strength.46 In general, the higher of the crystal field strength, the shorter is the emission wavelength. This agrees well with the redshift of the NIR emission band in Yb³⁺/Mn²⁺ codoped ABF₃ with increasing lattice constant (Figure 5c).

3. Discussion

In summary, we demonstrated tailoring of activator aggregation and super‐exchange in Mn²⁺‐Mn²⁺ effective dimers within the ABF₃ fluoride perovskites. Such tailoring enables the promotion of distinct photoluminescence phenomena, denoted as anomalous photoluminescence, in the near‐infrared spectral range. In contrast to normal photoluminescence, we attribute anomalous photoluminescence from divalent manganese to the relaxation reaction of ${}^6{A}_1{{(}^{6}S)}^4{T}_1{(}^{4}G){\to }^6{A}_1{{(}^{6}S)}^6{A}_1{(}^{6}S)$ that is facilitated by super‐exchange across Mn²⁺‐F‐Mn²⁺ bridges, i.e., effective dimers. This reaction occurs only when a sufficiently low interionic distance is obtained between Mn²⁺ species. We use a stochastic approach to estimate the crossover dopant concentrations for the occurrence of Mn²⁺ interaction within the first and second coordination shells. The results comply well with experimental observations of concentration quenching of photoluminescence from isolated Mn²⁺ (normal photoluminescence, quenched upon Mn²⁺—Mn²⁺ interaction) and from Mn²⁺—Mn²⁺ effective dimers (anomalous photoluminescence, quenched upon trimer formation). Tailoring of this procedure is achieved via adjusting the Mn—F—Mn angle and the Mn—F distance through substitution of the A⁺ and/or the B²⁺ species in the ABF₃‐type compound. This affects the local ligand field strength (interionic distance) as well as the crystal symmetry (angular constraints) and enables tuning of the near‐infrared emission wavelength within 760–830 nm. DFT computational calculations and EXAFS analyses were performed to confirm this picture.

We applied this principle to produce pure anti‐Stokes near‐infrared emission at ≈760 nm from codoped KMgF₃:Yb³⁺,Mn²⁺ upon excitation with a 976 nm laser diode, challenging the classical viewpoint where Mn²⁺ is used only for visible photoluminescence. In the present case, intense and tunable near‐infrared emission is generated. Such should be highly promising for future applications in biomedical imaging and labeling.

4. Experimental Section

Materials Synthesis: Perovskite fluorides of the type ABF₃:Mn²⁺ (Mn²⁺/Yb³⁺) (A = Na⁺, K⁺, Rb⁺, and Cs⁺; B = Mg²⁺, Zn²⁺, Mn²⁺, and Cd²⁺) were synthesized through modified hydrothermal or solvothermal methods according to ref. 44. Further experimental details are provided in the Supporting Information.

Characterization Methods: Powder X‐ray diffraction data of the samples were recorded on an X‐ray powder diffractometer (Philips Model PW1830) with Cu Kα radiation (λ = 1.5406 Å) at a step width of 0.02° with a speed of 4° min⁻¹. TEM images were carried out on a JEOL 2010 TEM operated at 200 kV. The room‐temperature (RT) excitation and emission spectra, and photoluminescence decay curves of the samples were recorded on an Edinburgh Instruments FLS920 spectrophotometer equipped with both continuous (450 W) and microsecond pulsed xenon (Xe) lamps as excitation sources. For temperature‐dependent emission and excitation spectra at 10–300 K, the samples were mounted on a cryostat (10–350 K, DE202, Advanced Research Systems). The UC emission spectra of the samples were measured with a Jobin–Yvon Triax 320 spectrofluorometer equipped with a R928 photomultiplier tube (PMT), in conjunction with a 976 nm diode laser as an excitation source. To characterize the thermal stability of UC PL at 300–473 K, the samples were placed on a TAP‐02 high‐temperature fluorescence instrument accessory (Tian Jin Orient‐KOJI Instrument Co., Ltd.). The X‐ray absorption fine structure (XAFS) data at Mn–K edge in both fluorescent and transmission mode were collected at the beamline BL14W1 in the Shanghai Synchrotron Radiation Facility (SSRF). The electron storage ring was operated at 3.5 GeV and 220 mA under a “top‐up” mode with a Si(111) double‐crystal monochromator for energy selecting. The photon energy was calibrated with the first inflection point of the Mn–K edge in a Mn metal foil. The raw XAFS data analysis was carried out using the IFEFFIT software package (Athena and Artemis).48

Theoretical Calculations: Geometry optimization for KMgF₃:Mn²⁺ was performed using first‐principle calculations based on the DFT to investigate the possibility of Mn²⁺ aggregation in KMgF₃. For this, the CASTEP (Cambridge Serial Total Energy Package, Accelrys, Inc.) code in Materials Studio was used.49 Details are provided in the Supporting Information.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

Song E., Ye S., Liu T., Du P., Si R., Jing X., Ding S., Peng M., Zhang Q., Wondraczek L. (2015). Tailored Near‐Infrared Photoemission in Fluoride Perovskites through Activator Aggregation and Super‐Exchange between Divalent Manganese Ions. Adv. Sci., 2: 1500089. doi: 10.1002/advs.201500089