Optimized parameter selection reveals trends in Markov state models for protein folding

Abstract

As molecular dynamics simulations access increasingly longer time scales, complementary advances in the analysis of biomolecular time-series data are necessary. Markov state models offer a powerful framework for this analysis by describing a system’s states and the transitions between them. A recently established variational theorem for Markov state models now enables modelers to systematically determine the best way to describe a system’s dynamics. In the context of the variational theorem, we analyze ultra-long folding simulations for a canonical set of twelve proteins [K. Lindorff-Larsen et al., Science 334, 517 (2011)] by creating and evaluating many types of Markov state models. We present a set of guidelines for constructing Markov state models of protein folding; namely, we recommend the use of cross-validation and a kinetically motivated dimensionality reduction step for improved descriptions of folding dynamics. We also warn that precise kinetics predictions rely on the features chosen to describe the system and pose the description of kinetic uncertainty across ensembles of models as an open issue.

I. INTRODUCTION

Understanding how proteins fold into their native three-dimensional structures is a long-standing problem that has inspired the development of several experimental, theoretical, and computational methods.^1,2 Molecular dynamics (MD) is one such technique in which a protein’s motions are simulated in atomic detail.^3,4 Due to a multitude of computational and algorithmic advances,^5–8 millisecond time scale MD simulations are now feasible, enabling the investigation of protein folding in silico.^9–24 The analysis of the enormous quantities of data generated by these simulations is currently a major challenge.

Markov state models (MSMs) are one class of methods that, parametrized from MD simulations, can provide interpretable and predictive models of protein folding.^{12–14,16,19–21,24–38} Building a MSM involves decomposing the phase space sampled by one or more MD trajectories into a set of discrete states and estimating the (conditional) transition probabilities between each pair of states. However, there are many ways to perform the state decomposition, and the choice of MSM building protocol can introduce subjectivity into the analysis.^31,39,40 Recently, a variational theorem for evaluating MSMs has been introduced, which enables the modeler to select the best MSM for a system based on its distance from a theoretical upper limit.^41,42

In this work, we reanalyze twelve ultra-long protein folding MD datasets.^5,18,34,43 For each system, we create MSMs with many protocol choices and utilize the variational theorem introduced by Noé and Nüske⁴¹ as a metric for cross-validation⁴⁴ to determine how different modeling choices affect the quality of the MSM as defined by its ability to detect and represent the systems’ long-time scale dynamical processes. Instead of focusing on a single specific system, we have directed our analysis toward elucidating general trends in MSM construction for protein folding datasets. Due to the diversity of proteins analyzed,¹⁸ we expect that our results will be extensible to other protein folding simulation data.

To this end, we first present a general overview of MSM construction that will inform experimental researchers about the MSM building pipeline as well as update method developers on our current recommendations for “best practices.” Next, we provide an abbreviated theoretical discussion that establishes the mathematical tools necessary to state the variational bound, evaluate it under cross-validation, and understand how it relates to the kinetic time scales predicted by a MSM. We then discuss four key recommendations that emerge from our variational analysis of protein folding MSMs: first, that cross-validation is necessary to avoid overfit models, second, that the incorporation of a kinetically motivated, optional step in MSM construction consistently produces better models, third, that the assignment of conformations in the MD dataset to system states is affected by the dimensionality of the system when states are assigned, and fourth, that the kinetics predicted by MSMs are highly sensitive to which features are chosen to represent the system.

II. MODELING CHOICES

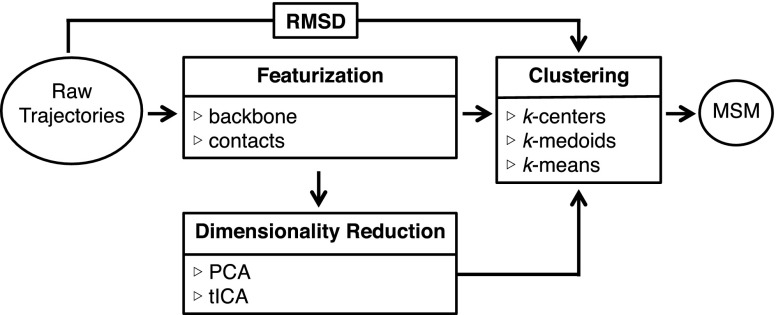
Constructing a MSM (i.e., generating state populations and pairwise transition probabilities) necessitates a state decomposition where each trajectory frame is assigned to a microstate. The state populations and pairwise transition probabilities provide the modeler with thermodynamic and kinetic information, respectively. When building a MSM from MD simulation data, it is sufficient to build the model directly from the raw MD output (atomic coordinates) but is also common to transform the data from atomic coordinates to an internal coordinate system (this transformation is often called “featurization” or “feature extraction”). Optionally, the dimensionality of these internal coordinates may be further reduced through a variance- or kinetically motivated transformation that precedes the requisite state decomposition (Fig. 1). Here, we discuss each step of the MSM building process in order to enumerate some of the options available to modelers.

FIG. 1.

The flow chart shows various options for the MSM construction starting from raw trajectory data. The state decomposition occurs in the clustering step, which is a requisite step in every MSM building protocol. The options presented in each box are intended to be a representative but not exhaustive set.

A. Featurization

The raw output of a MD trajectory consists of a time-series of frames, each of which contains the three Cartesian coordinates of every atom in the system. Optionally, a trajectory may be transformed (featurized) from its Cartesian coordinates into a system of internal coordinates. Many recent studies have constructed MSMs by initially featurizing Cartesian coordinates into a backbone-based^{21,35,38,45,46} or contact-based^45,47–49 internal coordinate system such as $\varphi$ and $\psi$ dihedral angles or inter-residue contact distances, respectively. Internal coordinate systems may also include combinations of different types of features.

1. A note on utilization of the root-mean-square deviation (RMSD) distance metric

Another common strategy is to proceed from Cartesian coordinates directly to state decomposition, which is achieved via clustering (see Sec. II C). In this case, the similarity of structures is judged by their root-mean-square deviation (RMSD) of atomic distances.^{14,19,20,30,33,34,36,50–53} While this process does not explicitly extract “features,” it can be interpreted as a replacement for explicit featurization.

B. Dimensionality reduction

Once the trajectories have been featurized into an internal coordinate system they can be immediately clustered into microstates for state decomposition (see Sec. II C) or pre-processed by further reducing the dimensionality of the dataset via another transformation. One type of dimensionality reduction commonly used in statistics is principal component analysis (PCA), which creates linear combinations from a dataset that account for variance in the data. A similar method, time-structure based independent component analysis (tICA), has also been recently incorporated into MSM analyses.^35,54,55 In contrast to PCA, tICA describes the slowest degrees of freedom in a dataset by finding linear combinations of features that maximize autocorrelation time. Both PCA^{39,47,56–62} and tICA^{21,35,38,39,46,49,55,63,64} have been used in the analysis of protein folding and conformational change. PCA or tICA reduces the dimensionality of each frame from its number of features to a user-specified number of components (either PCs or tICs), where each component is a linear combination of the features and the weight of each feature corresponds to its relevance to that component.

C. Clustering

The clustering step is where the requisite state decomposition occurs. In this step, every frame in the time-series is assigned to a microstate. Clustering into microstates can be performed directly from Cartesian coordinates using the RMSD distance metric or from explicitly featurized trajectories or the low-dimensional output of PCA or tICA using the Euclidean distance. The clustering step reduces the representation of each frame in the time-series to a single integer (the cluster assignment) and it is from this representation that the MSM is constructed. Commonly used clustering algorithms include k-centers,^{16,21,30,35,36,38,39,65} k-medoids,⁵³ and k-means.^44,66,67 More sophisticated methods, such as Ward’s method,^34,68,69 have also been used.

D. MSM construction

The MSM itself is generated from the state decomposition produced by clustering; i.e., the state populations and pairwise transition probabilities are determined. It is standard to find the maximum likelihood estimation (MLE) of the transition matrix under the constraint that the dynamics are reversible.³² The modeler must also select a model lag time. The Markovian assumption asserts that the system is memoryless at the chosen lag time, which means that the pathway by which the system enters any state does not affect the transition probabilities.

III. THEORY BACKGROUND

It is clear from Sec. II that there are many modeling choices involved in the MSM creation. Formally, the MSM building process offers a variety of ways to create a state decomposition (see Fig. 1). Traditionally, MSM building protocols have been determined heuristically and without an objective method to compare different models of the same system. In this section, we briefly overview the theory necessary to state the variational principle that enables the comparison of MSMs.^41,42,44 This variational principle provides the modeler with a systematic way to choose which of many modeling protocols most closely approximates the time scales on which the underlying dynamical processes of the system occur.

A. Propagator

We first present the essentials of continuous-time Markov processes.⁷⁰ We assert that our process, X_t, is homogeneous in time, ergodic, and reversible with respect to an equilibrium distribution, $\mu (x)$, which takes the continuous phase space $\mathrm{\Omega }$ to $ℝ$.

We are interested in the probability of transitioning from $x\in \mathrm{\Omega }$ to $y\in \mathrm{\Omega }$ after a duration of time $\tau$, on the condition that the system is already at x. This is given by

$$p(x,y)dy=\mathbb{P}(X_{t+\tau }\in B_{ϵ}(y)|X_t=x),\mathit{\hspace{1em}\hspace{1em}}$$ (1)

where $B_{ϵ}(y)$ is the open $ϵ$-ball centered at y with infinitesimal measure dy. Moreover, we are interested in the time-evolution of the entire system from time t to time $t+\tau$, which can be obtained by integrating over p_t(x) for all $x\in \mathrm{\Omega }$,

$$p_{t+\tau }(y)={\int }_{\mathrm{\Omega }}dx{p}_t(x)p(x,y)=\mathcal{P}(\tau )\circ p_t(y).\mathit{\hspace{1em}\hspace{1em}}$$ (2)

The propagator, $\mathcal{P}(\tau )$, admits a decomposition into a complete set of eigenfunctions and eigenvalues

$$\mathcal{P}(\tau )\circ {\varphi }_i={\lambda }_i{\varphi }_i,\mathit{\hspace{1em}\hspace{1em}}$$ (3)

where the eigenvalues ${\lambda }_i$ are real and indexed in decreasing order. The first eigenfunction ${\varphi }_1(x)$ corresponds to the equilibrium distribution $\mu (x)$ and has a unique largest eigenvalue ${\lambda }_1=1$. All subsequent eigenvalues lie within the unit interval $|{\lambda }_{i>1}|<1$ and their corresponding eigenfunctions represent the processes within the time-series.

The time scale of the ith process is given by $t_i\equiv -\tau /\text{ln}{\lambda }_i$. The propagator is often further approximated by retaining the m slowest time scales of the system (or the m largest eigenvalues). It can be shown that this is the closest possible rank-m approximation to the propagator.⁴⁴

B. Variational principle

The eigenfunctions that satisfy Eq. (3) can be interpreted as the m slowest dynamical processes from a collection of time-series (e.g., MD) data. However, we do not know the true eigenfunctions and must approximate them using a trial set of ansatz eigenfunctions. The variational theorem established by Noé and Nüske⁴¹ states that the sum of the eigenvalues corresponding to the ansatz eigenfunctions is bounded from above by the sum of the true eigenvalues, i.e.,

$$\text{GMRQ}\equiv \sum _{i=1}^m{\widehat{\lambda }}_i\le \sum _{i=1}^m{\lambda }_i,\mathit{\hspace{1em}\hspace{1em}}$$ (4)

where the GMRQ stands for generalized matrix Rayleigh quotient, which is the form of the approximator when the derivation is performed in the style of Ref. 44. The eigenvalues ${\widehat{\lambda }}_i$ are generated from the ansatz eigenfunctions in the same way as Eq. (3).

For our purposes, we highlight that there exists a theoretical upper bound on the GMRQ, which means that a dynamical process cannot be measured to occur on a slower time scale than its true time scale. This enables us to select the best set of trial ansatz eigenfunctions by choosing the set that yields the maximum GMRQ. The use of a variational approach to choose MSM construction protocol is not new⁷¹ and is similar to the variational selection of the ground-state wavefunction that yields the minimum energy in quantum mechanics.

Each set of ansatz eigenfunctions is a guess at how to represent the important degrees of freedom in the system. In practice, it corresponds to the set of features (Sec. II A) or PCs/tICs (Sec. II B) from which the state decomposition (i.e., clustering, Sec. II C) is performed. Thus, in the context of the variational bound, we denote the best MSM as the one that is constructed from the optimal set of ansatz eigenfunctions.

C. Cross-validation

To create a MSM that describes the kinetics of a system from raw MD data, the requisite state decomposition is achieved by one or more dimensionality-reducing steps (recall Sec. II), each of which may involve tunable parameters. We will refer to the transformation from raw MD data to states as our modeling “protocol.”⁷² A set of trial ansatz eigenfunctions is a function of both the input data and the protocol. We are interested in a procedure that compares how closely different trial sets of ansatz eigenfunctions approximate the true eigenfunctions for the same data. We have already shown that the GMRQ is a suitable metric for this purpose: to compare across different protocols, we construct MSMs using each protocol and choose the protocol that yields the largest sum of eigenvalues (Eq. (4)). The GMRQ, or sum of eigenvalues, thus serves as a model’s “score.”

However, our dataset is finite and thus possesses statistical noise in addition to information about the true dynamics. In order to determine the best protocol in the context of only the system’s dynamics, we must employ cross-validation to avoid overfitting to the noise in the data. This is achieved by splitting the dataset into a training set and a test set, constructing the MSM for the training set, but then evaluating its performance (i.e., calculating the GMRQ) on the test set. This process ensures that the protocol performance is evaluated only on dynamics that are present in both the training and test sets, which are expected to correspond to the system’s true dynamics when they have been sufficiently sampled. For conciseness, we will thus refer to the MSM predicting a system’s slowest time scales under cross-validation as the “best,” or optimal, MSM for that search space.

It is important to note that selecting the best MSM under cross-validation addresses different modeling challenges than validating the self-consistency of a single MSM, e.g., by assessing adherence to the Chapman-Kolmogorov property.^13,32,67 The comparison of models using cross-validation does not provide information about whether any single model is statistically consistent with the data (although we would expect inconsistent models to perform relatively poorly), whereas self-consistent validation does not evaluate how well a model has captured the system’s slow dynamics. Since our goal is to understand protein folding dynamics using MSMs, determining the most useful model, i.e., the model that best describes important collective degrees of freedom, requires the comparison of candidate models under cross-validation. For a representative self-consistent validation analysis, see the supplementary material, Figs. S3-S6.

IV. METHODS

The twelve MD datasets were generated by Lindorff-Larsen et al.¹⁸ via MD simulation in explicit solvent near the melting temperature. The proteins range from 10 to 80 amino acids in length. All datasets used contain a minimum of 100 μs of sampling and feature at least 10 instances each of folding and unfolding. For the analysis, we retain trajectory frames at every 2 ns. Unless otherwise specified, MSMs are created by first selecting a featurization scheme, dimensionality reduction option, and clustering algorithm (see Sec. II). Then, internal parameters relevant to those selections (e.g., the number of clusters) are optimized by generating 200 different models where internal parameters are determined by a random search (see the supplementary material, Table S2). The parameters of the highest-scoring model based on the mean of five cross-validation iterations are used for the analysis of trends in featurization, dimensionality reduction, and clustering choices.

V. RESULTS

In this section, we discuss results obtained from analyzing twelve ultra-long protein folding datasets¹⁸ in the context of choices in modeling protocol. We have chosen to highlight four key results for using MSMs to model protein folding that emerge from optimal parameter selection under cross-validation. Protocol choices corresponding to the best models as well as comparisons of different featurization, dimensionality reduction, and clustering choices for each system are reported in the supplementary material (Table S3 and Fig. S15ff, respectively). We emphasize, however, that there is no “magic bullet”: we deliberately do not recommend specific protocol choices but rather assert that the best practice for constructing MSMs is to determine the modeling protocol by systematically searching hyperparameter space (i.e., modeling choices) and evaluating the GMRQ of each model. The following discussion is thus designed to be extensible to MSM construction for protein folding in general.

A. A variational approach necessitates cross-validation

We established in Sec. III B that the time scale of a dynamical process cannot be estimated to be slower than its true time scale.⁴¹ However, it is a well-known result that a variational bound on a system’s eigenvalues only holds in the limit of complete data, i.e., in the absence of statistical noise.^41,42,73 In their analysis of octa-alanine dynamics,⁴⁴ used the GMRQ to show that with incomplete data, the models predicting the slowest time scales are likely describing statistical noise instead of the true dynamics, especially for models with a large number of states. Here, we extend this result to ultra-long protein folding trajectories. As an example, we created MSMs for $\lambda$-repressor (Protein Data Bank (PDB) ID: 1lmb), an 80-residue, 5-helix bundle analyzed by Lindorff-Larsen et al.¹⁸ This trajectory has previously been analyzed with MSMs by Bowman, Voelz, and Pande,¹⁹ who employed the k-centers clustering algorithm⁶⁵ to construct a model with 30 000 microstates.

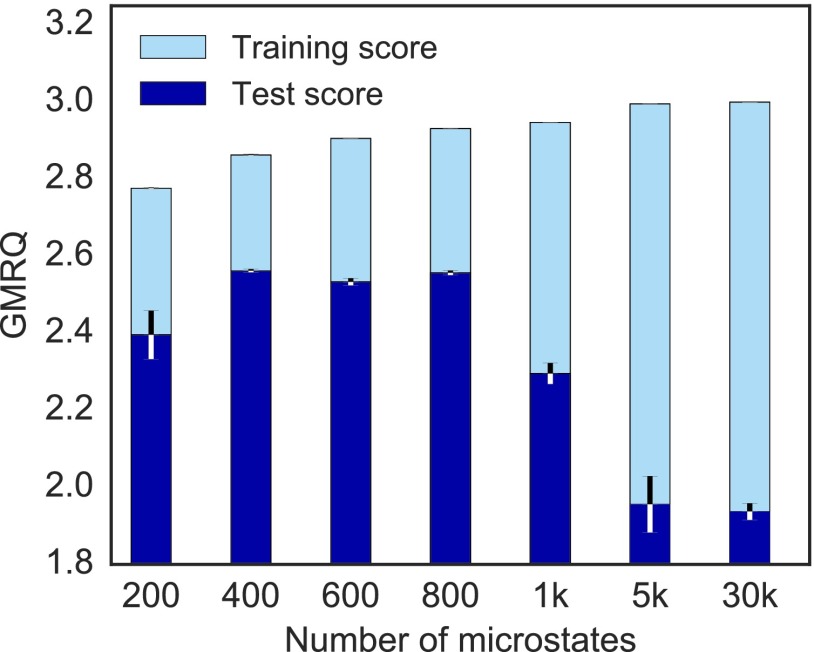
To create a new MSM for this system, we used the GMRQ under cross-validation (see Sec. III and the supplementary material, Table S2) to determine the optimal number of clusters for the dataset by creating 300 MSMs for randomly chosen numbers of microstates between 10 and 1000 using k-centers clustering with the RMSD distance metric. MSMs with 5000 and 30 000 microstates were also evaluated. Fig. 2 shows the average test and training GMRQ scores for models containing 200 to 30 000 microstates. Scores for the training datasets increase as the number of microstates increases, indicating the presence of increasingly slow processes. However, scores for the test datasets, which evaluate the ability of the model to describe data on which it was not fit, do not increase with the number of microstates. The best cross-validated model contains 400 microstates, while models containing 1000 or more microstates do not perform well when evaluated using unseen data. This is likely due to the fact that the slow transitions discovered while fitting the model on the training dataset are not present in the test dataset, indicating insufficient sampling of those processes. In some cases, the modeler may want to investigate these processes and sample them further. However, for a larger number of microstates, it becomes more difficult to sample all processes to equilibrium. Cross-validation therefore enables the modeler to choose a number of microstates that best partitions state space with respect to the slowest well-sampled processes, i.e., the processes present in both training and test sets.

FIG. 2.

GMRQ scores for two-time scale MSMs generated for $\lambda$-repressor (PDB ID: 1lmb) containing varying numbers of microstates show that the cross-validation is necessary to describe a system’s underlying dynamics. All models were constructed using k-centers clustering with the RMSD distance metric. The error bars signify the score standard deviation generated from five cross-validation iterations (the error bars on the training scores are negligibly small). The discrepancy between training and test scores (light blue and dark blue, respectively) as microstate number increases is likely due to overfitting during training; thus these models exhibit poorer performance on data that were hidden from the fitting process.

B. tICA systematically produces better models

The PCA and tICA algorithms (see Sec. II B) offer an additional, optional dimensionality reduction before clustering is performed. PCA finds orthogonal degrees of freedom that account for variance in the data, while tICA identifies degrees of freedom that explain slow decorrelation.^35,49,54,55 The incorporation of tICA into MSM construction was motivated by the desire to ensure, instead of assume, the retention of important kinetic information.³⁵ Here, we show that models made by clustering from tICs consistently produce the best models when compared to models clustered from PCs or directly from features.

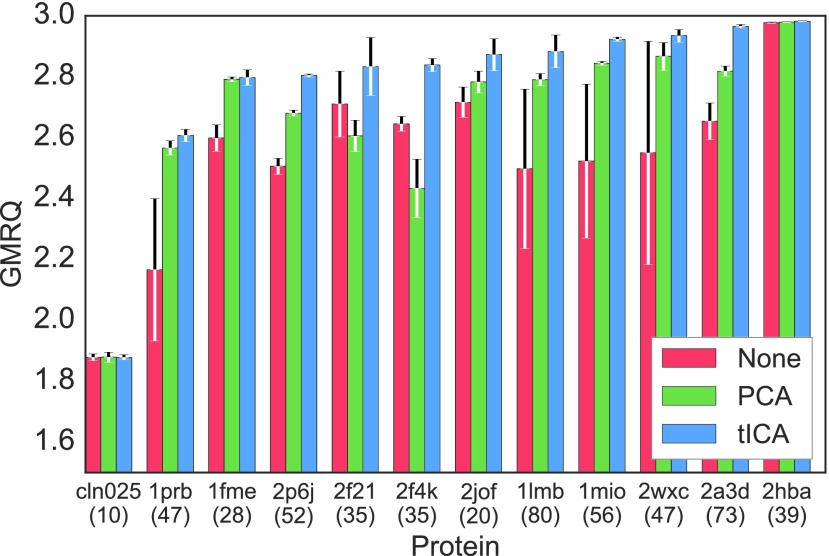
As an example, each of the twelve ultra-long protein trajectories was featurized using the dihedrals defined by every set of four consecutive α-carbons (α-angles⁷⁴). tICA or PCA was optionally performed on the α-angle features, further reducing the dataset dimensionality up to 10 tICs or PCs. The mini-batch k-means clustering algorithm⁶⁶ was then used to cluster from tICs, PCs, or α-angle features into states. For 11 of the 12 proteins, the best tICA model outperformed both the best PCA model and the best α-angles model. The one exception was chignolin, a 10-residue peptide that forms a β-hairpin in water,⁷⁵ for which the scores differed only in the fourth decimal place (two orders of magnitude smaller than the score standard deviations). Fig. 3 shows the scores for the best tICA, PCA, and α-angle models for each protein. Alternate choices of featurization and clustering may be used to demonstrate the same result; see the supplementary material, Fig. S15ff.

FIG. 3.

GMRQ scores for two-time scale MSMs generated for twelve ultra-long protein folding datasets¹⁸ where additional dimensionality reduction has been omitted (red), performed with PCA (green) or performed with tICA (blue) demonstrate that tICA systematically improves models. All MSMs were made using α-angle featurization and mini-batch k-means clustering. In all cases, the best tICA model performs better than or equivalently to both the best PCA model and the best model created directly from α-angle features. The error bars signify the score standard deviation generated from five cross-validation iterations. The number of amino acids of each protein is given below its PDB ID.

C. Different clustering algorithms perform similarly well on tICA data

Clustering trajectory frames into microstates produces the state decomposition that is essential for MSM construction. Various clustering algorithms have been used for MSMs of protein folding and conformational change (see Sec. II C), and the relative performance of different clustering algorithms has been compared.^32,76,77 McGibbon and Pande⁴⁴ used the GMRQ under cross-validation to show that for octaalanine, k-means produced the best models while k-centers performed poorly for several different featurization choices. The authors postulated that the poor performance of the k-centers algorithm is related to its tendency to choose outlier conformations as cluster centers. Schwantes and Pande³⁵ compared MSM time scales predicted using k-centers clustering with time scales from a hybrid k-medoids method,⁷⁷ and found them relatively unchanged when tICA was used to reduce the dimensionality of the trajectories before clustering. They suggested that problems with the k-centers algorithm were less influential when clustering is performed on low-dimensional data.

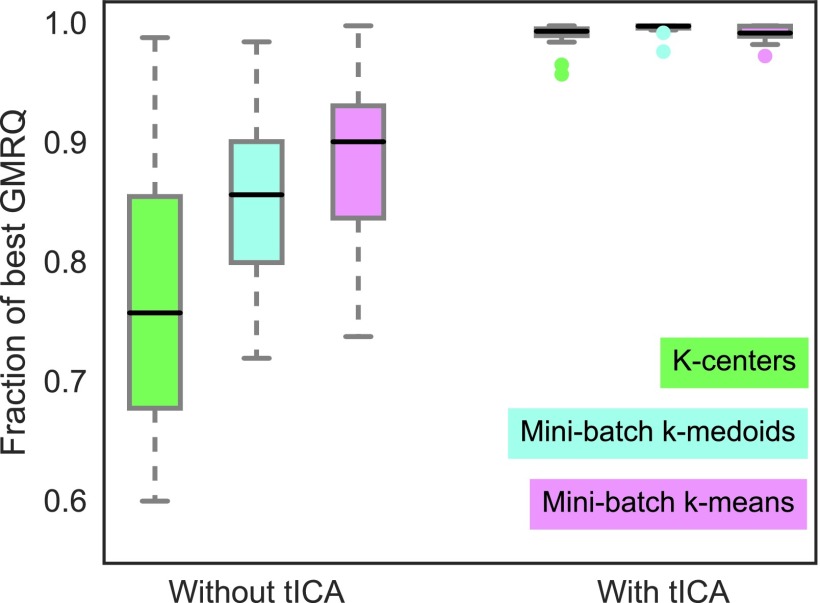
In Fig. 4, we compare mini-batch k-means, mini-batch k-medoids, and k-centers using the cross-validated GMRQs of the resulting MSMs. For this example, all twelve folding trajectories were featurized using contact distances between α-carbons, but other featurization choices will produce an equivalent result (see the supplementary material, Fig. S15ff). For each of the three clustering algorithms, two types of models were created: first directly from the contact distance features and second from tICA data generated from the same features. In order to integrate across the twelve systems, each of which has its own system-dependent upper bound on the GMRQ, we have transformed each model’s score into its ratio with the score of the best model produced for that system. We show that when protein folding trajectories are clustered from high-dimensional feature space, k-means clustering produces the best models and k-centers produce the worst models. However, when the trajectories are clustered from the lower-dimensional tICA data (chosen to be ${ℝ}^{10}$ or lower), k-means, k-medoids, and k-centers clustering all produce similar models. Importantly, the median score of the tICA models consistently exceeds the median score of the models clustered directly from their features. Thus we find that when clustering is preceded by tICA, which is typically chosen to reduce the dimensionality of the trajectories by one or two orders of magnitude, the clustering algorithms yield models that are not only similarly well-performing but also categorically superior to models created without tICA.

FIG. 4.

Aggregated score ratios for two-time scale MSMs generated for twelve ultra-long protein datasets¹⁸ using three different clustering algorithms with or without tICA show that different clustering algorithms produce similarly well-performing models when tICA is used. All models were made using α-carbon contact distances. When clustering is performed directly from features, the dimensionality is reduced by 2-3 orders of magnitude; whereas when clustering is performed from tICs, dimensionality is reduced from ${ℝ}^{10}$ or lower to $ℝ$. For large dimensionality reductions, k-means clustering produces the best models. For small dimensionality reductions via tICA, clustering algorithms produce similarly well-performing models that are categorically better than models created without tICA. (The best-performing algorithm at small dimensionality reductions is k-medoids; see the supplementary material, Fig. S9.)

D. Appropriate featurization is required to describe kinetics

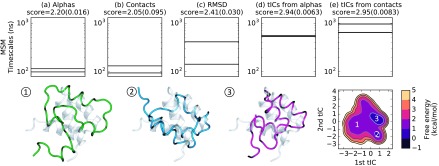
We have seen that omitting cross-validation from a MSM analysis may lead to an overfit model (Sec. V A) and that incorporating an intermediate dimensionality reduction step using tICA systematically improves models (Secs. V B and V C). In this section, we examine how the kinetic information contained within MSMs differs across models created for the same system. We constructed five MSMs for homeodomain (PDB ID: 2p6j)⁷⁸ from five different types of features: (a) α-angles, (b) α-carbon contact distances, (c) pairwise α-carbon RMSD, (d) tICs from α-angles, and (e) tICs from α-carbon contact distances. All clustering was performed with the mini-batch k-medoids algorithm.

The two slowest MSM time scales of each model are presented in Fig. 5 in order of increasing scores. The time scales differ by an order of magnitude from the worst model to the best model, which indicates that not all featurization choices optimally represent the system’s slow dynamics. To investigate the folding of homeodomain, we select the best model (e) for further analysis and create a free energy landscape from its first two tICs. Structures sampled from regions of the free energy landscape of model (e) provide a preliminary interpretation of the first two tICs: progress along the first tIC leads to the formation of a secondary structure while the second tIC may track the alignment of α-helices. The first tIC is highly correlated with RMSD to the folded state and can thus serve as a reaction coordinate for the folding of homeodomain (see the supplementary material, Figs. S11-S13).

FIG. 5.

Time scale plots for two-time scale MSMs generated for homeodomain (PDB ID: 2p6j) using the best model from each of five different featurization choices (a)-(e) show that kinetics are highly sensitive to the featurization choice. All models were made using mini-batch k-medoids clustering. Standard deviations for model scores generated from five cross-validation iterations are given in parentheses, and the thickness of each horizontal lines corresponding to estimated time scales represents two standard deviations in both directions from the estimate. The kinetics feature slower processes for better models; notably, the slowest time scale predicted by the best model is an order of magnitude slower than that predicted by the worst model. A free energy landscape for model (e) was created from its first two tICs. Structures sampled from the dataset (1-3) represent different regions on the free energy surface of model (e). Each sampled structure is an α-carbon trace superimposed upon the crystal structure. The first tIC (regions 1 $\to$ 3) appears to track the formation of secondary structure, while the second tIC (regions 2 $\to$ 3) corresponds to the aligning of α-helices.

When the system’s dynamics have been sufficiently sampled, we expect thermodyamic predictions, i.e., free energies, to be much less sensitive to featurization choices, since these calculations rely only on state populations (see the supplementary material, Fig. S14). In terms of kinetics, however, it is important to recognize that models can only describe processes captured by the collective degrees of freedom chosen as the system’s features.^{32,71,79,80,81} The GMRQ serves as an excellent tool to distinguish between the predictive capabilities of MSMs constructed from different types of features, which enables modelers to choose the most suitable features. This example demonstrates that it is crucial to investigate different featurization choices, since the best model created for a given set of features may be underestimating slow time scales if those features are not capable of describing the corresponding processes.

VI. CONCLUSIONS AND OUTLOOK

MSM construction for protein folding datasets involves many modeling choices. Historically, these decisions have been heuristically motivated. The utilization of a variational principle^41,42 under cross-validation enables the modeler to objectively optimize modeling protocol through the GMRQ score.⁴⁴ With this tool we have reanalyzed twelve ultra-long protein folding trajectories,¹⁸ in order to determine which modeling choices systematically produce superior MSMs and to suggest a set of recommendations for constructing MSMs of protein folding. We have shown that (1) cross-validation is necessary to avoid overfitting models, (2) the use of tICA to reduce trajectory dimensionality before clustering consistently produces higher-scoring models, (3) different clustering algorithms perform similarly on low-dimensionality data from tICA, and (4) the featurization choice is paramount for building kinetic models with predictive capabilities.

In Sec. V D, we reported that MSM time scales differ widely across models constructed from different features. To a lesser extent, this is also the case for time scales predicted by MSMs that have indistinguishable scores; in other words, time scales across indistinguishably good models differ more than their intra-model uncertainties^82–88 account for. This is likely due to the fact that each model is built from a different state decomposition and is thus describing a (perhaps subtly) different process. In the absence of an additional metric for distinguishing models, such as experimental results, the modeler may not be able to select the single best MSM. We therefore hypothesize that a system is better described by an ensemble of equivalently good models as opposed to a single best model. This motivates the need for new mathematical tools to describe ensembles of MSMs and their associated statistics, especially with regard to uncertainty in kinetics.

We anticipate that the advent of the GMRQ to evaluate MSMs will shift modelers from heuristic protocol choices toward systematic parameter searches informed by the results and practices presented in this work. The ability to construct MSMs capable of optimally describing slow processes in MD trajectories is invaluable to the theorist, whether those models are built to inform future experimental pursuits or to elucidate previous findings. It is important to be aware that the slow processes found by the best model may not correspond to the process of interest and instead may be artifacts of insufficient sampling or the force field used during simulation. A MSM that identifies uninformative slow processes may thus be an indicator of a problem with the raw data. We therefore stress that connection to experiment will continue to be crucial in evaluating model utility.

Free, open source software fully implementing all methods used in this work is available in the MDTraj,⁸⁹ MSMBuilder,⁹⁰ and Osprey⁹¹ packages available from http://mdtraj.org and http://msmbuilder.org.

SUPPLEMENTARY MATERIAL

See the supplementary material for specifics regarding MSM methods and cross-validation, supporting information, and individual protein results.