Abstract
Many features of virus populations make them excellent candidates for population genetic study, including a very high rate of mutation, high levels of nucleotide diversity, exceptionally large census population sizes, and frequent positive selection. However, these attributes also mean that special care must be taken in population genetic inference. For example, highly skewed offspring distributions, frequent and severe population bottleneck events associated with infection and compartmentalization, and strong purifying selection all affect the distribution of genetic variation but are often not taken into account. Here, we draw particular attention to multiple-merger coalescent events and background selection, discuss potential misinference associated with these processes, and highlight potential avenues for better incorporating them into future population genetic analyses.
Introduction
Viruses appear to be excellent candidates for studying evolution in real time; they have short generation times, high levels of diversity often driven by very large mutation rates and population sizes (both census and effective), and they experience frequent positive selection in response to host immunity or antiviral treatment. However, despite these desired attributes, standard population genetic models must be used with caution when making evolutionary inference.
First, population genetic inference is usually based on a coalescence model of the Kingman type, under the assumption of Poisson-shaped offspring distributions where the variance equals the mean and is always small relative to the population size; consequently, only two lineages may coalesce at a time. In contrast, viruses have highly variable reproductive rates, taken as rates of replication; these may vary based on cell or tissue type, level of cellular differentiation or stage in the lytic/lysogenic cycle (Knipe and Howley, 2007), resulting in highly skewed offspring distributions. This model violation is further intensified by the strong bottlenecks associated with infection and by strong positive selection (Neher and Hallatschek, 2013). Therefore, virus genealogies may be best characterized by multiple-merger coalescent (MMC) models (see, for example, Donnelly and Kurtz, 1999; Pitman, 1999; Sagitov, 1999; Schweinsberg, 2000; Möhle and Sagitov, 2001; Eldon and Wakeley, 2008), instead of the Kingman coalescent.
Second, the mutation rates of many viruses, particularly RNA viruses, are among the highest observed across taxa (Lauring et al., 2013; Cuevas et al., 2015). Although these high rates of mutation are what enables new beneficial mutations to arise, potentially allowing for rapid resistance to host immunity or antiviral drugs, they also render high mutational loads (Sanjuán, 2010; Lauring et al., 2013). Specifically, the distribution of fitness effects has now been described across taxa—demonstrating that the input of deleterious mutations far outnumbers the input of beneficial mutations (Acevedo et al., 2014; Bank et al., 2014; Bernet and Elena, 2015; Jiang et al., 2016). The purging of these deleterious mutants through purifying selection can affect other areas in the genome through a process known as background selection (BGS) (Charlesworth et al., 1993). Accounting for these effects is important for accurate evolutionary inference in general (Ewing and Jensen, 2016), but essential for the study of viruses because of their particularly high rates of mutation and compact genomes (Renzette et al., 2016).
Given these distinctive features of virus populations and the increasing use of population genetic inference in this area (see, for example, Renzette et al., 2013; Foll et al., 2014; Pennings et al., 2014; Renzette et al., 2016), it is crucial to account for these processes that are shaping the amount and distribution of variation across their genomes. We aim here to draw particular attention to MMC events and background selection, and the repercussions of ignoring them in population genetic inference, highlighting particular applications to viruses. We conclude with general recommendations for how best to address these topics in the future.
Skewed offspring distributions and the MMC
Inferring evolutionary history using the Wright–Fisher model: benefits and shortcomings
Many population genetic statistics and subsequent inference are based on the Kingman coalescent and the Wright–Fisher (WF) model (Wright, 1931; Kingman, 1982). With increasing computational power, the WF model has also been implemented in forward-time methods, allowing the modeling of more complex evolutionary scenarios versus backward-time methods. This also allows for the inference of population genetic parameters, including selection coefficients and effective population sizes (Ne), even from time-sampled data (that is, data collected at successive time points) (Ewens, 1979; Williamson and Slatkin, 1999; Malaspinas et al., 2012; Foll et al., 2014; Foll et al., 2015; Ferrer-Admetlla et al., 2016; Malaspinas, 2016). These methods are robust to some violations of WF model assumptions, such as constant population size, random mating, and non-overlapping generations, and have also been extended to accommodate selection, migration, and population structure (Neuhauser and Krone, 1997; Nordborg, 1997; Wilkinson-Herbots, 1998).
However, it has been suggested that violations of the assumption of a small variance in offspring number in the WF model, and in other models that result in the Kingman coalescent in the limit of large population size, lead to erroneous inference of population genetic parameters (Eldon and Wakeley, 2006). Biological factors such as sweepstake reproductive events, population bottlenecks, and recurrent positive selection may lead to skewed distributions in offspring number (Eldon and Wakeley, 2006; Li et al., 2014); examples include various prokaryotes (plague), fungi (Zymoseptoria tritici, Puccinia striiformis, rusts, mildew, oomycetes), plants (Arabidopsis thaliana), marine organisms (sardines, cods, salmon, oysters), crustaceans (Daphnia) and insects (aphids) (reviewed in Tellier and Lemaire, 2014). The resulting skewed offspring distributions can also result in elevated linkage disequilibrium despite frequent recombination, as linkage depends not only on recombination rate, but also on the degree of skewness in offspring distributions (Eldon and Wakeley, 2008; Birkner et al., 2013). Such events may also skew estimates of FST relative to those expected under WF models, as there is a high probability of alleles being identical by descent in subpopulations, where the expectation of coalescent times within subpopulations is less than that between subpopulations regardless of the timescale or magnitude of gene flow (Eldon and Wakeley, 2009).
The assumption of small variance in offspring number may often be violated in virus populations as well. For example, progeny RNA virus particles from infected cells can vary up to 100-fold (Zhu et al., 2009). Second, features such as diploidy, recombination, and latent stages are expected to increase the probability of multiple-merger events (Davies et al., 2007; Taylor and Véber, 2009; Birkner et al., 2013). Third, within their life cycle, viruses experience bottleneck events during transmission and compartmentalization, followed by strong selective pressure from both the immune system and drug treatments. Finally, at the epidemic level, extinction–colonization dynamics drive population expansion (Anderson and May, 1991).
All of these aspects characterize, for example, HIV, a diploid virus with extraordinary rates of recombination (Schlub et al., 2014). Transmitted and founder viruses undergo at least two distinct genetic bottlenecks (one at physical transmission and one at infection, respectively; Joseph and Swanstrom, 2015), followed by strong selection imposed by the immune system (Moore et al., 2002). At the epidemic scale, besides multiple events of colonization (Tebit and Arts, 2011), strong heterogeneity in the virus transmission chain has also been observed (see, for example, Service and Blower, 1995).
Beyond WF assumptions: the MMC
A more general coalescent class of models, summarized as the MMC class, can account for these violations, particularly for (non-Poisson) skewed offspring distributions, by allowing more than two lineages to coalesce at a time (Table 1). These are often derived from Moran models (Moran, 1958), generalized to allow multiple offspring per individual. In contrast to the Kingman coalescent (for which P(k>2)=0, where k is the number of lineages coalescing simultaneously), a probability distribution for k-merger events determines coalescence.
Table 1. Hierarchy of coalescent models in decreasing order of generality.
| Coalescent model | Allows MMs? | Allows simultaneous MMs? | Distribution and parameters | References |
|---|---|---|---|---|
| Ξ-Coalescent | Yes | Yes | MMC events occur at rate λ, with a specific measure ξ on the infinite simplex and which allows an arbitrary number of simultaneous mergers. | Schweinsberg (2000); Möhle and Sagitov (2001) |
| Λ-Coalescent | Yes | No | MMC events occur at rate λ (but ⩽1 event/time) | Donnelly and Kurtz (1999); Pitman (1999); Sagitov (1999) |
| Ψ-Coalescent | Yes | No | λ follows a distribution that depends on Ψ, that is,, the fraction of the population replaced by the offspring of a single individual | Eldon and Wakeley (2006); Eldon and Wakeley (2008); Eldon and Wakeley (2009); Eldon and Degnan (2012) |
| Beta-coalescent | Yes | No | λ follows β-distribution: β(α, 2-α) with 1⩽α<2 | Schweinsberg (2003); Berestycki et al. (2007); Berestycki et al. (2008); Birkner and Blath (2008); Birkner et al. (2013); Steinrücken et al. (2013) |
| Bolthausen–Sznitman | Yes | No | λ follows β-distribution with α=1: β(1,1)=uniform on [0,1] | Bolthausen and Snznitman (1998); Basdevant and Goldschmidt (2008); Neher and Hallatschek (2013) |
| Kingman coalescent | No | No | λ follows β-distribution with α=2; Λ has unit mass at 0 (Λ(dx)=δ0(x)dx) | Kingman (1982) |
Abbreviations: MM, multiple merger; MMC, multiple-merger coalescent.
Coalescent models listed in decreasing order with respect to generality.
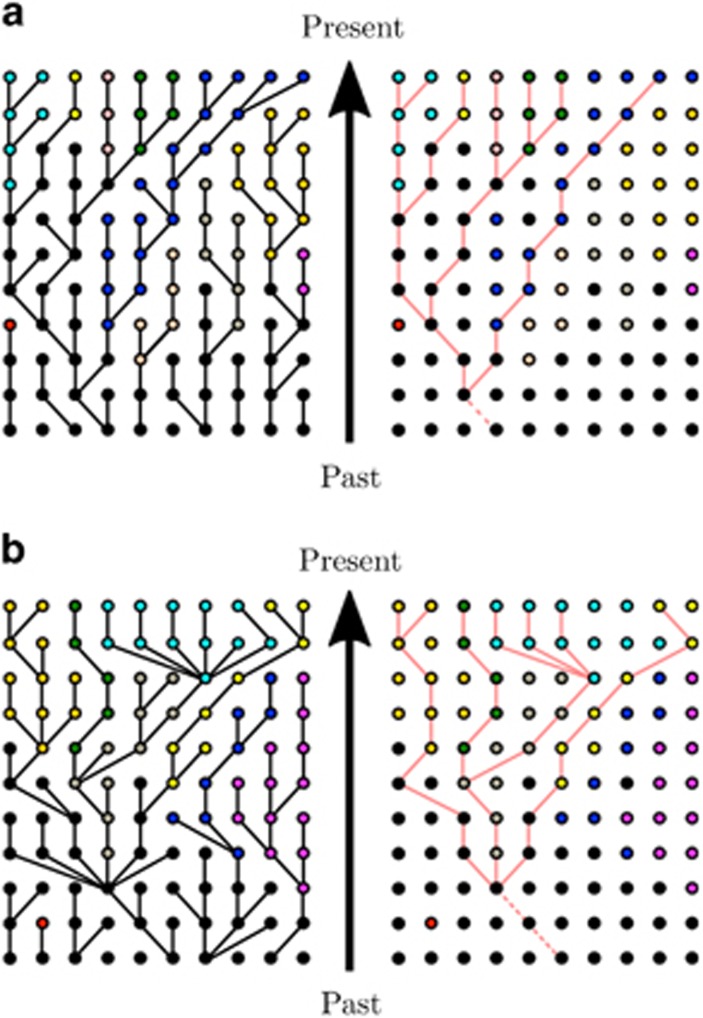
The parameters inferred under the MMC differ from those inferred under the Kingman coalescent in several notable respects. In the Kingman coalescent, effective size Ne scales linearly with census size N, whereas for the MMC it does not (Huillet and Möhle, 2011). Thus genetic diversity is a nonlinear function of population size. Coalescent trees under the MMC also have more pronounced star-like genealogies with longer branches (Figure 1), and their site frequency spectra (SFSs) are skewed toward an excess of low-frequency and high-frequency variants because of these branch lengths (Eldon and Wakeley, 2006; Blath et al., 2016), generating a more negative Tajima's D (Birkner et al., 2013). With similar migration and population size, alleles fix at a higher rate per population in the MMC than under the Kingman coalescent, and thus higher FST is expected between subpopulations (Eldon and Wakeley, 2009). Furthermore, the efficacy of selection increases, as selection acts almost deterministically between multiple-merger events; in the WF model, genetic drift counteracts selection fairly strongly (Der et al., 2011), but in generalized models where offspring distributions are wide, beneficial mutations may be more likely to escape stochastic loss and thus continue to fixation. Furthermore, the fixation probability of a new mutant with a positive selection coefficient approaches 1 as the population size increases, in stark contrast with traditional expectations under the standard WF model (Der et al., 2011).
Figure 1.
Multiple-merger and Kingman coalescent realizations. Example of genealogies and samples from (a) the Kingman coalescent and (b) a multiple-merger coalescent. Panels on the left show the evolutionary process of the whole population, whereas those on the right show a possible sampling and its resulting genealogy. Colors correspond to different (neutral) derived allelic states, where black denotes the wild type.
Not accounting for skewed offspring distributions can lead to misinference. For instance, Eldon and Wakeley (2006) showed that for Pacific oysters, which have been argued to undergo sweepstake-like reproductive events (Hedgecock, 1994a), the estimated population-wide mutation rate θ inferred under the Kingman coalescent is two orders of magnitude larger than that obtained from the Ψ-coalescent (see below)—9 vs 0.0308, respectively—and, indeed, provides a poor fit to the data.
The Ψ-coalescent
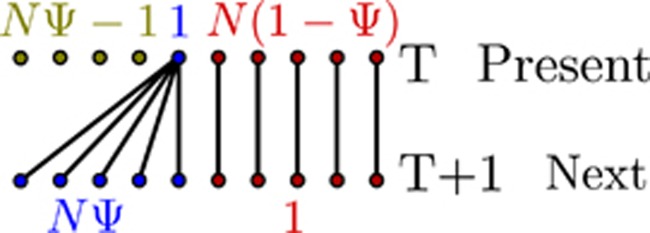
Introduced by Eldon and Wakeley (2006), the Ψ-coalescent (also called the ‘Dirac-coalescent') differentiates two possible reproductive events in the underlying forward process (Figure 2). Either a standard Moran model reproduction event occurs (with probability 1−ɛ), where a single individual is randomly chosen to reproduce and the (single) offspring replaces one randomly chosen nonparental individual; all other individuals, including the parent, persist. Alternatively, a ‘sweepstake' reproductive event occurs (with probability ɛ) (Hedgecock, 1994b), where a single parent replaces Ψ*N individuals. If these sweepstake events happen frequently enough, the rate of Ψ*N-reproduction events will be much greater than that of two-reproduction events, and the underlying coalescent process will consequently be characterized by MM events; if two or more parents were to replace Ψ*N individuals, simultaneous MM events may occur in a single generation resulting in a Ξ-coalescent. However, in contrast to other MMC models (for example, Ξ-coalescent or other Λ-coalescents), the parameter Ψ has a clear biological interpretation as the fraction of the population that is replaced in each sweepstake reproductive event. Though the assumption of a fixed Ψ (as in the normal Ψ-coalescent) seems biologically unrealistic, it can be avoided by treating Ψ as a Poisson parameter. Finally, despite its appealing connection to biologically relevant measures, the appropriateness of making inferences based on the Ψ-coalescent still depends on the biology of the specific virus being studied. Thus, model choice is still essential, and the best-fit coalescent should be assessed on a case-by-case basis.
Figure 2.
Depiction of the modified Moran model underlying the Ψ-coalescent. Lineages between the present and the next generation, where N is the population size, ɛ is the probability of a sweepstake event and Ψ is the fraction of the population that is replaced in each such event. Labels in the top row give the number of parental individuals reproducing in a given manner (represented by color), whereas labels in the bottom row give the number of corresponding offspring per parent.
Application to viruses
There are several reasons why a modified Moran model may better capture virus evolution than models converging to the Kingman coalescent, even though it does not account for fitness differences between individuals. First, virus evolution is driven by strong bottlenecks during host transmission and intrahost selection processes that likely result in skewed offspring distributions (Figure 3) (Gutiérrez et al., 2012; Tellier and Lemaire, 2014). Furthermore, viruses display the MMC-typical low Ne/N ratio (Pennings et al., 2014; Tellier and Lemaire, 2014), can adapt rapidly (Neher and Hallatschek, 2013), and may have sweepstake-like reproductive events in which a single virion can propagate a large fraction of the entire population (Grenfell et al., 2004; Pybus and Rambaut, 2009). For example, the influenza virus hemagglutinin segment appears to be under strong directional selection imposed by host immunity (and sometimes drug treatment), resulting in a ladder-like genealogy (as depicted in Figure 3a), suggesting that only a few viruses seed the entire next generation (Grenfell et al., 2004). That being said, some challenges remain (see Box 1), such as rigorously defining the term ‘generation' for virus populations, and subsequently confirming that the per-generation mutation rate is on the order of the coalescent timescale cN, a prerequisite for the use of any coalescent approach. Finally, viruses with little or no recombination may be prone to clonal interference, and this should be explicitly accounted for in population models and resulting coalescents (see, for example, Strelkowa and Lässig, 2012).
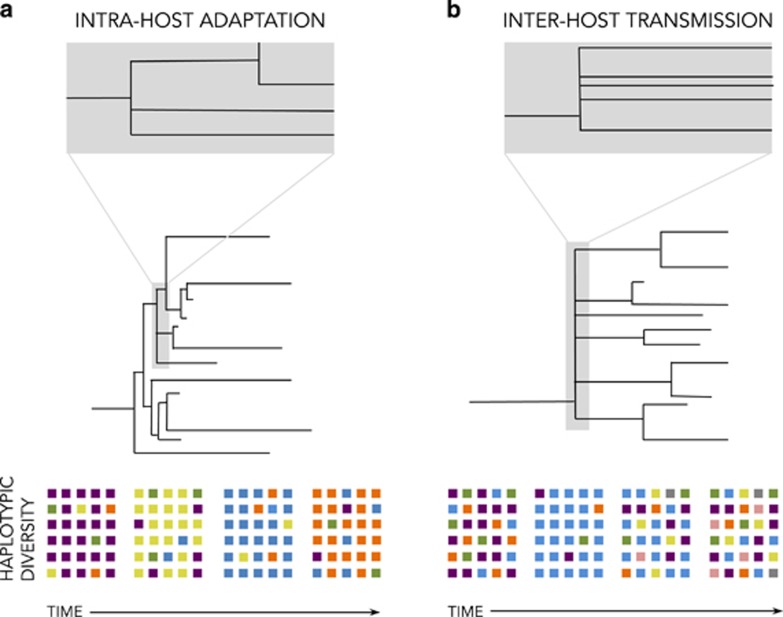
Figure 3.
Example of processes spurring MM events in virus populations. Examples include (a) intrahost adaptation (a selective process) and (b) interhost transmission (a demographic process). The tree in (a) characterizes, for example, neuraminidase (NA) or hemagglutinin (HA) evolution in the influenza A virus, driven by positive selection; selection by host immunity is ongoing, whereas that from drug treatment may be intermittent. The tree in (b) represents interhost transmission and its associated bottleneck; for viruses that compartmentalize (such as human cytomegalovirus and HIV), similar patterns follow transmission to new compartments. The colored squares below the trees roughly indicate the diversity of the population through time. Intrahost adaptation may temporally decrease diversity owing to genetic hitchhiking, though single snapshots may not reflect varying temporal levels of diversity. During interhost transmission, diversity decreases owing to the associated bottleneck but then may quickly recover in the new host.
Box 1 Future challenges in MMC models.
In order to make multiple-merger coalescent (MMC) models biologically relevant for viruses, a number of important tasks remain:
Describe summary statistics that capture demographic features and processes when offspring distributions are highly skewed; such patterns will be required for large-scale inference in a computationally efficient (for example, approximate Bayesian) framework.
Better understand the behavior of commonly used summary statistics under such models, as done for FST by Eldon and Wakeley (2009), for commonly used divergence, site frequency spectrum, and linkage disequilibrium-based statistics.
Determine which MMCs are best suited for different scales of virus evolution (that is, intrahost, interhost, global); develop novel models if necessary.
Investigate the effects of violations of MMC assumptions (for example, overlapping generations, number of multiple-merger events) on inference.
The processes that make viruses ideal candidates for MMCs can differ by scale (see Figure 3); for example, following transmission events, there are severe founder effects and potentially high recombination within the host (for example, HIV and human cytomegalovirus). Subsequent compartmentalization may introduce intrahost population structure through bottlenecks, colonization events, and extinction events (Renzette et al., 2013). To date, it remains unclear how often MMCs fit the patterns of variation observed in intrahost versus interhost virus populations—but such comparisons are increasingly feasible (Box 1). Finally, periods of latency—temporary virus inactivation with cessation of reproduction—should be incorporated in such modeling, potentially as recurring mass extinction events (Taylor and Véber, 2009). Thus, multiple MMC models are a necessary but not final step toward addressing the various patterns observed at different scales of virus evolution (Table 1).
The large data sets often generated from viruses may also prove impractical for the likelihood-based methods commonly employed for MMCs. This limitation has partially been overcome by Eldon et al. (2015), who proposed an approximate likelihood method along with an approximate Bayesian computation approach based on the SFS to distinguish between the MMC and exponential population growth. Although both effects are expected to result in very similar SFSs, characterized by an excess of singletons as compared with the Kingman coalescent, the bulk and tail of the SFS (that is, the higher-order frequency classes) typically differ, which can be assessed by approximate likelihood-ratio tests and approximate Bayes factors (Eldon et al., 2015; see Box 1).
Purifying selection and linkage in virus populations
Modeling background selection
The joint modeling of the effects of genetic drift and positive selection, including in experimental evolution studies of virus populations, has improved our ability to distinguish adaptive from neutral mutations by minimizing the chance that the rapid fixation of a neutral allele is incorrectly interpreted as strong positive selection (Li et al., 2012; Foll et al., 2014; see Box 2). However, there is another process that must be incorporated if we are to fully understand mutation trajectories in virus populations: background selection.
Box 2 Future challenges in identifying the effects of BGS.
As background selection (BGS) almost certainly affects inference in virus populations, accounting for its effects is critical. Future challenges include:
Account for BGS effects on the SFS by directly simulating weakly deleterious mutations, rather than by rescaling Ne.
Improve recombination maps for virus genomes.
Develop models combining the effects of nonequilibrium demography, positive selection, and BGS, ideally to allow for the joint estimation of all associated parameters.
Extend methods applied to other taxa to virus populations; for example, establishing a baseline of variation for use as a null expectation to estimate BGS levels across the genome, as done for Drosophila.
BGS was originally proposed to explain patterns of reduced diversity in regions of low recombination—patterns that were previously suggested to be the signature of genetic hitchhiking around strongly beneficial mutations (see Begun and Aquadro, 1992 and Charlesworth et al., 1993). It was argued that only neutral mutations present on the ‘least-loaded' chromosomes—that is, those with the fewest deleterious mutations—have appreciable probabilities of reaching high frequencies or fixation. Kimura and Maruyama (1966) showed that the proportion of chromosomes belonging to the least-loaded class is
where U is the rate of mutation to a deleterious state, s is the selection coefficient against homozygous mutations and h is the dominance coefficient. For simplicity of modeling, h is usually set to 1 for viruses that carry a single copy of their genome in each virion, although polyploid effects could arise in the case of multiple virions infecting the same cell.
The least-loaded class, and thus genetic diversity in the presence of BGS, is dependent on the balance between the influx of deleterious mutations (occurring at rate U) and their removal by natural selection (according to the product hs). Assuming that offspring exclusively originate from the least-loaded class of individuals, Charlesworth et al. (1993) expressed the expected neutral diversity due to background selection as
where Ne is the effective population size and μ is the mutation rate. As BGS reduces the number of reproducing individuals, genetic drift increases, thus reducing genetic diversity and increasing stochasticity in allele trajectories. Furthermore, as only the genetic diversity segregating in the least-loaded class can be observed, population size inferred from measures of genetic diversity may be underestimated if BGS is not properly taken into account (Ewing and Jensen, 2016).
In the BGS model described above, strongly deleterious mutations are maintained in mutation-selection balance such that no skew in the SFS is expected, as rare variants are rapidly purged. Thus, a simple rescaling of Ne is often used as a proxy for the effects of BGS (see, for example, Hudson and Kaplan, 1995; Zeng and Charlesworth, 2011; Prüfer et al., 2012; Zeng, 2013). However, recent work has demonstrated that although this rescaling is appropriate for strongly deleterious mutations, it is largely inappropriate for weakly deleterious mutations that may segregate in the population. Figure 4 shows the skew in estimates of population size obtained using an approximate Bayesian computation approach when BGS is prevalent for two populations A and B that have split at time τ=2Ne generations (reproduced from Ewing and Jensen, 2016). Furthermore, experimental work on the shape of the distribution of fitness effects in many organisms indicates that weakly deleterious mutations represent an important class (see, for example, Eyre-Walker and Keightley, 2007; Bank et al., 2014). These mutations may act to skew the SFS toward rare alleles as they decrease the expected frequency of linked neutral mutations relative to neutral expectations. As subsequent demographic inference is based on the shape of this SFS, this effect should be properly accounted for by directly simulating weakly deleterious mutations rather than implementing a simple rescaling, as is common practice (Box 2). Though important analytical progress has been made in this area (see, for example, McVean and Charlesworth, 2000), simulations remain the best option for the nonequilibrium demographic models and alternative coalescents recommended here for inference in virus populations.
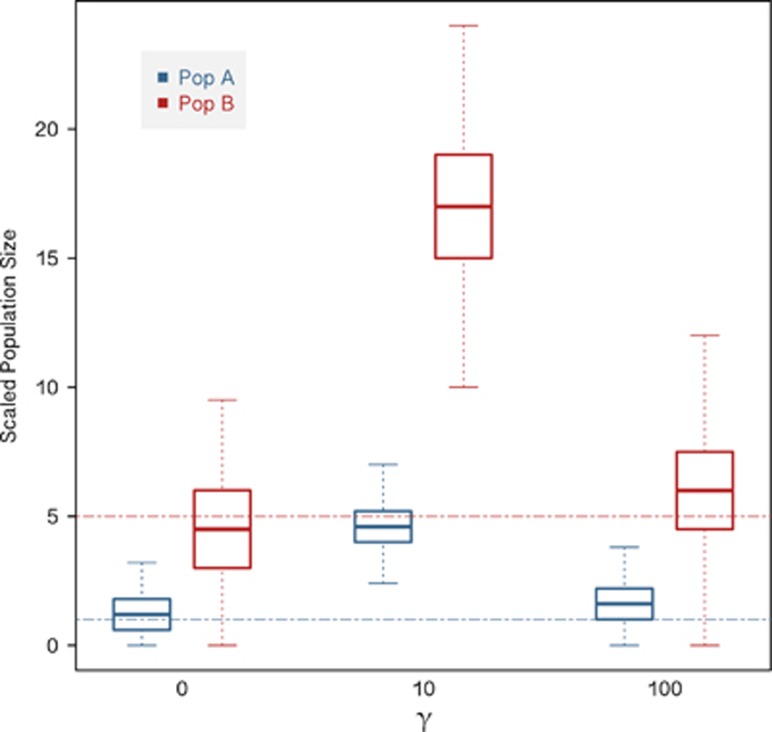
Figure 4.
Bias in parameter inference at intermediate levels of BGS. Bias in parameter inference for different levels of BGS, redrawn from Ewing and Jensen (2016). Posterior densities from approximate Bayesian computation (ABC) inference for population size are shown. The strength of purifying selection is given as γ, where γ=2Nes. Population A (Pop A) has a true scaled size of 1 (blue line), and population B (Pop B) a true scaled size of 5 (red line). Both population sizes are scaled relative to the size of the ancestral population. As shown, the greatest misinference occurs in the presence of weakly deleterious mutations and subsequent strong BGS effects.
The effects of background selection on inference in virus populations
Efforts to estimate the impact of BGS in nonviral organisms have been well reported. One of the most notable examples is that of Comeron (2014), who estimated levels of BGS in Drosophila melanogaster based on the results of Hudson and Kaplan (1995) and Nordborg et al. (1996) using a high-definition recombination map, with results indicating strong effects across the genome. For viruses, similar efforts are in their infancy (Box 2), with the first attempt at such estimation in a virus reported recently by Renzette et al. (2016), utilizing the theoretical predictions of Innan and Stephan (2003). Interestingly, the full spectrum of recombination frequencies is available in viruses—from non-recombining (for example, most negative-sense RNA viruses), to re-assorting (for example, influenza viruses), to rarely recombining (for example, hepatitis C and West Nile viruses), to frequently recombining (for example, HIV) — offering a highly promising framework for comparative analyses investigating the pervasiveness of BGS effects (Chare et al., 2003; Simon-Loriere and Holmes, 2011). Furthermore, given the high mutation rates and compact genomes of many viruses, evolutionary theory suggests effects at least equal to those seen in Drosophila.
In order to accomplish such inference, improved recombination maps for virus genomes will be important. With such maps in hand, and given the amenability of viruses to experimental perturbation, it may indeed be feasible to understand and account for BGS in models of virus evolution.
Future directions
Given that skewed offspring distributions and pervasive linked selection are likely important factors influencing the inference of virus population parameters, it is important to note that multiple backward and forward simulation programs have recently been developed that make the modeling of these processes feasible (Hernandez, 2008; Messer, 2013; Thornton, 2014; Eldon et al., 2015; Zhu et al., 2015). This will allow researchers to directly simulate from parameter ranges relevant for their population of interest, developing a better intuition for the importance of these processes in shaping the observed genomic diversity. More concretely, the ability to now simulate in a computationally efficient framework opens the possibility of directly implementing approximate Bayesian computation inference approaches under these models. Thus, by drawing mutations from a biologically realistic distribution of fitness effects and allowing offspring distributions to appropriately vary, it is now possible to reimplement common demographic estimation or genome scan approaches; these modified approaches would be based on more appropriate null expectations of the shape of the SFS, the extent of linkage disequilibrium, and the degree of population divergence.
Data archiving
As a review article, no new data were processed, analyzed, or used directly.
Acknowledgments
We thank Bjarki Eldon for helpful suggestions during the early stages of this manuscript as well as Valeria Montano and three anonymous referees for later comments. This work was funded by the European Research Council (ERC) Starting Grant to JDJ, as well as Swiss National Science Foundation (FNS) grants to JDJ (31003A_159835) and SV (PMPDP3_158381).
The authors declare no conflict of interest.
References
- Acevedo A, Brodsky L, Andino R. (2014). Mutational and fitness landscapes of an RNA virus revealed through population sequencing. Nature 505: 686–690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson RM, May RM. (1991) Infectious Diseases of Humans: Dynamics and Control. Oxford University Press: Oxford. [Google Scholar]
- Bank C, Hietpas RT, Wong A, Bolon DN, Jensen JD. (2014). A Bayesian MCMC approach to assess the complete distribution of fitness effects of new mutations: uncovering the potential for adaptive walks in challenging environments. Genetics 196: 841–852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Basdevant A, Goldschmidt C. (2008). Asymptotics of the allele frequency spectrum associated with the Bolthausen-Sznitmzn coalescent. Electron J Probab 13: 486–512. [Google Scholar]
- Begun DJ, Aquadro CF. (1992). Levels of naturally occurring DNA polymorphism correlate with recombination rates in D. melanogaster. Nature 356: 519–520. [DOI] [PubMed] [Google Scholar]
- Berestycki J, Berestycki N, Schweinsberg J. (2007). Beta-coalescents and continuous stable random trees. Ann Probab 35: 1835–1887. [Google Scholar]
- Berestycki J, Berestycki N, Schweinsberg J. (2008). Small-time behavior of beta coalescents. Ann I H Poincare-Pr 44: 214–238. [Google Scholar]
- Bernet GP, Elena SF. (2015). Distribution of mutational fitness effects and of epistasis in the 5' untranslated region of a plant RNA virus. BMC Evol Biol 15: 274–287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Birkner M, Blath J. (2008). Computing likelihoods for coalescents with multiple collisions in the infinitely many sites model. J Math Biol 57: 435–465. [DOI] [PubMed] [Google Scholar]
- Birkner M, Blath J, Eldon B. (2013). An ancestral recombination graph for diploid populations with skewed offspring distribution. Genetics 193: 255–290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blath J, Cronjäger MC, Eldon B, Hammer M. (2016). The site-frequency spectrum associated with Ξ -coalescents. Theor Popul Biol 110: 36–50. [DOI] [PubMed] [Google Scholar]
- Bolthausen E, Snznitman AS. (1998). On Ruelle's probability cascades and an abstract cavity method. Commun Math Phys 197: 247–276. [Google Scholar]
- Chare ER, Gould EA, Holmes EC. (2003). Phylogenetic analysis reveals a low rate of homologous recombination in negative-sense RNA viruses. J Gen Virol 84: 2691–2703. [DOI] [PubMed] [Google Scholar]
- Charlesworth B, Morgan MT, Charlesworth D. (1993). The effect of deleterious mutations on neutral molecular variation. Genetics 134: 1289–1303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Comeron JM. (2014). Background selection as a baseline for nucleotide variation across the Drosophila genome. PLoS Genet 10: e1004434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cuevas JM, Geller R, Garijo R, López-Aldeguer J, Sanjuán R. (2015). Extremely high mutation rate of HIV-1 in vivo. PLoS Biol 13: e1002251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davies JL, Simančík F, Lyngsø R, Mailund T, Hein J. (2007). On recombination-induced multiple and simultaneous coalescent events. Genetics 177: 2151–2160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Der R, Epstein CL, Plotkin JB. (2011). Generalized population models and the nature of genetic drift. Theor Popul Biol 80: 80–99. [DOI] [PubMed] [Google Scholar]
- Donnelly P, Kurtz TG. (1999). Particle representations for measure-valued population models. Ann Probab 27: 166–205. [Google Scholar]
- Eldon B, Birkner M, Blath J, Freund F. (2015). Can the site-frequency spectrum distinguish exponential population growth from multiple-merger coalescents? Genetics 199: 841–856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eldon B, Degnan JH. (2012). Multiple merger gene genealogies in two-species: Monophyly, paraphyly, and polyphyly for two examples of Lambda coalescents. Theor Popul Biol 82: 117–130. [DOI] [PubMed] [Google Scholar]
- Eldon B, Wakeley J. (2006). Coalesent processes when the distribution of offspring number among individuals is highly skewed. Genetics 172: 2621–2633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eldon B, Wakeley J. (2008). Linkage disequlibrium under skewed offspring distribution among individuals in a population. Genetics 178: 1517–1532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eldon B, Wakeley J. (2009). Coalescence times and Fst under a skewed offspring distirbution among individuals in a population. Genetics 181: 615–629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ewens WJ. (1979). Testing the generalized neutrality hypothesis. Theor Popul Biol 15: 205–216. [Google Scholar]
- Ewing GB, Jensen JD. (2016). The consequences of not accounting for background selection in demographic inference. Mol Ecol 25: 135–141. [DOI] [PubMed] [Google Scholar]
- Eyre-Walker A, Keightley PD. (2007). The distirbution of fitness effects of new mutations. Nat Rev Genet 8: 610–618. [DOI] [PubMed] [Google Scholar]
- Ferrer-Admetlla A, Leuenberger C, Jensen JD, Wegmann D. (2016). An approximate Markov model for the Wright-Fisher diffusion and its application to time series data. Genetics 203: 831–846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foll M, Poh Y, Renzette N, Ferrer-Admetlla A, Bank C, Shim H et al. (2014). Influenza virus drug resistance: a time-sampled population genetic perspective. PLoS Genet 10: e1004185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foll M, Shim H, Jensen JD. (2015). WFABC: a Wright-Fisher ABC-based approach for inferring effective population sizes and selection coefficients from time-sampled data. Mol Ecol Resour 15: 87–98. [DOI] [PubMed] [Google Scholar]
- Grenfell BT, Pybus OG, Gog JR, Wood JLN, Daly JM, Mumford JA et al. (2004). Unifying the epidemiological and evolutionary dynamics of pathogens. Science 303: 327–332. [DOI] [PubMed] [Google Scholar]
- Gutiérrez S, Michalakis Y, Blanc S. (2012). VIrus population bottlenecks during within-host progression and host-to-host transmission. Curr Opin Virol 2: 546–555. [DOI] [PubMed] [Google Scholar]
- Hedgecock D. (1994. a) Does variance in reproductive success limit effective population sizes of marine organisms? In: Beaumont AR (ed). Genetics and Evolution of Aquatic Organisms. Chapman & Hall: London. pp 122–133. [Google Scholar]
- Hedgecock D. (1994. b). Population genetics of marine organisms. US Globec News 6: 1–8. [Google Scholar]
- Hernandez R. (2008). A flexible forward simulator for populations subject to selection and demography. Bioinformatics 24: 2786–2787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudson RR, Kaplan NL. (1995). Deleterious background selection with recombination. Genetics 141: 1605–1617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huillet T, Möhle M. (2011). Population genetics models with skewed fertilities: a forward and backward analysis. Stoch Models 27: 521–554. [Google Scholar]
- Innan H, Stephan W. (2003). Distinguishing the hitchhiking and background selection models. Genetics 165: 2307–2312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang L, Liu P, Bank C, Renzette N, Prachanronarong K, Yilmaz LS et al. (2016). A balance between inhibitor binding and substrate processing confers influenza drug resistance. J Mol Biol 428: 538–523. [DOI] [PubMed] [Google Scholar]
- Joseph SB, Swanstrom R. (2015). A fitness bottleneck in HIV-1 transmission. Science 345: 136–173. [DOI] [PubMed] [Google Scholar]
- Kimura M, Maruyama T. (1966). The mutational load with epistatic gene interactions in fitness. Genetics 54: 1337–1351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kingman JFC. (1982). The coalescent. Stoch Proc Applicat 13: 235–248. [Google Scholar]
- Knipe DM, Howley PM. (2007) Fields Virology Vol 1, Lippincott Williams & Wilkins: Philadelphia. [Google Scholar]
- Lauring AS, Frydman J, Andino R. (2013). The role of mutational robustness in RNA virus evolution. Nat Rev Genet 11: 327–336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li J, Li H, Jakobsson M, Li S, Sjödin P, Lascoux M. (2012). Joint analysis of demography and selection in poulation genetics: where do we stand and where could we go? Mol Ecol 21: 28–44. [DOI] [PubMed] [Google Scholar]
- Li LM, Grassly NC, Fraser C. (2014). Genomic analysis of emerging pathogens: methods, application and future trends. Genome Biol 15: 541–550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malaspinas A-S. (2016). Methods to characterize selective sweeps using time serial samples: an ancient DNA perspective. Mol Ecol 25: 24–41. [DOI] [PubMed] [Google Scholar]
- Malaspinas A-S, Malaspinas O, Evans SN, Slatkin M. (2012). Estimating allele age and selection coefficient from time-serial data. Genetics 192: 599–607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McVean GAT, Charlesworth B. (2000). The effects of Hill-Robertson interference between weakly selected mutations on patterns of molecular evoultion and variation. Genetics 155: 929–944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Messer PW. (2013). SLiM: simulating evolution with selection and linkage. Genetics 194: 1037–1039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Möhle M, Sagitov S. (2001). A classification of coalescent processes for haploid exchangable population models. Ann Probab 29: 1547–1562. [Google Scholar]
- Moore CB, John M, James IR, Christiansen FT, Witt CS, Mallal SA. (2002). Evidence of HIV-1 adaptation to HLA-restricted immune responses at a population level. Science 296: 1439–1443. [DOI] [PubMed] [Google Scholar]
- Moran PAP. (1958). Random processes in genetics. Math Proc Camb Phil Soc 54: 60–71. [Google Scholar]
- Neher RA, Hallatschek O. (2013). Genealogies of rapidly adapting populations. Proc Natl Acad Sci USA 110: 437–442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neuhauser C, Krone SM. (1997). The genealogy of samples in models with selection. Genetics 145: 519–534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nordborg M. (1997). Structured coalescent processes on different time scales. Genetics 146: 1501–1514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nordborg M, Charlesworth B, Charlesworth D. (1996). The effect of recombination on background selection. Gen Res 67: 159–174. [DOI] [PubMed] [Google Scholar]
- Pennings PS, Kryazhimskiy S, Wakeley J. (2014). Loss and recovery of genetic diversity in adapting populations of HIV. PLoS Genet 10: e1004000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pitman J. (1999). Coalescents with multiple collisions. J Appl Probab 27: 1870–1902. [Google Scholar]
- Prüfer K, Munch K, Hellmann I, Akagi K, Miller JR, Walenz B et al. (2012). The bonobo genome compared with the chimpanzee and human genomes. Nature 486: 527–531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pybus OG, Rambaut A. (2009). Evolutionary analysis of the dynamics of viral infectious disease. Nat Rev Genet 10: 540–550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Renzette N, Gibson L, Bhattacharjee B, Fisher D, Schleiss MR, Jensen JD et al. (2013). Rapid intrahost evolution of human cytomegalovirus is shaped by demography and positive selection. PLoS Genet 9: e1003735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Renzette N, Kowalik TF, Jensen JD. (2016). On the relative roles of background selection and geneic hitchhiking in shaping human cytometgalovirus genetic diversity. Mol Ecol 25: 403–413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sagitov S. (1999). The general coalescent with asynchronous mergers of ancestral lines. J Appl Probab 36: 1116–1125. [Google Scholar]
- Sanjuán R. (2010). Mutational fitness effects in RNA and single-stranded DNA viruses: common patterns revealed by site-directed mutagenesis studies. Phil Trans R Soc B 365: 1975–1982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schlub TE, Grimm AJ, Smyth RP, Cromer D, Chopra A, Mallal S et al. (2014). Fifteen to twenty percent of HIV substitution mutations are associated with recombination. J Virol 88: 3837–3849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schweinsberg J. (2000). Coalescents with simultaneous multiple collisions. Electron J Probab 5: 1–50. [Google Scholar]
- Schweinsberg J. (2003). Coalescent processes obtained from supercritical Galton-Watson processes. Stoch Proc Applicat 106: 107–139. [Google Scholar]
- Service SK, Blower SM. (1995). HIV transmission in sexual networks: an empirical analysis. Proc R Soc Lond B Biol Sci 260: 237–244. [DOI] [PubMed] [Google Scholar]
- Simon-Loriere E, Holmes EC. (2011). Why do RNA viruses recombine? Nat Rev Microbiol 9: 617–626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steinrücken M, Birkner M, Blath J. (2013). Analysis of DNA sequence variation within marine species using Beta-coalescents. Theor Popul Biol 87: 15–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strelkowa N, Lässig M. (2012). Clonal interference in the evolution of influenza. Genetics 192: 671–682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor JE, Véber A. (2009). Coalescent processes in subdivided populations subject to recurrent mass extinctions. Electron J Probab 14: 242–288. [Google Scholar]
- Tebit DM, Arts EJ. (2011). Tracking a century of global expansion and evolution of HIV to drive understanding and to combat disease. Lancet Infect Dis 11: 45–46. [DOI] [PubMed] [Google Scholar]
- Tellier A, Lemaire C. (2014). Coalescence 2.0: a multiple branching of recent theoretical developments and their applications. Mol Ecol 23: 2637–2652. [DOI] [PubMed] [Google Scholar]
- Thornton KR. (2014). A C++ template library for efficient forward-time population genetic simulation of large populations. Genetics 198: 157–166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilkinson-Herbots HM. (1998). Genealogy and subpopulation differentiation under various models of population structure. J Math Biol 37: 535–585. [Google Scholar]
- Williamson EG, Slatkin M. (1999). Using maximum likelihood to estimate population size from temporal change in allele frequencies. Genetics 152: 755–761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright S. (1931). Evolution in Mendelian populations. Genetics 16: 97–159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeng K. (2013). A coalescent model of background selection with recombination, demography and variation in selection coefficients. Heredity 100: 363–371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeng K, Charlesworth B. (2011). The joint effects of background selection and genetic recombination on local gene genealogies. Genetics 189: 251–266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu S, Degnan JH, Goldstien SJ, Eldon B. (2015). Hybrid-Lambda: simulation of multiple merger and Kingman gene genealogies in species networks and species trees. BMC Bioinformatics 16: 292–298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu Y, Yongky A, Yin J. (2009). Growth of an RNA virus in single cells reveals a broad fitness distribution. Virology 385: 39–46. [DOI] [PMC free article] [PubMed] [Google Scholar]