A Novel Respiratory Motion Perturbation Model Adaptable to Patient Breathing Irregularities

Abstract

Purpose

To develop a physical, adaptive motion perturbation model to predict tumor motion using feedback from dynamic measurement of breathing conditions to compensate for breathing irregularities.

Methods and Materials

A novel respiratory motion perturbation (RMP) model was developed to predict tumor motion variations caused by breathing irregularities. This model contained 2 terms: the initial tumor motion trajectory, measured from 4-dimensional computed tomography (4DCT) images, and motion perturbation, calculated from breathing variations in tidal volume (TV) and breathing pattern (BP). The motion perturbation was derived from the patient-specific anatomy, tumor-specific location, and time-dependent breathing variations. Ten patients were studied, and 2 amplitude-binned 4DCT images for each patient were acquired within 2 weeks. The motion trajectories of 40 corresponding bifurcation points in both 4DCT images of each patient were obtained using deformable image registration. An in-house 4D data processing toolbox was developed to calculate the TV and BP as functions of the breathing phase. The motion was predicted from the simulation 4DCT scan to the treatment 4DCT scan, and vice versa, resulting in 800 predictions. For comparison, noncorrected motion differences and the predictions from a published 5-dimensional model were used.

Results

The average motion range in the superoinferior direction was 9.4 ± 4.4 mm, the average ΔTV ranged from 10 to 248 mm³ (−26% to 61%), and the ΔBP ranged from 0 to 0.2 (−71% to 333%) between the 2 4DCT scans. The mean noncorrected motion difference was 2.0 ± 2.8 mm between 2 4DCT motion trajectories. After applying the RMP model, the mean motion difference was reduced significantly to 1.2 ± 1.8 mm (P = .0018), a 40% improvement, similar to the 1.2 ± 1.8 mm (P = .72) predicted with the 5-dimensional model.

Conclusions

A novel physical RMP model was developed with an average accuracy of 1.2 ± 1.8 mm for interfraction motion prediction, similar to that of a published lung motion model. This physical RMP was analytically derived and is able to adapt to breathing irregularities. Further improvement of this RMP model is under investigation.

Introduction

Respiratory motion is a major source of uncertainty in external beam radiation therapy for lung, liver, and pancreatic cancer (1, 2). Despite the potential advantages of respiratory gating and tumor tracking, mobile tumors are often treated using the internal tumor volume method to target the trajectory envelope of the clinical tumor volume, with an additional 5- to 8-mm margin to cover setup uncertainty in the planning tumor volume. When an organ at risk (OAR) is adjacent to or overlapping with the tumor, a part of the OAR will be included inside the planning tumor volume and receive the full prescription dose. Therefore, the OAR dose tolerance can limit the prescription dose to the tumor, especially in stereotactic body radiation therapy (3-5). To spare the OARs, it is essential to improve stereotactic body radiation therapy using a high-precision targeting technique with reduced motion margins. Tumor tracking promises to minimize motion uncertainty, approaching the precision of the motion-free treatment achieved by temporary respiratory suspension (6, 7), beneficial for local control of lung tumors (8, 9), liver cancer (10, 11), and pancreatic cancer (12, 13). Maximal OAR sparing can enable further dose acceleration to overcome possible radioresistant hypoxic cores (14, 15). Currently, one of the obstacles to tumor tracking is the lack of a reliable, accurate tumor motion surrogate without implanted markers and/or high-frame-rate x-ray imaging. Although magnetic resonance (MR)-guided radiation therapy has recently been applied in radiation therapy clinics (16, 17), and more applications are expected (18, 19), it is associated with a substantial cost increase, additional personnel training, and dedicated resources. Furthermore, the MR-guided technology is still under intensive development to use its full capabilities (18).

Recently, optical surface imaging (OSI) has been applied to monitor all respiration-induced external torso motion (eg, breathing pattern), to provide spirometric measurements (tidal volume [TV] and airflow), and to detect body voluntary motion (registration shifts) (20, 21). These intrafraction motion parameters can be used to feed an adaptive respiratory motion model to accurately predict tumor motion and correct body shift–induced baseline drift and, thus, provide an alternative solution for tumor tracking. To date, most clinical motion prediction models have been based on the internal–external correlation, which is established before treatment but can be degraded during treatment owing to breathing irregularities. To confirm the validity of such a model, internal and external surrogates are often combined to predict tumor motion with reduced imaging radiation (22-24). However, the correlation model often requires model rebuilding multiple times during a treatment to cope with the changing breathing behavior.

Lung motion prediction, including tumors and OARs, has been studied using more advanced physical approaches, including biomechanical modeling with the finite element method (25, 26), motion vector modeling with deformable image registration (DIR) (27, 28), hybrid modeling with biomechanics and DIR (29, 30), and statistical modeling with respiratory parameters (31-33). Although the prediction accuracy might be clinically acceptable, the major limitations included a lack of real-time performance owing to the complex, iterative computation and lack of adaptations to changes of breathing behaviors or irregularities.

In the present study, we report a novel physical respiratory motion perturbation (RMP) approach to predict tumor motion based on a physical relationship using a perturbation method. Because only motion variation caused by irregularity was calculated, the computation workload was significantly reduced (34, 35). Additionally, separating the superoinferior (SI) from anteroposterior (AP) motions using breathing patterns (36, 37) simplified RMP modeling computation. The baseline tumor motion can be obtained from 4-dimensional computed tomography (4DCT) at simulation, and the motion perturbation can be calculated using the respiratory changes in TV and BP fed by the OSI-based technique (20, 21) during treatment. To investigate the feasibility, 2 sets of 4DCT images from 10 patients were used: both provide motion trajectories and corresponding breathing conditions (TV and BP, mimicking the OSI measurements). Beginning with motion trajectory from one 4DCT, we calculated the respiratory condition variations in TV and BP by comparing it with the second 4DCT. Next, we predicted the motion trajectory in the second 4DCT and then evaluated the prediction accuracy using the second motion trajectory as the ground truth. The predicted tumor motion trajectory is the sum of the baseline motion and motion perturbation. The prediction in reverse direction was also performed. For each patient, 40 bifurcation points were identified, tracked, and aligned in both 4DCT scans, leading to 800 predictions. We also compared the RMP predictions with the noncorrected (NC) motion difference and the results from a 5-dimensional (5D) model (31).

Methods and Materials

Patient data and prediction strategy

To predict patient breathing motion from simulation to treatment, 2 sets of 4DCT images for each of the 10 patients were acquired, the first at simulation and the second at treatment, approximately 2 weeks later, using an 8-slice LightSpeed scanner (GE Healthcare, Waukesha, WI) under an institutional review board–approved protocol. One 4DCT scan served as the starting data set, and the other was used as the ground truth for testing, and vice versa. Forty bifurcation points (5 for each of the anterior left and right lungs, 10 for each in the posterior left and right lungs, and 10 others randomly selected) in the bronchial tree were identified and tracked using an Insight Toolkits-based (38) in-house automatic bronchial bifurcation array (ABBA) segmentation tool. Independently, these points were tracked using DIR (39) throughout the breathing cycle and visually verified in both 4DCT images. Forty motion trajectories were produced by ABBA and DIR; however, only the DIR results were used, because they were less negatively affected by motion artifacts on the 4DCT scans (40). The native difference of the average displacement with NC was calculated for all corresponding trajectories between each 4DCT pair to serve as controls. We then applied the RMP model to predict a trajectory from one 4DCT to the other, and vice versa, and assess the accuracy using our 4D clinical multimodal image processing toolbox (41). The results were compared with an established 5D model (31). In total, 800 trajectory predictions were assessed.

RMP model

Because the AP and SI volume distributions were orthogonal and controlled by the intercostal muscles and diaphragm (sources of respiratory motion), respectively, the TV (TV = ΔV_torso = ΔV_thx + ΔV_abd) was attributed to the thoracic (ΔV_thx responsible for AP motion) and abdominal (ΔV_abd responsible for SI motion) motions. The BP (BP = ΔV_thx/TV), defined as the lung volume expansion change (AP) divided by the TV change, was used to quantify the involvement of the thorax (36, 37) and abdomen (1 – BP) in respiration. Therefore, the BP is a critical parameter that introduces directional information into the scalar spirometric TV data.

Previously, we defined the static BP ( $\mathit{\text{BP}}=\Delta V_{\mathit{\text{thx}}}^{\mathit{max}}/T{V}^{\mathit{max}}$) between full-exhalation and full-inhalation (36) and applied the dynamic BP(t) concept in the expandable piston respiration (EPR) model to predict the mean diaphragm motion (37). The dynamic BP was defined as a function of phase (t):

$$\mathit{\text{BP}}(t)=\frac{\Delta V_{\mathit{\text{thx}}}(t)}{\mathit{\text{TV}}(t)}=\frac{\Delta V_{\mathit{\text{thx}}}(t)}{\Delta V_{\mathit{\text{thx}}}(t)+\Delta V_{\mathit{\text{abd}}}(t)}$$ (1)

$$\mathit{\text{TV}}(t)=\Delta V_{\mathit{\text{torso}}}=\Delta V_{\mathit{\text{thx}}}(t)+\Delta V_{\mathit{\text{abd}}}(t)$$ (2)

The BP-related motion was estimated using our EPR model. The perturbation terms Δy^Pert (AP) and Δz^Pert (SI) were functions of the initial tumor position, BP, TV, and phase (t).

$$\Delta y^{\mathit{\text{Pert}}}(t)=\left(\frac{\Delta V_{\mathit{\text{thx}}}^{\mathit{\text{txt}}}(t)-\Delta V_{\mathit{\text{thx}}}^{\mathit{\text{sim}}}(t)}{{\mathit{\text{TV}}}_{\mathit{\text{ex}}}^{\mathit{\text{sim}}}}\right)•{\overline{H}}_{\mathit{\text{ex}}}^{\mathit{\text{sim}}}+\Delta y(\Delta z^{\mathit{\text{Pert}}}(t),\phi )$$ (3)

$$\Delta z^{\mathit{\text{Pert}}}(t)=(\frac{1-{\mathit{\text{BP}}}^{\mathit{\text{txt}}}(t)}{1-{\mathit{\text{BP}}}^{\mathit{\text{sim}}}(t)}•\frac{{\overline{\mathit{\text{TV}}}}^{\mathit{\text{txt}}}}{{\overline{\mathit{\text{TV}}}}^{\mathit{\text{sim}}}}-1)\times \Delta z^{\mathit{\text{sim}}}(t)$$ (4)

where the superscript “sim” and “txt” stand for simulation and treatment, respectively. These terms describe the motion perturbations (ΔMT) of the RMP model as a function of TV and BP: ΔMT(t) = f[TV^sim(t), BP^sim(t); TV^txt(t), BP^txt(t)], as shown in Eqs. 3 and 4. To avoid BP fluctuation, we used the median static BP = Median(ΔV_thx/TV) when TV was <25% of the maximum tidal volume. ${\overline{H}}_{\mathit{\text{ex}}}^{\mathit{\text{sim}}}$ is the tumor AP position. Δy(Δz^Pert(t), φ) is the result from Δz^Pert(t) motion, due to the curved rib cage (angle φ), which forces the SI displacement to move along the curved chest wall, resulting in an AP motion. Given a curvature of φ ≤ 15°, Δz′ = cosφ · Δz = 0:97 Δz ≈ Δz; thus, the effect is generally negligible in the SI direction. Detailed equation derivation is provided in Appendix E1 (available online at www.redjournal.org).

4DCT data extraction and analysis

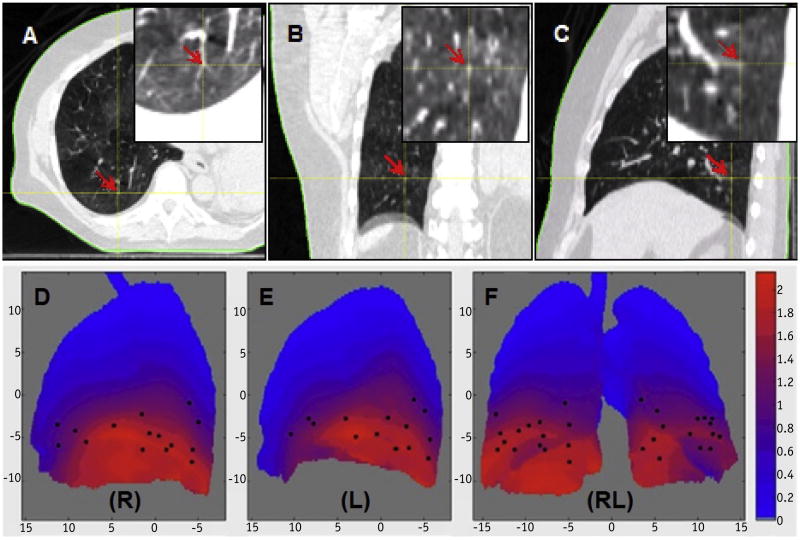
The patient 4DCT images were reconstructed using amplitude binning (42, 43) and processed using an in-house treatment planning system. The bronchial tree was segmented using an adaptive threshold algorithm, and the centerline was thinned to 1-voxel skeleton (44) to determine the bifurcation point using the in-house ABBA program. DIR was performed using full-exhalation CT as the reference, and the displacement vector field was used to generate the motion trajectories of 40 bifurcation points per 4DCT image. The point correspondence between the 2 4DCTs of the same patient was achieved by a rigid registration of first global and then local regions of interest (a 15-mm cubic box containing the bifurcation point and associated bronchial tree image). The selected points were visually verified (Fig. 1). Therefore, for each patient, 40-paired motion trajectories were generated in the middle-inferior lungs, serving as either the starting motion baseline for motion predictions or the ground truth for evaluation of the prediction accuracy.

Fig. 1.

Visual determination and verification of a bifurcation point in axial (A), coronal (B), and sagittal (C) views. The coordinates of the point were tracked through 10 breathing phases. The distribution of 30 bifurcation points (black dots) was detected using the automatic bronchial bifurcation array program (D-F). The points are displayed on a heat map of the lung mean motion (red) and the standard deviation (green) in centimeters for each pixel in the projection image. Note that the points are selected based on the image features and spread in the middle-inferior lungs (right [R] and left [L]).

An in-house 4D clinical multimodal image processing toolbox (41) was developed in MATLAB to facilitate 4DCT image processing and automated calculations of TV, BP, and breathing period. Automatic lung segmentation was performed, and both TV and BP were evaluated, based on Eqs. 1 and 2. The RMP model program took these calculated parameters, smoothed the motion trajectory baseline, evaluated the motion perturbation based on Eqs. 3 and 4, and compared the prediction results with the ground truth. Statistical analysis of the results was performed to demonstrate the accuracy of the RMP model prediction. The 2-tailed Student t test was used to assess the statistical significance between methods.

5D motion model and training

The 5D lung motion model is a function of 5 independent variables, including the initial tumor position P⃗(x₀, y₀, z₀), TV, and airflow (TV′) (31). When 2D motions in the AP (y) and SI (z) directions were considered, ignoring the negligible lateral motion, the tumor motion model relative to its initial position can be expressed as follows:

$$\overrightarrow{\Delta P}(x,y,z,\mathit{\text{TV}},{\mathit{\text{TV}}}^{\prime }){|}_t=\overrightarrow{P}(x,y,z,\mathit{\text{TV}},{\mathit{\text{TV}}}^{\prime }){|}_t-\overrightarrow{P}(x_0,y_0,z_0,{\mathit{\text{TV}}}_0,{\mathit{\text{TV}}}_0^{\prime }){|}_{t=0}=({\alpha }_y\overrightarrow{Y}+{\alpha }_z\overrightarrow{Z})\mathit{\text{TV}}+({\beta }_y\overrightarrow{Y}+{\beta }_z\overrightarrow{Z}){\mathit{\text{TV}}}^{\prime }$$ (5)

where α⃗ (α_y, α_z) and β⃗ (β_y, β_z) are the unit vectors for TV and TV′ and can be expressed as a function of Y⃗ and Z⃗ (unit vectors). The 4 unknown coefficients were estimated by fitting the model as dictated by Eq. 5 to the actual tumor motion trajectory using a linear regression procedure based on Euclidean (L₂) error norm. The 5D model does not consider the BP variable. The TV and TV′ values were extracted from the 4DCT scan and the associated breathing waveforms (36, 37). One 4DCT data set was used for training and the other for prediction.

Results

Bifurcation points and motion trajectories

Figure 1 shows an example of visual verification of a bifurcation point in sagittal, coronal, and transverse slices, and the distribution of 30 points in 1 patient. The trajectories generated by bifurcation point tracking and DIR methods are similar, with a mean vector difference of 1.2 ± 0.9 mm across all 400 points in all phases and patients. Motion artifacts present in 4DCT scans can cause the difference between the 2 methods, and the DIR results are less susceptible to motion artifacts than those of the bifurcation tracking method.

Patient breathing variation between simulation and treatment

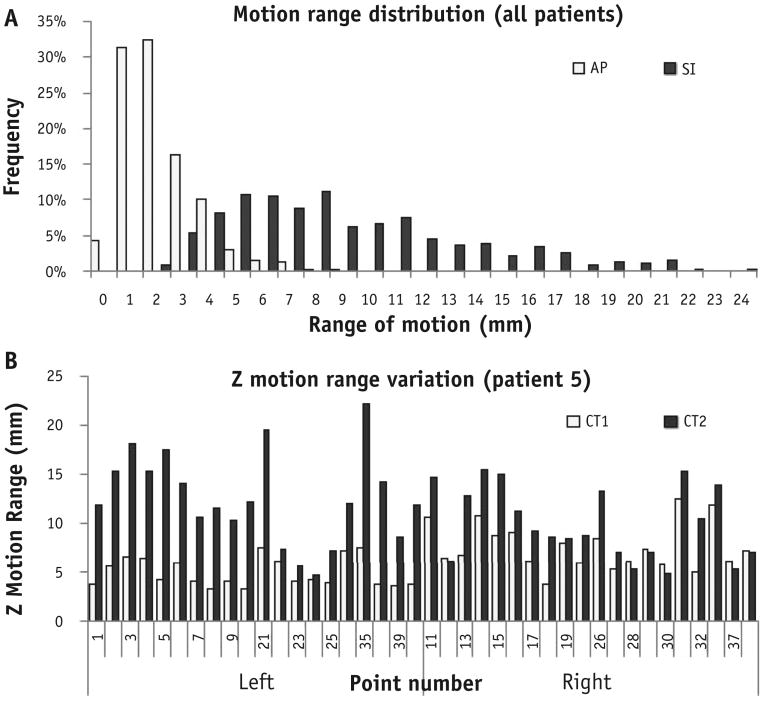
The basic respiratory characterization for the 10 patients, including TV, BP, and breathing period (T), are summarized in Table 1. The variations from CT1 to CT2 were −26% to 61% in TV, −71% to 333% in BP, and −62% to 90% in T (used for airflow calculation for the 5D model). The average range of SI motion was 9.4 ± 4.4 mm, and the AP motion range was far less at 2.7 ±1.4 mm (Fig. 2A). Therefore, the present study focused on SI motion prediction. Figure 2B illustrates the location-dependent range variation of SI motion for 40 bifurcation points tracked in a representative patient between 4DCT1 and 4DCT2.

Table 1. Variations in TV, BP, and T in 4-dimensional computed tomography scans 1 and 2.

	TV (mL)		BP		T (s)*		Relative variation [(X2 – X1)/X1] (%)
Patient number	CT1	CT2	CT1	CT2	CT1	CT2	TV	BP	T
1	587	436	0.06	0.26	8.7	3.3	−26	333	−62
2	297	286	0.49	0.34	3.0	2.9	−4	−31	−3
3	144	170	0.36	0.32	2.1	2.4	18	−11	14
4	328	338	0.24	0.22	2.8	3.0	3	−8	7
5	310	467	0.12	0.19	4.4	4.4	51	58	0
6	328	352	0.14	0.04	2.7	2.5	7	−71	−7
7	369	526	0.03	0.03	4.2	4.4	43	0	5
8	442	618	0.28	0.15	4.4	5.0	40	−46	14
9	215	346	0.18	0.21	2.1	4.0	61	17	90
10	839	1087	0.39	0.26	6.9	6.9	30	−33	0
Range of variation							−26 to 61	−71 to 333	−62 to 90

Abbreviations: BP = breathing pattern; CT1 = first 4-dimensional computed tomography scan; CT2 = second 4-dimensional computed tomography scan; T = period; TV = tidal volume.

^*The averaged period was obtained from a Fourier analysis of patients' breathing waveforms.

Fig. 2.

(A) Plot of motion range distribution in the superoinferior (SI) and anteroposterior (AP) directions of 800 trajectories (40 points for each patient, 2 sets of 4-dimensional computed tomography [4DCT] scans per patient; 10 patients). The mean motion was 9.4 ± 4.4 mm in the SI direction and 2.7 ± 1.4 mm in the AP direction. (B) Illustration of motion range variation between 4DCT1 and 4DCT2 in patient 5 for 40 points in the SI direction. Significant motion variation is shown across points at different anatomic locations.

Prediction from RMP and comparison with 5D model

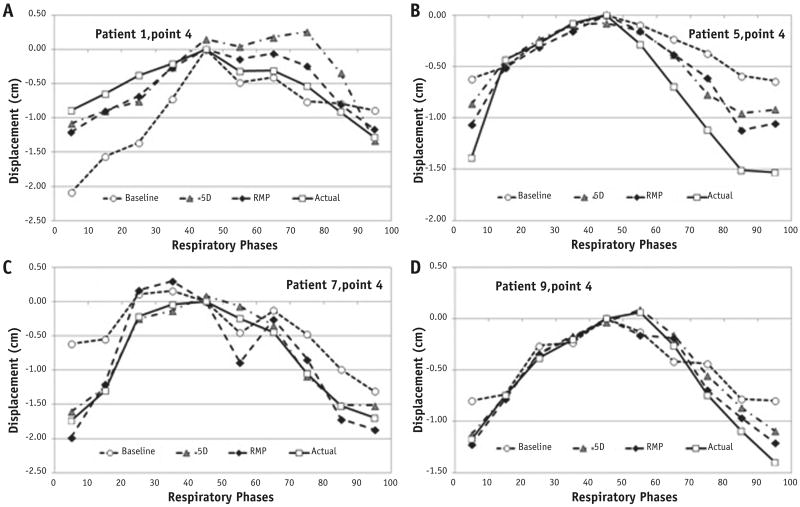
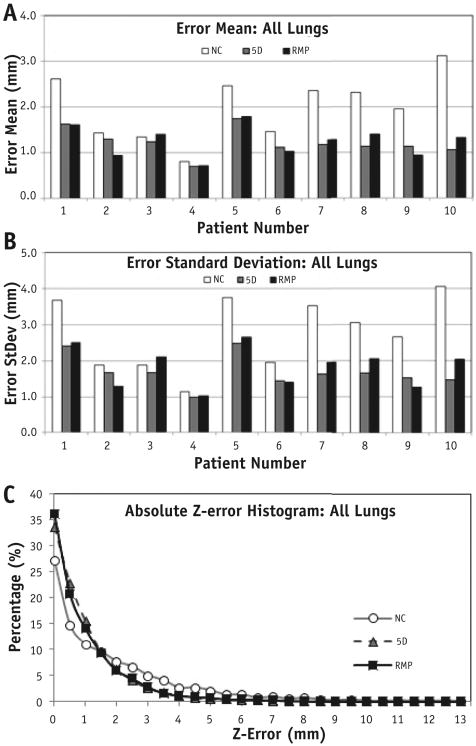
Figure 3 provides 4 typical prediction results where the full-exhalation phase was set as the reference. Figure 4 illustrates the error reductions using the RMP and 5D model predictions from NC errors and absolute error distributions. The mean errors and standard deviations for RMP prediction results between 4DCT1 and 4DCT2 are summarized in Table 2, and the t test showed that the RMP and 5D predictions were similar, significantly better than the NC predictions (P = .002). The reduced mean error (from 2.0 to 1.2 mm) and reduced standard deviation (from 2.8 to 1.8 mm) represent approximate 40% improvements in both measures (Fig. 4 and Table 2). Statistically, the predictions from the RMP and 5D models were similar (P = .72).

Fig. 3.

Illustration of respiratory motion perturbation (diamonds) and 5-dimensional (triangles) predictions from the initial motion (dot line) in 1 4-dimensional computed tomography (4DCT) scan to the actual motion (solid line) in another 4DCT scan in 4 patients (A-D).

Fig. 4.

Consistent error reduction (A, mean; B, standard deviation; and C, absolute error distribution) using respiratory motion perturbation (RMP) model predictions compared with noncorrected (NC) motions and 5-dimensional (5D) model predictions. (C) Distribution of absolute superoinferior (SI) errors of the RMP and 5D model predictions based on 800 trajectories (8000 points). The similarity between the RMP and 5D model predictions are shown, with improvement seen from the NC predictions between 4-dimensional computed tomography scan 1 and 2.

Table 2. Comparison of errors in NC, 5D, and RMP model predictions between 4DCT1 and 4DCT2.

		Prediction error (mm)		t Test P value
Points	Model	Mean	SD	vs NC	vs 5D
All points	NC	2.0	2.8	-	-
	5D	1.2	1.7	.004	-
	RMP	1.2	1.8	.002	.72
Left points	NC	2.1	3.0	-	-
	5D	1.3	1.7	.003	-
	RMP	1.2	1.8	.002	.57
Right points	NC	2.0	2.4	-	-
	5D	1.1	1.5	.004	-
	RMP	1.3	1.7	.013	.09

Abbreviations: BP = breathing pattern; 4DCT1 = first 4-dimensional computed tomography scan; 4DCT2 = second 4-dimensional computed tomography scan; 5D = 5-dimensional; NC = noncorrected; RMP = respiratory motion perturbation.

No significant difference was found between the 5D and RMP models using the Student t test (n = 800).

Discussion

Advantages of the RMP prediction model

Because the RMP model is derived from the physical relationship between lung motion variation (ΔMT) and respiratory conditions (TV and BP), it is capable of adapting to the changes in breathing conditions and, therefore, promises to be adjustable to breathing irregularities during the radiation treatment course. In contrast, most existing respiratory models were built based on pre-treatment data of a patient's breathing behavior, and the model contains fixed coefficients to the breathing behavior associated with the training data set (22, 45), although dynamic update can be performed. Therefore, changes in a patient's breathing behavior during treatment sessions may require model rebuilding (46). The RMP approach circumvents the fundamental limitation to the robustness of a correlation-based model. The 5D model, although it performs best with fresh-data training, provides a reasonable prediction using the 4DCT data and time-dependent internal parameters (TV and TV′) for updates, although the long-term prediction from the 5D model might not be as accurate as the short-term prediction (31). The RMP prediction result is similar to the 5D result and can be improved by introducing an airflow term.

The RMP prediction model requires updates from online respiratory measurements using an OSI-based technique (20, 21), which provides dynamic TV, TV′, and BP in various BPs, including free breathing, belly breathing, and chest breathing. Because the OSI-based technique captures all external torso motion induced by respiration (at 10 Hz), it has promise to be the most comprehensive external respiratory surrogate. In fact, no local external surrogates measure the BP values. By combining the RMP model and OSI measurements, this physics-based approach is potentially of great use in tumor motion prediction during radiation treatment. The RMP model is concise, efficient, and suitable for real-time prediction (the computation involved requires approximately 1 ms).

Compared with the 5D prediction model (31), the current RMP model predicts lung motion with similar accuracy (Fig. 4 and Table 2). Both RMP and 5D models reduced both mean and standard deviation of errors by about 40% compared with uncorrected data. As Eqs. 4 and 5 show, both models account for TV variation (−26% to 61%; Table 1), although the 5D model uses TV′ (T variation −61% to 90%) and the RMP model uses the BP variation (−71% to 333%). However, the RMP model can be further improved with introduction of the airflow and lung elasticity parameters.

The present study focused on motion prediction from different days, because the 2 sets of 4DCT scans were acquired 2 weeks apart. It was thus quite challenging and the prediction errors were greater than those with intra-imaging session prediction (0.75 ± 0.25 mm) as previously reported (31). Motion trajectories and breathing conditions extracted from 4DCT can only represent an average within the period of the 4DCT scan. Therefore, the results shown in the present study reflect day-to-day breathing irregularities, not intrasession irregularities.

Definition of BP and assumptions for RMP model

The quantitative definition of the BP concept (Eq. 1) is important to predict internal organ motion (36, 37). Physiologically, the BP usually refers to chest and belly breathing, which originate from 2 different driving forces: the intercostal muscles and the diaphragm. Therefore, the definition of BP quantifies the thoracic contribution volumetrically, and 1 – BP is a measure of the abdominal involvement. Physically, the definition of BP separates 2 orthogonal motions by quantifying the volumetric AP and SI motions. Thus, the BP definition is critical to RMP model prediction, because it reflects a major physiologic variation of the respiratory process.

The RMP model is established based on several assumptions that closely approximate the complex patient anatomy and respiratory motion, including the independence of SI and AP motions and the nondelayed motion response to TV and BP changes. The assumption of SI and AP motion independence was tested for its validity in predicting the mean diaphragm motion using an EPR model in a previous study (37). In that study, 11 of 14 patients followed this assumption and 3 patients had a conical rib cage at the diaphragm level. However, the volumetric difference was merely about 3%, which can be corrected in z-motion prediction by measuring the area within the rib cage across the motion range of the diaphragm. Owing to curvature of the rib cage, AP motion can depend on SI motion, and an anatomic correction term is needed (Eq. 3).

The implicit assumption of a negligible time difference between external motion and internal motion for the present model might only work for about 80% to 90% of patient populations, because 10% to 20% of patients were found to have phase shifts (≥0.5 second, or 1 phase) (47). Introducing the airflow (TV′) parameter into the RMP model is currently under investigation to account for the elasticity of the lung tissue, the primary cause of the phase shift.

Future directions

It is encouraging that the current RMP model, solely based on the physical relationship, is able to match the results of the established 5D model. The spirometric variation range is −26% to 61% in TV, −71% to 333% in BP, and −62% to 90% in breathing period (T, used for estimating airflow). With these large breathing variations, only 1 patient prediction will not reduce the NC error (already small); however, for the rest (9 of 10), the RMP reduces the NC error substantially or mildly (Fig. 4). In practice, if a base tumor motion trajectory is acquired at setup, smaller variations occurring the same day would be expected, and the prediction should be greatly improved (31) (Fig. 3D).

In addition, the inconsistency in the 2 sets of ground truths obtained from DIR and the bifurcation calculation mostly results from the binning artifacts, 2-mm slice thickness, and the intrinsic uncertainties of these 2 methods. Furthermore, using 2 sets of 4DCT images to evaluate the validity of the RMP model might only assess the long-term breathing variations, because the 2 4DCT scans were acquired in a 2-week interval. We suggest a further evaluation of the RMP model using dynamic magnetic resonance imaging (MRI) to serve the ground truth (48-50).

Because our RMP model is derived from a physical relationship (volume conservation and distribution) and other physical relationships are present that were not used, including biomechanics. Major efforts will be made to expand the RMP model to account for lung tissue elasticity. Although the complexity and heterogeneity of lung tissue portend challenges to deriving a physical model, we have demonstrated a promising physical approach to circumvent the breathing irregularity problem. We are currently pursuing improvements by accounting for additional physical parameters and further validation of the RMP model using dynamic MRI scanning. With further validation using time-resolved 4DMRI scanning, the potential of this RMP modeling approach with real-time volumetric updates would be to establish reliable and accurate respiratory gating or even tumor tracking in the presence of inter- and intrafraction breathing irregularities.

In summary, a novel RMP model has been developed and validated using 2 4DCT images. In practice, the RMP model can be integrated with the OSI-based technique to provide dynamic motion prediction in the presence of breathing irregularities. The clinical implication of this development is potentially to improve the accuracy and reliability of respiratory gating or even motion tracking in radiation therapy delivery, and therefore a tumor margin reduction can be expected in treatment planning.

Conclusions

The present study has demonstrated the feasibility of a novel physics-based, RMP model that can predict tumor motion between 2 different 4DCT scanning data sets. The strength of the RMP model is that it can adapt to breathing irregularities and overcome the limitation of correlation-based models when a patient's breathing behavior alters substantially. Investigations are ongoing for further improvement and validation of the RMP model.

Summary.

A novel physics law—based respiratory motion perturbation model was developed to predict tumor motion during breathing irregularities. This adaptive model predicts motion variations using tidal volume (TV) and breathing pattern (BP) updates and was validated using 2 4-dimensional computed tomography (4DCT) sets from 10 patients. Forty motion trajectories of 40 bifurcation points per 4DCT were tracked, and 800 4DCT1 ↔ 4DCT2 predictions were evaluated with known ground truth. An average accuracy (1.2 ± 1.8 mm) was achieved, similar to an established model and significantly improved from raw motion differences.