Reinforced Angle-based Multicategory Support Vector Machines

Abstract

The Support Vector Machine (SVM) is a very popular classification tool with many successful applications. It was originally designed for binary problems with desirable theoretical properties. Although there exist various Multicategory SVM (MSVM) extensions in the literature, some challenges remain. In particular, most existing MSVMs make use of k classification functions for a k-class problem, and the corresponding optimization problems are typically handled by existing quadratic programming solvers. In this paper, we propose a new group of MSVMs, namely the Reinforced Angle-based MSVMs (RAMSVMs), using an angle-based prediction rule with k − 1 functions directly. We prove that RAMSVMs can enjoy Fisher consistency. Moreover, we show that the RAMSVM can be implemented using the very efficient coordinate descent algorithm on its dual problem. Numerical experiments demonstrate that our method is highly competitive in terms of computational speed, as well as classification prediction performance. Supplemental materials for the article are available online.

1 Introduction

Classification is a standard supervised learning technique to handle problems with categorical response variables. Among various existing classifiers, the Support Vector Machine (SVM, Boser et al., 1992; Cortes and Vapnik, 1995) is a popular method originated from the machine learning community. It is a typical example of large-margin classifiers, that use a single classification function for prediction in binary problems. In particular, the binary SVM searches for a hyperplane in the feature space that maximally separates the two classes. It has been shown to be very useful and has achieved excellent performance on many applications in various disciplines. The corresponding theoretical properties, such as Fisher consistency and asymptotic convergence rates, are also well established. In particular, a classifier being Fisher consistent means that it can achieve the optimal prediction performance asymptotically, if the underlying functional space is rich enough. More details about Fisher consistency will be provided in Section 3. Cristianini and Shawe-Taylor (2000) and Hastie et al. (2009), among others, provide comprehensive reviews for existing classification methods.

In practice, it is prevalent to have more than two classes in the data. Despite the success on binary classification, it remains challenging to adapt SVMs to multicategory classification problems. To handle a multicategory problem with k classes using SVMs, there are two common approaches in the literature. The first approach is to train a sequence of binary SVMs and combine the results for multicategory classification. Examples include one-versus-one and one-versus-rest methods (Hastie and Tibshirani, 1998; Allwein et al., 2001). Although this approach is simple in concept and implementation, it has certain drawbacks. For example, the one-versus-one method can have a tie-in-vote problem, and the one-versus-rest method can suffer from inconsistency when there is no dominating class (Lee et al., 2004; Liu, 2007). The second approach is to consider all k classes in one optimization problem simultaneously. The common method is to use k classification functions to represent the k classes in the corresponding optimization, with a prediction rule based on which classification function is the maximum. Many existing simultaneous Multicategory SVM (MSVM) classifiers have been proposed in this framework. See, for example, Vapnik (1998), Weston and Watkins (1999), Crammer and Singer (2001), Lee et al. (2004), Liu and Shen (2006), Liu and Yuan (2011), and Guermeur and Monfrini (2011). In this paper, we focus our discussion on simultaneous MSVM methods. Among these MSVMs, Vapnik (1998), Weston and Watkins (1999), Crammer and Singer (2001) are not always Fisher consistent, whereas the MSVM proposed by Lee et al. (2004) is. Recently, Liu and Yuan (2011) proposed a new family of Fisher consistent MSVMs, namely, the Reinforced MSVMs (RMSVMs), which includes the method in Lee et al. (2004) as a special case. In particular, RMSVM uses a convex combination of the loss in Lee et al. (2004) and the naive SVM hinge loss to form a new group of Fisher consistent hinge loss functions for multicategory problems. To avoid confusion, we would like to point out that the reinforced MSVM in this paper refers to the MSVM using a convex combination of loss functions as in Liu and Yuan (2011), and is different from the reinforcement learning in the machine learning literature (Kaelbling et al., 1996; Barto, 1998).

For binary SVMs, one uses a single function for classification. Analogously, for a k-class multicategory problem, it should suffice to use k − 1 classification functions. Therefore, using k classification functions in the regular MSVMs can be redundant. To circumvent this difficulty, the existing MSVMs use different optimization formulations, which can be grouped into two main categories. Classifiers in the first group impose an explicit sum-to-zero constraint on the k classification functions, in order to reduce the function space and to ensure some theoretical properties such as Fisher consistency. Examples in this group include the MSVMs in Lee et al. (2004), Liu and Yuan (2011), and Guermeur and Monfrini (2011). For the second group, the corresponding optimization problem is based on pairwise differences among the k classification functions. One can verify that without an explicit sum-to-zero constraint, the obtained classification functions sum to zero automatically with an appropriate regularization term (Guermeur, 2012; Zhang and Liu, 2013). This can be regarded as an alternative way to reduce k functions to k − 1 by an implicit sum-to-zero property. The MSVM methods in Vapnik (1998), Weston and Watkins (1999), Crammer and Singer (2001), and Liu and Shen (2006) are examples in this group. Despite differences in the optimization formulation, the corresponding dual problems of all the aforementioned MSVMs involve linear equality constraints, and are typically solved via existing Quadratic Programming (QP) solvers. See more discussion in Section 4.4.

To facilitate comparison and implementation, Guermeur (2012) proposed a unified family of MSVMs, which includes the methods in Vapnik (1998), Weston and Watkins (1999), Crammer and Singer (2001), Lee et al. (2004), and Guermeur and Monfrini (2011) as special cases. Guermeur (2012) then studied the corresponding optimization problems of these MSVMs under this unified framework, and proposed to solve the dual problems using QP solvers. A corresponding powerful package “MSVMpack” was provided by aLauer and Guermeur (2011). For Liu and Yuan (2011), the authors also proposed to solve the dual problem by QP solvers. See Section 4.4 for more details.

Recently, Zhang and Liu (2014) proposed the multicategory angle-based large-margin classification framework, which uses only k − 1 classification functions, and implicitly transfers the sum-to-zero constraint onto the newly defined functional margins. As a result, the computational speed of the angle-based classifiers can be faster than the regular methods with the explicit or implicit sum-to-zero constraint. In particular, the angle-based classifiers consider a centered simplex with k vertices in a k − 1 dimensional space. Each vertex represents one class. The classification function naturally defines k angles with respect to the k vertex vectors, and the corresponding prediction rule is based on which angle is the smallest. Details of the least-angle prediction rule can be found in Section 2. Zhang and Liu (2014) introduced a new set of functional margins in the angle-based framework, and showed that the new functional margins sum to zero without an explicit constraint. Consequently, the angle-based classifiers can be more efficient than the regular multicategory classification methods.

Although the angle-based classification does not require the sum-to-zero constraint, the direct generalization of SVM in the angle-based classification structure is not Fisher consistent (Zhang and Liu, 2014). Therefore, the naive angle-based MSVM can be asymptotically suboptimal, and it is desirable to develop an MSVM classifier in the angle-based framework that enjoys Fisher consistency. To this end, we propose the Reinforced Angle-based Multicategory Support Vector Machine (RAMSVM). The loss function we employ for RAMSVM is a convex combination of two MSVM losses, and in Section 5 we show that such combination can lead to a stable classifier whose performance is often close to the optimum. In particular, we show through numerical examples that our proposed RAMSVM tends to have stable and competitive performance for many different cases. Our contribution in this paper is two fold. First, we modify existing MSVM losses in the angle-based classification framework, and introduce our RAMSVM loss family as a convex combination. We show that with a proper choice of the convex combination parameter, the new RAMSVM classifier enjoys Fisher consistency. Second, we show that the corresponding optimization can be reduced to minimizing a quadratic objective function with box constraints only. This can then be solved using the very efficient coordinate descent method (Fan et al., 2008; Friedman et al., 2010). We show in Section 5 that our new RAMSVM can enjoy a very fast computational speed. Moreover, RAMSVM is also highly competitive in terms of classification accuracy.

The rest of this article is organized as follows. In Section 2, we briefly review some existing MSVM methods, and introduce our RAMSVM classifier. In Section 3, we study Fisher consistency of the RAMSVM family. In Section 4, we develop the coordinate descent algorithm for solving the RAMSVM optimization problem. We also compare the dual problem of RAMSVM with those of the existing MSVM approaches. Numerical studies with simulated and real data sets are presented in Section 5. Some discussions are provided in Section 6. All proofs are collected in the appendix.

2 Methodology

For a multicategory classification problem with k classes, let (x₁, y₁), … , (x_n, y_n) be the observed training data points. Here x_i denotes a p-dimensional predictor vector, and y_i ∈ {1, …, k} is the corresponding label. The regular simultaneous multicategory large-margin classifiers use a k-dimensional classification function $\mathbf{f}\left(x\right)={(f_1\left(x\right),\cdots ,f_k\left(x\right))}^T$, and the prediction rule is $\widehat{y}\left(x\right)={\mathrm{argmax}}_{j\in \{1,\cdots ,k\}}{f}_j\left(x\right)$. The corresponding optimization can typically be written as

$$\underset{f\in F}{\min }\frac{1}{n}=\sum _{i=1}^{n}V(\mathbf{f}\left({\mathbf{x}}_i\right),y_i)+\frac{1}{2}\lambda J\left(\mathbf{f}\right),$$ (1)

where F denotes the function class, J (·) is the penalty term that controls the complexity of F to prevent overfitting, and λ is a tuning parameter that balances the loss and penalty terms. Here V (f (x), y) measures the loss of using f (x) as the classification function for (x, y). Different loss functions correspond to different classifiers. In the simultaneous MSVM literature, the following loss functions are commonly used as extensions from binary SVMs to MSVMs:

MSVM1 (Naive hinge loss) V (f (x), y) = [1 − f_y (x)]₊;

MSVM2 (Vapnik, 1998; Weston and Watkins, 1999) $V(\mathbf{f}\left(x\right),y)={[1-f_y\left(x\right)]}_{+}$;

MSVM3 (Crammer and Singer, 2001; Liu and Shen, 2006) $V(\mathbf{f}\left(x\right),y)={\sum }_{j\ne y}{[1-(f_y\left(x\right)-f_j\left(x\right))]}_{+}$;

MSVM4 (Lee et al., 2004) $V(\mathbf{f}\left(x\right),y)={\sum }_{j\ne y}{[1-{\min }_j(f_y\left(x\right)-f_j\left(x\right))]}_{+}$;

MSVM5 (Liu and Yuan, 2011) $V(\mathbf{f}\left(x\right),y)={\sum }_{j\ne y}{[1+f_j\left(x\right)]}_{+}$,

where [u]₊ = max(u, 0) and γ ∈ [0, 1] in MSVM5 is the convex combination parameter. As discussed in Section 1, MSVMs 1, 4 and 5 employ an explicit sum-to-zero constraint ${\sum }_{j=1}^k{f}_j=0$. Besides MSVMs 2-5, the MSVM method in Guermeur and Monfrini (2011) (MSVM6) cannot be formulated in the framework of (1). In particular, the primal optimization problem of MSVM6 can be written as

$$\underset{f,\xi }{\min }(\mid \mid M\xi \mid {\mid }_2^2+\lambda \mid \mid P_H\left(\mathbf{f}\right)\mid {\mid }_H^2),$$

$$\mathrm{s}.\mathrm{t}.\{\begin{array}{c}-f_j\left(x_i\right)\ge \frac{1}{k-1}-{\xi }_{ij}(i=1,\cdots ,n,j\ne y_i),\hfill \\ \sum _{j=1}^k{f}_j=0.\hfill \end{array}\phantom{\}}$$ (2)

Here M is a matrix of rank (k − 1)n, ξ is a vector of length (k − 1)n with its (in + j)^th element ξ_ij, the slack variable corresponding to the i^th subject and j^th class with j /= y_i, and ${\mid \mid P_H\left(\mathbf{f}\right)\mid \mid }_H^2$ is the squared norm of P_H(f) in a reproducing kernel Hilbert space H. Notice that each element of f involves an intercept, and P_H(f ) represents the projection of f onto the kernel space H. See Guermeur and Monfrini (2011) for details. Notice that Guermeur (2012) proposed a generic model of MSVMs, which cover MSVMs 2-4 and 6 as special cases. We discuss the corresponding dual problems of MSVMs 2-6 in Secion 4.4 and the appendix.

Although binary SVM is known to be Fisher consistent, MSVMs 1-3 are not. To overcome this challenge, Lee et al. (2004) proposed MSVM4, which can be shown to be Fisher consistent. Furthermore, Liu and Yuan (2011) proposed the Reinforced MSVM (RMSVM, MSVM5) method, which uses a convex combination of the naive hinge loss and the loss in Lee et al. (2004) as a new class of loss functions. Note that with γ = 0, RMSVM includes the MSVM of Lee et al. (2004) as a special case. Liu and Yuan (2011) showed that RMSVM is Fisher consistent when γ ∈ [0, 0.5].

As mentioned in Section 1, it can be inefficient to train a multicategory classifier with k classification functions, which are reduced to k − 1 by explicit or implicit sum-to-zero constraints. To overcome this difficulty, Zhang and Liu (2014) proposed the multicategory angle-based large-margin classification technique. The details of the angle-based classification are as follows. Consider a centered simplex with k vertices in a (k − 1)-dimensional space. Let W be a collection of vectors {W_j ; j = 1, … , k}, where

$${\mathbf{W}}_j=\{\begin{array}{cc}{(k-1)}^{-1∕2}1\hfill & \mathrm{if}j=1,\hfill \\ -\frac{1+\sqrt{k}}{{(k-1)}^{3∕2}}1+\sqrt{\frac{k}{k-1}{e}_{j-1}},\hfill & \mathrm{if}2\le j\le k.\hfill \end{array}\phantom{\}}$$

Here e_j ∈ ℝ^k−1 is a vector of 0’s except its j^th element is 1, and 1 ∈ ℝ^k−1 is a vector of 1. It can be verified that each vector W_j has Euclidean norm 1, and the angles between any pair (W_i, W_j ) are equal. Consequently, the vectors in W form a k-vertex simplex. For an observation x, we map it into ℝ^k−1 by the classification function vector $\mathbf{f}\left(x\right)=(f_1\left(x\right),\cdots ,f_{k-1}\left(x\right))\in {\mathbb{ℝ}}^{k-1}$. Note that f (x) defines k angles with respect to W_j (j = 1, …, k), namely, ∠(f (x), W_j) (j = 1, …, k). The label prediction for x is then based on which angle is the smallest. In other words, $\widehat{y}\left(x\right)={\mathrm{argmin}}_{j\in \{1,\cdots ,k\}}\angle (\mathbf{f}\left(x\right),{\mathbf{W}}_j)$. One can verify that the least angle prediction rule is equivalent to $\widehat{y}\left(x\right)={\mathrm{argmax}}_{j\in \{1,\cdots ,k\}}(\langle {\mathbf{W}}_j,\mathbf{f}\left(x\right)\rangle )$, where $\langle \cdot ,\cdot \rangle$ denotes the dot product. With this prediction rule, Zhang and Liu (2014) proposed the following optimization for the angle-based classification

$$\underset{f\in F}{min}\frac{1}{n}\sum _{i=1}^{n}l\left(\langle \mathbf{f}\left(x_i\right),{\mathbf{W}}_{yi}\rangle \right)+\frac{\lambda }{2}J\left(\mathbf{f}\right),$$ (3)

where £(·) is any binary large-margin classification loss function. Here the dot products 〈f (x), W_j) (j = 1, … , k〉 can be regarded as new functional margins of (x, y). Note that Lange and Wu (2008), Wu and Lange (2010) and Wu and Wu (2012) also used the simplex structure for multicategory classification with a different classification rule and the E-insensitive loss, and Hill and Doucet (2007) and Saberian and Vasconcelos (2011) studied MSVM and multicategory boosting in the simplex based structure as well.

The angle-based classification framework uses k − 1 classification functions directly, and it can be computed more efficiently. However, when using the regular hinge loss £(u) = [1 − u]₊ in (3), the corresponding angle-based SVM is not Fisher consistent. Therefore, it is desirable to have a generalization of the binary SVM classifier in the angle-based classification framework which enjoys Fisher consistency. Motivated by the convex combination idea in Liu and Yuan (2011), we propose the following Reinforced Angle-based Multicategory SVM (RAMSVM) classifier with the following optimization

$$\underset{f\in F}{\min }\frac{1}{n}\sum _{i=1}^n\left\{(1-\gamma )\sum _{j\ne y_i}{[1+\langle \mathbf{f}\left(x_i\right),{\mathbf{W}}_j\rangle ]}_{+}+\gamma {[(k-1)-\langle \mathbf{f}\left(x_i\right),{\mathbf{W}}_{y_i}\rangle ]}_{+}\right\}+\frac{\lambda }{2}J\left(\mathbf{f}\right),$$ (4)

where γ ∈ [0, 1] is the convex combination parameter. Note that the first part in the loss term of (4) can be regarded as a modified MSVM loss of Lee et al. (2004) in the angle-based classification framework. For many other existing MSVMs, we can generalize them into the angle-based classification framework accordingly. For example, the naive angle-based MSVM method studied in Zhang and Liu (2014) can be regarded as an extension of MSVM1 in the angle-based classification framework.

The motivation of using such a combination of loss functions in (4) is based on the prediction rule of the angle-based classification. Since the least angle prediction rule $\widehat{y}\left(x\right)={\mathrm{argmin}}_{j\in \{1,\cdots ,k\}}\angle (\mathbf{f}\left(x\right),{\mathbf{W}}_j)$ is equivalent to $\widehat{y}\left(x\right)={\mathrm{argmax}}_{j\in \{1,\cdots ,k\}}(\langle {\mathbf{W}}_j,\mathbf{f}\left(x\right)\rangle )$, we need to have (f (x), W_y ) to be the maximum among all the k dot products (f (x), W_j) (j = 1, … , k). To that end, the second part in the loss term of (4) encourages (f (x), W_y) to be large. On the other hand, observe that ${\sum }_{j=1}^k\langle \mathbf{f}\left(x\right),{\mathbf{W}}_j\rangle =0$ for all x, which means that the angle-based classification framework transfers the explicit sum-to-zero constraint onto the dot products. Hence, as the first part in the loss term of (4) encourages $\langle \mathbf{f}\left(x\right),{\mathbf{W}}_j\rangle (j\ne y)$ to be small, it implicitly encourages $\langle \mathbf{f}\left(x\right),{\mathbf{W}}_j\rangle$ to be large. As we will see in Section 5, encouraging $\langle \mathbf{f}\left(x\right),{\mathbf{W}}_j\rangle$ to be large explicitly and implicitly has their advantages respectively, and combining the two loss terms yields a classifier that is consistent, stable and highly competitive in accuracy.

Since most existing MSVMs can be cast into QP problems with linear constraints, they are typically implemented using existing QP solvers. For RAMSVM, we show in Section 4 that its dual problem is a QP with box constraints only, hence can be solved using the very efficient coordinate descent method. Compared to existing MSVM implementations using QP solvers, our RAMSVM can often enjoy a faster computational speed. We demonstrate the computational advantage of RAMSVM using numerical examples in Section 5.

In the next section, we introduce the details of Fisher consistency, and show that RAMSVM is Fisher consistent when γ ∈ [0, 1/2].

3 Fisher Consistency

For a classification method, Fisher consistency implies that the classifier can achieve the best classification performance asymptotically, when the underlying functional space is rich enough. In other words, under some conditions, the classifier can yield the Bayes classification rule with infinitely many training data points. In the literature, Lin (2004) explored the Fisher consistency of binary margin based classifiers, and a systematic study on Fisher consistency of regular multicategory large margin classification methods using k functions was provided by Zhang et al. (2014).

To introduce Fisher consistency, we need some extra notation. Let P_j (x) = Pr(Y = j|X = x) (j = 1, …, k) be the class conditional probabilities. For a given x, one can verify that $y^{\ast }\left(x\right)={\mathrm{argmax}}_{j\in \{1,\cdots ,k\}}{P}_j\left(x\right)$ attains the smallest expected classification error rate

$$Pr(y^{\ast }\left(x\right)\ne Y\mid x)$$ (5)

which can be regarded as a 0 − 1 loss function $E(I(y^{\ast }\ne Y)\mid x)$. Here one often refers to $y^{\ast }\left(x\right)={\mathrm{argmax}}_{j\in \{1,\cdots ,k\}}{P}_j\left(x\right)$ as the Bayes classifier. However, in practice, because the indicator function I(·) is discontinuous, the empirical minimizer of (5) is hard to find. To overcome this difficulty, in the large-margin classification literature, one can employ different surrogate loss functions, which correspond to different classification methods. Fisher consistency requires that prediction based on the conditional minimizer of a surrogate loss function is identical to $y^{\ast }\left(x\right)={\mathrm{argmax}}_{j\in \{1,\cdots ,k\}}{P}_j\left(x\right)$. In particular, for angle-based classifiers, Fisher consistency requires that ${\mathrm{argmax}}_{j\in \{1,\cdots ,k\}}\langle {\mathbf{f}}^{\ast }\left(x\right),{\mathbf{W}}_j\rangle ={\mathrm{argmax}}_{j\in \{1,\cdots ,k\}}{P}_j\left(x\right)$, and when $y^{\ast }\left(x\right)={\mathrm{argmax}}_{j\in \{1,\cdots ,k\}}{P}_j\left(x\right)$ is unique, so is ${\mathrm{argmax}}_{j\in \{1,\cdots ,k\}}\langle {\mathbf{f}}^{\ast }\left(x\right),{\mathbf{W}}_j\rangle$. Here f ^∗(x) is the minimizer of the conditional loss E[V (f (X), Y)|X = x]. In other words, Fisher consistency ensures that, if one uses f ^∗ as the classification function, then the predicted class has the largest class conditional probability, hence the corresponding error rate is minimized. For the RAMSVM classifier (4), we study its Fisher consistency in the following theorem.

Theorem 1

For multicategory classification problems with k > 2, the RAMSVM loss function (4) is Fisher consistent when γ ∈ [0, 0.5], and is not Fisher consistent when γ ∈ (0.5, 1].

From Theorem 1, we can conclude that the proposed RAMSVM provides a large family of consistent MSVM classifiers with γ ∈ [0, 1/2]. For γ > 1/2, the Fisher consistency cannot be guaranteed. In Section 5, we study the effect of different γ on the classification accuracy. Interestingly, we observed that the Fisher consistent RAMSVM with γ = 1/2 can provide a stable classifier with competitive classification accuracy. In particular, the numerical results show that RAMSVM with γ = 0 or γ = 1 can be suboptimal in certain cases, whereas γ = 1/2 gives a stable classifier whose performance is close to optimal in many situations. This demonstrates the advantage of the convex combination of MSVM loss functions in the angle-based classification structure.

In the MSVM literature, despite the fact that MSVMs 1-3 have shown to deliver reasonable performance for many problems with small or moderate sample sizes, they are not always Fisher consistent. An inconsistent classifier can yield suboptimal prediction results for certain problems. In contrast, the proposed RAMSVM is stable and competitive for finite sample applications, efficient for computation, and Fisher consistent.

In the next section, we develop an efficient algorithm to solve (4). In particular, we show that RAMSVM can be solved using the coordinate descent method, and within each step of the coordinate-wise optimization procedure, the update value can be calculated explicitly. This greatly boosts the computational speed.

4 Algorithm

In this section, we show how to solve the optimization problem (4). We demonstrate that with the intercepts penalized in linear learning (Fan et al., 2008) or kernel learning, RAMSVM can be solved using the coordinate descent method (Friedman et al., 2010) and consequently enjoys a fast computational speed. First, we focus on linear learning with the commonly used L₂ penalty. Then we develop the algorithm for kernel learning and weighted learning problems. Lastly, we discuss the difference of the dual problems among RAMSVM and the existing MSVM methods.

4.1 Linear Learning

For linear learning, we assume f_q (x) = x^Tβ_q (q = 1, … , k−1), where β_q (q = 1, …, k−1) are the parameters of interest. The penalty term J (f ) in (4) can be written as $J={\sum }_{q=1}^{k-1}{\beta }_q^T{\beta }_q$. Note that we include the intercepts in x to simplify notation. As a result, the obtained function margins would be slightly different from those margins obtained without regularization on the intercepts. In particular, consider the original space X and the augmented space $X^{\prime }=\{{(1,x^T)}^T:x\in X\}$. The original binary SVMs aim to maximize the smallest margins within X. On the other hand, if the intercept is penalized, one can verify that it is equivalent to maximizing the smallest margins within the augmented space X^′. However, the difference between these two types of margins is often negligible in binary problems (Fan et al., 2008). For MSVMs, the two types of function margins (i.e., with or without penalty on the intercepts) also differ slightly. Our numerical experience suggests that including the intercepts in the penalty term can still yield good classification performance.

We solve (4) in its dual form. Using new slack variables ξ_i,j (i = 1, … , n, j = 1, … , k), (4) with linear learning can be written as

$$\begin{array}{cc}\hfill & \underset{{\beta }_q,{\xi }_{i,j}}{\min }\frac{n\lambda }{2}\sum _{q=1}^{k-1}{\beta }_q^T{\beta }_q+\sum _{i=1}^n[\gamma {\xi }_{i,y_i}+(1-\gamma )\sum _{j\ne y_i}{\xi }_{i,j}],\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.{\xi }_{i,j}\ge 0(i=1),\cdots ,n,j=1,\cdots ,k),\hfill \\ \hfill & {\xi }_{i,y_i}+\langle \mathbf{f}\left(x_i\right),{{\mathbf{W}}_y}_i\rangle -(k-1)\ge 0(i=1,\cdots ,n),\hfill \\ \hfill & {\xi }_{i,j}+\langle \mathbf{f}\left(x_i\right),{\mathbf{W}}_j\rangle -1\ge (i=1,\cdots ,n,j\ne y_i).\hfill \end{array}$$

Define the corresponding Lagrangian function L as

$$\begin{array}{cc}\hfill & L=\frac{n\lambda }{2}\sum _{q=1}^{k-1}{\beta }_q^T{\beta }_q+\sum _{i=1}^n\left[\gamma {\xi }_{i,y_i}\right]+(1-\gamma )\sum _{i\ne y_i}^{{\xi }_{i,j}}\hfill \\ \hfill & -\sum _{i=1}^n{\alpha }_{i,y_i}[{\xi }_i,y_i+\langle \mathbf{f}\left(x_i\right),{\mathbf{W}}_{y_i}\rangle -(k-1)]-\sum _{i=1}^n\sum _{j\ne y_i}{\alpha }_{i,j}[{\xi }_{i,j}-\langle \mathbf{f}\left(x_i\right),{\mathbf{W}}_j\rangle -1],\hfill \end{array}$$

where α_i,j and τ_i,j (i = 1, … , n, j = 1, … , k) are the Lagrangian multipliers. One can verify that L can be rewritten as

$$\begin{array}{cc}\hfill & L=\frac{n\lambda }{2}\sum _{q=1}^{k-1}{\beta }_q^T{\beta }_q+\sum _{i=1}^n\sum _{j=1}^k[A_{i,j}-{\tau }_{i,j}-{\alpha }_{i,j}]{\xi }_{i,j}+\sum _{i=1}^n{\alpha }_{i,y_i}(k-1)+\sum _{i=1}^n\sum _{j\ne y_i}{\alpha }_{i,j}\hfill \\ \hfill & -\sum _{i=1}^n{\alpha }_{i,y_i}\langle \mathbf{f}\left(x_i\right),{\mathbf{W}}_{y_i}\rangle +\sum _{i=1}^n\sum _{j\ne y_i}{\alpha }_{i,j}\langle \mathbf{f}\left(x_i\right),{\mathbf{W}}_j\rangle ,\hfill \end{array}$$

where A_i,j = [γI(j = y_i) + (1 − γ)I(j /= y_i)].

After taking partial derivative of L with respect to β_q (q = 1, … , k − 1) and ξ_i,j (i = 1, … , n, j = 1, … , k), we have

$$\frac{\partial L}{\partial {\xi }_{i,j}}=A_{i,j}-{\tau }_{i,j}-{\alpha }_{i,j}=0(i=1,\cdots ,n,j=1,\cdots ,k),$$

$$\frac{\partial L}{\partial {\beta }_q}=n\lambda {\beta }_q-\sum _{i=1}^n{\alpha }_{i,y_i}{\mathbf{W}}_{y_i,q}{x}_i+\sum _{i=1}^n\sum _{j\ne y_i}{\alpha }_{i,j}{\mathbf{W}}_{j,q}{x}_i=0(q=1,\cdots ,k-1),$$

where W_j,q represents the q^th element of W_j . Hence

$${\beta }_q=\frac{1}{n\lambda }[\sum _{i=1}^n{\alpha }_{i,y_i}{\mathbf{W}}_{y_i,q}{x}_i-\sum _{i=1}^n\sum _{j\ne y_i}{\alpha }_{i,j}{\mathbf{W}}_{j,q}{x}_i].$$ (6)

Plug (6) in L, and one can obtain that, after simplification,

$$L=-\frac{n\lambda }{2}\sum _{q=1}^{k-1}{\beta }_q^T{\beta }_q+\sum _{i=1}^n{\alpha }_{i,y_i}(k-1)+\sum _{i=1}^n\sum _{j\ne y_i}{\alpha }_{i,j},$$ (7)

where β_q is given in (6). Because maximizing L with respect to α_i,j is equivalent to minimizing the negative of L, the dual form of (4) can be expressed as

$$\begin{array}{cc}\hfill & \underset{{\alpha }_{i,j}(i=1,\cdots ,n,j=1,\cdots ,k)}{\min }\frac{1}{2n\lambda }\sum _{q=1}^{k-1}{[\sum _{i=1}^n{\alpha }_{i,y_i}{\mathbf{W}}_{y_i,q}{x}_i-\sum _{i=1}^n\sum _{j\ne y_i}{\alpha }_{i,j}{\mathbf{W}}_{j,q}{x}_i]}^T\hfill \\ \hfill & [\sum _{i=1}^n{\alpha }_{i,y_i}{\mathbf{W}}_{y_i,q}{x}_i-\sum _{i=1}^n\sum _{j\ne y_i}{\alpha }_{i,j}{\mathbf{W}}_{j,q}{x}_i]\hfill \\ \hfill & -\sum _{i=1}^n{\alpha }_{i,y_i}(k-1)-\sum _{i=1}^n\sum _{j\ne y_i}{\alpha }_{i,j},\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.0\le {\alpha }_{i,j}\le A_{i,j}(i=1,\cdots n,j=1,\cdots ,k).\hfill \end{array}$$ (8)

In (7), one can verify that L is strictly concave with respect to β_q . Note that β_q ’s are linear functions of α_i,j ’s, hence L is a quadratic term of {α_i,j (i = 1, … , n, j = 1, … , k)}, and −L in (8) is strictly convex with respect to each α_i,j . Moreover, the constraints in (8) are box constraints. Therefore, the dual optimization (8) and can be solved by the well known coordinate descent method. Furthermore, because the object function is quadratic, within each step of coordinate-wise optimization the next update value can be calculated explicitly. This greatly boosts the computational speed. Compared to the regular MSVMs that involve linear equality constraints in the QP step (Lee et al., 2004; Liu and Yuan, 2011; Lauer and Guermeur, 2011), our proposed RAMSVM has box constraints only, hence can enjoy a faster computational speed. In Section 5, we show that RAMSVM often outperforms the MSVMs 2-6 in terms of computational speed. We point out that for RAMSVM using linear learning, the number of dual variables is O(nk). Hence, the implementation can be very fast for problems with high dimensional predictors and low sample sizes.

In the optimization literature, many authors have considered the general problem of quadratic programming with box constraints only (see, for example, Floudas and Gounaris, 2009, for a review). Moreover, there exist many packages that are aimed for such optimization problems (for example, Bochkanov and Bystritsky, 2013). For our RAMSVM, we provide an R package “ramsvm”, which is developed with focus on RAMSVM optimization. In Section 5, we show that our package can enjoy a fast computational speed.

4.2 Kernel Learning

Next, we briefly discuss the case with kernel learning. We show that with the regular squared norm regularization and the intercepts penalized, the optimization can also be solved using the coordinate descent method. To begin with, denote by K the corresponding kernel function, and by $\mathbf{K}={\left(K(x_i,x_{i^{\prime }})\right)}_{i=1,\cdots ,n,i^{\prime }=1,\cdots ,n}$ the gram matrix. Define A_i,j as in the linear case. If the penalty we choose is the squared norm penalty in the corresponding kernel space (see, for example, Shawe-Taylor and Cristianini, 2004, for details), then by the Representer Theorem (Kimeldorf and Wahba, 1971), we have $f_q\left(x\right)={\theta }_{q,0}+{\sum }_{i=1}^n{\theta }_{q,i}K(x_i,x)$ and $J\left(\mathbf{f}\right)={\sum }_{q=1}^{k-1}{\theta }_q^T\mathbf{K}{\theta }_q$. Here $\theta ={({\theta }_{q,1},\cdots ,{\theta }_{q,n})}^T$ is the kernel product coefficient vector, for q = 1, … , k − 1.

We introduce the slack variables ξ_i,j as in the linear case. If we impose penalization on the intercepts θ_q,0 for q = 1, … , k − 1 as well, (4) is equivalent to

$$\begin{array}{cc}\hfill & \underset{{\theta }_q,{\theta }_q,0,{\xi }_{i,j}}{\min }\frac{n\lambda }{2}\sum _{q=1}^{k-1}{\theta }_q^{T}K{\theta }_q+\frac{n\lambda }{2}\sum _{q=1}^{k-1}{\theta }_q^2,0+\sum _{i=1}^n[\gamma {\xi }_{i,y_i}+(1-\gamma )\sum _{j\ne y_i}{\xi }_{i,j}],\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.{\xi }_{i,j}\ge 0(i=1,\cdots ,n,j=1,\cdots ,k),\hfill \\ \hfill & {\xi }_{i,y_i}+\langle \mathbf{f}\left(x_i\right),{\mathbf{w}}_{y_i}\rangle -(k-1)\ge 0(i=1,\cdots ,n),\hfill \\ \hfill & {\xi }_{i,j}+\langle \mathbf{f}\left(x_i\right),{\mathbf{w}}_j\rangle -1\ge 0(i=1,\cdots ,n,j\ne y_i).\hfill \end{array}$$ (9)

Next, we introduce the Lagrangian multipliers τ_i,j and α_i,j , take partial derivative with respect to θ_q , θ_q,0 and ξ_i,j and set to zero, as in the linear case. Without loss of generality, assume that the gram matrix K is invertible. We have that

$${\theta }_q=\frac{1}{n\lambda }{\mathbf{K}}^{-1}[\sum _{i=1}^n{\alpha }_{i,y_i}{\mathbf{W}}_{y_i,q}{\mathbf{K}}_i-\sum _{i=1}^n\sum _{j\ne y_i}{\alpha }_{i,j}{\mathbf{W}}_{j,q}{\mathbf{K}}_i],$$ (10)

$${\theta }_{q,0}=\frac{1}{n\lambda }[\sum _{i=1}^n{\alpha }_{i,y_i}{\mathbf{W}}_{y_i,q}-\sum _{i=1}^n\sum _{j\ne y_i}{\alpha }_{i,j}{\mathbf{W}}_{j,q}],$$ (11)

where K_i is the i^th column of K. After plugging (10) and (11) in (9), (4) can be shown to be equivalent to

$$\begin{array}{cc}\hfill & \underset{{\alpha }_{i,j}(i=1,\cdots ,n,j=1,\cdots ,k)}{\min }\frac{1}{2n\lambda }\sum _{q=1}^{k-1}{[\sum _{i=1}^n{\alpha }_{i,y_i}{\mathbf{W}}_{y_i,q}{\mathbf{K}}_i-\sum _{i=1}^n\sum _{j\ne y_i}{\alpha }_{i,j}{\mathbf{W}}_{j,q}{\mathbf{K}}_i]}^T\hfill \\ \hfill & {\mathbf{K}}^{-1}[\sum _{i=1}^n{\alpha }_{i,y_i}{\mathbf{W}}_{y_i,q}{\mathbf{K}}_i-\sum _{i=1}^n\sum _{j\ne y_i}{\alpha }_{i,j}{\mathbf{W}}_{j,q}{\mathbf{K}}_i]\hfill \\ \hfill & +\frac{1}{2n\lambda }\sum _{q=1}^{k-1}{[\sum _{i=1}^n{\alpha }_{i,y_i}{\mathbf{W}}_{y_i,q}-\sum _{i=1}^n\sum _{j\ne y_i}{\alpha }_{i,j}{\mathbf{W}}_{j,q}]}^2\hfill \\ \hfill & -\sum _{i=1}^n{\alpha }_{i,y_i}(k-1)-\sum _{i=1}^n\sum _{j\ne y_i}{\alpha }_{i,j},\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.0\le {\alpha }_{i,j}\le A_{i,j}(i=1,\cdots ,n,j=1,\cdots ,k).\hfill \end{array}$$ (12)

Note that K⁻¹K_j is the j^th column of the identity matrix, and K^TK⁻¹K_j = K(x_i, x_j ). Therefore, we do not need to calculate the inverse matrix K⁻¹ in the optimization. One can verify that (12) can be solved in an analogous manner as (8).

4.3 Weighted Learning

So far we have focused on the optimization problem with equal weights of loss on different classes. In practice, it is prevalent to have one class whose size is significantly larger than that of another class. For example, in cancer research, the number of patients with a rare cancer can be very limited, while the number of healthy samples is large. In this case, standard classification without adjusting for the unbalanced sample sizes can lead to a suboptimal result. To overcome this difficulty, it has been proposed to use different weights of loss for different classes (Qiao and Liu, 2009). This weighted learning technique can also be applied to practical problems with possible biased sampling. See Zhang et al. (2013) for more discussions. Therefore, it is desirable to study the extension from standard classification to weighted learning. Next, we use linear learning as an example and demonstrate how to solve the corresponding optimization problems with given weights on different observations.

Let the weight of loss for the i^th observation be w_i, and assume that w_i > 0 (i = 1, … , n). In weighted learning, the optimization (4) becomes

$$\underset{f\in F}{\min }\frac{1}{n}\sum _{i=1}^n{w}_i\left\{(1-\gamma )\sum _{j\ne y_i}{[1+\langle \mathbf{f}(x_i,{\mathbf{W}}_j)\rangle ]}_{+}+\gamma {[(k-1)-\langle \mathbf{f}\left(x_i\right),{\mathbf{W}}_{y_i}\rangle ]}_{+}\right\}+\frac{\lambda }{2}J\left(\mathbf{f}\right),$$

which, after some calculation, can be rewritten as

$$\begin{array}{cc}\hfill & \underset{{\alpha }_{i,j}(i=1,\cdots ,n,j=1,\cdots ,k)}{\min }\frac{1}{2n\lambda }\sum _{q=1}^{k-1}{[\sum _{i=1}^n{\alpha }_{i,y_i}{\mathbf{W}}_{y_i,q}{x}_i-\sum _{i=1}^n\sum _{j\ne y_i}{\alpha }_{i,j}{\mathbf{W}}_{j,q}{x}_i]}^T\hfill \\ \hfill & [\sum _{i=1}^n{\alpha }_{i,y_i}{\mathbf{W}}_{y_i,q}{x}_i-\sum _{i=1}^n\sum _{j\ne y_i}{\alpha }_{i,j}{\mathbf{W}}_{j,q}{x}_i]\hfill \\ \hfill & -\sum _{i=1}^n{\alpha }_{i,y_i}(k-1)-\sum _{i=1}^n\sum _{j\ne y_i}{\alpha }_{i,j},\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.0\le {\alpha }_{i,j}\le {\stackrel{‒}{A}}_{i,j}(i=1,\cdots ,n,j=1,\cdots ,k),\hfill \end{array}$$ (13)

where ${\stackrel{‒}{A}}_{i,j}=w_i[\gamma I(j=y_i)+(1-\gamma )I(j\ne y_i)]$. Note that the difference between (8) and (13) is in the definition of A_i,j and ${\stackrel{‒}{A}}_{i,j}$. Because ${\stackrel{‒}{A}}_{i,j}\ge 0$, the optimization (13) can be solved in a similar manner as (8).

4.4 Comparison with Dual Problems in MSVMs 2-6

In this section, we provide a brief comparison between the dual problems of MSVMs 2-6 and our RAMSVM method. We first discuss the similarities among the dual problems of these classifiers, then illustrate the key difference between RAMSVM and other existing MSVMs. As a result, RAMSVM can be solved using the coordinate descent algorithm, while existing MSVMs typically rely on QP solvers. Numerical analysis in Section 5 suggests that the coordinate descent algorithm can be faster than QP solvers for solving the dual problems of MSVMs.

In the literature, Guermeur (2012) proposed a general form of primal optimization for MSVM methods, and MSVMs 2-4 and 6 are included as special cases in this framework. See Problem 1 and Table 1 in Guermeur (2012) for details. Guermeur (2012) then derived the corresponding dual problems for soft and hard margin MSVMs. For MSVM6, Liu and Yuan (2011) derived its dual problem in their (3.8). For better illustration, we include the dual problems of Guermeur (2012) and Liu and Yuan (2011) in (A.1), (A.2), and (A.3) in the appendix. The objective functions of these dual problems are all quadratic functions with respect to the dual variables. This is similar to the RAMSVM case, such as (8) and (12). Notice that the number of dual variables α_i,j in Guermeur (2012) is nk with α^i,yi = 0. Hence the number of effective dual variables is n(k − 1). For our RAMSVM method, the number of effective dual variable is generally nk, which is slightly larger than n(k − 1). This is because in RAMSVM we use the convex combination of loss functions as in (4), hence we introduce k more slack variables. Nevertheless, as we will see in Section 5, the combined loss function can provide stable classification performance under various settings, which is highly desirable. Notice that for γ = 0, our RAMSVM method also uses n(k − 1) effective dual variables, because α^i,yi = 0 by the box constraints. For RAMSVM, our numerical experience suggests that the difference between n(k − 1) or nk dual variables is small in terms of computational speed.

Table 1.

Prediction error rates and computational time in seconds for the simulated examples.

MSVM Method	Ex 1 Linear			Ex 2 Poly			Ex 3 Linear
	Error	Time	p-value	Error	Time	p-value	Error	Time	p-value
MSVM2	14.67	18	0.000	15.53	54	1.000	14.48	306	0.419
MSVM3	15.21	21	0.000	14.96	48	1.000	14.41	299	0.533
MSVM4	22.47	20	0.000	21.79	64	0.000	14.56	338	0.297
MSVM5	11.34	151	0.000	17.76	452	0.000	-	-	-
MSVM6	14.98	27	0.000	16.14	77	0.000	14.76	422	0.088
RAMSVM	9.80	13	-	15.71	23	-	14.43	115	-
MSVM Method	Ex 1 Gauss			Ex 2 Gauss			Ex 3 Poly
	Error	Time	p-value	Error	Time	p-value	Error	Time	p-value
MSVM2	8.64	13	1.000	11.62	17	0.000	14.64	599	0.109
MSVM3	9.16	11	0.000	12.88	21	0.000	14.91	478	0.010
MSVM4	11.71	15	0.000	15.19	23	0.000	14.88	705	0.013
MSVM5	14.09	277	0.000	15.82	298	0.000	-	-	-
MSVM6	11.57	15	0.000	13.57	30	0.000	14.29	818	0.581
RAMSVM	8.78	14	-	11.34	21	-	14.34	355	-

Poly: Second order polynomial kernel learning. Gauss: Gaussian kernel learning. The standard errors of the error rates range from 0.6% to 1.7%. The standard errors of the computational time range from 1 to 32 seconds. Note that MSVM5 cannot be computed for Example 3 due to its large n.

The key difference between MSVMs 2-6 and RAMSVM is that the former methods have equality constraints in the corresponding dual problems. See (A.1), (A.2), and (A.3) in the appendix. Hence, the coordinate descent algorithm cannot be directly implemented. Instead, existing QP solvers are typically employed to solve the corresponding optimization. Compared to these dual formations, our RAMSVM is free of equality constraints, and can be solved using the coordinate descent algorithm. More importantly, because the objective function is quadratic, each update value in the coordinate-wise minimization can be calculated explicitly, without any further loops such as those in Newton-Raphson methods (Friedman et al., 2010). This helps to alleviate the computational burden, and boosts the speed greatly. In the next section, we demonstrate that solving RAMSVM with coordinate descent algorithm is efficient to compute.

5 Numerical Results

In this section, we examine the numerical performance of RAMSVM. As we will see, the algorithms developed in Section 4 can provide an efficient way to solve the corresponding optimization problem. In particular, in Section 5.1, we compare the performance of RAMSVM with MSVMs 2-6 via three simulated examples, and in Section 5.2, we study six real world data sets. For MSVMs 2-4 and 6, we use the MSVMpack package developed by Lauer and Guermeur (2011). For RAMSVM, we apply the same stopping criterion as in the MSVMpack package, which is to stop the iteration when the ratio of the dual objective function is larger than 98% of the primal value. For RMSVM, the R code is publicly available, and we follow the suggestion in Liu and Yuan (2011) to use γ = 0.5. For RAMSVM, we demonstrate the effect of γ on the classification accuracy using simulated examples. We show that RAMSVM can often enjoy a faster computational speed, and the Fisher consistent RAMSVM with γ = 0.5 yields a stable and competitive classifier.

All numerical analyses are done with R (R Core Team, 2015) on a computer with an Intel(R) Core(TM) i7-4770 processor at 3.4GHz and 16GB of memory. The core code of the coordinate descent algorithm for RAMSVM is written in C. An R package “ramsvm”, which contains the code to perform RAMSVM classification, is provided in the Supplementary Materials. Notice that both MSVMpack and our ramsvm implement parallel computing to train the classifiers. In particular, the algorithm splits the data into small chunks, and the dual variables for each chunk are updated using parallel threads. Hence, for problems with large data sets, parallel computing can significantly reduce the computational time. However, as Lauer and Guermeur (2011) mentioned, sometimes the algorithm for one chunk of data needs output from previous steps. If the computation in the previous steps is not finished before the next update step, the corresponding thread would be idle for a while, and this can reduce the corresponding efficiency. How to determine the chunk size can be an issue, and is discussed in the ramsvm reference manual. Moreover, for our ramsvm package, we observe that for small data sets (hundreds of observations), using parallel computing in R can indeed be slower. This is because creating threads in R can take some time, and is not efficient for small problems. Hence, in our ramsvm package, we provide the option to use parallel computing or not. For numerical results in the following sections, we report the smaller computational time of RAMSVM and MSVMpack with or without parallel computing.

5.1 Simulated Examples

We consider three simulated examples in this section. The first example is constructed such that linear learning suffices, and we apply linear learning as well as the Gaussian kernel learning. For the second example, we design the marginal distribution of X such that linear classification boundaries cannot separate the classes well. Therefore, we use the second order polynomial kernel and the Gaussian kernel for this example. For Gaussian kernel learning, the kernel parameter σ is chosen to be the median of all the pairwise distances between one category and others. The third example is a simulated data set from the UCI machine learning website (Bache and Lichman, 2015). We apply linear and second order polynomial kernel learning for this example.

We let the convex combination parameter γ vary in {0, 0.1, 0.2, … , 0.9, 1} and study the effect of γ on the classification accuracy for RAMSVM. To select the best tuning parameter λ, we use a grid search. In particular, we train the classifiers on a training data set. The classifier that has the smallest prediction error rate on an independent tuning data set is then selected, and we record the prediction error rate on a separate testing data set. The size of the testing data is 10⁶ for the first and second examples. We repeat this procedure 50 times and report the average prediction error rate on the testing data set. To compare the computational speed among different methods, in each replication we record the total time of training the classifiers for 50 different tuning parameters, selecting the best parameter λ and predicting on the testing data set. We report the average time used for one replication as a measurement of computational speed. For RAMSVM, we only report the time for γ = 1/2, since the differences in terms of computational time for various γ values are small.

Example 1

This is an eight class example with equal probabilities Pr(Y = j) (j = 1, … , 8). The marginal distribution of X for each class is normal, and the mean vectors for different classes form a simplex in ℝ⁷. We choose the covariance matrices of the normal distributions so that the corresponding Bayes classification error is 5%. We use 150 observations for training and another 150 for tuning.

Example 2

We generate four classes with Pr(Y = j) = 1/4 (j = 1, … , 4) on ℝ². For each class, the predictor vector X | Y = j follows a mixed normal distribution. In particular, for class j, X follows 0.5N ((cos(jπ/4), sin(jπ/4))^T, Σ) + 0.5N ((cos(jπ/4 + π), sin(jπ/4 + π))^T, Σ). Here Σ is chosen such that the Bayes error is 5%. Both the training and tuning data are of size 150.

Example 3

This is the three-class Waveform Database Generator (Version 1) data set from the UCI machine learning website. The number of observations for the three classes are 1657, 1647 and 1696, respectively. There are 21 predictors. For each replicate, we divide the data into six parts of roughly the same size. Four parts are used as the training data, one as the tuning, and the rest as the testing data set.

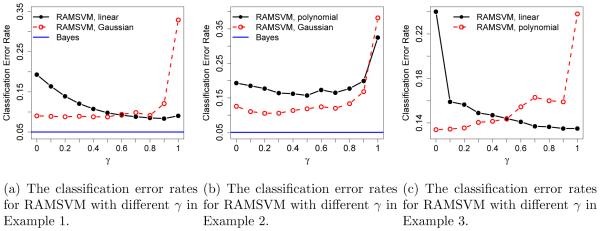
The effect of γ on classification error rates for RAMSVM is illustrated in Figure 1. For linear learning, the classification error rate decreases as γ increases from 0 to 1/2. When γ ranges in [1/2, 1], the change in classification accuracy is small. However, for kernel learning, the pattern is reversed according to Figure 1. In particular, the classification error rates increase as γ increases from 1/2 to 1, and when γ is in [0, 1/2], the classification accuracy does not change much. The results suggest that although RAMSVM with γ > 1/2 is not Fisher consistent, in linear learning where the functional class F is relatively simple, encouraging $\langle \mathbf{f},{\mathbf{W}}_y\rangle$ to be large explicitly (the second part of loss in (4)) may work better than doing so implicitly (the first part of loss). However, for kernel learning problems where F is more flexible, Fisher consistency can become more relevant and the classification accuracy of RAMSVM with γ > 1/2 may suffer from being inconsistent. From Figure 1, one can conclude that the classification accuracy of RAMSVM with γ = 1/2 is close to the optimum for all situations, hence choosing γ = 1/2 provides a Fisher consistent and stable classifier. We recommend using γ = 1/2 for all classification problems.

Figure 1.

The left panel displays the effect of different γ values on the classification performance of RAMSVM for simulated Example 1. The standard errors of the classification error rates in Example 1 range from 0.001 to 0.012. The middle panel reports the pattern for Example 2, and the corresponding standard errors range from 0.001 to 0.010. The right panel shows the effect of different γ values on classification error rates for Example 3. The corresponding standard errors range from 0.003 to 0.023.

We report the comparison among RAMSVM and MSVMs 2-6 in Table 1. In particular, we calculate the p-values for testing the null (alternative) hypotheses that the classification error of RAMSVM is larger than or equal to (smaller than) that of the other methods, using the two sample proportion test. Based on the p-values, our RAMSVM with γ = 1/2 can work better than all the considered existing MSVMs in Example 1 using linear learning, and in Example 2 using Gaussian learning. For other cases, one can see that RAMSVM is still very competitive. In terms of computational speed, compared to MSVMpack, RAMSVM has computational advantages on linear and polynomial learning, which is also demonstrated in Section 5.2. For Gaussian kernel learning, the speed of RAMSVM is comparable with respect to MSVMpack.

5.2 Real Data Analysis

In this section, we test the performance of RAMSVM using six real data sets, among which five data sets can be found on the UCI machine learning repository website. The Glioblastoma data can be found in Verhaak et al. (2010). A summary of these data sets is provided in Table 2. The predictors of these real data sets are standardized. For the Vertebral, Optical, and Glioblastoma data sets, we perform a 5-fold cross validation to select the best tuning parameters. We report the average prediction error rates among 50 replicates. As a measurement of computational speed, we report the average time for solving the optimization problems with the entire training data sets throughout the 50 replicates. The Gaussian kernel parameters are chosen analogously as in Section 5.1.

Table 2.

Summary of the real data sets used in Section 5.2.

Data	# classes	# predictors	# training obs	# testing obs
Gas	6	129	11592	2318
Glioblastoma	4	16548	296	60
Isolet	26	617	6238	1559
Optical	10	64	3823	1797
Pendigits	10	16	7494	3498
Vertebral	3	6	258	52

For the Gas, Isolet, and Pendigits data sets, because their sizes are relatively large, we choose a small proportion of observations to select the tuning parameters. Then we report the computational time of optimization with the entire training data set as a measurement of computational speed. Moreover, we report the prediction error rates. Notice that we only perform one replicate for the Gas, Isolet, and Pendigits data sets to assess the corresponding classification accuracy and computational speed, due to the large sample sizes of these problems.

The real data results are reported in Table 3. One can verify that RAMSVM can enjoy a very efficient computational speed, especially with linear learning. This is consistent with the findings in the simulation study. For Gaussian kernel learning, the computational speed of RAMSVM and MSVMpack is comparable. In terms of classification accuracy, RAMSVM with γ = 1/2 is a stable classifier, and the corresponding prediction error rates are close to the optimum. Overall, RAMSVM is a very competitive classifier. Notice that the code for MSVM5 does not converge for Gas, Isolet, and Pendigits data sets after 48 hours.

Table 3.

Prediction error rates and computational time for the real examples.

Data & Kernel	Method	Error	Time
Gas Linear	MSVM2	1.57	01:33:24
	MSVM3	1.72	32:19:17
	MSVM4	1.92	48:00:00*
	MSVM5	-	-
	MSVM6	1.78	48:00:00*
	RAMSVM	1.51	00:47:42
Glioblastoma Linear	MSVM2	24.21	00:00:02
	MSVM3	23.17	00:00:02
	MSVM4	24.28	00:00:02
	MSVM5	23.80	00:00:21
	MSVM6	23.92	00:00:02
	RAMSVM	22.95	00:00:02
Isolet Linear	MSVM2	9.07	44:26:09
	MSVM3	8.93	29:16:35
	MSVM4	9.41	48:00:00*
	MSVM5	-	-
	MSVM6	9.39	48:00:00*
	RAMSVM	8.92	07:26:04
Optical Gaussian	MSVM2	2.63	00:00:15
	MSVM3	2.58	00:00:18
	MSVM4	2.74	00:00:31
	MSVM5	-	-
	MSVM6	2.68	00:01:44
	RAMSVM	2.56	00:00:16
Pendigits Gaussian	MSVM2	5.13	00:03:19
	MSVM3	6.60	00:00:29
	MSVM4	4.93	00:01:20
	MSVM5	-	-
	MSVM6	5.11	00:05:17
	RAMSVM	5.06	00:00:52
Vertebral Gaussian	MSVM2	18.26	00:00:01
	MSVM3	18.41	00:00:01
	MSVM4	18.63	00:00:01
	MSVM5	18.20	00:00:12
	MSVM6	18.39	00:00:01
	RAMSVM	17.92	00:00:01

For Vertebral, Optical, and Glioblastoma, the standard errors of the error rates range from 0.05% to 0.24%, and the standard errors of the computational time range from 0.001 to 2 seconds. Note that MSVM5 cannot be computed for Gas, Isolet, and Pendigits, due to the large n.

^*Here means the MSVMpack algorithm did not converge according to the stopping rule within 48 hours, and the iteration was manually stopped. The models at 48 hours were used to assess the performance. See Lauer and Guermeur (2011) for more details.

6 Discussion

In this paper, we propose the RAMSVM as a new angle-based MSVM method. We show that the RAMSVM has two advantages. First, it is free of the sum-to-zero constraint, hence the corresponding optimization procedure can be more efficient. In particular, we develop a new algorithm to train the classifier using coordinate descent method, which does not rely on existing QP solvers. Second, the RAMSVM overcomes the difficulty of inconsistency, compared to the existing angle-based MSVM method. Numerical comparisons between the RAMSVM and some existing MSVMs demonstrate the usefulness of our method. Although one can treat γ as an additional tuning parameter, it requires more computational time. We recommend using the RAMSVM with γ = 1/2, which yields a Fisher consistent classifier whose performance is stable and often close to the optimum.