Imaging Brain Source Extent from EEG/MEG by Means of an Iteratively Reweighted Edge Sparsity Minimization (IRES) Strategy

Abstract

Estimating extended brain sources using EEG/MEG source imaging techniques is challenging. EEG and MEG have excellent temporal resolution at millisecond scale but their spatial resolution is limited due to the volume conduction effect. We have exploited sparse signal processing techniques in this study to impose sparsity on the underlying source and its transformation in other domains (mathematical domains, like spatial gradient). Using an iterative reweighting strategy to penalize locations that are less likely to contain any source, it is shown that the proposed iteratively reweighted edge sparsity minimization (IRES) strategy can provide reasonable information regarding the location and extent of the underlying sources. This approach is unique in the sense that it estimates extended sources without the need of subjectively thresholding the solution. The performance of IRES was evaluated in a series of computer simulations. Different parameters such as source location and signal-to-noise ratio were varied and the estimated results were compared to the targets using metrics such as localization error (LE), area under curve (AUC) and overlap between the estimated and simulated sources. It is shown that IRES provides extended solutions which not only localize the source but also provide estimation for the source extent. The performance of IRES was further tested in epileptic patients undergoing intracranial EEG (iEEG) recording for pre-surgical evaluation. IRES was applied to scalp EEGs during interictal spikes, and results were compared with iEEG and surgical resection outcome in the patients. The pilot clinical study results are promising and demonstrate a good concordance between noninvasive IRES source estimation with iEEG and surgical resection outcomes in the same patients. The proposed algorithm, i.e. IRES, estimates extended source solutions from scalp electromagnetic signals which provide relatively accurate information about the location and extent of the underlying source.

Introduction

Electroencehalography (EEG)/magnetoencephalography (MEG) source imaging is to estimate the underlying brain activity from scalp recorded EEG/MEG signals. The locations within the brain involved in a cognitive or pathological process can be estimated using associated electromagnetic signals such as scalp EEG or MEG (He et al., 2011; Baillet et al., 2001). The process of estimating underlying sources from scalp measurements is a type of inverse problem referred to as electrophysiological source imaging (ESI) (Michel et al., 2004b; Michel & He, 2011; He & Ding, 2013).

There are two main strategies to solve the EEG/MEG inverse problem (source imaging), namely the equivalent dipole models (Scherg & von Cramon 1985; He et al, 1987) and the distributed source models (Hämäläinen et al., 1984; Dale & Sereno, 1993; Pascual-Marqui et al., 1994). The dipole models assume that the electrical activity of the brain can be represented by a small number of equivalent current dipoles (ECD) thus resulting in an over-determined inverse problem. This, however leads to a nonlinear optimization problem, which ultimately estimates the location, orientation and amplitude of a limited number of equivalent dipoles, to fit the measured data. The number of dipoles has to be determined a priori (Bai & He, 2006). On the other hand, the distributed source models use a large number of dipoles (Hämäläinen et al., 1984; Dale & Sereno, 1993; Pascual-Marqui et al., 1994) or monopoles (He et al, 2002) distributed within the brain volume or the cortex. In such models, the problem becomes linear, since the dipoles (monopoles) are fixed in predefined grid locations, but the model is highly underdetermined as the number of unknowns is much more than the number of measurements. Given that functional areas within the brain are extended and not point-like, the distributed models are more realistic. Additionally, determining the number of dipoles to be used in an ECD model is not a straightforward process (Michel et al., 2004b).

Solving under-determined inverse problems calls for regularization terms (in the optimization problem) or prior information regarding the underlying sources. Weighted minimum norm solutions were one of the first and most popular algorithms. In these models, the regularization term is the weighted norm of the solution (Lawson & Hanson, 1974). Such regularization terms will make the process of inversion (going from measurements to underlying sources) possible and will also impose additional qualities to the estimation such as smoothness or compactness. Depending on what kind of weighting is used within the regularization term, different solutions can be obtained. If a uniform weighting or identity matrix is used, the estimate is known as the minimum norm (MN) solution (Hämäläinen et al., 1984). The MN solution is the solution with least energy (L2 norm) within the possible solutions that fit the measurements. It is due to this preference for sources with a small norm that MN solutions are well-known to be biased towards superficial sources (Hämäläinen et al., 1994). One modification to this setback is to use the norm of the columns of the lead field matrix to weight the regularization term in such a manner to penalize superficial sources more than the deep sources, as the deep sources do not present well in the scalp potential (Lawson & Hanson, 1974). In this manner the tendency towards superficial sources is alleviated. This is usually referred to as the weighted minimum norm (WMN) solution. Another popular choice is the low resolution brain electromagnetic tomography (LORETA) (Pascual-Marqui et al., 1994). LORETA is basically a WMN solution where the weighting is a discrete Laplacian. The solution’s second spatial derivative is minimized so the estimation is smooth. Many inverse methods apply the L2 norm, i.e. Euclidean norm, in the regularization term. This causes the estimated solution to be smooth, resulting in solutions that are overly smoothed and extended all over the solution space. Determining the active cortical region by distinguishing desired source activity from background activity (to determine source extent) proves difficult in these algorithms, as the solution is overly smooth and poses no clear edges between background and active brain regions (pertinent or desired activity, epileptic sources for instance as compared to background activity or noise). This is one major drawback of most conventional algorithms including the ones discussed so far.

In order to overcome the extremely smooth solutions, the L2 norm can be supplanted by the L1 norm. This idea is inspired from sparse signal processing literature where the L1 norm has been proposed to model sparse signals better and more efficiently, specifically after the introduction of the least absolute shrinkage selection operator (LASSO) (Tibshirani, 1996). While optimization problems involving L1 norms do not have closed form solutions, they are easy to solve as they fall within the category of convex optimization problems (Boyd & Vandenberghe, 2004).

Selective minimum norm method (Matsura & Okabe, 1995), minimum current estimate (Uutela et al., 1999) and sparse source imaging (Ding & He, 2008) are examples of such methods. These methods seek to minimize the L1 norm of the solution. Another algorithm in this category, which uses a weighted minimum L1 norm approach to improve the stability and “spiky-looking” character of L1-norm approaches, is the vector-based spatio-temporal analysis using L1-minimum norm (VESTAL) (Huang et al., 2006). These algorithms encourage extremely focused solutions. Such unrealistic solutions root from the fact that by penalizing the L1 norm of the solution a sparse solution is being encouraged. As discussed by Donoho (Donoho, 2006) under proper conditions regularizing the L1 norm of a solution will result in a sparse solution; a solution which has only a few number of non-zero elements. Sparsity is definitely not a desired quality for underlying sources which produce EEG/MEG signals as EEG/MEG signals are the result of synchronous activity of neurons from a certain extended cortical region (Baillet et al., 2001; Nunez et al., 2000).

To overcome the aforementioned shortcomings while still benefiting from the advantages of sparse signal processing techniques, new regularization terms which encourage sparsity in other domains have been proposed. The idea is to find a domain in which the solution has a sparse representation. This basically means that while the solution might not be sparse itself (as is usually the case for underlying sources generating the EEG/MEG) it still might be sparsely represented in another domain such as the spatial gradient or wavelet coefficient domain. This amounts to the fact that the signal still has redundancies that can be exploited in other domains.

Haufe et al. (Haufe et al., 2008) penalized the Laplacian of the solution instead and showed focal results which are realistically extended. They have shown the effect of considering implicit domain sparsity in improving the results by comparing their estimation with that of conventional methods using L2 norm regularization terms or simple L1 norm terms. Ding (Ding, 2009) has tried penalizing the gradient instead of Laplacian. Due to the selected penalization term which penalizes the solution discontinuities or jumps, the solution is piecewise constant and needs thresholding to discard the low level semi-constant background activity. Liao et al. (Liao et al., 2012) have used the faced-based wavelet in the penalty term and have shown focal results. Chang et al. (Chang et al., 2010) and Zhu et al. (Zhu et al., 2014) proposed to impose sparsity on multiple domains to better capture the redundancies of the underlying sources and have shown positive results. Zhu et al. combined the gradient and wavelet transform in the regularization term and Chang et al. used two strategies to combine domain sparsity. The first strategy is to impose sparsity on the solution and the Laplacian of the solution, and the second strategy is to impose sparsity on the solution and its wavelet transform. Another piece of work worthy of mentioning is the Elastic Net (ENET) (Zou and Hastie, 2005) and ENET L (Vega-Hernández et al, 2008). In the ENET algorithm both the L1 norm and L2 norm of the solution are regularized to obtain estimations that are more robust than LASSO-type solutions. ENET L regularizes the L1 and L2 norm of the Laplacian to obtain smooth and focal solutions. While imposing sparsity on multiple domains improves the results and seems to be a good approach for estimating extended sources, the solutions presented in the discussed papers cannot yet determine the extent of the underlying source objectively, i.e. still a threshold needs to be applied to reject the background activity.

Another successful class of inverse algorithms is Bayesian inverse techniques. In these methods, the problem is formulated within a Bayesian framework starting with prior distributions (of the dipole current density) to converge to a posterior distribution of the underlying source. Wipf and Nagarajan (Wipf and Nagarajan, 2009) have discussed this approach thoroughly. In this work many conventional algorithms such as MN, WMN and FOCUSS (Gorodnitsky et al., 1995) are re-introduced within this framework. Another well-known Bayesian algorithm is the maximum entropy on the mean (MEM) approach (Grova et al., 2006) where the cortical surface is clustered in a data driven manner to obtain active and inactive regions on the cortex by regularizing the mean entropy. The idea of MEM has been further pursued by Chowdhury et al. (Chowdhury et al., 2013) and Lina et al. (Lina et al., 2014) in a parcelization framework, where the cortical surface is divided into segments and then it is determined if each parcel is within the active source patch or not (through statistical analysis). The proposed method in the present work is not defined within the Bayesian framework, but as a series of convex optimization problems, as will be discussed.

Model based algorithms inspired by the sparse signal processing literature have also been proposed in recent years. Spatial or temporal basis functions which are believed to model the underlying source activity of the brain are defined a priori in a huge data set called the dictionary (Bolstad et al., 2009; Limpiti et al., 2006). Later on a solution which best fits the measurements is sought within the dictionary. Haufe et al. proposed a Gaussian basis to spatially model extended brain sources (Haufe et al., 2011). These methods can be effective in solving the inverse problem as long as the underlying assumption about the basis functions holds true (since the solution is basically subsumed within the dictionary elements). For instance, the design of the basis function in (Haufe et al., 2011) might include very compact Gaussian kernels to provide a chance for the solver to select these kernels and give more compact estimates (although extent estimation is not pursued in that work). Furthermore, for a given spatial extent for the Gaussian kernel infinitely many different standard deviations can be assumed. If the kernel includes a good amount of such cases, in order to be unbiased and to avoid selecting parameters a priori (like subjective thresholding,) the dictionary can be huge and the problem might become intractable. However similar approaches undertaken by other groups have not been able to resolve this issue completely. Other studies (Chang et al., 2010; Liao et al., 2014; Zhu et al., 2014) adopted a similar approach using wavelets (wavelets that have many levels of precision and spatial extent) and their results still needed a minor thresholding to reject the weak sources. The proposed method in the present work does not assume any prior dictionaries or basis functions prior to solving the inverse problem.

Mixed-norm estimates have also gained attention in recent years (Gramfort et al., 2012; Gramfort et al., 2013a). These algorithms have also been incorporated in an iterative reweighting scheme (Strohmeier et al., 2014, 2015). These algorithms define two-level (or multi-level) mixed norms (usually combining L1 and L2 norms) to obtain focal solutions. Since the regularization is enforced on the solution, very focal estimates are obtained. Basically not much information regarding the source extent can be extracted from these algorithms currently, although it is suggested that newer implementations or combination with other algorithms may provide such capabilities in the future (Gramfort et al., 2013a).

Estimating the extent of the underlying source is a challenge but also highly desirable in many applications. Determining the epileptogenic brain tissue is one important application. EEG/MEG source imaging is a non-invasive technique making its way into the presurgical workup of epilepsy patients undergoing surgery. EEG/MEG source imaging helps the physician in localizing the location of activity and if it can more reliably and objectively estimate the extent of the underlying epileptogenic tissue, the potential merits to improve patient care and quality of life are obvious since EEG and MEG are noninvasive modalities. Another important application is mapping brain functions, elucidating roles of different regions of the brain responsible for specific functional tasks using EEG/MEG (He et al., 2013).

In order to come up with an algorithm that is able to objectively determine the extent of the underlying sources, we move along the lines of multiple domain sparsity and also introduce the notion of iterative reweighting within the sparsity framework to achieve this goal. If the initial estimation of the underlying source is relaxed enough to provide an overestimation of the extent, it is possible to use this initial estimation and launch a series of subsequent optimization problems to gradually converge to a more accurate estimation of the underlying source. The sparsity is imposed on both the solution and the gradient of the solution. This is the basis of the proposed algorithm, which is called iteratively reweighted edge sparsity minimization (IRES).

The notion of edge sparsity or imposing sparsity on the gradient of the solution is also referred to as the total-variation (TV) in image processing literature (Adde et al. 2005; Rudin et al., 1992). Recently some fMRI studies have shown the usefulness of working within the TV framework to obtain focal hot-spots within fMRI maps without noisy spiky-looking results (Dohmatob et al., 2014; Gramfort et al., 2013b). The results presented in the aforementioned works still need to set a threshold to reject background activity. These approaches are similar to the approach adopted in IRES with the difference that IRES initiates a sequence of reweighting iterations based on obtained solutions to suppress background activity and create clear edges between sources and background. One example has been presented in the supplementary materials to show the effect of thresholding on IRES estimates (Fig. S1).

A series of computer simulations were performed to assess the performance of the IRES algorithm in estimating source extent from the scalp EEG. The estimated results were compared with the simulated target sources and quantified using different metrics. To show the usefulness of IRES in determining the location and extent of the epileptogenic zone in case of focal epilepsy, the algorithm has been applied to source estimation from scalp EEG recordings and compared to clinical findings such as resection and seizure onset zone (SOZ) determined from intracranial EEG by the physician.

Materials and Methods

Iteratively reweighted edge sparsity minimization (IRES)

The brain electrical activity can be modeled by current dipole distributions. The relation between the current dipole distribution and the scalp EEG/MEG is constituted by Maxwell’s equations. After discretizing the solution space and numerically solving Maxwell’s equations, a linear relationship between the current dipole distribution and the scalp EEG/MEG can be derived:

$$\phi =Kj+n_0$$ (1)

where φ is the vector of scalp EEG (or MEG) measurements, K is the lead field matrix which can be numerically calculated using the boundary element method (BEM) modeling, j is the vector of current dipoles to be estimated and n₀ models the noise. For EEG source imaging, φ is an M x 1 vector, where M refers to the number of sensors; K is an M x D matrix, where D refers to the number of current dipoles; j is a vector of D x 1, and n₀ is an M x 1 vector.

Following the multiple domain sparsity in the regularization terms, the optimization problem is formulated as a second order cone programming (SOCP) (refer to Boyd & Vandenberghe, 2004 for more details) in (2). While problems involving L1 norm minimization do not have closed-form solutions and may seem complicated, such problems are easy to solve as they fall within the convex optimization category (Boyd & Vandenberghe, 2004). There are many efficient methods for solving convex optimization problems.

$$\begin{array}{l}{j}^{\mathit{est}}={\text{argmin}}_j{\left|\right|Vj\left|\right|}_1+\alpha {\left|\right|j\left|\right|}_1\\ \mathit{subject}to{(\phi -Kj)}^T{\mathrm{\sum }}^{-1}(\phi -Kj)\le \beta \end{array}$$ (2)

Where V is the discrete gradient defined based on the source domain geometry (T x D, where T is the number of edges as defined by (4), later on), β is a parameter to determine noise level and Σ is the covariance matrix of residuals, i.e. measurement noise covariance. Under the assumption of additive white Gaussian noise (AWGN), Σ is simply a diagonal matrix with its diagonal entries corresponding to the variance of noise for each recording channel. In more general and realistic situations, Σ is not diagonal and has to be estimated from the data (refer to simulation protocols for more details on how this can be implemented). Under the uncorrelated Gaussian noise assumption it is easy to see that the distribution of the residual term will follow the ${\chi }_n^2$ distribution, where ${\chi }_n^2$ is the chi-squared distribution with n degrees of freedom (n is the number of recording channels, i.e. number of EEG/MEG sensors). In case of correlated noise, the noise whitening process in (2) will eliminate the correlations and hence is an important step. This de-correlation process is achieved by multiplying the inverse of the covariance matrix (Σ⁻¹) by the residuals, as formulated in the constraint of the optimization problem in (2). In order to determine the value of β the discrepancy principle is applied (Morozov, 1966). This translates to finding a value for β for which it can be guaranteed that the probability (p) of having the residual energy within the [0 β] interval is high (p). Setting p=0.99 (Zhu et al., 2014; Malioutov et al., 2005), β was calculated using the inverse cumulative distribution function of the ${\chi }_n^2$ distribution.

The optimization problem proposed in (2) is an SOCP-type problem that needs to be solved at every iteration of IRES. In each iteration, based on the estimated solution, a weighting coefficient is assigned to each dipole location. Intuitively, locations which have dipoles with small amplitude will be penalized more than locations which have dipoles with larger amplitude. In this manner, the optimization problem will gradually slim down to a better estimate of the underlying source. The details of how to update the weights at each iteration and why to follow such a procedure is given in Appendix A. Mathematically speaking, the following procedure is repeated until the solution does not change significantly in two consecutive iterations as outlined in (3):

At iteration L:

$$\begin{array}{l}{j}^L={\text{argmin}}_j{\left|\right|W_d^{L-1}(Vj)\left|\right|}_1+\alpha {\left|\right|W^{L-1}j\left|\right|}_1\\ \mathit{subject}to{(\phi -K{j}^L)}^T{\mathrm{\sum }}^{-1}(\phi -K{j}^L)\le \beta \end{array}$$ (3)

where W^L and $W_d^L$ are updated based on the estimation j^L (refer to appendix A for details).

The procedure is depicted in Fig. 1. The idea of data-driven weighting is schematically depicted. Although the number of iterations cannot be determined a priori, the solution converges pretty fast, usually within two to three iterations. One of the advantages of IRES is that it uses data-driven weights to converge to a spatially extended source. Following the idea proposed in the sparse signal processing literature (Candès et al., 2008; Wipf and Nagarajan, 2010), the heuristic that locations with smaller dipole amplitude need to be penalized more than other locations, will be formalized. In the sparse signal processing literature it is well known that under some general conditions (Donoho, 2006) the L1-norm can produce sparse solutions; in other words “L0-norm” can be replaced with L1-norm. In reality, “L0-norm” is not really a norm, mathematically speaking. It assigns 0 to the elements of the input vector when those elements are 0 and 1 otherwise. It is easy to imagine that when sparsity is considered, such a measure or pseudo-norm is intended (as this measure will impose the majority of the elements of the vector to be zero, when minimized). However this measure is a non-convex function and including it in an optimization problem makes it hard or impossible to solve, so it is replaced by the L1-norm which is a convex function and under general conditions the solutions of the two problems are close enough. When envisioning “L0-norm” and L1-norm, it is evident that while “L0-norm” takes a constant value as the norm of the input vector goes to infinity, L1-norm is unbounded and goes to infinity. In order to use a measure which better approximates the L0-norm and yet has some good qualities (for the optimization problem to be solvable), Fazel et al. (Fazel, 2002; Fazel et al., 2003) proposed that a logarithm function be used instead of the “L0-norm”. Logarithmic functions are concave but also quasi-convex (refer to (Boyd and Vandenberghe, 2004) for the definition and for more properties), thus the problem would be solvable. However, finding the global minimum (which is a promise in the convex optimization problems) is no more guaranteed. This means that the problem is replaced with a series of optimization problems, which could converge to a local minimum; thus the final outcome of the problem depends on the initial estimation. Our results in this paper indicate that initiating the problem formulated in (3) with identity matrices, provide good estimates in most of the cases, hopefully indicating that the algorithm might not be getting trapped in local minima. More detailed mathematical analysis is presented in Appendix A.

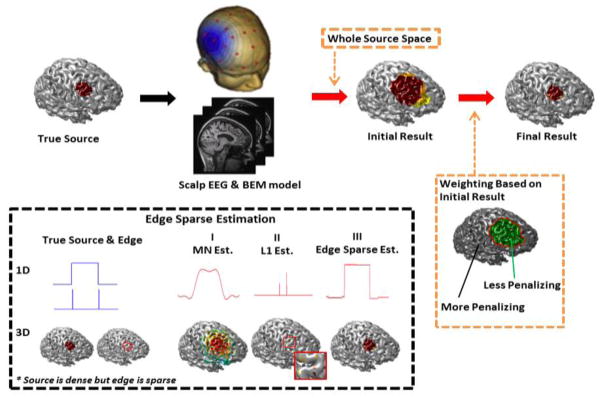
Fig. 1.

Schematic diagram of the proposed method. Two novel strategies (edge sparse estimation and iterative reweighting) were proposed to accurately estimate the source extent. The edge sparse estimation is based on the prior information that source is densely distributed but the source edge is sparse. The source extent can thus be obtained by adding the edge-sparse term into the source optimization solution. The iterative reweighting is based on a multistep approach. Initially an estimate of the underlying source is obtained. Consequently the locations which have less activity (smaller dipole amplitude) are penalized based on the solutions obtained in previous iterations. This process is continued until a focal solution is obtained with clear edges.

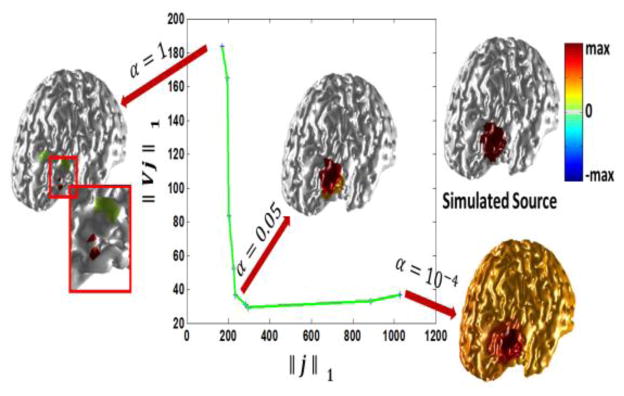
Selecting the hyper-parameter α is not a trivial task. Selecting hyper-parameters can be a dilemma in any optimization problem and most optimization problems inevitably face such a selection. It is proposed to adopt the L-curve approach to objectively determine the suitable value for α (Hansen et al. 1990; He et al., 2011). Referring to Fig. 2 it can be seen how selecting different values for α can affect the problem. In this example a 20 mm extent source is simulated and a range of different α values ranging from 1 to 10⁻⁴ are used to solve the inverse problem. As it can be seen, selecting a large value for α will result in an overly focused solution (underestimation of the spatial extent). This is due to the fact that by selecting a large value for α the optimization problem focuses more on the L1-norm of the solution rather than the domain sparsity (TV term) so the solution will be sparse. In the extreme case when α is much larger than 1 the optimization problem turns into a L1 estimation problem which is known to be extremely sparse, i.e. focused. Conversely selecting very small values for α may result in spread solutions (overestimation of the spatial extent). Selecting an α value near the bend (knee) of the curve is a compromise to get a solution which minimizes both terms involved in the regularization. The L-curve basically looks at different terms within the regularization and tries to find an α for which all the terms are small and also changing α minimally along each axis will not change the other terms drastically. In other words the bend of the L-curve gives the optimal α as changing α will result in at least one of the terms in the regularization term to grow which is counterproductive in terms of minimizing (2). In this example an α value of 0.05 to 0.005 seems to give reasonable results)

Fig. 2.

Selecting the hyper-parameter α using the L-curve technique. In order to select α which is a hyper-parameter balancing between the sparsity of the solution and gradient domain, the L-curve technique is adopted. As it can be seen a large value of α will encourage a sparse solution while a small value of α encourages a piecewise constant solution which is over-extended. The selected α needs to be a compromise. Looking at the curve it seems that an α corresponding to the knee is optimum as perturbing α will make either of the terms in the goal function grow and thus would not be optimal. The L-curve in this figure is obtained when a source with an average radius of 20 mm was simulated. The SNR of the simulated scalp potential is 20 dB.

Another parameter to control for is the number of iterations. Although this cannot be theoretically dealt with now, it is suggested to continue iteration until the estimation of two consecutive steps do not vary much. The actual number of iterations needed is usually 2 to 4 iterations, as our experience with the data suggests. This is also reported by Candès et al (Candès et al., 2008). This means that within a few iterations an extended solution with distinctive edges from the background activity is reached. Fig. 3 shows one example. In this case a 10 mm extent source is estimated and the solution is depicted through 10 iterations. As it can be seen, the solution stabilizes after 3 iterations and it stays stable even after 10 iterations. It is also interesting that these iterations do not cause the solution to shrink and produce an overly concentrated solution like the well-known algorithm FOCUSS (Gorodnitsky et al., 1995). This is due to the fact that the regularization term in IRES contains TV and L1 terms which in turn balance between sparsity and edge-sparsity, avoiding overly spread or focused solutions.

Fig. 3.

The effect of iteration. A 10 mm source is simulated and IRES estimation at each iteration, is depicted. As it can be seen the estimated solution converges to the final solution after a few iterations and more so the continuation of the iterations does not affect the solution, i.e. shrink it. The bottom right graph shows the norm of the solution (blue) and the gradient of the solution (green) and also the goal function (red) at each iteration. The goal function (penalizing terms) is the term minimized in (2).

Neighborhood and edge definition

In order to form matrix V which approximates some sort of total variation among the dipoles on the cortex, it is necessary to constitute the concept of neighborhood. Since the cortical surface is triangulated for the purpose of solving the forward problem (using the boundary element model) to form the lead field matrix K, there exists an objective and simple way to define neighboring relationship. The center of each triangle is taken as the location of the dipoles to be estimated (amplitude) and as each triangle is connected to only three other triangles via its edges, each dipole is neighbor to only three other dipoles. Based on this simple relation, neighboring dipoles can be detected and the edge would be defined as the difference between the amplitude of two neighboring dipoles. Based on this explanation it is easy to form matrix V (Ding, 2009) as presented in (4):

$$\begin{array}{l}V=\left(\begin{array}{ccc}{v}_{11}& \cdots & v_{1n}\\ ⋮& \ddots & ⋮\\ v_{T1}& \cdots & v_{Tn}\end{array}\right)\\ \{\begin{array}{ll}{v}_{ij}=1\mathit{and}{v}_{ik}=-1\hfill & if\mathit{dipole}j\mathit{and}k\mathit{are}\mathit{neighbors}\mathit{over}\mathit{edge}i\hfill \\ v_{ij}=0\hfill & \mathit{otherwise}\hfill \end{array}\end{array}$$ (4)

The number of edges is denoted by T. Basically each row of matrix V corresponds to an edge that is shared between two triangles and the +1 and −1 values within that row are located such as to differentiate the two dipoles that are neighbors over that particular edge. The operator V can be defined regardless of mesh size, as the neighboring elements can be always formed and determined in a triangular tessellation (always three neighbors). However reducing the size of the mesh to very small values (less than 1mm) is not reasonable as M/EEG recordings are well-known to be responses from ensembles of postsynaptic neuronal activity. Having small mesh grids will increase the size of V relentlessly without any meaningful improvement. On the other hand increasing the grid size to large values (>1 cm) will also give coarse grids that can potentially give coarse results. It is difficult to give a mathematical expression on this but a grid size of 3~4 mm was chosen to avoid too small a grid size and too coarse a tessellation.

Computer simulation protocol

In order to analyze IRES performance, a series of computer simulations were conducted in a realistic cortex model. The cortex model was derived from MR images of a human subject. The MR images were segmented into three layers, namely the brain tissue, the skull and the skin. Based on this segmentation a three layer BEM model was derived to solve the forward problem and obtain the lead field matrix, constituting the relation between current density dipoles and the scalp potential. The conductivity of the three layers, i.e. brain, skull and skin, were selected respectively as 0.33 S/m, 0.0165 S/m and 0.33 S/m (Oostendorp et al, 2000; Lai et al., 2005; Zhang et al., 2006). The number of recording electrodes used in the simulation is 128 channels. 100 random locations on the cortex were selected and at each location sources with different extent sizes were simulated, ranging from 10 mm to 30 mm in radius size. The amplitude of the dipoles were set to unity, so the cortical surface was partitioned into active (underlying source) and non-active (not included within the source) area. The orientation of the sources were taken to be normal to the cortical surface, as the pyramidal cells located in the gray matter responsible for generating the EEG signals are oriented orthogonal to the cortical surface (Baillet et al., 2001; Nunez et al., 2000). The orientation of the dipoles was accordingly fixed when solving the inverse problem. Different levels of white Gaussian noise were added to the generated scalp potential maps to make simulation more realistic. The noise power was controlled to obtain different levels of desired signal to noise ratio (SNR), namely 10 dB and 20 dB (another set of simulations with 6dB SNR was also conducted as explained in the next paragraph). These SNR values are realistic in many applications including epileptic source imaging. The inverse solutions were obtained using IRES and the estimated solutions were compared to the ground truth (simulated sources) for further assessment. The results of these simulations are presented in Figs. 4 to 6.

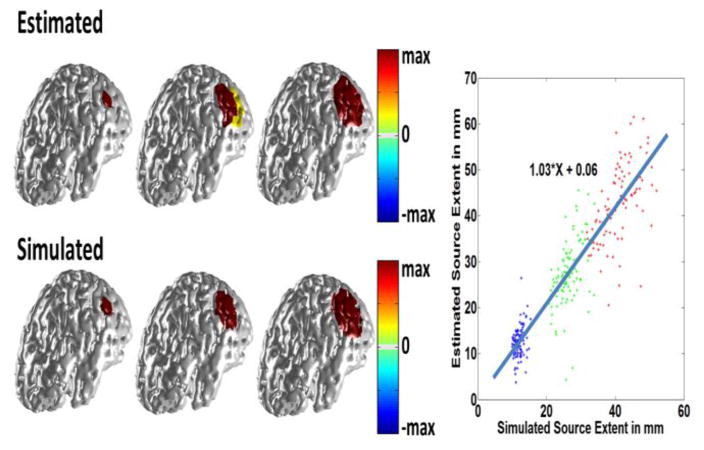
Fig. 4.

Simulation results. In the left panel three different source sizes were simulated with extents of 10 mm, 20 mm and 30 mm (lower row). White Gaussian noise was added and the inverse was solved using the proposed method. The results are shown in the top row. The same procedure was repeated for random locations over the cortex. The extent of the estimated source is compared to that of the simulated source in the right panel. The SNR is 20 dB.

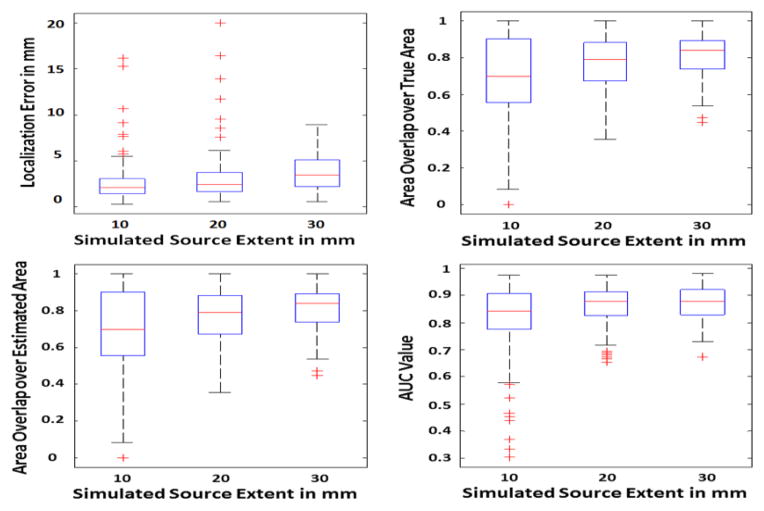
Fig. 5.

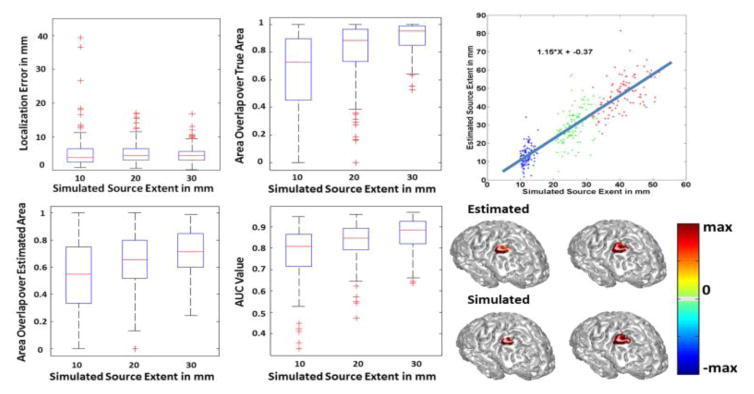
Simulation statistics. The performance of the simulation study is quantified using the following measures, localization error (upper left), AUC (upper right) and the ratio of the area of the overlap between the estimated and true source to either the area of the true source or the area of the estimated source (lower row). The SNR is 20 dB in this study. The simulated sources are roughly categorized as small, medium and large with average radius sizes of 10 mm, 20 mm and 30 mm, respectively. The LE, AUC and NOR are then calculated for the sources within each of these classes. The boxplots show the distribution of each metric to provide a brief statistical review of the distribution of these metrics for all of the data. For more explanation about the metrics and how to interpret them please refer to the methods section of the paper.

Fig. 6.

Simulation statistics and performance of the simulation study when the SNR is 10 dB. Results are quantified using the following measures, localization error, AUC and the ratio of the area of the overlap between the estimated and true source to either the area of the true source or the area of the estimated source. The statistics are shown in the left panel. In the right panel, the relation between the extent of the estimated and simulated source is delineated (top row). Two different source sizes namely, 10 mm and 15 mm, were simulated and the results are depicted in the right panel (bottom row).

In order to compare the effect of modeling parameters on the inverse algorithm and also to avoid the most obvious form of “inverse crime”, another series of simulations were also conducted for which the forward and inverse model was different (in addition to the previous results presented in Figs. 4 to 6). The mesh used for the forward problem was very fine with 1mm spacing consisting of 225,879 elements on the cortex. A BEM model consisting of three layers, i.e. brain, skull and skin with conductivities of 0.33 S/m, 0.015 S/m and 0.33 S/m was used for the forward model. For the inverse model a coarse mesh of 3mm spacing consisting of 28,042 elements was used. The inverse BEM model consists of three layers, i.e. brain, skull and skin with conductivities of 0.33 S/m, 0.0165 S/m and 0.33 S/m. Basically the conductivity ratio is changed by 10% in the inverse model compared to the forward model and also a different and much finer grid is used for the forward model in comparison to the inverse model (Auranen et al, 2005; Auranen et al., 2007). In this manner we reduced the dependency of IRES performance to modeling parameters such as grid size and conductivity values (by using different lead field matrices for forward and inverse). In addition to that, we used realistic noise recorded from a human subject as the additive noise so as to avoid using only white noise. Low SNR of 5~6 dB was also tested following (Gramford et al., 2013), to make sure IRES can be used in noisier conditions. The results of these simulations are presented in Fig. 7 and Fig. 8.

Fig. 7.

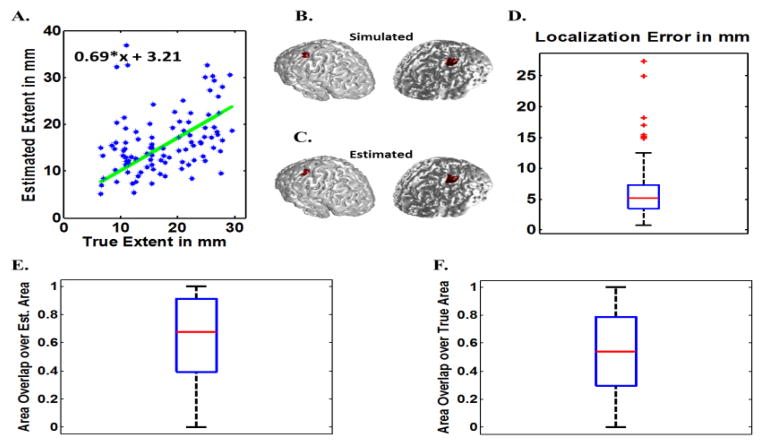
Monte Carlos simulations for differing BEM models with 6 dB SNR (IRES). The estimated source extent is graphed against the true (simulated source) extent (A). Two examples of the target (true) sources (B) and their estimated sources (C) are provided. The localization Error (D), Normalized overlaps defined as overlap area over estimated source area (F) and overlap area over true source area (F), are presented to evaluate the performance of IRES (all data). The boxplots show the distribution of each metric to provide a brief statistical review of the distribution of these metrics for all of the data. For more explanation about the metrics and how to interpret them please refer to the methods section of the paper.

Fig. 8.

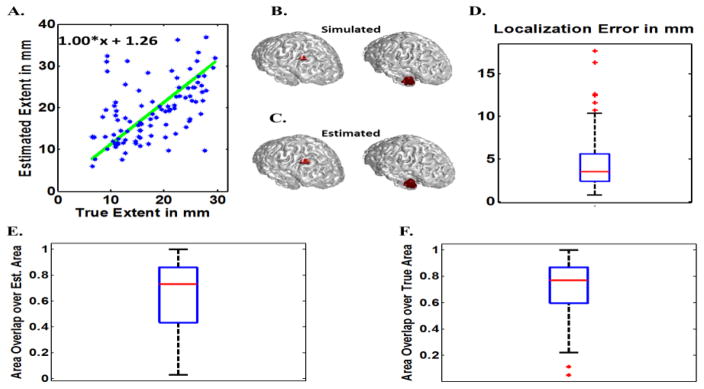
Monte Carlos simulations for differing BEM models with 20 dB SNR (IRES). The estimated source extent is graphed against the true (simulated source) extent (A). Two examples of the target (true) sources (B) and their estimated sources (C) are provided. The localization Error (D), Normalized overlaps defined as overlap area over estimated source area (F) and overlap area over true source area (F), are presented to evaluate the performance of IRES (all data). The boxplots show the distribution of each metric to provide a brief statistical review of the distribution of these metrics for all of the data. For more explanation about the metrics and how to interpret them please refer to the methods section of the paper.

To further assess the effect of slight differences in conductivities on inverse algorithms’ performance, another inverse model was formed and used as well. This inverse model is the same as the inverse model described in the previous paragraph, meaning that in these simulations the grids used for the forward and inverse model were different but the conductivity values were not. The results of the simulations are presented in Fig. S2 and Fig. S3 in the supplementary materials.

Model violations such as non-constant sources (amplitude) and multiple simultaneous active sources were also tested. Additionally cLORETA (Wagner et al., 1996) and focal vector field reconstruction (FVR) (Haufe et al., 2008) were used to estimate solutions and the results from these inverse algorithms were compared with IRES (these results are presented in Figs. S4 and S5 of the supplementary materials).

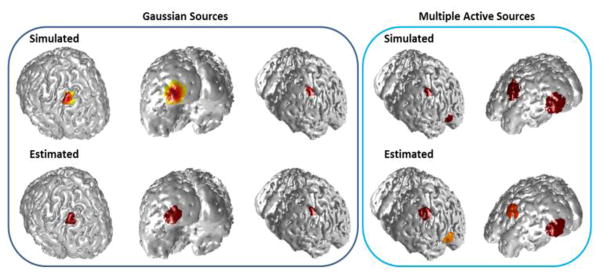
To further evaluate the performance of IRES non-constant sources (for which the dipoles within the source patch did not have constant amplitudes and varied in amplitude) and multiple simultaneously active sources were also simulated and tested. Results of IRES performance are presented in Fig. 9 for multiple cases in these scenarios. More detailed results and analyses are presented in Figs. S6 to S9 of the supplementary materials.

Fig. 9.

Model violation scenarios. Examples of IRES performance when Gaussian sources (left panels) and multiple active sources (right panel) are simulated as underlying sources for a 6 dB SNR. Simulated (true) sources are depicted in the top row and estimated sources on the bottom row. More detailed analysis is provided in the supplementary materials.

Performance measures

In order to evaluate IRES performance, multiple metrics were used. As extended sources are being considered in this study, appropriate metrics being able to compare extended sources need to be used. The first measure is the localization error (LE). The localization error calculates the Euclidean distance between the center of mass of the simulated and estimated sources. In order to compare the shape and relative position of the estimated and simulated sources the overlap metric is used. The amount of overlap between the estimated and simulated sources is calculated and divided by either the simulated source area or the estimated source area to derive a normalized overlap ratio (NOR). This normalized overlap shows how well the two distributions match each other. These measures should both be as close as possible to 1. If an overestimated or underestimated solution is obtained, one of the two measures can be close to 1 while the other decreases significantly. Another important measure is the area under curve (AUC) analysis (Grova et al., 2006). The curve mentioned is the receiver operating characteristics (ROC) curve (Kay, 2011). The AUC enables us to compare two source distributions (one is the estimated source distribution and the other one is the simulated source). The closer this AUC value is to 1, the better our estimation of the simulated source will be.

Clinical data

In order to determine if IRES could be used in practical settings and ultimately translated into clinical settings, the proposed algorithm was also tested in patients suffering from partial (focal) epilepsy. Three patients were included in this study. All clinical studies were conducted according to a protocol approved by the institutional review board (IRB) of Mayo Clinic, Rochester and the University of Minnesota. All patients had pre-surgical recordings with multiple inter-ictal spikes in their EEG recording. Two of the patients were suffering from temporal lobe epilepsy (TLE) and one was diagnosed with fronto-parietal lobe epilepsy. All three patients underwent surgery and were seizure free at one year post-operation follow-up. Two of the patients also had intracranial EEG recordings (before surgery) from which the seizure onset zone (SOZ) and spread activity electrodes were determined (Fig. 10). All patients had pre-surgical MRI as well as post-surgical MRI images (An example of pre/post-surgical MRI images is presented in Fig. S10 of the supplementary materials). The pre-surgical MRI was used to form individual realistic geometry head models, i.e. BEM models, for every patient. The BEM model composed of three layers. The conductivity of the three layers, i.e. brain, skull and skin, were selected respectively as 0.33 S/m, 0.0165 S/m and 0.33 S/m (Oostendorp et al, 2000; Lai et al., 2005; Zhang et al., 2006). The post-op MRI was used to locate and segment the surgical resection to later compare with IRES estimated solution. The EEG recordings were filtered with a band-pass filter with cut-off frequencies set at 1 Hz and 50 Hz. Inter-ictal spikes were searched for, through patient EEG recordings prior to operation, and were checked for scalp map consistency and temporal similarities. The spikes that were repeated more often were included in the analysis. The spikes were averaged around the peak of their mean global field power (MGFP) to produce a single averaged spike; on average 10 spikes were averaged for this study. These averaged spikes were then used for further source imaging analysis. The electrode montage used for these patients contained 76 electrodes (Yang et al., 2011) and the electrode locations were digitized and used in the inverse calculation. The estimated solution by IRES is compared to the surgical resection surface (as IRES is currently confined to cortical surface) and SOZ whenever available.

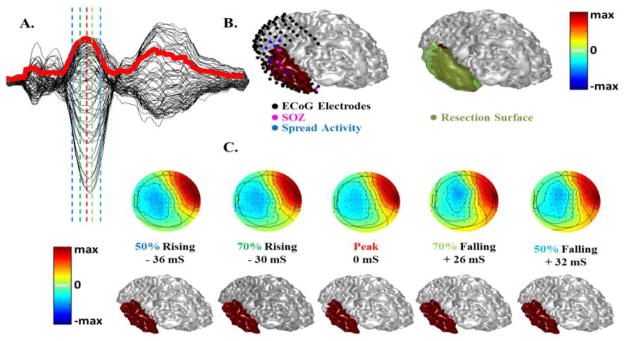
Fig. 10.

Source extent estimation results in a patient with temporal epilepsy. (A) Scalp EEG waveforms of the inter-ictal spike in butterfly plot on top of the mean global field power (in red). (B) The estimated solution at Peak time (by VIRES) is shown on top of the ECoG electrodes and SOZ (left) and the surgical resection (right). (C) Scalp potential maps and estimation results of source extent at different latency of the interictal spike.

Implementation

The BEM based forward problem was solved using CURRY 7 (Compumedics, Chalotte, NC). The cortical surface was triangulated into 1 mm and 3 mm mesh for the computer simulations and clinical data analysis. In order to solve the SOCP problem which is the backbone of IRES a convex problem solver called CVX (Grant & Boyd, 2008; Grant & Boyd, 2013) was used. CVX contains many solvers including the self-dual-minimization (SeDuMi) (Strum, 1999) which is a MATLAB (Mathworks, Natick, MA) compatible package implementing an interior path method (IPM) for solving the SOCP problems. It takes about 2–4 minutes to solve (3) at each iteration on widely available desktop computers (3.4 GHz CPU and 4 Gbytes RAM). Although such a computation time is about 20 times that of MN-like algorithms, it is not too lengthy and IRES can be solved in reasonable time. While we have not developed a specific solver for IRES and used a general solver, i.e. CVX, it is reasonable to assume that the running time can be improved with tailored algorithms specifically designed for IRES.

Results

Computer Simulations

Fig. 4 through Fig. 6 show simulation results using the same lead field matrix for forward and inverse problem. The results presented in figures 4 and 5 pertain to the case were the SNR of the simulated scalp potential is 20 dB and the same results are presented in figure 6 for the 10 dB case. As it can be seen in Fig. 4 IRES can distinguish between different source sizes and estimate the extent with good accuracy. In the left panel of Fig. 4, three different cases are presented with extents of 10, 20 and 30 mm, respectively. Comparing the simulated sources and estimation results shows that IRES can distinguish between different sources reasonably. The right panel in Fig. 4 shows the relation between the extent of the estimated and simulated source. The fitted line shows that IRES has small bias and minimal under/over-estimation on average. The variance of the estimated solutions is comparable to the estimated extent (about 50% of source extent). The overall trend is positive and indicates that IRES is relatively unbiased in estimating underlying source extent.

Other measures such as LE, NOR and AUC are also important to assess the performance of IRES. In Fig. 5 the results of such different metrics can be seen. The localization error in sources with different extent is less than 5 mm over all. Note that the simulated sources were approximately categorized into three classes with average extent of 10, 20 and 30 mm, corresponding to the three colors seen in Fig. 4. This value is less for smaller sources and closer to 3 mm. Such a low localization error shows that IRES can localize the underlying extended sources with low bias. Actually there a few cases (where the LE is greater than 12 mm) for which the simulated sources were split between the two hemispheres with an unconventional geometry, thus the solution was a bit widespread and not good. However some of the cases simulated in deeper regions like the medial temporal lobe or the medial wall of the inter-hemisphere have errors in the range of 5–10 mm. Results of some difficult simulation cases are provided in Fig. 12 and discussed further in the Discussion section. Additionally, to better understand the combined effect of LE and extent estimation, the normalized overlaps should be studied. Looking at Fig. 5 one can see that the overlap between the estimated and simulated source is relatively high and over 70% for smaller sources (on average) and close to 85% for larger sources. The fact that both NOR values are high show that not only the estimated and simulated sources overlap extensively with each other, but the estimation is neither an overestimation nor an underestimation of the spatial extent (in either case only one of the NOR values would be high and the other would be small). The high AUC values for various source sizes also indicate the overall high sensitivity and specificity of IRES as an estimator.

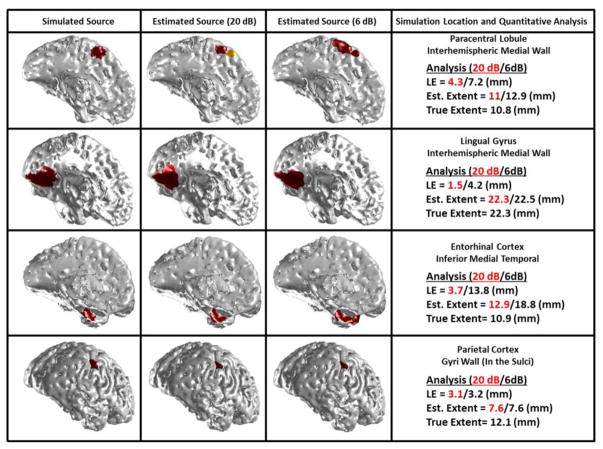
Fig. 12.

IRES sensitivity to source location and depth. Simulation results for four difficult cases are presented in this figure for two SNRs, i.e. 20 and 6 dB. The sources were simulated in the medial wall located in the interhemispheric region, medial temporal wall and sulci wall. The orientation of some of these deep sources is close to tangential direction.

Fig. 6 shows the same results for the 10 dB case. Comparing Fig. 6 with Fig. 5 and Fig. 4 similar trends can be observed.

Fig. 7 and Fig. 8 show simulation results when different forward and inverse models (in terms of grid size and conductivity) are used for two cases of 6 dB and 20 dB SNR. The results in Fig. 7 show an underestimation for the extent. The localization error is as low as 5 mm and the NOR is ~60%–70% on average. Comparing the same results when SNR is set to 20 dB, much better results can be obtained. Referring to Fig. 8 it can be seen that the extent estimation is with minimal bias with localization error of 3 mm (on average) and high NOR metrics (80% for both values on average). The slight decline in IRES performance in noisier conditions (Fig. 6 and Fig. 7) is expected due to increased levels of noise interference.

A few examples when source amplitude is not constant and also when multiple sources are simultaneously active, are presented in Fig. 9. The variation of source amplitude was governed by a normal distribution, meaning that the amplitude of the dipoles decreased exponentially as the distance of the dipoles increased from the center of the source distribution (patch). More detailed analysis and explanations are presented in supplementary materials.

These simulation results show that IRES is robust against noise and changes in model parameters such as grid size and conductivity. IRES can perform well when multiple sources are active or when source amplitude varies within the source extent.

Clinical Data Analysis

The patient data analysis is summarized in figures 10 and 11. Fig. 10 shows the results of a temporal lobe epilepsy patient who underwent invasive EEG recording and ultimately surgical resection. In this case different timing was tested to examine the effect of estimation results at different time instances around the peak. It can be seen in Fig. 10a, that five different timings (instances) were tested, two prior to peak time, the peak time and two after the peak corresponding to 50% and 70% rising phase, peak and 70% and 50% falling time. Looking at the estimated solution at different timings, it is clear that the solution is stable within tens of milliseconds around the peak and the epileptic activity does not propagate too much. This might be due to the fact that the averaged inter-ictal spikes arise from the irritative zone which is larger than the SOZ, so the propagation of activity might not even be observable using the average spike. Comparing the results of IRES with the resection in Fig. 10b it can be seen that the estimated solution coincides within the resection very well. Looking at the SOZ electrodes colored pink in Fig. 10b it is also observed that the SOZ electrodes are covered by the solution. SOZ region is very focal so it is challenging to obtain a solution which can be in full concordance with it and as it can be seen, sometimes the SOZ region is not continuous (electrodes are not always right next to each other); nonetheless the estimated solution by IRES is in concordance with the clinical findings.

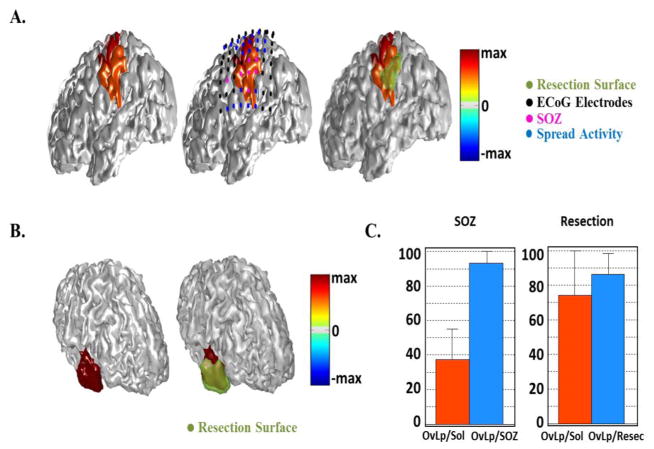
Fig. 11.

Source extent estimation results in all patients. (A) Estimated results by IRES in a parietal epilepsy patient compared with SOZ determined from the intracranial recordings (middle) and surgical resection (right). (B) Estimation results of source extent computed by VIRES in another temporal epilepsy patient compared with surgical resection. (C) Summary of quantitative results of the source extent estimation by calculating the area overlapping of the estimated source with SOZ and resection. The overlap area is normalized by either the solution area or resection/SOZ area.

In order to further test the proposed IRES approach two more patients were studied; one temporal case with anterior tip of temporal lobe resection (and thus a smaller resection area) and an extra-temporal case (fronto-parietal). Referring to Fig. 11a it can be seen that the estimated solution includes most of the SOZ electrodes and coincides well with the resection. This implies that IRES does well for extra-temporal lobe cases as well as temporal cases. Given the fact that not all the SOZ electrodes are close to the resection, the estimated solution is a bit spread towards those SOZ electrodes and the neighboring regions thus extending beyond the resected region. In Fig. 11b the results of the second temporal case can be found. This patient did not have any intra-cranial EEG recordings. Fig. 11c reports the quantitative analyses for these three patients. In order to assess how well the estimated results match the clinical findings, the overlap between the solution and the resection and the SOZ was calculated. Then this overlap area was either divided by the solution area or the resection/SOZ area. The results are classified as resection and SOZ indicating the clinical finding, i.e. SOZ or resection, used to assess the estimated solutions.

Looking at Fig. 11c it can be seen that the IRES solution generally covers the SOZ very well but also extends beyond the SOZ giving an overestimated solution. Looking at the right bar-plot it can be seen that this is not the case when comparing the IRES solution to resected area.

Note that for temporal lobe epilepsy cases, due to more geometrical complexity of the cortex in the temporal region (compared to other locations within the brain) and the fact that mesio-temporal region is not directly recorded by the electrodes over the temporal region, Vector-based IRES (VIRES) was used instead of IRES (mathematical details of VIRES are given in Appendix B). VIRES basically relaxes the orientation constraint of the dipoles (being orthogonal to the cortical surface as implemented by IRES) and leaves that as a variable to be estimated.

In this paper the clinical analysis presented was intended as a proof-of-concept study to show the feasibility of using IRES for epilepsy source imaging. Further investigation in a large number of patients and also with different number of electrodes, needs to be done in the future. Careful comparison of the IRES results to existing techniques is also necessary for future studies, although we have presented a comparison with cLORETA in one case (as an example) (Fig. S11 supplementary materials). Some recent literature in identifying extended sources of inter-ictal spikes is noteworthy (Chowdhury et al., 2013; Heers et al., 2015). In these works the MEM-type optimization alongside cortical parcelization is proposed to find extended sources.

Testing IRES on Public Data Sets

In order to further evaluate IRES, the algorithm was tested on the Brainstorm epilepsy data (Tadel et al., 2011) which is publicly available at (http://neuroimage.usc.edu/brainstorm). This tutorial includes the anonymous data of a patient suffering from focal fronto-parietal epilepsy, who underwent surgery and is seizure-free within a 5 year follow-up duration (http://neuroimage.usc.edu/brainstorm/Tutorials/Epilepsy). The data in this tutorial were originally analyzed and published in a paper by Dümpelmann et al. (Dümpelmann et al., 2012). The patient underwent iEEG recording prior to surgery. The iEEG study results as well as the post-operational MRI are not available in the data set but are presented in the published paper (Dümpelmann et al., 2012). The procedure outlined in the Brainstorm tutorial was followed to get the average spikes and the head model, with the exception of the head model conductivity (ratio) for which we used the conductivities we have used so far, throughout the paper.

Fig. S12 (supplementary materials) shows the IRES solutions in this data set. Comparing these results with the clinical findings reported in (Dümpelmann et al., 2012), the obtained results are in well accordance with such findings. Additionally the source localization is performed using the cMEM algorithm (Grova et al., 2006) on another Brainstorm tutorial (http://neuroimage.usc.edu/brainstorm/Tutorials/EpilepsyBest?highlight=%28cMEM%29). Comparing IRES and cMEM results, it can be seen that the two solutions are concordant.

Discussion

In this paper a new inverse algorithm is proposed, namely the iterative reweighted edge sparsity (IRES). As the simulation results suggest, this algorithm is capable of distinguishing between sources with different sizes. The simulation results suggest that IRES not only localizes the underlying source but can also provide an estimate of the extent of the underlying source, as well. Moreover one of the main merits of IRES is that it produces extended sources without the need for any kind of thresholding. The initial clinical evaluation study in focal epilepsy patients also shows good concordance between clinical findings (such as resection and SOZ) with IRES solution. This suggests the practicality of IRES in clinical applications such as pre-surgical planning for pharmacoresistant focal epilepsy. Although we tested the IRES in imaging focal epilepsy sources, IRES is not limited to epilepsy source localization, but is applicable to imaging brain sources in other disorders or in healthy subjects from noninvasive EEG (or MEG).

Merits and novelty of IRES and parameter selection

Many algorithms have been proposed in the recent years that work within the sparse framework and are thus capable of producing relatively focal solutions. Some of these methods enforce sparsity on multiple domain like IRES (Chang et al., 2010; Haufe et al., 2008; Zhu et al., 2014), but neither of the aforementioned algorithms provide solutions with clear edges between background and desired activity and thus determining how to discard the tails of the solution distribution, i.e. thresholding, is difficult. IRES, on the other hand, achieves this by imposing sparsity on the spatial gradient which in turn creates visible edges. It is essential to note that some of the aforementioned algorithms do not intend to find the extent of the underlying sources like IRES and instead aim to model other physiologically plausible characteristics. Furthermore, it should not be assumed that all the existing methods in the literature resort to thresholding to separate brain activity from noisy background activity. Examples of these methods are the Gaussian dictionary based method by Haufe et al. (Haufe et al., 2011) and the Bayesian methods (Grova et al., 2006; Chowdhury et al., 2013; Lina et al., 2014).

Algorithms formulated and operating within the Bayesian framework seem to be promising algorithms, such as MEM-type algorithms (Grova et al., 2006). Additionally the combination of cortex parcelization with these algorithms (Chowdhury et al., 2013; Lina et al., 2014) makes it even stronger. These algorithms use Otsu’s thresholding method (Otsu, 1979) to separate the background noise from active sources objectively. However, there is an implicit assumption in Otsu’s method that classes (say, background and desired signal) are distinguished enough, to be separated well with a threshold. In our experience this depends on the inverse method used. Most conventional methods do not provide strong discriminants. This means that the threshold might not be “unique” in practice. Furthermore, no parcelization is used in IRES. Additionally IRES does not work within the Bayesian framework and is formulated as a series of convex optimization problems. Bayesian methods usually have complex formulations and take long to run.

Mixed norm methods have also proven to be effective in analyzing spatio-temporal activity of underlying brain sources (Gramfort et al., 2012; Gramfort et al., 2013a). However as mentioned before these methods enforce sparsity on solution and are thus highly focused (Gramfort et al., 2013a).

IRES basically operates within a TV-L1 framework. This means that the sparsity is enforced on the edges as well as the solution itself. Within this framework data driven iterative reweighting are applied to IRES estimates at each step to get rid of small amplitude dipoles to obtain more accurate estimates. The formulation of IRES is simple yet effective and as tested by our extensive simulations, provides useful information about the source extent.

Solutions derived based on sparse signal theory are proven to be mathematically optimal under certain mathematical conditions (Candès et al., 2006a) whether sparsity is applied on the solution or another appropriate domain such as wavelet coefficients (Candès et al., 2006b). This means that no other algorithm can provide solutions that are fundamentally better. Although these mathematical conditions do not hold for the electrophysiological source imaging (ESI) problem (due to ill-conditioned lead field matrices), still there is an increasing trend in applying sparse methods to ESI problems in recent years as indicated by the recent literature and the results presented in this work.

Another feature of IRES is its iterative reweighting technique. This procedure has enabled IRES to improve the estimation by disregarding the locations that are more probable to lie outside the extent of the underlying source. Since the amplitude of the dipoles corresponding to locations outside the underlying source is smaller than dipoles closer to or within the underlying source (this is due to the formulation of the problem where spatially focused sources with zero background are preferred) it is reasonable to focus less on locations for which the associated dipoles have very low amplitudes. Additionally, after a few iterations, IRES converges to a solution which is zero in the background, i.e. a focused solution is obtained, so an extended solution is reached without applying any threshold. Due to the limited number of iterations and mostly due to the way existing convex optimization problems solvers work (Bolstad et al., 2009) a perfect zero background might not be obtained but the amplitude of dipoles located in the background is typically less than 3% of dipoles with maximum amplitude.

The two features of IRES, namely the iteration and use of sparse signal processing techniques, makes IRES unique and can also explain the good performance of IRES in providing extended solutions which estimate the extent of the underlying source well. The parameters of the SOCP optimization problem in (3) need to be selected carefully, for IRES to work well. As discussed previously the L-Curve approach is adopted to determine α. The L-Curve in general is a tool to examine the dependency of level sets of the optimization problem to a certain parameter of the problem when the constraints are fixed. In our problem when β is determined (β intuitively determines noise level and is calculated based on the discrepancy principle) the constraint is fixed and then for different values of α the optimization problem is solved to find the optimum solution of the optimization problem for the given α. For the obtained solution j^* the pair (||j||₁* and ||Vj||₁*) are graphed in a plot like Fig. 2 (||j||₁ and ||Vj||₁are the two terms of the goal function in (2)). The curve obtained for different values of α (level set of the goal function) which are the best pair of (||j||₁, ||Vj||₁) that can be achieved given a fixed constraint and a fixed α value, can show the dependency of the two terms on parameter α. If the curve has a clear pointed bending (knee), selecting the value of α around the knee is equal to selecting the Pareto-optimal pair (this means that for any other value of α that is selected, either ||j||₁ or ||Vj||₁ will be larger than the values of ||j||₁ or ||Vj||₁ of the knee). In this manner the (Pareto) optimal value of α is selected (Boyd and Vandenberghe, 2004). Another way to think about this is to imagine that for a fixed budget (β) the dependence curve of costs (||j||₁ and ||Vj||₁) are obtained (also called “utility curve” in other fields such as microeconomics). The best way to minimize costs is to find the cost pair (||j||₁* and ||Vj||₁*) for which all other pairs are (Pareto) greater, meaning that either one will be larger (compared to ||j||₁* and ||Vj||₁*). In the framework of Pareto-optimality the L-Curve formed from the level sets of the optimization problem, can determine the optimal value of α. The hyper-parameter β is determined using the discrepancy principle (Morozov, 1966). β ultimately determines the probability of capturing noise. Another way to look at this is to note that β determines how large the constraint space will be. In other words, selecting a larger β corresponds to searching for an optimal solution within a larger solution space; this translates into relaxing the parameters of the optimization problem. The manner in which the hyperparameters of IRES are defined is intuitive and bares physical meaning and thus tuning the hyperparameters can be done easily and objectively (as opposed to hyperparameters that are merely mathematical).

Model Validity

Considering the domain in which sparsity is imposed in IRES one might wonder if this model is completely right, that is to assume that underlying sources are spatially focused activities with constant value within their extent. It is not easy to answer this question. In practice EEG/MEG signals arise from the mass response of a large number of neurons which fire synchronously. Thus it is reasonable to assume that variations within the source extent, are hard to be detected from EEG/MEG recordings. Even in data recorded from intracranial EEG the region defined as SOZ by the physician seem to have a uniform activity, i.e., piecewise continuous activity over the recording grid (Lu et al., 2012b). From a simplistic modeling point of view (and as a first step) the assumption is defendable. Face-based wavelets (Zhu et al., 2014) and spherical wavelet transforms (Chang et al., 2010) have also been used to model sources but none of the clinical data analysis presented in these papers shows solutions with varying amplitudes.

Ill-posedness of the problem and geometrical complexities of the cortex

Note that while IRES provides information regarding the extent of the underlying source, it is still dealing with an underdetermined system and thus the extent information is not exact. Referring to Figs. 4 to 8 it can be seen that there is still a noticeable amount of variance in extent estimation (almost half of the true extent). Yet the fact that the general trend of IRES in estimating the extent is correct and distinguishes between sources with extents as small as 8 mm to as large as 50 mm is encouraging.

Sensitivity to source location, depth and orientation

The accuracy of ESI results can vary depending on the source location and orientation. It is well-known that deep sources are more difficult to resolve than superficial sources. Additionally tangential source orientations might be more difficult for EEG to detect (as normal orientations are more difficult to be detected by MEG). This adds further complexity to the already difficult inverse problem. IRES is not different from all other ESI algorithms in this aspect and will not function well under every circumstance. Some difficult cases where the simulated sources were deep or more tangentially located (in the inter-hemisphere wall or on the medial wall of the temporal lobe) are presented as examples in Fig. 12 (these cases are included in the statistical results presented so far). As it can be seen, specifically in the first row image, in highly noisy conditions (SNR of 6 dB, third column), IRES did not do very well in determining the extent or shape of the source. Still IRES does not totally fail in determining the location and extent of the source in these very difficult conditions. In less noisy conditions (second row), IRES does well.

Future works and improvements on IRES

In this work the focus was not to develop a specific solver for IRES. It is more a proof-of-concept project where the capabilities and usefulness of IRES are evaluated. As a result the CVX software which is a general solver for convex optimization problems was used. To name a few of the recent solvers and algorithms that have gained attention in the recent years one should mention the alternating direction method of multipliers (ADMM) (Boyd et al., 2011) and the fast iterative shrinkage thresholding algorithm (FISTA) (Beck and Teboulle, 2009). Implementing these algorithms for solving IRES can improve the speed and efficiency of the solver (compared to general solvers such as CVX).

Referring to the clinical data analyzed in this study it is observed that the area of the estimated source is on average 2 times the SOZ area while comparable to resected area. Although we did not attempt to directly answer whether IRES can provide estimates that are comparable to SOZ or not, this is an important question that needs further investigation. This does not solely depend on IRES or the inverse algorithm per se, but also to the input fed into the inverse algorithm. In the clinical data analysis presented here, inter-ictal spikes have been analyzed. It is generally agreed upon that inter-ictal spikes arise from the irritative zone which is known to be larger than the SOZ (Rosenow & Luders, 2001). High frequency oscillations on the other hand are shown to be very focal and more concordant with SOZs compared to inter-ictal spikes (Worrell et al., 2008). Lu et al. performed a study to show that source localization based on HFO’s detected in scalp EEG are more accurate than inter-ictal spikes (Lu et al., 2014). Thus it is interesting to extract HFOs from scalp EEG recordings of focal epilepsy patients and feed them into IRES to see if better results can be achieved; better in the sense that the estimated solution area is comparable to SOZ.

The idea of trying to determine the underlying epileptic source is important since one third of epilepsy patients do not respond to medication (Cascino, 1994). Surgical resection is a viable option for patients with focal epilepsy within this pharmacoresistant population. Currently the gold standard is to use intracranial EEG to determine SOZ (Engel, 1987). This is highly invasive with all the risks associated with such procedures. Being able to non-invasively determine the SOZ and assist the physician in determining the location and size of the epileptogenic tissue can improve the quality of life for many patients.

In the current work, only a limited number of patients were studied as a proof-of-concept for potential clinical application of IRES to localize and image epileptogenic zone in patients. Further investigation in a large number of patients is needed to determine the usefulness of IRES in aiding pre-surgical planning in epilepsy patients. Additionally, it would be interesting to study the effect of electrode number on solution precision (within the new framework). While there are several studies suggesting that increasing the number of electrodes helps improve source localization results significantly (Brodbeck et al., 2011; Lantz et al., 2003; Michel et al., 2004a; Sohrabpour et al., 2015; Srinivasan et al., 1998), determining the relation between the number of electrodes and solution precision awaits future experimentation. Whether plateauing effects will be observed as suggested by Sohrabpour et al. (Sohrabpour et al., 2015) or not, can only be determined after further investigations (specifically in clinical data).

In the current work, the solution space was limited to the cortical space. It is necessary to investigate if IRES can be generalized to include a solution space that encompasses the three dimensional brain volume.

The presented form of IRES in this paper was intended for single time-points as opposed to spatio-temporal analysis. This is due to the fact that it was intended to show the feasibility of this algorithm and its applicability in real data recordings. Spatio-temporal algorithms (Gramfort et al., 2013a; Ou et al., 2009) are important as the dynamics of the underlying brain sources captured by EEG/MEG has to be studied properly to better understand brain networks. Following Ou et al. (Ou et al., 2009), a temporal basis can be extracted from the EEG recordings onto which the data is projected. This basis can be derived from principle component analysis (PCA), independent component analysis (ICA) and time-frequency analysis of the data (Gramfort et al., 2013a; Yang et al, 2011). In any case, IRES can be incorporated into the spatio-temporal basis and by no means is limited to single time-points, at all. We present here the IRES strategy and results for single time-points source imaging as this problem is fundamental to spatio-temporal source imaging. Spatio-temporal IRES imaging needs further investigation and will be pursued in the future.

Conclusion

We have proposed the iteratively reweighted edge sparsity minimization (IRES) strategy for estimating the source location and extent from EEG/MEG. We demonstrated, using sparse signal processing techniques, that it is possible to extract information about the extent of the underlying source objectively. The merits of IRES have been demonstrated in a series of computer simulations and tested in epilepsy patients undergoing intracranial EEG recordings and surgical resections. The present simulation and clinical results indicate that IRES provides source solutions that are spatially extended without the need to threshold the solution to separate background activity from active sources under study. This gives IRES a unique standing within the existing body of inverse algorithms. The present results suggest that IRES is a promising algorithm for source extent estimation from noninvasive EEG/MEG, which can be applied to epilepsy source imaging, determining the location and extent of the underlying epileptic source, as well as other brain source imaging applications.

Highlights.

• A new inverse imaging strategy suitable for estimating extended sources from EEG/MEG is proposed.

• The sparsity of the source is exploited in multiple domains using an iterative method.

• No thresholding is required to obtain extended-source solutions.

• The proposed algorithm can estimate the source extent within reasonable error bounds.

• A potential application of the method is to estimate the source extent in epilepsy patients.

Appendix A

Weighting Strategy for IRES

Assuming that our problem is the following, where C is a convex set:

$$\begin{array}{l}{x}^{\mathit{est}}={\text{argmin}}_x{\left|\right|x\left|\right|}_1\\ \mathit{subject}tox\in C\end{array}$$ (A1)

It is reformulated as follows where ε is a positive number,

$$argminln(\frac{\mid x\mid }{\epsilon }+1)x\in C$$ (A2)

In order to solve (A2) we linearize the logarithm function about the solution obtained in the previous step using the Taylor expansion’s series as follows,

$$\begin{array}{l}{x}^{k+1}={\text{argmin}}_{x}ln(\frac{\mid x\mid }{\epsilon }+1)x\epsilon C\\ ln(\frac{\mid x\mid }{\epsilon }+1)=ln\left(\frac{\mid x^k\mid }{\epsilon }+1\right)+\frac{1}{\epsilon }·\left(\frac{1}{\frac{\mid x^k\mid }{\epsilon }+1}\right)·(x-x^k)+O(x^2)\end{array}$$ (A3)

Substituting the linearized logarithm into the optimization problem and noting that x^k is treated as a constant (as the minimization is with respect to x) the following optimization problem is achieved,

$$\begin{array}{l}{x}^{k+1}={\text{argmin}}_x\left(\frac{x}{\frac{\mid x^k\mid }{\epsilon }+1}\right)={\text{argmin}}_x{W}^{k}xs.t.x\epsilon C\\ W^k=\left(\frac{x}{\frac{\mid x^k\mid }{\epsilon }+1}\right)\end{array}$$ (A4)

Note that x was treated as a scalar here. In our case where x is a vector the weighting is derived for each element individually and finally placed into a diagonal matrix format. This is how (3) is derived. Treating (Vj)as a vector, i.e. y = Vj, the same procedure can be followed to update W_d.

Appendix B

Vector-based iteratively reweighted edge sparsity minimization (VIRES)

Applying the same idea as in IRES to the case where the orientation is not fixed can be easily done. It is also possible to assume that each of the three dimensions of the dipole is an independent variable; in that case following the procedure described in Appendix A and (3) needs to be followed. Another way to approach the problem is to penalize the amplitude of the vector in the penalization terms as the variable under study is a vector now. It is necessary to note that matrix V which approximates the discrete gradient must be expanded three time using the Kronecker product, V_New = V ⊗ I₃ where I₃ is the 3×3 identity matrix. Following what was derived in (3) it is easy to get the following,

$$\begin{array}{l}{j}^L=\underset{j}{\text{argmin}}\sum _{i=1}^T{W}_d^{L-1}(i,i){\left|\right|V_{\mathit{New}(i,:)}j\left|\right|}_2+\alpha \sum _{p=1}^n{W}^{L-1}(p,p){\left|\right|[j_p(x),j_p(y),j_p(z)||}_2\\ \mathit{subject}to{(\phi -Kj)}^T{\mathrm{\sum }}^{-1}(\phi -Kj)\le \beta \\ W^L,W_d^L\to \mathit{Updated}\mathit{based}on{j}^L\end{array}$$ (B1)

Where T is the number of edges and n is the number of dipole locations. Also V_New(i,:) denotes the rows of V_New that correspond to the i^th edge. These correspond to the 3*i-2^th to the 3*i^th rows of V_New.

Following the steps in Appendix A it is easy to obtain the update rule for the weights at iteration L as follows,

$$W^L(p,p)=\left(\frac{1}{\frac{{\left|\right|\left[j_p^{L-1}(x),j_p^{L-1}(y),j_p^{L-1}(z)\right]\left|\right|}_2}{\epsilon }+1}\right)\mathit{for}p=1,2,\dots ,n$$ (B2)

$$W_d^L(i,i)=\left(\frac{1}{\frac{{\left|\right|V_{\mathit{New}(i,:)}{j}^{L-1}\left|\right|}_2}{\epsilon }+1}\right)\mathit{for}i=1,2,\dots ,T$$ (B3)