Abstract
Monaural speech separation is a fundamental problem in robust speech processing. Recently, deep neural network (DNN)-based speech separation methods, which predict either clean speech or an ideal time-frequency mask, have demonstrated remarkable performance improvement. However, a single DNN with a given window length does not leverage contextual information sufficiently, and the differences between the two optimization objectives are not well understood. In this paper, we propose a deep ensemble method, named multicontext networks, to address monaural speech separation. The first multicontext network averages the outputs of multiple DNNs whose inputs employ different window lengths. The second multicontext network is a stack of multiple DNNs. Each DNN in a module of the stack takes the concatenation of original acoustic features and expansion of the soft output of the lower module as its input, and predicts the ratio mask of the target speaker; the DNNs in the same module employ different contexts. We have conducted extensive experiments with three speech corpora. The results demonstrate the effectiveness of the proposed method. We have also compared the two optimization objectives systematically and found that predicting the ideal time-frequency mask is more efficient in utilizing clean training speech, while predicting clean speech is less sensitive to SNR variations.
Keywords: Deep neural networks, ensemble learning, mapping-based separation, masking-based separation, monaural speech separation, multicontext networks
I. Introduction
Monaural speech separation aims to separate the speech signal of a target speaker from background noise or interfering speech from a single-microphone recording. In this paper, we focus on the problem of separating a target speaker from an interfering speaker. This problem is challenging because the target and interfering speakers have similar spectral shapes. A solution is important for a wide range of applications, such as speech communication, speech coding, speaker recognition, and speech recognition (e.g. [23], [33]). It is theoretically an ill-posed problem with a single microphone, and to solve this problem, various assumptions have to be made. Recently, supervised (data-driven) speech separation has received much attention [30]. Based on the definition of the training target, supervised separation methods can be categorized to (i) masking-based methods and (ii) mapping-based methods.
Masking-based methods learn a mapping function from a mixed signal to a time-frequency (T-F) mask, and then use the estimated mask to separate the mixed signal. These methods typically predict the ideal binary mask (IBM) or ideal ratio mask (IRM). For the IBM [29], a T-F unit is assigned 1, if the signal-to-noise ratio (SNR) within the unit exceeds a local criterion, indicating target dominance. Otherwise, it is assigned 0, indicating interference dominance. For the IRM [24], a T-F unit is assigned some ratio of target energy and mixture energy. Kim et al. [20] used Gaussian mixture models (GMM) to learn the distribution of target and interference dominant T-F units and then built a Bayesian classifier to estimate the IBM. Jin and Wang [19] employed multilayer perceptron with one hidden layer, to estimate the IBM, and their method demonstrates promising results in reverberant conditions. Han and Wang [12] used support vector machines (SVM) for mask estimation and produced more accurate classification than GMM-based classifiers. May and Dau [22] first used GMM to calculate the posterior probabilities of target dominance in T-F units and then trained SVM with the new features for IBM estimation. Their method can generalize to a wide range of SNR variation.
Recently, motivated by the success of deep neural networks (DNN) with more than one hidden layer, Wang and Wang [32] first introduced DNN to perform binary classification for speech separation. Their DNN-based method significantly outperforms earlier separation methods. Subsequently, Wang et al. [31] examined a number of training targets and suggested that the IRM should be preferred over the IBM in terms of speech quality. Huang et al. [14], [15] used DNN and recurrent neural network (RNN) to minimize the reconstruction loss of the spectra of two premixed speakers by embedding the IRM into the loss function (later called signal approximation in [35]). The method demonstrates significant performance improvement over standard NMF based methods. Weninger et al. [35] took signal approximation (SA) as the optimization objective and introduced long short-term memory (LSTM) structure into RNN which outperforms DNN and NMF based methods. Erdogan et al. [9] and Weninger et al. [34] further extended the SA to a phase-sensitive case and used LSTM for speech denoising. Williamson et al. [36] proposed complex ratio masking for DNN based monaural speech separation, which learns the real and imaginary components of complex spectrograms jointly in the Cartesian coordinate system instead of learning magnitude spectrograms only in the traditional polar coordinate system. The method improves speech quality significantly.
Mapping-based methods learn a regression function from a mixed signal to clean speech directly, which differs from masking-based methods in optimization objectives. Xu et al. [37]–[38] trained DNN as a regression model to perform speech separation and showed a significant improvement over conventional speech enhancement methods. Han et al. [13], [11] used DNN to learn a mapping from reverberant and reverberant-noisy speech to anechoic speech. Their spectral mapping approach substantially improves SNR and objective speech intelligibility. Du et al. [8] improved the method in [37] with global variance equailization, dropout training, and noise-aware training strategies. They demonstrated significant improvement over a GMM-based method and good generalization to unseen speakers in testing. Tu et al. [27] trained DNN to estimate not only the target speech but also the interfering speech. They showed that using dual outputs improves the quality of speech separation.
Speech signal is highly structured, and leveraging temporal context is important for improving the performance of a speech processing method. Generally, a learning machine uses the concatenation of neighboring frames instead of a single frame as its input for predicting the output. A good choice of input expansion is to select a fixed contextual window that performs the best among several candidate windows. For example, in [14], the masking-based method sets the window length to 3; in [8], the mapping-based method sets the window length to 7. However, different candidate windows may provide complementary information that can further improve the performance.
In addition, ensemble learning, which integrates multiple weak learners to create a stronger one, has not been systematically explored for speech separation. Ensemble learning is a methodology applicable to various machine learning methods. There are two key elements for ensemble learning to succeed: (i) weak learners are at least stronger than random guess, and (ii) strong diversity exists among the weak learners [7]. For the former, DNN is a good choice; for the latter, there are a number of ways to enlarge the diversity by manipulating input features, output targets, training data, and hyperparameters of base learners [7]. We should point out that Le Roux et al. [21] proposed to integrate the outputs of multiple base learners by majority voting or shallow meta learners, e.g. support vector machines, for speech denoising.
Motivated by the above considerations as well as the recent success of the multi-resolution cochleagram feature [1] and the relationship between the feature and its components [39], we investigate DNN-based speech separation by incorporating DNN into the framework of ensemble learning [7] in this paper. We propose the multi-context networks, where the term “context” denotes a window of neighboring frames. In addition, we analyze the differences between the two optimization objectives, i.e. ideal masking and spectral mapping, systematically. The contributions of this paper are summarized as follows:
Multi-context networks for speech separation. Multi-context networks are ensembles of DNNs. Each DNN uses the IRM or SA as the training target. The first multi-context network is multi-context averaging (MCA), which simply averages the outputs of the DNNs. Each DNN in MCA takes the expansion of raw features in a contextual window as its input. The DNNs have different windows. The second multi-context network is multi-context stacking (MCS), which is a stack of DNN ensembles. Each DNN in a module of the stack first concatenates original acoustic features and the estimated ratio masks from the lower module as a new acoustic feature, and then takes the expansion of the new feature in a contextual window as its input. The DNNs in the same module have different windows. Multi-context networks improve the accuracy of DNN by ensembling and stacking, and enlarge the diversity between the DNNs with the multi-context scheme which manipulates the input features of DNNs.
Comparison of masking and mapping for DNN-based speech separation. The methods in comparison use the same type of DNN in multi-context networks. Our systematic comparison leads to the following conclusions. (i) The masking-based approach is more effective in utilizing the clean training speech of a target speaker. (ii) The mapping-based method is less sensitive to the SNR variation of a training corpus. (iii) Given a training corpus with a fixed mixture SNR and plenty of clean training speech from the target speaker, the mapping and masking-based methods tend to perform equally well.
We have conducted extensive experiments on the corpora of speech separation challenge [3], TIMIT [10], and IEEE [17], and found that the proposed methods outperform previous mapping- and masking-based methods in all experiments.
This paper is organized as follows. In Section II, we present the multi-context networks. In Section III, we analyze the differences between mapping and masking. In Section IV and Section V, we present the results. Finally, we conclude in Section VI.
II. Multicontext Networks
In this section, we introduce two multi-context networks, present three optimization objectives, introduce the DNN model in the multi-context networks, and discuss related work.
A. Multicontext Averaging
MCA averages the outputs of multiple DNNs whose inputs employ different contexts. Specifically, in the preprocessing stage of MCA training, given a mixed signal and the corresponding clean signals of a target speaker and an interfering speaker, we extract the magnitude spectra of their short time Fourier transform (STFT) features, denoted as , , and , respectively, where M is the number of frames for the mixed signal, and subscript a denotes the target speaker and subscript b the interfering speaker. We further calculate the IRM of the target speaker, denoted as , from the STFT features (see Section II-C for the definitions of the IRM and SA).
In the training stage, suppose that MCA contains P DNNs (P > 1). The pth DNN learns a mapping function IRMm = fp(vm,p) where the input vm,p is an expansion of the raw feature ym at a half-window length Wp:
| (1) |
Note that if the SA, which is the squared loss between and its estimation, is used as the optimization objective, the pth DNN learns IRMm = fp(vm,p) implicitly, and the output of the DNN in the test stage is an estimated ratio mask.
In the test stage of MCA, given a mixed signal of two speakers in the time domain, we first extract by STFT, where ym and θm represent the magnitude vector and phase vector of the mth frame respectively. We use the expansions of as the inputs of the DNNs and get the estimated ratio masks, denoted as . We average the outputs of the DNNs by:
| (2) |
Then, we get the estimated magnitude spectra by . Finally, we transform back to the time-domain signals via the inverse STFT, where the operator ⊙ denotes the element-wise product. Note that we use the noisy phase to do resynthesis, and the Hamming window in STFT.
B. Multicontext Stacking
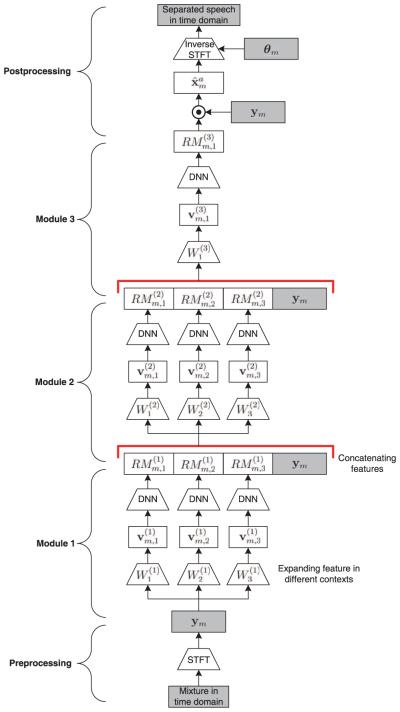
MCS is a stack of ensemble learning machines, as shown in Fig. 1. The learning machines in a module of the stack have different contextual window lengths; they take the concatenation of the output predictions of their lower module and the original acoustic features as their input. MCS can be either mapping-based, masking-based, or a combination of mapping and masking. In this paper, we instantiate the learning machines by DNN and use the IRM or SA as the optimization objective. Compared to MCA, MCS fuses the outputs of the base DNNs in a nonlinear way.
Fig. 1.
Diagram of multi-context stacking. The symbols in the figure are defined in Section II. Trapezoid modules represent contextual windows or DNNs. Rectangle modules represent features.
The preprocessing stage of MCS training is the same as that of MCA training. In the training stage, MCS learns a mapping function IRM = f(y) given a training corpus of mixed signals. Suppose MCS trains S modules, and the sth module has Ps learning machines, denoted as , each of which has a unique half-window length (see Eq. (3) below). The pth DNN learns the mapping function where the input is an expansion of the feature at a half-window length :
| (3) |
with defined as:
| (4) |
where are the estimated IRMs of yn produced by the (s − 1)th module , and is an integer. Note that we usually train only one model with an empirically optimal window length at the top module, as illustrated in Fig. 1.
In the test stage of MCS, we use the magnitude vectors as the input of MCS and get the estimated ratio masks in each module. After getting the estimated ratio masks from the top module, we first get the estimated magnitude spectra by and then transform back to the time-domain signals via the inverse STFT.
C. Optimization Objectives
The general training objective of DNN-based speech separation methods is given as follows:
| (5) |
where ℓ(·) measures training loss, dm represents the desired output at frame m, and α is the parameter set of the speech separation algorithm f(·).
1) Direct Mapping
Mapping-based DNN methods learn a mapping function from the spectrum of the mixed signal to the spectrum of the clean speech of the target speaker directly, which can be formulated as the following minimum mean squared error problem:
| (6) |
where ∥ · ∥2 is the squared loss. In the test stage, mapping-based methods transform the prediction back to the time-domain signal by inverse STFT.
2) Ratio Masking
Masking-based DNN methods learn a mapping function from the spectrum of the mixed signal to the ideal time-frequency mask of the clean utterance of the target speaker:
| (7) |
where IRMm is the ideal mask, and the output of fα(ym) is restricted to the range [0, 1]. In the test stage, we first apply the estimated mask RMm to the spectrum of the mixed signal ym by and then transform the estimated spectrum back to the time-domain signal by inverse STFT.
The ideal ratio mask in MCS is defined as:
| (8) |
where and denote and at frequency k respectively, ϵ is a very small positive constant to prevent the denominator from being zero, and K is number of STFT frequency bins.
Wang et al. [31] point out that masking as a form of normalization reduces the dynamic range of target values, leading to different training efficiency compared to mapping.
3) Signal Approximation
SA-based DNN methods learn a mapping function from the spectrum of the mixed signal to the IRM, which is the same as IRM-based methods. However, different from common IRM-based methods which evaluate the squared training loss between the IRM and the estimated mask, SA-based methods evaluate the squared training loss between the spectrum of the target speech and the estimated spectrum, which is the same as the direct mapping. The SA is defined formally as follows:
| (9) |
The output of fα(ym) is restricted to the range [0, 1] and bounded as the IRM.
D. DNN in Multicontext Networks
A DNN model has a number of nonlinear hidden layers plus an output layer. Each layer has a number of model neurons (or mapping functions). The model can be described as follows:
| (10) |
where l = 1,…,L denotes the lth hidden layer from the bottom, hl(·) denotes nonlinear activation functions of the lth hidden layer, g(·) activation functions of the output layer, and y is the input feature vector. Common activation functions for the hidden layers include the sigmoid function tanh function, and more recently rectified linear function b = max(0, a) where a is the input and b the output of a neuron. Common activation functions in the output layer include the linear function b = a, softmax function, and sigmoid function. Because the rectified linear function is shown to result in faster training and better learning of local patterns, we use it as the activation function for the hidden layers of DNN. As the training target is the IRM whose value varies between [0, 1], we use the sigmoid function for the output layer.
Traditionally, DNN employs full connections between consecutive layers, which tends to overfit data and be sensitive to different hyperparameter settings. Dropout [4], which randomly deactivates a percentage of neurons, was proposed recently to alleviate the problem. It has been analyzed that dropout provides as a regularization term for DNN training. Due to this regularization, we are able to train much larger DNN model. Therefore, we use dropout for DNN training.
Although early research in deep learning uses pretraining to prevent poor local minima, recent experience shows that, when data sets are large enough, pretraining does not further improve the performance of DNN. Therefore, we do not pretrain DNN. In addition, we use the adaptive stochastic gradient descent algorithm [5] with a momentum term [25] to accelerate gradient descent and to facilitate parallel computing.
E. Related Work
The MCS described above is different from our preliminary work in [40] which used MCS for separating speech from non-speech noise, boosted DNN as the base weak learner, the ideal binary mask as the optimization objective, and multi-resolution cochleagram [1] as the acoustic feature.
The method in [18] fuses multiple DNNs that have different optimization objectives and hidden layers. This method is designed for separating speech from nonspeech signals, such as random noise and music. Note that our work was developed independently at about the same time (see [40]).
The proposed method is also different from deep convex networks [6] and tensor deep stacking networks [16]. Although these two methods take the raw feature and the output of the lower module as the input to the upper module, each module of these networks is a single shallow network, while each module of our method is an ensemble of deep networks that emphasizes the importance of contextual information. Moreover, these methods are mainly developed for speech recognition.
III. Mapping and Masking
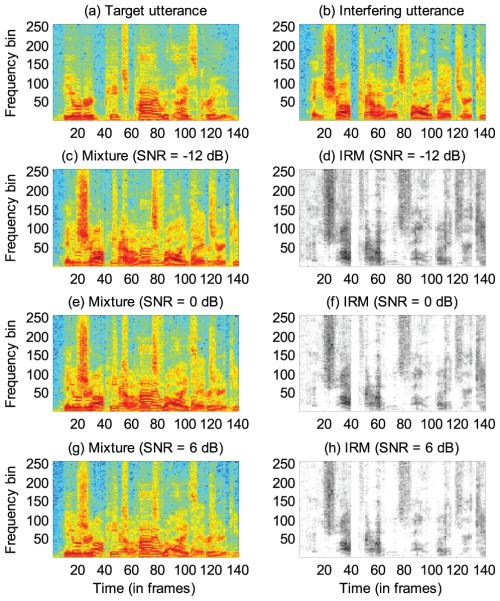
Here, we report two novel differences between mapping- and masking-based methods. Mapping-based methods are less sensitive to the SNR variation of training data than masking-based methods. Specifically, the optimization objective min tends to recover the spectra xa that have large energy and sacrifice those that have small energy, so that the overall loss is minimized. Fig. 2 illustrates such an example, where a target utterance (Fig. 2a) is mixed with an interfering utterance (Fig. 2b) at multiple SNR levels (Figs. 2c, 2e, and 2g). For mapping-based methods, no matter how the SNR changes, the reference xa (Fig. 2a) is unchanged, which means that only the energy of y affects the optimization. On the contrary, for masking-based methods, the energy of the ideal masks IRM (Figs. 2d, 2f, and 2h) becomes small with the decrease of the SNR. One can imagine that when the SNR is low, the estimated ratio mask tends to suffer a larger loss than the estimated reference in mapping-based methods. As a result, when the SNR of a training corpus varies in a wide range, masking-based methods likely perform worse than mapping-based methods at low SNR levels.
Fig. 2.
Comparison of mapping and masking when the SNR of the mixed signal varies in a wide range. (a) The spectrogram of an utterance of a target speaker. (b) The spectrogram of an utterance of an interfering speaker. (c) The spectrogram of the mixed signal with SNR = −12 dB. (d) The IRM of the target speaker with SNR = −12 dB. (e) The spectrogram of the mixed signal with SNR = 0 dB. (f) The IRM of the target speaker with SNR = 0 dB. (g) The spectrogram of the mixed signal with SNR = 6 dB. (h) The IRM of the target speaker with SNR = 6 dB.
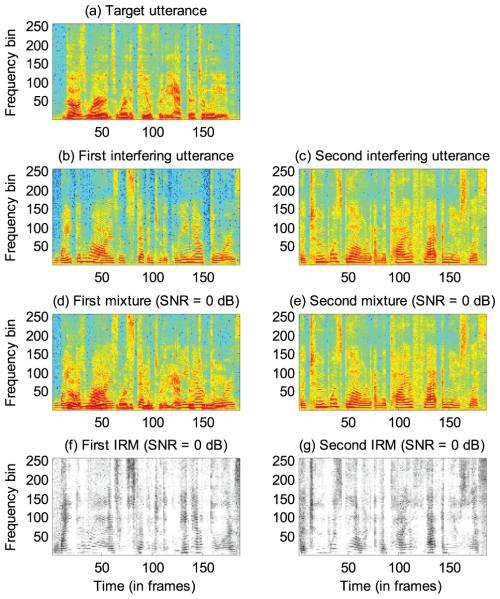
Masking-based methods can explore the mutual information between target and interfering speakers better than mapping-based methods. Specifically, data-driven methods, such as DNN, need a large number of different patterns to train a good machine. When a target speaker has a limited number of utterances, we usually create a large training corpus by mixing each utterance of the target speaker with many utterances of interfering speakers. Fig. 3 illustrates such a process where one utterance of a target speaker (Fig. 3a) is mixed with two utterances of an interfering speaker (Figs. 3b and 3c), each at 0 dB, which produces two spectrograms from the two mixed signals (Figs. 3d and 3e) and two ideal ratio masks (Figs. 3f and 3g). In the IRM illustrations of Figs. 3f and 3g, white corresponds to 1 and black to 0. Mapping-based methods learn a mapping function from the spectrograms in Figs. 3d and 3e to the same output pattern in Fig. 3a. On the contrary, masking-based methods learn a mapping function that projects the spectrogram in Fig. 3d to the ideal ratio mask in Fig. 3f, and the spectrogram in Fig. 3e to the ideal ratio mask in Fig. 3g, respectively. In other words, training targets are different depending on interfering utterances (see also [31]). Therefore, masking-based methods can potentially utilize the training patterns better than mapping-based methods, and hence likely achieve better performance. SA-based methods optimize the IRM implicitly, and evaluate the training loss between the spectrograms of the clean speech and separated speech [14]–[15]. In a way, SA combines the aforementioned merits of the IRM and direct mapping.
Fig. 3.
Comparison of mapping and masking when the number of the utterances of the target speaker is limited. (a) The spectrogram of the utterance of the target speaker. (b) The spectrogram of the first utterance of the interfering speaker. (c) The spectrogram of the second utterance of the interfering speaker. (d) The spectrogram of the mixed signal produced from the target utterance (i.e. Fig. 3a) and the first interfering utterance (i.e. Fig. 3b). (e) The spectrogram of the mixed signal produced from the target utterance and the second interfering utterance (i.e. Fig. 3c). (f) The IRM of the target utterance given the first interfering utterance. (g) The IRM of the target utterance given the second interfering utterance.
IV. Results With Speaker-Pair Dependent Training
In this section, we evaluate multi-context networks and compare the optimization objectives of mapping and masking systematically when target and interfering speakers are the same in the training and test corpora, i.e. speaker-pair dependent training. We trained hundreds of DNN models and reported the average results over the 4 possible gender pairs in all experiments, where the first speaker of a gender pair is the target speaker and the other one interfering speaker. See Supplementary Material for the detailed results on each gender pair.
As analyzed in Section III, two factors affect the performance of mapping- and masking-based methods: (i) insufficiency of the clean training utterances and (ii) the variation of SNR in the training set. The two factors lead to different training scenarios, analyzed in Sections IV-B to IV-E.
A. Experimental Settings
1) Datasets
We used the speech separation challenge (SSC) [3] dataset as the separation corpus. SSC has predefined training and test corpora. The training corpus contains 34 speakers, each of which has 500 clean utterances. Each mixed signal in the test corpus is also produced from a pair of speakers in the training corpus. Because each pair of speakers contains at most 2 test mixtures, we did not use the test corpus. Instead, we randomly picked 2 pairs of speakers for each gender pair from the training corpus, which generated 8 separation tasks. See Sections IV-B to IV-E for the description of the training sets of the four training scenarios. Each task had 7 test SNR levels ranging from {−12, −9, −6, −3, 0, 3, 6} dB. The test set at each SNR level contained 50 mixed signals. Each component of a mixed signal was a clean utterance from the last 50 utterances of the corresponding speaker.
We resampled all corpora to 8 kHz, and extracted the STFT features with the frame length set to 25 ms and the frame shift set to 10 ms.
2) Comparison Methods and Parameter Settings
We compared the DNN-, MCA- and MCS-based speech separation methods with direct mapping (Map), IRM, or SA as the objective. The comparison methods, which were denoted in the format of model + objective, were DNN+Map, DNN+IRM, MCA+IRM, MCS+IRM, DNN+SA, MCA+SA, and MCS+SA respectively. For all comparison methods, we used DFT to extract acoustic features. For the MCA-based method, we trained 3 base DNNs with parameters W1, W2, W3 set to 1, 2, and 3 respectively. For the MCS-based method, we trained two modules (i.e. parameter S = 2). For the bottom module of MCS, we trained 3 DNNs with parameters , , set to 1, 2, and 3 respectively. For the top module of MCS, we trained 1 DNN with set to 1.
We searched for the optimal parameter settings of DNN using a development task, and used the optimal settings in all evaluation tasks. The development task was constructed from two male speakers of SSC. Its training set contained 1000 mixtures, and its test set contained 50 mixtures, both of which were at −12 dB.
The selected parameter settings are as follows. DNN was optimized by the minimum mean square error criterion. Each DNN has 2 hidden layers, each of which consists of 2048 rectified linear neurons. The output neurons of the DNN for the mapping-based method are the linear neurons. The output neurons of the DNNs for the masking-based methods were the sigmoid functions. The number of epoches for backpropagation training was set to 50. The batch size was set to 128. The scaling factor for the adaptive stochastic gradient descent was set to 0.0015, and the learning rate decreased linearly from 0.08 to 0.001. The momentum of the first 5 epoches was set to 0.5, and the momentum of other epoches was set to 0.9. The dropout rate of the hidden neurons was set to 0.2. The half-window length W (defined in Eq. (3)) was set to 3 for the mapping-based method, and set to 1 for the masking-based methods.
We normalized data before training. For DNN+Map, we first normalized the training data to zero mean and unit standard deviation in each dimension, and then used the same normalization factor to normalize both the training references and the test data. After getting the predictions in the test stage, we converted the predictions back to the original scale by the same normalization factor. For the IRM-based methods, we first normalized and then used the same normalization factor to normalize the test data. For the SA-based methods, we did not normalize the input and output of the training data due to the definition of the SA.
3) Evaluation Metrics
We used the short-time objective intelligibility (STOI) [26] as the evaluation metric. STOI evaluates the objective speech intelligibility of time-domain signals. It has been shown empirically that STOI scores are well correlated with human speech intelligibility scores. The higher the STOI value is, the better the predicted intelligibility is. STOI is a standard metric for evaluating speech separation performance [31], [8], [15].
B. Comparison With Single-SNR Training and Sufficient Clean Training Data
This scenario aims to evaluate the comparison methods without the complicating factors of SNR variation and insufficient training data. For each test SNR level of a task, we generated 1000 mixed signals at the same SNR level as the corresponding training set. Each component of a mixture in the training set was a clean utterance randomly selected from the first 450 utterances of the corresponding speaker.
We conducted a comparison at each SNR level of each separation task, and report the average results of the 8 tasks. Table I lists the comparison results. From the table, we observe that (i) all methods improve STOI scores over the original mixed signals significantly, particularly at low SNR levels; (ii) the proposed methods slightly outperform the DNN-based methods; (iii) MCA and MCS perform equally well; (iv) DNN+Map and DNN+IRM perform equally well; (v) the SA-based methods outperform the Map- and IRM-based methods.
TABLE I.
STOI (in Percent) Comparison Between Speech Separation Methods With Single-SNR Speaker-Pair Dependent Training on SSC Corpus. The Results Are Averaged Over 8 Speaker Pairs
| −12 dB | −9 dB | −6 dB | −3 dB | O dB | 3 dB | 6 dB | |
|---|---|---|---|---|---|---|---|
| Noisy | 46.4 | 52.2 | 58.8 | 65.8 | 72.7 | 79.2 | 84.8 |
| DNN+Map | 71.4 | 76.7 | 81.0 | 84.9 | 88.3 | 91.2 | 93.5 |
| DNN+IRM | 72.1 | 76.5 | 80.5 | 84.5 | 87.8 | 90.9 | 93.2 |
| MCA+IRM | 73.9 | 78.3 | 82.2 | 86.0 | 89.1 | 91.7 | 93.9 |
| MCS+IRM | 73.7 | 78.5 | 82.4 | 86.3 | 89.4 | 92.1 | 94.2 |
| DNN+SA | 76.9 | 81.0 | 84.7 | 88.0 | 90.8 | 93.3 | 95.3 |
| MCA+SA | 77.8 | 82.2 | 85.8 | 88.9 | 91.6 | 93.8 | 95.6 |
| MCS+SA | 78.4 | 82.2 | 86.1 | 88.9 | 91.8 | 93.9 | 95.7 |
C. Comparison With Single-SNR Training and Insufficient Clean Training Data
This scenario aims to evaluate how insufficient clean training utterances affect the performance. For each test SNR level of a task, we generated 1000 mixed signals at the same SNR level as the training set. Different from Section IV-B, the 1000 mixed signals were generated from only 20 clean training utterances, in which 10 clean training utterances were randomly selected from the target speaker and the other 10 from the interfering speaker. Each mixture in the training set was constructed by first randomly selecting 2 clean utterances, each from the 10 utterances of a speaker, then shifting the interfering utterance randomly, wrapping the shifted utterance circularly, and finally mixing the two utterances together. Note that the random shift operation was used to synthesize a large number of mixtures from a small number of clean utterances.
Table II lists the average comparison results of the 8 tasks. From the table, we observe that (i) all methods improve the STOI scores at the low SNR levels. (ii) The IRM-based methods significantly outperform DNN+Map, except for MCS+IRM which is slightly inferior to DNN+Map at −12dB. (iii) The SA-based methods significantly outperform DNN+Map and IRM-based methods. (iv) The MCA-based methods outperform DNN-based methods. (v) MCS+IRM is inferior to DNN+IRM. (vi) MCS+SA outperforms DNN+SA and is identical to MCA+SA at low SNR levels. The comparison results between DNN, MCA, and MCS suggest that, if we do not have sufficient clean training data, we should use MCA to aggregate the base DNNs.
TABLE II.
STOI Comparison Between Speech Separation Methods With Single-SNR Speaker-Pair Dependent Training on SSC Corpus With Insufficient Clean Training Data
| −12 dB | −9 dB | −6 dB | −3 dB | O dB | 3 dB | 6 dB | |
|---|---|---|---|---|---|---|---|
| Noisy | 46.4 | 52.2 | 58.8 | 65.8 | 72.7 | 79.2 | 84.8 |
| DNN+Map | 57.1 | 62.4 | 67.8 | 72.6 | 76.7 | 80.3 | 83.1 |
| DNN+IRM | 58.8 | 65.1 | 71.1 | 76.8 | 81.1 | 84.4 | 86.9 |
| MCA+IRM | 58.7 | 65.2 | 71.5 | 77.2 | 81.7 | 84.9 | 87.2 |
| MCS+IRM | 56.8 | 63.5 | 70.2 | 76.1 | 80.6 | 83.0 | 84.4 |
| DNN+SA | 66.0 | 71.6 | 77.0 | 81.4 | 85.2 | 88.2 | 90.5 |
| MCA+SA | 66.7 | 72.3 | 77.7 | 82.1 | 85.7 | 88.5 | 90.6 |
| MCS+SA | 66.7 | 72.3 | 77.7 | 82.0 | 85.4 | 88.1 | 90.1 |
Moreover, comparing Table I and Table II, we find that DNN+Map works well with sufficient clean training utterances, while the IRM- and SA-based methods work well on both corpora, consistent with our analysis in Section III. Not surprisingly, the STOI improvements are smaller when the dataset has much fewer clean training utterances for each speaker.
Note that, in this paper, we only used a simple pattern augmentation method—random shift of interfering utterances— to enlarge the noisy training set. It is worthy further exploring other pattern augmentation methods, such as noise rate perturbation, vocal tract length perturbation, and frequency perturbation [2].
D. Comparison With Multi-SNR Training and Sufficient Clean Training Data
This scenario aims to evaluate how the variation of training SNR affects the performance. We used the experimental settings in Section IV-A1 and made 8 speech separation tasks, each of which had 7 test sets. Different from Section IV-B where each task had 7 training sets, we had only 1 training set for each task encompassing various SNRs. Each training set of SSC contained 10,000 mixed signals. Each training mixture had a random SNR level varying between −13 dB and 10 dB with the increment of 1 dB.
For each speech separation task, we tested the model on all 7 test sets at different SNRs. Then, we report the average results of the 8 tasks. Table III lists the comparison results on the SSC corpus. From the table, we observe that (i) all methods improve the STOI scores over the original mixed signals significantly. (ii) The MCS-based methods perform overall the best across all SNR levels, while the performance of the MCA-based methods is close to that of the MCS-based methods. (iii) DNN+IRM underperforms DNN+Map at low SNR levels, while the SA-based methods outperform DNN+Map and the IRM-based methods, consistent with our analysis in Section III.
TABLE III.
STOI Comparison Between Speech Separation Methods With Multi-SNR Speaker-Pair Dependent Training on SSC Corpus
| −12 dB | −9 dB | −6 dB | −3 dB | O dB | 3 dB | 6 dB | |
|---|---|---|---|---|---|---|---|
| Noisy | 46.4 | 52.2 | 58.8 | 65.8 | 72.7 | 79.2 | 84.8 |
| DNN+Map | 74.9 | 80.4 | 84.6 | 87.8 | 90.3 | 92.3 | 93.7 |
| DNN+IRM | 72.0 | 77.8 | 82.7 | 86.6 | 89.7 | 92.1 | 94.0 |
| MCA+IRM | 74.2 | 79.7 | 84.3 | 87.9 | 90.8 | 93.0 | 94.6 |
| MCS+IRM | 75.1 | 81.0 | 85.6 | 89.1 | 91.8 | 93.7 | 95.1 |
| DNN+SA | 78.9 | 83.5 | 86.9 | 89.6 | 91.8 | 93.6 | 95.0 |
| MCA+SA | 80.8 | 84.9 | 88.1 | 90.6 | 92.5 | 94.2 | 95.5 |
| MCS+SA | 81.4 | 85.7 | 88.9 | 91.2 | 93.1 | 94.6 | 95.9 |
E. Comparison With Multi-SNR Training and Insufficient Clean Training Data
We followed the same construction method of the training sets as in Section IV-D and made 8 speech separation tasks, each of which had 1 training set and 7 test sets. Each training set had 10,000 mixed signals, each of which was generated in the same way and from the same 20 randomly selected utterances as in Section IV-C and had a random SNR level as in Section IV-D. We trained and evaluated the models in the same way as in Section IV-D.
Table IV lists the comparison results. From the table, we observe a similar performance profile and that the insufficiency of clean training data has a larger effect on the performance than the variation of the training SNR, albeit STOI improvements are lower compared to the results with the full SSC corpus.
TABLE IV.
STOI Comparison Between Speech Separation Methods With Multi-SNR Speaker-Pair Dependent Training on SSC Corpus With Insufficient Clean Training Data
| −12 dB | −9 dB | −6 dB | −3 dB | O dB | 3 dB | 6 dB | |
|---|---|---|---|---|---|---|---|
| Noisy | 46.4 | 52.2 | 58.8 | 65.8 | 72.7 | 79.2 | 84.8 |
| DNN+Map | 56.0 | 62.6 | 68.4 | 73.1 | 76.6 | 79.1 | 80.8 |
| DNN+IRM | 57.0 | 64.4 | 71.3 | 77.2 | 81.9 | 85.2 | 87.5 |
| MCA+IRM | 57.6 | 65.1 | 72.0 | 77.9 | 82.5 | 85.7 | 87.8 |
| MCS+IRM | 56.7 | 64.6 | 71.7 | 77.6 | 82.0 | 84.9 | 86.7 |
| DNN+SA | 63.9 | 70.8 | 76.7 | 81.5 | 85.3 | 88.1 | 90.1 |
| MCA+SA | 65.5 | 72.1 | 77.8 | 82.4 | 85.9 | 88.4 | 90.2 |
| MCS+SA | 65.8 | 72.3 | 77.8 | 82.2 | 85.5 | 87.9 | 89.6 |
Moreover, comparing Table III with Table I, we find that, when a training set is generated from a large number of clean utterances (each speaker has 450 clean utterances), enlarging the size of the training set from 1000 mixed signals in Table I to 10,000 mixed signals in Table III significantly elevates the performance. On the other hand, we find that, when a training set is constructed from limited clean utterances (each speaker has only 10 utterances), enlarging the size of the training set from 1000 mixed signals in Table II to 10,000 mixed signals in Table IV does not elevate the performance. This can be seen from the fact that the results at low SNR levels in Table IV are worse than those in Table II.
V. Results With Target Dependent Training
In this section, we evaluate the generalization ability of the MCA- and MCS-based methods when interfering speakers in the test set are different from those in the training set, but the target speakers of the training and test corpora are the same. Also, SNR levels of the test corpus are different from those of the training corpus.
A. Experimental Settings
1) Datasets
We used the IEEE corpus as the source of target speakers [17] and TIMIT [10] as the source of interfering speakers. We call this the IEEE-TIMIT corpus. The IEEE corpus has one male speaker and one female speaker. Each speaker utters 720 clean utterances. TIMIT contains 630 speakers, each of which has 10 clean utterances. We constructed two tasks, each of which took a speaker in the IEEE corpus as the target speaker and took the speakers in the TIMIT corpus as the interfering speakers.
Each task had one training set. The training set had 6000 mixed signals with the SNR in dB varying in the range of [−13, −11, −10, −8, −7, −5, −4, −2, −1, 1, 2, 4, 5, 7, 8, 9, 10]. The utterance of a target speaker in a mixed signal was randomly selected from the first 640 utterances of the speaker. The utterance of an interfering speaker in a mixed signal was randomly selected from the first 8 utterances of the randomly selected 620 speakers (out of 630 speakers) of TIMIT (4960 utterances in total).
Each task had 7 test sets with the SNR levels ranging at −12, −9, −6, −3, 0, 3, and 6 dB. Each test set had 80 mixed signals. The target component of a mixture was a clean utterance selected from the last 80 clean utterances of a speaker in the IEEE corpus. The interfering utterance of a mixture was selected from the first 8 utterances of the remaining 10 speakers of TIMIT which include 6 male and 4 female speakers.
Note that because the SSC corpus does not have sufficient speakers for training target-dependent models, we used the TIMIT corpus as the source of interfering speakers. Since TIMIT utterances have durations close to those of IEEE and are much longer than those of SSC, we used the IEEE corpus as the source of target speakers.
2) Comparison Methods
Besides the 7 comparison methods in Section IV, we further evaluated the proposed methods with a concatenation of the estimations of both the IRM and SA. Specifically, we trained 3 IRM-based DNNs and 3 SA-based DNNs in the bottom module of MCA or MCS as in Section IV. For MCA, we averaged the outputs of the 6 DNNs; the method was denoted as MCA+IRM+SA. For MCS, we concatenated the outputs of the 6 DNNs as part of the input of the upper module, and used the SA as the optimization objective of the DNN in the upper module; the method was denoted as MCS+IRM+SA. The parameter settings of all DNN models followed those described in Section IV-A2.
3) Evaluation Metrics
Besides STOI, we used the source to distortion ratio (SDR) [28], a metric similar to SNR for evaluating the quality of separation.
B. Main Results
Tables V and VI list the comparison results on the IEEE-TIMIT corpus in terms of STOI and SDR respectively. From the tables, we observe the following results. (i) All methods improve the STOI and SDR scores over the original mixed signals significantly. (ii) The MCA- and MCS-based methods out-perform the DNN-based methods at all SNR levels. (iii) MCS outperforms MCA at all SNR levels, particularly when the IRM is used as the optimization objective. (iv) DNN+IRM outperforms DNN+Map between −6 dB and 6 dB, whereas DNN+Map outperforms DNN+IRM at −12 dB and −9 dB. The SA-based methods outperform DNN+Map and the IRM-based methods. The relative performance of DNN+Map and DNN+IRM is consistent with our analysis in Section III. Note also that the relative performance profiles are similar in STOI and SDR.
TABLE VI.
SDR Comparison Between Speech Separation Methods With Target Dependent Training on IEEE-TIMIT Corpus
| −12 dB | −9 dB | −6 dB | −3 dB | O dB | 3 dB | 6 dB | |
|---|---|---|---|---|---|---|---|
| Noisy | −10.86 | −8.32 | −5.59 | −2.74 | 0.18 | 3.14 | 6.12 |
| DNN+Map | 2.61 | 4.09 | 5.49 | 6.97 | 8.61 | 10.32 | 12.05 |
| DNN+IRM | 2.48 | 4.21 | 5.89 | 7.61 | 9.45 | 11.32 | 13.16 |
| MCA+IRM | 2.92 | 4.61 | 6.27 | 7.97 | 9.77 | 11.61 | 13.41 |
| MCS+IRM | 3.71 | 5.53 | 7.24 | 8.92 | 10.67 | 12.44 | 14.12 |
| DNN+SA | 4.20 | 5.47 | 6.98 | 8.47 | 10.14 | 11.92 | 13.71 |
| MCA+SA | 4.54 | 5.80 | 7.33 | 8.84 | 10.49 | 12.24 | 14.01 |
| MCS+SA | 4.75 | 6.09 | 7.49 | 9.05 | 10.74 | 12.53 | 14.32 |
| MCA+IRM+SA | 4.31 | 5.71 | 7.16 | 8.73 | 10.43 | 12.21 | 13.98 |
| MCS+IRM+SA | 4.79 | 6.13 | 7.54 | 9.10 | 10.80 | 12.61 | 14.43 |
Comparing Table V with Tables I and III, we find that even if the interfering speakers are unseen during training, target dependent training can still reach similar performance to that of speaker-pair dependent training. This demonstrates the strong generalization of the DNN-based speech separation methods.
TABLE V.
STOI Comparison Between Speech Separation Methods With Target Dependent Training on IEEE-TIMIT Corpus
| −12 dB | −9 dB | −6 dB | −3 dB | O dB | 3 dB | 6 dB | |
|---|---|---|---|---|---|---|---|
| Noisy | 48.9 | 54.9 | 61.4 | 68.0 | 74.5 | 80.4 | 85.5 |
| DNN+Map | 72.6 | 77.0 | 80.9 | 84.5 | 87.7 | 90.4 | 92.5 |
| DNN+IRM | 71.2 | 76.6 | 81.2 | 85.2 | 88.6 | 91.5 | 93.7 |
| MCA+IRM | 73.4 | 78.3 | 82.6 | 86.3 | 89.6 | 92.2 | 94.2 |
| MCS+IRM | 75.1 | 80.2 | 84.4 | 87.9 | 90.8 | 93.1 | 94.8 |
| DNN+SA | 75.0 | 79.4 | 83.0 | 86.3 | 89.1 | 91.5 | 93.5 |
| MCA+SA | 76.5 | 80.8 | 84.3 | 87.4 | 90.0 | 92.3 | 94.0 |
| MCS+SA | 76.9 | 81.4 | 85.1 | 88.1 | 90.7 | 92.9 | 94.6 |
| MCA+IRM+SA | 76.9 | 81.1 | 84.7 | 87.8 | 90.6 | 92.9 | 94.6 |
| MCS+IRM+SA | 77.4 | 81.9 | 85.5 | 88.5 | 91.1 | 93.3 | 95.0 |
C. MCS Variants
We investigate several MCS variants below. To simplify the discussion, we take the IRM as the optimization objective.
1) Effects of Number of Modules of MCS
The reported results so far are produced with only two modules of MCS. In this subsection, we investigate MCS with three modules, where the parameter setting of the DNN in the top module (i.e. module 3) is the same as that in the middle module (i.e. module 2) and the bottom module (i.e. module 1). STOI results are presented in Table VII. From the table, we observe that stacking the third module improves the performance.
TABLE VII.
STOI Comparison Between Different Modules in MCS
| −12 dB | −9 dB | −6 dB | −3 dB | O dB | 3 dB | 6 dB | |
|---|---|---|---|---|---|---|---|
| Module 1 | 71.2 | 76.6 | 81.2 | 85.2 | 88.6 | 91.5 | 93.7 |
| Module 2 | 75.1 | 80.2 | 84.4 | 87.9 | 90.8 | 93.1 | 94.8 |
| Module 3 | 75.9 | 80.8 | 84.8 | 88.1 | 91.0 | 93.2 | 95.0 |
2) Effects of Number of Training Utterances of Target Speaker
We have observed that when the clean utterances of the target speaker are limited, the performance improvement of all DNN-based methods is limited. In this subsection, we examine how this factor affects the separation performance.
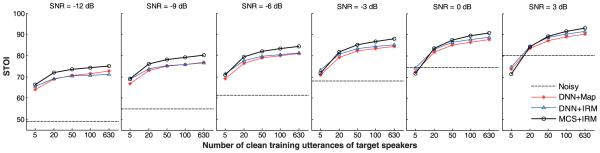
We constructed 5 training sets for each target speaker in the same way as described above, except for the only difference that the 6,000 mixed signals of each training set were generated from 5, 20, 50, 100, and 640 clean utterances of the target speaker. Fig. 4 shows the average STOI results on the two separation tasks at various SNR levels. From the figures, we observe that (i) the MCS-based method outperforms the DNN-based methods, particularly at the low SNR levels; (ii) when the SNR is lower than −3 dB, DNN+Map and DNN+IRM perform about the same; (iii) when the SNR is higher than −3 dB, DNN+IRM performs slightly better than DNN+Map; (iv) consistent with our analysis, DNN+IRM performs better than DNN+Map with fewer target training utterances; (v) the effects of the number of target training utterances weaken with the decrease of the SNR.
Fig. 4.
STOI comparison of DNN+Map, DNN+IRM, and MCS+IRM with respect to the number of the utterances of the target speaker in training.
3) Effects of Raw Feature in MCS
We investigate the effects of the raw feature in the upper modules of MCS by comparing the proposed MCS with an MCS method that does not take the raw feature as the input of the upper modules. The hyperparameter settings of the two comparison methods were the same. The data set was the same as in Section V-A1. The comparison result given in Table VIII shows that taking the raw feature as part of the input of the upper modules is important.
TABLE VIII.
STOI Comparison Between the Proposed MCS With and the MCS Without the Raw Feature as the Inputs of Upper Modules
| −12 dB | −9 dB | −6 dB | −3 dB | O dB | 3 dB | 6 dB | |
|---|---|---|---|---|---|---|---|
| MCS without raw feature | 73.1 | 78.4 | 82.8 | 86.6 | 89.9 | 92.5 | 94.5 |
| MCS with raw feature | 75.1 | 80.2 | 84.4 | 87.9 | 90.8 | 93.1 | 94.8 |
4) MCS Versus Best Single DNN
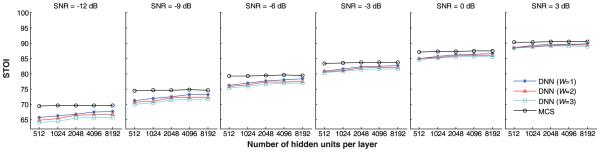
In this subsection, we investigate whether the effectiveness of MCS over a single DNN is simply due to more model parameters in MCS. The parameter setting of the single DNN was as follows. The number of hidden layers was set to 2. The number of units per hidden layer was selected from {512, 1024, 2048, 4096, 8192}. All other parameters were the same as in Section IV-A2. The parameter setting of MCS was as follows. The number of modules was set to 2. As shown in experimental results, setting the number of units per hidden layer of the DNNs in the first module to 4096 is sufficient in terms of performance. So we set the number of hidden units of the three DNNs in the bottom module of MCS to 4096 (per layer), while the number of units in each hidden layer of the DNN in the top module was selected from {512, 1024, 2048, 4096, 8192}.
We reduced the training set of IEEE-TIMIT to 1000 mixed signals in this comparison. The STOI results are summarized in Fig. 5. From the figure, we observe that the MCS with 512 hidden units per layer in the top module outperforms the best single DNN (with the half-window length W = 1) even when its number of units in each hidden layer is 8192, particularly at lower input SNRs. Specifically, the DNN model with 8192 units per hidden layer has 75,514,112 parameters, while the MCS with 512 units per hidden layer in Module 2 has 70, 149, 632 parameters (20, 979, 968 + 23, 077, 120 + 25, 174, 272 parameters for the three DNNs in Module 1, and 918, 272 parameters for the DNN model in Module 2). That is to say, the smallest MCS outperforms the best single large DNN model with more parameters. The experimental results indicate that it is the structure of MCS, not simply more parameters, that contributes to the performance improvement of MCS over DNN.
Fig. 5.
STOI comparison of DNN-, and MCS-based methods with respect to the number of units per hidden layer of DNN.
Note that the comparison methods do not overfit data, as we can see from Fig. 5 that the performance of each comparison method does not drop with respect to the increase of the number of parameters.
5) MCS Versus Best Single-Context Stacking
We investigate the effect of the multi-context scheme by comparing MCS with the best single-context stacking (SCS), which is a deep ensemble method that concatenates the raw feature and the output of the best single DNN model in the bottom module as the input of the upper module. We used the same data set as in Section V-A1. The comparison result in Table IX shows that the multi-context scheme provides some improvements at low SNR levels.
TABLE IX.
STOI COMPARISON (IN PERCENT) BETWEEN MCS AND SCS
| −12 dB | −9 dB | −6 dB | −3 dB | 0 dB | 3 dB | 6 dB | |
|---|---|---|---|---|---|---|---|
| SCS | 74.5 | 79.6 | 83.8 | 87.5 | 90.5 | 93.0 | 94.8 |
| MCS | 75.1 | 80.2 | 84.4 | 87.9 | 90.8 | 93.1 | 94.8 |
VI. Concluding Remarks
In this paper, we have proposed a deep ensemble learning method—multi-context networks—for speech separation. The first multi-context network, named multi-context averaging, averages the outputs of an ensemble of DNNs that exploits different contextual information by using different window lengths. The second one, named multi-context stacking, is a stack of DNN ensembles. Each DNN model in a module of the stack takes the concatenation of original acoustic features and the estimated masks from its lower module as the input. The DNN models in the same module explore different contexts. The key idea for exploring different contexts is to enlarge the diversity between the based DNNs.
Moreover, we have compared the two commonly adopted training objectives for DNN-based speech separation— masking and mapping—systematically, where the objectives of the masking-based methods include the IRM and SA. We have found that (i) masking is more effective than mapping in utilizing clean training utterances of a target speaker, and therefore masking-based methods are more likely to achieve better performance when a target speaker has a limited number of training utterances. (ii) Masking is more sensitive to the SNR variation of a training corpus than mapping, and hence, masking-based methods are more likely to perform worse at low SNRs in the test stage when the SNR of the training corpus varies in a wide range. (iii) Signal approximation appears to combine the benefits of both masking and mapping.
To evaluate the proposed multi-context networks and the differences between mapping and masking, we trained the DNN-, MCA-, and MCS-based methods with the three optimization objectives. After testing hundreds of models with speaker-pair dependent training or target dependent training, we have observed that the multi-context networks outperform the DNN-based methods uniformly, which implies that exploiting deep ensemble learning methods is a simple and effective way for further improving the performance of DNN-based methods. We have also observed that the relative performances between the mapping- and masking-based methods are consistent with our analysis.
Acknowledgment
The authors would like to thank Yuxuan Wang for providing his DNN code, Ke Hu for helping with the SSC, TIMIT, and IEEE corpora, and Jun Du, Yong Xu, and Yanhui Tu for assistance in using their code. The authors would also like to thank the Ohio Supercomputing Center for providing computing resources.
This work was supported in part by the AFOSR under Grant FA9550-12-1-0130 and in part by the NIDCD under Grant R01 DC012048. The associate editor coordinating the review of this manuscript and approving it for publication was Dr. Hirokazu Kameoka.
Biographies

Xiao-Lei Zhang (S’08–M’12) received the Ph.D. degree in information and communication engineering from Tsinghua University, Beijing, China, in 2012. He is currently a Postdoctoral Researcher with the Department of Computer Science and Engineering, The Ohio State University, Columbus, OH, USA. He was a Visitor of the Perception and Neurodynamics Laboratory at The Ohio State University, and a Visitor of the Center of Intelligent Acoustics and Immersive Communications at Northwestern Polytechnical University, Xi’an, China, since 2013. His research interests include audio signal processing, machine learning, statistical signal processing, and artificial intelligence. He has published over 20 peer-reviewed articles in journals and conference proceedings including IEEE TASLP, IEEE SPL, IEEE TPAMI, IEEE TCYB, IEEE TSMC, ICASSP, and Interspeech. He has translated one text book in statistics. He is a Member of the ISCA. He was a recipient of the first-class Beijing Science and Technology Award, the Science and Technology Achievement awarded by Ministry of Education of China, and the first-class Scholarship of Tsinghua University.
DeLiang Wang (F’04), photograph and biography not provided at the time of publication.
References
- [1].Chen J, Wang Y, Wang DL. A feature study for classification-based speech separation at very low signal-to-noise ratio. IEEE/ACM Trans. Audio Speech Lang. Process. 2014 Dec;22(12):1993–2002. [Google Scholar]
- [2].Chen J, Wang Y, Wang DL. Noise perturbation for supervised speech separation. Speech Commun. 2016;78:1–10. doi: 10.1016/j.specom.2015.12.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Cooke M, Lee T-W. Speech Separation Challenge [Online] 2006 Available: http://staffwww.dcs.shef.ac.uk/people/M.Cooke/SpeechSeparationChallenge.htm.
- [4].Dahl GE, Sainath TN, Hinton GE. Improving deep neural networks for LVCSR using rectified linear units and dropout. Proc. IEEE Int. Conf. Acoust. Speech Signal Process. 2013:8609–8613. [Google Scholar]
- [5].Dean J, et al. Large scale distributed deep networks. Proc. Adv. Neural Inf. Process. Syst. 2012:1232–1240. [Google Scholar]
- [6].Deng L, Yu D. Deep convex network: A scalable architecture for speech pattern classification. Proc. Interspeech. 2011:2285–2288. [Google Scholar]
- [7].Dietterich TG. Ensemble methods in machine learning. Multiple Classifier Syst. 2000;1:1–15. [Google Scholar]
- [8].Du J, Tu Y, Xu Y, Dai L, Lee C-H. Speech separation of a target speaker based on deep neural networks. Proc. IEEE Int. Conf. Signal Process. 2014:473–477. [Google Scholar]
- [9].Erdogan H, Hershey JR, Watanabe S, Le Roux J. Phase-sensitive and recognition-boosted speech separation using deep recurrent neural networks. Proc. IEEE Int. Conf. Acoust. Speech Signal Process. 2013:708–712. [Google Scholar]
- [10].Garofolo J, Lamel L, Fisher W, Fiscus J, Pallett D, Dahlgren N. DARPA TIMIT acoustic-phonetic continuous speech corpus CD-ROM. NTIS order number PB91-100354. 1993 [Google Scholar]
- [11].Han K, Wang Y, Wang DL, Woods WS, Merks I, Zhang T. Learning spectral mapping for speech dereverberation and denoising. IEEE/ACM Trans. Audio Speech Lang. Process. 2015 Jun;23(6):982–992. [Google Scholar]
- [12].Han K, Wang DL. A classification based approach to speech segregation. J. Acoust. Soc. Amer. 2012;132(5):3475–3483. doi: 10.1121/1.4754541. [DOI] [PubMed] [Google Scholar]
- [13].Han K, Wang Y, Wang DL. Learning spectral mapping for speech dereverberation. Proc. IEEE Int. Conf. Acoust. Speech Signal Process. 2014:4628–4632. [Google Scholar]
- [14].Huang P-S, Kim M, Hasegawa-Johnson M, Smaragdis P. Deep learning for monaural speech separation. Proc. IEEE Int. Conf. Acoust. Speech Signal Process. 2014:1562–1566. [Google Scholar]
- [15].Huang P-S, Kim M, Hasegawa-Johnson M, Smaragdis P. Joint optimization of masks and deep recurrent neural networks for monaural source separation. IEEE/ACM Trans. Audio Speech Lang. Process. 2015 Dec;23(12):2136–2147. [Google Scholar]
- [16].Hutchinson B, Deng L, Yu D. Tensor deep stacking networks. IEEE Trans. Pattern Anal. Mach. Intell. 2013 Aug;35(8):1944–1957. doi: 10.1109/tpami.2012.268. [DOI] [PubMed] [Google Scholar]
- [17].IEEE IEEE recommended practice for speech quality measurements. IEEE Trans. Audio Electroacoust. 1969 Jun;AE-17(3):225–246. [Google Scholar]
- [18].Jaureguiberry X, Vincent E, Richard G. Fusion Methods for Audio Source Separation [Online] 2014 Available: https://hal.archives-ouvertes.fr/hal-01120685/document.
- [19].Jin Z, Wang DL. A supervised learning approach to monaural segregation of reverberant speech. IEEE Trans. Audio Speech Lang. Process. 2009 May;17(4):625–638. [Google Scholar]
- [20].Kim G, Lu Y, Hu Y, Loizou PC. An algorithm that improves speech intelligibility in noise for normal-hearing listeners. J. Acoust. Soc. Amer. 2009;126(3):1486–1494. doi: 10.1121/1.3184603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Le Roux J, Watanabe S, Hershey JR. Ensemble learning for speech enhancement. Proc. IEEE Workshop Appl. Signal Process. Audio Acoust. 2013:1–4. [Google Scholar]
- [22].May T, Dau T. Computational speech segregation based on an auditory-inspired modulation analysis. J. Acoust. Soc. Amer. 2014;136(6):3350–3359. doi: 10.1121/1.4901711. [DOI] [PubMed] [Google Scholar]
- [23].Rennie SJ, Hershey JR, Olsen P. Single-channel multitalker speech recognition. IEEE Signal Process. Mag. 2010 Nov;27(6):66–80. [Google Scholar]
- [24].Srinivasan S, Roman N, Wang DL. Binary and ratio time-frequency masks for robust speech recognition. Speech Commun. 2006;48:1486–1501. [Google Scholar]
- [25].Sutskever I, Martens J, Dahl G, Hinton G. On the importance of initialization and momentum in deep learning. Proc. Int. Conf. Mach. Learn. 2013:1–8. [Google Scholar]
- [26].Taal CH, Hendriks RC, Heusdens R, Jensen J. An algorithm for intelligibility prediction of time–frequency weighted noisy speech. IEEE Trans. Audio Speech Lang. Process. 2011 Sep;19(7):2125–2136. [Google Scholar]
- [27].Tu Y, Du J, Xu Y, Dai L, Lee C-H. Speech separation based on improved deep neural networks with dual outputs of speech features for both target and interfering speakers. Proc. Int. Symp. Chin. Spoken Lang. Process. 2014:250–254. [Google Scholar]
- [28].Vincent E, Gribonval R, Févotte C. Performance measurement in blind audio source separation. IEEE Trans. Audio Speech Lang. Process. 2006 Jul;14(4):1462–1469. [Google Scholar]
- [29].Wang DL. On ideal binary mask as the computational goal of auditory scene analysis. Speech Sep. Humans Mach. 2005;60:63–64. [Google Scholar]
- [30].Wang Y. Ph.D. dissertation, Dept. Comput. Sci. Eng. Ohio State Univ.; Columbus, OH, USA; May, 2015. Supervised speech separation using deep neural networks. [Google Scholar]
- [31].Wang Y, Narayanan A, Wang DL. On training targets for supervised speech separation. IEEE/ACM Trans. Audio Speech Lang. Process. 2014 Dec;22(12):1849–1858. doi: 10.1109/TASLP.2014.2352935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Wang Y, Wang DL. Towards scaling up classification-based speech separation. IEEE Trans. Audio Speech Lang. Process. 2013 Jul;21(7):1381–1390. [Google Scholar]
- [33].Weng C, Yu D, Seltzer ML, Droppo J. Deep neural networks for single-channel multi-talker speech recognition. IEEE/ACM Trans. Audio Speech Lang. Process. 2015 Oct;23(10):1670–1679. [Google Scholar]
- [34].Weninger F, et al. Speech enhancement with LSTM recurrent neural networks and its application to noise-robust ASR. Proc. Int. Conf. Latent Variable Anal. Signal Sep. 2015:91–99. [Google Scholar]
- [35].Weninger F, Hershey JR, Le Roux J, Schuller B. Discriminatively trained recurrent neural networks for single-channel speech separation. Proc. IEEE Global Conf. Signal Inf. Process. 2014:577–581. [Google Scholar]
- [36].Williamson DS, Wang Y, Wang DL. Complex ratio masking for monaural speech separation. IEEE/ACM Trans. Audio Speech Lang. Process. 2016 Mar;24(3):483–492. doi: 10.1109/TASLP.2015.2512042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Xu Y, Du J, Dai L-R, Lee C-H. An experimental study on speech enhancement based on deep neural networks. IEEE Signal Process. Lett. 2014 Jan;21(1):65–68. [Google Scholar]
- [38].Xu Y, Du J, Dai L-R, Lee C-H. A regression approach to speech enhancement based on deep neural networks. IEEE/ACM Trans. Audio Speech Lang. Process. 2015 Jan;23(1):7–19. [Google Scholar]
- [39].Zhang X-L, Wang DL. Boosted deep neural networks and multi-resolution cochleagram features for voice activity detection. Proc. Interspeech. 2014:1534–1538. [Google Scholar]
- [40].Zhang X-L, Wang DL. Multi-resolution stacking for speech separation based on boosted DNN. Proc. Interspeech. 2015:1745–1749. [Google Scholar]