Abstract
Research examining models of memory has focused on differences in the shapes of ROC curves across tasks and has used these differences to argue for and against the existence of multiple memory processes. ROC functions are usually obtained from confidence judgments, but the reaction times associated with these judgments are rarely considered. The RTCON2 diffusion model for confidence judgments has previously been applied to data from an item recognition paradigm. It provided an alternative explanation for the shape of the z-ROC function based on how subjects set their response boundaries and these settings are also constrained by reaction times. In our experiments, we apply the RTCON2 model to data from associative recognition tasks to further test the model’s ability to accommodate non-linear z-ROC functions. The model is able to fit and explain a variety of z-ROC shapes as well as individual differences in these shapes while simultaneously fitting reaction time distributions. The model is able to distinguish between differences in the information feeding into a decision process and differences in how subjects make responses (i.e., set decision boundaries and confidence criteria). However, the model is unable to fit data from a subset of subjects in these tasks and this has implications for models of memory.
Keywords: Response time, Confidence judgments, Associative recognition memory, Receiver operating characteristics, Diffusion model
Introduction
Associative memory is memory for combinations of items (i.e., do you remember whether these items were presented together or separately during the study list). Compared to simple item recognition memory (i.e., do you remember an item or not) associative recognition shows greater declines with age (e.g., Bastin & Van der Linden, 2006; Craik, Luo, & Sakuta, 2010; Naveh-Benjamin, 2000, 2012; Ratcliff, Thapar, & McKoon, 2011), is less susceptible to decay and interference (Hockley, 1992), has different patterns of false alarm rates (Hockley, 1994; Malmberg & Xu, 2007), has a different time course (Gronlund & Ratcliff, 1989), and shows different word frequency effects (Clark, 1992), among other differences.
In this paper, we apply the RTCON2 model to an associative recognition task for which subjects used a six-point scale to rate the confidence with which they believed a pair of test items had or had not appeared together earlier in the experiment. This is the more common method of collecting confidence responses, especially in memory research, although some researchers have had subjects make a two-choice response followed by a confidence rating (Baranski & Petrusic, 1998; Merkle & Van Zandt, 2006; Pleskac & Busemeyer, 2010; Van Zandt, 2000; Van Zandt & Maldonado-Molina, 2004; Vickers, 1979; Vickers & Lee, 1998, 2000). In the model, evidence is accumulated toward a set of decision thresholds and the relative heights of these thresholds explains both the location and shape of subjects’ reaction time distributions and also the shape of their z-ROC functions. This means that z-ROC shape does not solely provide information about memory representations as has been assumed to date but also reflects individual differences in how subjects use confidence response scales. Application of the RTCON2 model to associative recognition is especially interesting because this type of memory task often produces z-ROC functions with different shapes than item recognition, and these differences have previously been used to motivate the development of various memory models (Glanzer, Hilford, & Kim, 2004; Hilford, Glanzer, Kim, & DeCarlo, 2002; Kelley & Wixted, 2001; Qin, Raye, Johnson, & Mitchell, 2001; Slotnick & Dodson, 2005; Slotnick, Klein, Dodson, & Shimamura, 2000; Wixted, 2007; Yonelinas, 1997, 1999) and in neuroscience research (Eichenbaum, Yonelinas, & Ranganath, 2007; Henson, Rugg, Shallice, & Dolan, 2000; Kim & Cabeza, 2007; Kirwan, Wixted, & Squire, 2008; Moritz, Glascher, Sommer, Buchel, & Braus, 2006; Rissman, Greely, & Wagner, 2010; Stark & Squire, 2001; Wais, 2011; Yonelinas, Hopfinger, Buonocore, Kroll, & Baynes, 2001). However, these memory models typically focus only on the kind of evidence being fed into a decision, ignore or over-simplify the process of making a decision based on that evidence, and may not produce the same estimates of evidence that a full decision model would. In contrast, our research attempts to model the process of making confidence-judgments in an associative recognition paradigm and investigate to what degree experimental findings can be accounted for with a decision-making model.
In an associative recognition memory experiment, participants study pairs of words and are then asked to distinguish between pairs of words that were previously studied together (“intact”) or studied separately (“rearranged”). In an item recognition memory experiment, participants study individual items and are then asked to distinguish between items that were previously studied (“old”) and items that were not previously studied (“new”). Most of the work investigating either type of recognition memory has relied on Signal Detection theory (Banks, 1970; Bernbach, 1967; Donaldson & Murdock, 1968; Egan, 1958; Grasha, 1970; Kintsch, 1967; Kintsch & Carlson, 1967; Lockhart & Murdock, 1970; Norman & Wickelgren, 1969; Ratcliff, McKoon, & Tindall, 1994; Ratcliff, Sheu, & Gronlund, 1992; Yonelinas, 1994). In the signal detection framework, it is assumed that each tested pair has some value of associative strength that is normally distributed for each category of tested items (for example, “intact” or “rearranged” word pairs). The intact/rearranged decision can then be modeled by placing a single criterion on a dimension representing the associative strength of the test items. If the associative strength value for a test item is above the criterion, then an ‘intact’ response is made; otherwise, if the associative strength value is below the criterion, then a ‘rearranged’ response is made. Bias toward one of the response choices can be modeled by changes in the placement of the decision criterion, and multiple response options (such as confidence judgments) can be modeled by including additional decision criteria.
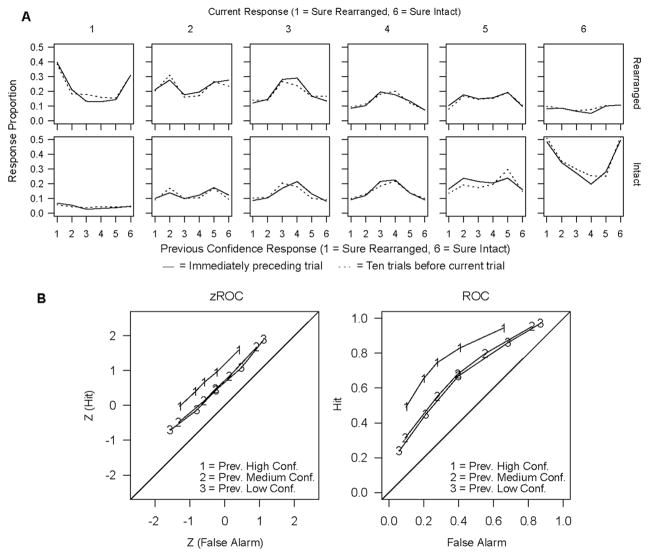
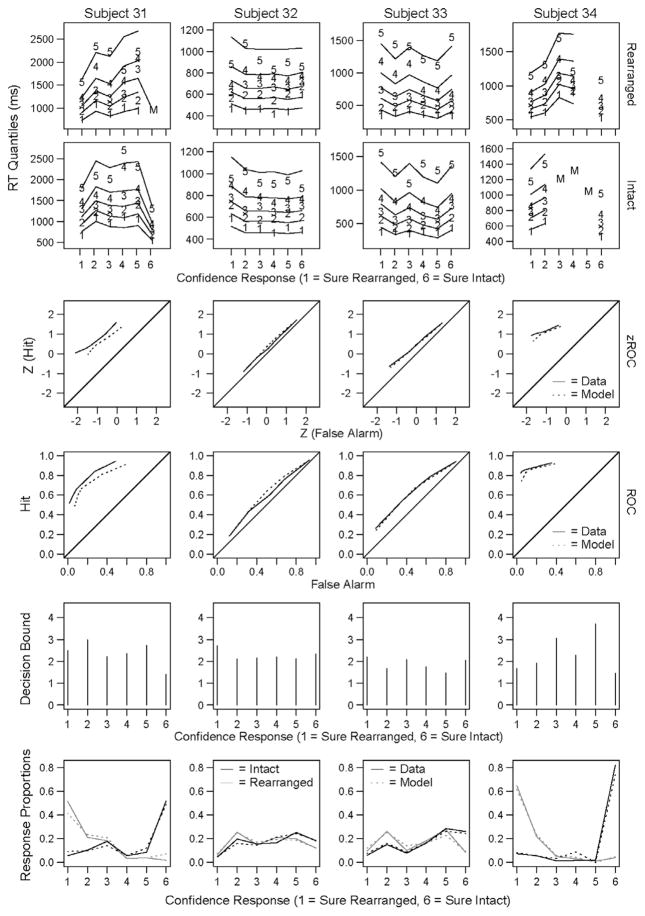
In confidence judgment procedures, subjects rate their confidence that an item is intact or rearranged using a response scale with levels ranging from ‘very sure intact’ to ‘very sure rearranged’. To model these multiple response options, additional decision criteria are used to divide the memory strength dimension into multiple response regions. Fig. 1 depicts two normal distributions, one for intact items and one for rearranged items, and three possible decision criteria. These decision criteria partition the match dimension into four response regions corresponding to four confidence categories: from left to right, high confidence rearranged, low confidence rearranged, low confidence intact, high confidence intact. As the decision criterion moves from left to right, both the hit and false alarm rates decrease.
Fig. 1.
The standard Signal Detection model with one normal distribution each for the intact and rearranged items respectively, four response regions created by three confidence criteria, the z-ROC obtained from the two distributions, and the equation relating the z-transformed hit and false alarm rates.
These decision criteria can then be used to create receiver operating characteristic (ROC) functions, which are plots of the hit rate (“intact” responses to intact word pairs) against the false alarm rate (“intact” responses to rearranged word pairs). To create an ROC function from the data, each criterion is treated as if it were the only criterion and the hit and false alarm rates for that criterion are calculated and plotted against each other as a single point on the ROC curve. Hit and false alarm rates are calculated first for the rightmost criterion, representing the highest confidence intact category, then for the two rightmost categories (adding together the number of responses in those two categories), then for the three rightmost, and so on.
These hit and false alarm rates are frequently converted to z-scores, resulting in a function called a z-ROC. The assumption of normal distributions of memory evidence predicts linear z-ROC functions with a slope equal to the ratio of the standard deviations of the “intact” and “rearranged” item distributions (Ratcliff et al., 1992). The lower portion of Fig. 1 depicts the z-ROC function obtained from the two distributions. However, linear z-ROC functions are also consistent with other kinds of distributions such as poisson, gamma, and even a combination of ramp and rectangular distributions (Banks, 1970; Lockhart & Murdock, 1970; Murdock, 1974). With different distributions of evidence, the slope of the z-ROC function is not the ratio of the standard deviations of the distributions as it is when the distributions are normal.
As predicted by SDT with normal distributions, most of the z-ROC functions found in the memory literature on item recognition have been approximately linear. However, a number of studies have demonstrated systematically non-linear z-ROC functions and these findings have prompted theoretical elaborations of the standard single-process signal-detection theory (DeCarlo, 2002; Malmberg & Xu, 2006; Ratcliff et al., 1994; Ratcliff & Starns, 2013; Rotello, Macmillan, & Reeder, 2004; Rotello, Macmillan, & Van Tassel, 2000; Yonelinas, 1994, 1997; Yonelinas, Dobbins, Szymanski, Dhaliwal, & King, 1996). Several of these theories have focused on explaining the slightly U-shaped z-ROC functions observed in some associative recognition and source-memory experiments (Glanzer et al., 2004; Hilford et al., 2002; Kelley & Wixted, 2001; Qin et al., 2001; Slotnick & Dodson, 2005; Slotnick et al., 2000; Wixted, 2007; Yonelinas, 1997, 1999).
There are a number of problems with this SDT approach to memory modeling. First, this approach often ignores differences between individuals. ROC analyses are frequently conducted on data that has been averaged across subjects, so any differences between subjects are ignored or relegated to an Appendix A. As the present study will demonstrate, there can be substantial differences in how subjects utilize confidence response scales such that it is not appropriate to only analyze averaged data (Malmberg & Xu, 2006; Ratcliff et al., 1994). Second, the SDT approach ignores the reaction time associated with each response. Although there is a well-known relationship between the speed and accuracy with which people make decisions (Pachella, 1974; Wickelgren, 1977), most memory researchers only collect and analyze accuracy data. In order to provide a complete account of the confidence decision process, it is important to consider both reaction time and accuracy. Third, the SDT approach assumes that the only source of variability in the decision process is the variability in memory strength between items. This assumption leads to inappropriate conclusions about the z-ROC functions (Ratcliff & Starns, 2009, 2013; Starns, Ratcliff, & McKoon, 2012). Fourth, elaborations of SDT often include additional memory processes or additional sources of information in order to accommodate non-linear z-ROC functions (Arndt & Reder, 2002; DeCarlo, 2002, 2003; Hilford et al., 2002; Kelley & Wixted, 2001; Rotello et al., 2004; Yonelinas, 1994; Yonelinas & Parks, 2007). With the inclusion of reaction time data and individual differences, the present study will demonstrate that these additional processes are not always necessary to produce non-linear z-ROC functions. All of these problems with SDT can potentially be addressed by using the RTCON2 model. This model produces both accuracy and reaction time predictions for individual subjects, it includes several sources of variability related to the decision process, and it has been able to fit a variety of item recognition z-ROC functions without additional memory processes (Ratcliff & Starns, 2009, 2013). The RTCON2 model is not a memory model in the same way SDT is not a memory model. A complete description of processing would have a memory model provide the distributions of memory evidence used in making the decision as in SDT. However, the model has been able to explain various z-ROC shapes observed in item recognition tasks, including non-linear functions. The explanation for these shapes is based on how subjects set their decision boundaries and is constrained by reaction time data. As such, the explanation for these shapes is based on the process of making a decision as opposed to the type of information entering into the decision process from memory. The goal of these experiments is to determine whether the RTCON2 model can similarly account for the non-linear z-ROC functions commonly observed in associative recognition tasks.
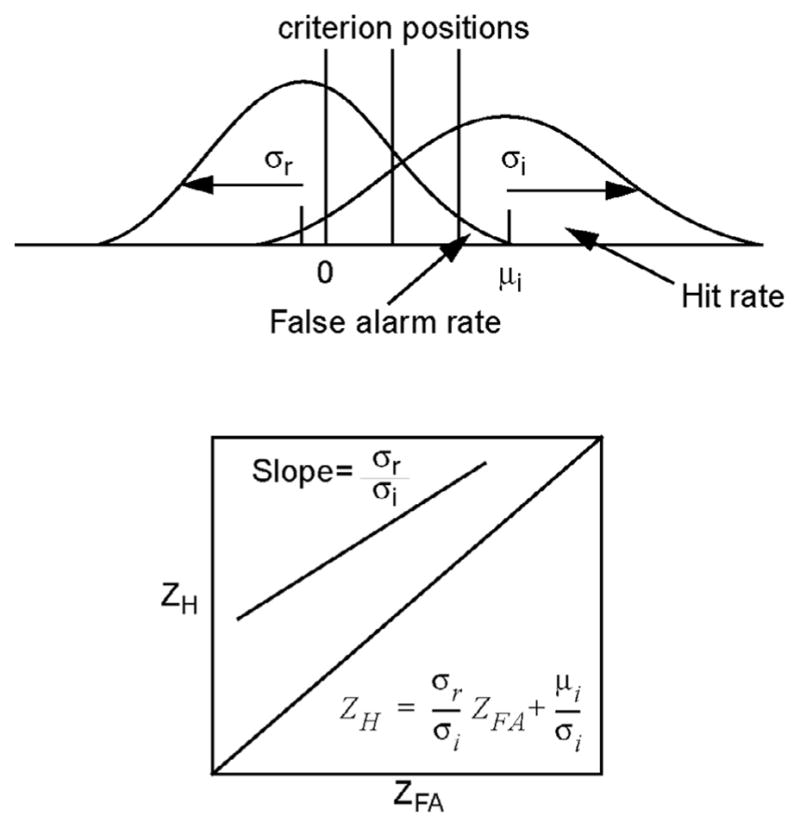
The RTCON2 model has previously been applied to confidence judgments in item recognition and motion discrimination tasks and was shown to provide a better fit to the data than several competing decision models (Ratcliff & Starns, 2013). In the RTCON2 model, the evidence available to the decision process on a single trial (i.e., the memory strength for a particular item) is assumed to be a distribution across the evidence-strength dimension instead of a single value (cf. Beck et al., 2008; Gomez, Ratcliff, & Perea, 2008; Jazayeri & Movshon, 2006; Ratcliff, 1981; Ratcliff & Starns, 2009). These item distributions have a standard deviation of 1 and their mean location varies from trial to trial (as in SDT). The bottom portion of Fig. 2 illustrates how the distribution of evidence for a single item is mapped to the decision process. As in SDT, multiple confidence criteria are used to divide the match dimension into multiple response regions corresponding to different levels of confidence.
Fig. 2.
RTCON2. The distribution of evidence for an item on a given trial drives six mutually inhibitory accumulators (one for each confidence category). The proportion of the distribution between the confidence criteria on the match dimension drives the drift rate for each confidence category. When one of the accumulators reaches its decision boundary, the corresponding response is made. Each time one accumulator takes a step up of size x, the accumulators on the opposite side take a x/(N/2) step down (where N is the number of accumulators) such that the amount of evidence stays constant (i.e., if an ‘intact’ accumulator is incremented, then the ‘rearranged’ accumulators are all decremented and the other ‘intact’ accumulators are unchanged).
Each response region has its own accumulator and decision boundary, as shown in the top portion of Fig. 2, and the diffusion processes race until one of the processes reaches its decision boundary and the corresponding response is made. Evidence for each confidence response accumulates separately over time toward a decision boundary. This is similar to other sequential sampling models that assume that noisy evidence is accumulated separately for each response alternative (as in the dual-diffusion model, Ratcliff, Hasegawa, Hasegawa, Smith, & Segraves, 2007; and the Leaky-Competing Accumulator model, Usher & McClelland, 2001).
The mean position of the distribution of evidence (μ) is determined by the quality of information extracted from the stimulus and determines the rate of accumulation (ν) for each accumulator. In an experiment, the value of μ would be different for stimulus conditions of differing difficulty. For example, in an associative recognition experiment, μ would represent the quality of the match between a given word pair and memory. A pair of words that had been presented together during the study period should have a higher degree of match (i.e., a higher value of μ) than a pair of words that had been presented in different pairs during the study period. The quality of information from stimuli of the same type is allowed to vary across trials to reflect differences in the encoding and retrieval of associative information across pairs of items. This between-trial variability in μ is assumed to be normally distributed with standard deviation s. The average rate of accumulation (ν) for each response is determined by the proportion of the within-trial distribution of evidence in each of the response regions. This accumulation process is subject to moment-to-moment variability such that processes with the same accumulation rates will not always terminate at the same time or with the same confidence response.
Several aspects of this model affect the relationship between the level of confidence and the evidence in favor of a particular choice. Specifically, a particular confidence judgment is determined by the decision boundaries of the response accumulators and by the criteria that divide the strength dimension into response regions as well as by the amount of evidence in favor of a particular confidence response. For example, a high confidence response region may have a higher decision boundary such that more evidence must be accumulated for that response to be selected. The height of the decision boundary would cause that particular response to be selected less often and with a longer reaction time than if that response region had a lower decision boundary, even for items that have a high mean value of evidence. Thus in RTCON2 confidence is not merely a function of accuracy.
The RTCON models are an extension of the diffusion model (Audley & Pike, 1965; Ratcliff, 1978, 1988, 2006; Ratcliff & McKoon, 2008), and were developed to accommodate both accuracy and reaction time distributions from multi-choice confidence judgment tasks (Ratcliff & Starns, 2009, 2013). RTCON2 differs from the original RTCON model in that it uses a slightly different decision process (RTCON2 uses constant summed evidence whereas RTCON uses an OU diffusion process) and allows accumulators to go below zero (in fact, because it is a linear process, there is no true zero point; a constant could be added to the base evidence level and decision bounds and the behavior of the model would be the same).
In the constant summed evidence algorithm, the increment to evidence (Δx) on each time step (Δt) is determined by its drift rate (v) and noise (Eq. (1)). On each time step, one of the response accumulators is selected randomly and increased (Eq. (1)) and some of the other response accumulators are decreased such that the sum of the total decrease is equal to the increase in the selected accumulator (Eq. (2)).
| (1) |
| (2) |
There are several possible variants of this algorithm. For example, all of the response accumulators could be competing (i.e., an increase on one accumulator would cause all of the other N accumulators to decrease) or only some of the accumulators could be competing (i.e., if one of the ‘intact’ accumulators was increased, only the ‘rearranged’ accumulators would decrease – the other ‘intact’ accumulators would be unchanged). For this application, we used the variant of the model where an increase in evidence in one of the ‘intact’ accumulators would cause a decrease in evidence only in the ‘rearranged’ accumulators (this is shown in Eq. (2)), but not the other ‘intact’ accumulators. This version of the constant-summed evidence algorithm makes intuitive sense in that evidence for one type of response (intact or rearranged) should not compete with other confidence levels of that same response. This version of the algorithm also provides parameter values that are more consistent across different numbers of response options. The expressions for the changes in evidence for each accumulator are given in Eqs. (1) and (2). Eq. (1) describes the update in evidence for the selected accumulator and Eq. (2) describes the corresponding change in activity for the non-selected accumulators (note that, due to noise from the second terms in the right-hand side of Eq. (1), Δxi could also be a negative value such that the other accumulators would all take a proportional step up). If the selected accumulator was one of the ‘intact’ accumulators, then Eq. (2) would be used to adjust the ‘rearranged’ accumulators, but the other intact accumulators would be unchanged (and vice versa, if a ‘rearranged’ accumulator was selected). In these equations, as is a scaling parameter that adjusts drift rate (the area under the distribution in the bottom of Fig. 2), σ is within-trial variability in the accumulation process, η is a normally distributed random variable with mean 0 and SD 1, and N is the total number of accumulators. The constant summed evidence algorithm has been shown to provide a better fit to empirical data than a competing class of models because it is better able to account for shifts in the RT distributions across confidence responses (Ratcliff & Starns, 2013).
Reaction time distributions are obtained by combining the decision time (the time taken for one of the evidence accumulators to reach a decision boundary) with a uniformly distributed non-decision component. The non-decision component is assumed to have mean Ter and range st, and it encompasses both encoding and response output processes. Reaction time distributions are also dependent on the height of the decision boundaries, which vary from trial to trial over a uniform distribution with a range of sb.
Although both RTCON2 and SDT use normal distributions of stimulus information, they produce considerably different interpretations of z-ROC functions. In SDT, the proportion of hit and false alarm rates can only be manipulated through the placement of the decision criterion. In RTCON2, the proportion of hit and false alarm responses can be manipulated either by adjusting the height of the decision boundaries or by adjusting the confidence criteria. A shift in the heights of the decision boundaries will shift the response time distributions and have an effect on the leading edge of the RT distribution whereas a shift in the confidence criteria will have a smaller effect on the leading edge. Thus, the two ways of adjusting response proportions in RTCON2 are identifiable based on reaction time distributions. Because the response proportions depend on both the height of the decision boundaries and the placement of the confidence criteria, RTCON2 is able to fit a wider variety of z-ROC functions than standard SDT. In contrast to SDT, which deals only with accuracy, RT distributions provide additional severe constraints on RTCON2 because the model not only has to account for z-ROC functions but also RT distributions.
As mentioned previously, standard SDT with normal distributions of evidence is unable to account for the non-linear z-ROC functions observed in some associative recognition experiments (Glanzer et al., 2004; Hilford et al., 2002; Kelley & Wixted, 2001; Qin et al., 2001; Slotnick & Dodson, 2005; Slotnick et al., 2000; Wixted, 2007; Yonelinas, 1997, 1999). This has prompted theorists to add extra memory processes (Yonelinas, 1994; Yonelinas & Parks, 2007) or extra sources of information (DeCarlo, 2002, 2003; Hilford et al., 2002; Kelley & Wixted, 2001) to standard SDT in order to account for these findings. Because the RTCON2 model has different ways of adjusting response proportions (but additional constraints because of RT distributions), it can potentially account for non-linear z-ROC functions through changes in the decision-making process as opposed to changes in the memory process. Moreover, because RTCON2 is fit to both accuracy and RT data, applications of the model in other paradigms have demonstrated a relationship between the shape of the z-ROC function and the behavior of response time distributions that had not previously been observed.
Another important difference between SDT and RTCON2 is that SDT contains only a single source of variability. In SDT, the variability in the distribution of memory strength is the only source of variability that affects the decision. In RTCON2, however, there is variability across trials in the quality of evidence from a stimulus (the variability in the mean value of the evidence distribution across trials), variability in the evidence accumulation process, and variability in the decision boundaries. These three sources of variability are identifiable and are needed to account for decision time, that is, RT distributions for responses for the various confidence categories (see Ratcliff & Starns, 2009, for some discussion of parameter recovery and lack of parameter correlations for RTCON). In standard SDT, the slope of the z-ROC function represents the ratio of the standard deviations of the distributions of old and new stimulus evidence. But because there are several sources of variability in the decision process, the slope of the z-ROC function is not a measure of the ratio of stimulus variability for the two choices as in SDT.
RTCON2 is able to account for both accuracy and reaction time values for confidence judgments, distinguishes between several sources of variability in the decision process, and provides an alternative explanation for the shape of z-ROC functions. The aim of these experiments is to investigate whether this model can account for data from an associative recognition task.
Experiment 1
The first experiment was designed to collect a large number of observations for a few subjects to provide stringent tests of the RTCON2 model performance on an associative recognition task. The aim is to determine whether this one-process model can account for the type of accuracy (and RT) data that has been assumed to provide evidence for different memory processes (DeCarlo, 2002, 2003; Healy, Light, & Chung, 2005; Kelley & Wixted, 2001; Rotello et al., 2000; Yonelinas, 1994). In this experiment, subjects studied lists of pairs of words and then were presented with pairs of test words and had to distinguish between intact and rearranged versions of the study pairs.
Method
Subjects
Five Ohio State University undergraduate students participated in 8 sessions and earned $10 for each completed session.
Materials
The stimuli were drawn from a pool of 814 high-frequency words, 859 low-frequency words, and 741 very-low-frequency words. Low-frequency words ranged from 4 to 6 occurrences per million (M = 4.41), very-low-frequency words ranged from 0 to 1 occurrence per million (M = 0.365), and high-frequency words ranged from 78 to 10,595 occurrences per million (M = 323.22; Kučera & Francis, 1967). Study lists were composed of 12 high-frequency words, 12 low-frequency words, and 4 very-low-frequency words selected randomly (without replacement) from the word pools. These words were randomly paired within frequency to create 14 word pairs (6 high-frequency pairs, 6 low-frequency pairs, and 2 very-low-frequency pairs). The two very-low-frequency word pairs served as buffer items for the study list and were presented in the first and last positions of the study list, and the remaining pairs were target items. All of the target word pairs were presented twice within each list. The 12 target pairs were randomly assigned to the middle study list positions with the restriction that there was at least one intervening word pair between the two presentations of each pair.
Test lists consisted of the two buffer word pairs (presented in the first and last positions of the test list) and the 12 target pairs. Each pair was presented only once during the test list and exactly half of the target pairs were randomly rearranged within frequency (i.e., a low-frequency word pair could only be rearranged with another low-frequency word pair). Words also maintained the same positions within pairs, such that a word presented as the first item in a pair during study would also be the first item of a pair during test, regardless of what word it was paired with. Thus each test list consisted of 6 rearranged pairs and 6 intact pairs. Intact pairs consisted of words which had appeared together in the study list and rearranged pairs consisted of words which appeared in different pairs in the study list.
Procedure
Each experimental session lasted approximately 50 min. The first two sessions for each subject consisted of a response-key practice block, 3 study/test blocks, a second response-key practice block, and 20 more study/test blocks. The second response-key practice block was dropped after the first two sessions, because subjects were familiar with the response keys and no longer needed the additional practice. Subjects responded using a PC keyboard on which the Z, X, C, comma, period, and slash keys were labeled with the symbols “− − −”, “− −”, “−”, “+”, “+ +”, and “+ + +”. Subjects were instructed to place their left-hand ring, middle, and index fingers on the “− − −”, “− −”, and “−” keys and their right-hand index, middle, and ring fingers on the “+”, “+ +”, and “+ + +” keys.
During the response-key practice, each of the symbols marked on the keyboard (e.g., “− −”) would appear on the screen one at a time and the subjects were told to press the designated key as quickly as possible. If a subject took longer than 800 ms to respond to one of the symbols, a “TOO SLOW” message would appear on the screen for 1000 ms. Each practice block consisted of 10 repetitions of each of the six response key options resulting in 60 trials total in each block. The symbols appeared in random order within the block with the restriction that repeated symbols had to have at least one intervening symbol.
For the remainder of the experiment, subjects were told that they would be presented with pairs of words during the study portions of the experiment and their job was to learn these pairs. During the study/test blocks, subjects initiated the start of each study list by pressing the spacebar. Each word pair in the study list was displayed for 3000 ms followed by 200 ms of blank screen. Immediately after the final study-list word pair, a message appeared directing subjects to press the space bar to begin the test list. During the test-list, subjects were required to distinguish between the word pairs that had not appeared during the study-list (rearranged word pairs) and those that had (intact word pairs). Each word pair remained on the screen until the subject had made a response. Subjects were instructed to use the different response-key options to indicate whether a word pair had appeared in the study-list and their confidence in their response. They were told to use one of the “−” keys to indicate that the word pair had not appeared in the study-list, and to use one of the “+” keys to indicate that it had. Subjects were instructed to use the different levels of “+” and “−” to indicate their amount of confidence in their response (e.g., if a subject felt very confident that a word pair was intact they would use the “+ + +” key, whereas if they felt only moderately confident they would use the “+ +” key). Subjects were encouraged to respond quickly and accurately and to try to spread their responses among all six response-keys throughout the course of the experiment. If a subject took less than 280 ms to respond to one of the test items, a “TOO FAST” message would appear on the screen for 1500 ms. Subjects were given error feedback throughout all test blocks in the form of the words “CORRECT” or “ERROR” displayed for 300 ms after their response to each test item.
Model fitting
The RTCON2 model was fit to each individual subject’s response proportion and reaction time quantiles (.1, .3, .5, .7, .9) for each of the 6 confidence response for each of the 4 conditions (rearranged high frequency, rearranged low frequency, intact high frequency, and intact low frequency word pairs). The RT quantiles divide the response proportion data into six bins for each confidence category. Initial parameter values were chosen that produced predictions similar to the empirical data, and then a simplex function (Nelder & Mead, 1965) was used to adjust the parameters of the model until the predictions matched the data as closely as possible. The match between the empirical data and the model predictions was quantified by a chi-square (χ2) statistic, which was minimized by the simplex function (see Ratcliff & Tuerlinckx, 2002 for more detail). Because there are no exact solutions for this model, simulations are used to generate predicted values from the model. To simulate the process of accumulation given by Eqs. (1) and (2), we used the simple Euler’s method with 1-ms steps (cf. Brown, Ratcliff, & Smith, 2006; Usher & McClelland, 2001). For each millisecond step, one accumulator was chosen randomly, and the evidence in it was incremented or decremented according to Eq. (1) and opposite accumulators were incremented or decremented according to Eq. (2) (e.g., if the selected accumulator was for one of the ‘intact’ responses, then the evidence in the ‘rearranged’ accumulators would be adjusted according to Eq. (2) and the other ‘intact’ accumulators would be unchanged). For each condition, 20,000 simulations of the decision process were used to generate the response proportions and RT quantiles for each confidence category. Note that we use the term ‘model predictions’ to refer to data generated by the model for a specific set of parameter values. These predictions are thus the data predicted by the model structure and a given parameter set, as opposed to predictions about some future data based on fits of the current data.
There are six RT bins for each confidence response, which gives 36 degrees of freedom for the 6-choice task. But these response proportions have to add to 1, which reduces the degrees of freedom to 35 for each condition. With four conditions, this gives a total of 140 degrees of freedom in the data. For this experiment there are 23 free parameters in RTCON2. Of these, 12 are used to represent the memory strength feeding into the decision (3 mean drift values – one is fixed to zero, 4 between-trial variability in the mean of the drift distribution, and 5 confidence criteria) and the remaining 11 parameters are used to model the decision process (6 decision boundaries, non-decision time, variability in non-decision time, the scaling parameter on drift, variability in the decision boundaries, and within-trial noise in the diffusion process). These 11 additional parameters are what enable the model to produce response times as well as accuracy. Note that an accuracy-only SDT model with the same representation of memory strength would require 12 parameters (the same ones for RTCON2) for data with only 20 degrees of freedom. Additionally, although RTCON2 has a fairly large number of parameters, a change in any one of the parameter values will affect predictions across multiple conditions or response categories such that it is not possible to remedy misfits in a single condition by simply adjusting a single parameter.
Results and discussion
There are two main results of this experiment. First, the model fits both the proportion of responses and the RT quantiles for each confidence category. Second, because the model fits the proportions of responses, it also fits the ROC and z-ROC functions for all but one subject reasonably well.
Data from this experiment consisted of response proportions and reaction-time quantiles for each subject from each condition and each confidence response. There were four conditions in this experiment: rearranged high frequency, rearranged low frequency, intact high frequency, and intact low frequency word pairs. Reaction time latencies less than 300 ms or greater than 4000 ms were excluded from these analyses (less than 0.3% of all data).
We analyzed response rates across all levels of confidence for word frequency effects. There was a higher hit-rate for LF word pairs (M = 0.81, SD = 0.07) than HF word pairs (M = 0.66, SD = 0.10) and this difference was significant (t(4) = −9.3, p < .05). There was also a higher false-alarm rate for LF word pairs (M = 0.34, SD = 0.22) than HF word pairs (M = 0.25, SD = 0.14) but this difference was not significant (t(4) = −2.3, p > .05).
The model was fit to data from individual subjects and the best-fitting model parameters are shown in Table 1. For each subject, these parameter values were used to generate predicted reaction time quantiles and response proportions for each condition. These predicted values can then be compared with the empirical data using a χ2 test to quantitatively assess the model fit. The mean χ2 value for this experiment was 254 with a SD of 36. This mean is 1.5 times the critical χ2 value (168.6) which indicates a mismatch between the model’s predictions and the data. However, the size of this mismatch is comparable to those obtained in other experiments with diffusion models. Ratcliff, Thapar, Gomez, and McKoon (2004) demonstrated that a miss as large as .1 in the proportion of responses between quantiles could produce χ2 values 2–3 times the critical value. Similarly, Ratcliff and Starns (2009) demonstrated that 10 ms perturbations of the quantile reaction times could produce large increases in χ2 values. The significance of the χ2 values is also, at least partially, a power issue. In order to fit RCON2, we need good RT quantile estimates and so need to collect a sizeable amount of data from each subject. For this experiment, we collected an average of 550 responses per condition from each subject. With this many responses, even small differences between the empirical data and the model predictions will be significant. For comparison, if we had observed these same response proportions and quantile RTs from about 358 responses per condition (65% of the actual 550) then the same χ2 test yields a mean value of 153.29 (4 out of 5 subjects have values less than the critical value) and the model would be considered to be a reasonably good match to the data. Additionally, the original RTCON model produces an average χ2 value of 331 when fit to these data. This demonstrates that this new version of the RTCON model is indeed an improvement over the original version in that it provides a closer fit to the data. The original RTCON model primarily had difficulty producing the bowed RT quantiles that were observed in this experiment.
Table 1.
Experiment 1 best fitting model parameters.
| Subject | Ter | st | as | σ | sb | χ2 | ||
|---|---|---|---|---|---|---|---|---|
| 1 | 389 | 358 | 0.021 | 0.13 | 1.47 | 196 | ||
| 2 | 363 | 178 | 0.047 | 0.11 | 0.90 | 256 | ||
| 3 | 292 | 162 | 0.067 | 0.12 | 1.04 | 250 | ||
| 4 | 476 | 383 | 0.040 | 0.15 | 0.71 | 294 | ||
| 5 | 535 | 357 | 0.049 | 0.17 | 1.39 | 273 | ||
| b1 | b2 | b3 | b4 | b5 | b6 | |||
|
|
||||||||
| 1 | 1.81 | 1.57 | 1.76 | 1.32 | 1.17 | 1.42 | ||
| 2 | 2.30 | 2.03 | 2.46 | 2.19 | 1.76 | 1.37 | ||
| 3 | 1.68 | 1.71 | 2.48 | 2.40 | 1.65 | 1.52 | ||
| 4 | 2.80 | 2.91 | 2.72 | 2.10 | 2.36 | 2.01 | ||
| 5 | 3.00 | 2.49 | 2.27 | 2.67 | 2.27 | 2.26 | ||
| c1 | c2 | c3 | c4 | c5 | ||||
|
|
||||||||
| 1 | −0.81 | 0.00 | 0.87 | 2.04 | 3.23 | |||
| 2 | −1.20 | −0.04 | 0.76 | 1.46 | 2.51 | |||
| 3 | −0.84 | 0.08 | 0.95 | 1.96 | 2.81 | |||
| 4 | −0.69 | 0.00 | 1.15 | 1.73 | 2.18 | |||
| 5 | −0.90 | −0.25 | 0.85 | 1.93 | 3.00 | |||
| μrH | μrL | μiH | μiL | srH | srL | siH | siL | |
|
|
||||||||
| 1 | 0.00 | 0.87 | 0.42 | 2.49 | 0.61 | 0.63 | 0.65 | 0.53 |
| 2 | 0.00 | −0.07 | 1.18 | 1.71 | 0.31 | 0.52 | 0.57 | 0.48 |
| 3 | 0.00 | −0.15 | 1.82 | 2.14 | 0.40 | 0.41 | 0.63 | 0.61 |
| 4 | 0.00 | −0.44 | 1.29 | 1.73 | 0.53 | 0.69 | 0.66 | 0.61 |
| 5 | 0.00 | 0.68 | 1.28 | 1.82 | 0.57 | 0.74 | 0.86 | 0.63 |
Ter is the mean nondecision time, st is the range in nondecision time, σ is the SD in within trial variability, as is the scaling factor that multiplies drift rate, sb is the range in variability in the decision boundaries, b1–b6 are the decision boundaries, c1–c5 are the confidence criteria, the μ values are the mean values of the drift rate distributions for each experimental condition, and the s values are the between-trial variability values for each experimental condition (r represents rearranged items, i represents intact items, H represents high-frequency items, and L represents low frequency items).
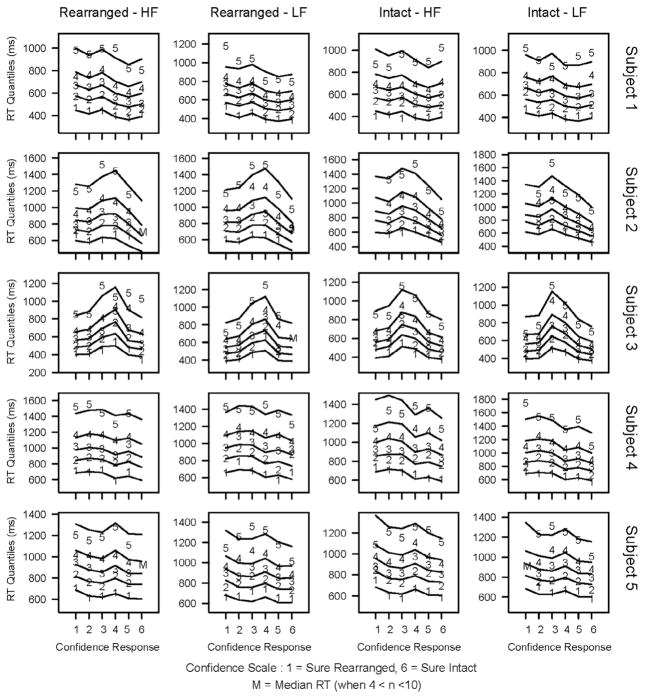
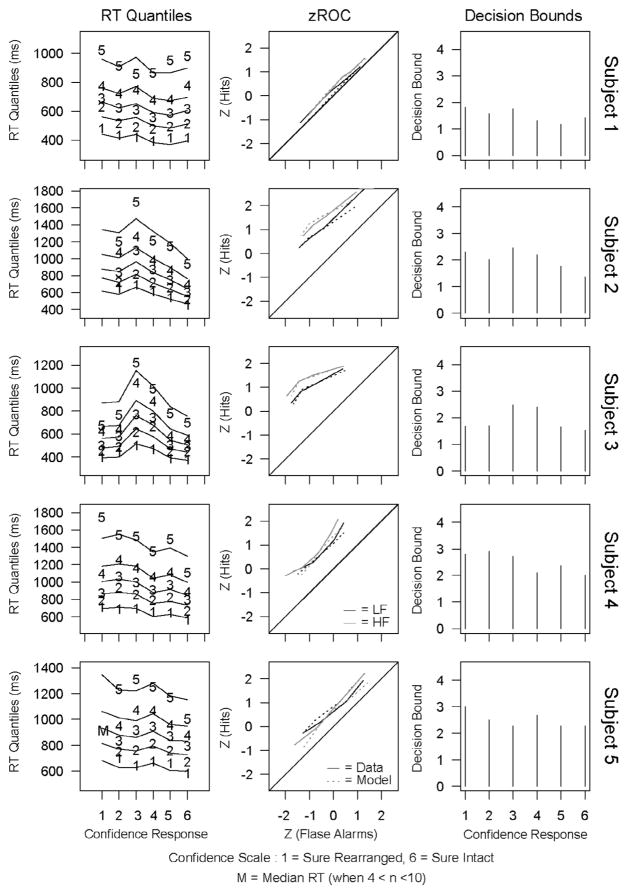
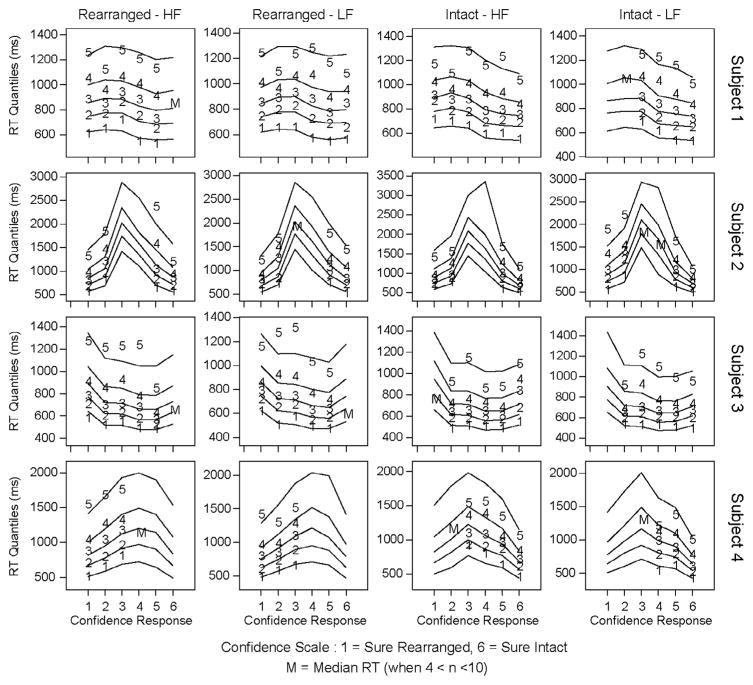
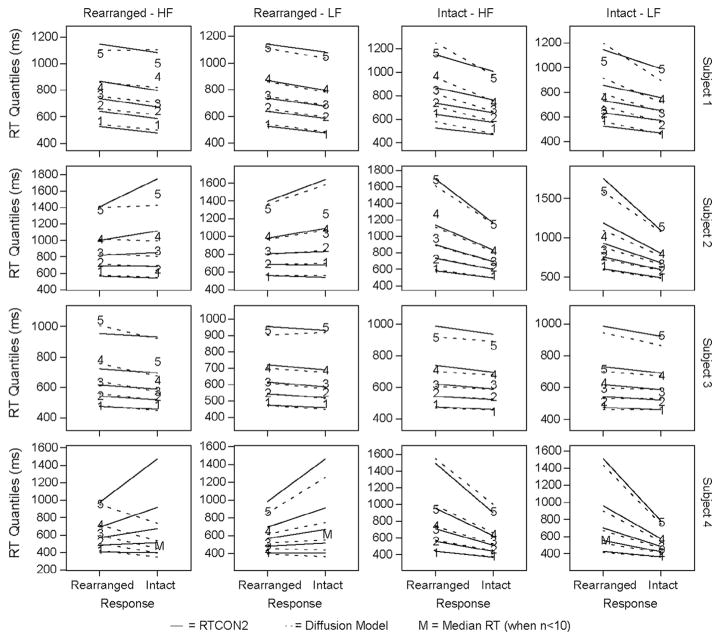
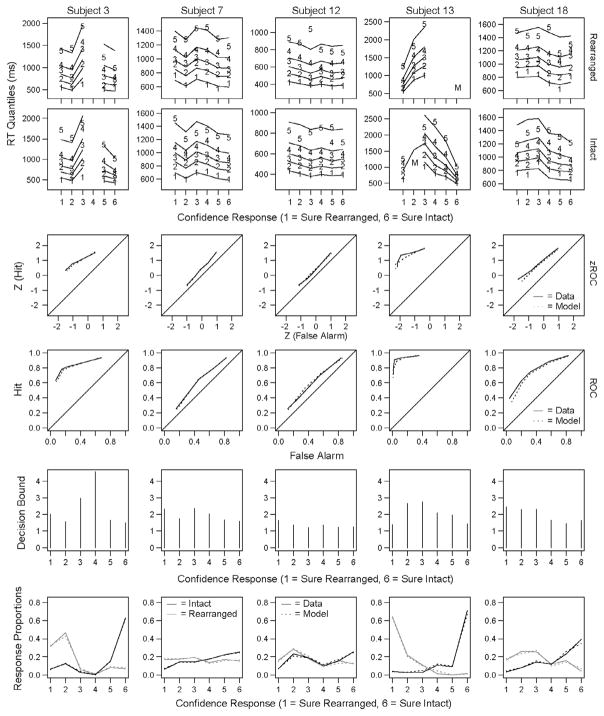
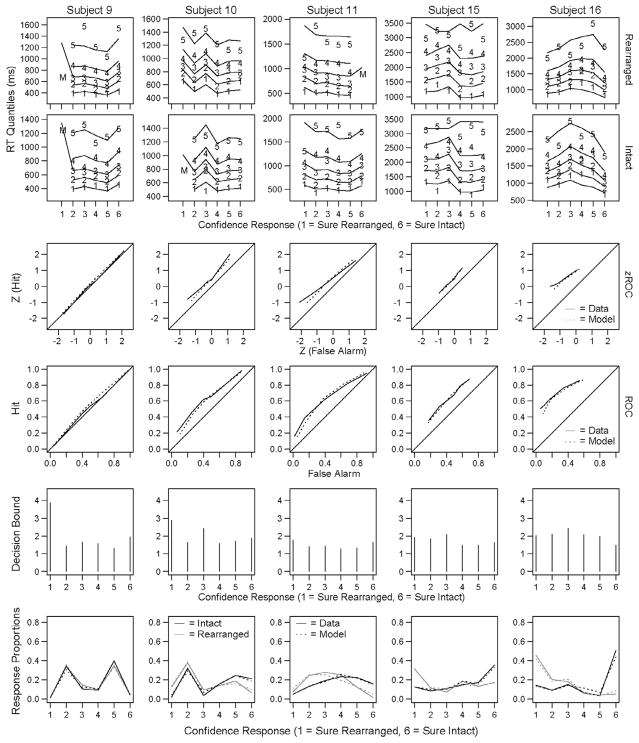
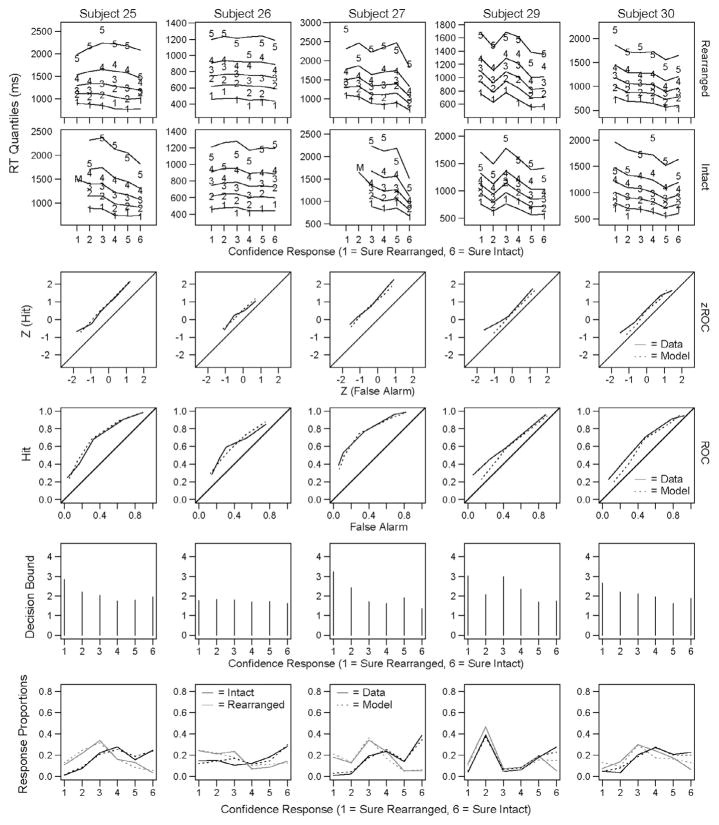
In addition to the quantitative comparison, the model predictions for each condition can also be compared with the empirical data to qualitatively assess the model fit. Quantile reaction-times for each subject for each of the four experimental conditions are shown in Fig. 3. In each of these plots, the six confidence responses are plotted across the x-axis (the “sure rearranged” category is labeled 1 and the “sure intact” category is labeled 6) and each line represents a quantile (with the lowest line depicting the .1 quantile, followed by .3, .5, .7 and .9). The numbers plotted in these figures represent the empirical data and the lines represent the predicted data from the model’s best fitting parameters. From these plots, it is apparent that there is consistency in the quantile response patterns of individual subjects across experimental conditions as well as wide differences between subjects in the quantile response patterns. For example, subjects 2 and 3 exhibit bowed reaction time quantiles where the high confidence responses are made more quickly than the low confidence responses. This is a response pattern that has been observed in previous confidence response paradigms (Murdock, 1974; Murdock & Dufty, 1972; Ratcliff & Murdock, 1976), but for which the original RTCON model was unable to account (see Ratcliff & Starns, 2013 for a discussion of why models with a decay term, such as RTCON, have difficulty capturing changes in the leading edge of RT distributions across response options). The fits to these data show that RTCON2 is able to capture this behavior of RT distributions.
Fig. 3.
Experiment 1: Quantile reaction times for each condition for each subject. Confidence responses are plotted along the x-axis (ranging from 1: Sure Rearranged to 6: Sure Intact). The numbers 1–5 depict the RT quantiles from the behavioral data and the corresponding lines depict the predictions from RTCON2. In conditions where subjects made between 4 and 10 responses the median RT is plotted as an ‘M’ and the other quantiles are not included. Conditions where subjects made fewer than 5 responses are omitted from the figure (e.g., subject 2 made fewer than 5 ‘Sure Rearranged’ responses to intact low-frequency word pairs so there are no behavioral data plotted for that condition).
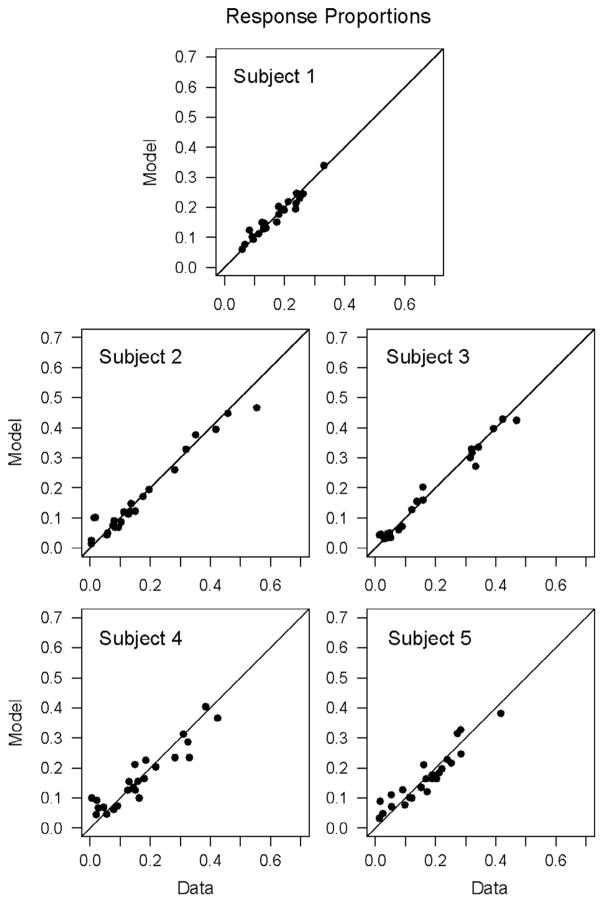
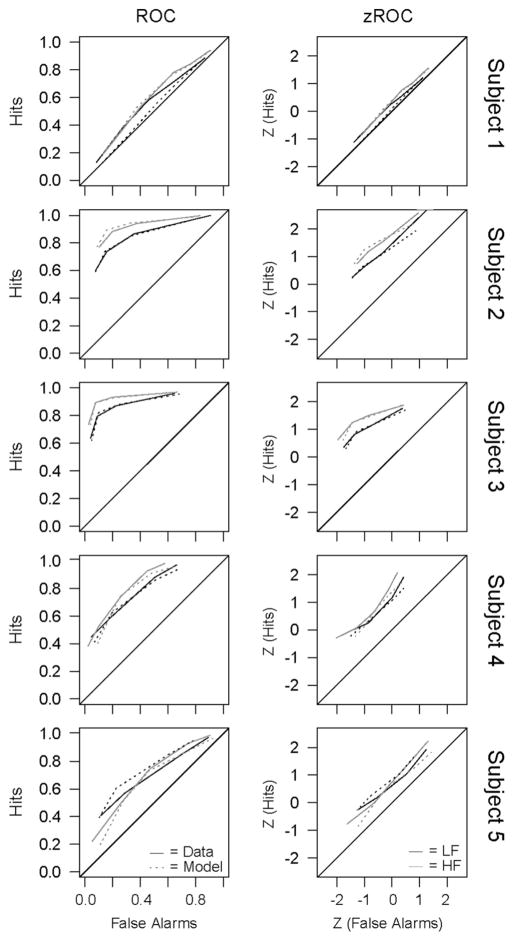
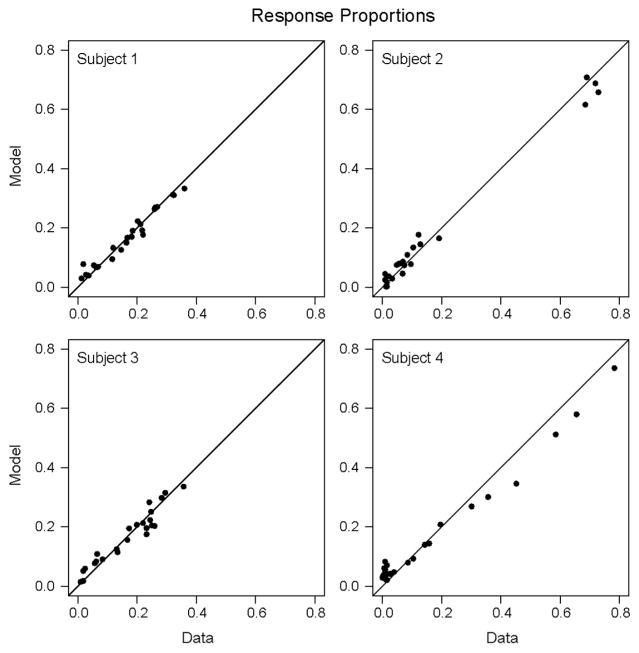
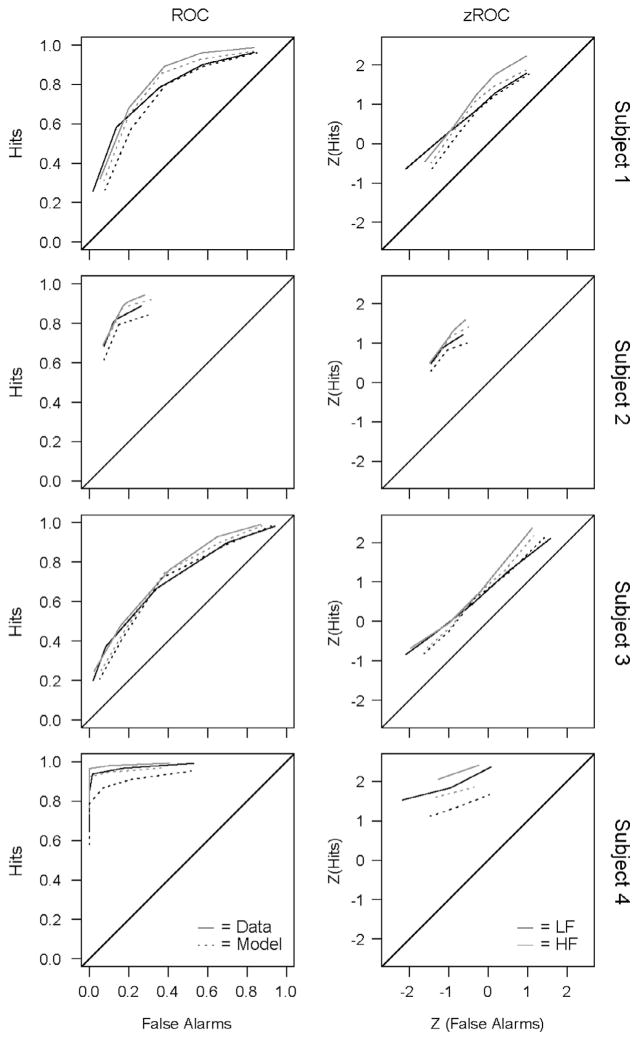
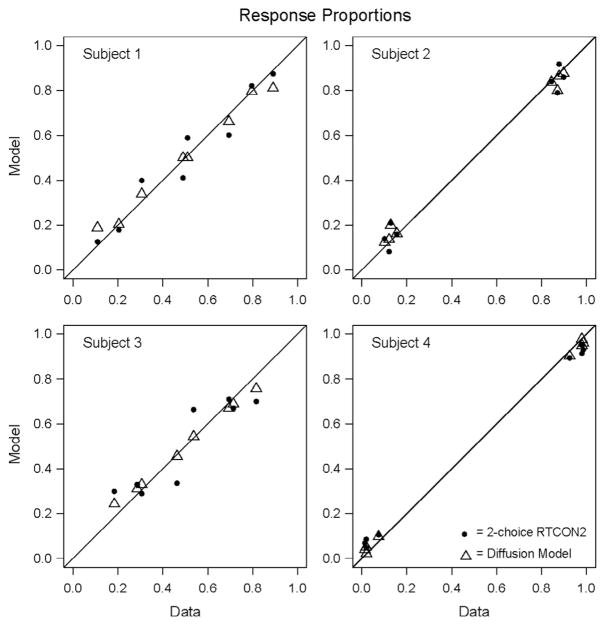
RTCON2 was also able to capture the proportion of responses in each condition and confidence category. In Fig. 4, the empirical response proportions for each subject are plotted against the predicted response proportions for that subject (with a reference line with an intercept of 0 and a slope of 1). We can see that the model matches the data reasonably well for all subjects. ROC and z-ROC functions from both the model predictions and the empirical data for each subject are plotted in Fig. 5. The solid lines depict the empirical data, the dashed lines are the predictions from the model, the black lines are for HF word pairs and the gray lines are for LF word pairs. If the model is successful at capturing the response patterns of the subjects, then the dashed lines should match the solid lines. The linearity of each of the individual z-ROC curves was tested using maximum likelihood estimation (Ogilvie & Creelman, 1968) and subjects 3, 4, and 5 were all found to have z-ROC curves that are significantly different from linear (χ2 values are reported in Table 2). Subjects 1 and 2 have z-ROC functions that are not significantly different from linear, subject 3 has inverted U-shaped z-ROC functions, and subjects 4 and 5 have U-shaped z-ROC functions. The model’s predicted ROC and z-ROC functions are relatively close to the empirical functions and exhibit the same linear and nonlinear patterns found in the empirical data for the first three subjects, but the model predicts linear z-ROC functions for subjects 4 and 5. These misfits can occur for several reasons, which will be discussed in greater detail following Experiment 3. In short, mismatches between the empirical data and model predictions occur for subjects and conditions with low numbers of observations or certain patterns of response proportions which are difficult for RTCON2 to handle. Specifically, subject 2 made very few high-confidence errors in any condition (fewer than 1.8%) and the model had difficulty producing such extreme response proportions so that a small difference between predicted and observed proportions leads to a miss in the predictions for the extreme points on the z-ROC. Similarly, subject 4 also made very few high-confidence errors. While such misses were numerically small (for example, the model predicted that subject 4 would make high confidence errors about 9.3% of the time instead of 2.2%), such small misses are exaggerated in the z-transformed ROC function. More crucially, as will be discussed following Experiment 3, certain patterns of data give rise to u-shaped z-ROC functions that are difficult for RTCON2 to produce.
Fig. 4.
Experiment 1: Empirical response proportions plotted against predicted response proportions (for the six confidence conditions and four experimental conditions for each subject) with a reference line with an intercept of 0 and a slope of 1.
Fig. 5.
Experiment 1: ROC and z-ROC functions for each subject and each condition. The solid lines are the functions from the behavioral data and the dashed lines are the predictions from RTCON2. The black lines are the functions for HF words and the gray lines are the functions for LF words. Conditions where subjects made fewer than 10 responses are omitted from the figure.
Table 2.
Linearity analysis of behavioral z-ROC curves – Experiment 1.
| Subject 1 | Subject 2 | Subject 3 | Subject 4 | Subject 5 | Average | |
|---|---|---|---|---|---|---|
| LF | 4.85 | 4.65 | 26.18* | 56.84* | 17.86* | 30.15* |
| HF | 2.30 | 5.61 | 10.39* | 75.00* | 18.59* | 20.17* |
df = 3, critical value = 7.815.
χ2 is significant at the p < .05 level.
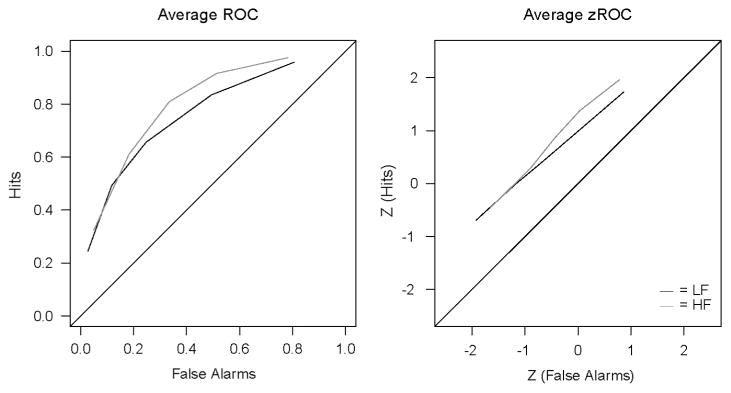
Additionally, as noted earlier, in much of the research investigating memory models it is common practice to examine only group data. For illustrative purposes, Fig. 6 shows the ROC and z-ROC functions for this experiment averaged across subjects. The linearity of the averaged z-ROC curve was also tested using the maximum likelihood estimation method (see the last column of Table 2). While the χ2 values indicate that the averaged z-ROC function is still significantly different from linear, we can see that the variety present in the individual z-ROC shapes is largely obscured by averaging.
Fig. 6.
Experiment 1: ROC and z-ROC functions for data averaged across subjects. The gray lines are the low-frequency condition and the black lines are the high-frequency condition.
In RTCON2, the shape of the z-ROC function is primarily dependent on the relative heights of the individual decision boundaries, provided the proportion of responses in each confidence category is not tiny (e.g., less than 1%). Simulations of the original RTCON model demonstrated that inverted u-shaped decision boundaries can yield inverted u-shaped z-ROC functions (Ratcliff & Starns, 2009) and fits of RTCON2 to item recognition also demonstrated this relationship (Ratcliff & Starns, 2013). In this experiment we see that the relative shape of the decision boundaries across categories corresponds to the shape of the z-ROC curves for some of the subjects. The setting of these decision boundaries is assumed to be entirely under the control of the subject, although it can be affected by instructions (Ratcliff & Starns, 2009), and so reflects an individual decision-making preference. Moreover, the relative shape of the decision boundaries is primarily constrained by the reaction time data. If a subject’s boundary for a given confidence response is set higher than the other boundaries, those responses will be slower (and the proportion of responses will be lower than if the boundary was set lower). This relationship is illustrated in Fig. 7, where the shape of the decision boundaries matches the shape of both the reaction time quantile functions for most of the subjects. The relationship between the shape of the z-ROC function and the decision boundaries is apparent for some subjects (e.g., subject 3) but not for others.
Fig. 7.
Experiment 1: Comparison of RT quantile shapes (from Intact – LF condition), z-ROC functions, and the relative heights of the decision boundaries for each subject. Plotting conventions are the same as for Figs. 3 and 5.
This experiment demonstrates that RTCON2 can fit both RT and accuracy data from an associative recognition experiment with confidence responses. The RTCON2 model distinguishes between different sources of variability, can fit individual differences in how people use confidence response scales, and provides an alternative explanation for the shape of ROC and z-ROC functions that is linked to reaction time and decision-related processes rather than changes in the nature of information from memory.
RTCON2 is able to fit both response proportions and reaction time distributions from a confidence judgment paradigm, and does so without a 1:1 mapping between accuracy and confidence. Additionally, the model is able to account for individual differences in how subjects use the confidence scale and as a result can produce a variety of ROC and z-ROC shapes. This explanation for various ROC and z-ROC shapes is entirely based on the decision-making process and individual differences in how people make confidence judgments. Therefore, some of the behavioral evidence that has been the primary support for additional memory processes may be alternatively explained through the addition of an explicit model of the decision-making process. These findings demonstrate the importance of focusing not only on what kind of information is used in a decision, but also on how the decision-making process handles that information and makes a decision.
Experiment 2
The RTCON2 model distinguishes between the representation of information from memory and how that information is used to make a decision. As such, it is important to demonstrate the validity of the representation of information in RTCON2. To this end, the second experiment was designed to compare the RTCON2 model with the standard two-choice diffusion model (Ratcliff, 1978; Ratcliff & McKoon, 2008). If these models explain individual differences in decision-making in the same way, then their parameter values should be consistent when fit to the same data. Additionally, the two-choice diffusion model’s ability to explain decision making behavior over a wide range of tasks is well-established so comparison of the two models can lend validity to the RTCON2 model. This experiment allows us to compare 6-choice and two-choice data using the RTCON2 model and then compare the RTCON2 and the diffusion model for the two-choice data. The parameters from the diffusion and RTCON2 models should be consistent when fit to the two-choice data, and the RTCON2 model should be able to fit both 6-choice and two-choice data with select parameters held constant across the number of response options.
Since most decision models focus on two-choice tasks (Busemeyer & Townsend, 1992; Laming, 1968; Link, 1975; Ratcliff, 1978; Ratcliff & McKoon, 2008; Ratcliff & Rouder, 1998; Ratcliff, Van Zandt, & McKoon, 1999; Usher & McClelland, 2001; Wagenmakers, 2009), these models are well-established and provide a benchmark for model performance. Because RTCON2 can be seen as an extension of the diffusion model, the models are quite similar. Just like RTCON2, the diffusion model has parameters that describe the non-decision process (non-decision time and variability in non-decision time, st), drift rate parameters that describe the quality of evidence entering the decision process (mean ν and between-trial variability η), and starting point (z) and boundary (a) parameters that control the amount of evidence needed to make a decision (as well as any bias toward a particular response). However, there are a few differences between the models which make their comparison worthwhile. First, the models represent the accumulation rate differently. In the diffusion model, the rate of evidence accumulation is represented as a discrete value that varies between items. In RTCON2, the rate of evidence accumulation for each response is determined by the area between the confidence criteria under a normal distribution with SD of 1 whose mean value (μ) varies between items. The area of this distribution in each response region is then scaled by a parameter (as) to produce an accumulation rate for each confidence response. Second, unlike the diffusion model, RTCON2 has no closed form solution and so must be fit by simulation methods.
In this task, subjects will alternate between using a 6-choice confidence response scale, and a two-choice response scale (corresponding to a simple intact/rearranged decision).
Method
Subjects
Four Ohio State University undergraduate students participated in 7 sessions and earned $10 for each completed session.
Materials
The stimuli were drawn from the same high-frequency, low-frequency, and very-low-frequency word pools described in the first experiment. Study lists were composed of 12 high-frequency words, 12 low-frequency words, and 4 very-low-frequency words selected randomly (without replacement) from the word pools. These words were randomly paired within frequency to create 14 word pairs (6 high-frequency pairs, 6 low-frequency pairs, and 2 very-low-frequency pairs). As in the first experiment, the 2 very-low-frequency word pairs served as buffer items for the study list and were presented in the first and last position within each list. All of the target word pairs were presented twice within each study list and were assigned to study-list positions randomly with the restriction that repeated pairs had at least one intervening word pair.
As in experiment one, test lists consisted of the two buffer word pairs (which were again presented in the first and last positions of the test list) and the 12 target pairs. Each pair was presented only once during the test list and exactly half of the target pairs were randomly rearranged within frequency and number of presentations. Thus each test list consisted of 2 buffer word pairs, 6 rearranged word pairs and 6 intact word pairs. Intact pairs consisted of words which had appeared together in the study list and rearranged pairs consisted of words which appeared in different pairs in the study list.
Procedure
Each experimental session lasted approximately 50 min. The first two sessions for each subject consisted of a response-key practice block, 3 study/test blocks, a second response-key practice block, and 20 more study/test blocks. The second response-key practice block was dropped after the first two sessions, because subjects were familiar with the response keys and no longer needed the additional practice. During the first three study/test blocks, subjects alternated between using 6 or 2 response-keys between each list (one 6-choice list, then one two-choice list, then another 6-choice list). During the last twenty study/test blocks, subjects alternated between blocks of lists (three two-choice lists, then seven 6-choice lists, then three two-choice lists, then seven 6-choice lists). Subjects responded using a PC keyboard on which the Z, X, C, comma, period, and slash keys were labeled with the symbols “− − −”, “− −”, “−”, “+”, “+ +”, and “+ + +”. Subjects were instructed to place their left-hand ring, middle, and index fingers on the “− − −”, “− −”, and “−” keys and their right-hand index, middle, and ring fingers on the “+”, “+ +”, and “+ + +” keys.
During the response-key practice, each of the symbols marked on the keyboard (e.g., “− −”) would appear on the screen one at a time and the subjects were told to press the designated key as quickly as possible. If a subject took longer than 800 ms to respond to one of the symbols, a “TOO SLOW” message would appear on the screen for 1000 ms. Each practice block consisted of 10 repetitions of each of the six response key options resulting in 60 trials total in each block. The symbols appeared in random order within the block with the restriction that repeated symbols had to have at least one intervening symbol.
For the remainder of the experiment, subjects were told that they would be presented with pairs of words during the study portions of the experiment and their job was to learn these pairs. Additionally, subjects were informed at the beginning of each study-list and each test-list how many different response-keys were to be used for that study/test block (e.g., ‘Please use all 6 confidence categories for the next study list’). During the study/test blocks, subjects initiated the start of each study list by pressing the spacebar. Each word pair in the study list was displayed for 3000 ms followed by 200 ms of blank screen. Immediately after the final study-list word pair, a message appeared directing subjects to press the space bar to begin the test list. During the test-list, subjects were required to distinguish between the word pairs that had not appeared during the study-list (rearranged word pairs) and those that had (intact word pairs). Each word pair remained on the screen until the subject had made a response.
On the 6-choice study/test blocks subjects were instructed to use all 6 response-keys to indicate whether a pair was intact or rearranged and their confidence in their response. They were told to use one of the “−” keys to indicate that the word pair had not appeared in the study-list, and to use one of the “+” keys to indicate that it had. Subjects were instructed to use the different levels of “+” and “−” to indicate their amount of confidence in their response (e.g., if a subject felt very confident that a word pair was intact they would use the “+ + +” key, whereas if they felt only moderately confident they would use the “+ +” key). On the two-choice study/test blocks, subjects were instructed to use only the two most extreme response-keys (“+ + +” and “− − −”) to indicate only whether a pair was intact or rearranged. Subjects were encouraged to respond quickly and accurately and to try to spread their responses among all six response-keys throughout the course of the experiment. If a subject took less than 280 ms to respond to one of the test items, a “TOO FAST” message would appear on the screen for 1500 ms. Subjects were given error feedback throughout all test blocks in the form of the words “CORRECT” or “ERROR” displayed for 300 ms after their response to each test item.
Model fitting
The two-choice and 6-choice versions of the RTCON2 model are fit using the same procedure described for the first experiment. To facilitate comparison between RTCON2 and the diffusion model, within-trial variability in the decision process (σ) was fixed to 0.1. All other RTCON2 parameters were allowed to vary freely when fitting the 6-choice data, and then select parameters were fixed when fitting the two-choice data. For the two-choice data, the mean value of the drift rate distributions, the between-trial variability in these mean values, and the between-trial variability in the height of the decision boundaries were fixed to the values estimated from the 6-choice data. As in the first experiment, there are 35 degrees of freedom per condition in the 6-choice task. In the two-choice task, there are also six RT bins for each response key, which gives 12 degrees of freedom, but these 12 proportions have to add to 1, which reduces the degrees of freedom to 11 per condition. With four conditions, this gives a total of 140 degrees of freedom in the 6-choice task and 44 degrees of freedom in the two-choice task. For these fits there were 23 free parameters in RTCON2 for the 6-choice data and 6 free parameters for the two-choice data, and 13 free parameters for the diffusion model.
Results and discussion
Data for this experiment consisted of response proportions and reaction-time quantiles for each subject from each condition and for each response category. Reaction time latencies less than 300 ms or greater than 4000 ms were excluded from this analysis (less than 0.1% of all data).
This experiment was designed to compare the performance of RTCON2 with the diffusion model. There are three main results of this experiment. First, all of the models fit both the proportions of responses in each confidence category and their RT quantiles well for the appropriate tasks. Second, as in the previous experiment, the RTCON2 model also fits the empirical ROC and z-ROC functions for the 6-choice task. Third, there is consistency in the model parameters across the diffusion model and RTCON2, and the RTCON2 model is able to fit data from 6-choice and two-choice task with appropriate parameters fixed across tasks.
For data collapsed over the 6-choice and two-choice tasks, there was a higher hit-rate for LF word pairs (M = 0.88, SD = 0.08) than HF word pairs (M = 0.79, SD = 0.13) and this difference was significant (t(3) = −3.5, p < .05). There was again a higher false-alarm rate for LF word pairs (M = 0.24, SD = 0.19) than HF word pairs (M = 0.21, SD = 0.16) but this difference was not significant (t(4) = −1.9, p > .05).
The diffusion model and two versions of the RTCON2 model (one for 6-choice decisions and one for two-choice decisions) were fit to the data from individual subjects. The RTCON2 model was fit to the 6-choice data and both the diffusion model and RTCON2 model were fit to the two-choice data. The RTCON2 and diffusion models were both able to fit both the quantile reaction-times and response proportions for each condition and response-key. The best-fitting parameters for each model are shown in Tables 3–5. Table 3 contains the parameters for the 6-choice version of RTCON2, Table 4 contains the parameters from the two-choice version of RTCON2, and Table 5 contains the parameters from the diffusion model.
Table 3.
Experiment 2 6-choice RTCON2 model parameters.
| Subject | Ter | st | as | σ | sb | χ2 | ||
|---|---|---|---|---|---|---|---|---|
| 1 | 436 | 280 | 0.03 | 0.1 | 0.48 | 109 | ||
| 2 | 392 | 263 | 0.04 | 0.1 | 0.47 | 129 | ||
| 3 | 373 | 137 | 0.03 | 0.1 | 1.02 | 214 | ||
| 4 | 278 | 252 | 0.03 | 0.1 | 0.86 | 152 | ||
| b1 | b2 | b3 | b4 | b5 | b6 | |||
|
|
||||||||
| 1 | 1.80 | 1.87 | 1.78 | 1.41 | 1.33 | 1.41 | ||
| 2 | 1.59 | 2.15 | 5.52 | 3.21 | 1.92 | 1.45 | ||
| 3 | 2.32 | 1.50 | 1.42 | 1.21 | 1.31 | 1.62 | ||
| 4 | 1.85 | 2.16 | 2.64 | 2.53 | 2.34 | 1.66 | ||
| c1 | c2 | c3 | c4 | c5 | ||||
|
|
||||||||
| 1 | −1.31 | 0.00 | 0.85 | 1.77 | 2.89 | |||
| 2 | −0.48 | 0.00 | 1.19 | 1.29 | 2.18 | |||
| 3 | −0.89 | −0.12 | 0.92 | 1.90 | 2.48 | |||
| 4 | −0.82 | 0.09 | 0.87 | 1.59 | 2.64 | |||
| μrH | μrL | μiH | μiL | srH | srL | siH | siL | |
|
|
||||||||
| 1 | 0.00 | −0.06 | 1.92 | 2.24 | 0.85 | 0.87 | 1.10 | 0.96 |
| 2 | 0.00 | −0.17 | 2.01 | 2.31 | 0.53 | 0.81 | 1.18 | 0.98 |
| 3 | 0.00 | −0.13 | 1.78 | 2.00 | 0.66 | 1.07 | 1.00 | 1.03 |
| 4 | 0.00 | −0.49 | 2.33 | 2.97 | 0.59 | 0.67 | 0.92 | 1.03 |
Ter is the mean nondecision time, st is the range in nondecision time, σ is the SD in within trial variability, as is the scaling factor that multiplies drift rate, sb is the range in variability in the decision boundaries, b1–b6 are the decision boundaries, c1–c5 are the confidence criteria, the μ values are the mean values of the drift rate distributions for each experimental condition, and the s values are the between-trial variability values for each experimental condition (r represents rearranged items, i represents intact items, H represents high-frequency items, and L represents low frequency items).
Table 5.
Experiment 2 diffusion model parameters.
| Subject | Ter | st | a | z | sz | χ2 | ||
|---|---|---|---|---|---|---|---|---|
| 1 | 536 | 350 | 0.13 | 0.05 | 0.09 | 62 | ||
| 2 | 500 | 280 | 0.20 | 0.09 | 0.16 | 39 | ||
| 3 | 463 | 170 | 0.11 | 0.05 | 0.09 | 42 | ||
| 4 | 305 | 10 | 0.17 | 0.08 | 0.08 | 30 | ||
| νrH | νrL | νiH | νiL | ηrH | ηrL | ηiH | ηiL | |
|
|
||||||||
| 1 | −0.21 | −0.28 | 0.20 | 0.09 | 0.29 | 0.36 | 0.27 | 0.31 |
| 2 | −0.32 | −0.39 | 0.24 | 0.23 | 0.32 | 0.36 | 0.14 | 0.22 |
| 3 | −0.02 | −0.18 | 0.10 | 0.15 | 0.23 | 0.17 | 0.01 | 0.16 |
| 4 | −0.23 | −0.38 | 0.26 | 0.37 | 0.14 | 0.15 | 0.01 | 0.15 |
Ter is the mean nondecision time, st is the range in nondecision time, a is the boundary separation, z is the starting point of the accumulation process, sz is the range in variability in the starting point, the ν values are the mean drift rate values for each experimental condition, and the η values are the between-trial variability values for each experimental condition (r represents rearranged items, i represents intact items, H represents high-frequency items, and L represents low-frequency items).
Table 4.
Experiment 2, 2-choice RTCON2 model parameters.
| Subject | Ter | st | as | b1 | b2 | c1 | χ2 |
|---|---|---|---|---|---|---|---|
| 1 | 456 | 295 | 0.01 | 2.10 | 1.51 | 0.61 | 84 |
| 2 | 405 | 233 | 0.02 | 3.07 | 2.46 | 0.84 | 45 |
| 3 | 410 | 108 | 0.01 | 1.72 | 1.49 | 1.10 | 57 |
| 4 | 266 | 60 | 0.02 | 2.88 | 2.42 | 1.14 | 35 |
Ter is the mean nondecision time, st is the range in nondecision time, as is the scaling factor that multiplies drift rate, b1–b2 are the decision boundaries, and c1 is the decision criteria.
For the 6-choice version of the RTCON2 model, the mean χ2 value for this experiment was 151 with a SD of 45. This mean is less than the critical value for χ2 with 140 degrees of freedom and α = 0.05 (168.6) indicating that the model provides an adequate fit to the data. For comparison, the original RTCON model produces an average χ2 value of 211 when fit to this data. For the two-choice version of the RTCON2 model, the mean χ2 value was 55 with a SD of 21. For the standard two-choice diffusion model, the mean χ2 value was 43 with a SD of 13. These means are both less than the critical value for χ2 with 44 degrees of freedom and α = 0.05 (60.5) indicating that both models provide an adequate fit to the data.
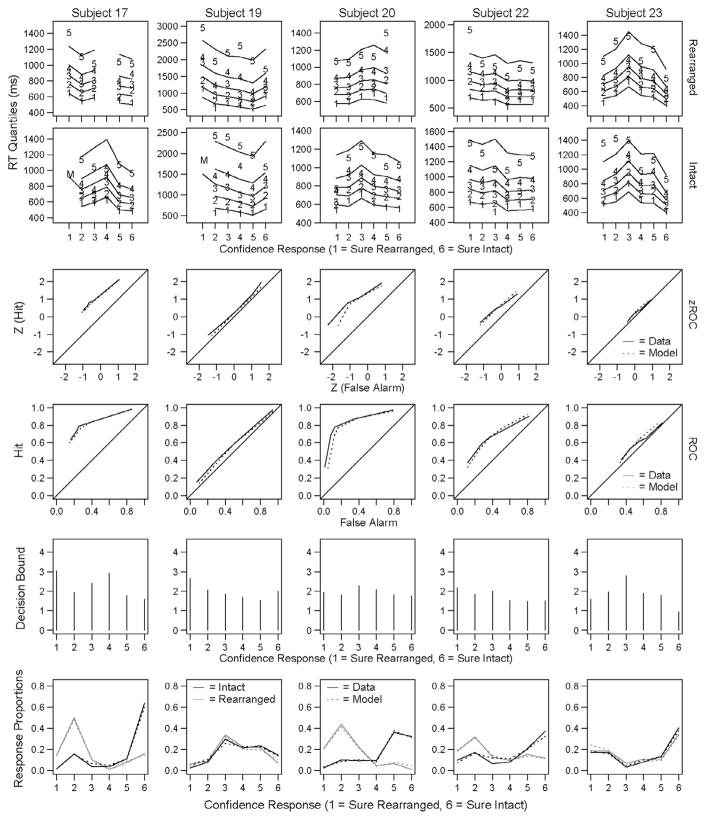
For each subject, their parameter values were used to generate predicted reaction time quantiles and response proportions for each model. These predicted values can then be compared with the empirical data to qualitatively assess the fit of the various models. For the 6-choice task, quantile reaction-times for each subject for each of the four experimental conditions (rearranged high frequency, rearranged low frequency, intact high frequency, and intact low frequency word pairs) are shown in Fig. 8 along with predicted values from the 6-choice version of RTCON2. As in the previous experiment, the 6 response keys are plotted on the x-axis and each line represents a reaction time quantile. The numbers plotted in the figures represent the subject data and the lines represent predicted data. As before, there is considerable consistency in the shapes of the subjects’ RT quantiles across conditions and considerable differences across subjects, and RTCON2 is successful at capturing these effects. Note that there is considerably less 6-choice data for this experiment compared to the first (since subjects in this experiment were alternating between using a 6-choice response scale and a two-choice response scale), so there are more conditions where subjects made fewer than 10 responses over the course of all of the sessions.
Fig. 8.
Experiment 2: Quantile reaction times from the 6-choice task for each condition for each subject. Confidence responses are plotted along the x-axis (ranging from 1: Sure Rearranged to 6: Sure Intact). The numbers 1–5 depict the RT quantiles from the behavioral data and the corresponding lines depict the predictions from RTCON2. In conditions where subjects made between 4 and 10 responses the median RT is plotted as an ‘M’ and the other quantiles are not included. Conditions where subjects made fewer than 5 responses are omitted from the figure (e.g., subject 4 made fewer than 5 ‘Intact’ responses of any confidence level to rearranged low-frequency word pairs so there are no behavioral data plotted for those conditions).
Despite these small numbers of observations, RTCON2 was still able to capture the proportion of responses in each condition and confidence category. In Fig. 9, the empirical response proportions for each subject are plotted against the model’s predicted response proportions for that subject (with a reference line with an intercept of 0 and a slope of 1). We can see that the model matches the data quite well for all subjects. ROC and z-ROC functions from both the model predictions and the empirical data for each subject are plotted in Fig. 10. The solid lines depict the empirical data, the dashed lines are the predictions from the model, the gray lines are the LF word pairs, and the black lines are the HF word pairs. If the model is successful at capturing the response patterns of the subjects, then the dashed lines should match the solid lines. The model’s predicted ROC and z-ROC functions are close to the empirical functions and generally exhibit the same linear and nonlinear patterns found in the empirical data, although there are slightly larger mismatches for subjects with extremely low numbers of observations in some conditions (such as subject 4, who made very few errors across all of the sessions).
Fig. 9.
Experiment 2: Empirical response proportions from the 6-choice task plotted against predicted response proportions (for the six confidence conditions and four experimental conditions for each subject) with a reference line with an intercept of 0 and a slope of 1.
Fig. 10.
Experiment 2: ROC and z-ROC functions from the 6-choice task for each subject and each condition. The solid lines are the functions from the behavioral data and the dashed lines are the predictions from RTCON2. The black lines are the functions for HF words and the gray lines are the functions for LF words. Conditions where subjects made fewer than 10 responses are omitted from the figure.
The linearity of the subjects’ z-ROC curves was tested using maximum likelihood estimation (Ogilvie & Creelman, 1968) and two subjects had z-ROC curves that were significantly different from linear: the low-frequency condition for subject 3 and both conditions for subject 4 (χ2 values are reported in Table 6).
Table 6.
Linearity analysis of behavioral zROC curves – Experiment 2.
df = 3, critical value = 7.815.
χ2 is significant at the p < .05 level.
For the two-choice task, Fig. 11 compares the predicted RT values from the two-choice version of RTCON2 and the diffusion model with the individual subjects’ data. Data in each row are from a single subject and data in each column are from a single experimental condition (rearranged high frequency, rearranged low frequency, intact high frequency, and intact low frequency word pairs) with the 2 response keys on the x-axis (1 representing ‘rearranged’ and 2 representing ‘intact’). The numbers plotted in the figures represent the subject data, the solid lines represent predicted data generated from RTCON2, and the dashed lines represent predicted data generated from the diffusion model. The predicted data from both models fit the empirical RT data relatively well. Both models are also able to capture the proportion of responses in each condition and response category. In Fig. 12, the empirical response proportions for each subject are plotted against the RTCON2 model’s predicted response proportions (the dots) and against the diffusion model’s predicted response proportions (the x’s) with a reference line with an intercept of 0 and a slope of 1. Although both models match the data reasonably well, the diffusion model’s predictions provide a slightly better match to the empirical data.
Fig. 11.
Experiment 2: Quantile reaction times from the two-choice task for each condition for each subject. The numbers 1–5 depict the RT quantiles from the behavioral data, the solid lines depict the predictions from RTCON2, and the dashed lines depict the predictions from the diffusion model. In conditions where subjects made fewer than 10 responses the median RT is plotted as an ‘M’ and the other quantiles are not included.
Fig. 12.
Experiment 2: Empirical response proportions from the two-choice task plotted against predicted response proportions from the RTCON2 model (the triangles) and the diffusion model (the dots) for each subject (for the two responses and four experimental conditions) with a reference line with an intercept of 0 and a slope of 1.
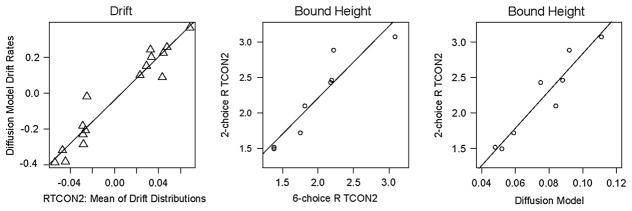
Parameters from the 6-choice version of RTCON2 were fixed for fits of the two-choice version of RTCON2, and parameters from the two-choice version of RTCON2 were compared with corresponding diffusion model parameters. Not all of the model parameters are directly comparable given that the models have different numbers of confidence criteria and decision boundaries. However, parameters that represent the quality of evidence from the stimuli (such as drift rate) and parameters that reflect individual differences in decision making (such as decision boundaries) should be consistent across all the models and tasks. A comparison of drift rate values and boundary heights across models is shown in Fig. 13. In the figure on the left, drift rate values from the diffusion model are plotted against the mean of the drift distributions from the RTCON2 model (based on fits of the 6-choice data) along with a linear regression line. The RTCON2 model fixes the mean of one of the drift distributions to zero, and allows the other drift distributions and confidence criteria to vary (see Table 3). The diffusion model allows all of the drift values to vary. For comparison purposes, for this figure the drift values from the RTCON2 model have been adjusted to match the diffusion model (mean drift values were shifted such that the middle confidence criterion was at zero) and multiplied by the scaling parameter. The two models produced very similar estimates of drift rate. This demonstrates that the RTCON2 model is able to produce estimates of the quality of evidence used in a decision that are comparable to the estimates produced by the more established standard diffusion model. In the figures in the middle and on the right of Fig. 13, the decision boundaries from the two-choice RTCON2 model are plotted against the boundaries from the 6-choice RTCON2 model and the diffusion model. For the 6-choice model, the heights of the ‘intact’ and ‘rearranged’ response options were averaged over confidence level to produce two values to compare to the parameters estimated from the two-choice task. For the diffusion model, the total distance between the two decision boundaries (a) was split into the distance from the starting point (z) to produce two values (z and a–z) to compare to the parameters estimated from the two-choice task. For both figures, a linear regression line is included for reference. Overall, the models produce similar estimates of decision boundary heights. This demonstrates both that the RTCON2 model is able to produce estimates of response caution that are comparable to estimates produced by the diffusion model and that individual differences in response caution appear consistent across response options.
Fig. 13.
Experiment 2: Comparison of drift rates and decision bounds across the models along with best-fitting linear regression lines. In the figure on the left, drift rate values have been shifted and adjusted to account for differences in how the models parameterize drift rates. In the middle figure, for the 6-choice RTCON2 model the heights of the ‘intact’ and ‘rearranged’ response options were averaged over confidence level. In the figure on the right, for the diffusion model the total distance between the two decision boundaries (a) was split into the distance from the starting point (z) to produce two values (z and a–z). Original values for all parameters are available in Tables 3–5.
This experiment provided another demonstration of RTCON2’s ability to fit a variety of z-ROC functions as well as bowed reaction time quantiles. Additionally, this experiment demonstrated consistency in model parameters within subjects and across tasks. The RTCON2 model was able to fit data from both a 6-choice task and a two-choice task with a reasonable subset of the parameters held constant across tasks. We also observed considerable correspondence between the drift rates across models. This indicates that, regardless of task differences (which likely affect other parameters such as those related to making a decision), the quality of evidence extracted from the stimulus can be held constant across task conditions.
Experiment 3
The third experiment was designed to collect a moderate number of observations from a larger group of subjects with the goal of providing more examples of non-linear z-ROC shapes to be fit by the model. As in the previous experiments, subjects in this experiment studied lists of pairs of words and then were presented with pairs of test words and had to distinguish between intact and rearranged versions of the study pairs. For this experiment, the study lists were slightly longer and each item was presented for a shorter duration in order to collect more observations from each session.
Method
Subjects
34 Ohio State University undergraduate students participated in 2 sessions each and earned research credit for an introductory Psychology course for each completed session.
Materials
The stimuli were drawn from the same high-frequency, low-frequency, and very-low-frequency word pools described in the first experiment. Study lists were composed of 20 high-frequency words, 20 low-frequency words, and 4 very-low-frequency words selected randomly (without replacement) from the word pools. These words were randomly paired within frequency to create 22 word pairs (10 high-frequency pairs, 10 low-frequency pairs, and 2 very-low-frequency pairs). As in the first experiment, the 2 very-low-frequency word pairs served as buffer items for the study list and were presented in the first and last position within each list. All of the target word pairs were presented twice within each study list and were assigned to study-list positions randomly with the restriction that repeated pairs had at least one intervening word pair.
As in Experiment 1, test lists consisted of the two buffer word pairs (which were again presented in the first and last positions of the test list) and the 20 target pairs. Each pair was presented only once during the test list and exactly half of the target pairs were randomly rearranged within frequency and number of presentations. Thus each test list consisted of 2 buffer word pairs, 10 rearranged word pairs and 10 intact word pairs. Intact pairs consisted of words which had appeared together in the study list and rearranged pairs consisted of words which appeared in different pairs in the study list.
Procedure
Each experimental session lasted approximately 50 min. Each session consisted of a response-key practice block, one practice study/test block, and 16 more study/test blocks. Subjects responded using a PC keyboard on which the Z, X, C, comma, period, and slash keys were labeled with the symbols “− − −”, “− −”, “−”, “+”, “+ +”, and “+ + +”. Subjects were instructed to place their left-hand ring, middle, and index fingers on the “− − −”, “− −”, and “−” keys and their right-hand index, middle, and ring fingers on the “+”, “+ +”, and “+ + +” keys.
During the response-key practice, each of the symbols marked on the keyboard (e.g., “− −”) would appear on the screen one at a time and the subjects were told to press the designated key as quickly as possible. If a subject took longer than 800 ms to respond to one of the symbols, a “TOO SLOW” message would appear on the screen for 1000 ms. The practice block consisted of 10 repetitions of each of the six response key options resulting in 60 trials total. The symbols appeared in random order within the block with the restriction that repeated symbols had to have at least one intervening symbol.
For the remainder of the experiment, subjects were told that they would be presented with pairs of words during the study portions of the experiment and their job was to learn these pairs. During the study/test blocks, subjects initiated the start of each study list by pressing the spacebar. Each word pair in the study list was displayed for 2500 ms followed by 200 ms of blank screen. Immediately after the final study-list word pair, a message appeared directing subjects to press the space bar to begin the test list. During the test-list, subjects were required to distinguish between the word pairs that had not appeared during the study-list (rearranged word pairs) and those that had (intact word pairs). Each word pair remained on the screen until the subject had made a response. Subjects were instructed to use the different response-key options to indicate whether a word pair had appeared in the study-list and their confidence in their response. They were told to use one of the “−” keys to indicate that the word pair had not appeared in the study-list, and to use one of the “+” keys to indicate that it had. Subjects were instructed to use the different levels of “+” and “−” to indicate their amount of confidence in their response (e.g., if a subject felt very confident that a word pair was intact they would use the “+ + +” key, whereas if they felt only moderately confident they would use the “+ +” key). Subjects were encouraged to respond quickly and accurately and to try to spread their responses among all six response-keys throughout the course of the experiment. If a subject took less than 280 ms to respond to one of the test items, a “TOO FAST” message would appear on the screen for 1500 ms. Subjects were given error feedback throughout all test blocks in the form of the words “CORRECT” or “ERROR” displayed for 300 ms after their response to each test item.
Model fitting
The 6-choice version of the RTCON2 model was fit using the same procedure described for the first experiment. As in the first experiment, there are 35 degrees of freedom per condition in this task. With two conditions, this gives a total of 70 degrees of freedom. For these fits there were 19 free parameters in RTCON2.
Results and discussion
This experiment was designed to elicit a larger variety of z-ROC shapes and investigate the performance of the RTCON2 model when fitting these data. To yield more observations per condition for fitting the model, the high and low frequency conditions were combined resulting in two conditions: rearranged and intact word pairs. Prior to collapsing across word-frequency we analyzed hit and false alarm rates and the results were similar to those observed in the first two experiments. There was a higher hit-rate for LF word pairs (M = 0.74, SD = 0.10) than HF word pairs (M = 0.66, SD = 0.12) and this difference was significant (t(33) = −6.5, p < .05). There was again a higher false-alarm rate for LF word pairs (M = 0.39, SD = 0.18) than HF word pairs (M = 0.31, SD = 0.16) and this difference was significant (t(33) = −5.9, p > .05). Although the change in false-alarm rate was significant for this experiment, the mean of the difference across subjects (M = −0.08) was in-line with those observed in the first two experiments (Experiment 1: M = −0.09; Experiment 2: M = −0.03).
Data for this experiment consisted of response proportions and reaction-time quantiles for each subject from each condition and for each response category. Reaction time latencies less than 300 ms or greater than 4000 ms were excluded from this analysis (less than 0.1% of all data).
The model was fit to data from individual subjects and the best-fitting model parameters are shown in Table 7. The mean χ2 value for this experiment was 91.3 with a SD of 28.8. This is slightly larger than the critical χ2 value (90.5) indicating a mismatch between the model’s predictions and the data. Half the subjects, however, had χ2 values less than the critical value.
Table 7.
Experiment 3 best fitting model parameters.
| Subject | Ter | st | as | σ | sb | χ2 | c1 | c2 | c3 | c4 | c5 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 418 | 187 | 0.09 | 0.15 | 0.94 | 107 | −0.48 | −0.07 | 0.12 | 0.84 | 1.45 |
| 2 | 366 | 287 | 0.01 | 0.14 | 1.02 | 83 | −0.76 | −0.50 | 0.66 | 0.94 | 1.75 |
| 3 | 305 | 138 | 0.04 | 0.10 | 1.17 | 64 | −0.56 | 0.14 | 0.89 | 1.08 | 1.69 |
| 4 | 323 | 213 | 0.001 | 0.09 | 0.88 | 99 | −0.63 | 0.34 | 0.81 | 1.43 | 2.38 |
| 5 | 392 | 207 | 0.03 | 0.08 | 0.76 | 139 | −0.32 | 0.20 | 0.77 | 1.38 | 2.02 |
| 6 | 409 | 247 | 0.003 | 0.09 | 0.75 | 75 | −0.88 | 0.00 | 0.57 | 1.22 | 2.26 |
| 7 | 503 | 394 | 0.02 | 0.13 | 0.43 | 68 | −0.68 | −0.57 | 0.84 | 1.78 | 2.48 |
| 8 | 541 | 286 | 0.03 | 0.11 | 0.92 | 84 | −0.68 | −0.02 | 0.81 | 1.71 | 1.92 |
| 9 | 251 | 216 | 0.02 | 0.10 | 1.19 | 43 | −0.83 | 0.15 | 0.44 | 0.64 | 2.72 |
| 10 | 369 | 315 | 0.03 | 0.12 | 1.01 | 74 | −0.55 | 0.51 | 0.93 | 1.12 | 2.06 |
| 11 | 263 | 255 | 0.02 | 0.07 | 1.14 | 71 | −0.98 | −0.20 | 0.54 | 1.20 | 1.80 |
| 12 | 315 | 158 | 0.03 | 0.10 | 1.15 | 78 | −0.87 | 0.35 | 0.82 | 1.15 | 1.63 |
| 13 | 361 | 194 | 0.05 | 0.07 | 0.80 | 50 | −0.63 | 0.29 | 1.00 | 1.68 | 2.36 |
| 14 | 392 | 322 | 0.05 | 0.08 | 0.81 | 110 | −0.50 | 0.17 | 0.66 | 1.16 | 1.69 |
| 15 | 441 | 294 | 0.01 | 0.06 | 0.90 | 81 | −0.34 | 0.04 | 0.60 | 1.03 | 1.27 |
| 16 | 487 | 250 | 0.03 | 0.08 | 1.02 | 131 | −0.57 | −0.01 | 0.75 | 1.32 | 1.73 |
| 17 | 401 | 209 | 0.04 | 0.14 | 0.74 | 72 | −0.59 | 0.74 | 1.28 | 2.09 | 2.22 |
| 18 | 567 | 325 | 0.04 | 0.11 | 0.42 | 120 | −0.98 | −0.07 | 0.92 | 1.36 | 2.11 |
| 19 | 252 | 178 | 0.01 | 0.08 | 1.19 | 121 | −1.23 | −1.08 | 0.40 | 1.19 | 1.59 |
| 20 | 455 | 218 | 0.06 | 0.13 | 1.03 | 85 | −0.86 | 0.04 | 0.85 | 1.21 | 2.10 |
| 21 | 240 | 189 | 0.01 | 0.07 | 0.75 | 76 | −0.84 | −0.06 | 0.63 | 1.70 | 2.45 |
| 22 | 457 | 316 | 0.02 | 0.10 | 1.18 | 142 | −0.50 | 0.49 | 1.17 | 1.27 | 1.87 |
| 23 | 417 | 252 | 0.02 | 0.12 | 1.40 | 96 | −0.98 | 0.14 | 0.88 | 1.48 | 2.64 |
| 24 | 516 | 249 | 0.03 | 0.06 | 0.56 | 32 | −0.80 | −0.08 | 0.57 | 1.11 | 1.92 |
| 25 | 440 | 271 | 0.03 | 0.07 | 1.44 | 79 | −1.17 | −0.24 | 0.68 | 1.42 | 2.13 |
| 26 | 333 | 412 | 0.02 | 0.11 | 1.04 | 112 | −0.57 | 0.39 | 1.21 | 1.34 | 1.78 |
| 27 | 487 | 190 | 0.03 | 0.07 | 1.00 | 114 | −0.63 | 0.00 | 0.65 | 1.39 | 2.21 |
| 28 | 323 | 322 | 0.03 | 0.06 | 0.41 | 93 | −0.60 | 0.03 | 0.61 | 1.37 | 2.12 |
| 29 | 422 | 266 | 0.02 | 0.12 | 0.91 | 102 | −0.55 | 1.62 | 2.18 | 2.43 | 2.68 |
| 30 | 357 | 265 | 0.01 | 0.10 | 0.52 | 109 | −0.67 | −0.63 | 0.69 | 1.92 | 2.11 |
| 31 | 431 | 297 | 0.05 | 0.09 | 1.05 | 96 | −0.58 | 0.34 | 0.94 | 1.39 | 2.27 |
| 32 | 310 | 158 | 0.04 | 0.16 | 0.05 | 150 | −1.63 | −0.51 | −0.02 | 0.71 | 1.54 |
| 33 | 194 | 186 | 0.01 | 0.10 | 1.21 | 107 | −1.01 | 0.00 | 0.77 | 1.39 | 1.97 |
| 34 | 378 | 229 | 0.08 | 0.09 | 0.82 | 39 | −0.56 | 0.04 | 0.66 | 1.36 | 1.46 |
| b1 | b2 | b3 | b4 | b5 | b6 | μr | μi | sr | si | ||
|
|
|||||||||||
| 1 | 1.55 | 2.22 | 2.52 | 2.87 | 1.86 | 1.47 | 0 | 0.99 | 0.48 | 0.67 | |
| 2 | 2.16 | 1.60 | 2.08 | 2.23 | 1.56 | 1.90 | 0 | 1.60 | 0.47 | 0.81 | |
| 3 | 2.00 | 1.56 | 2.97 | 4.56 | 1.64 | 1.50 | 0 | 1.61 | 0.35 | 0.97 | |
| 4 | 2.66 | 1.56 | 2.18 | 1.96 | 1.23 | 1.45 | 0 | 1.09 | 0.48 | 0.54 | |
| 5 | 2.74 | 1.60 | 1.74 | 2.01 | 1.60 | 1.21 | 0 | 1.04 | 0.81 | 0.93 | |
| 6 | 2.20 | 1.73 | 2.29 | 1.15 | 1.07 | 4.24 | 0 | 3.31 | 0.39 | 0.63 | |
| 7 | 2.31 | 1.74 | 2.35 | 2.02 | 1.67 | 1.59 | 0 | 1.31 | 0.92 | 0.69 | |
| 8 | 2.62 | 2.12 | 1.91 | 1.92 | 1.43 | 1.79 | 0 | 0.97 | 0.54 | 0.90 | |
| 9 | 3.88 | 1.42 | 1.66 | 1.57 | 1.30 | 1.94 | 0 | 0.30 | 0.69 | 0.80 | |
| 10 | 2.89 | 1.63 | 2.42 | 1.57 | 1.72 | 1.86 | 0 | 1.05 | 0.97 | 0.86 | |
| 11 | 1.75 | 1.41 | 1.43 | 1.28 | 1.31 | 1.65 | 0 | 0.91 | 0.35 | 0.60 | |
| 12 | 1.62 | 1.37 | 1.20 | 1.37 | 1.23 | 1.26 | 0 | 0.84 | 0.74 | 0.73 | |
| 13 | 1.39 | 2.65 | 2.75 | 2.09 | 1.96 | 1.44 | 0 | 2.06 | 0.52 | 0.87 | |
| 14 | 2.80 | 2.20 | 1.89 | 2.18 | 1.82 | 1.95 | 0 | 0.67 | 0.58 | 0.72 | |
| 15 | 1.90 | 1.85 | 2.08 | 1.48 | 1.48 | 1.62 | 0 | 0.94 | 0.81 | 0.62 | |
| 16 | 2.01 | 2.11 | 2.44 | 2.06 | 1.97 | 1.49 | 0 | 0.94 | 0.34 | 0.77 | |
| 17 | 3.05 | 1.93 | 2.41 | 2.93 | 1.77 | 1.58 | 0 | 2.30 | 0.80 | 1.06 | |
| 18 | 2.45 | 2.29 | 2.31 | 1.65 | 1.44 | 1.63 | 0 | 1.40 | 0.70 | 1.08 | |
| 19 | 2.65 | 2.05 | 1.86 | 1.70 | 1.54 | 2.01 | 0 | 0.56 | 0.53 | 0.57 | |
| 20 | 1.93 | 1.79 | 2.27 | 2.08 | 1.82 | 1.76 | 0 | 1.40 | 0.33 | 0.40 | |
| 21 | 2.90 | 2.18 | 0.99 | 1.31 | 1.98 | 1.90 | 0 | 1.31 | 1.12 | 0.97 | |
| 22 | 2.17 | 1.84 | 2.01 | 1.53 | 1.46 | 1.51 | 0 | 1.30 | 0.48 | 0.92 | |
| 23 | 1.57 | 1.95 | 2.79 | 1.89 | 1.78 | 0.94 | 0 | 0.66 | 0.67 | 0.68 | |
| 24 | 2.37 | 1.91 | 1.96 | 1.87 | 1.49 | 1.82 | 0 | 1.12 | 0.74 | 1.10 | |
| 25 | 2.84 | 2.19 | 2.02 | 1.74 | 1.79 | 1.95 | 0 | 1.12 | 0.92 | 0.89 | |
| 26 | 1.75 | 1.81 | 1.80 | 1.69 | 1.70 | 1.62 | 0 | 1.38 | 0.61 | 0.80 | |
| 27 | 3.25 | 2.42 | 1.70 | 1.61 | 1.92 | 1.36 | 0 | 1.19 | 0.64 | 0.83 | |
| 28 | 2.63 | 1.94 | 1.31 | 1.76 | 1.68 | 2.04 | 0 | 1.04 | 0.67 | 1.07 | |
| 29 | 3.01 | 2.07 | 2.99 | 2.34 | 1.69 | 1.73 | 0 | 1.45 | 0.47 | 0.72 | |
| 30 | 2.66 | 2.21 | 2.11 | 1.96 | 1.61 | 1.86 | 0 | 1.22 | 0.66 | 0.35 | |
| 31 | 2.49 | 2.99 | 2.23 | 2.36 | 2.72 | 1.41 | 0 | 1.36 | 0.63 | 1.02 | |
| 32 | 2.71 | 2.11 | 2.15 | 2.20 | 2.12 | 2.33 | 0 | 0.61 | 0.71 | 0.66 | |
| 33 | 2.20 | 1.66 | 2.08 | 1.75 | 1.47 | 2.05 | 0 | 2.78 | 0.79 | 0.47 | |
| 34 | 1.67 | 1.93 | 3.06 | 2.29 | 3.71 | 1.44 | 0 | 1.22 | 0.27 | 0.65 | |
Ter is the mean nondecision time, st is the range in nondecision time, σ is the SD in within trial variability, as is the scaling factor that multiplies drift rate, sb is the range in variability in the decision boundaries, b1–b6 are the decision boundaries, c1–c5 are the confidence criteria, the μ values are the mean values of the drift rate distributions for each experimental condition, and the s values are the between-trial variability values for each experimental condition (r represents rearranged items, i represents intact items).
The linearity of the subjects’ z-ROC curves was tested using maximum likelihood estimation (Ogilvie & Creelman, 1968). Out of 34 total subjects, 17 subjects had a z-ROC curve that was significantly different from linear (χ2 values are reported in Table 8).
Table 8.
Linearity analysis of behavioral zROC curves – Experiment 3.
| Subject | χ2 | Subject | χ2 |
|---|---|---|---|
| 1 | 23.85* | 18 | 6.52 |
| 2 | 11.48* | 19 | 5.02 |
| 3 | 3.36 | 20 | 4.68 |
| 4 | 1.15 | 21 | 15.94* |
| 5 | 29.33* | 22 | 1.46 |
| 6 | 2.69 | 23 | 5.27 |
| 7 | 3.98 | 24 | 11.38* |
| 8 | 29.31* | 25 | 20.88* |
| 9 | 3.86 | 26 | 18.45* |
| 10 | 24.01* | 27 | 11.34* |
| 11 | 3.58 | 28 | 35.10* |
| 12 | 6.54 | 29 | 24.67* |
| 13 | 20.81* | 30 | 11.19* |
| 14 | 29.50* | 31 | 14.57* |
| 15 | 7.56 | 32 | 2.95 |
| 16 | 7.63 | 33 | 2.98 |
| 17 | 10.45* | 34 | 3.43 |
df = 3, critical value = 7.815.
χ2 is significant at the p < .05 level.
For each subject, these parameter values were used to generate predicted reaction time quantiles and response proportions for each condition. These predicted values can then be compared with the empirical data to qualitatively assess the fit of the various models. The model was able to produce the various RT and response proportion patterns quite well for most of the subjects, however there were slight but systematic misses for most of the subjects with u-shaped z-ROC functions. Fits for select subjects are shown in Figs. 14 and 15 and fits for the remaining individual subjects are in Appendix A. The subjects in Fig. 14 were chosen to illustrate the model’s ability to capture a variety of ROC and z-ROC shapes and patterns of response proportions. The subjects in Fig. 15 were chosen to illustrate the model’s slight misfits to u-shaped z-ROC functions.
Fig. 14.
Experiment 3: Data and model fits. The first two rows plot the RT quantiles for each confidence response with the 6 response keys plotted on the x-axis (the “sure rearranged” category is labeled 1 and the “sure intact” category is labeled 6) and the RT quantiles plotted vertically with each line representing a reaction time quantile. The numbers plotted represent the empirical data and the lines represent predicted data from the model. In conditions where subjects made between 4 and 10 responses the median RT is plotted as an ‘M’ and the other quantiles are not included. Conditions where subjects made fewer than 5 responses are omitted from the figure. In conditions where the model predicted between 5 and 10 responses only the median RT is plotted and the other quantiles are not included. Conditions where the model predicted fewer than 5 responses are omitted from the figure. The third and fourth row in each figure plot the empirical and predicted z-ROC and ROC curves for each subject. The solid lines depict the empirical data and the dashed lines depict the model predictions. The fifth row plots the decision boundaries for each confidence response and the sixth row plots the response proportions (both empirical data and model predictions) for each confidence response and condition. The solid lines depict the empirical data, the dashed lines depict the model predictions, the black lines depict responses for ‘intact’ pairs and the gray lines depict responses for ‘rearranged’ pairs.
Fig. 15.
Experiment 3: Data and model fits. Same plotting conventions as Fig. 14.
The first two rows in Figs. 14 and 15 plot the RT quantiles for each confidence response with the 6 response keys plotted on the x-axis (the “sure rearranged” category is labeled 1 and the “sure intact” category is labeled 6) and the RT quantiles plotted vertically with each line representing a reaction time quantile. The numbers plotted represent the empirical data and the lines represent predicted data from the model. Note that there is considerably less data for this experiment compared to the first (since subjects only completed 2 sessions), so there are more conditions where subjects made fewer than 10 responses over the course of all of the sessions. The third and fourth row in each figure plot the empirical and predicted z-ROC and ROC curves for each subject. The solid lines depict the empirical data and the dashed lines depict the model predictions. The fifth row plots the decision boundaries for each confidence response and the sixth row plots the response proportions (both empirical data and model predictions) for each confidence response and condition. The solid lines depict the empirical data, the dashed lines depict the model predictions, the black lines depict responses for ‘intact’ pairs and the gray lines depict responses for ‘rearranged’ pairs.
The model predictions match the data quite closely for the subjects in Fig. 14 (there is a significant difference between the model predictions and the data only for subject 18). The model predicted ROC curves match the data closely, even for subjects whose performance is near ceiling (e.g., subject 13) or floor (e.g., subject 12). The model is also able to reproduce the response proportions from subjects who spread their responses fairly evenly across the confidence categories (e.g., subjects 7 and 18) as well as those who used some confidence responses much more often than others (e.g., subjects 3 and 13). The model is able to produce both linear z-ROC functions (e.g., subjects 7 and 18) and non-linear z-ROC functions (e.g., subject 13).
The model predictions also match the data quite closely for the subjects in Fig. 15, despite the small misfits of the z-ROC functions for most of the subjects (there is a significant difference between the model predictions and the data for subjects 14 and 28, but not the others in this figure). All of the subjects in this figure have z-ROC functions that are significantly non-linear. Although there is not a significant difference between the model predictions and the data for most of these subjects, the model fails to produce the non-linearity in the z-ROC function for most of these subjects (the z-ROC predicted by the model for subject 21 is slightly non-linear).
There are several aspects of these u-shaped z-ROC functions that are difficult for the model to capture. First, the model has difficulty producing u-shaped z-ROC functions for subjects whose RT quantiles are not u-shaped across the confidence responses. For example, subject 24 has a u-shaped z-ROC function but relatively fast high-confidence responses. The model is able to account for the shape of the RT distributions, but misses the slight non-linearity of the z-ROC function. In contrast, subject 21 has both u-shaped RT quantiles and a u-shaped z-ROC function and the model is able to produce a non-linear z-ROC function for this subject. This was also an issue in Experiment 1, where subjects 4 and 5 had u-shaped z-ROC functions but relatively flat RT quantiles. Second, the transformation of the ROC to the z-ROC causes small misses at the ends of the ROC function to be amplified. As shown in Fig. 15, the misses in ROC space that lead to changes in linearity in z-ROC space are relatively small. In fact, for these five subjects the average absolute difference between the response proportions predicted by the model and the empirical response proportions ranged from 2% to 3% (with maximum absolute differences ranging from 3% to 7%). Moreover, the model is quite constrained in its ability to accommodate the entire pattern of response proportions and RT quantiles. For example, the model over-predicted by 7% the number of high-confidence ‘intact’ responses to rearranged word pairs made by subject 8. In order to reduce the number of false alarms for this response, the decision bound for this response could be raised, but this would also reduce the number of correct responses for this response option (since other responses would be more likely to be chosen over that response) and change the RT for this response. Similarly, the right-most confidence criteria could be moved further to the right to reduce the number of false alarms, but this would also reduce the number of hits and change the proportion of responses made in the neighboring medium-confidence response region. Overall, the model is quite constrained in its ability to fit response patterns since small changes in confidence criteria and decision boundaries affect the overall patterns of both the response times and response proportions across all of the conditions. Third, the model has difficulty producing patterns of response proportions that have very low discriminability between intact and rearranged items for the medium and low confidence responses but higher discriminability for high confidence responses. For example, note that the solid black and gray lines (empirical response proportions) for subject 14 in the bottom row of Fig. 15 nearly overlie each other for the middle four confidence responses and then separate for the high confidence responses. This indicates that this subject’s performance was close to chance when he or she was responding using the middle four confidence responses (as demonstrated by the fact that there is little separation between the black and gray curves for those responses) and only performed better than chance for the highest confidence responses. While the model is able to capture this general pattern, the model produces values that are less extreme than the pattern observed in the data (i.e., the model predictions for the middle confidence responses are slightly more accurate than the data and the predictions for the highest confidence responses are slightly less accurate than the data). A similar pattern is observed with subject 8, especially for the “intact” response options. This pattern can be difficult for the model to account for given the representation of evidence in RTCON2. Memory strength is represented by a normal distribution on each trial, and the area under the curve of that distribution in each response region drives the accumulation for that response. To produce a comparable number of correct and incorrect responses for a particular confidence response, there must be similar evidence in that response region for both ‘intact’ and ‘rearranged’ stimuli (i.e., the drift distributions for ‘intact’ and ‘rearranged’ items will need to overlap in that region). On the other hand, to produce different numbers of correct and incorrect responses for a particular confidence response, there must be more evidence (i.e., larger area under the curve) in that response region for one condition over the other.
The model can handle low discriminability in the medium and low confidence responses when the overall pattern of responses is consistent with the representation of evidence in RTCON2. For example, subject 21 had low discriminability for the medium and low confidence responses and higher discriminability for high confidence responses and a smaller proportion of high confidence responses overall. The model is able to handle this pattern of responses because it is consistent with having overlapping drift distributions such that there will be less difference between the two distributions around the middle of the response region (where they overlap) and a greater difference in the tails of the distributions (in the higher confidence regions). This representation will also tend to produce more low and medium confidence responses and relatively fewer high confidence responses, as is the case for subject 21. In contrast, the model has difficulty producing response patterns like those of subject 14, who made a relatively large number of correct high confidence responses but was at chance at the other confidence levels. It is also worth noting that the cumulative nature of the ROC and z-ROC functions obscures most of this information about response pattern. For subjects like 14, the model predictions are missing as much on the middle confidence regions as the extremes, but the ROC functions make it appear that the model is only missing the tails since the misses in the middle confidence regions compensate for the misses in the high confidence regions when using cumulative values.
Previous application of the original RTCON model demonstrated that the slope of subjects’ z-ROC functions showed sequential effects (i.e., the slope of the z-ROC changed as a function of the prior response; Ratcliff & Starns, 2009). In that study, subjects were biased in favor of repeating a particular response (i.e., if they made an ‘old’ response on the previous trial, they were more likely to make another ‘old’ response on the current trial). In this experiment we observed sequential effects of confidence level. Subjects were more likely to make a high confidence response if their previous response was a high confidence response and similarly for medium and low confidence responses. In Fig. 16A, response proportions for each confidence response (1–6) and each condition (intact and rearranged) are plotted separately as a function of a previous response. The solid lines show the response proportions for each condition and response option sorted based on the response from the immediately preceding trial and the dashed lines show the response proportions sorted based on response from a trial ten trials before the current trial. That is, the upper left plot shows the proportion of ‘sure rearranged’ responses made to rearranged pairs as a function of the previous response (solid line) and as a function of the response ten trials previous (dashed line), the upper right plot shows the proportion of ‘sure intact’ responses made to rearranged pairs, and so on. From these plots we can see that subjects were likely to respond with the same level of confidence on subsequent trials. For example, in the upper left plot we see that subjects made more ‘sure rearranged’ responses to rearranged stimuli if they had previously made a high confidence response (i.e., a 1 or a 6 in this figure) than if they had previously made a medium or low confidence response (i.e., a 2–5). Similarly, in the second plot in the top row we see that subjects made more ‘medium-confident rearranged’ responses to rearranged stimuli if they had previously made a medium confidence response (i.e., a 2 or a 5) than if they had previously made a low or high confidence response. Similar results were observed across all confidence response options and conditions and for both lags (i.e., the immediately preceding trial or one ten trials before the current trial). This was an unexpected result. Although Ratcliff and Starns (2009) observed a bias in favor of repeating a particular response, that bias was based on the category of the response (e.g., intact vs. rearranged), not the confidence level of the response. We discuss two possible explanations for this type of behavior.
Fig. 16.
Experiment 3: Sequential effects. (A) Response proportions as a function of previous responses. Response proportions for each confidence response (1–6) and each condition (intact and rearranged) are plotted separately as a function of a previous response. The solid lines show the response proportions for each condition and response option sorted based on the response from the immediately preceding trial and the dashed lines show the response proportions sorted based on response from a trial ten trials before the current trial. So the upper left plot shows the proportion of ‘sure rearranged’ responses made to rearranged pairs as a function of the previous response (solid line) and as a function of the response ten trials previous (dashed line), the upper right plot shows the proportion of ‘sure intact’ responses made to rearranged pairs, and so on. (B) z-ROC and ROC functions for averaged data as a function of previous responses. Data were collapsed across previous ‘intact’ and ‘rearranged’ responses to produce three conditions based just on the confidence level of the immediately preceding response (1: high, 2: medium, and 3: low).
First, it is possible that, rather than distributing their responses across the entire confidence scale, subjects were switching around which pair of intact/rearranged responses they were using (i.e., essentially making two-choice decisions and mapping those responses onto a particular pair of response keys). Subjects were told to try to use all of the confidence levels over the course of the experiment to discourage them from using just two responses (i.e., using just one confidence level throughout the whole experiment), so this type of behavior may have been a strategic way of following those instructions.
Second, it is possible that subjects were using the confidence levels based on general changes in attention or motivation. For example, subjects may have been more attentive or motivated during some blocks (and would likely perform better on those blocks in terms of accuracy) and then made their confidence responses based on how they felt they were performing during those periods of time (as opposed to making confidence responses solely based on their perceived memory strength for each word pair). If this were the case, we would also expect to see differences in performance based on previous confidence levels. To examine this, we generated ROC and z-ROC functions as a function of previous responses averaged over all the subjects. Fig. 16B shows average ROC and z-ROC functions sorted according to the previous response (here collapsed across ‘intact’ and ‘rearranged’ responses to produce three conditions based just on the confidence level of the immediately preceding response). Accuracy was indeed higher on trials made following a high confidence response, and the z-ROC functions were more u-shaped following a low or medium confidence response. Standard memory and decision-making models do not produce these types of effects (without including additional assumptions) and so the data produced by subjects using these types of strategies are challenging for standard models.
This experiment demonstrated the ability of RTCON2 to fit a wide variety of ROC and z-ROC shapes in an associative recognition task while simultaneously fitting RT distributions. By collecting data from a larger group of subjects we were able to demonstrate when RTCON2 is able to produce various z-ROC functions and when it has difficulty. The model is able to reproduce the z-ROC shapes when the shape of the RT quantiles across confidence levels matches the shape of the z-ROC, when there are sufficient numbers of observations in the extreme confidence categories, and when the response patterns across confidence levels are consistent with the model’s continuous representation of evidence. The model has difficulty producing non-linear z-ROC shapes when these conditions are not met, which tends to be the case when u-shaped z-ROC shapes occur. However, the misfits in these cases were quite small. The average absolute deviation between the model and the data ranged from 2% to 3% for the subjects in Fig. 15, and the χ2 values for the model fits were non-significant for three of these five subjects. It is possible that a different representation of memory information would enable the model to fit these u-shaped functions, but such a representation should not hinder the model’s ability to fit the other patterns of data as well. We also identified some possible strategies (based on sequential effects) that subjects may use when responding with confidence scales and these effects should be considered when modeling and interpreting this type of data. Note that these effects were not observed in Experiments 1 and 2 which used paid subjects who were more practiced at the task.
General discussion
These experiments were designed to test the ability of the RTCON2 model to fit both the properties of confidence responses and reaction times in an associative recognition paradigm. This would be a substantial advance over signal-detection based models that address only choice proportions and could provide an alternative account for the z-ROC patterns that have been observed in this paradigm. While the model was able to account for most of the response patterns and reaction times in these experiments, the model was not able to account for some of the non-linear z-ROC shapes which are of particular interest to memory modelers. However, although the model was not able to produce the u-shaped z-ROC functions, the response proportions predicted by the model did not always significantly differ from the empirical response proportions (based on χ2) and the differences between the model predictions and the data were quite small.
Previous research has demonstrated an alternative explanation for the shapes of the ROC and z-ROC functions that is based on how subjects set their decision boundaries (Ratcliff & Starns, 2013). In the RTCON2 model, if the response proportions for the different confidence responses are not close to zero (see appendix of Ratcliff & Starns, 2013), there is a relationship between the shape of the z-ROC function, the RT quantiles, and the decision boundaries. Intuitively, the height of the decision boundary affects the amount of evidence required to make a response and therefore affects reaction times. But the relative heights of the decision boundaries also affect the response proportions for the different confidence responses. If one of the confidence categories has a lower decision boundary than the others, the accumulator for that response will be able to reach its boundary more quickly and that response will be chosen a higher proportion of the time. These changes in the response proportions for different confidence responses directly affect the shape of the z-ROC function. The experiments in this paper demonstrate a relationship between the shape of the z-transformed receiver operating characteristic and the behavior of response time distributions for subjects with linear z-ROC functions and inverted u-shaped z-ROC functions, and this relationship is explained by the behavior of the decision boundaries in the RTCON2 model.
The model had difficulty, however, producing most of the u-shaped z-ROC functions observed in these experiments. Specifically, the model had trouble producing these z-ROC shapes when the shapes of the RT quantiles were not consistent with the shapes of the z-ROC functions, or when there was a low number of high-confidence responses. In the model, evidence is represented as a normal distribution (with an SD of 1) on some memory strength dimension and the position of this normal distribution varies across trials (according to another normal distribution with mean μ and SD s). This representation of evidence restricts the possible response patterns that the model can produce. For example, in order to produce chance performance for some response option, the evidence distributions for ‘intact’ and ‘rearranged’ items must have similar area in that response region. However, such a restriction affects the area of these evidence distributions in all of the other response regions since they are all determined by the location of the normal distribution of evidence. Thus the model has difficulty producing, for example, extreme changes in performance for neighboring response options. Although the placement of the confidence criteria and decision boundaries will also affect response patterns (by adjusting the area of the response region and adjusting the amount of evidence required to make a particular response), these parameters are constrained by the response time data as well as the response proportions and so are unable to take on extreme values to produce any possible pattern of responses (e.g., a very low decision boundary would lead to chance performance, but would also result in faster RTs and an increase in the number of responses predicted for that particular confidence response). This representation of evidence was used because it has previously provided a good fit to data (Ratcliff & Starns, 2013). However, as discussed in Ratcliff and Starns (2013), the distribution of memory strength across trials does not need to be a normal distribution and could instead take the form of some distribution predicted by a memory model. In recent years, much of the research attempting to distinguish between models of memory has been focused on slight differences in the shape of these z-ROC functions. Such variation in the shapes of the z-ROC has been used to make claims about the number of processes involved in a memory decision, the nature of the evidence involved in the decision, and specific characteristics of the decision process.
In the associative memory literature, non-linear z-ROC functions are a violation of the normal distributions of evidence usually assumed in SDT, and have prompted theorists to elaborate upon the basic theory. One such elaboration is the dual-process signal detection (DPSD) model (Yonelinas, 1994; Yonelinas & Parks, 2007), which assumes that recognition consists of an equal-variance signal-detection process referred to as “familiarity” plus a discrete threshold process referred to as “recollection”. According to this model, some recognition decisions are based on a vague sense of familiarity while others are based on recollection of a qualitative detail of the learning event (e.g., “this word was followed by ‘house’ in the study list”). When responding is based entirely on familiarity, the DPSD model predicts asymmetrical curvilinear ROC functions and linear z-ROC functions with a slope equal to one. When responding is based on recollection for some proportion of the word pairs, the model predicts linear ROC functions and slightly non-linear (i.e., slightly U-shaped) z-ROC functions with slopes less than one.
In an associative recognition paradigm, the familiarity of the individual words should not help discriminate between intact and rearranged pairs since all of the words were seen during the previous study period. Therefore, according to the DPSD model, performance in an associative paradigm should be based primarily on the “recollection” process and should result in linear ROC and non-linear z-ROC functions. This prediction has been supported by linear associative recognition ROC functions reported by Yonelinas (1997) and replicated by Rotello et al. (2000) as well as linear source memory ROC functions reported by Yonelinas (1999). However, Kelley and Wixted (2001) and Verde and Rotello (2004) reported curvilinear associative recognition ROC functions and Healy et al. (2005) reviewed 13 associative recognition studies and found that a curvilinear ROC function provided a better fit to the data than a linear ROC function. There were a number of task differences that may have produced these discrepancies in the shapes of the ROC functions. In the experiments reported by Yonelinas (1997) and Rotello et al. (2000) that produced linear associative recognition ROC functions, subjects were making both item and associative recognition judgments for the same lists. When these tasks are mixed, subjects may rely on different response strategies than they would in a pure associative recognition task. Rotello et al. (2000) also demonstrated that an additional guessing process could influence the linearity of the ROC and z-ROC functions.
In our experiments we did not observe systematically linear ROC functions. Although some of the subjects in Experiment 3 did have relatively linear ROC functions (e.g., subjects 5 and 29), the majority of the subjects across all three experiments had curved ROC functions (although note that ROC functions will necessarily become more linear as performance goes to chance). Some of our subjects did have slightly U-shaped z-ROC functions, but other subjects had linear z-ROC functions or inverted U-shaped z-ROC functions, which are at odds with the predictions of DPSD.
However, even when curvilinear ROC functions are found in associative recognition and source memory studies, these were not as curvilinear as would be predicted by an unequal-variance signal-detection model (Hilford et al., 2002; Kelley & Wixted, 2001). In order to explain these effects, Hilford et al. (2002) assumed that on some proportion of trials, the information necessary for the memory decision, either associative or source, was not available. Hilford et al. (2002) proposed that subjects failed to encode the information for some proportion of items during the study phase. Similarly, DeCarlo (2002, 2003) demonstrated that nonlinear z-ROC functions can be produced if the memory strength distributions are mixtures of two different distributions, such as a distribution from items that were encoded during study and a distribution from items that were not encoded during study.
All of the approaches described above use the shape of the ROC and z-ROC functions to draw conclusions about the nature of memory evidence. In DeCarlo (2002, 2003), Hilford et al. (2002) and Kelley and Wixted (2001), evidence comes from a mixture of qualitatively similar processes. In Yonelinas’ (1994) model, evidence comes from two qualitatively different processes. Support for these models has come from observations of the shape of ROC and z-ROC functions sources across tasks and conditions. For example, Kelley and Wixted (2001) found that ROCs in an associative recognition experiment were more curvilinear for strong (i.e., studied more often) word pairs than weak pairs. This change in ROC shape across conditions was consistent with a mixture model that included continuously distributed item and associative information (as opposed to a high-threshold model or a signal-detection type model with a single source of evidence). However, changes in ROC shape can also be produced by RTCON2 with just changes in the mean of the drift distribution (see Appendix of Ratcliff & Starns, 2013).
Additionally, these accuracy-only memory models were designed solely to account for accuracy and completely ignore the amount of time required to make a particular memory decision. Using a model like RTCON2 allows us to investigate how many of the observed patterns of responses could be explained through the addition of a model for making confidence judgments. Explicitly modeling both the information feeding into a decision and the decision-making process allows us to distinguish between effects on z-ROC shapes that are a result of how subjects set confidence criteria and decision boundaries (aspects of the decision-making process), and effects that are a result of changes in the information being provided from memory. This model can handle some of the observed response patterns, but is unable to account for the subset of subjects who exhibited u-shaped z-ROC functions. However, the misfits for these subjects are quite small – there is an average difference of 2–3% between the model predictions and the data for these subjects. It remains to be seen if adjusting the memory information feeding into the decision (e.g., combining the memory strength predictions of a memory model with the decision-making process of RTCON2) will enable the model to handle these patterns. Such an approach could also be informative for models of memory based on the additional constraint provided by RTs. This type of combined modeling approach would allow researchers to take advantage of the ability of RTCON2 to distinguish between the information feeding into a confidence response and individual differences in how the confidence response scale is used. However, the adjusted model would still need to be able to handle all of the patterns observed in these experiments that RTCON2 was able to fit. So far, none of the existing memory models can handle the full observed pattern of RTs and response proportions across confidence levels and none of them, to our knowledge, would predict the diversity of z-ROC shapes observed in these experiments. Without assuming more than a relatively simple single distribution of memory strength, RTCON2 was able to produce a variety of ROC and z-ROC shapes. Thus the specific ROC and z-ROC shapes cannot be used solely to infer the nature of evidence from memory but are also indicative of differences in how different subjects choose to set decision boundaries when using confidence response scales.
In many memory experiments, data from individual subjects are averaged together and conclusions are made based on these averaged data. Differences between individual subjects are, at best, presented only to illustrate that most of the subjects exhibit the same general pattern of results as the average. These experiments demonstrate the importance of considering individual differences when reporting ROC and z-ROC experiments. Subjects in these experiments exhibited a wide variety of z-ROC functions with some subjects having linear z-ROCs and other subjects having nonlinear z-ROCs. These experiments, as well as work by Ratcliff et al. (1994) and Ratcliff and Starns (2013), demonstrate dramatic individual differences in the shapes of the z-ROC functions that appear to be relatively stable across tasks (although these effects are some-what susceptible to specific response instructions; Ratcliff & Starns, 2009). Other models, such as the dual-process signal-detection account (Yonelinas, 1997), would have difficulty explaining these consistent individual differences, except possibly as a result of individual differences in response or encoding strategies, and are unable to explain the inverted u-shaped z-ROCs exhibited by some subjects.
This research also demonstrates the advantages of the new version of the RTCON model compared to the original. This version of the model was able to fit the bowed reaction time quantiles that the other model was unable to handle. While practice and specific instructions can eliminate these bowed effects (Ratcliff & Starns, 2009), this pattern of reaction time behavior is relatively common in confidence response paradigms (Murdock, 1974; Murdock & Dufty, 1972; Norman & Wickelgren, 1969; Ratcliff & Murdock, 1976) and a model designed to account for data from these paradigms should be capable of handling this pattern. As shown, RTCON2 was able to produce the necessary bowed RT quantiles which were slower for low confidence responses than high confidence responses (as well as the other observed RT quantile patterns). The ability of the model to handle these shifts in RT distributions is crucial given the relationship between these shifts and the shape of the z-ROC function.
The RTCON2 model also provides a better fit to two-choice data then the original RTCON model (Starns et al., 2012), as demonstrated in the second experiment. In order to be considered a viable model of multi-choice data, RTCON2 should be able accommodate two-choice data as well as 6-choice. In the second experiment, subjects alternated between using a 6-choice response scale and a two-choice response scale. The data from both tasks was then fit with the RTCON2 model, and the two-choice data was also fit with the standard diffusion model. The RTCON2 model was able to fit data from a two-choice task nearly as well as the diffusion model (Ratcliff, 1978; Ratcliff & McKoon, 2008), and was able to do so with some of the parameters constrained across the 6-choice and two-choice tasks (i.e., some of the same parameters were used to fit the RTCON2 model to data from both the two-choice and 6-choice tasks).
Although RTCON2 has a relatively large number of parameters, there are considerably more degrees of freedom in the data than in the model because of the need to fit RT distributions. Additionally, because of the structure of the model, a change in any one parameter value will affect predictions across multiple conditions or response categories. This means that it is not possible to remedy misfits in a single condition by simply adjusting single parameters. The model is also not overly flexible. While it was able to fit most of the patterns of individual differences found in these two experiments, it was not able to fit a set of artificial data created by combining some subjects’ accuracy data with other subjects’ reaction time data. In this analysis, we rearranged subjects’ data into artificial data sets consisting of one subject’s response proportions and a different subject’s reaction time quantiles from Experiment 1. When the model was fit to these artificial data sets, the resulting mean χ2 value was 445 (more than twice as large as the observed mean value in the first experiment). The misfits were largest for data sets that consisted of data from subjects with different z-ROC function shapes. For example, when trying to fit a data set consisting of subject 3’s bowed reaction times (see Fig. 3) and subject 5’s accuracy (see Fig. 5), the model’s best fitting parameter values yielded a χ2 of 1029 (compared with χ2 values of 250 and 273 for subjects 3 and 5 respectively).
This research demonstrates the strengths of RTCON2 as a model of multi-choice confidence judgments as well as areas for future development. The model is able to fit a wide range of reaction time and response proportion behaviors and is able to do so without assuming any additional memory processes. However, the model slightly misses some of the observed u-shaped z-ROC functions for associative recognition such that it may be necessary to adjust the information feeding into the model to account for these patterns. RTCON2 performs as well as the standard diffusion model when applied to two-choice data, and provides parameter estimates that are consistent across models and response paradigms. With the addition of reaction time and decision-related processing, RTCON2 is able to distinguish between the information feeding into a decision and aspects of the decision-making process, and in some cases is able to provide an alternative interpretation of z-ROC functions that is based on individual differences in the decision-making process.
Acknowledgments
This article was supported by Grants NIA R01-AG041176 and AFOSR # FA9550-11-1-0130 to Roger Ratcliff. We thank Jeffrey Starns for comments on the article.
Appendix A
Fig. A1.
Experiment 3: Data and model fits. The first two rows plot the RT quantiles for each confidence response with the 6 response keys plotted on the x-axis (the “sure rearranged” category is labeled 1 and the “sure intact” category is labeled 6) and the RT quantiles plotted vertically with each line representing a reaction time quantile. The numbers plotted represent the empirical data and the lines represent predicted data from the model. In conditions where subjects made between 4 and 10 responses the median RT is plotted as an ‘M’ and the other quantiles are not included. Conditions where subjects made fewer than 5 responses are omitted from the figure. In conditions where the model predicted between 5 and 10 responses only the median RT is plotted and the other quantiles are not included. Conditions where the model predicted fewer than 5 responses are omitted from the figure. The third and fourth row in each figure plot the empirical and predicted z-ROC and ROC curves for each subject. The solid lines depict the empirical data and the dashed lines depict the model predictions. The fifth row plots the decision boundaries for each confidence response and the sixth row plots the response proportions (both empirical data and model predictions) for each confidence response and condition. The solid lines depict the empirical data, the dashed lines depict the model predictions, the black lines depict responses for ‘intact’ pairs and the gray lines depict responses for ‘rearranged’ pairs.
Fig. A2.
Experiment 3: Data and model fits. Same plotting conventions as Fig. A1.
Fig. A3.
Experiment 3: Data and model fits. Same plotting conventions as Fig. A1.
Fig. A4.
Experiment 3: Data and model fits. Same plotting conventions as Fig. A1.
Fig. A5.
Experiment 3: Data and model fits. Same plotting conventions as Fig. A1.
References
- Arndt J, Reder LM. Word frequency and receiver operating characteristic curves in recognition memory: Evidence for a dual-process interpretation. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2002;28:830–842. doi: 10.1037//0278-7393.28.5.830. http://dx.doi.org/10.1037/0278-7393.28.5.830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Audley RJ, Pike AR. Some alternative stochastic models of choice. British Journal of Mathematical and Statistical Psychology. 1965;18:207–225. doi: 10.1111/j.2044-8317.1966.tb00351.x. [DOI] [PubMed] [Google Scholar]
- Banks WP. Signal detection theory and human memory. Psychological Bulletin. 1970;74:81–99. http://dx.doi.org/10.1037/h0029531. [Google Scholar]
- Baranski JV, Petrusic WM. Probing the locus of confidence judgments: Experiments on the time to determine confidence. Journal of Experimental Psychology: Human Perception and Performance. 1998;24:929–945. doi: 10.1037//0096-1523.24.3.929. http://dx.doi.org/10.1037/0096-1523.24.3.929. [DOI] [PubMed] [Google Scholar]
- Bastin C, Van der Linden M. The effects of aging on the recognition of different types of associations. Experimental Aging Research. 2006;32:61–77. doi: 10.1080/03610730500326291. http://dx.doi.org/10.1080/03610730500326291. [DOI] [PubMed] [Google Scholar]
- Beck JM, Ma WJ, Kiani R, Hanks T, Churchland AK, Roitman J, … Pouget A. Probabilistic population codes for Bayesian decision making. Neuron. 2008;60:1142–1152. doi: 10.1016/j.neuron.2008.09.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernbach HA. Decision processes in memory. Psychological Review. 1967;74:462–480. doi: 10.1037/h0025132. http://dx.doi.org/10.1037/h0025132. [DOI] [PubMed] [Google Scholar]
- Brown S, Ratcliff R, Smith PL. Evaluating methods for approximating stochastic differential equations. Journal of Mathematical Psychology. 2006;50:402–410. doi: 10.1016/j.jmp.2006.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Busemeyer JR, Townsend JT. Fundamental derivations from decision field theory. Mathematical Social Sciences. 1992;23:255–282. [Google Scholar]
- Clark SE. Word frequency effects in associative and item recognition. Memory & Cognition. 1992;20:231–243. doi: 10.3758/bf03199660. http://dx.doi.org/10.3758/BF03199660. [DOI] [PubMed] [Google Scholar]
- Craik FM, Luo L, Sakuta Y. Effects of aging and divided attention on memory for items and their contexts. Psychology and Aging. 2010;25:968–979. doi: 10.1037/a0020276. http://dx.doi.org/10.1037/a0020276. [DOI] [PubMed] [Google Scholar]
- DeCarlo LT. Signal detection theory with finite mixture distributions: Theoretical developments with applications to recognition memory. Psychological Review. 2002;109:710–721. doi: 10.1037/0033-295x.109.4.710. http://dx.doi.org/10.1037/0033-295X.109.4.710. [DOI] [PubMed] [Google Scholar]
- DeCarlo LT. An application of signal detection theory with finite mixture distributions to source discrimination. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2003;29:767–778. doi: 10.1037/0278-7393.29.5.767. http://dx.doi.org/10.1037/0278-7393.29.5.767. [DOI] [PubMed] [Google Scholar]
- Donaldson W, Murdock BB. Criterion change in continuous recognition memory. Journal of Experimental Psychology. 1968;76:325–330. doi: 10.1037/h0025510. http://dx.doi.org/10.1037/h0025510. [DOI] [PubMed] [Google Scholar]
- Egan JP. USAF Operational Applications Laboratory Technical Note, 58-51, 32. 1958. Recognition memory and the operating characteristic. [Google Scholar]
- Eichenbaum HH, Yonelinas AP, Ranganath CC. The medial temporal lobe and recognition memory. Annual Review of Neuroscience. 2007:30123–30152. doi: 10.1146/annurev.neuro.30.051606.094328. http://dx.doi.org/10.1146/annurev.neuro.30.051606.094328. [DOI] [PMC free article] [PubMed]
- Glanzer M, Hilford A, Kim K. Six regularities of source recognition. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2004;30:1176–1195. doi: 10.1037/0278-7393.30.6.1176. http://dx.doi.org/10.1037/0278-7393.30.6.1176. [DOI] [PubMed] [Google Scholar]
- Gomez P, Ratcliff R, Perea M. A model of letter position coding: The overlap model. Psychological Review. 2008;115:577–601. doi: 10.1037/a0012667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grasha AF. Detection theory and memory processes: Are they compatible? Perceptual and Motor Skills. 1970;30:123–135. http://dx.doi.org/10.2466/pms.1970.30.1.123. [Google Scholar]
- Gronlund SD, Ratcliff R. Time course of item and associative information: Implications for global memory models. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1989;15:846–858. doi: 10.1037//0278-7393.15.5.846. http://dx.doi.org/10.1037/0278-7393.15.5.846. [DOI] [PubMed] [Google Scholar]
- Healy MR, Light LL, Chung C. Dual-process models of associative recognition in young and older adults: Evidence from receiver operating characteristics. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2005;31:768–788. doi: 10.1037/0278-7393.31.4.768. http://dx.doi.org/10.1037/0278-7393.31.4.768. [DOI] [PubMed] [Google Scholar]
- Henson RA, Rugg MD, Shallice TT, Dolan RJ. Confidence in recognition memory for words: Dissociating right prefrontal roles in episodic retrieval. Journal of Cognitive Neuroscience. 2000;12:913–923. doi: 10.1162/08989290051137468. http://dx.doi.org/10.1162/08989290051137468. [DOI] [PubMed] [Google Scholar]
- Hilford A, Glanzer M, Kim K, DeCarlo LT. Regularities of source recognition: ROC analysis. Journal of Experimental Psychology: General. 2002;131:494–510. doi: 10.1037//0096-3445.131.4.494. http://dx.doi.org/10.1037/0096-3445.131.4.494. [DOI] [PubMed] [Google Scholar]
- Hockley WE. Item versus associative information: Further comparisons of forgetting rates. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1992;18:1321–1330. http://dx.doi.org/10.1037/0278-7393.18.6.1321. [Google Scholar]
- Hockley WE. Reflections of the mirror effect for item and associative recognition. Memory & Cognition. 1994;22:713–722. doi: 10.3758/bf03209256. http://dx.doi.org/10.3758/BF03209256. [DOI] [PubMed] [Google Scholar]
- Jazayeri M, Movshon JA. Optimal representation of sensory information by neural populations. Nature Neuroscience. 2006;9:690–696. doi: 10.1038/nn1691. [DOI] [PubMed] [Google Scholar]
- Kelley R, Wixted JT. On the nature of associative information in recognition memory. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2001;27:701–722. http://dx.doi.org/10.1037/0278-7393.27.3.701. [PubMed] [Google Scholar]
- Kim H, Cabeza R. Trusting our memories: Dissociating the neural correlates of confidence in veridical versus illusory memories. The Journal of Neuroscience. 2007;27:12190–12197. doi: 10.1523/JNEUROSCI.3408-07.2007. http://dx.doi.org/10.1523/JNEUROSCI.3408-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kintsch W. Memory and decision aspects of recognition learning. Psychological Review. 1967;74:496–504. doi: 10.1037/h0025127. http://dx.doi.org/10.1037/h0025127. [DOI] [PubMed] [Google Scholar]
- Kintsch W, Carlson WJ. Changes in the memory operating characteristic during recognition learning. Journal of Verbal Learning and Verbal Behavior. 1967;6:891–896. http://dx.doi.org/10.1016/S0022-5371(67)80155-5. [Google Scholar]
- Kirwan CB, Wixted JT, Squire LR. Activity in the medial temporal lobe predicts memory strength, whereas activity in the prefrontal cortex predicts recollection. The Journal of Neuroscience. 2008;28:10541–10548. doi: 10.1523/JNEUROSCI.3456-08.2008. http://dx.doi.org/10.1523/JNEUROSCI.3456-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kučera H, Francis WN. Computational analysis of present-day American English. Providence: Brown University Press; 1967. [Google Scholar]
- Laming DJ. Information theory of choice-reaction times. Oxford, England: Academic Press; 1968. [Google Scholar]
- Link SW. The relative judgment theory of two choice response time. Journal of Mathematical Psychology. 1975;12:114–135. http://dx.doi.org/10.1016/0022-2496(75)90053-X. [Google Scholar]
- Lockhart RS, Murdock BB. Memory and the theory of signal detection. Psychological Bulletin. 1970;74:100–109. http://dx.doi.org/10.1037/h0029536. [Google Scholar]
- Malmberg KJ, Xu J. The influence of averaging and noisy decision strategies on the recognition memory ROC. Psychonomic Bulletin & Review. 2006;13:99–105. doi: 10.3758/bf03193819. [DOI] [PubMed] [Google Scholar]
- Malmberg KJ, Xu J. On the flexibility and the fallibility of associative memory. Memory & Cognition. 2007;35:545–556. doi: 10.3758/bf03193293. http://dx.doi.org/10.3758/BF03193293. [DOI] [PubMed] [Google Scholar]
- Merkle EC, Van Zandt T. An application of the poisson race model to confidence calibration. Journal of Experimental Psychology: General. 2006;135:391–408. doi: 10.1037/0096-3445.135.3.391. http://dx.doi.org/10.1037/0096-3445.135.3.391. [DOI] [PubMed] [Google Scholar]
- Moritz S, Glascher J, Sommer T, Buchel C, Braus DF. Neural correlates of memory confidence. NeuroImage. 2006;33:1188–1193. doi: 10.1016/j.neuroimage.2006.08.003. http://dx.doi.org/10.1016/j.neuroimage.2006.08.003. [DOI] [PubMed] [Google Scholar]
- Murdock BB. Human memory: Theory and data. Oxford, England: Lawrence Erlbaum; 1974. [Google Scholar]
- Murdock BB, Dufty PO. Strength theory and recognition memory. Journal of Experimental Psychology. 1972;94:284–290. http://dx.doi.org/10.1037/h0032795. [Google Scholar]
- Naveh-Benjamin M. Adult age differences in memory performance: Tests of an associative deficit hypothesis. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2000;26:1170–1187. doi: 10.1037//0278-7393.26.5.1170. http://dx.doi.org/10.1037/0278-7393.26.5.1170. [DOI] [PubMed] [Google Scholar]
- Naveh-Benjamin M. Age-related differences in explicit associative memory: Contributions of effortful-strategic and automatic processes. In: Naveh-Benjamin M, Ohta N, editors. Memory and aging: Current issues and future directions. New York, NY, US: Psychology Press; 2012. pp. 71–95. [Google Scholar]
- Nelder JA, Mead R. A simplex method for function minimization. Computer Journal. 1965;7:308–313. [Google Scholar]
- Norman DA, Wickelgren WA. Strength theory of decision rules and latency in retrieval from short-term memory. Journal of Mathematical Psychology. 1969;6:192–208. http://dx.doi.org/10.1016/0022-2496(69)90002-9. [Google Scholar]
- Ogilvie J, Creelman C. Maximum-likelihood estimation of receiver operating characteristic curve parameters. Journal of Mathematical Psychology. 1968;5:377–391. [Google Scholar]
- Pachella RG. The interpretation of reaction time in information processing research. In: Kantowitz B, editor. Human information processing: Tutorials in performance and cognition. New York: Halstead Press; 1974. pp. 41–82. [Google Scholar]
- Pleskac TJ, Busemeyer JR. Two-stage dynamic signal detection: A theory of choice, decision time, and confidence. Psychological Review. 2010;117:864–901. doi: 10.1037/a0019737. http://dx.doi.org/10.1037/a0019737. [DOI] [PubMed] [Google Scholar]
- Qin J, Raye CL, Johnson MK, Mitchell KJ. Source ROCs are (typically) curvilinear: Comment on yonelinas (1999) Journal of Experimental Psychology: Learning, Memory, and Cognition. 2001;27:1110–1115. http://dx.doi.org/10.1037/0278-7393.27.4.1110. [PubMed] [Google Scholar]
- Ratcliff R. A theory of memory retrieval. Psychological Review. 1978;85:59–108. http://dx.doi.org/10.1037/0033-295X.85.2.59. [Google Scholar]
- Ratcliff R. A theory of order relations in perceptual matching. Psychological Review. 1981;88:552–572. [Google Scholar]
- Ratcliff R. Continuous versus discrete information processing: Modeling accumulation of partial information. Psychological Review. 1988;95:238–255. doi: 10.1037/0033-295x.95.2.238. http://dx.doi.org/10.1037/0033-295X.95.2.238. [DOI] [PubMed] [Google Scholar]
- Ratcliff R. Modeling response signal and response time data. Cognitive Psychology. 2006;53:195–237. doi: 10.1016/j.cogpsych.2005.10.002. http://dx.doi.org/10.1016/j.cogpsych.2005.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Hasegawa YT, Hasegawa RP, Smith PL, Segraves MA. Dual diffusion model for single-cell recording data from the superior colliculus in a brightness-discrimination task. Journal of Neurophysiology. 2007;97:1756–1774. doi: 10.1152/jn.00393.2006. http://dx.doi.org/10.1152/jn.00393.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, McKoon G. The diffusion decision model: Theory and data for two-choice decision tasks. Neural Computation. 2008;20:873–922. doi: 10.1162/neco.2008.12-06-420. http://dx.doi.org/10.1162/neco.2008.12-06-420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, McKoon G, Tindall M. Empirical generality of data from recognition memory receiver-operating characteristic functions and implications for the global memory models. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1994;20:763–785. doi: 10.1037//0278-7393.20.4.763. http://dx.doi.org/10.1037/0278-7393.20.4.763. [DOI] [PubMed] [Google Scholar]
- Ratcliff R, Murdock BB. Retrieval processes in recognition memory. Psychological Review. 1976;83:190–214. http://dx.doi.org/10.1037/0033-295X.83.3.190. [Google Scholar]
- Ratcliff R, Rouder JN. Modeling response times for two-choice decisions. Psychological Science. 1998;9:347–356. http://dx.doi.org/10.1111/1467-9280.00067. [Google Scholar]
- Ratcliff R, Sheu C, Gronlund SD. Testing global memory models using ROC curves. Psychological Review. 1992;99:518–535. doi: 10.1037/0033-295x.99.3.518. http://dx.doi.org/10.1037/0033-295X.99.3.518. [DOI] [PubMed] [Google Scholar]
- Ratcliff R, Starns JJ. Modeling confidence and response time in recognition memory. Psychological Review. 2009;116:59–83. doi: 10.1037/a0014086. http://dx.doi.org/10.1037/a0014086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Starns JJ. Modeling confidence judgments, response times, and multiple choices in decision making: Recognition memory and motion discrimination. Psychological Review. 2013;120:697–719. doi: 10.1037/a0033152. http://dx.doi.org/10.1037/a0033152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Thapar A, Gomez P, McKoon G. A diffusion model analysis of the effects of aging in the lexical-decision task. Psychology and Aging. 2004;19:278–289. doi: 10.1037/0882-7974.19.2.278. http://dx.doi.org/10.1037/0882-7974.19.2.278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Thapar A, McKoon G. Effects of aging and IQ on item and associative memory. Journal of Experimental Psychology: General. 2011;140:464–487. doi: 10.1037/a0023810. http://dx.doi.org/10.1037/a0023810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Tuerlinckx F. Estimating parameters of the diffusion model: Approaching to dealing with contaminant reaction and parameter variability. Psychonomic Bulletin & Review. 2002;9:438–481. doi: 10.3758/bf03196302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Van Zandt T, McKoon G. Connectionist and diffusion models of reaction time. Psychological Review. 1999;106:261–300. doi: 10.1037/0033-295x.106.2.261. http://dx.doi.org/10.1037/0033-295X.106.2.261. [DOI] [PubMed] [Google Scholar]
- Rissman J, Greely HT, Wagner AD. Detecting individual memories through the neural decoding of memory states and past experience. Proceedings of the National Academy of Sciences of the United States of America. 2010;107:9849–9854. doi: 10.1073/pnas.1001028107. http://dx.doi.org/10.1073/pnas.1001028107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rotello CM, Macmillan NA, Reeder JA. Sum-difference theory of remembering and knowing: A two-dimensional signal-detection model. Psychological Review. 2004;111:588–616. doi: 10.1037/0033-295X.111.3.588. http://dx.doi.org/10.1037/0033-295X.111.3.588. [DOI] [PubMed] [Google Scholar]
- Rotello CM, Macmillan NA, Van Tassel G. Recall-to-reject in recognition: Evidence from ROC curves. Journal of Memory and Language. 2000;43:67–88. http://dx.doi.org/10.1006/jmla.1999.2701. [Google Scholar]
- Slotnick SD, Dodson CS. Support for a continuous (single-process) model of recognition memory and source memory. Memory & Cognition. 2005;33:151–170. doi: 10.3758/bf03195305. [DOI] [PubMed] [Google Scholar]
- Slotnick SD, Klein SA, Dodson CS, Shimamura AP. An analysis of signal detection and threshold models of source memory. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2000;26:1499–1517. doi: 10.1037//0278-7393.26.6.1499. http://dx.doi.org/10.1037/0278-7393.26.6.1499. [DOI] [PubMed] [Google Scholar]
- Stark CL, Squire LR. Simple and associative recognition memory in the hippocampal region. Learning & Memory. 2001;8:190–197. doi: 10.1101/lm.40701. http://dx.doi.org/10.1101/lm.40701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Starns JJ, Ratcliff R, McKoon G. Evaluating the unequal-variance and dual-process explanations of zROC slopes with response time data and the diffusion model. Cognitive Psychology. 2012;64:1–34. doi: 10.1016/j.cogpsych.2011.10.002. http://dx.doi.org/10.1016/j.cogpsych.2011.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Usher M, McClelland JL. The time course of perceptual choice: The leaky, competing accumulator model. Psychological Review. 2001;108:550–592. doi: 10.1037/0033-295x.108.3.550. http://dx.doi.org/10.1037/0033-295X.108.3.550. [DOI] [PubMed] [Google Scholar]
- Van Zandt T. ROC curves and confidence judgments in recognition memory. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2000;26:582–600. doi: 10.1037//0278-7393.26.3.582. http://dx.doi.org/10.1037/0278-7393.26.3.582. [DOI] [PubMed] [Google Scholar]
- Van Zandt T, Maldonado-Molina M. Response reversals in recognition memory. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2004;30:1147–1166. doi: 10.1037/0278-7393.30.6.1147. http://dx.doi.org/10.1037/0278-7393.30.6.1147. [DOI] [PubMed] [Google Scholar]
- Verde MF, Rotello CM. Strong memories obscure weak memories in associative recognition. Psychonomic Bulletin & Review. 2004;11:1062–1066. doi: 10.3758/bf03196737. [DOI] [PubMed] [Google Scholar]
- Vickers D. Decision processes in visual perception. New York, London: Academic Press; 1979. [Google Scholar]
- Vickers D, Lee MD. Dynamic models of simple judgments: I. properties of a self-regulating accumulator module. Nonlinear Dynamics, Psychology, and Life Sciences. 1998;2:169–194. http://dx.doi.org/10.1023/A:1022371901259. [Google Scholar]
- Vickers D, Lee MD. Dynamic models of simple judgments: II. Properties of a self-organizing PAGAN (parallel, adaptive, generalized accumulator network) model for multi-choice tasks. Nonlinear Dynamics, Psychology, and Life Sciences. 2000;4:1–31. http://dx.doi.org/10.1023/A:1009571011764. [Google Scholar]
- Wagenmakers E. Methodological and empirical developments for the Ratcliff diffusion model of response times and accuracy. European Journal of Cognitive Psychology. 2009;21:641–671. http://dx.doi.org/10.1080/09541440802205067. [Google Scholar]
- Wais PE. Hippocampal signals for strong memory when associative memory is available and when it is not. Hippocampus. 2011;21:9–21. doi: 10.1002/hipo.20716. http://dx.doi.org/10.1002/hipo.20716. [DOI] [PubMed] [Google Scholar]
- Wickelgren WA. Speed-accuracy tradeoff and information processing dynamics. Acta Psychologica. 1977;41:67–85. http://dx.doi.org/10.1016/0001-6918(77)90012-9. [Google Scholar]
- Wixted JT. Dual-process theory and signal-detection theory of recognition memory. Psychological Review. 2007;114:152–176. doi: 10.1037/0033-295X.114.1.152. http://dx.doi.org/10.1037/0033-295X.114.1.152. [DOI] [PubMed] [Google Scholar]
- Yonelinas AP. Receiver-operating characteristics in recognition memory: Evidence for a dual-process model. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1994;20:1341–1354. doi: 10.1037//0278-7393.20.6.1341. http://dx.doi.org/10.1037/0278-7393.20.6.1341. [DOI] [PubMed] [Google Scholar]
- Yonelinas AP. Recognition memory ROCs for item and associative information: The contribution of recollection and familiarity. Memory & Cognition. 1997;25:747–763. doi: 10.3758/bf03211318. [DOI] [PubMed] [Google Scholar]
- Yonelinas AP. The contribution of recollection and familiarity to recognition and source-memory judgments: A formal dual-process model and an analysis of receiver operating characteristics. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1999;25:1415–1434. doi: 10.1037//0278-7393.25.6.1415. http://dx.doi.org/10.1037/0278-7393.25.6.1415. [DOI] [PubMed] [Google Scholar]
- Yonelinas AP, Dobbins I, Szymanski MD, Dhaliwal HS, King L. Signal-detection, threshold, and dual-process models of recognition memory: ROCs and conscious recollection. Consciousness and Cognition: An International Journal. 1996;5:418–441. doi: 10.1006/ccog.1996.0026. http://dx.doi.org/10.1006/ccog.1996.0026. [DOI] [PubMed] [Google Scholar]
- Yonelinas AP, Hopfinger JB, Buonocore MH, Kroll NA, Baynes KK. Hippocampal, parahippocampal and occipital–temporal contributions to associative and item recognition memory: An fMRI study. Neuroreport: For Rapid Communication of Neuroscience Research. 2001;12:359–363. doi: 10.1097/00001756-200102120-00035. http://dx.doi.org/10.1097/00001756-200102120-00035. [DOI] [PubMed] [Google Scholar]
- Yonelinas AP, Parks CM. Receiver operating characteristics (ROCs) in recognition memory: A review. Psychological Bulletin. 2007;133:800–832. doi: 10.1037/0033-2909.133.5.800. http://dx.doi.org/10.1037/0033-2909.133.5.800. [DOI] [PubMed] [Google Scholar]