Modular modelling with Physiome standards

Abstract

Key points

• The complexity of computational models is increasing, supported by research in modelling tools and frameworks. But relatively little thought has gone into design principles for complex models.

• We propose a set of design principles for complex model construction with the Physiome standard modelling protocol CellML.

• By following the principles, models are generated that are extensible and are themselves suitable for reuse in larger models of increasing complexity.

• We illustrate these principles with examples including an architectural prototype linking, for the first time, electrophysiology, thermodynamically compliant metabolism, signal transduction, gene regulation and synthetic biology.

• The design principles complement other Physiome research projects, facilitating the application of virtual experiment protocols and model analysis techniques to assist the modelling community in creating libraries of composable, characterised and simulatable quantitative descriptions of physiology.

Abstract

The ability to produce and customise complex computational models has great potential to have a positive impact on human health. As the field develops towards whole‐cell models and linking such models in multi‐scale frameworks to encompass tissue, organ, or organism levels, reuse of previous modelling efforts will become increasingly necessary. Any modelling group wishing to reuse existing computational models as modules for their own work faces many challenges in the context of construction, storage, retrieval, documentation and analysis of such modules. Physiome standards, frameworks and tools seek to address several of these challenges, especially for models expressed in the modular protocol CellML. Aside from providing a general ability to produce modules, there has been relatively little research work on architectural principles of CellML models that will enable reuse at larger scales. To complement and support the existing tools and frameworks, we develop a set of principles to address this consideration. The principles are illustrated with examples that couple electrophysiology, signalling, metabolism, gene regulation and synthetic biology, together forming an architectural prototype for whole‐cell modelling (including human intervention) in CellML. Such models illustrate how testable units of quantitative biophysical simulation can be constructed. Finally, future relationships between modular models so constructed and Physiome frameworks and tools are discussed, with particular reference to how such frameworks and tools can in turn be extended to complement and gain more benefit from the results of applying the principles.

Key points

• The complexity of computational models is increasing, supported by research in modelling tools and frameworks. But relatively little thought has gone into design principles for complex models.

• We propose a set of design principles for complex model construction with the Physiome standard modelling protocol CellML.

• By following the principles, models are generated that are extensible and are themselves suitable for reuse in larger models of increasing complexity.

• We illustrate these principles with examples including an architectural prototype linking, for the first time, electrophysiology, thermodynamically compliant metabolism, signal transduction, gene regulation and synthetic biology.

• The design principles complement other Physiome research projects, facilitating the application of virtual experiment protocols and model analysis techniques to assist the modelling community in creating libraries of composable, characterised and simulatable quantitative descriptions of physiology.

Abbreviations

ATP

adenosine triphosphate

GFP

green fluorescent protein

IP3

inositol trisphosphate

NFAT

nuclear factor of activated T‐cells

ODE

ordinary differential equation

PMR

Physiome Model Repository

SBML

Systems Biology Markup Language

SED‐ML

Simulation Experiment Description Markup Language

Introduction

The complexity demanded of computational models is increasing, both in terms of the detail required at a given spatial or temporal scale, and in terms of the number of scales to be considered. Recent initiatives focus on describing and exploring large numbers of connected processes such as interacting pathways (Büchel et al. 2013). Models that address whole‐cell level complexity, a goal of Systems Biology for some time (Snoep et al. 2006), are now being constructed (Karr et al. 2012).

With the increase in complexity comes difficulties in communicating the meaning of model components, maintaining such models in the light of new biophysical information, and extending them to deal with new physiological scenarios of interest. Reuse of existing models, particularly in combination with other models to form mathematical descriptions that simulate more complex and realistic biophysical situations, will in the near future become less of ‘an advantage’ and more of ‘a necessity’.

Over the last decade, the associated sub‐field of model representation has developed. Community standards such as CellML (Cuellar et al. 2003) and the Systems Biology Markup Language (SBML) (Hucka et al. 2003) have addressed some of the issues in model communication by virtue of their functions as XML‐based model exchange protocols. Such declarative protocols focus on the mathematical representation of entities of interest and the relationships between them. In contrast to procedural approaches such as object‐oriented programming, they separate the solver from the model, thereby allowing flexibility in model simulation; this is important as large‐scale models are constructed from many smaller‐scale efforts. CellML in particular is used in cellular and physiological modelling and allows modular construction of models via component instances and encapsulation hierarchies, and is accepted by many journals as a community standard.

Despite this work, a modeller who today wishes to construct a complex model in an efficient fashion still faces several challenges. Ideally, their model could be composed of modules from existing models, with perhaps a few additional modules as required. They will, therefore, want some way of finding existing models that cover their own area of interest, and be apprised of, or at least have access to information to readily discern, what physiological conditions the models do and do not cater for. The larger model will need to be assembled from different modules, so the modules will need to be connectable in some fashion, and making those connections should be computer‐assisted and automated as much as possible. The modeller must ensure that the final model behaves appropriately enough to facilitate investigation of the research question at hand, so ideally it would be easy to test input–output responses for the module components, either separately or in concert, to both confirm model development directions and aid ‘debugging’. The behaviour of the resulting model should also be readily presentable to facilitate validation, and ultimately the validation process should itself be automated where possible. Finally, the resulting model should be able to be treated, in future model building efforts, as a reusable module itself, with information about the assumptions and physiological coverage of the model readily discernable by future re‐users. While not all of these goals are achievable today, a number of research projects have led to the development of tools and frameworks to begin to address these challenges.

A key enabler is the Physiome Model Repository (PMR; models.physiomeproject.org; see Yu et al. 2011) which provides an online centre for groups of researchers to develop models, either publicly or privately, with full provenance information (Miller et al. 2011). Model versions can be ‘released’ via public ‘exposures’, and may contain links to other models within the repository. These links provide a dynamic mechanism for reuse of models from the community of modellers during the composition of new models.

The ApiNATOMY framework (de Bono et al. 2012) uses links between model elements and ontologies to provide efficient and accurate model search and retrieval in order to facilitate reuse. In addition, it is also possible to automate the sending of retrieved models to a numerical simulator so that the modeller can discover not simply what models are available but what quantitative behaviour is available (de Bono et al. 2015).

The Cardiac Electrophysiology Web Lab initiative (Cooper et al. 2016) provides an automated method for simulating models according to well‐defined protocols (each being a ‘virtual experiment’) and testing the behaviour of the models against defined expected behaviour – in a similar manner to automated unit‐testing frameworks for software development. Where the protocols represent some real‐world experimental conditions, with care this system can also be used to identify whether a given model behaves ‘properly’ in a physiological sense. Thus, after some initial setup, violation or compliance of assumptions can largely be checked automatically.

OpenCOR (Garny & Hunter, 2015) is a desktop‐based software package that allows a modeller to construct, simulate and interact with CellML models. The focus here is on the user experience and providing a usable gateway to the various frameworks and protocols. Via an extensible system of plugins, it is also capable of providing an interface for interacting with PMR and virtual experimental protocols (such as the Simulation Experiment Description Markup Language (SED‐ML), as discussed below) and for linking model elements to ontologies by providing an interface for annotation with metadata.

SemGen (Neal et al. 2015) provides an interface to the SemSim framework that enables more complex annotations to be made. SemGen allows the modeller to use this metadata for visual module definition and combination where module interfaces are defined dynamically, guided by the modeller and biological and physical information encompassed in metadata provided by OpenCOR or SemGen (Neal et al. 2014).

Underpinning these tools is a set of standards that allow the various software components to interoperate and to help ensure clarity about what model components represent. The CellML Metadata Framework (Cooling & Hunter, 2015) connects model components with biophysical concepts such as proteins and metabolites, cellular components, and anatomical features. SED‐ML is used to clearly define virtual experiments, including which models to simulate, simulation parameters, and which model results are of particular interest and can be considered ‘output’ (Waltemath et al. 2011).

These standards provide the connections between models and tools and ontologies, but what of the models themselves? We observe that, beyond providing a general composition framework, comparatively little thought has been given thus far to the structural design of models within those frameworks. Many models found in journals are monolithic and not designed with reuse in mind. Others are modular within their own contexts but require refactoring to reuse. As in wider engineering or construction, as construct size and complexity increases, design principles will be necessary to ensure a consistent, understandable and extensible aggregation of concepts in encoded mathematical models. Such principles would be applicable to modelling in general but particularly relevant to cardiac models which have reached a level of sophistication and complexity that justifies careful thinking about the design principles used and model formulation.

For example, the CellML protocol embodies a number of concepts for model representation that a modeller is free to choose from. This freedom can stimulate innovation but can also result in models that require modifications to integrate. CellML has a proven track record in multi‐scale simulations (Nickerson, 2006), and integrated physiology modelling (Beard et al. 2012). Models have been published in the domains of cellular electrophysiology (Nickerson et al. 2008), signal transduction (Cooling et al. 2007), metabolism (Wimalaratne et al. 2009), cell contraction (Terkildsen et al. 2008) and synthetic biology (Cooling et al. 2010). Although these models are in some sense mathematically compatible, and were all architected with extension and reuse in mind, the style of model structure differs between them. There was no clear set of CellML design principles that would lead to modellers being able to easily recombine models from all the domains without significant refactoring. In order to construct larger models, such as whole‐cell models and models that allow investigation of the physiological context of the cell, it is necessary to restructure some or all of them according to some set of common CellML design principles. What should these principles be? How can we structure our models to facilitate reuse in complicated contexts?

Here we develop a set of design principles that yield models that are more easily reused and extended in order to support complex, more physiologically relevant model development. Example models are constructed from these principles. The first example provides a relatively simple illustration in an intracellular signalling context. The second example provides a more complex illustration linking one example from each of several different subdomains including electrophysiology, thermodynamically sensitive metabolism, signal transduction, gene regulation and synthetic biology. This second example is an architectural prototype for an approach towards whole‐cell modelling [albeit limited to compartmentalised ordinary differential equation (ODE)‐based formulations], as it covers a ‘core set’ of domains for whole‐cell modelling with genetic human intervention, and is also used to demonstrate some of the practical considerations in providing harnesses for model testing and characterisation.

All models and components are available in the online collaborative repository for computational physiological models: the Physiome Repository (http://models.physiomeproject.org), providing a publicly extensible library of modelling modules across multiple domains to facilitate complex cellular model construction.

Design principles for modularity in CellML

There are some similarities between mathematical models and software. Both are encoded into sets of character strings, representing relationships and/or processes. Some have commented that model composition challenges are equivalent to those in software composability (Bartholet et al. 2004). As the software field matured, concerns such as those outlined above were met by giving careful thought to the design and structure of code and languages. Inspired by this, and informed by our collective experience in modelling scenarios in the domains above, we here propose a set of modelling design principles to guide reusable and extensible model development.

Our design principles can be grouped into three categories: those dealing with the structuring of mathematics into modules; those dealing with specifying interfaces between those modules; and those dealing with the definition of units and ‘data’ for the modules – specifically model parameters and initial conditions. Each category will be explained in turn. These principles can be applied fruitfully in any order and combination to new model construction, or to the wrapping or refactoring of legacy monolithic models to enhance model extension.

Module structures

Many models have constructs that are repetitions of the same biophysics represented with the same mathematical formulation but with different parameters. For example, consider a simple reaction where two reactants D and E combine to form F (and the stoichiometry of all reactants and products is 1). If another reaction in the model similarly combines G and H to form I, then both of these reactions will use the same mathematical formulation, more generally as J = a × b × kf, where J represents the flux of the reactions (in, for example, microlitres per second), kf is a rate constant, and a and b are reactant concentrations. This commonality suggests the opportunity for reuse. In the field of software engineering, it has been found that modularisation on the basis of design decision is fruitful, rather than on the basis of mere function or process sequence which might at first seem more natural (Parnas, 1972). How to represent common biophysical processes mathematically is the modeller's design decision here. This decision may in many cases only need to be made once for many instances of the same biophysics. But, this principle is not limited to representations of biophysics. Thus, while we will also consider modularisation by function below, these considerations lead us to our first principle: (1) common mathematics should be abstracted into separate modules and reused wherever possible.

It is natural to group biological processes and entities into functional modules. One of the guiding principles of good modules is that they exhibit high cohesion (Stevens et al. 1974), that is, they have a well‐defined set of responsibilities that are strongly related, and all responsibilities of that kind in the larger system reside in that module. One of the strongest forms of cohesion is ‘functional cohesion’ which in software engineering can be considered in terms of deriving output data from input data in a particular way. In a computational biology model, we propose that this could be considered in terms of outputs based on biological processes. For example: a single reaction component may be considered as transforming concentrations of reactants and rate constants into fluxes of products. A ‘calcium handing’ component may derive a calcium flux or transient based on various inputs such as channel shear stresses, voltage changes, stored calcium levels, etc. Some of the elements of a functional module may be functional modules in their own right, e.g. some lower‐level biological process such as a particular channel, or a calcium store. Such modules could conceivably be reused in different ways, depending on how the larger‐scale components are partitioned. Rather than building large, tightly cohesive structures, as is common in monolithic model construction, we propose constructing larger functional modules from smaller modules in a nested fashion, in what may be termed a composition hierarchy. Simply put: (2) build large, cohesive functional modules from smaller, cohesive functional modules. Ideally, the smallest cohesive modules (at the leaves of the compositional hierarchy) would be at the level of individual species and ‘atomic processes’ (such as a particular reaction). However, if one is refactoring an existing module that contains a ‘lumped parameter’ formalism, practically speaking it may not be easy or even possible to arrive at quite that level of detail.

High cohesion of modules tends to be accompanied by low coupling – a reduction in the number and kind of connections between modules. While connections between mathematical modules may not be undesirable per se, care should be taken that such connections do not reflect assumptions that one module makes about the inner workings of another. In this we reflect, and have surely been forewarned by, the citing of similar concerns during the beginnings of software engineering (Parnas, 1971). It is sometimes tempting, if the modeller knows that a module needs to communicate with another, to embed target module‐specific mechanisms in the source or target module. In our experience, the most common scenario is where several modules need to communicate in order to produce some result, for example in the production of a sum of fluxes of a second messenger which has many possible sources and sinks. We can avoid other‐module‐specific mechanisms by ensuring that, instead of attempting to encode the connection in one of a set of components, we (3) form separate modules to handle multi‐module communication.

Module interfaces

Consideration of highly cohesive, loosely coupled modules leads naturally to the concept of ‘information hiding’ where the inner workings of a module are simply not accessible to other modules. When done well, this ‘separation of concerns’ (Dijkstra, 1982) allows parts of a model to be reformulated without affecting other parts. But it is possible to hide information that could become important if the module were used in other contexts. It is helpful to distinguish between design decisions of a mathematical nature (which probably can be hidden), and information of a biological nature (such as the concentration of a particular metabolite, or density of a receptor on a membrane). In the latter case, it is often difficult to be certain that that information would not be useful elsewhere in the wider model – new relationships between biological entities are uncovered as scientific research continues, and the scope of encompassing models may change over time. Hiding that kind of information may lead to the module having to be redesigned later, or, in the worst case, a larger model may unwittingly include the same biological entity more than once. For these reasons we propose that modellers (4) expose information relating to the amounts and rates of change of biological entities.

Mathematical modelling languages may allow, or even demand, the definition of units for parameters and variables. In such cases, it is common for modules that have been created by different researchers and/or for different purposes to expose parameters or variables that one would wish to connect, at different scales or in different units (that may or may not be dimensionally consistent with one another). A conversion may be necessary, and a decision may need to be made on where to do the conversion. Rather than selecting one module or the other, and thus coupling them to the conversion, we instead advocate that modellers (5) use separate modules to perform unit conversions. This could be considered somewhat analogous to the ‘Adaptor Pattern’ in software engineering (Gamma et al. 1994).

Module units and data

Models typically require many parameters and initial conditions, each set of which may be specific to a virtual biological scenario or experiment. Coupling these ‘data’ tightly with the mathematical modules that utilise them may make it difficult for these data to be changed without unintended side‐effects, and may lock the modules into describing one particular scenario. These undesirable effects can be reduced by ensuring that we (6) separate all parameter and initial condition definitions from the mathematical modules and place them in their own dedicated modules. This parallels the notion of ‘data independence’ developed for ‘Structured Modeling’ of decision support systems (Geoffrion, 1991), especially if one considers a complex mathematical model to be a system for decision support, be it decisions on what scientific hypothesis to adopt or what set of real experiments to plan next, with multiple simulations as ‘what‐if’ analyses on how the biology may be functioning. Following this principle makes it easier to find and alter parameter values when refining virtual experimental conditions. It also facilitates the potential replacement of parameter values with additional modules should, for example, a constant need to be replaced with a variable governed by some new process.

For protocols that allow the definition of new units, the question of where, in a large model, to define them arises. In Principle (2) we advocated a composition hierarchy where leaf nodes are, ideally, individual biological entities and processes. Since such leaf nodes should be able to be recombined into different higher‐level compositions, it seems logical that units should be defined at the simplest level of module in which they are used, thus keeping the simpler modules cohesive with respect to their units. Unit definitions themselves represent a design decision, and as such could be considered a module in their own right. Hence if the modelling language allows it, we propose that modellers (7) define units at the lowest level of the composition hierarchy possible.

Some unit and parameter or initial condition definitions may be common across many models; units may be defined according to the SI system of units and some parameters may in fact be universal constants. In both cases it seems helpful to define these once and promote consistency amongst models and modules within models by advocating that modellers (8) use standard unit and universal constant modules where possible.

Summary of the design principles

For ease of reference, the set of design principles is reproduced below, in the order to be discussed.

1. Common mathematics should be abstracted into separate modules and reused wherever possible.

2. Build large, cohesive functional modules from smaller, cohesive functional modules.

3. Form separate modules to handle multi‐module communication.

4. Expose information relating to the amounts and rates of change of biological entities.

5. Use separate modules to perform unit conversions.

6. Separate all parameter and initial condition definitions from the mathematical modules and place them in their own dedicated modules.

7. Define units at the lowest level of the composition hierarchy possible.

8. Use standard unit and universal constant modules where possible.

Examples

This section describes two example models formulated from model modules that were constructed using the principles. The first is a relatively simple example model in a signalling context by which the application of the principles can be described. The second example, which reuses parts from the first example, shows how the principles can be used to define an architectural prototype for whole‐cell modelling. This ‘Core Domains’ example provides more advanced examples of reuse that following the design principles facilitates.

Signalling model example

We apply the principles to the construction of a signal transduction model. This endothelial cell model combines the shear‐stress sensitive channels of Kang et al. (2007) with the calcium handling of Plank et al. (2006) to form a model for calcium dynamics on shear‐stress from blood flow, as shown in Fig. 1.

Figure 1. Biological schematic diagram of the Signalling Model Example .

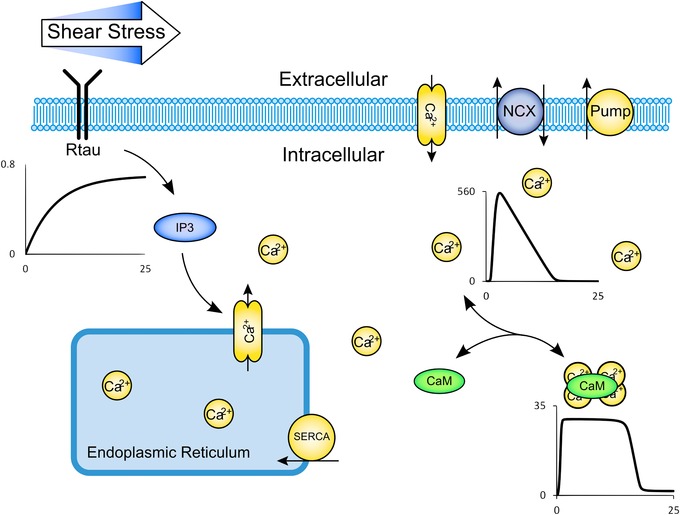
Shear stress sensed by receptors (Rtau) leads to IP₃ production and store calcium release. Calcium is also transferred between the extra‐ and intracellular compartments via stress‐sensitive calcium channels, calcium/sodium exchanger, a calcium pump, a basal calcium leak and capacitative calcium entry. Calcium leads to activation of calmodulin (CaM). Representative traces of Rtau, free intracellular calcium, and activated calmodulin over a 25 s simulated time period are shown (please see the Supporting information for more details on the traces).

The model can be simulated in OpenCOR (all example models and their components are available online; please see the Supporting information for more details on retrieving and simulating the models). Please note that while these are quantitative models, the actual parameter values and scales of the output are not particularly important here; our contribution lies in how such models can be structured and composed. Broad qualitative behaviour is shown in order to illustrate how some of the different kinds of models may be composed, but this work is not concerned with parameter, variable or output value accuracy per se in this or in further models considered here.

Model modules are implemented as CellML components, which encompass module variables and, optionally, mathematics. Components for a model can be distributed among multiple files and copies of components from other files can be made in‐memory using what is known as a CellML import (more details can be found in Cuellar et al. 2003). The import feature is used to implement Principle (1) (abstraction of common mathematics), as reusable mathematics can be defined once and then copies made for each required use of those mathematics, as shown in Fig. 2.

Figure 2. Common template components being imported to form biological entities (A) and processes (B) .

Squares are CellML components, and arrows show the direction of the import: for example, ‘Ca_if’ is an imported instance of ‘Template_Species_uM’. Ca_if and Ca_st are free and store calcium respectively, ‘CaM’ is calmodulin, and the ‘_star’ suffix denotes the activated version.

Principle (2) (a compositional hierarchy of modules) was followed by considering the natural division between larger scale processes related to shear‐stress, calcium‐handling and calmodulin activation. A schematic diagram of the component hierarchy is shown in Fig. 3.

Figure 3. The biological component hierarchy of the Signalling Example model .

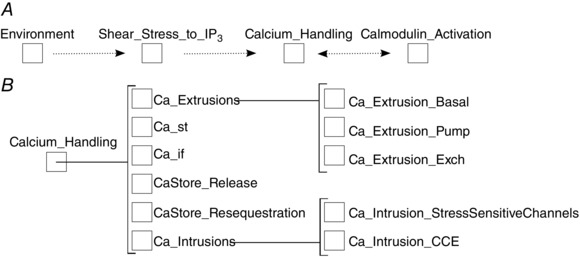
A, the top level of the hierarchy, with large cohesive modules (dotted lines indicate general flow of information; free intracellular calcium modulates both IP₃ generation and calmodulin activation). B, the nested nature (brackets indicate encapsulation relationships) of the Calcium_Handling module, which are constructed from smaller cohesive components representing sub‐modules. Similar sub‐hierarchies could be drawn for Shear_Stress_to_IP₃ and Calmodulin_Activation components.

Large scale processes are constructed from aggregations of finer‐grained components that represent particular biological entities or processes, implemented using CellML's group construct (Cuellar et al. 2003). Large scale processes could themselves be included in even larger models, as will be shown in a later example. Variables that are required inputs or outputs at lower levels become candidate input or output variables at higher levels – design decisions where achieving high cohesiveness and low coupling should, in general, be priorities.

Principle (3) (separate modules for multi‐module communication) is implemented as a separate component for each species that participates in more than one process. The aggregation of the resulting fluxes is handled in components with a ‘_delta’ suffix as shown in Fig. 4. As shown in that figure, it may also include multiplication by factors to account for different volumes between compartments. The output of this component is fed into components that would be interested in the net rate of change (via CellML connections; Cuellar et al. 2003), such as the component that implements the species of interest.

Figure 4. Variables of the ‘Ca_st_delta’ component, which handles multi‐module communication between Ca_st (store calcium) and other components, with respect to flux .

Arrows represent input or output on variables listed by name. The component includes ‘input’ variables for fluxes (positive or negative) from store resequestration and release processes, as well as any external processes (see the example models for more details). There is also a variable for converting between different volumes (in this case, cytoplasm/store). The net flux is component output, named ‘JNet’. The ‘Ca_st’ component will use ‘JNet’ to update the total amount of calcium in the store, across a given time interval.

Principle (4) (exposing entity information) is implemented by considering what entity amounts and rates of change exist in the model. These are then exposed in the interfaces of the higher level components that encompass them. The ‘Calcium_Handling’ component exposes ‘Ca_if’ and ‘J_Ca_if’ – the current intracellular calcium concentration and the rate of change of that species, respectively. Similar values are exposed for other entities. Those values can simply be ‘read’ via connections (from higher level components as will be shown in the example models) without having to understand the inner workings of the source component. For example, the ‘Calmodulin_Activation’ component uses the ‘Ca_if’ value from ‘Calcium_Handling’ as an input (the source of the dotted line between the two components in Fig. 3 A). A more subtle requirement is revealed by considering that the activation of calmodulin decreases the free intracellular calcium concentration, and this ‘drain’ on calcium should be reflected in the ‘Calcium_Handling’ component. Hence, in addition to exposing values to be read, the higher level components also provide input variables ‘J_<species>_External’ to represent fluxes contingent on a species from processes external to that component. In the case mentioned above, the flux of calmodulin activation is connected to a ‘J_Ca_if_External’ variable exposed by the ‘Calcium_Handling’ component (noted in Fig. 3 A by the bidirectional arrow), so that the free intracellular calcium flux summation can include it. Additional fluxes could be connected by summing them in a separate component first, then passing that component's output to the ‘_External’ variable. In general, each biological entity likely to be of interest should have exposed, in any component that encapsulates it, the current concentration and the current flux, and take as inputs both the initial value and a net flux from processes external to the immediate parent component or its immediate ancestors.

Additional components are also used to perform unit conversions (Principle (5)), necessary here as the amount of inositol trisphosphate (IP₃) in the system is handled differently between the Kang et al. and Planck et al. models. In the former it is a dimensionless construct, whereas the latter considers the IP₃ concentration. This is handled relatively simply by a component at the top level of the hierarchy, that performs a multiplication of the dimensionless value from the ‘Shear_Stress_to_IP₃’ component by a concentration scaling factor, before passing the result to the ‘Calcium_Handling’ component.

Each of the components requires parameters or initial conditions pertaining to the low‐level components that they encompass. Following Principle (6) (separation of initial conditions and parameters from mathematics), these sets are each housed in their own component which is then connected to the components representing those processes and entities, as shown in Fig. 5.

Figure 5. Parameters and initial conditions are placed in their own components, here for each high level biological component .

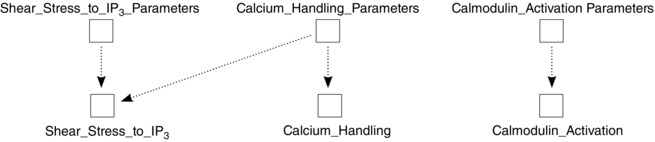
Each has their own parameter set, but the separation allows for parameters to come from other sources too. Shear_Stress_to_IP₃ can run using its own parameters; however, when linked with other modules (such as Calcium_Handling) it may be more appropriate for some parameters to come from that source instead. Following Principle (6) allows such ‘parameter collisions’ to be resolved by the model builder.

In CellML, units are housed in models that encompass the components we have mentioned, their units and connections between components at that level. Following Principle (7), units are defined not at the top level, but at the lowest level possible (see Fig. 6), ensuring that every level has the units that it needs to be well defined.

Figure 6. Units reuse .

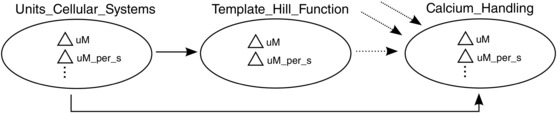
Units (triangles) are defined at the lowest level and imported into the models (circles) housing low‐level components so that those components can be reused in other models along with consistent and expected unit information (continuous arrows show unit import directions). Units for higher level modules (‘Calcium_Handling’, in this case) may be (dotted arrows) imported from lower levels or from other ‘child’ models. Additionally, following Principle (8), we include a ‘Units_’ model that houses standard units providing a library of such units for many models to use promoting inter‐model consistency. Higher level constructs can import all units directly from that common source, reducing coupling that the former strategy would incur.

Additionally, all unit definitions have been collected in a single file that serves as an evolving ‘standard library’ of units for intracellular models, thus implementing the unit‐related aspect of Principle (8).

Note that CellML allows some flexibility with respect to where models and components are stored on the file system. Here our discussion centred on how to organise components following the principles defined earlier, independently of where the components are stored on the file system. We do, however, note an inherent design trade‐off in having many files and thus being able to locate components easily, but also having then to work between perhaps a great many files at once, which may make enhancing and maintaining the models more difficult without a suitable tool.

Core domains example

Having devised the implementation of the principles in CellML, we now apply them to the construction of a more complex model with modules from multiple domains, in an effort to illustrate how structured whole‐cell modelling might occur. Our simplified model, the ‘Core Domains’ model, does not contain all the processes in a cell, rather it contains some processes from each of several domains that one might expect in a whole‐cell model, in order to demonstrate the architecture. More processes could be added in a similar fashion to achieve the desired level of cellular complexity.

This example, shown in Fig. 7, considers an electrically active cell with one ion channel (an L‐type calcium channel from Nickerson & Buist, 2008). The channel is sensitive to pH and adenosine triphosphate (ATP), hence is also sensitive to the myosin ATPase activity as implemented in the metabolic models of Vanlier et al. (2009). The resulting intracellular calcium flux signals calmodulin activation (reusing a high level component from the Signalling Example model) which in turn activates calcineurin and cycling of the transcription factor nuclear factor of activated T‐cells (NFAT) between nucleus and cytoplasm (model from Cooling et al. 2009). This transcription factor binds to a promoter of a variant of a green fluorescent protein (GFP)‐producing synthetic biology device (modified here to represent a eukaryotic system). The extensible nature of the components is used to our advantage by additionally attaching a stimulus current on the virtual plasma membrane, to depolarise the cell leading to a calcium signal and subsequent increase in GFP signal (Fig. 7). In order to readily demonstrate time courses showing key activities, several rate constants were scaled in this example. The model can be run in OpenCOR (please see the online Supporting information for more details).

Figure 7. Biological schematic diagram of the Core Domains model .

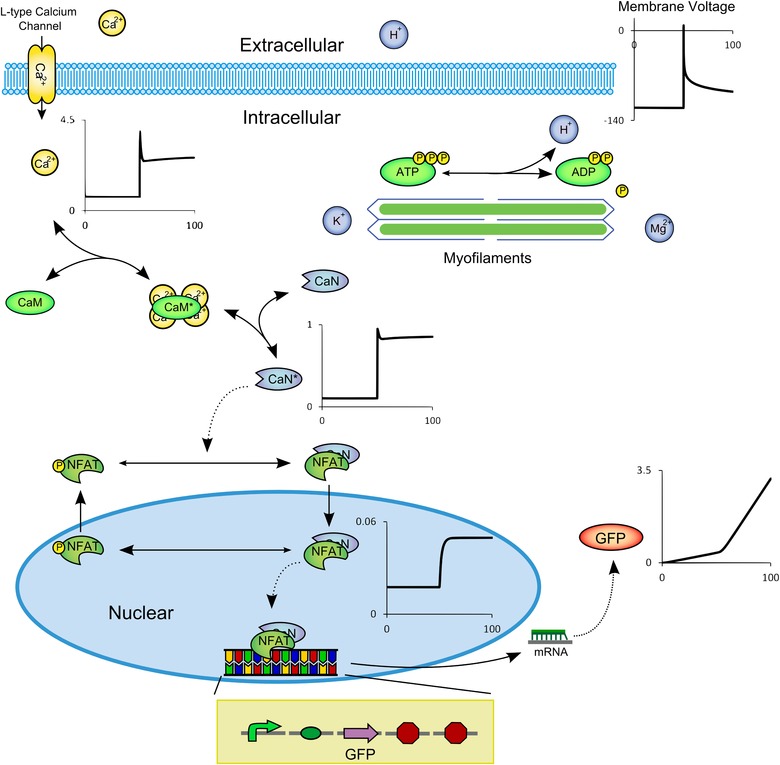
The membrane is depolarised at t = 50s (voltage trace shown, scale is mV), resulting in calcium influx (trace shown in μm) through L‐type calcium channels (electrophysiology). The channels are sensitive to pH and [ATP], both of which are influenced by myosin ATPase reaction (metabolism). Calcium activates calmodulin and calcineurin (trace of ratio of active calcineurin–calmodulin complex shown), leading to NFAT cycling (signalling). NFAT (trace shown in nm) is a transcription factor for a sample ‘device’ (gene regulation and synthetic biology) resulting in mRNA production that is translated outside the nucleus to form a GFP signal (trace shown in nm), which increases as the membrane is depolarised. Please see the Supporting information for more details.

Exploiting Principle (2), it is possible to structure the large composite models so that they can be run and simulated by themselves without modification, as well as being connected to a larger model. That is, it is possible to define a model composed of the ‘main’ component and some parameter and time components, and also define a larger model that connects different parameters (and perhaps uses outputs from other components for those parameters). An example of this is shown in Fig. 8 A. The former model can be thought of as a ‘test harness’ for the ‘main’ component, allowing an exploration and debugging if necessary of that model with different parameters, before attempting to simulate the complete model.

Figure 8. Simultaneous model reuse and characterisation .

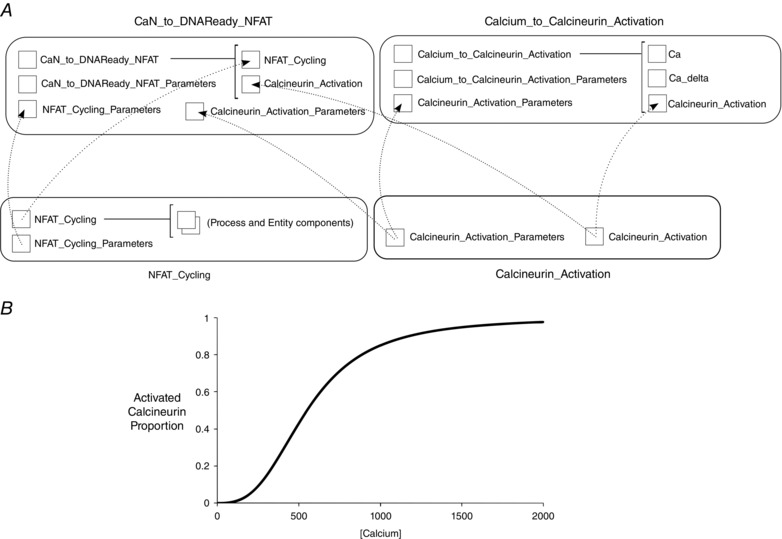
A, model aggregation and re‐parameterisation. Here all models (rounded boxes) are complete and simulatable in their own rights. Components (squares) imported (dotted arrows) from ‘NFAT_Cycling’ and ‘Calcineurin_Activation’ form part of the higher level model ‘CaN_to_DNAReady_NFAT’, which includes parameter components related to the child components by default, but could equally source parameter values from other components. ‘Calcium_to_Calcineurin_Activation’ model imports the ‘Calcineurin_Activation components’, but also includes a calcium species whose concentration varies over time, hence replaces the constant calcium concentration parameter with the output of the ‘Ca’ component. B, output of the ’Calcium_to_Calcineurin’ model. The trace of activated calcineurin proportion for increasing calcium concentration is shown (calcineurin and calmodulin concentrations are fixed in that model).

We extend this to a more complex test harness. We have included a ‘Calcium_to_Calcineurin_Activation’ model that incorporates both the ‘Calcineurin_Activation’ component (used in the Core Domains model) and a separate implementation of intracellular calcium, which is set to increase steadily over time. When this model is run, it effectively tests the calcineurin activation component, generating a characterising sigmoidal activation curve (Fig. 8 B). This is useful for testing the dynamic range of the model with a given set of parameters, independently from any larger model, aiding parameterisation and debugging.

This example of a complex harness also illustrates how Principle (2) helps to resolve conflicts between two models. Both the Core Domains model and the described test harness implement intracellular calcium. If a biological entity or process is implemented in both models as a constant parameter value, then it is simply a matter of choosing which parameter to use from the two possibilities (facilitated by Principle (6)). If, as in this case, the processes and entities are implemented as components, then only one component for each conflicting element can be chosen. Principle (2) means that sub‐components of the components of interest can be separated out, and desired components connected together, allowing conflict resolution.

Principle (4) is more completely implemented in this model such that the top level model is provided an interface similar to its children. All the children's input and output variables are similarly exposed at the next level up, unless a sibling component provides or exclusively consumes that information. The notion of time and the parameters and initial conditions are always exposed as inputs to be provided by higher level modules. This means that not only can a module be run or tested by itself, but this entire Core Domains model can be incorporated into a future larger model (including, for example, extracellular detail, other cells or tissue‐level effects) in exactly the same way as its children have been incorporated into it.

Universal constants are separated from the mathematics (Principle (8)), in the ‘mohr_taylor_newell_2008_subset’ model, using values derived from Mohr et al. (2008).

When building components from scratch, it is easy to apply the principles from the beginning. However, some advantages can still be gained from legacy models by applying only some of the principles to wrap existing structures. The Core Domains example imports the L‐type calcium channel model from Nickerson & Buist (2008) largely unchanged. The processes in the metabolic model (from Vanlier et al. 2009) are also partly retained in their original monolithic form. However, in both cases care has been taken here to wrap the components in the interfaces appropriate for implementing Principles (4) and (6), demonstrating that they can take advantage of the modular architecture of the larger model and be thus usefully included. Principle (8) was also followed with units being imported from our evolving standard units file. These principles are relatively easy to apply to existing modules to facilitate composability of higher level models without necessarily having to re‐factor all the processes as Principle (2) would require. This could also be a useful strategy if the advantages of following Principle (2) were not needed in a particular situation. For example, if there are no common species or processes that change over time between one model and any foreseeable model that connects to or encompasses it, then the ability to resolve such a collision by importing only non‐overlapping components would not be needed.

Finally note that while parameter and initial conditions are separated from the rest of the model (Principle (6)), their source is flexible and not necessarily centralised. For example, the synthetic biology modules are designed to be transferred with embedded parameters, and the ‘ExampleDevice’ component maintains this custom: if run by itself it uses the embedded parameters from its children. By contrast, the Core Domains model defines all parameters centrally and passes them down to its children, including ‘ExampleDevice’. Either, or combinations of the two, are valid options made possible by following the principles.

Discussion

The scope and complexity demanded of mathematical models increases as the field moves towards whole‐cell, multi‐scale and clinically relevant modelling. Therefore, the ability to design model structures such that their compositional utility is increased will become more important. Modelling work that follows the principles described here will therefore have a greater chance of directly contributing to new discoveries as the biological modelling field increases in scope.

Following the principles, CellML models are structured in a considered, coherent fashion, aiding the understandability and communicability of the models (once the design is understood). This, and the separation of parameters from the mathematics of the model, provides a high level of maintainability as cohesive modules – whether they represent low‐level mathematical constructs, simple biological constructs, or complex biological scenarios – can be readily found and considered in isolation. Additionally, parameters can be changed without having to alter the modules themselves. The model design also provides reuse without modification, as shown in our examples by the calmodulin activation module. Importantly, the design greatly increases extensibility; models can be subsumed into other or larger models without modification, even (if desired) while they continue to be part of still other models.

We validated the principles’ utility in a series of example models, culminating in the successful composition of a model covering several key intracellular domains central to whole‐cell modelling. While the principles are important in this work, rather than the model per se, that example is, to our knowledge, also the first model to incorporate all of these cellular domains together, reflecting the utility of the principles.

Elements of the principles can be found in earlier work. For example, Principles (1) and (7) unify approaches advocated in Cooling et al. (2007), Nickerson & Buist (2008) and Wimalaratne et al. (2009). Cooling et al. (2007) also advocated an early, CellML‐specific version of Principle (3), and Terkildsen et al. (2008) noted the importance of what we have developed into Principle (5). Elements of some of the principles are perhaps used by modelling groups already. Here we present principles that are coherent as a set, together with detailed examples, to enable better reuse and extension of models from different domains.

While the most gain is in following all the principles, trade‐offs in resulting code complexity (due to fine granularity and interface construction) against extensibility and clarity must be weighed by the modeller. A model of small scope that is to be put together quickly to explore some idea, or constructed as a learning exercise, and crucially is not intended to be significantly built upon or shared, may, if all the principles were followed, accrue too great an ‘overhead cost’ for the extra effort and structure to be worthwhile. We demonstrate that even partial application of the principles can yield gains, in particular in wrapping existing models that are differently structured. Complete refactoring can be an iterative process to be conducted if required, given the modelling situation at hand. There are also trade‐offs with the set of principles. For example, in Principle (4), there is a potential tension between reducing coupling and designing larger module–module interfaces. If one wishes to reduce the coupling that this principle promotes, a viable compromise may be to connect a second, removable component which presents a reduced interface to other components rather than the full interface of the original component – somewhat analogous to the ‘Façade Pattern’ known in object‐oriented software design (Gamma et al. 1994). The principles are named as such as we hope to facilitate thought rather than replace it.

While we are concerned with CellML in this work, commonalities and differences between these principles and those possible in other modelling paradigms would be an interesting area of research. This includes protocols that are semantically close to CellML (such as SBML) and those that share a more distant common ancestor, such as object oriented programming.

Models of physiology are concerned with biophysical mechanisms and quantification of behaviour. CellML is a powerful modelling protocol for representing such models. Our principles greatly facilitate the potential for CellML models to have a longer life cycle than one or two modelling studies. For example, the response of cells to external signals, and the feedback from those cells to the wider physiological environment, can be modelled in greater detail by the careful construction of smaller models which are later combined to yield more detailed representations of the workings of a cell. While CellML has been used to provide a library of components in Synthetic Biology (Cooling et al. 2010), libraries of CellML components for the various domains needed by systems of physiological complexity that interoperate without modification have not been constructed. In part, this is because a coherent set of design principles that covers all domains did not exist. Hierarchies of small, cohesive, loosely coupled modules allow the iterative and partitioned development of cellular physiology models and their validation. As more biophysical details emerge from physiological research, ‘swapping out’ older modules for modules embodying new knowledge will be facilitated. Separation of the data from the model allows easier application of models to new physiological scenarios. Models that can be recombined without modification and do not have to be partially recoded for new questions of interest will, as a resource, facilitate the reuse of physiological studies at the model level.

Realising the full potential of the principles will depend on the interaction of the resulting models with Physiome tools, frameworks, and standards. PMR already has facility for linking ‘workspaces’ together so that enhancements to a component model can influence higher level models if desired. This functionality has already been demonstrated in previous work (Cooling et al. 2010) and, as in that work, components from the Core Domains Model provide the seed of an extensible CellML module library, available to the international modelling community.

Retrieving the modules from PMR via ApiNATOMY would rely on thorough annotation of the modules with links to appropriate anatomical and biophysical concepts. While that is not the focus of this work, many of the required elements exist, as briefly described in the Introduction. Development of a standard annotation process to complement the standard metadata framework is a current research project.

The principles do not directly address the content of the models. It is possible to completely follow the principles and still connect models together that do not make good sense. Unresolved duplications of entities or processes, missing processes, or not updating the notions of species or processes based on new additions are all still entirely possible. In the Core Domains model, for example, if more electrophysiological modules are added that impact potassium ions, their impact on the potassium ion species in the metabolic model, and vice versa, must be considered. The principles make it easier to address these modelling considerations, but the fact that they may exist in a particular model is still up to the model builder to realise. Appropriate tagging of components with metadata and automated model ‘sanity checking’ will help. The enhancement of model generation tools, whether metadata‐driven or not, such that the resulting models follow the design principles above, is likely to be of great practical benefit to the builders of complex models. Annotation will also facilitate the modules’ inclusion in SED‐ML‐defined experimental protocols.

As the number of reusable model modules grows, tools such as the Cardiac Electrophysiology Web Lab will become valuable in both testing the assumptions and behaviour of the modules, and checking that the relevant assumptions hold when the modules are composed with others. Characterisation of modules’ behaviour would be valuable to modellers searching for components to reuse, and future work to determine how best to define and present these characterisations is likely to be beneficial to the modelling community. Extending the information available on a given module to include sensitivity analysis will also benefit both search and model composition.

Separation of the model parameters from the mathematical relationships provides clear entry points for parameter modification by virtual experiment protocols. It will similarly facilitate parameter modification from tools and platforms that use clinical information to constrain and contextualise mathematical models (Nickerson et al. 2016).

Tools such as SemGen may generate CellML models from user directives at the biophysical level, or from semantically driven model composition. Another development that may assist with composition is the recent application of bond graphs to intracellular modelling (Gawthrop et al. 2015). This provides a method for sketching the main players in a system and the effort or flows between them, and generating mathematical models that are automatically appropriately constrained by, for example, mass, charge, or Gibbs free energy. This will provide implicit biophysical constraints on signalling, metabolic, electrophysiological and other models. Future developments may include the generation of CellML code from such models. Whether models are crafted by hand or generated algorithmically, as in the above two examples, following the principles described above will help ensure that they are maintainable as testable modules that can be directly reused in the composition of simulatable quantitative descriptions of larger systems.

Additional information

Competing interests

None declared.

Author contributions

M.T.C. conceived the work, led the discussions that developed the principles, developed the example models, and drafted the manuscript. D.P.N. contributed to the development of the principles and the example models, and revised the manuscript. P.M.F.N. motivated a preliminary study, contributed to the development of the principles, and revised the manuscript. P.J.H. conceived the work and revised the manuscript. All authors have approved the final version of the manuscript, agree to be accountable for all aspects of the work, and qualify for authorship. All those who qualify for authorship are listed.

Funding

Portions of this work were supported by a Marsden Fast‐Start Grant from the Royal Society of New Zealand UOA1007 to M.T.C. M.T.C. was also supported by the Maurice Wilkins Centre for Molecular Biodiscovery and the Aotearoa Foundation. D.P.N. was supported by the Maurice Wilkins Centre for Molecular Biodiscovery and the Virtual Physiological Rat Project, NIH grant P50‐GM094503. P.J.H. was supported by a Marsden Grant from the Royal Society of New Zealand UOA1205.

Supporting information

Disclaimer: Supplementary materials have been peer‐reviewed but not copyedited.

Supporting material S1. Guidance on how to obtain the example models and simulate them in OpenCOR.

Supporting material S2. Signalling Example: simulation output (plotted in Fig. 1). Full modelling details of the input and output for the traces shown in the Signalling Example.

Supporting material S3. Core Domains Example: simulation output (plotted in Fig. 7). Full modelling details of the input and output for the traces shown in the Core Domains Example.