Networks of conforming or nonconforming individuals tend to reach satisfactory decisions

Significance

Many real-life decisions where one out of two actions must be chosen can be modeled on networks consisting of individuals who are either coordinating, that is, take an action only if sufficient neighbors are also doing so, or anticoordinating, that is, take an action only if too many neighbors are doing the opposite. It is not yet known whether such networks tend to reach a state where every individual is satisfied with his decision. We show that indeed any network of coordinating, and any network of anticoordinating individuals always reaches a satisfactory state, regardless of how they are connected, how different their preferences are, and how many simultaneous decisions are made over time.

Abstract

Binary decisions of agents coupled in networks can often be classified into two types: “coordination,” where an agent takes an action if enough neighbors are using that action, as in the spread of social norms, innovations, and viral epidemics, and “anticoordination,” where too many neighbors taking a particular action causes an agent to take the opposite action, as in traffic congestion, crowd dispersion, and division of labor. Both of these cases can be modeled using linear-threshold–based dynamics, and a fundamental question is whether the individuals in such networks are likely to reach decisions with which they are satisfied. We show that, in the coordination case, and perhaps more surprisingly, also in the anticoordination case, the agents will indeed always tend to reach satisfactory decisions, that is, the network will almost surely reach an equilibrium state. This holds for every network topology and every distribution of thresholds, for both asynchronous and partially synchronous decision-making updates. These results reveal that irregular network topology, population heterogeneity, and partial synchrony are not sufficient to cause cycles or nonconvergence in linear-threshold dynamics; rather, other factors such as imitation or the coexistence of coordinating and anticoordinating agents must play a role.

The sharing of resources, division of labor, and dispersion of crowds represent a few examples of collective behaviors that can emerge on networks of interacting agents when the adoption of a particular action by too many individuals deters others from adopting that action. On the other hand, when individuals’ taking an action makes it more likely that others will adopt that action, behaviors such as the spread of social norms, technological innovations, and viral infections can occur. In either case, various factors are thought to contribute to the emergence of such collective behaviors, including network topology, interaction payoffs, strategy update rules, and population diversity (1–3). In particular, when agents can take one of a finite number of states at a given time, whether by voluntary decisions or involuntary reactions, the fundamental questions include (i) whether the agents will eventually settle on a fixed state/action, (ii) which distribution of actions the network will converge to, and (iii) how long it will take for the network to converge. Although most of the literature focuses on the second and especially third questions, particularly for homogeneous populations where individuals share the same utility function (4–7), the first question is perhaps more fundamental because it deals with convergence at the agent level. Undoubtedly, this action settling is crucial to a wide range of decision-making populations, from collective nest selection by ants (8) to stabilization of financial markets (9). Moreover, without establishing such convergence, answers to questions ii and iii cannot be used to design policies at the local or neighborhood level (10), which may help to improve cost efficiency by targeting influential nodes in a complex network.

“Best-response dynamics” is one of the most widely used models to study the types of problems mentioned above; this is due in part to its rational nature as well as its broad applicability. Indeed, recent experimental studies have shown that humans often use myopic best responses when making decisions in social networks (11). The idea behind best-response dynamics is simple: in a network of interacting agents, each agent takes the action that results in the best cumulative outcome against its neighbors. This framework is frequently considered in a game-theoretic context (12–15), but its impact is further broadened by the fact that when there are two available actions for each agent, it is equivalent to a “linear-threshold model” (16). This comes with an alternative yet also intuitive interpretation: when a sufficient fraction of my neighbors are taking action A, I will also take action A. The reverse is also possible: if too many of my neighbors are taking action A, I will switch to action B. We call agents of the former type “coordinating” and the latter, “anticoordinating,” according to the standard coordination and anticoordination games, which are also sometimes referred to as games of strategic complements and strategic substitutes, respectively (17). These switches may be considered voluntary as in changing an opinion, preference, or habit, or involuntary, as getting infected by virus or defaulting on a loan. In general, the thresholds of the agents need not be the same, and this is equivalent to agents having asymmetric payoffs in the corresponding matrix game. Depending on the application, this can represent differences in the willingness to follow a crowd, susceptibility to infection, perceived value of interactions, and many other individual characteristics (18). Variation in thresholds can thus be thought of as heterogeneity of a population.

The linear-threshold model was first motivated and discussed by Mark Granovetter (18) in the context of fully connected networks, with an example of how the incitement of riots in crowds depends critically on the distribution of individual thresholds that will cause each person to join the riot. Since then, a rich literature has developed around questions related to stability and convergence of best-response dynamics in matrix games on well-mixed populations (19, 20). Convergence of homogeneous well-mixed populations under more general nonmatrix games has been established in ref. 21 in the context of congestion games, using potential functions. The convergence properties of networks with arbitrary structure has also been investigated under various conditions, particularly in the homogeneous (symmetric) case (22–24). Recently in ref. 17, a combination of mean-field approximations and simulations were used to show that synchronous best-response dynamics in symmetric coordination or anticoordination games tend to always converge to Nash equilibria. However, in the case of asymmetric coordination games, it was shown in ref. 25 that synchronous best-response dynamics may not converge to a single action but rather to a cycle of alternating actions. Symmetry thus seems to be a significant factor in the convergence of the threshold model, but we will show that asynchrony perhaps plays an even more important role, because regardless of the symmetry, the network always converges in the asynchronous case. In addition to making the convergence more likely, compared with synchronous models, asynchronous dynamics can provide a more realistic model of the timeline over which independent agents make decisions and receive information, and they are particularly suitable when the payoff dynamics can be thought of as fast compared with the update dynamics. For example, decisions on matters such as which product to buy, which political party to vote for, or which traffic route to take may be the culmination of many individual interactions. Nevertheless, our results do not require that only one agent can update at a time; in fact, we show that even small asynchronous perturbations to fully synchronous dynamics lead to equilibrium convergence.

In this paper, we show that every network consisting of anticoordinating agents with asynchronous best-response dynamics will eventually reach an equilibrium state, even if each agent has a different threshold. Moreover, we show that the same result holds for networks of coordinating agents. As a corollary, we establish the existence of pure-strategy Nash equilibria in both cases for arbitrary networks and arbitrary payoffs. On the question of convergence time, we show that, in such networks, the total number of strategy switches is no greater than six times the number of edges in the network. In the case of partial synchrony, when a random number of agents can update simultaneously, we show that the network still almost surely reaches an equilibrium. It follows that irregular network topology, population heterogeneity, and synchrony of decisions between two or more agents (as long as random asynchronous updating is not completely excluded) are not sufficient to cause nonconvergence or cycles in best-response dynamics; rather, possible causes include the occasional use of non–best-response strategies, randomization, or a mixture of coordinating and anticoordinating agents. Indeed, we provide a small example demonstrating the possibility of cycles in networks containing both coordinating and anticoordinating agents.

Asynchronous Best-Response Dynamics

Consider an undirected network $\mathbb{G}=\left(\mathcal{V},\mathrm{ℰ}\right)$ where the nodes $\mathcal{V}=\left\{1,\dots ,n\right\}$ correspond to agents and each edge in the set $\mathrm{ℰ}\subseteq \mathcal{V}\times \mathcal{V}$ represents a 2-player game between neighboring agents. Each agent $i\in \mathcal{V}$ chooses pure strategies from a binary set $\mathcal{S}≔\left\{A,B\right\}$ and receives a payoff upon completion of game according to the matrix:

$$\begin{array}{l}\begin{array}{ccc}& \hspace{1em}A& B\end{array}\\ \begin{array}{c}A\\ B\end{array}\left(\begin{array}{ll}{a}_i& b_i\\ c_i& d_i\end{array}\right),\hspace{1em}{a}_i,b_i,c_i,d_i\in \mathrm{ℝ}.\end{array}$$

The dynamics take place over a sequence of discrete time $k=\mathrm{0,1,2},\dots$. Let $x_i\left(k\right)\in \mathcal{S}$ denote the strategy of agent i at time k, and denote the number of neighbors of agent i playing A and B at time k by $n_i^A\left(k\right)$ and $n_i^B\left(k\right)$, respectively. When there is no ambiguity, we may sometimes omit the time k for compactness of notation. The total payoffs to each agent i at time k are accumulated over all neighbors, and are therefore equal to $a_i{n}_i^A\left(k\right)+b_i{n}_i^B\left(k\right)$ when $x_i\left(k\right)=A$, or $c_i{n}_i^A\left(k\right)+d_i{n}_i^B\left(k\right)$ when $x_i\left(k\right)=B$.

In asynchronous (myopic) best-response dynamics, one agent at a time becomes active and chooses a single action to play against all neighbors. The active agent at time k updates at time $k+1$ to the strategy that achieves the highest total payoff, that is, is the best response, against the strategies of its neighbors at time k:

$$x_i\left(k+1\right)=\{\begin{array}{cc}A,& \text{if}\hspace{0.17em}{a}_i{n}_i^A+b_i{n}_i^B>c_i{n}_i^A+d_i{n}_i^B\\ B,& \text{if}\hspace{0.17em}{a}_i{n}_i^A+b_i{n}_i^B<c_i{n}_i^A+d_i{n}_i^B\\ z_i,& \text{if}\hspace{0.17em}{a}_i{n}_i^A+b_i{n}_i^B=c_i{n}_i^A+d_i{n}_i^B\end{array}.$$

In the case that strategies A and B result in equal payoffs, both strategies are best responses and we use the notation $z_i$, which is defined to be A, B, or $x_i\left(k\right)$, to allow for several possibilities for this equality case. Note that we do not require all agents to have the same $z_i$. That is, when both A and B are best responses, some agents may choose A, others may choose B, and others may keep their current strategy; however, the agents cannot change their choice of $z_i$ over time.

It is convenient to rewrite these dynamics in terms of the number of neighbors playing each strategy. Let ${\mathrm{deg}}_i$ denote the total number of neighbors of agent i. We can simplify the conditions above by using the fact that $n_i^B={\mathrm{deg}}_i-n_i^A$ and rearranging terms:

$$\begin{array}{c}{a}_i{n}_i^A+b_i\left({\mathrm{deg}}_i-n_i^A\right)>c_i{n}_i^A+d_i\left({\mathrm{deg}}_i-n_i^A\right)\\ n_i^A\left(a_i-c_i+d_i-b_i\right)>{\mathrm{deg}}_i\left(d_i-b_i\right)\\ {\delta }_i{n}_i^A>{\gamma }_i{\mathrm{deg}}_i,\end{array}$$

where ${\delta }_i≔a_i-c_i+d_i-b_i$ and ${\gamma }_i≔d_i-b_i$. The cases of “$<$” and “$=$” can be handled similarly. Consider the case when ${\delta }_i\ne 0$, and let ${\tau }_i≔{\gamma }_i/{\delta }_i$ denote a “threshold” for agent i. Depending on the sign of ${\delta }_i$, we have two possible types of best-response update rules. If ${\delta }_i>0$, the update rule is given by the following:

$$x_i\left(k+1\right)=\{\begin{array}{cc}A& \text{if}\hspace{0.17em}{n}_i^A\left(k\right)>{\tau }_i{\mathrm{deg}}_i\\ B& \text{if}\hspace{0.17em}{n}_i^A\left(k\right)<{\tau }_i{\mathrm{deg}}_i\\ z_i& \text{if}\hspace{0.17em}{n}_i^A\left(k\right)={\tau }_i{\mathrm{deg}}_i\end{array}.$$ [1]

These agents switch to strategy A if a sufficient fraction of neighbors are using that strategy, and likewise for strategy B. On the other hand, for ${\delta }_i<0$, if a sufficient fraction of neighbors are playing A, the agent will switch to B, and vice versa. This update rule is given by the following:

$$x_i\left(k+1\right)=\{\begin{array}{cc}A& \text{if}\hspace{0.17em}{n}_i^A\left(k\right)<{\tau }_i{\mathrm{deg}}_i\\ B& \text{if}\hspace{0.17em}{n}_i^A\left(k\right)>{\tau }_i{\mathrm{deg}}_i\\ z_i& \text{if}\hspace{0.17em}{n}_i^A\left(k\right)={\tau }_i{\mathrm{deg}}_i\end{array}.$$ [2]

In the case that ${\tau }_i\notin \left[\mathrm{0,1}\right]$, it is straightforward to show that there exists a strictly dominant strategy, and the update rule Eq. 1 or 2 is equivalent to one in which ${\tau }_i\in \left\{\mathrm{0,1}\right\}$ and $z_i\in \left\{A,B\right\}$. The same holds for when ${\delta }_i=0$. Agents for which ${\delta }_i\ge 0$ are called coordinating and can be modeled by Eq. 1. Agents for which ${\delta }_i\le 0$ are called anticoordinating and can be modeled by Eq. 2. Therefore, every agent can be described as a coordinating or an anticoordinating agent (or both).

Let $\mathrm{\Gamma }≔\left(\mathbb{G},\tau ,\left\{+,-,\pm \right\}\right)$ denote a “network game,” which consists of the network $\mathbb{G}$, a vector of agent thresholds $\tau ={\left({\tau }_1,\dots ,{\tau }_n\right)}^{\mathrm{\top }}$, and one of $+$, $-$, or $\pm$, corresponding to the cases of all coordinating, all anticoordinating, or a mixture of both types of agents, respectively. The dynamics in Eqs. 1 and 2 are in the form of the standard linear-threshold model (18). An equilibrium state in the threshold model is a state in which the number of A-neighbors of each agent does not violate the threshold that would cause them to change strategies. For example, in a network of anticoordinating agents in which $z_i=B$ for all i, this means that for each agent $i\in \mathcal{V}$, $x_i\left(k\right)=A$ implies $n_i^A\left(k\right)<{\tau }_i{\mathrm{deg}}_i$ and $x_i\left(k\right)=B$ implies $n_i^A\left(k\right)\ge {\tau }_i{\mathrm{deg}}_i$. Note that this notion of equilibrium is equivalent to a pure-strategy Nash equilibrium in the corresponding network game.

Convergence Results

We investigate the equilibrium convergence properties of the agent-based threshold models in Eqs. 1 and 2 that we defined in the previous section.

Before providing the main results, we precisely define the nature of the asynchronous dynamics. We require only that at any given time step, each agent is guaranteed to be active at some finite future time. Let $i^k$ denote the agent who is active at time k and let ${\left(i^k\right)}_{k=0}^{\infty }$ denote a sequence of active agents. We say that such a sequence is “persistent” if for every agent $j\in \mathcal{V}$ and every time $k\ge 0$, there exists some finite later time $k\prime >k$ at which agent j is again active ($i^{k\prime }=j$).

Assumption 1.

Every activation sequence driving the dynamics in Eq. 1 or Eq. 2 is persistent.

Remark 1.

In stochastic settings, Assumption 1 holds almost surely whenever agents activate infinitely many times with probability one, for example, if each agent activates at a rate determined by a Poisson process.

We divide the convergence analysis into two main parts corresponding to the cases of anticoordinating and coordinating agents. In what follows, we use 1 to denote the n-dimensional vector containing all ones. We refer the reader to SI Appendix for the detailed proofs of the results.

All Agents Are Anticoordinating

Theorem 1.

Every network of anticoordinating agents who update asynchronously under Assumption 1 will reach an equilibrium state in finite time.

The sketch of the proof is as follows. We begin by showing that an arbitrary network game $\mathrm{\Gamma }=\left(\mathbb{G},\left(1/2\right)\mathbf{1},-\right)$ consisting of anticoordinating agents in which the threshold of each agent is $1/2$ will reach an equilibrium in finite time. Then we extend the result to a heterogeneous-threshold network game $\mathrm{\Gamma }=\left(\mathbb{G},\tau ,-\right)$ by constructing a homogeneous-threshold “augmented” network game $\widehat{\mathrm{\Gamma }}=\left(\widehat{\mathbb{G}},\left(1/2\right)\mathbf{1},-\right)$ that is dynamically equivalent to $\mathrm{\Gamma }$. We complete the proof by showing that if the augmented network game $\widehat{\mathrm{\Gamma }}$ reaches an equilibrium, then $\mathrm{\Gamma }$ does as well. The following lemma establishes convergence of the homogeneous-threshold network game $\left(\mathbb{G},\left(1/2\right)\mathbf{1},-\right)$.

Lemma 1.

Every network of anticoordinating agents who update asynchronously under Assumption 1, with ${\tau }_i=1/2$ for each agent $i\in \mathcal{V}$, will reach an equilibrium state in finite time.

The proof of the lemma revolves around the following potential function:

$${\mathrm{\Phi }}_i\left(k\right)=\{\begin{array}{ll}{n}_i^A\left(k\right)-{\widehat{n}}_i^A\hfill & \text{if}\hspace{0.17em}{x}_i\left(k\right)=A\hfill \\ {\widehat{n}}_i^A+1-n_i^A\left(k\right)\hfill & \text{if}\hspace{0.17em}{x}_i\left(k\right)=B\hfill \end{array},$$

where ${\widehat{n}}_i^A$ denotes the maximum number of A-neighbors of agent i that will not cause agent i to switch to B when playing A. The proof follows from the fact that the function is lower bounded and decreases every time an agent in the network switches strategies.

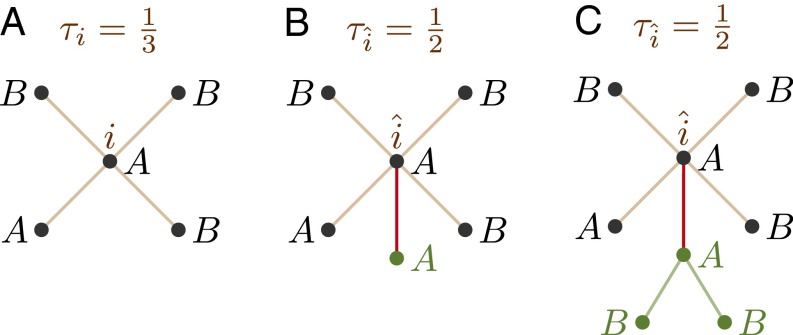
To motivate our approach for extending this result to an arbitrary distribution of thresholds, consider for example an agent i with 4 neighbors whose threshold is $1/3$. When playing A, this agent can tolerate up to 1 A-neighbor (Fig. 1A), but 2 or more will cause a switch to B. Similarly, when playing B, the agent needs at least 2 A-neighbors to remain playing B, whereas 1 or fewer will cause a switch to A. Now consider an agent $\widehat{i}$ whose threshold is $1/2$ but who has one additional neighbor who always plays A, for a total of 5 neighbors, as shown in Fig. 1B. When playing A, this agent can tolerate up to 2 A-neighbors before switching to B, and as a B-agent needs at least 3 A-neighbors, whereas 2 or fewer will cause a switch to A. Notice, however, that with respect to the original 4 neighbors, the dynamics of agents i and $\widehat{i}$ are indistinguishable. It turns out that whenever ${\tau }_i<1/2$, by adding a sufficient number of fixed A-neighbors, we can always construct a dual node $\widehat{i}$ with threshold $1/2$ whose dynamics are equivalent to the dynamics of the original node i. Moreover, if ${\tau }_i>1/2$, we can achieve the same result by adding fixed B-neighbors. To ensure that the added nodes do not change strategies, we simply add two opposite strategy neighbors to these nodes (Fig. 1C). It is then straightforward to show that the strategies of all added nodes remain constant. We now formalize this argument for arbitrary networks of anticoordinating agents, using some techniques similar to those that have already proven useful in studying the convergence of synchronous networks (25).

Fig. 1.

(A and B) Agents i and $\widehat{i}$ have thresholds ${\tau }_i=1/3$ and ${\tau }_{\widehat{i}}=1/2$, but because an extra A-neighbor has been added to $\widehat{i}$, they are dynamically equivalent. (C) To ensure that the added node does not switch, two B neighbors are added who also will not switch, forming a V-block.

We define the “augmented network game” $\widehat{\mathrm{\Gamma }}≔\left(\widehat{\mathbb{G}},\left(1/2\right)\mathbf{1},-\right)$ based on $\mathrm{\Gamma }$ as follows. Let $\widehat{\mathbb{G}}=\left(\widehat{\mathcal{V}},\widehat{\mathrm{ℰ}}\right)$. Define a “V-block” as a triplet of nodes $\left\{v_1,v_2,v_3\right\}\subseteq \widehat{\mathcal{V}}$ along with the edges $\left\{\left\{v_1,v_2\right\},\left\{v_1,v_3\right\}\right\}\subseteq \widehat{\mathrm{ℰ}}$. For each agent $i\in \mathcal{V}$, we introduce a “dual agent” $\widehat{i}\in \widehat{\mathcal{V}}$ with the same initial strategy, that is, $x_{\widehat{i}}\left(0\right)=x_i\left(0\right)$, and with $z_{\widehat{i}}=z_i$. Corresponding to each dual agent $\widehat{i}$, there are $m_i$ number of V-blocks in $\widehat{\mathbb{G}}$ such that the $v_1$-node of each block is connected to $\widehat{i}$, with $m_i$ being defined as follows: if ${\tau }_i=1/2$, then $m_i=0$; otherwise, $m_i$ depends on which one of the following three conditions on ${\tau }_i$ holds:

$$m_i=\{\begin{array}{ll}\left|\left(1-2{\tau }_i\right){\mathrm{deg}}_i\right|\hfill & {\tau }_i{\mathrm{deg}}_i\in \mathrm{\mathbb{Z}}\hfill \\ \left|{\mathrm{deg}}_i-r-1\right|\hfill & \exists r\in 2\mathrm{\mathbb{Z}}:\frac{r}{2}<{\tau }_i{\mathrm{deg}}_i<\frac{r+1}{2}\hfill \\ \left|{\mathrm{deg}}_i-r\right|\hfill & \exists r\in 2\mathrm{\mathbb{Z}}+1:\frac{r}{2}\le {\tau }_i{\mathrm{deg}}_i<\frac{r+1}{2}\hfill \end{array},$$

where $2\mathrm{\mathbb{Z}}$ and $2\mathrm{\mathbb{Z}}+1$ denote the set of even and odd numbers, respectively. If ${\tau }_i<1/2$, then the initial strategies of each V-block connected to the dual agent $\widehat{i}$ are $x_{v_1}\left(0\right)=A$ and $x_{v_2}\left(0\right)=x_{v_3}\left(0\right)=B$; and if ${\tau }_i>1/2$, then $x_{v_1}\left(0\right)=B$ and $x_{v_2}\left(0\right)=x_{v_3}\left(0\right)=A$. In total, $\widehat{\mathcal{V}}$ has $n+{\displaystyle {\sum }_{i=1}^n{m}_i}$ agents, the thresholds of all of which are set to $1/2$. For $\widehat{\mathrm{ℰ}}$, in addition to the edges for the V-blocks, there is an edge between any two dual agents $\widehat{i}$ and $\widehat{j}$ in $\widehat{\mathcal{V}}$, if and only if there is an edge between i and j in $\mathcal{V}$.

Next, we show that if whenever an agent in $\mathbb{G}$ activates, its dual in $\widehat{\mathbb{G}}$ also activates (while neglecting the time steps that a V-block agent is active), then the dynamics of each node in $\mathbb{G}$ are the same as the dynamics of its dual node in $\widehat{\mathbb{G}}$ (again while neglecting the time steps that a V-block agent is active). Then Theorem 1 can be proven accordingly.

As a result of Theorem 1, we have the following corollary, which to the best of our knowledge has not been shown in the literature to date.

Corollary 1.

Every network of anticoordinating agents admits a pure-strategy Nash equilibrium.

All Agents Are Coordinating

Theorem 2.

Every network of coordinating agents who update asynchronously under Assumption 1 will reach an equilibrium state in finite time.

The proof of Theorem 2 follows similar steps as the anticoordinating case. The key difference is that the potential function becomes the following:

$${\mathrm{\Phi }}_i\left(k\right)=\{\begin{array}{ll}{\check{n}}_i^A-n_i^A\left(k\right)\hfill & \text{if}\hspace{0.17em}{x}_i\left(k\right)=A\hfill \\ n_i^A\left(k\right)-{\check{n}}_i^A+1\hfill & \text{if}\hspace{0.17em}{x}_i\left(k\right)=B\hfill \end{array},$$ [3]

where ${\check{n}}_i^A$ is defined as the minimum number of A-neighbors required for an A-playing agent to continue playing A. The maximum number of A-neighbors that a B agent can tolerate before switching to A is then given by ${\check{n}}_i^A-1$. We refer the reader to SI Appendix for a complete proof of the theorem.

Theorem 2 also leads to a corollary on existence of equilibria for networks of coordinating agents, but in this case we confirm an already known result (e.g., ref. 26).

Corollary 2.

Every network of coordinating agents admits a pure-strategy Nash equilibrium.

The following corollary follows directly from Theorem 1 and Theorem 2, and the fact that a network of homogeneous agents can always be described as all coordinating or all anticoordinating.

Corollary 3.

Every network of homogenous agents who update asynchronously under Assumption 1 will reach an equilibrium state in finite time.

Coordinating and Anticoordinating Agents Coexist.

Given the previous two results, the natural question arises of what we can say about convergence when both coordinating and anticoordinating agents are present in a network. Although there may be particular configurations that converge, we can demonstrate that this will not hold in general with a simple example on a network consisting of only two agents connected to each other, namely a path of length one, that is, $\mathcal{V}≔\left\{\mathrm{1,2}\right\},\mathrm{ℰ}≔\left\{\left(\mathrm{1,2}\right),\left(\mathrm{2,1}\right)\right\}$. Suppose that agent 1 is coordinating, agent 2 is anticoordinating, and their thresholds are both equal to $1/2$. Given their respective update rules in Eqs. 1 and 2, agent 1 will always switch to match agent 2 while agent 2 will always switch to oppose the strategy of agent 1. In other words, the following transitions will occur with probability one: $\left(A,A\right)\to \left(A,B\right)\to \left(B,B\right)\to \left(B,A\right)\to \left(A,A\right)$, resulting in a neverending cycle. This formulation is equivalent to a repeated version of the well-known matching pennies game. From this, we can conclude that convergence is not a trivial result to be expected in all cases, and can only be guaranteed when all agents are either coordinating or anticoordinating.

Convergence Time.

The following corollary follows from the fact that the potential function $\mathrm{\Phi }\left(k\right)$ is bounded from above and below and decreases by at least one every time an agent switches strategies.

Corollary 4.

Every network of all coordinating or all anticoordinating agents will reach an equilibrium state after no more than $6\left|\mathrm{ℰ}\right|$ agent switches.

This implies that agents cannot switch an arbitrary number of times before the network reaches equilibrium. It follows that when agent activation times are independent and identically distributed, the upper bound on the expected time to reach equilibrium is linear in the number of edges in the network.

Synchronous and Partially Synchronous Updating

So far, any network of all coordinating or all anticoordinating agents is shown to reach an equilibrium state, as long as the agents update asynchronously. However, the importance of asynchronous updating to the convergence results remains an open problem. In this section, we show that, although full synchrony may not always result in convergence, the results indeed still hold for partial synchrony, in which a random number of agents update at each time step.

Synchronous Updating.

We show that networks in which updates are fully synchronous may never reach an equilibrium state, by presenting counterexamples with only two agents.

First, suppose that both agents are anticoordinating and start from the strategy vector $\left(A,A\right)$. The agents update synchronously, that is, at each time step, both agents activate and update their strategies according to the update rule in Eq. 2. Therefore, the dynamics will be deterministic, and the following transitions will occur on the strategies of the agents: $\left(A,A\right)\to \left(B,B\right)\to \left(A,A\right)$, resulting in a cycle of length 2.

Now suppose that both agents are coordinating and they start from the strategy vector $\left(A,B\right)$. Following the update rule in Eq. 1, the following transitions take place under the synchronous updating: $\left(A,B\right)\to \left(B,A\right)\to \left(A,B\right)$, again resulting in a cycle of length 2.

The above examples prove that equilibrium convergence is no longer guaranteed if the agents update in full synchrony. However, it is known that any network game governed by synchronous best-response dynamics will reach a cycle of length at most 2, even when both coordinating and anticoordinating agents coexist in the network (27).

Partially Synchronous Updating.

To understand what happens in the case of partially synchronous updates, we need to relax the assumption that only one agent can update at a given time. We must therefore decouple the activation sequence from the discrete-time dynamics, and consider the activations to occur in continuous time. Let ${\left\{t^j\right\}}_{j=1}^{\infty }$ denote a sequence of times and ${\left\{i^j\right\}}_{j=1}^{\infty }$, a sequence of agents such that agent $i^j$ activates at time $t^j$. Fig. 2 shows the relationship of the discrete time steps with the agent activation sequence.

Fig. 2.

In the partially synchronous update model, multiple agents can activate in a single discrete time step. All agents who are active in the absolute time interval $\left[k,k+1\right)$ update at time $k+1$ based on the information at time k. The colors red, blue, and green represent three different agents.

It is now possible that multiple agents update between consecutive time steps. In particular, all agents who are active in the time interval $\left[k,k+1\right)$ update at time $k+1$ based on the state of the network at time k. Let ${\mathcal{A}}_k$ denote the set of all agents who are active during the time interval $\left[k,k+1\right)$. We can express the partially synchronous dynamics as follows:

$$x_i\left(k+1\right)=\{\begin{array}{ll}{x}_i^{br}\left(k\right)\hfill & \text{if}\hspace{0.17em}i\in {\mathcal{A}}_k\hfill \\ x_i\left(k\right)\hfill & \text{otherwise}\hfill \end{array},$$

where $x_i^{br}\left(k\right)$ denotes the best response of agent i to the strategies of its neighbors at time k. To provide a general framework for independent stochastic activation sequences, we make the following assumption.

Assumption 2.

The interactivation times for each agent are drawn from mutually independent probability distributions with support on ${\mathrm{ℝ}}_{\ge 0}$.

One standard model that satisfies Assumption 2 is to use exponential distributions with mean $1/\lambda$. This represents the case in which each agent updates according to a Poisson clock with rate λ, and the expected number of agents updating in one unit of time is $\lambda n$.

From the previous sections, we know that the best-response dynamics do not necessarily converge to an equilibrium when the updating is synchronous, yet do converge when the updating is asynchronous. Therefore, the natural question arising is the following: how much asynchrony do the partially synchronous best-response dynamics need for convergence? It turns out that, even under the relatively mild assumption on the partially synchronous updates in Assumption 2, we still have convergence to an equilibrium state almost surely.

Theorem 3.

Every network of all coordinating or all anticoordinating agents who update with partially synchronous dynamics that satisfy Assumption 2 almost surely reaches an equilibrium state in finite time.

To prove the theorem, we model the network game as a Markov chain and show that it is absorbing (28). We refer the reader to SI Appendix for a detailed proof.

Note that one technically equivalent but perhaps less practical modeling of the partially synchronous updates would be to simply assume that at each time step $k=\mathrm{0,1},\dots$, a random number of random agents activate simultaneously and then update at $k+1$. In other words, there is a fixed probability that a particular group of agents activate simultaneously at every time step. Then Theorem 3 still holds because the probability that each agent activates asynchronously is bounded below by a positive constant. From a broader point of view, Theorem 3 holds whenever random asynchronous activations are not completely excluded from the partially synchronous dynamics. Convergence, however, may not be achieved for particular nonrandom activation sequences, as discussed in the following.

Zero-Probability Nonconvergence.

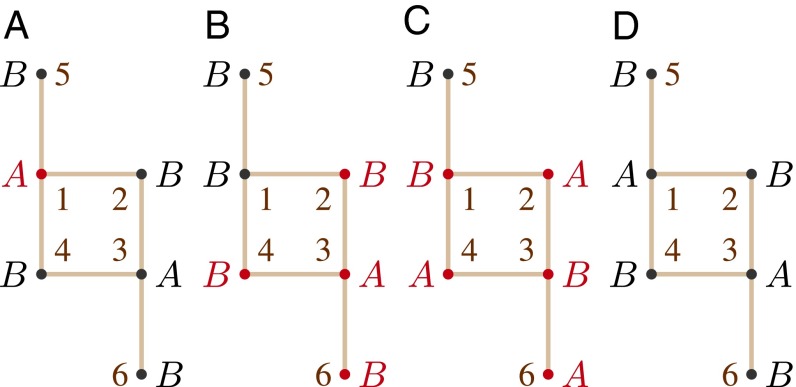
We now show that Theorem 3 holds only almost surely. In other words, there exist activation sequences generated under Assumption 2 that do not result in equilibrium convergence; however, the probability of such sequences happening is zero. Consider the network game $\mathrm{\Gamma }=\left(\mathbb{G},\left(1/2\right)\mathbf{1},+\right)$ where $\mathbb{G}$ and the initial strategies $x\left(0\right)$ are as in Fig. 3A. First, we show that if any single agent activates when the strategy state equals $x\left(0\right)$, then there exists a finite sequence of agent activations that return the state to $x\left(0\right)$. Consider the case when agent 1 activates exclusively at $k=0$ (Fig. 3A), and hence, switches to B at $k=1$. Then if agents 2, 3, 4, 6 activate at $k=1$ and agents 1, 2, 3, 4, 6 at $k=2$, the strategy state returns to $x\left(0\right)$ at $k=3$, that is, $x\left(3\right)=x\left(0\right)$; the process is shown in Fig. 3 B–D. Denote the corresponding activation subsequence by ${\alpha }_1=\left(\left\{1\right\},\left\{\mathrm{2,3,4,6}\right\},\left\{\mathrm{1,2,3,4,6}\right\}\right)$. Similarly, as shown in Fig. 4, there exists an activation sequence that returns the state of the system to $x\left(0\right)$ when agent 2 activates at $k=0$. The corresponding activation subsequence would be ${\alpha }_2=\left(\left\{2\right\},\left\{\mathrm{1,3,4,5,6}\right\},\left\{\mathrm{1,2,3,4,5,6}\right\}\right)$. Moreover, due to the symmetric distribution of the strategies $x\left(0\right)$ in the network, the same can be shown for when agents 3, 4, or 6 are activated at $k=0$ (which are similar to agents 1, 2, and 5, respectively). Denote the corresponding activation subsequences by ${\alpha }_3,{\alpha }_4$, and ${\alpha }_6$. Now consider the event X made by ${\alpha }_1$ and ${\alpha }_2$ as follows:

$$X={\left(x_i\right)}_{i=1}^{\infty },\hspace{1em}{x}_i\in \left\{{\alpha }_1,{\alpha }_2\right\}.$$

Any activation sequence in X can be generated under Assumption 2 and has the property that all agents activate exclusively infinitely many times. However, no sequence in X results in convergence of the network game $\mathrm{\Gamma }$. However, this does not contradict Theorem 3 because $\mathrm{\mathbb{P}}\left[X\right]=0$, under Assumption 2.

Fig. 3.

(A–D) Strategy evolution in the network game $\mathrm{\Gamma }=\left(\mathbb{G},\left(1/2\right)\mathbf{1},+\right)$ under the activation subsequence ${\alpha }_1=\left(\left\{1\right\},\left\{\mathrm{2,3,4,6}\right\},\left\{\mathrm{1,2,3,4,6}\right\}\right)$. Red circles indicate those nodes that are activated at the corresponding time step.

Fig. 4.

(A–D) Strategy evolution in the network game $\mathrm{\Gamma }=\left(\mathbb{G},\left(1/2\right)\mathbf{1},+\right)$ under the activation subsequence ${\alpha }_2=\left(\left\{2\right\},\left\{\mathrm{1,3,4,5,6}\right\},\left\{\mathrm{1,2,3,4,5,6}\right\}\right)$.

Concluding Remarks

We have shown that arbitrary networks consisting of all coordinating or all anticoordinating agents who update with asynchronous best responses will reach equilibrium in finite time. Moreover, when updates are partially synchronous, we have shown that the network still almost surely reaches an equilibrium under mild conditions on the independence and randomness of agent updates. For the case of anticoordinating agents, these results have important implications in social contexts where individuals prefer an action only if a small enough portion of neighbors are using that action, for example, deciding which route to take to avoid traffic congestion, volunteering for a dangerous but important public service position, contributing money or time toward a crowd-sourced project, etc. For coordinating agents, the results apply to social contexts where each agents prefer an action only if a sufficient number of neighbors are using that action, for example, the spread of social behaviors, technological innovations, viral infections. Our results suggest that, in both cases, no matter how different the individuals are, which neighbors affect their decisions, or how many simultaneous decisions are made, everyone will tend to settle on a particular action with which they are satisfied. This means that the presence of cycles or nonconvergence must result from other factors such as imitation or other unmodeled effects in the update dynamics, or a mixture of coordinating and anticoordinating agents. These results also open the door to characterizing the equilibria and investigating possibilities for payoff-based incentive control of the network.