Significance
Artificial neural networks are some of the most widely used tools in data science. Learning is, in principle, a hard problem in these systems, but in practice heuristic algorithms often find solutions with good generalization properties. We propose an explanation of this good performance in terms of a nonequilibrium statistical physics framework: We show that there are regions of the optimization landscape that are both robust and accessible and that their existence is crucial to achieve good performance on a class of particularly difficult learning problems. Building on these results, we introduce a basic algorithmic scheme that improves existing optimization algorithms and provides a framework for further research on learning in neural networks.
Keywords: machine learning, neural networks, statistical physics, optimization
Abstract
In artificial neural networks, learning from data is a computationally demanding task in which a large number of connection weights are iteratively tuned through stochastic-gradient-based heuristic processes over a cost function. It is not well understood how learning occurs in these systems, in particular how they avoid getting trapped in configurations with poor computational performance. Here, we study the difficult case of networks with discrete weights, where the optimization landscape is very rough even for simple architectures, and provide theoretical and numerical evidence of the existence of rare—but extremely dense and accessible—regions of configurations in the network weight space. We define a measure, the robust ensemble (RE), which suppresses trapping by isolated configurations and amplifies the role of these dense regions. We analytically compute the RE in some exactly solvable models and also provide a general algorithmic scheme that is straightforward to implement: define a cost function given by a sum of a finite number of replicas of the original cost function, with a constraint centering the replicas around a driving assignment. To illustrate this, we derive several powerful algorithms, ranging from Markov Chains to message passing to gradient descent processes, where the algorithms target the robust dense states, resulting in substantial improvements in performance. The weak dependence on the number of precision bits of the weights leads us to conjecture that very similar reasoning applies to more conventional neural networks. Analogous algorithmic schemes can also be applied to other optimization problems.
There is increasing evidence that artificial neural networks perform exceptionally well in complex recognition tasks (1). Despite huge numbers of parameters and strong nonlinearities, learning often occurs without getting trapped in local minima with poor prediction performance (2). The remarkable output of these models has created unprecedented opportunities for machine learning in a host of applications. However, these practical successes have been guided by intuition and experiments, whereas obtaining a complete theoretical understanding of why these techniques work seems currently out of reach, due to the inherent complexity of the problem. In other words, in practical applications, large and complex architectures are trained on big and rich datasets using an array of heuristic improvements over basic stochastic gradient descent (SGD). These heuristic enhancements over a stochastic process have the general purpose of improving the convergence and robustness properties (and therefore the generalization properties) of the networks, with respect to what would be achieved with a pure gradient descent (GD) on a cost function.
There are many parallels between the studies of algorithmic stochastic processes and out-of-equilibrium processes in complex systems. Examples include jamming processes in physics, local search algorithms for optimization and inference problems in computer science, regulatory processes in biological and social sciences, and learning processes in real neural networks (see, e.g., refs. 3–7). In all these problems, the underlying stochastic dynamics are not guaranteed to reach states described by an equilibrium probability measure, as would occur for ergodic statistical physics systems. Sets of configurations that are quite atypical for certain classes of algorithmic processes become typical for other processes. Although this fact is unsurprising in a general context, it is unexpected and potentially quite significant when sets of relevant configurations that are typically inaccessible for a broad class of search algorithms become extremely attractive to other algorithms.
Here, we discuss how this phenomenon emerges in learning in large-scale neural networks with low precision synaptic weights. We further show how it is connected to an out-of-equilibrium statistical physics measure that suppresses the confounding role of exponentially many deep and isolated configurations (local minima of the error function) and also amplifies the statistical weight of rare but extremely dense regions of minima. We call this measure the robust ensemble (RE). Moreover, we show that the RE allows us to derive novel and exceptionally effective algorithms. One of these algorithms is closely related to a recently proposed stochastic learning protocol used in complex deep artificial neural networks (8), implying that the underlying geometrical structure of the RE may provide an explanation for its effectiveness.
In the present work, we consider discrete neural networks with only one or two layers, which can be studied analytically. However, we believe that these results should extend to deep neural networks of which the models studied here are building blocks, and in fact to other learning problems as well.
Interacting Replicas As a Tool for Seeking Dense Regions
In statistical physics, the canonical ensemble describes the equilibrium (i.e., long-time limit) properties of a stochastic process in terms of a probability distribution over the configurations of the system , where is the energy of the configuration, an inverse temperature, and the normalization factor is called the partition function and can be used to derive all thermodynamic properties. This distribution is thus defined whenever a function is provided, and indeed it can be studied and provide insight even when the system under consideration is not a physical system. In particular, it can be used to describe interesting properties of optimization problems, in which has the role of a cost function that one wishes to minimize; in these cases, one is interested in the limit , which corresponds to assigning a uniform weight over the global minima of the energy function. This kind of description is at the core of the well-known simulated annealing (SA) algorithm (9).
In the past few decades, equilibrium statistical physics descriptions have emerged as fundamental frameworks for studying the properties of a variety of systems that were previously squarely in the domain of other disciplines. For example, the study of the phase transitions of the random -satisfiability problem (SAT) was linked to the algorithmic difficulty of finding solutions (10, 11). It was shown that the system can exhibit different phases, characterized by the arrangement of the space of solutions in one, many, or a few connected clusters. Efficient (polynomial-time) algorithms seem to exist only if the system has so-called “unfrozen” clusters: extensive and connected regions of solutions in which at most a sublinear number of variables have a fixed value. If, on the contrary, all solutions are “frozen” (belonging to clusters in which an extensive fraction of the variables take a fixed value, thus confined to subspaces of the space of configurations), no efficient algorithms are known. In the limiting case in which all variables—except at most a sublinear number of them—are fixed, the clusters are isolated point-like regions, and the solutions are called “locked” (12).
For learning problems with discrete synapses, numerical experiments indicate that efficient algorithms also seek unfrozen solutions. In ref. 13, we showed that the equilibrium description in these problems is insufficient, in the sense that it predicts that the problem is always in the completely frozen phase in which all solutions are locked (14), despite the fact that efficient algorithms seem to exist. This motivated us to introduce a different measure, which ignores isolated solutions and enhances the statistical weight of large, accessible regions of solutions:
| [1] |
Here, is a parameter that has the formal role of an inverse temperature and is a “local free entropy”:
| [2] |
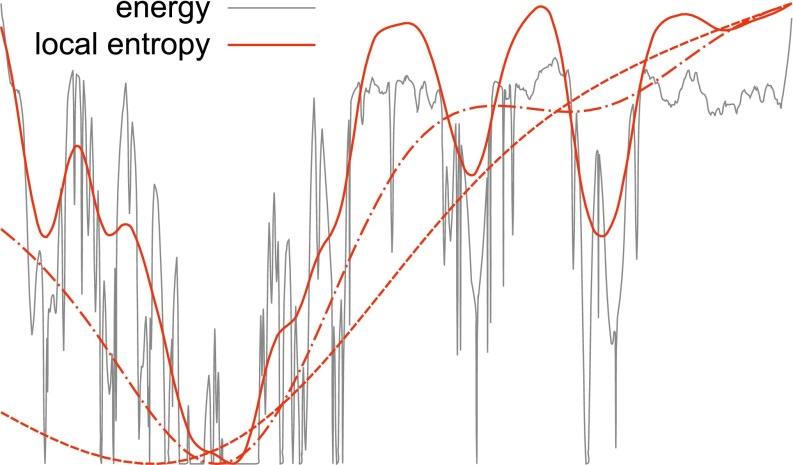
where denotes some monotonically increasing function of the distance between configurations, defined according to the model under consideration. In the limit , this expression reduces (up to an additive constant) to a “local entropy”: It counts the number of minima of the energy, weighting them (via the parameter ) by the distance from a reference configuration . Therefore, if is large, only the configurations that are surrounded by an exponential number of local minima will have a nonnegligible weight. By increasing the value of , it is possible to focus on narrower neighborhoods around , and at large values of the reference will also with high probability share the properties of the surrounding minima. This is illustrated in Fig. 1. These large-deviation statistics seem to capture very well the behavior of efficient algorithms on discrete neural networks, which invariably find solutions belonging to high-density regions when these regions exist, and fail otherwise. These solutions therefore could be rare (i.e., not emerge in a standard equilibrium description), and yet be accessible (i.e., there exist efficient algorithms that are able to find them), and they are inherently robust (they are immersed in regions of other “good” configurations). As discussed in ref. 13, there is a relation between the robustness of solutions in this sense and their good generalization ability: This is intuitively understood in a Bayesian framework by considering that a robust solution acts as a representative of a whole extensive region.
Fig. 1.
Energy landscape compared with local entropy landscape in an illustrative toy example. The energy landscape (gray curve) can be very rugged, with a large number of narrow local minima. Some isolated global minima can also be observed on the right. On the left, there is a region of denser minima that coalesce into a wide global optimum. The red curves show the local entropy landscape (Eq. 2 with the opposite sign) computed at increasing values of the interaction parameter (i.e., at progressively finer scales). At low values of (dashed curve), the landscape is extremely smooth and the dense region is identifiable on a coarse-grained scale. At intermediate values of (dot-dashed curve) the global minimum is narrower and located in a denser region, but it does not correspond to a global energy minimum yet. At large values of (solid curve) finer-grain features appear as several local minima, but the global minimum is now located inside a wide global optimum of the energy. As a consequence of this general picture, a process in which a local search algorithm driven by the local entropic landscape is run at increasing values of will end up in such wide minima, even though in the limit the local entropy landscape tends to the energy landscape. Note that in a high-dimensional space the isolated global minima can be exponentially more numerous and thus dominate the equilibrium measure, but they are “filtered out” in the local entropy description.
It is therefore natural to consider using our large-deviation statistics as a starting point to design new algorithms, in much the same way that SA uses equilibrium statistics. Indeed, this was shown to work well in ref. 15. The main difficulty of that approach was the need to estimate the local (free) entropy , which was addressed there using the belief propagation (BP) algorithm (16).
Here, we demonstrate an alternative, general, and much simpler approach. The key observation is that, when is a nonnegative integer, we can rewrite the partition function of the large deviation distribution Eq. 1 as
| [3] |
This partition function describes a system of interacting replicas of the system, one of which acts as reference while the remaining are identical, subject to the energy and the interaction with the reference . Studying the equilibrium statistics of this system and tracing out the replicas is equivalent to studying the original large deviations model. This provides us with a very simple and general scheme to direct algorithms to explore robust, accessible regions of the energy landscape: replicating the model, adding an interaction term with a reference configuration, and running the algorithm over the resulting extended system.
In fact, in most cases, we can further improve on this scheme by tracing out the reference instead, which leaves us with a system of identical interacting replicas describing what we call the RE:
| [4] |
| [5] |
In the following, we will demonstrate how this simple procedure can be applied to a variety of different algorithms: SA, SGD, and BP. To demonstrate the utility of the method, we will focus on the problem of training neural network models.
Neural Network Models
Throughout this paper, we will consider for simplicity one main kind of neural network model, composed of identical threshold units arranged in a feed-forward architecture. Each unit has many input channels and one output and is parameterized by a vector of “synaptic weights” . The output of each unit is given by , where is the vector of inputs.
Because we are interested in connecting with analytical results, for the sake of simplicity all our tests have been performed using binary weights, , where denotes a hidden unit and an input channel. We should, however, mention that all of the results generalize to the case of weights with multiple bits of precision (17). We denote by the total number of synaptic weights in the network, which for simplicity is assumed to be odd. We studied the random classification problem: Given a set of random input patterns , each of which has a corresponding desired output , we want to find a set of parameters such that the network output equals for all patterns . Thus, for a single-layer network (also known as a perceptron), the condition could be written as , where if and otherwise. For a fully connected two-layer neural network (also known as committee or consensus machine), the condition could be written as (note that this assumes that all weights in the output unit are , because they are redundant in the case of binary ’s). A three-layer fully connected network would need to satisfy , and so on. In this work, we limited our tests to one- and two-layer networks.
In all tests, we extracted all inputs and outputs in from unbiased, identical, and independent distributions.
To use methods such as SA and gradient descent, we need to associate an energy or cost to every configuration of the system . One natural choice is just to count the number of errors (misclassified patterns), but this is not a good choice for local search algorithms because it hides the information about what direction to move toward in case of error, except near the threshold. Better results can be obtained by using the following general definition instead: We define the energy associated to each pattern as the minimum number of synapses that need to be switched to classify the pattern correctly. The total energy is then given by the sum of the energy for each pattern, . In the single-layer case, the energy of a pattern is thus , where . Despite the simple definition, the expression for the two-layer case is more involved and is provided in SI Appendix. For deeper networks, the definition is conceptually too naive and computationally too hard, and it should be amended to reflect the fact that more than one layer is affected by training, but this is beyond the scope of the present work.
We also need to define a distance function between replicas of the system. In all our tests, we used the squared distance , which is proportional to the Hamming distance in the binary case.
Replicated SA
We claim that there is a general strategy that can be used by a system of interacting replicas to seek dense regions of its configuration space. The simplest example of this is by sampling the configuration space with a Monte Carlo method (18), which uses the objective functions given by Eqs. 3 or 4, and lowering the temperature via an SA procedure, until either a zero of the energy (“cost”) or a “give-up condition” is reached. For simplicity, we use the RE, in which the reference configuration is traced out (Eq. 4), and we compare our method to the case in which the interaction between the replicas is absent (i.e., , which is equivalent to running parallel independent standard SA algorithms on the cost function). Besides the annealing procedure, in which the inverse temperature is gradually increased during the simulation, we also use a “scoping” procedure, which consists of gradually increasing the interaction , with the effect of reducing the average distance between the replicas. Intuitively, this corresponds to exploring the energy landscape on progressively finer scales (Fig. 1).
Additionally, we find that the effect of the interaction among replicas can be almost entirely accounted for by adding a prior on the choice of the moves within an otherwise standard Metropolis scheme, while still maintaining the detailed balance condition (of course, this reduces to the standard Metropolis rule for ). The SA procedure is described in Materials and Methods and in more detail in SI Appendix.
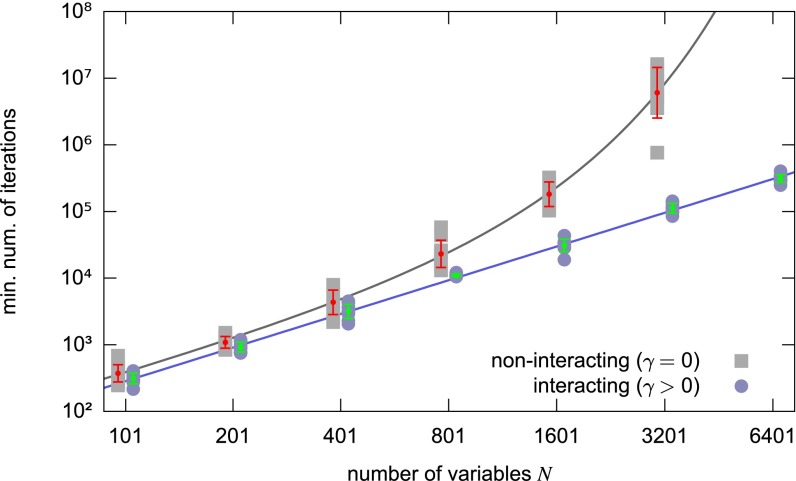
In Fig. 2, we show the results for the perceptron; an analogous figure for the committee machine, with similar results, is shown in SI Appendix, Fig. S1. The analysis of the scaling with demonstrates that the interaction is crucial to finding a solution in polynomial time: The noninteracting version scales exponentially and it rapidly becomes impossible to find solutions in reasonable times. Our tests also indicate that the difference in performance between the interacting and noninteracting cases widens greatly with increasing the number of patterns per synapse . As mentioned above, this scheme bears strong similarities to the entropy-driven Monte Carlo (EdMC) algorithm that we proposed in ref. 15, which uses the BP algorithm to estimate the local entropy around a given configuration. The main advantage of using a replicated system is that it avoids the need to use BP, which makes the procedure much simpler and more general. However, in systems where BP is able to provide a reasonable estimate of the local entropy, it can do so directly at a given temperature, and thus avoids the need to thermalize the replicas. Therefore, the landscapes explored by the replicated SA and EdMC are in principle different, and it is possible that the latter has fewer local minima; this, however, does not seem to be an issue for the neural network systems considered here.
Fig. 2.
Replicated SA on the perceptron, comparison between the interacting version (i.e., which seeks regions of high solution density) and the noninteracting version (i.e., standard SA), at patterns per synapse using replicas. With optimized annealing/scoping parameters, the minimum number of iterations required to find a solution scales exponentially with for the standard case and polynomially for the interacting case. Ten samples were tested for each value of (the same samples in both cases). The bars represent averages and standard deviations (taken in logarithmic scale) and the lines represent fits. The interacting case was fitted by a function with , , and the noninteracting case was fitted by a function with , , , . Data are not available for the noninteracting case at because we could not solve any of the problems in a reasonable time (the extrapolated value according to the fit is ). The two datasets are slightly shifted relative to each other for presentation purposes. All of the details are reported in SI Appendix.
Replicated GD
Monte Carlo methods are computationally expensive and may be infeasible for large systems. One simple alternative general method for finding minima of the energy is using GD or one of its many variants. All these algorithms are generically called backpropagation algorithms in the neural networks context (19). Indeed, GD—in particular SGD—is the basis of virtually all recent successful “deep learning” techniques in machine learning. The two main issues with using GD are that it does not in general offer any guarantee to find a global minimum and that convergence may be slow [in particular for some of the variables; cf. the “vanishing gradient” problem (20) that affects deep neural network architectures]. Additionally, when training a neural network for the purpose of inferring (generalizing) a rule from a set of examples, it is in general unclear how the properties of the local minima of the energy on the training set are related to the energy of the test set (i.e., to the generalization error).
GD is defined on differentiable systems, and thus it cannot be applied directly to the case of systems with discrete variables considered here. One possible work-around is to introduce a two-level scheme, consisting of using two sets of variables, a continuous one and a discrete one , related by a discretization procedure , and in computing the gradient over the discrete set but adding it to the continuous set: (where is a gradient step, also called learning rate in the machine learning context). For the single-layer perceptron with binary synapses, using the energy definition provided above, in the case when the gradient is computed one pattern at a time (in machine learning parlance, using SGD with a minibatch size of ), this procedure leads to the so-called clipped perceptron algorithm (CP). This algorithm is not able to find a solution to the training problem in the case of random patterns, but simple (although nontrivial) variants of it are (SBPI and CP+R; see refs. 21 and 22). In particular, CP+R was adapted to two-layer networks (using a simplified version of the two-level SGD procedure described above) and was shown in ref. 13 to be able to achieve near-state-of-the-art performance on the MNIST database (23). The two-level SGD approach was also more recently applied to multilayer binary networks with excellent results in refs. 24 and 25, along with an array of additional heuristic modifications of the SGD algorithm that have become standard in application-driven works (e.g., batch renormalization). In those cases, however, the back-propagation of the gradient was performed differently, either because the output of each unit was not binary (24) or as a work-around for the use of a different definition for the energy, which required the introduction of additional heuristic mechanisms (25).
Almost all of the above-mentioned results are purely heuristic (except in the online generalization setting, which is not considered in the present work). Indeed, even just using the two-level SGD is heuristic in this context. Nevertheless, here we demonstrate that, as in the case of SA of the previous section, replicating the system and adding a time-dependent interaction term (i.e., performing the GD over the RE energy defined in Eq. 5) leads to a noticeable improvement in the performance of the algorithm, and that when a solution is found it is indeed part of a dense region, as expected (Materials and Methods). We showed in ref. 13 that solutions belonging to maximally dense regions have better generalization properties than other solutions; in other words, they are less prone to overfitting.
It is also important to note here that the stochastic nature of the SGD algorithm is essential in this case in providing an entropic component that counters the purely attractive interaction between replicas introduced by Eq. 5, because the absolute minima of the replicated energy of Eq. 4 are always obtained by collapsing all of the replicas in the minima of the original energy function. Indeed, the existence of an entropic component allowed us to derive the RE definition by using the interaction strength to control the distance via a Legendre transform in the first place in Eq. 2; to use this technique with a nonstochastic minimization algorithm, the distance should be controlled explicitly instead.
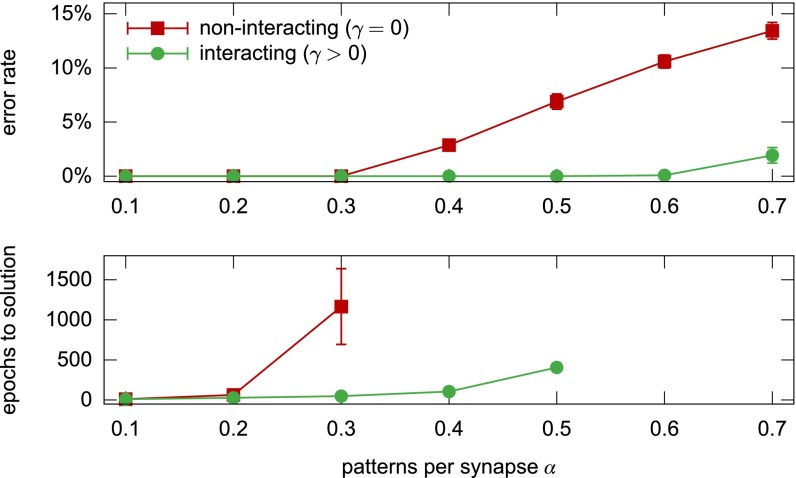
In Fig. 3 we show the results for a fully connected committee machine, demonstrating that the introduction of the interaction term greatly improves the capacity of the network (from to almost patterns per synapse), finds configurations with a lower error rate even when it fails to solve the problem, and generally requires fewer presentations of the dataset (epochs). The graphs show the results for replicas in which the gradient is computed for every patterns (the so-called minibatch size); we observed the same general trend for all cases, even with minibatch sizes of (in SI Appendix, Fig. S2 we show the results for and minibatch size ). We also observed the same effect in the perceptron, although with less extensive tests, where this algorithm has a capacity of at least . All technical details are provided in SI Appendix. These results are in perfect agreement with the analysis of the next section, on BP, which suggests that this replicated SGD algorithm has near-optimal capacity.
Fig. 3.
Replicated SGD on a fully connected committee machine with ,605 synapses and units in the second layer, comparison between the noninteracting (i.e., standard SGD) and interacting versions, using replicas and a minibatch size of patterns. Each point shows averages and standard deviations on samples with optimal choice of the parameters, as a function of the training set size. (Top) Minimum training error rate achieved after epochs. (Bottom) Number of epochs required to find a solution. Only the cases with success rate are shown (note that the interacting case at has success rate but an error rate of just ).
It is interesting to note that a very similar approach—a replicated system in which each replica is attracted toward a reference configuration, called elastic averaged SGD (EASGD)—was proposed in ref. 8 (see also ref. 26) using deep convolutional networks with continuous variables, as a heuristic way to exploit parallel computing environments under communication constraints. Although it is difficult in that case to fully disentangle the effect of replicating the system from the other heuristics (in particular the use of “momentum” in the GD update), their results clearly demonstrate a benefit of introducing the replicas in terms of training error, test error, and convergence time. It seems therefore plausible that, despite the great difference in complexity between their network and the simple models studied in this paper, the general underlying reason for the effectiveness of the method is the same (i.e., the existence of accessible robust low-energy states in the space of configurations).
Replicated BP
BP, also known as sum-product, is an iterative message-passing method that can be used to describe a probability distribution over an instance described by a factor graph in the correlation decay approximation (27, 28). The accuracy of the approximation relies on the assumption that, when removing an interaction from the network, the nodes involved in that interaction become effectively independent, an assumption linked to so-called replica symmetry (RS) in statistical physics.
Algorithmically, the method can be briefly summarized as follows. The goal is to solve a system of equations involving quantities called messages. These messages represent single-variable cavity marginal probabilities, where the term “cavity” refers to the fact that these probabilities neglect the existence of a node in the graph. For each edge of the graph there are two messages going in opposite directions. Each equation in the system gives the expression of one of the messages as a function of its neighboring messages. The expressions for these functions are derived from the form of the interactions between the variables of the graph. The resulting system of equations is then solved iteratively, by initializing the messages in some arbitrary configuration and updating them according to the equations until a fixed point is eventually reached. If convergence is achieved, the messages can be used to compute various quantities of interest; among those, the most relevant in our case are the single-site marginals and the thermodynamic quantities such as the entropy and the free energy of the system. From single-site marginals, it is also possible to extract a configuration by simply taking the of each marginal.
In the case of our learning problem, the variables are the synaptic weights, and each pattern represents a constraint (i.e., an “interaction”) between all variables, and the form of these interactions is such that BP messages updates can be computed efficiently. Also note that, because our variables are binary, each of the messages and marginals can be described with a single quantity: We generally use the magnetization, that is, the difference between the probability associated to the states and . We thus generally speak of the messages as “cavity magnetizations” and the marginals as “total magnetizations.” The factor graph, the BP equations, and the procedure to perform the updates efficiently are described in detail in SI Appendix, closely following the work of ref. 29. Here, we give a short summary. We use the notation for the message going from the node representing the weight variable to the node representing pattern at iteration step , and for the message going in the opposite direction, related by the BP equation:
| [6] |
where indicates the set of all factor nodes connected to . The expressions for the total magnetizations are identical except that the summation index runs over the whole set . A configuration of the weights is obtained from the total magnetizations simply as . The expression for as a function of is more involved and it is reported in SI Appendix.
As mentioned above, BP is an inference algorithm: When it converges, it describes a probability distribution. One particularly effective scheme to turn BP into a solver is the addition of a “reinforcement” term (29): A time-dependent local field is introduced for each variable, proportional to its own marginal probability as computed in the previous iteration step, and is gradually increased until the whole system is completely biased toward one configuration. This admittedly heuristic scheme is quite general, leads to very good results in a variety of different problems, and can even be used in cases in which unmodified BP would not converge or would provide a very poor approximation (see, e.g., ref. 30). In the case of the single-layer binary network such as those considered in this paper, it can reach a capacity of patterns per synapse (29), which is consistent with the value at which the structure of solution-dense regions breaks (13).
The reason for the effectiveness of reinforced BP has not been clear. Intuitively, the process progressively focuses on smaller and smaller regions of the configuration space, with these regions determined from the current estimate of the distribution by looking in the “most promising” direction. This process has thus some qualitative similarities with the search for dense regions described in the previous sections. This analogy can be made precise by writing the BP equations for the system described by Eq. 3. There are in this case two equivalent approaches. The first is to use the local entropy as the energy function, using a second-level BP to estimate the local entropy itself. This approach is very similar to the so-called one-step replica-symmetry-breaking (1RSB) cavity equations (see ref. 16 for a general introduction). The second approach is to replicate the system, considering vector variables of length , and assuming an internal symmetry for each variable, that is, that all marginals are invariant under permutation of the replica indices, similarly to what is done in ref. 31: . The result in the two cases is the same. Because BP assumes replica symmetry, the resulting message-passing algorithm reproduces quite accurately the analytical results at the RS level. As explained in ref. 13, these results can, however, become wrong, in particular for high values of , , and , due to the onset of correlations [the so-called replica-symmetry-breaking (RSB) effect (16)]. More specifically, in this model the RS solution assumes that there is a single dense region comprising the RE, whereas the occurrence of RSB implies that there are several maximally dense regions. As a consequence, this algorithm is not a very good candidate as a solver. A more correct description—which could then lead to a more controlled solver—would thus require a third level of BP equations, or equivalently an assumption of symmetry breaking in the structure of the marginals .
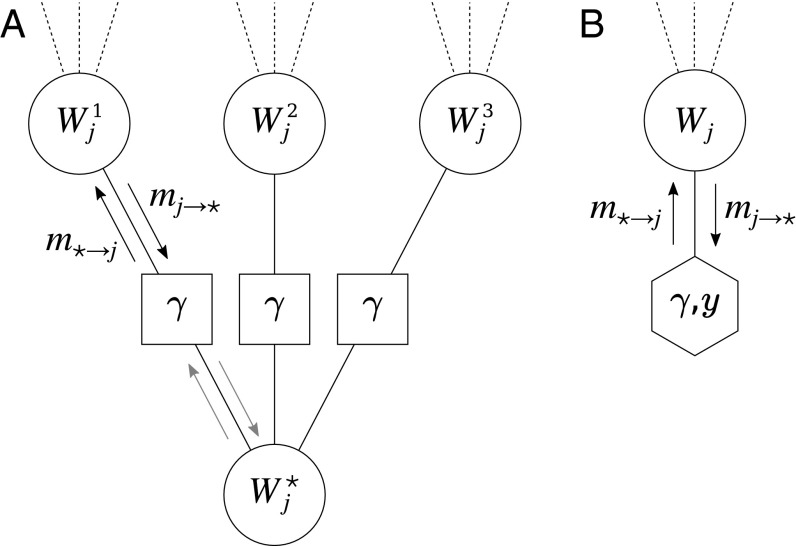
Fortunately, it turns out that that there is a different way of applying BP to the replicated system, leading to an efficient solver that is both very similar to the reinforced BP algorithm and reasonably well described by the theoretical results. Instead of considering the joint distribution over all replicated variables at a certain site , we simply replicate the original factor graph times; then, for each site , we add an extra variable , and interactions, between each variable and . Finally, because the problem is symmetric, we assume that each replica of the system behaves in exactly the same way, and therefore that the same messages are exchanged along the edges of the graph regardless of the replica index. This assumption neglects some of the correlations between the replicated variables but allows us to work only with a single system, which is identical to the original one except that each variable now also exchanges messages with identical copies of itself through an auxiliary variable (which we can just trace away at this point, as in Eq. 4). The procedure is shown graphically in Fig. 4. At each iteration step , each variable receives an extra message of the form
| [7] |
where is the cavity magnetization resulting from the rest of the factor graph at time , and is the interaction strength. This message simply enters as an additional term in the sum in the right-hand side of Eq. 6. Note that even though we started from a system of replicas, after the transformation we are no longer constrained to keep in the integer domain. The reinforced BP (29), in contrast, has a term of the form
| [8] |
Fig. 4.
(A) Portion of a BP factor graph for a replicated variable with replicas and a reference configuration . The dashed lines represent edges with the rest of the factor graph. The squares represent the interactions . All BP messages (arrows) are assumed to be the same in corresponding edges. (B) Transformed graph that represents the same graph as in A but exploits the symmetry to reduce the number of nodes, keeping only one representative per replica. The hexagon represents a pseudoself-interaction, that is, it expresses the fact that depends on and is parametrized by and .
The latter equation uses a single parameter instead of two and is expressed in terms of the total magnetization instead of the cavity magnetization . Despite these differences, these two terms induce exactly the same BP fixed points if we set and (SI Appendix). This result is somewhat incidental, because in the context of our analysis the limit should be reached gradually; otherwise, the results should become trivial (Fig. 1), and the reason why this does not happen when setting in Eq. 7 is only related to the approximations introduced by the simplified scheme of Fig. 4. As it turns out, however, choosing slightly different mappings with both and diverging gradually (e.g., and with increasing from to ) can lead to update rules with the same qualitative behavior and very similar quantitative effects, such that the performances of the resulting algorithms are hardly distinguishable, and such that the aforementioned approximations do not thwart the consistency with the theoretical analysis. This is shown and discussed in SI Appendix. Using a protocol in which is increased gradually, rather than being set directly at , also allows the algorithm to reach a fixed point of the BP iterative scheme before proceeding to the following step, which offers more control in terms of the comparison with analytical results, as discussed in the next paragraph. In this sense, we therefore have derived a qualitative explanation of the effectiveness of reinforced BP within a more general scheme for the search of accessible dense states. We call this algorithm focusing BP (fBP).
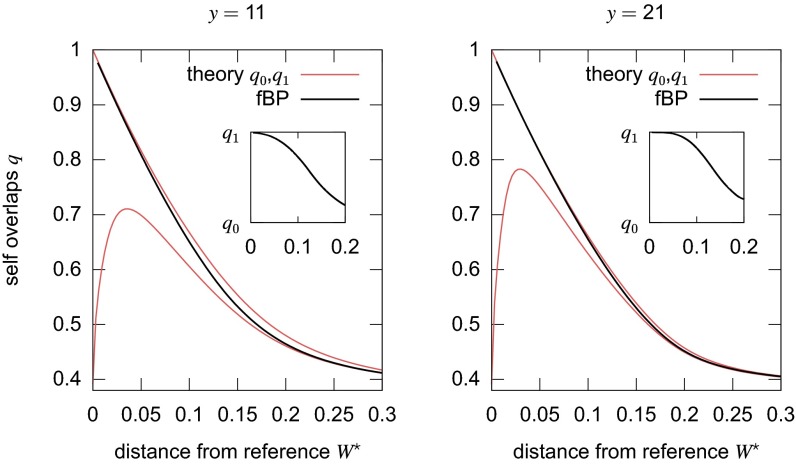
Apart from the possibility of using fBP as a solver, by gradually increasing and until a solution is found, it is also interesting to compare its results at fixed values of and with the analytical predictions for the perceptron case that were derived in refs. 13 and 15, because at the fixed point we can use the fBP messages—using the standard BP formulas—to compute such values as the local entropy, the distance from the reference configuration, and the average overlap between replicas (defined as for any and , where denotes the thermal averaging). The expressions for these quantities are provided in SI Appendix. The results indicate that fBP is better than the alternatives described above in overcoming the issues arising from RSB effects. The 1RSB scheme describes a nonergodic situation that arises from the breakup of the space of configurations into a collection of several separate equivalent ergodic clusters, each representing a possible state of the system. These states are characterized by the typical overlap inside the same state (the intracluster overlap ) and the typical overlap between configurations from any two different states (the intercluster overlap ). Fig. 5 shows that the average overlap between replicas computed by the fBP algorithm transitions from to when is increased (and the distance with the reference is decreased as a result). This suggests that the algorithm has spontaneously chosen one of the possible states of high local entropy in the RE, achieving an effect akin to the spontaneous symmetry breaking of the 1RSB description. Within the state, RS holds, so that the algorithm is able to eventually find a solution to the problem. Furthermore, the resulting estimate of the local entropy is in very good agreement with the 1RSB predictions up to at least (SI Appendix, Fig. S5).
Fig. 5.
fBP spontaneously breaks replica symmetry: The overlap order parameter (black thick curves) gradually transitions from the intercluster overlap and the intracluster overlap of the replica theory (red thin curves, ) as the distance to the reference goes to (i.e., as ). (Insets) An alternative visualization of this phenomenon, plotting against the distance. These results were obtained on a perceptron with ,001 at , averaging over samples. The two panels shows that the transition occurs at larger distances (i.e., at smaller ) at larger .
Therefore, although this algorithm is not fully understood from the theoretical point of view, it offers a valuable insight into the reason for the effectiveness of adding a reinforcement term to the BP equations. It is interesting in this context to observe that the existence of a link between the reinforcement term and the RE seems consistent with some recent results on random bicoloring constraint satisfaction problems (32), which showed that reinforced BP finds solutions with shorter “whitening times” with respect to other solvers: This could be interpreted as meaning they belong to a region of higher solution density, or are more central in the cluster they belong to. Furthermore, our algorithm can be used to estimate the point up to which accessible dense states exist, even in cases, such as multilayer networks, where analytical calculations are prohibitively complex.
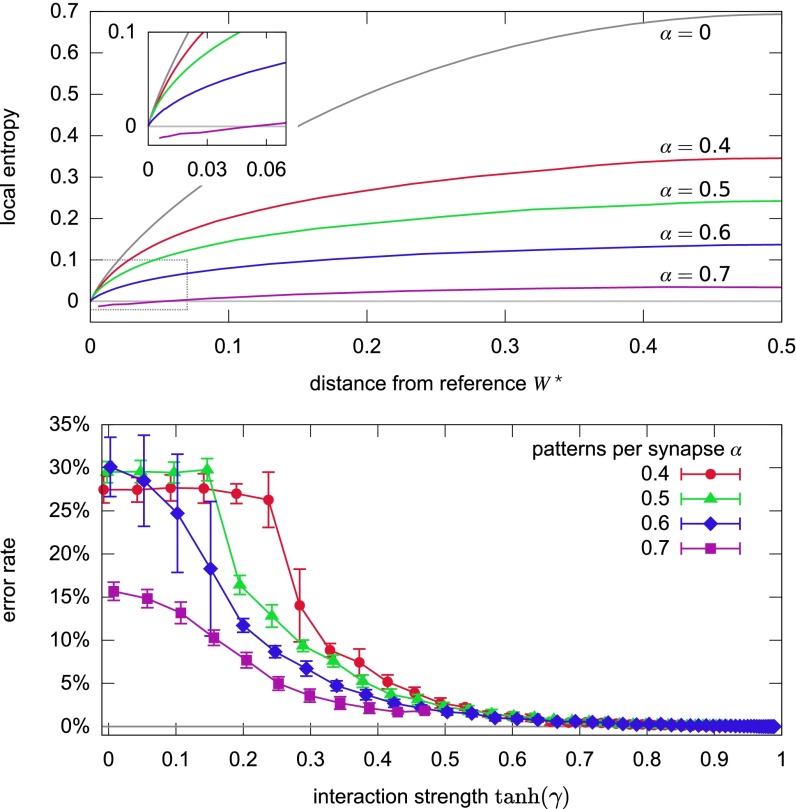
Fig. 6 shows the result of experiments performed on a committee machine with the same architecture and same of Fig. 3 (Materials and Methods). The figure shows that fBP finds that dense states (where the local entropy curves approach the upper bound at small distances) exist up to nearly patterns per synapse, and that when it finds those dense states it is correspondingly able to find a solution, in perfect agreement with the results of the replicated GD algorithm.
Fig. 6.
Results of fBP on a committee machine with ,605, , , increasing the interaction from to , averages on samples. (Top) Local entropy versus distance to the reference for various (error bars not shown for clarity). The topmost gray curve () is an upper bound, representing the case where all configurations within some distance are solutions. (Inset) Enlargement of the region near the origin indicated by the rectangle in the main plot. This shows that dense states exist up to almost patterns per synapse: At this value of , dense states are only found for a subset of the samples (in which case a solution is also found). Negative local entropies (curve at ) are unphysical, and fBP fails shortly after finding such values. (Bottom) Error rates as a function of . For , all curves eventually get to . However, only out of samples reached a sufficiently high at , whereas in three cases the fBP equations failed. The curve for is interrupted because fBP failed for all samples, in each case shortly after reaching a negative local entropy. The plateaus at and are regions where the solution to the equations are symmetric with respect to the permutation of the hidden units: fBP spontaneously breaks that symmetry as well.
Finally, we also performed some exploratory tests applying fBP on the random -satisfiability problem, and we found clear indications that the performance of this algorithm is similar to that of survey-propagation-based algorithms (10, 33), although a more detailed analysis is required to draw a more precise comparison. The results are reported in SI Appendix.
Discussion
In this paper, we have presented a general scheme that can be used to bias the search for low-energy configurations, enhancing the statistical weight of large, accessible states. Although the underlying theoretical description is based on a nontrivial large deviation measure, its concrete implementation is very simple—replicate the system and introduce an interaction between the replicas—and versatile, in that it can be generally applied to a number of different optimization algorithms or stochastic processes. We demonstrated this by applying the method to SA, GD, and BP, but it is clear that the list of possible applications may be much longer. The intuitive interpretation of the method is also quite straightforward: A set of coupled systems is less likely to get trapped in narrow minima, and will instead be attracted to wide regions of good (and mostly equivalent) configurations, thus naturally implementing a kind of robustness to details of the configurations.
The utility of this kind of search depends on the details of the problem under study. Here we have mainly focused on the problem of training neural networks, for a number of reasons. The first is that, at least in the case of single-layer networks with discrete synapses, we had analytical and numerical evidence that dense, accessible states exist and are crucial for learning and improving the generalization performance, and we could compare our findings with analytical results. The second is that the general problem of training neural networks has been addressed in recent years via a sort of collective search in the space of heuristics, fueled by impressive results in practical applications and mainly guided by intuition; heuristics are evaluated based on their effectiveness in finding accessible states with good generalization properties. It seems reasonable to describe these accessible states as regions of high local entropy (i.e., wide, very robust energy minima): The center of such a region can act as a Bayesian estimator for the whole extensive neighborhood. Here we showed a simple way to exploit the existence of such states efficiently, whatever the optimization algorithm used. This not only sheds light on previously known algorithms but also suggests improvements or even entirely new algorithms. Further work is required to determine whether the same type of phenomenon that we observed here in simple models actually generalizes to the deep and complex networks currently used in machine learning applications (the performance boost obtained by the EASGD algorithm of ref. 8 being a first indication in this direction), and to investigate further ways to improve the performance of learning algorithms, or to overcome constraints (such as being limited to very-low-precision computations).
It is also natural to consider other classes of problems in which this analysis may be relevant. One application would be solving other constraint satisfaction problems. For example, in ref. 15 we demonstrated that the EdMC algorithm can be successfully applied to the random -satisfiability problem, even though we had to resort to a rough estimate of the local entropy due to RS breaking effects. We have shown here that the fBP algorithm presented above is also effective and efficient on the same problem. It is also interesting to note here that large-deviation analyses—although different from the one of the present paper—of a similar problem, the random bicoloring constraint satisfaction problem, have shown that atypical “unfrozen” solutions exist (and can be found with the reinforced BP algorithm) well beyond the point in the phase diagram where the overwhelming majority of solutions have become “frozen” (32, 34). Finally, an intriguing problem is the development of a general scheme for a class of out-of-equilibrium processes attracted to accessible states: Even when describing a system that is unable to reach equilibrium in the usual thermodynamic sense or is driven by some stochastic perturbation, it is still likely that its stationary state can be characterized by a large local entropy.
Materials and Methods
Replicated SA.
The SA procedure used an elementary Metropolis–Hastings Monte Carlo iteration step that can be summarized as follows: i) We choose a replica uniformly at random; ii) we choose a candidate weight to flip for that replica according to a prior computed from the state of all of the replicas; and iii) we estimate the single-replica energy cost of the flip and accept it according to a standard Metropolis rule with a (usually very small) extra term.
The sampling technique (step ii above) uses a prior to choose which spin to flip. The prior for a spin that, if flipped, would result in a contribution to the interaction energy, Eq. 5, is computed from the number of spins in the same replica that would produce the same contribution, , and the number of those which would either produce the same contribution or its opposite, . For , the prior is
| [9] |
where , with the hypergeometric function, and is the Kronecker delta symbol. The prior for the case is . The move is accepted (step iii above) with probability , where is the single-replica energy shift (without the interaction). This procedure is derived and explained in more detail in SI Appendix.
The annealing procedure consisted of starting from a given inverse temperature and interaction strength and increasing them both by a constant factor after a certain number of accepted moves, until either a solution was found (by any one of the replicas or by the center, computed as their spinwise mode) or a give-up criterion was met. The details are provided in SI Appendix.
Replicated GD.
Our replicated SGD scheme uses continuous internal variables and associated binary variables , where is a synaptic index and is a replica index. The gradient is used in the update of the continuous variables, but it is computed using the discrete variables; the formula for the update of a given weight is simply the usual SGD formula plus an extra term that comes from the RE interaction, Eq. 5, with an additional step parameter :
| [10] |
This formula is derived and discussed in more detail in SI Appendix.
We used a standard SGD protocol with fixed minibatch size. During the training process, we kept the gradient steps fixed but increased in regular steps after each epoch. The training was stopped whenever a solution was found (by any one of the replicas or by their spinwise mode), or after epochs. The details are provided in SI Appendix.
Replicated BP.
Our implementation of the fBP algorithm closely follows ref. 29 with the addition of the self-interaction Eq. 7, except that great care is required to correctly estimate the local entropy at large , due to numerical issues. The formulas and the numerical issues are discussed in detail in SI Appendix.
Supplementary Material
Acknowledgments
We thank Y. LeCun and L. Bottou for encouragement and interesting discussions about future directions for this work. This work was supported by European Research Council Grant 267915 (to C. Baldassi, C.L., and R.Z.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
Data deposition: The code for the Replicated Stochastic Gradient Descent algorithm is available at https://github.com/carlobaldassi/BinaryCommitteeMachineRSGD.jl. The code for the Focusing Belief Propagation algorithm is available at https://github.com/carlobaldassi/BinaryCommitteeMachineFBP.jl.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1608103113/-/DCSupplemental.
References
- 1.LeCun Y, Bengio Y, Hinton G. Deep learning. Nature. 2015;521(7553):436–444. doi: 10.1038/nature14539. [DOI] [PubMed] [Google Scholar]
- 2.Ngiam J, et al. 2011. On optimization methods for deep learning. Proceedings of the 28th International Conference on Machine Learning (ICML-11)(International Machine Learning Society), pp 265–272. [Google Scholar]
- 3.Charbonneau P, Kurchan J, Parisi G, Urbani P, Zamponi F. Fractal free energy landscapes in structural glasses. Nat Commun. 2014;5:3725. doi: 10.1038/ncomms4725. [DOI] [PubMed] [Google Scholar]
- 4.Ricci-Tersenghi F, Semerjian G. On the cavity method for decimated random constraint satisfaction problems and the analysis of belief propagation guided decimation algorithms. J Stat Mech Theor Exp. 2009;2009:P09001. [Google Scholar]
- 5.Bressloff PC. Stochastic Processes in Cell Biology. Vol 41 Springer; Berlin: 2014. [Google Scholar]
- 6.Easley D, Kleinberg J. Networks, Crowds, and Markets: Reasoning About a Highly Connected World. Cambridge Univ Press; Cambridge, UK: 2010. [Google Scholar]
- 7.Holtmaat A, Svoboda K. Experience-dependent structural synaptic plasticity in the mammalian brain. Nat Rev Neurosci. 2009;10(9):647–658. doi: 10.1038/nrn2699. [DOI] [PubMed] [Google Scholar]
- 8.Zhang S, Choromanska AE, LeCun Y. Deep learning with elastic averaging SGD. In: Cortes C, Lawrence ND, Lee DD, Sugiyama M, Garnett R, editors. Advances in Neural Information Processing Systems 28. Curran Associates; Red Hook, NY: 2015. pp. 685–693. [Google Scholar]
- 9.Kirkpatrick S, Gelatt CD, Jr, Vecchi MP. Optimization by simmulated annealing. Science. 1983;220(4598):671–680. doi: 10.1126/science.220.4598.671. [DOI] [PubMed] [Google Scholar]
- 10.Mézard M, Parisi G, Zecchina R. Analytic and algorithmic solution of random satisfiability problems. Science. 2002;297(5582):812–815. doi: 10.1126/science.1073287. [DOI] [PubMed] [Google Scholar]
- 11.Krzakala F, Montanari A, Ricci-Tersenghi F, Semerjian G, Zdeborova L. Gibbs states and the set of solutions of random constraint satisfaction problems. Proc Natl Acad Sci USA. 2007;104(25):10318–10323. doi: 10.1073/pnas.0703685104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Zdeborová L, Mézard M. Locked constraint satisfaction problems. Phys Rev Lett. 2008;101:078702. doi: 10.1103/PhysRevLett.101.078702. [DOI] [PubMed] [Google Scholar]
- 13.Baldassi C, Ingrosso A, Lucibello C, Saglietti L, Zecchina R. Subdominant dense clusters allow for simple learning and high computational performance in neural networks with discrete synapses. Phys Rev Lett. 2015;115(12):128101. doi: 10.1103/PhysRevLett.115.128101. [DOI] [PubMed] [Google Scholar]
- 14.Huang H, Kabashima Y. Origin of the computational hardness for learning with binary synapses. Phys Rev E Stat Nonlin Soft Matter Phys. 2014;90(5):052813. doi: 10.1103/PhysRevE.90.052813. [DOI] [PubMed] [Google Scholar]
- 15.Baldassi C, Ingrosso A, Lucibello C, Saglietti L, Zecchina R. Local entropy as a measure for sampling solutions in constraint satisfaction problems. J Stat Mech Theor Exp. 2016;2016(2):P023301. [Google Scholar]
- 16.Mézard M, Montanari A. Information, Physics, and Computation. Oxford Univ Press; New York: 2009. [Google Scholar]
- 17.Baldassi C, Gerace F, Lucibello C, Saglietti L, Zecchina R. Learning may need only a few bits of synaptic precision. Phys Rev E. 2016;93(5):052313. doi: 10.1103/PhysRevE.93.052313. [DOI] [PubMed] [Google Scholar]
- 18.Moore C, Mertens S. The Nature of Computation. Oxford Univ Press; New York: 2011. [Google Scholar]
- 19.Rumelhart DE, Hinton GE, Williams RJ. Learning representations by back-propagating errors. Nature. 1988;323:533–536. [Google Scholar]
- 20.Hochreiter S. 1991. Untersuchungen zu dynamischen neuronalen netzen. Master’s thesis (Institut fur Informatik, Technische Universitat, Munich)
- 21.Baldassi C, Braunstein A, Brunel N, Zecchina R. Efficient supervised learning in networks with binary synapses. Proc Natl Acad Sci USA. 2007;104:11079–11084. doi: 10.1073/pnas.0700324104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Baldassi C. Generalization learning in a perceptron with binary synapses. J Stat Phys. 2009;136:902–916. [Google Scholar]
- 23.LeCun Y, Bottou L, Bengio Y, Haffner P. Gradient-based learning applied to document recognition. Proc IEEE. 1998;86(11):2278–2324. [Google Scholar]
- 24.Courbariaux M, Bengio Y, David JP. Binaryconnect: Training deep neural networks with binary weights during propagations. In: Cortes C, Lawrence ND, Lee DD, Sugiyama M, Garnett R, editors. Advances in Neural Information Processing Systems 28. Curran Associates; Red Hook, NY: 2015. pp. 3105–3113. [Google Scholar]
- 25.Courbariaux, Matthieu Hubara I, Soudry D, El-Yaniv R, Bengio Y. 2016. Binarized neural networks: Training deep neural networks with weights and activations constrained to +1 or -1. arXiv:1602.02830.
- 26.Zhang S. 2016. Distributed stochastic optimization for deep learning. Ph.D. thesis (New York University, New York). arXiv:1605.02216.
- 27.MacKay DJ. Information Theory, Inference and Learning Algorithms. Cambridge Univ Press; New York: 2003. [Google Scholar]
- 28.Yedidia JS, Freeman WT, Weiss Y. Constructing free-energy approximations and generalized belief propagation algorithms. IEEE Trans Inform Theor. 2005;51(7):2282–2312. [Google Scholar]
- 29.Braunstein A, Zecchina R. Learning by message-passing in neural networks with material synapses. Phys Rev Lett. 2006;96:030201. doi: 10.1103/PhysRevLett.96.030201. [DOI] [PubMed] [Google Scholar]
- 30.Bailly-Bechet M, et al. Finding undetected protein associations in cell signaling by belief propagation. Proc Natl Acad Sci USA. 2011;108(2):882–887. doi: 10.1073/pnas.1004751108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Kabashima Y. Replicated bethe free energy: A variational principle behind survey propagation. J Phys Soc Jpn. 2005;74(8):2133–2136. [Google Scholar]
- 32.Braunstein A, Dall’Asta L, Semerjian G, Zdeborová L. The large deviations of the whitening process in random constraint satisfaction problems. J Stat Mech Theor Exp. 2016;2016(5):053401. [Google Scholar]
- 33.Marino R, Parisi G, Ricci-Tersenghi F. 2015. The backtracking survey propagation algorithm for solving random K-SAT problems. arXiv:1508.05117. [DOI] [PMC free article] [PubMed]
- 34.Dall’Asta L, Ramezanpour A, Zecchina R. Entropy landscape and non-gibbs solutions in constraint satisfaction problems. Phys Rev E. 2008;77(3):031118. doi: 10.1103/PhysRevE.77.031118. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.