Development of array piezoelectric fingers towards in vivo breast tumor detection

Abstract

We have investigated the development of a handheld 4 × 1 piezoelectric finger (PEF) array breast tumor detector system towards in vivo patient testing, particularly, on how the duration of the DC applied voltage, the depression depth of the handheld unit, and breast density affect the PEF detection sensitivity on 40 patients. The tests were blinded and carried out in four phases: with DC voltage durations 5, 3, 2, to 0.8 s corresponding to scanning a quadrant, a half, a whole breast, and both breasts within 30 min, respectively. The results showed that PEF detection sensitivity was unaffected by shortening the applied voltage duration from 5 to 0.8 s nor was it affected by increasing the depression depth from 2 to 6 mm. Over the 40 patients, PEF detected 46 of the 48 lesions (46/48)—with the smallest lesion detected being 5 mm in size. Of 28 patients (some have more than one lesion) with mammography records, PEF detected 31/33 of all lesions (94%) and 14/15 of malignant lesions (93%), while mammography detected 30/33 of all lesions (91%) and 12/15 of malignant lesions (80%), indicating that PEF could detect malignant lesions not detectable by mammography without significantly increasing false positives. PEF’s detection sensitivity is also shown to be independent of breast density, suggesting that PEF could be a potential tool for detecting breast cancer in young women and women with dense breasts.

I. INTRODUCTION

In the US, there will be 234 190 invasive breast cancer cases and 63 440 carcinoma in situ (CIS) diagnosed in 2015.¹ Breast cancer is the second leading cause of cancer death and about 40 000 deaths are expected in the US in 2015. Worldwide, 500 000 women are estimated to die from breast cancer each year.² Current methods of breast cancer detection include clinical breast examination (CBE), mammography, ultrasound imaging (US), and magnetic resonance imaging (MRI). CBE relies on a physician’s palpation to detect lumps in the breast³ and is not sensitive to detect early stage breast cancers including ductal carcinoma in situ (DCIS).^4–6 So far, mammography is the only FDA approved breast cancer screening tool that can detect early stage breast cancers to lead to more effective treatments. However, mammography is not very effective for young women under 40 and women with dense breasts^7,8—the detection sensitivity decreases sharply from 87% for non-dense breasts (density score 1/4) to 62.9% for extremely dense breasts (density score 4/4).^9,10 Although US can differentiate cysts from solid tumor, it does not detect all types of breast malignancy.¹¹ Therefore it is mostly used as an auxiliary test to mammography to identify cysts.^12–14 MRI is capable of detecting small lesions undetected by mammography.¹⁵ However it has many false positives^16,17 and is prohibitively expensive.¹⁸ Besides women under 40, 43% of women 40-74 yrs old¹⁹ and most of Eastern Asian women have dense breasts.^20,21 Furthermore, breast density has been shown to be a strong predictor of the breast cancer risk^22–25—a higher breast density (core >3/4) is correlated with a 4- to 6-fold increase in breast cancer risk^25–27 while there has been little progress in how to advise women with dense breasts.²⁸ Radiology studies have shown that supplemental ultrasound imaging can detect some cancers that mammography misses in women with dense breasts but it will also substantially increase the number of false positives.^29,30 Recent clinical study with dual-energy contrast-enhanced digital mammography (CEDM) has shown better diagnostic accuracy than mammography alone and mammography plus ultrasound in dense breasts.³¹ However, CEDM is not widely used due to high cost, limited availability, and high radiation dosage.³² As such, it would be desirable to have a method that can detect breast cancer in young women and women with dense breasts without increasing false positives and also is low-cost.

Studies have shown that breast cancers are stiffer than surrounding breast tissues.^33–37 Increasingly researchers have sought to detect breast tumors by means of tissue stiffness contrast by mechanical^{33,34,38–46} or optical^47,48 means. Ultrasound elastography (UE) detects breast tumors by measuring the difference in the distribution of the echo times with and without applying pressure which is further analyzed with inversion simulations.^49–52 Breast mechanical imager (BMI or “SureTouch”) detects breast tumors with great promise by measuring the compressive stress distribution with a pressure sensor array followed by the inversion simulation analysis.^38–40 In recent years, more studies were also aiming to detect breast tumors using mechanical means. For example, a new study used an indenter to measure the normal and lateral forces which were further analyzed by artificial neural network to differentiate hard inclusions from the surrounding matrix.⁴¹ Lee and Won have investigated an optical tactile sensation imaging system (TSIS) in which stresses and strains were determined by the scattered light.^47,48 Uribe et al. used the resonance frequency shift of a vibrating piezoelectric bimorph sensor (VPBS) to relate to the stiffness of gelatin samples of different concentrations.^42,43 All the above methods including the UE,^49–52 the BMI,^39,40 the indenter technique,⁴¹ the TSIS,^47,48 and the VPBS^42,43 do not measure tissue stiffness directly. Rather, they measure the stress or strain distribution on the surface and use an inversion technique or a neural network technique to determine if there is a tumor and the location and size of the tumor if there is one. In addition, all these methods have not been proven capable of detecting breast cancer in dense breasts.

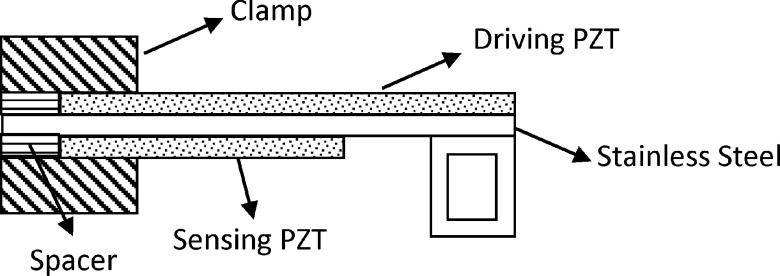
A piezoelectric finger (PEF) is a new type of tissue elasticity sensor in a cantilever form with two piezoelectric layers (see Fig. 1) that can directly measure tissue elastic modulus in situ as well as in vivo simply by placing the PEF on the tissue.^{44,45,53–56} Applying a direct-current (DC) voltage in the driving piezoelectric layer imparts a force on the tissue. The corresponding tissue displacement in turn generates an induced voltage in the sensing piezoelectric layer. Tissue elastic moduli can be directly determined from the induced voltages as described earlier.^54–57 A lesion is directly detected by contrasting the elastic modulus measured above the lesion with that measured above the surrounding tissues^44,54,55 without the need of inversion simulations or pattern recognition software. PEF has been tested on 77 cases of excised breast tissues⁴⁵ and demonstrated capable of detecting most types of breast tumors including invasive carcinoma (IC), hyperplasia, fibrocystic, DCIS, micro-calcifications, and even a 3-mm satellite IC missed by mammography and by physician’s palpation. While the above results illustrated the potential of PEF as a sensitive breast tumor detecting tool, all were obtained with a single PEF manually moved from spot to spot by an xyz positioner, which is time consuming and unfit for in vivo testing. To investigate the feasibility of PEF as a potential breast tumor detecting tool, we have fabricated a handheld unit containing a 4 × 1 PEF array and the associated electronic circuit (see Figs. 2(a)–2(c)) to test it in vivo. For the PEF array to be a viable in vivo breast tumor detection tool, it must be able to scan both breasts in a reasonable amount of time. A critical factor that can affect the time needed to scan the breasts is the duration for an applied DC voltage to the driving piezoelectric layer—it must be long enough for the induced voltage across the sensing piezoelectric layer to be accurately captured but short enough to allow speedier breast scan.

FIG. 1.

A schematic of a piezoelectric finger (PEF).

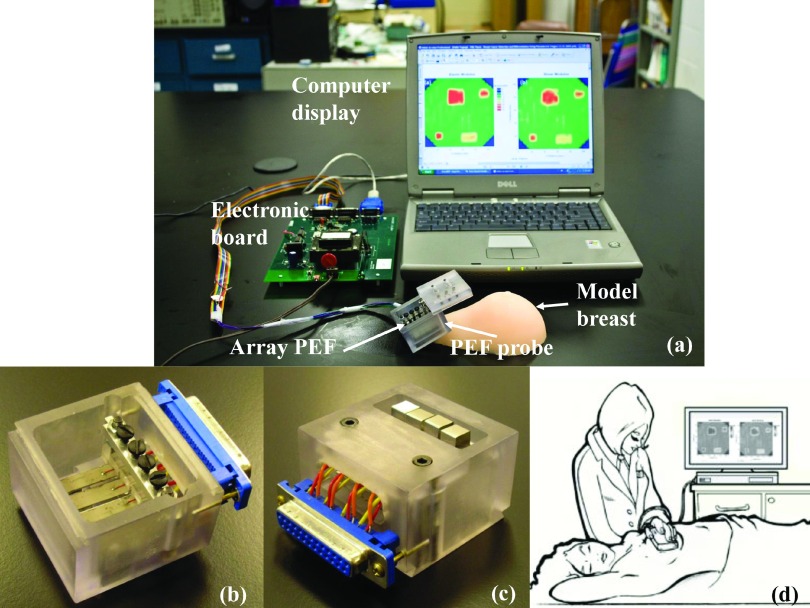
FIG. 2.

(a) A photograph of PEF breast cancer detection system which consists of PEF probe, electronic board, and a laptop for control and display; (b) the top view of the PEF probe; (c) the bottom view of the PEF probe; (d) a schematic showing how the PEF breast cancer detection system is performed on patients.

The purpose of this study is to investigate the development of this PEF array together with the custom-made electronic circuit board towards in vivo breast tumor detection. Particularly, we will investigate how (1) the DC voltage duration, (2) the depth at which the handheld unit is pressed against the breast, and (3) the breast density affect the detection sensitivity. The real-time tissue elastic modulus measurement was carried out through LabVIEW (National Instruments) programing, and the final display of a color-coded breast tissue elastic modulus map (E map) was carried out using MATLAB (MathWorks).

II. METHODS

A. Fabrication of piezoelectric finger (PEF) and the handheld unit

The handheld unit consists of a polycarbonate housing (Figs. 2(a)–2(c)) and the 4 × 1 PEF array. All four PEFs were 6.5 ± 0.5 mm wide which consists of a 127-μm thick, 22 ± 0.5 mm long lead zirconate titanate (PZT) layer (T105-H4E-602, Piezo Systems, Inc.) at the top for driving, a 50-μm thick, 22 ± 0.5 mm stainless steel layer (Alfa Aesar) in the middle, and a 127 μm thick 12 ± 0.5 mm PZT layer at the bottom for sensing as schematically shown in Fig. 1 made using a combination of a conductive epoxy (ITW Chemtronics) and a nonconductive epoxy (Henkel Loctite) and cured at room temperature overnight. A stainless steel strip was bent into a rectangular loop and glued to the free end of the cantilever (see Fig. 1) using the nonconductive epoxy. The effective spring constants of the four PEFs were determined to be 224 ± 4, 226 ± 5, 219 ± 4, and 231 ± 5 m/N using the method described in earlier publications.^55,56 The effective spring constant of each individual PEF was used together with Eq. (1) to quantify the elastic modulus of tissue measured by that PEF.

B. PEF breast tumor detection system

Fig. 2(a) shows the PEF array breast tumor detection system including the handheld 4-PEF array unit, a custom-built electronic board, and a laptop computer. Figs. 2(b) and 2(c) show a top and bottom view of the PEF array unit. As can be seen from Fig. 2(c), the bottom surface of the handheld unit was mostly flat to flatten out tissues surrounding the area under testing and make sure that the contact area of each of the four PEF was fully in contact with the tissue. Note that, because the PEFs were in a cantilever geometry, they had only one end fixed to the housing, which is different from sensors in “SureTouch”^38–40 that have all edges fixed to the housing of the device. This allowed the probe surface of a PEF at the free end of the cantilever to be free from the pressure exerted on the housing as long as the PEF was “recessed” from the bottom surface of the housing (see Fig. 2(c)). Such an arrangement allows (1) protection of the PEFs from unintentional touching of the PEF tip which can damage the PZT layer and (2) desensitization of the PEFs from the pressure exerted by the hand on the housing against the breast (see Sec. III A). Fig. 2(d) is an illustration of the PEF measurement with the patient in a supine position.

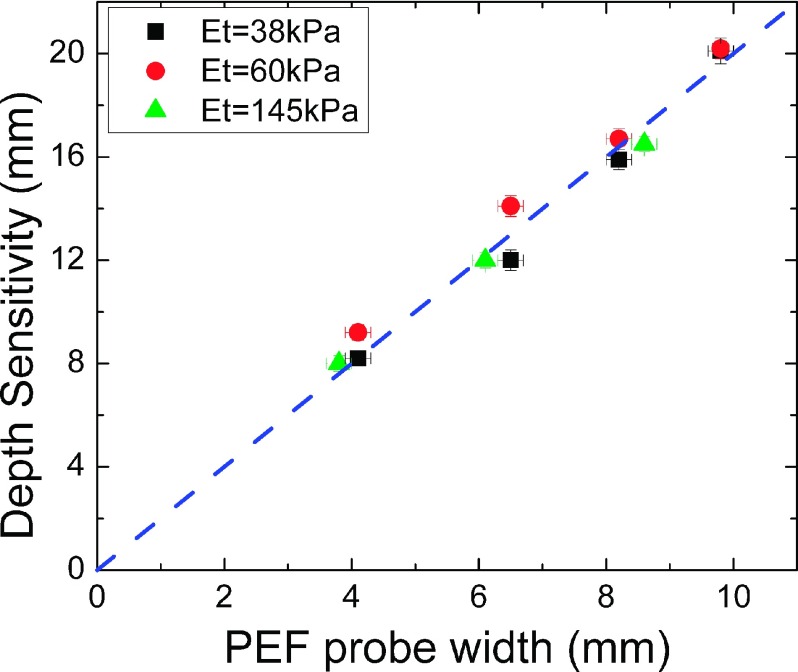
PEF is an indentation technique. It can only assess the mechanical properties of tissues within a certain depth beneath the surface. We define the depth sensitivity of a PEF as the depth within which the mechanical properties of tissues can be assessed by the PEF. The depth sensitivity of a PEF could be determined by elastic modulus measurements over model tissues containing an array of model tumors of different depths, and it was empirically determined as the depth of a model tumor at which the measured effective elastic modulus of the model tumor no longer differed from that of the surrounding model tissues.⁵³ In earlier studies with a single PEF without a housing, the depth sensitivity of a PEF was shown to be about twice the probe width. Using a similar approach, we had determined the depth sensitivities of the PEFs with the housing gently placed on the model tissue surface without depressing the model tissue. The obtained depth sensitivity versus PEF contact (probe) width is shown in Fig. 3. As can be seen, the depth sensitivity of a PEF inside the handheld housing was still about twice the width of the probe size and insensitive to the elastic moduli of the model tumors. This indicates that the current PEF array with a 6.5 mm wide probe had depth sensitivity about 13-15 mm. By further pushing the probe housing to depress the breast by 4-6 mm (see Sec. III A), the depth sensitivity could reach over 2 cm. As we would show below, this seems to be sufficient for detecting tumors in a normal-size breast as illustrated by the encouraging results from the 40 patients tested. For larger breasts and deeper tumors, PEFs with a larger probe width can be used, which was not within the scope of this study. Although one advantage of using a PEF array is that all PEFs can carry out measurements simultaneously, in the current study, the PEFs were used to do measurements sequentially to avoid the interference from the neighboring PEFs when more than one PEF were activated simultaneously. Studies using a PEF array that can mitigate the interference of neighboring PEFs and carry out simultaneous measurements are not within the scope of this study and will be examined in a future publication. The electronic board as designed and fabricated by M Squared Electronics was used to generate the applied voltages on the driving PZT of a selected PEF and to read the induced voltages from the sensing PZT of the PEF. It communicates with the laptop through a USB port.

FIG. 3.

A PEF’s depth sensitivity versus its probe width where the black squares, red circles, and green triangles represent data obtained with the elastic moduli of the inclusions being 38 ± 4 kPa, 60 ± 5 kPa, and 145  ± 10 kPa, respectively. The blue dashed line with a slope of 2. Clearly, the depth sensitivity of a PEF was twice of the probe width, regardless of the elastic moduli of the inclusions. *Note the green triangles were taken from Ref. 38.

C. PEF indentation elastic modulus measurements

A PEF measures the tissue stiffness as follows. Applying a direct current (DC) voltage to the top PZT layer of a PEF causes the PEF to bend due to the converse piezoelectric effect. Furthermore, the bending of the PEF generates an induced piezoelectric voltage in the sensing PZT layer.⁵⁶ It has been shown^44,56 that the induced voltage is proportional to the PEF tip displacement, d. Therefore, the induced voltage can be used to represent the d.^44,56 As a result, the elastic modulus, E, of the tissue is deduced as

$${\displaystyle E=\frac{1}{2}{\left(\frac{\pi }{A}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left(1-{\nu }^2\right)\frac{K(V_{\mathit{in},0}-V_{\mathit{in}})}{V_{\mathit{in}}},}$$ (1)

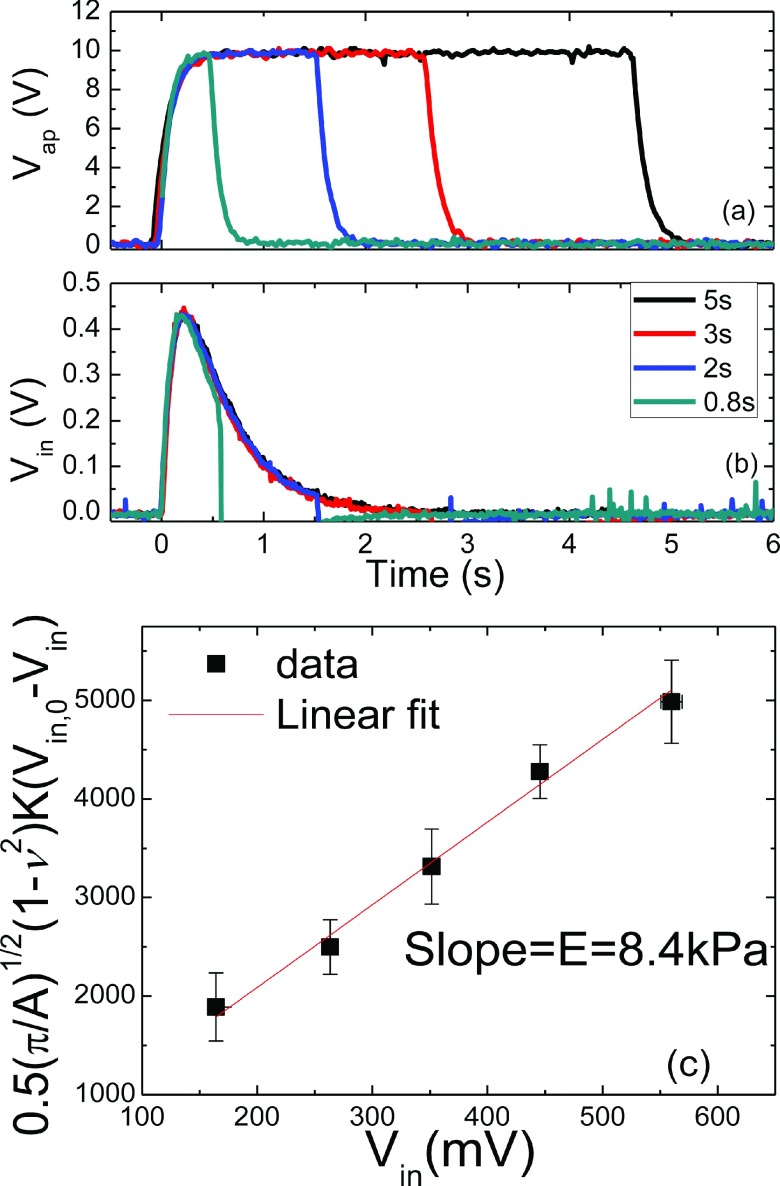
where V_in,0 and V_in are the induced voltages without and with the tissue, respectively, ν is the Poisson’s ratio of the tissue, A is the contact area defined by the stainless steel probe at the tip of the PEF, and K is the effective spring constant of the PEF. As an example, we show the applied voltage, V_ap, versus time in Fig. 4(a) and the induced voltage, V_in, versus time in Fig. 4(b) for durations of 5, 3, 2, and 0.8 s in black, red, blue, and green curves, respectively. As can be seen, for V_ap = 10 V, V_in increased rapidly from zero at t = 0 and reached a maximum of about 0.43 V at around t = 0.21 s for all four durations. For convenience, in what follows, we simply refer to V_in as the maximum of V_in reached at around t = 0.21 s. With a measurement time frame of about 0.2 s after indentation is initiated, the PEF measurements are not likely to be affected by the relaxation of tissues which requires a much longer time (>10 s).⁵⁸ In addition, PEF typically exerted small strains (<0.1%) at which there was negligible viscoelastic effect on the measured elastic modulus in vitro.⁵⁹ For these reasons we neglected the viscoelastic effect in the present study. However, living tissues may exhibit different viscoelastic behavior from those removed from the body. It is important to examine if the viscoelastic effect on the measured elastic modulus can be similarly negligible in vivo and it may be a topic of a future publication.

FIG. 4.

(a) V_ap versus time, (b) V_in versus time for durations of 5, 3, 2, and 0.8 s, and (c) an example of $0.5{\left(\pi /A\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left(1-{\nu }^2\right)K(V_{\mathit{in},0}-V_{\mathit{in}})$ versus V_in, where the slope of the linear fitting was 8.4 kPa which was taken as the elastic modulus of the model gelatin.

To use Eq. (1) to deduce the elastic modulus, E, at a particular location of the tissue, a series of five different V_ap’s were applied to a free PEF to obtain the corresponding induced voltages without the tissue, V_in,0’s. The PEF probe was then brought in contact with the tissue. The same series of five V_ap’s were applied to the PEF, and the corresponding induced voltages, V_in’s, which were different from the V_in,0 were recorded. To deduce E of the tissue, $(1/2){\left(\pi /A\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left(1-{\nu }^2\right)K(V_{\mathit{in},0}-V_{\mathit{in}})$ was then plotted versus V_in as shown in Fig. 4. E of the tissue (gelatin in this case) was deduced to be 8.4 kPa as determined by the slope of the curve. LabVIEW programming was used to conduct the measurement, record and plot the data, and deduce the E values.

D. Breast models and the measurement procedures

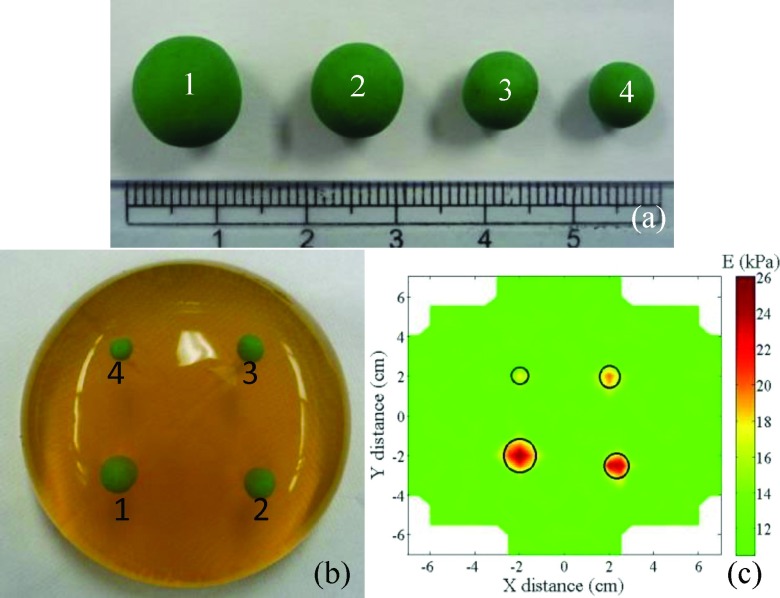
As an example, a model breast tissue consisting of a gelatin (Now Foods, Bloomingdale, IL) matrix with four suspended model tumors of green modeling clay (Crayola) (see Fig. 5(a)) was shown in Fig. 5(b). The concentration of the gelatin matrix was 0.10 g/ml, and its E was similar to that of normal breast tissues, about 10 kPa.^13,45,60,61 The model clay was chosen because its E of 60 kPa was similar to those of breast tumors measured ex vivo using PEF reported in Ref. 45 as well as in this study (not shown). In addition, these choices were consistent with the E values of normal breast tissues and those of breast tumors reported in the literature, which were 3-33 kPa and 6-107 kPa, respectively^{35–37,62–64} as shown in Table SI in the supplementary material. The diameters of model tumors were 11.5 ± 0.3 mm, 10.3 ± 0.3 mm, 7.8 ± 0.2 mm, and 6.2 ± 0.2 mm, respectively. The depths of model tumors—which measure how far the top of the model tumors was under the gelatin surface—were 6.8 ± 0.4 mm, 9.3 ± 0.3 mm, 8.0 ± 0.3 mm, and 5.5 ± 0.2 mm, respectively. Before the measurement, a grid was drawn on the model surface for location tracking. The PEF probe was placed on the first location and the E measurements were performed by activating the four PEFs sequentially. Each elastic modulus measurement required five applied voltages to the driving PZT of a PEF and deducing the elastic modulus as the slope of $(1/2){\left(\pi /A\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left(1-{\nu }^2\right)K(V_{\mathit{in},0}-V_{\mathit{in}})$ versus V_in as described above. Three repeated elastic modulus measurements were made for each location to obtain an average elastic modulus and the standard deviation. Using the average elastic modulus, E obtained at each location, a color-coded E map was then created to visualize where and how big the tumor was. As an example, Fig. 5(c) shows a color-coded E map of the model tissue shown in Fig. 5(b), where the green color represents the E of the gelatin matrix while the red color represents the elevated E of the modeling clay. The actual locations of the tumors were marked by the black circles. As can be seen, the PEF system indeed detected all the model tumors. The locations of model tumors determined by the PEF system also agreed with their actual locations. The lateral sizes of the model tumors as determined by the widths of the half peak heights are listed in Tables I and II. Also shown were the actual sizes measured with a caliper. The sizes estimated by PEF were larger than the actual ones by about 1-2 mm in the direction parallel to the PEFs and by about 1.5-3 mm in the direction perpendicular to the PEFs. The larger errors in the direction perpendicular to the PEFs were presumably due to the larger interval perpendicular to the PEF array—1 cm as opposed to the 7.5 mm in the parallel direction—between two adjacent measurements.

FIG. 5.

(a) Model tumors 1, 2, 3, and 4 made of green modeling clay. The diameters of the model tumors were 11.5 ± 0.3 mm, 10.3 ± 0.3 mm, 7.8 ± 0.2 mm, and 6.2 ± 0.2 mm, respectively; (b) a photograph of the model breast made of gelatin with the four model tumors suspended in it. The distances from the top of the model tumors to the gelatin surface were 6.8 ± 0.4 mm, 9.3 ± 0.3 mm, 8.0 ± 0.3 mm, and 5.5 ± 0.2 mm, respectively; (c) elastic modulus (E) map of the model breast of gelatin with clay model tumors scanned by the PEF breast cancer detection system. The actual locations of the tumors are marked with black circles.

TABLE I.

The sizes of model tumors in Fig. 5(a) measured in the direction parallel to the PEF array.

	Size in the direction parallel to the PEF array
Model tumor	Measured (mm)	Actual (mm)	Error (mm)
1	13.1 ± 0.6	11.5 ± 0.3	1.6
2	12.2 ± 0.5	10.3 ± 0.3	1.9
3	9.1 ± 0.7	7.8 ± 0.2	1.3
4	7.0 ± 0.5	6.2 ± 0.2	0.8

TABLE II.

The sizes of model tumors in Fig. 5(a) measured in the direction perpendicular to the PEF array.

	Size in the direction perpendicular to the PEF array
Model tumor	Measured (mm)	Actual (mm)	Error (mm)
1	13.0 ± 0.5	11.5 ± 0.3	1.5
2	13.0 ± 0.6	10.3 ± 0.3	2.7
3	10.7 ± 0.5	7.8 ± 0.2	2.9
4	8.1 ± 0.6	6.2 ± 0.2	1.9

E. In vivo measurements

40 patients were recruited under the institutional review board (IRB), and blinded in vivo tests were carried out on these patients in a supine position as illustrated in Fig. 2(d) in the outpatient clinic of AB from May 2011 to April 2012 before their breast cancers were removed by surgery. 39 of the patients had a breast abnormality identified by either palpation, mammography, or ultrasound, and 1 patient had no breast abnormality. In all patients, the operator had no knowledge if there was a tumor within the tested area nor did she know the location or the extent of the tumor. The accuracy of the PEF measurement was assessed by comparing with the PEF results with the pathology reports. The PEF results were also compared to those of mammography and other imaging modalities when available.

Due to the limited scanning time (30 min) of in vivo measurements, we carried out our study in four phases. In the beginning, a long duration time of 5 s was used for each applied DC voltage to fulfill to the requirement of DC voltages. Under such conditions, only a quadrant of a breast could be completed in 30 min (phase I, n = 18). Because of this constraint, the surgeon would tell the operator which breast and which quadrant to test. Other than that, the operator had no knowledge if there was a tumor in that quadrant, or the size, or the location of the tumor. In phase II (n = 9) the duration of applied DC voltage was shortened to 3 s. As a result, one half of the breast could be completed. Because of this, the surgeon would tell the operator which half of the breast to test. Other than that the operator did not know if there was a tumor in that half of the breast, or the location, or the size of the tumor. In phase III (n = 7), we decreased the duration of the applied voltage to 2 s so that a whole breast could be completed in 30 min. Because of this, the surgeon would tell the operator which breast to scan. However, again the operator did not know if there was a tumor in that breast, or the location, or the size of the tumor. In phase IV (n = 6) we further reduced the duration of the applied DC voltage to 0.8 s. As a result, both breasts could be completed in 30 min. In this final phase, the operator would scan both breasts while having no knowledge as to whether there was a tumor in either breast, or the location, or the size of the tumor. Note that all testing protocols such as shortening of the DC voltage duration time and the automated data acquisition were all well validated in model tissue studies before testing in vivo.

To create a coordinate system on a breast, a rectangular grid with a 1-cm increment was created on the breast with a washable marker. At each spot, the handheld unit was pressed against the breast with the same depression depth as marked on the outside of the housing (see the illustration by Fig. 6(a)). Three independent measurements were made to obtain an average and a standard deviation of the elastic modulus of the spot. The step size of the measurement was 7.5 mm in the x direction (which was parallel to the PEF array) and 1 cm in the y direction (which was perpendicular to the PEF array). The measurements were repeated until the entire assigned area was scanned. A 2-D elastic modulus (E) map of the scanned area of the breast was then created with green representing the E values of the normal breast tissues and red representing the elevated E values of the tumors as illustrated above for model tissues in Fig. 5(c).

FIG. 6.

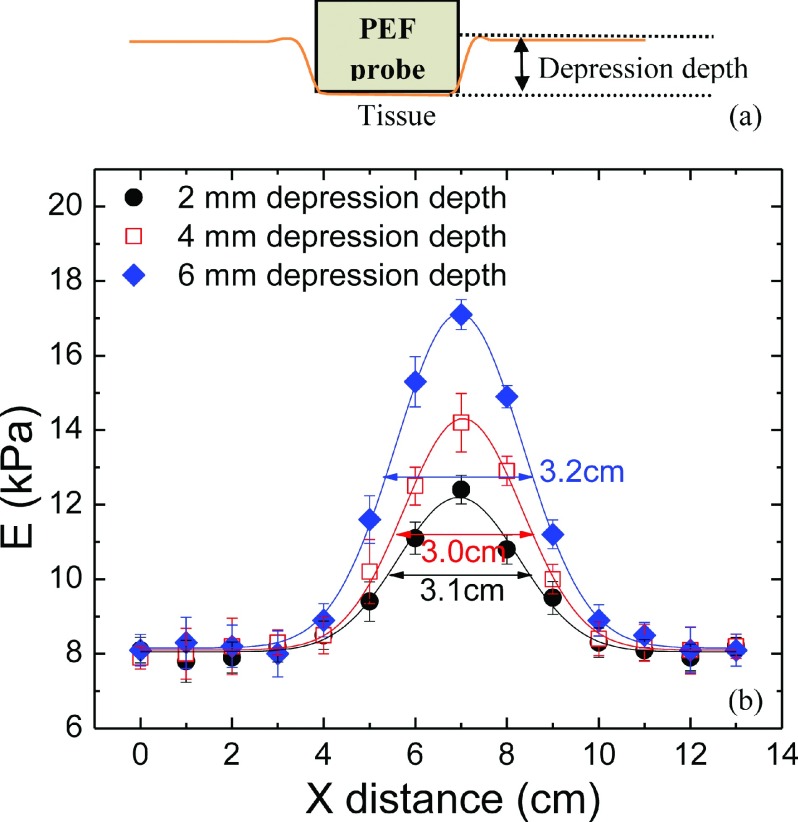
(a) A schematic of the probe of PEF being pushed in with a depression depth during the in vivo measurement, and (b) the measured elastic modulus at y = 5 cm versus distance around a tumor center at x = 7 mm with a 2-mm (full circles) depression depth, 4-mm (open squares), and a 6-mm (full diamonds) depression depth. Note that the elastic modulus of the normal tissue away from the tumor remained unchanged regardless the depression depths. Although the measured elastic modulus at the center of the tumor became larger, the size of the tumor taken as the width at the half peak height of the Gaussian fit was 3.1 cm with a 2-mm depression depth, 3.0 cm with a 4-mm depression depth, and 3.2 cm with a 6-mm depression depth, which was essentially the same within the experimental uncertainty of about 10%.

III. RESULTS AND DISCUSSIONS

A. Lateral tumor size determination and effect of depression depth

During measurements, the handheld unit was pressed against the breast with a depression depth as illustrated in Fig. 6(a). To examine the effect of the depression depth on the detection of the tumors, we examined the effect of different depression depths: 2 m, 4 mm, and 6 mm on the tumor size determination in 15 patients. To determine the size of the tumor at a certain y with a certain depression depth, the elastic modulus, E, at that y value with that depression depth was plotted as a function of x. As an example, E versus x at y = 5 cm obtained with 2-mm, 4-mm, and 6-mm depression depths is shown as black full circles, red open squares, and blue full diamonds in Fig. 6(b). The curve was then fitted to a Gaussian distribution (solid line). The size of the tumor with each depression depth was determined as the width at the half peak height of the Gaussian fit, which was 3.1 cm, 3.0 cm, and 3.2 cm, respectively, as shown in Fig. 6(b), indicating that the choice of the depression depth did not alter the measured tumor size. The reason is that increasing the depression depth did not alter the elastic moduli of the normal tissues at the bottom of the bell-shaped curves but only heightened the elastic moduli within the perimeter of the tumor as the depression pushed the PEFs closer to the tumor.

For the 15 cases tested with three depression depths (2 mm, 4 mm, and 6 mm) during phases I and II, PEF detected 16 out of 17 lesions with all three depths. The one lesion missed was due to the fact that the area with the lesion was not scanned. Furthermore, the sizes of the same tumor as determined by the three different depression depths were all within 10% of each other as similar to the results shown in Fig. 6(b), indicating that for practical purpose, the measured tumor size was largely independent of the depression depth of 2 mm, 4 mm or 6 mm, which is also supported by a more systematic study on model breast tumors presented in the supplementary material. Since the resultant tumor sizes were fairly insensitive to the choice of the depression depth, in the following, unless specified, all PEF measurements were carried out with a 4-mm depression depth. The size of the tumor in the y direction at a certain x was obtained in a similar fashion. The reported tumor sizes in the x and y directions were the largest in those directions. Note that in the current study, with only one probe size, it was insufficient for tumor depth (z) profile determination.

B. Tumor detection performance in the four phases

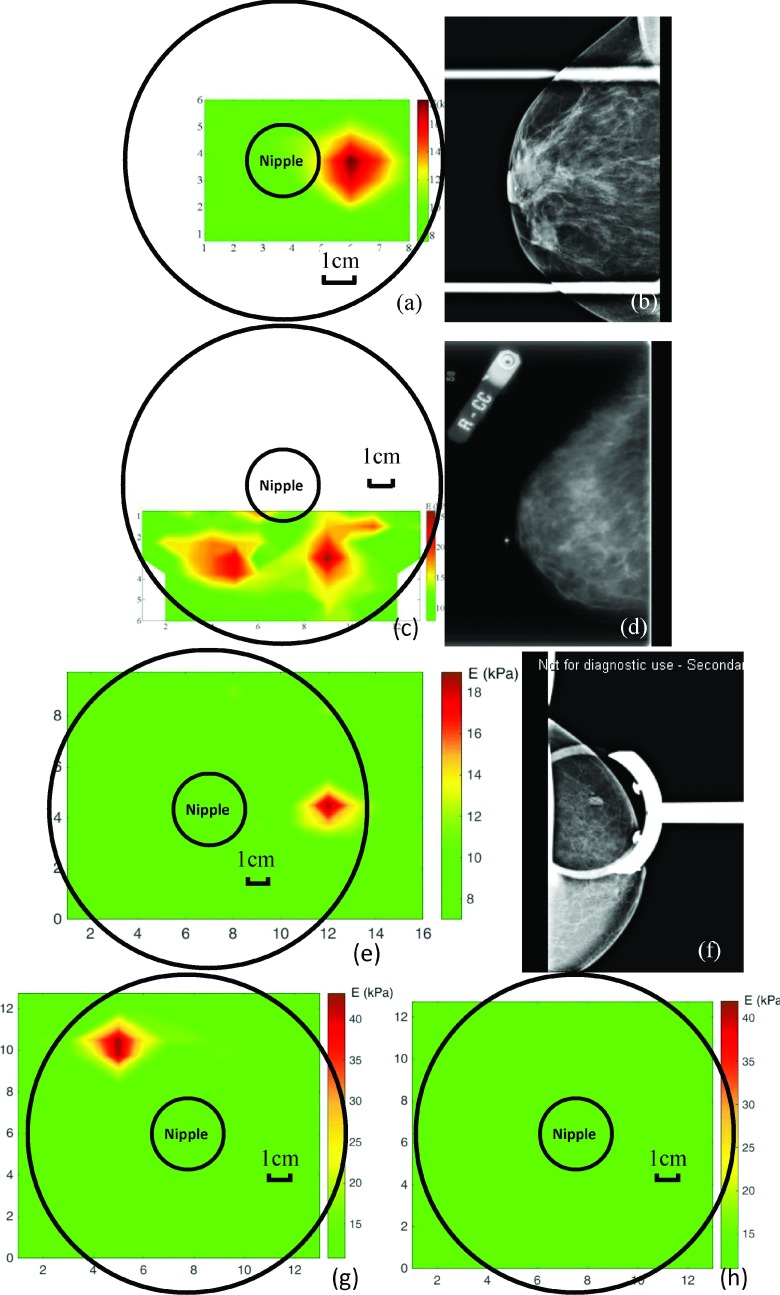
A summary of the age, race, and tumor type distributions of the 40 subjects is given in Table III. The result of the PEF scan on each subject was presented as a color-coded E map on a breast in polar coordinates in angle (in o’clock) and distance (in centimeter) with the nipple as the origin. As an example, the E map of subject 1 obtained in phase I and that of subject 2 in phase II is shown in Figs. 7(a) and 7(c), respectively. These represent two of the partial scans obtained in phase I and phase II due to the time limitation as mentioned above. The green color represents the E values of the normal breast tissues ranging from 8 to 11 kPa, and the red color represents the elevated E values of ≥15 kPa (which was at least 35% larger than the E values of the normal tissues as we will show in Figs. 8(a)–8(d)). Note that most of the patients had an E value of the normal breast tissues ranging from 8 to 11 kPa. Within the same patient the E values of the normal breast tissues were quite uniform with a standard deviation less than 15%. The E map in Fig. 7(a) shows that PEF detected a 2.4 cm × 2.5 cm lesion at 3 o’clock on the border of the nipple, which was consistent with the mammogram shown in Fig. 7(b) that exhibited a spiculated lesion in the subareolar region. The E map in Fig. 7(c) shows the PEF detected two lesions: a 1.5 cm × 2.1 cm lesion at 5 o’clock and 4 cm from the nipple and a 2.4 cm × 2.0 cm lesion at 7 o’clock and 4 cm from the nipple. These lesions were missed by the mammogram shown in Fig. 7(d) but were confirmed as two DCIS by the pathology report. Furthermore, subject 2’s mammography report indicated that the breast was dense with a density score of 3-4. These results illustrate that PEF could detect tumors in dense breasts that were difficult to detect by mammography. It is of interest to note that the two lesions in subject 2 were also found by MRI (not shown). Fig. 7(e) represents an E map of a complete scan of the left breast of subject 3 obtained in phase III which indicated a 1.9 × 1.3 cm lesion at 3 o’clock and 5 cm from the nipple, consistent with a lesion found in mammogram of the craniocaudal projection (see Fig. 7(f)) and was confirmed as an invasive carcinoma by the pathology report. The E maps of right and left breasts obtained in phase IV are shown in Figs. 7(g) and 7(h), respectively. As can be seen, PEF detected a 1.9 × 2.1 cm lesion at 10 o’clock and 6 cm from nipple in right breast which was confirmed as an invasive carcinoma by the pathology report while no lesions were detected in the left breast which was consistent with the results of mammography.

TABLE III.

Summary of the 40 subjects in the in vivo study.

Age (20-77)	20-40	15
	41-50	10
	51-60	8
	61-80	7
Race	African American	24
	Asian	2
	Caucasian	14
Tumor type	Malignant	14
	Ductal carcinoma in situ (DCIS)	2
	Invasive ductal carcinoma (IDC)	12
	Benign	25
	Cyst	5
	Fibroadenoma	7
	Adenosis stromal fibrosis	1
	Apocrine metaplasia	1
	Fat necrosis	3
	Stromal fibrosis	1
	Usual ductal hyperplasia	2
	Other	5
	No tumor	1

FIG. 7.

(a) The E map of the right breast of subject 1 in phase I indicating a 2.4 × 2.5 cm lesion at 3 o’clock on the border of nipple, consistent with an irregular mass with a spiculated margin in the subareolar region found in (b) the mammography of the same breast shown in (a); (c) the E map of the right breast of subject 2 in phase II, indicating a 1.5 × 2.1 cm lesion at 5 o’clock and 4 cm from nipple and a 2.4 × 2.0 cm lesion at 7 o’clock and 4 cm from nipple, both confirmed by pathology as DCIS but missed by (d) the mammography of the same breast shown in (c), which showed a dense breast with no visible sign of lesions; (e) the E map of the left breast of subject 3 in phase III, indicating a 1.9 × 1.3 cm lesion at 3 o’clock and 5 cm from nipple, which was confirmed by biopsy as an invasive carcinoma and shown by (f) the mammogram of the same breast in (e); (g) the E map of the right breast and (h) that of the left breast of subject 4 in phase IV obtained within 30 min indicating a 1.9 × 2.1 cm lesion at 10 o’clock and 6 cm from the nipple in the right breast which was confirmed as an invasive carcinoma by biopsy while no lesions in the left breast, which was consistent with the results of mammography.

FIG. 8.

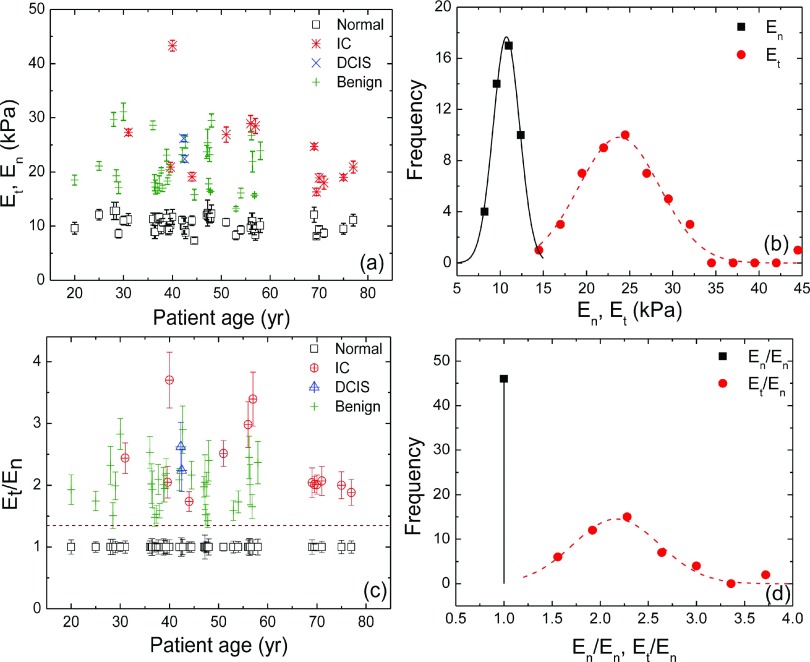
(a) E_t, E_n versus age of 40 patients, (b) distributions of E_t (red) and E_n (black) as obtained from (a), (c) E_t/E_n and E_n/E_n versus age, and (d) distribution of E_t/E_n and E_n/E_n, where E_n stands for the elastic moduli of normal breast tissues (□) and E_t is the maximum elastic moduli in the tumor regions: benign tumor (+), DICS (×), and IC (*) and the solid and dashed bell-shaped curves in (b) represent the Gaussian fits to the distributions of E_n and E_t, respectively and the dashed bell-shaped curve in (d) represents the Gaussian fit to the distribution of E_t/E_n.

1. Consistency of tumor detection sensitivity throughout the four phases

From the examples shown in Figs. 7(a)–7(h), it seemed that increasing the detection speed did not adversely affect the capability of the PEFs to detect tumors over the four different phases of the study. This was indeed the case. In the 40 subjects enrolled in the study, a total of 48 lesions were confirmed by pathology or other imaging modalities such as mammography, ultrasound, and MRI. PEF detected 20 out of 20 lesions (20/20) in phase I, 10 of 11 lesions (10/11) in phase II, 7 out of 8 lesions (7/8) in phase III, and 9 of 9 lesions (9/9) in phase IV. As can be seen, PEF detected all the lesions in phase I and phase IV and missed only 1 lesion which was malignant in phase II and 1 lesion which was benign in phase III. The reason that PEF missed a malignant lesion in phase II was because PEF scanned only half of the breast and did not scan the part containing the lesion while the missed benign tumor in phase III was a nonpalpable lesion detected by mammography. Clearly, as PEF progressed to faster scans with a shorter duration of each applied voltage, the detection accuracy remained consistent through the four phases, indicating that the shortened duration time of each applied DC voltage did not affect PEF’s detection sensitivity. With all four phases, PEF detected 45 of the 47 lesions (45/47) including 15 malignant lesions (15/16) with only 1 missed malignant tumor in phase II and 1 missed benign tumor in phase III as explained above. A breakdown of the detection sensitivity in terms malignant or benign lesions in each of the phases is shown in Table IV.

TABLE IV.

Summary of the detection sensitivity of PEF in different phases in terms of lesions and in terms of patients.

	Detection sensitivity in terms of lesions		Detection sensitivity in terms of patients
	Lesions detected by PEF	Malignant lesions detected by PEF	Patients detected by PEF	Malignant patients detected by PEF
Phase I	20/20 (100%)	7/7 (100%)	18/18 (100%)	6/6 (100%)
Phase II	10/11 (91%)	5/6 (83%)	8/9 (89%)	4/5 (80%)
Phase III	7/8 (88%)	2/2 (100%)	5/6 (83%)	2/2 (100%)
Phase IV	9/9 (100%)	1/1 (100%)	6/6 (100%)	1/1 (100%)
Total	46/48 (96%)	15/16 (94%)	37/39 (95%)	13/14 (93%)

2. Difference between elastic moduli of tumors and those of normal breast tissues

Denoting the maximum elastic modulus measured by PEF using Equation (1) within the region above the tumor as E_t, and the elastic modulus of the normal breast tissue away from the tumor as E_n, we plot E_t (various colored symbols) and E_n (open squares) of the 40 subjects versus subject age in Fig. 8(a). Note that E_t was the effective elastic modulus of the tumor embedded/surrounded by normal breast tissues. The actual elastic modulus was not measurable in an in vivo study as the breast tumors were not removed from the patients. As can be seen from Fig. 8(a), E_n hovered around 10 kPa, while E_t were much larger than E_n for all patients from phase I to IV. The distributions of E_t (red circles) and E_n (black squares) are plotted in Fig. 8(b) with the solid and dashed bell-shaped curves indicating the Gaussian fits to distributions of E_n and E_t, respectively. Figs. 8(a) and 8(b) together indicated that the distribution of E_t and that of E_n barely overlapped. To further illustrate the separation of E_t and E_n, the ratio E_t/E_n of the patient is plotted in Fig. 8(c) where the E_n was normalized as unity for each patient. The distribution of E_t/E_n is plotted in Fig. 8(d) with the dashed bell-shaped curve indicating the Gaussian fit to the distribution of E_t/E_n. Since all elastic moduli were normalized with E_n, the distribution of E_n/E_n is a vertical line at unity. Clearly, E_t/E_n was well separated from unity with a cutoff of about E_t/E_n = 1.35, indicating that E_t was larger than E_n by at least 35%, which was 2.3 times larger than the standard deviation of E_n (not shown). This cutoff worked well for all ages and the p value of the t test between E_t and E_n was much smaller than 0.001 indicating they are indeed different.

3. Comparison of PEF tumor detection sensitivity and location with mammography

There were 28 patients with mammography records. In Table V, we compare the detection sensitivity of PEF with that of mammography within these 28 patients throughout each of the four phases. Because we had different number of patients in different phases, the PEF detected 17/17, 7/8, 4/5, and 3/3 lesions for phase I-IV, respectively, and 31/33 overall while mammography detected 16/17, 6/8, 5/5, and 3/3 lesions for the corresponding phases and 30/33 overall. Overall, PEF detected about the same numbers of lesions as mammography for patients with mammography records, indicating that PEF do not generate more false positives than mammography. We also compare the detection sensitivity of malignant tumors between PEF and mammography in Table V for patients with mammography records as well. The PEF detected 7/7, 5/6, 1/1, and 1/1 malignant lesions for phase I-IV, respectively, and 14/15 (93%) overall while mammography detected 6/7, 4/6, 1/1, and 1/1 malignant lesions for phases I-IV, respectively, and 12/15 (80%) overall. Note the one malignant tumor was missed by PEF in phase II because PEF did not scan that half of the breast. That PEF had higher malignant tumor detection sensitivity (93%) than mammography (80%) while had similar all-tumor detection sensitivity with mammography indicates that PEF could detect malignant tumors not detectable by mammography without significantly increasing false positives.

TABLE V.

Detection sensitivity of PEF and mammography based on 28 patients with mammography reports.

	Detection sensitivity of PEF		Detection sensitivity of Mammography
	Total lesions detected by PEF	Malignant lesions detected by PEF	Total lesions detected by mammography	Malignant lesions detected by mammography
Phase I	17/17 (100%)	7/7 (100%)	16/17 (94%)	6/7a (86%)
Phase II	7/8 (88%)	5/6 (83%)	6/8 (75%)	4/6b (67%)
Phase III	4/5 (90%)	1/1 (100%)	5/5 (100%)	1/1 (100%)
Phase IV	3/3 (100%)	1/1 (100%)	3/3 (100%)	1/1 (100%)
Total	31/33 (94%)	14/15 (93%)	30/33 (91%)	12/15 (80%)

^aMammography missed 1 invasive carcinoma.

^bMammography missed 2 DCIS as shown in Fig. 7(d).

We also compared the locations of the lesions found in these 28 mammography reports as determined by PEF and by mammography. The position of a tumor determined by a different method may differ due to the fact that breasts are soft and movable and different methods may manipulate the breasts differently and thus produce somewhat different tumor locations. For example, PEF and US examined un-compressed breasts when the patients are supine while mammography and MRI require breasts to be compressed between two plates when the patients are standing or on the stomach, and pathology examined surgically excised breast tissues ex vivo. Because PEF does not require compressing a breast between two plates like mammography or MRI, the location, i.e., polar angle in o’clock determined by PEF may not be the same as that determined by mammography. For these reasons, we allowed some angular tolerance when comparing the tumor locations found by PEF to those found by mammography. With the 2 o’clock tolerance, we found that the locations determined by PEF agreed with those determined by mammography among tumors found by both PEF and mammography.

C. Comparison with palpation

Compared to palpation, PEF detected 32/32 palpable tumors (11 malignant and 21 benign). More importantly, PEF detected 12 of the 14 non-palpable lesions (12/14) including 2 of 3 non-palpable cancers (2/3). As mentioned above, one non-palpable malignant lesion was not scanned by PEF in phase II because PEF did not scan the area containing the tumor. Not counting this one, the sensitivity for the non-palpable lesions would be 92% (12/13) instead of 86% (12/14).

D. Tumor size comparison

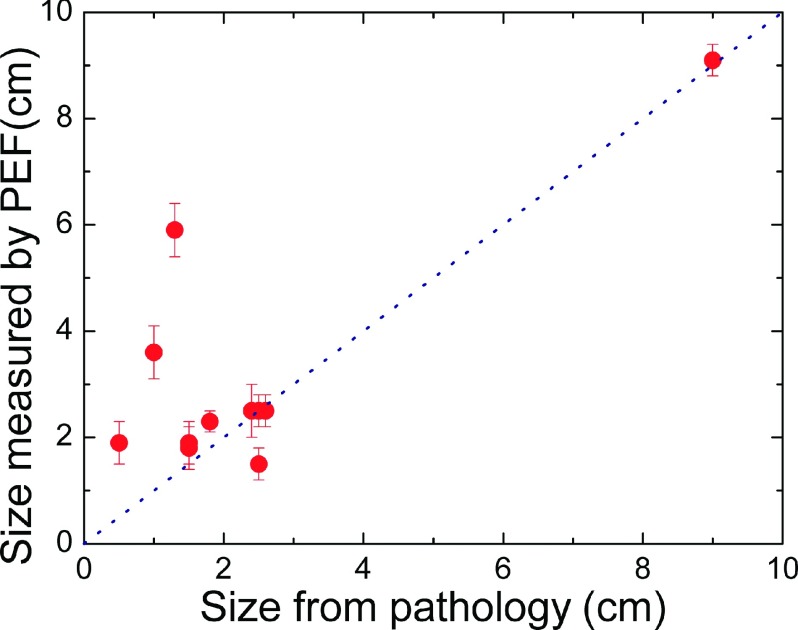
We compared to the tumor sizes reported in the pathological reports which were available only for malignant tumors. Since the orientation of the tumor during PEF measurement might not be exactly the same as that during pathological analysis, we defined the size of the tumor as the largest dimension by both the PEF and pathology. The size determined by PEF versus the size by pathology is plotted in Fig. 9. The size of the smallest cancer PEF detected was 0.5 cm. For some of the cancers (6/11), the size obtained by PEF was the same as that determined by pathology, for others (4/11) PEF indicated a larger size than pathology. Since PEF was able to determine the model tumor sizes fairly accurately, we speculate that the larger size obtained by PEF for some of the cancers might be the manifestation of the stroma surrounding the cancer as stroma was made of collagens which were also stiffer than normal breast tissues. Note that in one subject, the size determined by PEF was 5.9 ± 0.5 cm, which was much larger than the pathological size of 1.3 cm. This was because the patient had three cancerous lesions that were close to one another. The sizes of these three lesions were 1.3 cm, 0.7 cm, and 0.4 cm from the pathology report. Because they were close together, PEF could not resolve them as separate tumors. As a result, the PEF size was much larger than the size determined by pathology.

FIG. 9.

Tumor size determined by PEF versus tumor size measured by pathology.

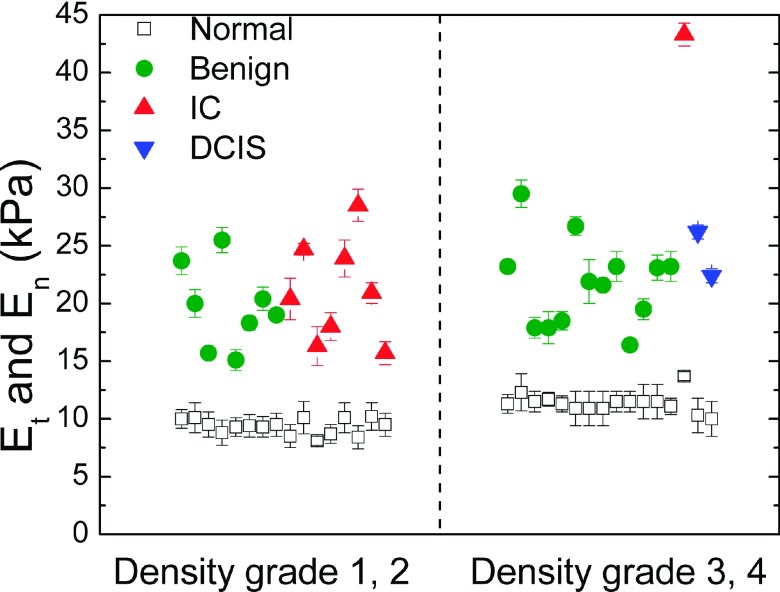
E. Breast density

PEF uses tissue elastic modulus contrast, i.e., E_t/E_n instead of density contrast to detect tumors. Therefore, the sensitivity of PEF does not depend on the mammography density of the breast. To illustrate this point, we separate the patients into two groups, low-density group (with density score 1 or 2) and high density group (density score 3 or 4), and separate E_n and E_t versus patient number into these two groups in Fig. 10. The breast density score is classified using the BI-RADS (American College of Radiology Breast Imaging Reporting and Data System) scoring system. Density score 1 indicates that the breast is entirely fat and grade 4 means the breast is extremely dense. The result shows that denser breasts had a larger E_n. However, for all density scores, the E_t were well separated from E_n, indicating that PEF was able to detect tumors in both dense breasts and non-dense breasts. Remarkably, PEF detected tumors with 100% sensitivity in women 40 years old or younger who generally have dense breasts and for whom mammography is not very sensitive.⁶⁵ Combining this with the results PEF detected more malignant tumors than mammography (Sec. III B 3) without significantly increasing false positives indicates that PEF could be a potential tool for detecting breast cancer in young women and women with dense breasts.

FIG. 10.

Maximum elastic modulus of tumor region E_t (full symbols), and elastic modulus of normal tissues, E_n (open squares), versus mammography density score.

IV. CONCLUSION

We have investigated the development of a handheld 4 × 1 PEF array breast tumor detector system towards in vivo patient testing, particularly on how the duration of the DC applied voltage, the depression depth of the handheld unit, and the breast density affect the results of the blinded testing. The tests were carried out in four phases: with DC voltage durations 5, 3, 2, to 0.8 s corresponding to scanning a quadrant, a half, a whole breast, and both breasts within in 30 min, respectively. The detection results for all four phases showed similar sensitivity, indicating that shortening the duration of the applied voltage did not affect the accuracy of the measurements. It is also shown that for the 15 cases tested for depression depths of 2-6 mm, the detection results in terms of detection sensitivity and tumor size were unaffected by different depression depths. Overall, PEF detected 46 of the 48 lesions (46/48). The smallest malignant tumor detected by PEF in this study was 5 mm. For the 28 patients with mammography reports, PEF detected 31/33 of all lesions and 14/15 of malignant lesions as compared with 30/33 of all lesions and 12/15 of malignant lesions by mammography, indicating that PEF could detect malignant tumors which are not detectable by mammography without significantly increasing false positives. Furthermore, PEF detection was independent of breast density, suggesting that PEF could be a potential tool for detecting breast cancer in young women and women with dense breasts. We envision that PEF will be used as a prescreening tool to detect breast cancer in the office of a family physician or a gynecologist. If the PEF detects something, the patient may be followed up with further testing with mammography, ultrasound, or MRI. As a start, it can be an aid to clinical breast exam (CBE) and eventually can replace the CBE as it is more sensitive than CBE and can provide a quantitative location of the tumor. In developing countries such as India and China where mammography is not widely available, such a breast cancer prescreening tool will be particularly useful.

SUPPLEMENTARY MATERIAL

See supplementary material for the effects of depression depth on the determination of tumor size and a summary of elastic moduli of various breast tissues from literature.