Large numbers of vertebrates began rapid population decline in the late 19th century

Significance

The current rate of species extinction is ∼1,000 times the background rate of extinction and is attributable to human impact, ecological and demographic fluctuations, and inbreeding due to small population sizes. The rate and the initiation date of rapid population decline (RPD) can provide important clues about the driving forces of population decline in threatened species, but they are generally unknown. We analyzed the genetic diversity data in 2,764 vertebrate species. Our population genetics modeling suggests that in many threatened vertebrate species the RPD on average began in the late 19th century, and the mean current size of threatened vertebrates is only 5% of their ancestral size. We estimated a ∼25% population decline every 10 y in threatened vertebrate species.

Abstract

Accelerated losses of biodiversity are a hallmark of the current era. Large declines of population size have been widely observed and currently 22,176 species are threatened by extinction. The time at which a threatened species began rapid population decline (RPD) and the rate of RPD provide important clues about the driving forces of population decline and anticipated extinction time. However, these parameters remain unknown for the vast majority of threatened species. Here we analyzed the genetic diversity data of nuclear and mitochondrial loci of 2,764 vertebrate species and found that the mean genetic diversity is lower in threatened species than in related nonthreatened species. Our coalescence-based modeling suggests that in many threatened species the RPD began ∼123 y ago (a 95% confidence interval of 20–260 y). This estimated date coincides with widespread industrialization and a profound change in global living ecosystems over the past two centuries. On average the population size declined by ∼25% every 10 y in a threatened species, and the population size was reduced to ∼5% of its ancestral size. Moreover, the ancestral size of threatened species was, on average, ∼22% smaller than that of nonthreatened species. Because the time period of RPD is short, the cumulative effect of RPD on genetic diversity is still not strong, so that the smaller ancestral size of threatened species may be the major cause of their reduced genetic diversity; RPD explains 24.1–37.5% of the difference in genetic diversity between threatened and nonthreatened species.

Although preservation of biodiversity is vital to a sustainable human society, rapid population decline (RPD) continues to be widespread across taxa (1–3). When RPD occurs, it is accompanied by a loss of genetic diversity. Genetic diversity is reflected in the genetic differences among individuals and is essential for populations to adapt to changing environments (4). The start date and the rate of RPD provide useful information for effective conservation of threatened species and are important for promotion of public awareness of the threat. However, these two key parameters are difficult to estimate because there are virtually no time-series data on population size over hundreds of years. For most species, the population size may only be traced back to 40 y (2). Therefore, an alternative approach is to estimate the start date and the rate of RPD, using mathematical modeling.

Changes in population size over thousands of years could be inferred for a species from genome-wide DNA polymorphism data (5–7). However, it remains a formidable technical challenge to infer the event of RPD because the signal of such an event is weak in the typical time scale of observable polymorphisms (8). To overcome the limited resolution power of the genetic data from a single species, we propose an approach that draws conclusions based on the collective support from many species. The central premise of our approach is that the threat of extinction of thousands of species was primarily due to a common cause in the past that led to a significant depletion of available habitats and resources. Consequently, we were able to draw conclusions based on present-day polymorphism data from a large number of threatened species and their nonthreatened relatives. Our method is depicted in Fig. 1. Here we studied RPD in vertebrates, because vertebrates have been more extensively investigated in the past. However, our conclusions should have some generality because vertebrate species live in a wide range of ecosystems. Moreover, the proposed method is also suitable for studying nonvertebrate species.

Fig. 1.

Schematic inference on the start date and the rate of RPD under one particular demographic model. The coalescence simulations were conducted conditional on the sample sizes, the numbers of loci, the pattern of missing data, the generation times, the census sizes, the species distributions, and the years of sampling. The data were summarized as the relative difference in four genetic diversity measurements between two species groups. The species categorized as near threatened (NT) and least concern (LC) are treated as the nonthreatened species. The threatened species include those listed as critically endangered (CR), endangered (EN), and vulnerable (VU) (6). The uncategorized species include those that are listed as data deficient and have not been evaluated by the IUCN.

Results and Discussion

Data Collected.

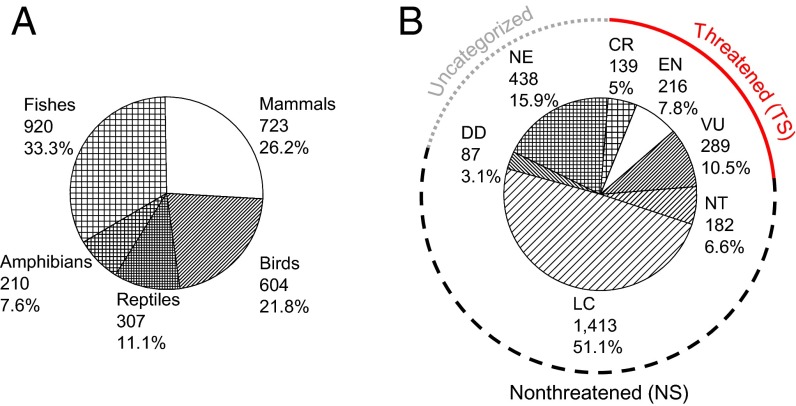
We reviewed more than 10,000 peer-reviewed papers published in the last two and half decades, among which ∼2,500 papers in 164 scientific journals were found to have surveyed the genetic diversity of at least one vertebrate species. The level of genetic diversity was measured with one of the following summary statistics (9): the expected and observed heterozygosity ($H_e$ and $H_o$), the number of alleles per locus ($\alpha$) at the microsatellite loci, Watterson’s ${\theta }_w$ (10), and the mean number of nucleotide differences per nucleotide site between two mitochondrial sequences ($\pi$). The collected dataset includes 2,764 vertebrate species belonging to 1,466 genera and 465 families (Fig. 2). Then, we used the International Union for Conservation of Nature (IUCN) Red List categories (3) to determine the level of extinction risk for each species, and the species were categorized into three groups: nonthreatened species (NS), threatened species (TS), and uncategorized species (Fig. 2B). The uncategorized species include (i) those that are listed as data deficient and (ii) those that have not been evaluated by the IUCN. A taxon is listed as data-deficient when there is inadequate information to make an assessment of its risk of extinction (3). The uncategorized species were excluded from our analyses (Fig. 1), unless noted otherwise.

Fig. 2.

Categories of the 2,764 vertebrate species used in this study. (A) The number and relative proportion of the species in each taxon category. (B) IUCN Red List categories of the examined species and their relative proportions. CR, critically endangered; DD, data deficient; EN, endangered; LC, least concern; NE, not evaluated; NT, near threatened; VU, vulnerable. The threatened species include the species of critically endangered, endangered, and vulnerable, and the nonthreatened species include the near-threatened and least-concern species.

Comparison of Genetic Diversity Between Nonthreatened and Threatened Species.

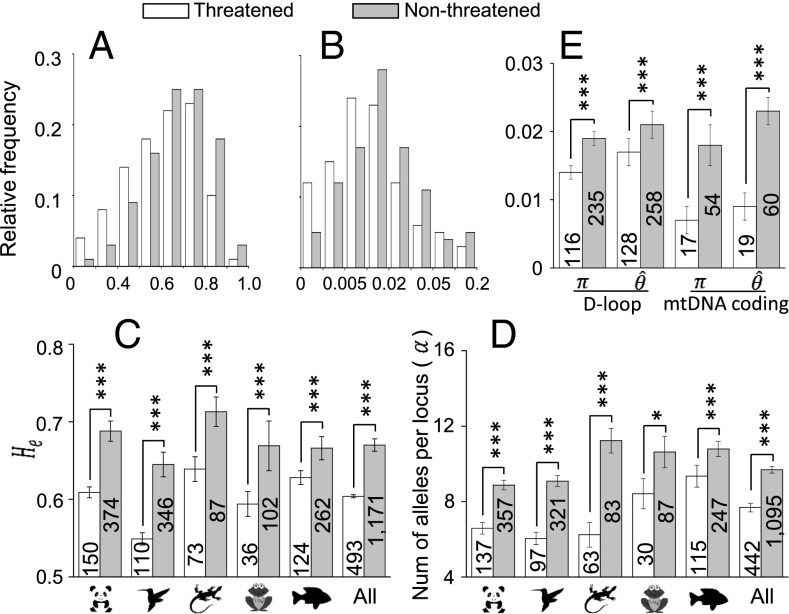
Following a previous study (11), we compared the genetic diversity between nonthreatened and threatened vertebrate species using the permutation test (12). The establishment of those IUCN categories does not rely on the information of genetic diversity. Although the distributions of genetic diversity of nonthreatened and threatened species overlap (Fig. 3 A and B and SI Appendix, Fig. S1), the mean genetic diversity of nonthreatened species is significantly higher than that of related threatened species in all 16 comparisons (Fig. 3 C–E and SI Appendix, Table S1), generally agreeing with the previous finding (11). The results remain the same when we recompiled the data with different numbers of microsatellite loci ($<\text{or}\ge 10$ loci) or different sequenced lengths of the D-loop ($<\text{or}\ge 500$ bp) (SI Appendix, Fig. S2).

Fig. 3.

Comparisons of genetic diversity between nonthreatened and threatened vertebrate species. (A) Empirical distributions of $H_e$ on microsatellite loci. (B) Empirical distributions of Watterson’s ${\theta }_w$ calculated from sequence variation in the D-loop (control region) of mitochondrial DNA. (C) Results of the permutation test on $H_e$ of microsatellite loci between nonthreatened and threatened species. (D) Results of the permutation test on the number of alleles per microsatellite locus ($\alpha$) between nonthreatened and threatened species. (E) Results of the permutation test on Watterson’s ${\theta }_w$ and the mean pairwise nucleotide differences ($\pi$) in the D-loop and coding regions in the mitochondrial genome. The null hypothesis of the permutation test is that the mean genetic diversity of nonthreatened species is equal to that of threatened species. The numbers of species examined are shown on the columns, and the one-tailed P values of the test are shown above the columns. The SEM is presented as an error bar. To ensure a reliable estimation of genetic diversity for a species, we required a sample size of $n\ge 20$ individuals. *P < 0.05, ***P < 0.01.

To examine whether differences in population structure can explain the reduction in genetic diversity of threatened species, we first compared the Fst values (an indicator of recent population structure estimated from microsatellite loci) between two species groups and found no significant difference (P = 0.25) (SI Appendix, Table S2). Next, we calculated the one-tailed P values of Tajima’s D (13) for the mitochondrial DNA polymorphism data, which is sensitive to ancient but not recent population structure (14). There was also no significant difference between the two species groups (P = 0.67) (SI Appendix, Table S2). Thus, population structure differences are unlikely the principle cause of the difference in genetic diversity between nonthreatened and threatened species.

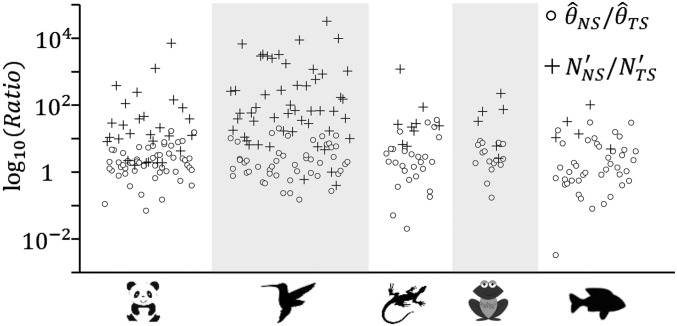
To assess the impact of recent demographic change on genetic diversity of threatened species, we considered pairs of nonthreatened and threatened species from the same family. For each pair we calculated the ratio of the long-term effective population size ($N_e$) and the ratio of the effective population size at present $N\left(0\right)$. The observed genetic diversity provides an estimate of $N_e=\theta /4\mu$ for autosomes (15) or $N_e=\theta /\mu$ for mitochondrial DNA (10), where $\mu$ is the mutation rate per generation. Therefore, the ratio of $N_e$ between two species groups was estimated as ${\widehat{\theta }}_{NS}/{\widehat{\theta }}_{TS}$ for either autosomal or mitochondrial loci, where the subscripts NS and TS stand for nonthreatened and threatened species, respectively. Also, the ratio of $N\left(0\right)$ was approximated by the ratio of the current census size $N\prime$. This is based on the finding that the ratio of effective to actual population size ($f=N\left(0\right)/N\prime$) has a mean value of 0.1 (16) and is largely independent of $N\prime$. We found that $N_{e,NS}/N_{e,TS}$ (median 1.89, the 5th and 95th percentiles 0.16 and 15.32, respectively) is remarkably smaller than $N_{NS}\left(0\right)/N_{TS}\left(0\right)$ (median 36.95, the 5th and 95th percentiles 1.9 and 3,282.9, respectively) ($P<{10}^{-5}$) (Fig. 4 and SI Appendix, Tables S3 and S4). This may indicate a much larger ancestral size and a RPD across all or most of the threatened taxa.

Fig. 4.

Ratios of long-term effective population size (circles, measured as ${\widehat{\theta }}_{NS}/{\widehat{\theta }}_{TS}$) and ratios of effective population size at present (crosses, measured as ${N\prime }_{NS}/{N\prime }_{TS}$) between nonthreatened and threatened species for five vertebrate classes. Species group pairs are from the same family. $\widehat{\theta }$ was calculated using the D-loop of mitochondrial DNA (10) and allelic variation at microsatellite loci (15).

We suggest that the recent impacts on population size could be measured by $N_{NS}\left(0\right)/N_{TS}\left(0\right)$ and normalized by ${\widehat{\theta }}_{NS}/{\widehat{\theta }}_{TS}$. Then we examined which families of species were affected the most or the least (SI Appendix, Table S5). A larger impact index indicates that one or a few threatened species in the family experienced a more severe population decline.

Demographic Models.

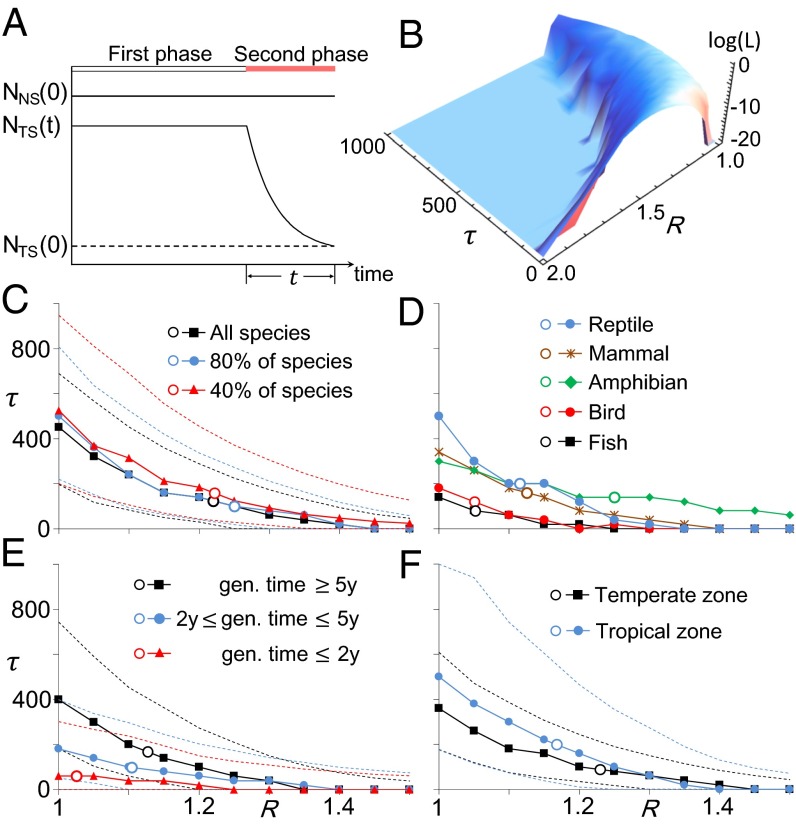
We used a model-based approach to quantify the RPD. One model is illustrated in Fig. 5A. The essential premise is that many threatened species began the RPD at similar times due to the increased impact of human activities and habitat losses. Specifically, the model assumes that each threatened species began an exponential decrease in size $t$ years ago, which follows a distribution with the mean equal to $\tau$, whereas nonthreatened species have maintained a constant population size (the case of nonthreatened species with nonconstant size is examined below). Naturally, the time $t$ splits the population history into two phases (Fig. 5A). We define $R=E\left({\theta }_{w,NS}\left(t\right)\right)/E\left({\theta }_{w,TS}\left(t\right)\right)\approx E\left(N{\prime }_{NS}\left(t\right)\right)/E\left(N{\prime }_{TS}\left(t\right)\right)$, which is the ratio of the ancestral genetic diversity of nonthreatened species to that of threatened species at time $t$ and represents the difference in census size between the two species groups before RPD.

Fig. 5.

Coalescence-based modeling and analysis. (A) The two-phase model of exponential population decline for threatened species with a constant effective population size of nonthreatened species during both phases. (B) The likelihood surface obtained from the analysis. (C) The estimates based on the data from all studied species and subgroups of species. The estimates ($\widehat{R}$, $\widehat{\mathrm{\tau }}$) are shown by open circles, the estimates of τ conditional on R are shown in solid lines, and their 95% confidence intervals are given in dashed lines. The estimates for the case of 40% species were averaged over five random replicates. (D) The estimates based on the microsatellite data from five taxa. (E) The estimates based on the data from species with different generation times. (F) Results from species categorized as temperate and tropical zones.

To estimate the two parameters ($R$ and $\tau$), a numerical approximation of their likelihood $L\left(R,\tau \right)$ was obtained using the principle of rejection sampling (5, 17, 18) after representing the data as the relative differences in the mean genetic diversity between the two species groups (Methods). Then we explored each of the scenarios with the start date of RPD that follows the normal, the exponential, and the one-point (i.e., constant) distribution with the mean $\tau$. The SD of the normal distribution was estimated as the SD of $\widehat{t}$ among 18 well-documented mammal and bird species (SI Appendix, Table S6). The estimated $\widehat{\tau }$ is 111, 154, and 123 y, respectively. Judging from the amount of uncertainty associated with these estimates, it seems that $\widehat{\tau }$ is robust with regard to the assumption of the distribution of $t$. However, assuming a nonconstant $t$ will lead to a substantial increase in computation/simulation time in subsequent analyses. Therefore, only the one-point distribution of $t$ was implemented in the subsequent analyses.

The surface of the likelihood $L\left(R,\tau \right)$ is shown in Fig. 5B. The estimate $\widehat{R}$ is 1.22 (Fig. 5C) with a 95% confidence interval between 1.11 and 1.35, implying that the ancestral size of threatened vertebrate species was, on average, 22% smaller than that of nonthreatened vertebrate species. As expected, $R$ is more precise than $N_{e,NS}/N_{e,TS}$ estimated above because the latter was estimated from the small number of species and had a very large variance. The corresponding $\widehat{\tau }$ is 123 y with a 95% confidence interval of 20–260 y, and the rate of RPD ($\widehat{\lambda }$) implies a 24.5% population decline every 10 y. The results suggest that the difference in genetic diversity between the two species groups (Fig. 3) was due to the joint effect of the smaller ancestral size of threatened species and the RPD that began on average in the late 19th century. Then, the effect of RPD was quantified by comparing the simulated genetic diversity between the cases of RPD and no RPD. We found that RPD explains 24.1–37.5% of the difference in genetic diversity between the two species groups (SI Appendix, Table S7). The effect varies with different measurements of genetic diversity because the number of alleles per locus ($\alpha$) and Watterson’s ${\theta }_w$ are more sensitive to RPD than the expected heterozygosity ($H_e$) and $\pi$ (19, 20).

The effect of RPD on the reduction in genetic diversity is relatively weak because the time period of RPD is short and because the observed differences in genetic diversity between the two species groups were small. For example, the initial simulated heterozygosity of threatened species was 0.572, and the reduced heterozygosity after RPD was 0.558. That is, only 2.4% of the heterozygosity was lost due to RPD because the time period of RPD was only 123 y.

Comparison with Historical Data.

It has been documented that accelerated land use by humans might have caused the decrease of biodiversity since the middle of the 19th century (21) and extinction rates increased sharply over the past 200 y (22). Therefore, our estimated $\widehat{\tau }$ agrees with these two studies. $\widehat{\tau }$ also agrees with the estimated $\widehat{t}$ for 18 well-documented species [ranging from 55 to 415 y, and $\text{mean}\left(\widehat{t}\right)\approx 166$ y] (SI Appendix, Table S6). The Living Planet Index (2), based on vertebrate population time series between 1970 and 2010, reported a less rapid population decline than we inferred. This may have occurred because conservation efforts had slowed down the rate of population decline in the last 40 y, or populations of nonthreatened vertebrate species were also included to track global biodiversity change in their analysis (23, 24).

Unbiasedness and Robustness of the Method.

We examined the bias of our inference method. First, the sampling effect among species was studied, and it was found that smaller subsets of data gave unbiased estimates but with large variances, as expected (Fig. 5C). Second, RPDs were simulated (10,000 replicates) with the parameter values $R=1.2$ and $\tau =120$, and the obtained mean $\widehat{\mathit{R}}$ and $\widehat{\mathit{\tau }}$ were 1.20 and 128, respectively, showing little bias (SI Appendix, Fig. S3).

The robustness of our estimates was investigated in a number of ways. Several scenarios of the ancient demography before RPD were simulated, and we found that the ancient demography has almost no impact on the estimates (SI Appendix, Fig. S4). We also found that even if the population size of species categorized as near-threatened was assumed to decrease by half since RPD the estimates were virtually unchanged (SI Appendix, Fig. S5A). We also considered the uncertainty of assessment on the genetic diversity due to small sample size, the uncertainty of assessment on the threatened status of species, the uncertainty of estimating $N\left(0\right)$, and the uncertainty of the evolutionary model of microsatellite loci (SI Appendix, Fig. S6). We found that these factors have no visible impacts on the estimates (SI Appendix, Fig. S5 B–E). It has been found that positive and negative selection have acted on mitochondrial genomes (25, 26), which may invalidate the neutral assumption of the model. Moreover, the two short highly hypervariable regions in the D-loop region have been preferentially selected for study, and we observed an increased genetic diversity in mtDNA sequencing data when a short region (<500 bp) was sequenced. To avoid this potential bias, we conducted an analysis by completely excluding the mitochondrial dataset but we found that the estimates $\widehat{\mathit{R}}$ and $\widehat{\mathit{\tau }}$ remained approximately the same (SI Appendix, Fig. S5F).

Our large collection of species allowed us to conduct refined inferences. First, we reanalyzed each taxon class (Fig. 5D). We found that threatened birds and fish species seem to have experienced a more recent RPD than other threatened vertebrates. Thus, the estimated $\widehat{\mathit{\tau }}$ should be interpreted as the average starting date of RPD among different threatened species/taxa. Interestingly, a threatened species with a longer generation time might have an earlier start of RPD (Fig. 5E). This might be due to a positive correlation between generation time and body size (27) and the possibility that a threatened species with a larger body size may be affected earlier by human activities. Second, our analysis of temperate/tropical species suggested that tropical threatened species might have been affected earlier than other threatened species (Fig. 5F), which coincides with the greater habitat loss in the tropics than in other parts of the world. However, we did not observe a large difference in the estimated $\mathit{\tau }$ between threatened terrestrial and aquatic species (SI Appendix, Fig. S7A) or among low/mid/high-income geographic regions (SI Appendix, Fig. S7B). Finally, because the genetic diversity could be different between different IUCN threatened categories (critically endangered, endangered, and vulnerable) (SI Appendix, Table S8), we compared the nonthreatened species with the threatened species belonging to different threatened categories. We found that the different IUCN threatened categories have almost no impact on the estimated $\widehat{\mathit{\tau }}$ (SI Appendix, Fig. S7C). Overall, recent RPDs were observed in all of the examined cases, which strengthened our view that RPD on average widely began in the late 19th century.

In summary, this study demonstrates a utility of genetic polymorphism data in conservation biology. The model with the two parameters $R$ and $\mathrm{\tau }$ (Fig. 5A) is able to capture the crucial features in the observed patterns of polymorphism, and the estimates are robust against various conditions (SI Appendix, Figs. S4 and S5). The estimated start date of RPD coincides with that of widespread industrialization and a profound change in global living ecosystems in the late 19th century, reinforcing the belief that human activity is the primary cause for recent massive extinction. $\widehat{R}$ ranges between 1.1 and 1.3 (Fig. 5 and SI Appendix, Figs. S4, S5, and S7), indicating that the ancestral size of threatened species was 10–30% smaller than that of nonthreatened species. Overall, a species with small population size is likely more vulnerable to environmental change (4). Therefore, an important question is raised whether a relatively small ancestral size of a species is an important factor for its current threatened status. This could be investigated with the genome-wide polymorphism data from the recently initiated Genome 10K Project (28) in the future. Finally, if current conservation efforts are generally enacted when population sizes are low, the historical inferences of this study suggest that recovery may be compromised by delaying action as population sizes continue to decline.

Methods

Collecting Genetic Diversity Data.

For over a decade we carefully examined 2,475 peer-reviewed papers published in 164 scientific journals (Dataset S1) and collected DNA polymorphism data for vertebrate species living in various ecosystems. We focused on vertebrate species because available data were mostly from vertebrates. The genetic diversity in each of these species was typically assayed by one or two molecular techniques: allelic variation at microsatellite loci and sequence variation in the control (D-loop) and coding regions of the mitochondrial DNA. Therefore, the genetic diversity data presented here represent the polymorphism level in both nuclear and mitochondrial genomes.

To ensure data quality, if an inconsistency (in the sample size, the number of haplotypes, the number of alleles, or any related key information) was found in a paper we contacted the authors for their confirmation or discarded the data if we received no response. We also excluded studies using museum samples because the number of such studies is very limited. To increase nomenclatural consistency, the standard world checklists (version 2014.3) on the IUCN Red List were used (www.iucnredlist.org/technical-documents/information-sources-and-quality).

The within-species polymorphism data of 2,764 vertebrate species are presented in Dataset S1. In this dataset, there were 400 vertebrate species surveyed by more than one method, so we have 3,219 nonredundant entries in total, where each entry is composed of one to three summary statistics. If the microsatellite loci of a vertebrate species were surveyed, the sample size (n), the number of microsatellite loci, the expected heterozygosity ($H_e$), the observed heterozygosity ($H_o$), the mean number of alleles per locus ($\alpha$), $F_{ST}$ (29), and the year of publication were recorded and later used in simulations. If the D-loop region of the mitochondrion was sequenced in a vertebrate species, we recorded the sample size (n), the length of the sequenced region, the mean number of pairwise nucleotide differences per base pair ($\pi$) between the DNA sequences examined, Watterson’s ${\theta }_w$ per base pair (10), and the year of publication. When it was necessary and possible, we downloaded mitochondrial sequences from EMBL/GenBank and aligned them by DNASTAR, checked the alignment by eye, and then calculated $\pi$ and Watterson’s ${\theta }_w$. The haplotype frequencies were obtained from the original articles, and the sites containing insertions and deletions were excluded in our analysis. To investigate population structure, we calculated Tajima’s D (13) and its P value, as the summary statistic for the ancient population structure (14). The $\pi$ and Watterson’s ${\theta }_w$ were rescaled according to the length of the sequenced fragment that was used to calculate Tajima’s D. We also collected a small dataset of genetic diversity for the coding regions of mitochondrial DNA. The collection process was similar to that described above, and we used the dataset only in the description analysis because the number of available species is small.

According to the IUCN, the threatened species (TS) include those listed as critically endangered (CR), endangered (EN), and vulnerable (VU) (3). The species categorized as near threatened (NT) and least concern (LC) are treated as the nonthreatened species (NS). The uncategorized species include those that are listed as data deficient (DD) and have not been evaluated by the IUCN. A taxon is listed as data deficient when there is inadequate information to make an assessment of its risk of extinction (3). Generally, the uncategorized species were excluded from our analyses (Fig. 1), unless stated otherwise.

Collecting Species Distribution and Generation Time Data.

The geographic distributions of 2,552 vertebrate species were retrieved from the IUCN Red List (version 2014.3) and a reptile database (www.reptile-database.org). The data are given in Dataset S1. The generation times of 3,146 vertebrate species were obtained from different published resources (Dataset S1), which formed the basis for our generation time estimates. Assume that the generation time of a species is $\beta \rho$, where $\rho$ is the sexual maturity age of the species. $\beta$ is equal to the generation time divided by the sexual maturity age and is species/genus-dependent. If the generation time of a species is unknown but its age of sexual maturity is documented, its generation time was estimated using the mean $\beta$ from closely related well-studied species.

Ratio of Effective Population Sizes Between Nonthreatened and Threatened Species.

It is difficult to estimate the effective population size at a specific time of a species with fluctuating population size (5–7). However, the ratio of $N\left(0\right)$ between two species groups, each composed of a large number of related species, can be approximated by the ratio of their current census size $N\prime$. It has been inferred that the ratio of the effective to the actual population size [$f=N\left(0\right)/N\prime$] is of the order of 0.1 (16), and $f$ is usually independent of $N\prime$. When both nonthreatened and threatened species groups are each composed of a large number of related species, it is reasonable to assume $E\left(f_{NS}\right)\approx E\left(f_{TS}\right)$, where subscripts NS and TS represent nonthreatened and threatened species, respectively. Consequently,

$$\omega =\frac{E({\theta }_{NS}\left(0\right))}{E({\theta }_{TS}\left(0\right))}=\frac{E(N_{NS}\left(0\right))}{E(N_{TS}\left(0\right))}=\frac{E\left(f_{NS}{N}_{NS}^{\prime }\right)}{E\left(f_{TS}{N}_{TS}^{\prime }\right)}\approx \frac{E\left(N_{NS}^{\prime }\right)}{E\left(N_{TS}^{\prime }\right)},$$ [1]

where $N\left(t\right)$ denotes the effective population size at time $t$ (counting backward) and $N\prime$ the current census size.

Based on the current census of 1,868 vertebrate species obtained from IUCN, a professional book (30), and peer-reviewed literature (Dataset S1), we estimated $\widehat{\omega }\approx 25$ for mammals, 146 for birds, 32 for amphibians, 26 for reptiles, and 14 for fish (SI Appendix, Table S9). Therefore, we set $\widehat{\omega }=25$ in the modeling study, but we also used $\widehat{\omega }=10$ and 100 to examine the robustness of the results.

Demographic Model and Likelihood Inference of RPD.

Demographic model.

We assumed that the effective population size of a nonthreatened species remains constant. Denote the ancestral effective population size of a threatened species at time $t$ by $N_{TS}\left(t\right)$, and assume that at $t$ years ago its population size started declining exponentially (Fig. 5A); time $t$ is counted backward. We assumed that the start date of RPD in threatened species follows the normal, the exponential, or the one-point (i.e., constant) distribution with the mean $\tau$. Once $\omega =E\left(N_{NS}\left(0\right)\right)/E\left(N_{TS}\left(0\right)\right)$ was estimated by Eq. 1, the demographic model was characterized by two parameters, $R=E\left({\theta }_{NS}\left(t\right)\right)/E\left({\theta }_{TS}\left(t\right)\right)$ and $\tau =E\left(t\right)$. Then, the two parameters $R$ and $\tau$ were estimated from an analysis in the likelihood framework as described below.

Under the assumption of constant population size during the first phase and $E\left(f_{NS}\right)\approx E\left(f_{TS}\right)$, we have $R=E\left(N_{NS}\left(t\right)\right)/E\left(N_{TS}\left(t\right)\right)\approx E\left(N{\prime }_{NS}\left(t\right)\right)/E\left(N{\prime }_{TS}\left(t\right)\right)$, where $N{\prime }_{NS}\left(t\right)$ and $N{\prime }_{TS}\left(t\right)$ are the census sizes of the nonthreatened and threatened species at the start date of RPD. Thus, R represents the ratio of census size at the start date of RPD between the two species groups. If the assumption of constant size during the first phase is invalid, R represents the long-term ratio of census size between two species groups before the start of RPD.

Assumption about sampling times.

The sampling time is likely different in different studies, but the time duration between the time of sampling and the time of publication is generally much shorter than $t$. We assumed that the sampling happened 3 y before the year of publication. In this study, the term “at present” means “2015,” so the sampling of the i-th species happened at ${\gamma }_i\prime$ ($=2015-{\gamma }_i+3$) years ago, where ${\gamma }_i$ is the year of publication. The duration between the start date of RPD and the year of sampling is $t_i\prime =t-{\gamma }_i\prime$.

Coalescence-based simulations.

The coalescence-based simulations followed the standard procedure (31, 32). To simulate the microsatellite polymorphism data for the i-th species, we (randomly) chose ${\theta }_i({\gamma }_i\prime )=4N_i({\gamma }_i\prime )\mu$ from the ${\theta }_{obs}$ value(s) of its nonthreatened related species, where $\mu$ is the mutation rate per locus per generation, and the sampling happened ${\gamma }_i\prime$ years ago. The details are given below.

We first calculated ${\theta }_{obs}$ from the observed within-species polymorphism data of nonthreatened species with a reasonable sample size ($\mathit{n}\ge 20$) based on the stepwise mutation model (15). Then, we denoted the set of ${\theta }_{obs}$ values in the group of nonthreatened species related to the i-th species as ${\mathbf{\theta }}_{\mathbf{i}}=\{{\theta }_{obs,1},\hspace{0.17em}{\theta }_{obs,2},\hspace{0.17em}\dots \}$. If ${\mathbf{\theta }}_{\mathbf{i}}=\varnothing$ at the genus level, ${\mathbf{\theta }}_{\mathbf{i}}$ would be obtained at the family level, or even at the phylum level. Then a value ${\theta }_s$ was (randomly) drawn from ${\mathbf{\theta }}_{\mathbf{i}}$. The value ${\theta }_s$ would be used as $\theta \hspace{0.17em}(=4N_{NS,i}\left(0\right)\mu =4N_{NS,i}({\gamma }_i\prime )\mu )$ if the i-th species is nonthreatened. If the i-th species is threatened, the value ${\theta }_s$ was rescaled according to its effective population size at the time of sampling, $N_{TS,i}({\gamma }_i\prime )$. Then, we have

$${\theta }_{TS,i}\left({\gamma }_i^{\prime }\right)=\{\begin{array}{cc}\frac{e^{\lambda t_i^{\prime }}}{\widehat{\omega }{e}^{\lambda t}}{\theta }_s,& t_i^{\prime }>0\\ \frac{1}{R}{\theta }_s,& t_i^{\prime }\le 0\end{array},$$ [2]

where $\lambda$ is the rate of RPD, and a negative $t_i^{\text{'}}$ indicates the sampling happened before the start of RPD. From the definitions of $R$ and $\omega$ and Eq. 1, we have

$$\lambda =\ln \left(\frac{R}{\widehat{\omega }}\right)/t,$$ [3]

where $t$ was randomly sampled from the distribution described above.

To model the heterogeneity of mutation rates among microsatellite loci, we assumed that the mutation rate for a randomly selected locus follows a lognormal distribution, with the coefficient of variation equal to 1 (33). We also assumed that the microsatellite loci are independent and are autosomal.

If the evolution of the i-th species followed a nonconstant size model, the time in the unit of years was transformed to the unit of $2N_i\left(0\right)$ generations (31, 32), where $N_i\left(0\right)=E\left(f\right)N_i\prime$, $E\left(f\right)=0.1$ (16), and $N_i\prime$ is the current census size of the i-th species.

To simulate the single-nucleotide polymorphism data on the D-loop region, we followed the procedures described above with two modifications. First, ${\theta }_{obs}$ was estimated as Watterson’s ${\theta }_w$ (10), based on the within-species sequence variation in the D-loop of nonthreatened species with $\text{n}\ge 20$; the cases of ${\theta }_{obs}=0$ were discarded because those estimated values represent $N\left(0\right)=0$ or $\mu =0$. Second, the rescaled decline time was multiplied by 4 because the effective population size of a mitochondrial locus is only one-fourth that of an autosomal locus.

Likelihood inference of RPD.

The observed genetic diversity of a species can be represented by a vector $\mathbf{S}=\{H_e,\alpha ,{\theta }_w,\pi \}$ in which at least one element was observed. The corresponding likelihood function is $L\left(R,\tau \right)={\displaystyle \prod }_{i}P\left({\mathbf{S}}_i\right|R,\tau )$, where the i-th species is designated by subscript i. Although there is no exact method for computing $L\left(R,\tau \right)$, numerical approximations can be obtained by following the principle of rejection sampling (5, 17, 18) and by representing the data as the relative differences in the mean genetic diversity between nonthreatened and threatened species. The details are as follows.

For the summary statistic H_e on the microsatellite loci, we denote ${\mathrm{\Delta }}_{H_e}=\left(\overline{H_{e,NS}}-\overline{H_{e,TS}}\right)/\overline{H_{e,NS}}$. Denote ${\mathrm{\Delta }}_{H_e,simu}$ and ${\mathrm{\Delta }}_{H_e,obs}$ as the simulated and observed relative difference of mean H_e between nonthreatened and threatened species. The likelihood function $L_{H_e}(R,\tau )$ is then estimated as a numerical approximation of $P\left(|{\mathrm{\Delta }}_{H_e,simu}-{\mathrm{\Delta }}_{H_e,obs}\left|\le \epsilon \right|R,\tau \right)$, where $\epsilon$ is a fixed tolerance. When $\epsilon$ is very small, the computational load is very large, whereas the precision of the estimate will be poor when $\epsilon$ is large. Our experience suggests that $\epsilon =0.05$ works well, and the estimate of $\tau$ is not sensitive to $\epsilon$. We also set $\epsilon =0.01$, 0.1, or 0.2, and the results remained almost unchanged. The estimation procedure of $P\left(|{\mathrm{\Delta }}_{H_e,simu}-{\mathrm{\Delta }}_{H_e,obs}\left|\le \epsilon \right|R,\tau \right)$ is given below. In step 1, we simulated the microsatellite polymorphic dataset using the procedure described above and calculated ${\mathrm{\Delta }}_{H_e,simu}$. The pattern of missing data, the information of sample size and the number of loci have been properly considered in the simulation and also in the related calculation. In step 2, we introduced an indicator variable $I\left(H_e\right)=\{\begin{array}{ll}1,\hfill & \left|{\mathrm{\Delta }}_{H_e,simu}-{\mathrm{\Delta }}_{H_e,obs}\right|\le \epsilon \hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}$. In step 3, we repeated steps 1 and 2 B times. The likelihood $L_{H_e}(R,\tau )$ was then estimated by ${\widehat{L}}_{H_e}\left(R,\tau \right)\approx \frac{1}{B}{{\displaystyle \sum }}^{}I\left(H_e\right)$, where $B={10}^4$.

The above procedure was applied to multiple summary statistics with only minor modifications. For the microsatellite dataset, we jointly considered H_e and $\alpha$, which are not independent. Then we have $L_{micro}\left(R,\tau \right)=L_{H_e,\alpha }\left(R,\tau \right)=P\left(\left|{\mathrm{\Delta }}_{H_e,simu}-{\mathrm{\Delta }}_{H_e,obs}\right|\le \epsilon ,\left|{\mathrm{\Delta }}_{\alpha ,simu}-{\mathrm{\Delta }}_{\alpha ,obs}\right|\le \epsilon |R,\tau \right)$. Similarly, we have $L_{mtDNA}\left(R,\tau \right)=L_{\theta ,\pi }\left(R,\tau \right)$. Finally, we have $L\left(R,\hspace{0.17em}\tau \right)=L_{micro}\left(R,\tau \right)L_{mtDNA}\left(R,\tau \right)$.

Then, $R$ and $\tau$ are estimated by a two-step process through a likelihood framework. The first step is to calculate the profile likelihood for $R$ [$L_1\left(R\right)={\max }_{\tau }L(R,\tau )$] and then the mean $\widehat{\mathit{R}}$, which is the mean of $R$’s weighted by the relative profile likelihood values (Fig. 5 C–F). The second step is to obtain the maximum likelihood estimate $\widehat{\tau }$ of $\tau$ conditional on $R=\widehat{R}$. In general, if $R>1$, which indicates that the ancestral genetic diversity of nonthreatened species is higher than that of threatened species, a small $\tau$ is needed to explain the observed low genetic diversity in the present-day threatened species. In particular, if $R\ge 1.35$, we have $\tau \le 40$ (Fig. 5C). Because it has been documented that the RPD of threatened species happened at least 40 y ago (2), we set 1.35 as the upper bound of $R$. Moreover, it is likely that, on average, the ancestral size of nonthreatened species was larger than that of its related threatened species. Thus, we assumed $R\ge 1$.

All of the collected species, including those with small sample size ($n<20$), were taken in the coalescence-based modeling, unless noted otherwise. This is because the modeling was conducted conditional on the values of n.

Likelihood ratio test.

To conduct the likelihood ratio test and obtain likelihood-based confidence intervals, we obtained the empirical distribution of the likelihood ratio $\zeta =\log (max\hspace{0.17em}{L}_1/max\hspace{0.17em}{L}_0)$ by analyzing 10⁴ simulated datasets conditional on $R$ and $\tau$, where $L_1$ and $L_0$ are the likelihoods for the alternative and null models, respectively. An example of the empirical distribution of $\zeta$ is shown (SI Appendix, Fig. S8). In this case, the 95% critical value (${\zeta }_{95\%}$) is 1.792. Note that, for a different dataset, or for different $R$ and $\tau$, ${\zeta }_{95\%}$ could be different. Therefore, the corresponding empirical distribution of $\zeta$ was used to obtain ${\zeta }_{95\%}$ for the likelihood ratio test.

Effect of RPD on the Difference in Genetic Diversity Between Nonthreatened and Threatened Species.

We first conducted the coalescence-based modeling described above, conditional on $R=1.22$ and $\tau =0$ or 123. We used ${\theta }_{NS}\left(\tau \right)=2$ (microsatellite loci, per locus) and 0.02 (mitochondrial locus, per base pair). We then compared the case of $\tau =123$ (the estimated RPD) with the case of $\tau =0$ (indicating no RPD) to estimate the effect of PRD on the difference in genetic diversity between nonthreatened and threatened species. We denoted ${\mathrm{\Delta }}_{M,\tau }=\left(\overline{M_{\tau ,NS}}-\overline{M_{\tau ,TS}}\right)/\overline{M_{\tau ,NS}}$, where $M$ stands for $H_e$, the mean number of alleles per locus ($\alpha$), $\pi$, or Watterson’s ${\theta }_w$. The effect of PRD was calculated as $\left({\mathrm{\Delta }}_{M,\tau =123}-{\mathrm{\Delta }}_{M,\tau =0}\right)/{\mathrm{\Delta }}_{M,\tau =123}$ (SI Appendix, Table S7). In the considered model, we have $\overline{M_{\tau =123,NS}}=\overline{M_{\tau =0,NS}}$, so the effect of RPD can be simplified as $(\overline{M_{\tau =0,TS}}-\overline{M_{\tau =123,TS}})/(\overline{M_{\tau =123,NS}}-\overline{M_{\tau =123,TS}})$. In the mitochondrial case of $\tau =0$, the values of ${\mathrm{\Delta }}_{\pi ,\tau =0}$ and ${\mathrm{\Delta }}_{{\theta }_w,\tau =0}$ can be computed analytically, which agree with the simulation.

Robustness Analysis Under Various Demographic Models.

To examine the robustness of the estimates, we conducted reanalyses under various demographic models. The likelihood method described above is very flexible, and little modification is needed to analyze other demographic models. First, we considered a slow population decline in a nonthreatened vertebrate species categorized as near-threatened (NT) based on the rationale that human activities may also have an impact on those nonthreatened vertebrate species. We assumed that their population size declined by half $(E\left(N_{NT}\left(\tau \right)\right)/E\left(N_{NT}\left(0\right)\right)=2)$. We assumed that the populations of those near-threatened vertebrate species also started to decline at time $\tau$.

Second, we considered an ancestral population with varying size (SI Appendix, Fig. S4). Under the ancestral instantaneous expansion model (SI Appendix, Fig. S4 A and B), we assumed that $t_1$ follows a uniform distribution in [100,000, 1,000,000] (in unit of years), and $N_2/N_1$ is uniformly distributed between [2, 5], where $N_1$ and $N_2$ are the effective population size before and after the expansion, respectively. For the ancestral instantaneous bottleneck model (SI Appendix, Fig. S4 C and D), we assumed that $t_0$ follows a uniform distribution of [10,000, 100,000], $t_1$ follows a uniform distribution of [100,000, 1,000,000], and $N_2/N_1$ is uniformly distributed between [2, 5], where $N_1$ is the effective population size during the bottleneck and $N_2$ the effective population size before and after the bottleneck. Then we assigned the ancestral expansion or the ancestral bottleneck model with equal probability (0.5 vs. 0.5) for a species, as its demographic scenario before the RPD.

To ensure that the simulated genetic diversity level is equal to the observed one in a nonthreatened species with varying population size, ${\theta }_{NS}\left(0\right)$ was determined as follows. Based on the constant size model, $\theta$ was first estimated from the observed polymorphic data (10, 15). Then we simulated 50 random coalescent trees given the desired demographic model and denoted the mean tree length by $\overline{l}$. Then we have $\sigma =\overline{l}/{\displaystyle \sum _{i=1}^{n-1}}\frac{2}{i}$, and ${\theta }_{NS}\left(0\right)=\theta /\sigma$.

To determine ${\theta }_{TS}\left(0\right)$ of a threatened species, we reconstructed a demographic model of the nonthreatened species. During the first phase, the model is the same as that of the threatened species. During the second phase, however, the population size is constant. Then ${\theta }_{TS}\left(\tau \right)$ was obtained by the method described above, and ${\theta }_{TS}\left(0\right)$ was rescaled from ${\theta }_{TS}\left(\tau \right)$. The effect of different sampling time was also considered and Eq. 2 was slightly revised.