On the (un)predictability of a large intragenic fitness landscape

Significance

The study of fitness landscapes is fundamentally concerned with understanding the relative roles of stochastic and deterministic processes in adaptive evolution. Here, the authors present a uniquely large and complete multiallelic intragenic fitness landscape of 640 systematically engineered mutations in the heat-shock protein Hsp90 in yeast. Using a combination of traditional and recently proposed theoretical approaches, they study the accessibility of the global fitness peak and the potential for predictability of the fitness landscape topography. They report local ruggedness of the landscape and the existence of epistatic hotspot mutations, which together make extrapolation and hence predictability inherently difficult if mutation-specific information is not considered.

Abstract

The study of fitness landscapes, which aims at mapping genotypes to fitness, is receiving ever-increasing attention. Novel experimental approaches combined with next-generation sequencing (NGS) methods enable accurate and extensive studies of the fitness effects of mutations, allowing us to test theoretical predictions and improve our understanding of the shape of the true underlying fitness landscape and its implications for the predictability and repeatability of evolution. Here, we present a uniquely large multiallelic fitness landscape comprising 640 engineered mutants that represent all possible combinations of 13 amino acid-changing mutations at 6 sites in the heat-shock protein Hsp90 in Saccharomyces cerevisiae under elevated salinity. Despite a prevalent pattern of negative epistasis in the landscape, we find that the global fitness peak is reached via four positively epistatic mutations. Combining traditional and extending recently proposed theoretical and statistical approaches, we quantify features of the global multiallelic fitness landscape. Using subsets of the data, we demonstrate that extrapolation beyond a known part of the landscape is difficult owing to both local ruggedness and amino acid-specific epistatic hotspots and that inference is additionally confounded by the nonrandom choice of mutations for experimental fitness landscapes.

Since first proposed by Sewall Wright in 1932 (1), the idea of a fitness landscape relating genotype (or phenotype) to the reproductive success of an individual has inspired evolutionary biologists and mathematicians alike (2–4). With the advancement of molecular and systems biology toward large and accurate datasets, the fitness landscape concept has received increasing attention across other subfields of biology (5–9). The shape of the fitness landscape carries information on the repeatability and predictability of evolution, the potential for adaptation, the importance of genetic drift, the likelihood of convergent and parallel evolution, and the degree of optimization that is (theoretically) achievable (4). Unfortunately, the dimensionality of a complete fitness landscape of an organism—that is, a mapping of all possible combinations of mutations to their respective fitness effects—is much too high to be assessed experimentally. With the development of experimental approaches that allow for the assessment of full fitness landscapes of tens to hundreds of mutations, there is growing interest in statistics that capture the features of the landscape and that relate an experimental landscape to theoretical landscapes of similar architecture, which have been studied extensively (10). It is, however, unclear whether this categorization allows for an extrapolation to unknown parts of the landscape, which would be the first step toward quantifying predictability—an advancement that would yield impacts far beyond the field of evolutionary biology, in particular for the clinical study of drug-resistance evolution in pathogens and the development of effective vaccine and treatment strategies (8).

Existing research in this rapidly growing field comes from two sides. Firstly, different empirical landscapes have been assessed (reviewed in ref. 4), generally based on the combination of previously observed beneficial mutations or on the dissection of an observed adaptive walk (i.e., a combination of mutations that have been observed to be beneficial in concert). Secondly, theoretical research has proposed different landscape architectures [such as the House-of-Cards (HoC), the Kauffman NK (NK), and the Rough Mount Fuji (RMF) model], studied their respective properties, and developed a number of statistics that characterize the landscape and quantify the expected degree of epistasis (i.e., interaction effects between mutations) (10–14).

The picture that emerges from these studies is mixed, reporting both smooth (15) and rugged (16, 17) landscapes with both positive epistasis [i.e., two mutations in concert are more advantageous than expected; (18)] and negative epistasis [i.e., two mutations in concert are more deleterious than expected (refs. 19 and 20 but see refs. 21 and 22)]. Current statistical approaches have been used to rank the existing landscapes by certain features (10, 14) and to assess whether the landscapes are compatible with Fisher’s Geometric Model (23). A crucial remaining question is the extent to which the nonrandom choice of mutations for the experiment affects the topography of the landscape and whether the local topography is indeed informative as to the rest of the landscape.

Here, we present an intragenic fitness landscape of 640 amino acid-changing mutations in the heat-shock protein Hsp90 in Saccharomyces cerevisiae in a challenging environment imposed by high salinity. With all possible combinations of 13 mutations of various fitness effects at 6 positions, the presented landscape is not only uniquely large but also distinguishes itself from previously published work regarding several other experimental features—namely, by its systematic and controlled experimental setup using engineered mutations of various selective effects and by considering multiple alleles simultaneously. We begin by describing the landscape and identifying the global peak, which is reached through a highly positively epistatic combination of four mutations. Based on a variety of implemented statistical measures and models, we describe the accessibility of the peak, the pattern of epistasis, and the topography of the landscape. To accommodate our data, we extend several previously used models and statistics to the multiallelic case. Using subsets of the landscape, we discuss the predictive potential of such modeling and the problem of selecting nonrandom mutations when attempting to quantify local landscapes to extrapolate global features.

Results and Discussion

We used the EMPIRIC approach (24, 25) to assess the growth rate of 640 mutants in yeast Hsp90 (Materials and Methods). Based on previous screenings of fitness effects in different environments (26) and on different genetic backgrounds (20), and on expectations of their biophysical role, 13 amino acid-changing point mutations at 6 sites were chosen for the fitness landscape presented here (Fig. 1). The fitness landscape was created by assessing the growth rate associated with each individual mutation on the parental background and all possible mutational combinations. A previously described Monte Carlo Markov chain (MCMC) approach was used to assess fitness and credibility intervals (ref. 27 and Materials and Methods).

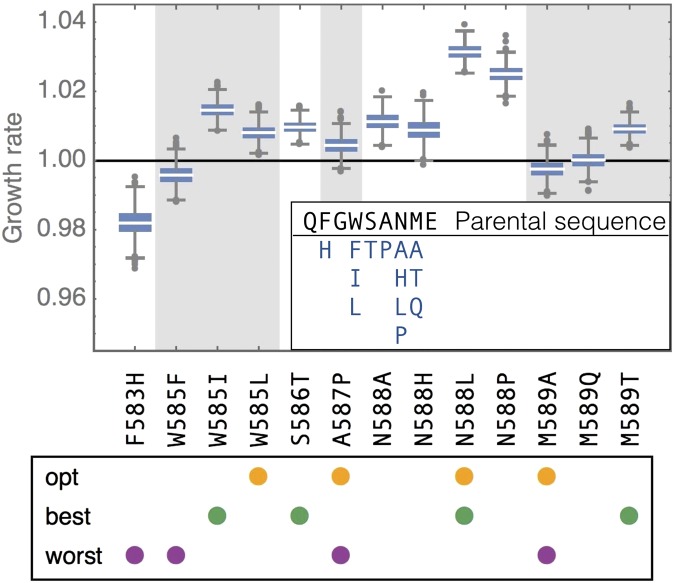
Fig. 1.

Individual amino acid substitutions and their effect on the parental background in elevated salinity, obtained from 1,000 samples from the posterior distribution of growth rates. Boxes represent the interquartile range [i.e., the 50% confidence interval (CI)], whiskers extend to the highest/lowest data point within the box $\pm$1.5 times the interquartile range, and circles represent outliers; gray and white background shading alternates by amino acid position. The box below indicates with colored dots which mutations are involved in the focal landscapes discussed throughout the main text: the four mutations leading from the parental type to the global optimum (“opt”), the four individually most beneficial mutations on the parental background (“best”), and the four mutations with the individually lowest growth rates on the parental background (“worst”). (Inset) Parental sequence at positions 582–590 and assessed amino acids by position.

The Fitness Landscape and Its Global Peak.

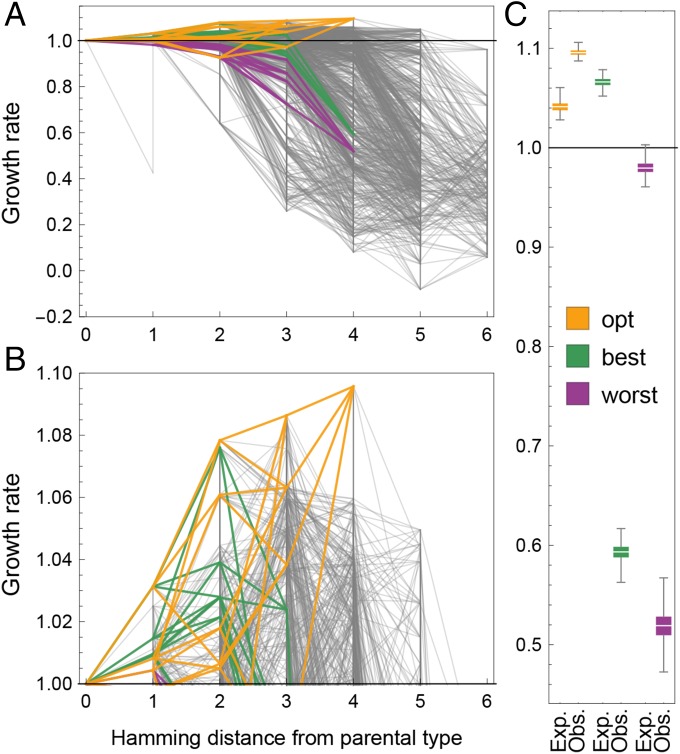
Fig. 2 presents the resulting fitness landscape, with each mutant represented based on its Hamming distance from the parental genotype and its median estimated growth rate. Lines connect single-step substitutions, with vertical lines occurring when there are multiple mutations at the same position (Fig. 1). With increasing Hamming distance from the parental type, many mutational combinations become strongly deleterious. Thus, we observe strong negative epistasis between the substitutions that, as single steps on the parental background, have small effects. This pattern is consistent with Fisher’s Geometric Model (28) when combinations of individually beneficial or small-effect mutations overshoot the optimum and with classic arguments predicting negative epistasis based on mutational load (29). It is also intuitively comprehensible on the protein level, where the accumulation of too many mutations is likely to destabilize the protein and render it dysfunctional (30).

Fig. 2.

(A) Empirical fitness landscape by mutational distance to parental type. Each line represents a single substitution. Vertical lines appear when multiple alleles have been screened at the same position. There is a global pattern of negative epistasis. The three focal landscapes are highlighted. (B) Close-up on the beneficial portion of the landscape. (C) Expected (“Exp.”) versus observed (“Obs.”) fitness for the focal landscapes, obtained from 1,000 posterior samples. We observe strong positive epistasis in the landscape that contains the global optimum, whereas the other two are dominated by negative epistasis. In A–C, the y axis depicts growth rate as a proxy for fitness.

The global peak of the fitness landscape is located four mutational steps away from the parental type (Fig. 2B), with 98% of posterior samples identifying the peak. The fitness advantage of the global peak reaches nearly 10% over the parental type and is consistent between replicates (Materials and Methods and SI Appendix, Fig. S3_1). Perhaps surprising given the degree of conservation of the studied genomic region (figure S5 in ref. 24), it is important to note that these fitness effects are measured under highly artificial experimental conditions including high salinity, which are unlikely to represent a natural environment of yeast. The effects of the individual mutations comprising the peak in a previous experiment without added NaCl were −0.04135, −0.01876, −0.03816, and −0.02115 for mutations W585L, A587P, N588L, and M589A, respectively, emphasizing the potential cost of adaptation associated with the increased salinity environment (data from ref. 20; see also ref. 26).

Curiously, the global peak is not reached by combining the most beneficial single-step mutations on the parental background but via a highly synergistic combination of one beneficial and three “neutral” mutations (i.e., mutations that are individually indistinguishable from the parental type in terms of growth rate). In fact, each of the five beneficial local optima shows a similar signature of positive epistasis (SI Appendix, Fig. S3_2). Fig. 2C demonstrates that a combination of the four mutations involved in the global peak (opt) predicts only a 4% fitness advantage. Furthermore, even a combination of the four individually most-beneficial, single-step mutations on the parental background in the dataset (best) (considering at most one mutation per position) only predicts a benefit of 6%. Notably, the actual combination of these four mutations on the parental background is highly deleterious and thus exhibits strong negative epistasis. Although negative epistasis between beneficial mutations during adaptation has been reported more frequently, positive epistasis has also been observed occasionally (18, 31), particularly in the context of compensatory evolution. In fact, negative epistasis between beneficial mutations and positive epistasis between neutral mutations has been predicted by de Visser et al. (32). Furthermore, our results support the pattern recently found in the gene underlying the antibiotic resistance enzyme TEM-1 $\beta$-lactamase in Escherichia coli, showing that large-effect mutations interact more strongly than small-effect mutations such that the fitness landscape of large-effect mutations tends to be more rugged than the landscape of small-effect mutations (13) and that mutations that were selected for their combined beneficial effect on a wild-type background tend to interact synergistically, whereas mutations selected for their individual effects interact antagonistically (4, 13).

Adaptive Walks on the Fitness Landscape.

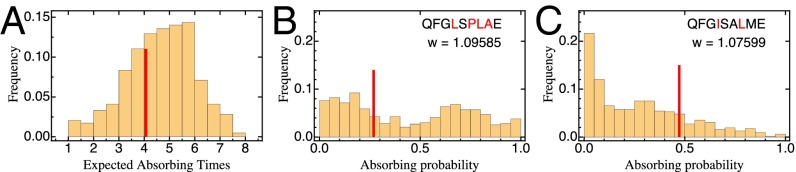
Next, we studied the empirical fitness landscape within a framework recently proposed by Draghi and Plotkin (33). Given the empirical landscape, we simulated adaptive walks and studied the accessibility of the six observed local optima. In addition, we evaluated the length of adaptive walks starting from any mutant in the landscape, until an optimum is reached. In the strong selection weak mutation limit (34), we can express the resulting dynamics as an absorbing Markov chain, where local optima correspond to the absorbing states, and in which the transition probabilities correspond to the relative fitness increases attainable by the neighboring mutations (Materials and Methods). This approach allowed us to derive analytical solutions for the mean and variance of the number of steps to reach a fitness optimum (SI Appendix, Supporting Information 1: Extended Materials and Methods), and the probability to reach a particular optimum starting from any given mutant in the landscape (Fig. 3 and SI Appendix, Figs. S3_3 and S3_4).

Fig. 3.

(A) Distribution of average lengths of adaptive walks starting from any type in the full landscape (i.e., absorbing times of the Markov chain). The red line indicates mean path length for adaptive walks from the parental genotype. (B and C) Distribution of absorbing probabilities, that is, the probability to reach a specific optimum starting from a given genotype computed for all genotypes in the dataset. The red line corresponds to the respective probability when starting from the parental sequence. The global optimum (B) is, in general, reached with a very high probability, but there are starting points from which it is poorly accessible.

Using this framework, we find that the global optimum can be reached with nonzero probability from almost 95% of starting points in the landscape, and is reached with high probability from a majority of starting points - indicating high accessibility of the global optimum (Fig. 3). The picture changes when restricting the analysis to adaptive walks initiating from the parental type (Fig. 3 and SI Appendix, Figs. S3_3 and S3_4). Here, although 73% of all edges and 78% of all vertices are included in an adaptive walk to the global optimum, it is reached with only 26% probability. A local optimum two substitutions away from the parental type (Fig. 3C) is reached with a much higher probability of 47%. Hence, adaptation on the studied landscape is likely to stall at a suboptimal fitness peak. This observation indicates that the local and global landscape pattern may be quite different, an observation that is confirmed and discussed in more detail below (see Predictive Potential of Landscape Statistics). In line with the existence of multiple local fitness peaks, we find that pairs of alleles at different loci show pervasive sign (30%) and reciprocal sign (8%) epistasis (35), whereas the remaining 62% are attributed to magnitude epistasis (i.e., there is no purely additive interaction between alleles; for a discussion of the contribution of experimental error, see SI Appendix, Fig. S3_5).

Epistasis Measures and the Topography of the Fitness Landscape.

Next, we considered the global topography of the fitness landscape. Various measures of epistasis and ruggedness have been proposed, most of them correlated and hence capturing similar features of the landscape (10). However, drawing conclusions has proven difficult because the studied landscapes were created according to different criteria. Furthermore, the majority of published complete landscapes are too small to be divided into subsets (but see refs. 10 and 12), preventing tests for the consistency and hence the predictive potential of landscape statistics. The landscape studied here provides us with this opportunity. Moreover, because multiple alleles at the same site are contained within the landscape, we may study whether changes in the shape of the landscape are site- or amino acid-specific.

We computed various landscape statistics (roughness-to-slope ratio, fraction of epistasis, and the recently proposed gamma statistics; SI Appendix, Supporting Information 1: Extended Materials and Methods) (10, 11, 14) and compared them with expectations from theoretical landscape models [NK (36–38), RMF (39, 40), HoC (41), egg-box landscapes (14); for brief definitions of these terms, see SI Appendix, Supporting Information 2: Overview of Different Fitness Landscape Models Introduced in the Main Text]. Whenever necessary, we provide an analytical extension of the used statistic to the case of multiallelic landscapes (Materials and Methods). To assess consistency and predictive potential, we computed the whole set of statistics for (i) all landscapes in which 1 amino acid was completely removed from the landscape (a cross-validation approach (42), subsequently referred to as the “drop-one” approach), (ii) all possible 360 diallelic sublandscapes, and (iii) for all 1,570 diallelic, 4-step landscapes containing the parental genotype, highlighting as special examples the three focal landscapes discussed.

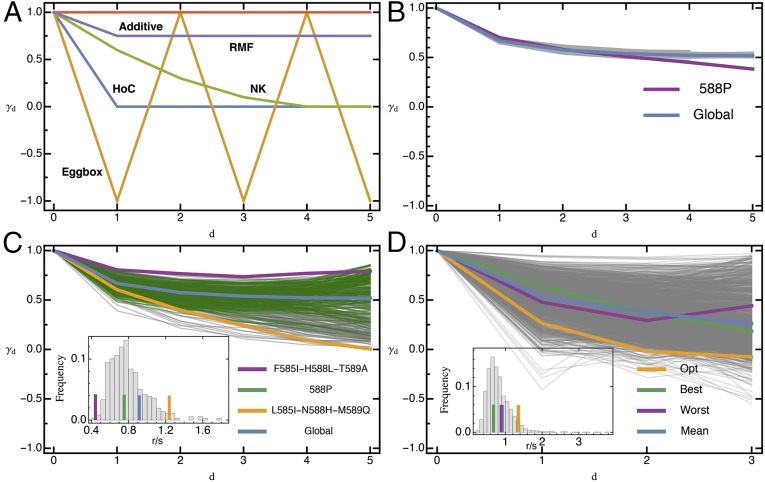
We find that the general topography of the fitness landscape resembles that of a RMF landscape with intermediate ruggedness, which is characterized by a mixture of a random HoC component and an additive component (Fig. 4 A and B). Whereas the whole set of landscape statistics supports this topography and our conclusions, the gamma statistics measuring landscape-averaged correlations in fitness effects, recently proposed in ref. 14, proved to be particularly illustrative. We will therefore focus on these in the main text; we refer to SI Appendix for additional results (e.g., measurement uncertainty and adaptive walks).

Fig. 4.

(A) Expected pattern of landscape-wide epistasis measure ${\gamma }_d$ (SI Appendix, Eq. S1_15) with mutational distance for theoretical fitness landscapes with 6 loci from ref. 14. (B) Observed decay of ${\gamma }_d$ with mutational distance under the drop-one approach is quite homogenous, except when hot spot mutation 588P is removed; 95% CIs are contained within the lines for the global landscape. (C) Observed decay of ${\gamma }_d$ for all diallelic six-locus sublandscapes. Depending on the underlying mutations, ${\gamma }_d$ is vastly different, suggesting qualitative differences in the topography of the underlying fitness landscape and in the extent of additivity in the landscape. Three focal landscapes representative of different types and ${\gamma }_d$ for the full landscape have been highlighted. (D) Observed decay of ${\gamma }_d$ for all diallelic four-locus sublandscapes containing the parental type, indicative of locally different landscape topographies. Highlighted are the three focal landscapes. (Insets) Histograms of the roughness-to-slope ratio $r\mathrm{/}s$ for the respective subset, with horizontal lines indicating values for highlighted landscapes [$r\mathrm{/}s$ for global landscape (blue) is significantly different from HoC expectation, $p\mathrm{=}\mathrm{0.01}$]. Similar to ${\gamma }_d$, there is a huge variation in $r\mathrm{/}s$ for subparts of the fitness landscape, especially when considering the four-locus subsets.

Predictive Potential of Landscape Statistics.

When computed based on the whole landscape and on a drop-one approach, the landscape appears quite homogeneous, and the gamma statistics show relatively little epistasis (Figs. 4B and 5B). At first sight, this result contradicts our earlier statement of strong negative and positive epistasis but can be understood, given the different definitions of the epistasis measures used: above, we have measured epistasis based on the deviation from the multiplicative combination of the single-step fitness effects of mutations on the parental background. Because these effects were small, epistasis was strong in comparison. Conversely, the gamma measure is independent of a reference genotype and captures the fitness decay with a growing number of substitutions as a dominant and quite additive component of the landscape.

Fig. 5.

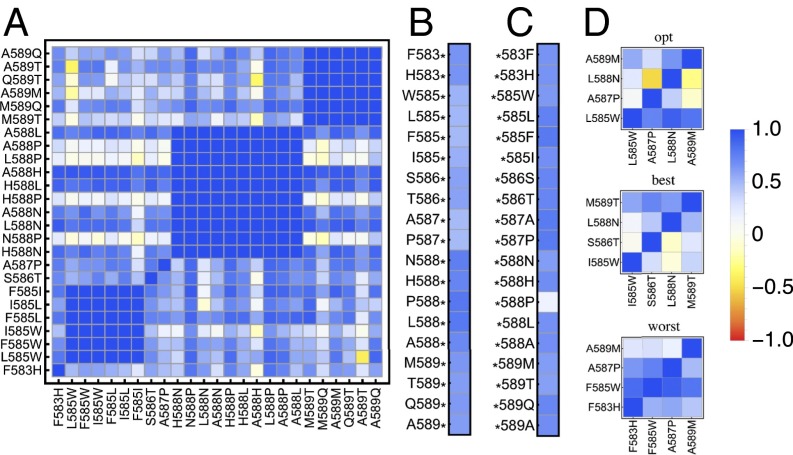
(A) Epistasis measure ${\gamma }_{(A_i,B_i)\to (A_j,B_j)}$ (SI Appendix, Eq. S1_8; $(A_i,B_i)$ on the x axis) between any two substitutions, averaged across the entire landscape. The majority of interactions are small to moderate (blue). Parts of the fitness landscape show highly localized and mutation-specific epistasis, ranging from strong magnitude epistasis (white) to sign and reciprocal sign epistasis (yellow). (B) The average epistatic effect ${\gamma }_{A_i\to }$ (SI Appendix, Eq. S1_10) of a mutation occurring on any background is always small. (C) The average epistatic effect ${\gamma }_{\to A_j}$ (SI Appendix, Eq. S1_13) of a background on any new mutation is usually small, except for mutations to *588P, which shows a strong magnitude effect. (D) Locus-specific gamma for the four mutations leading to the global optimum (Top), the four largest single-effect mutations (Middle), and the single-effect mutations with the lowest fitness (Bottom). The opt landscape exhibits strong sign epistasis between loci 587 and 588 and between loci 588 and 589. Also, the best landscape exhibits pervasive epistasis with sign epistasis between locus 588 and loci 585 and 586, respectively. We observe almost no epistasis in the worst landscape.

Only mutation 588P has a pronounced effect on the global landscape statistics and seems to act as an epistatic hotspot by making a majority of subsequent mutations (of individually small effect) on its background strongly deleterious (clearly visible in Figs. 4B and 5C). This finding can be explained by looking at the biophysical properties of this mutation. In wild-type Hsp90, amino acid 588N is oriented away from solvent and forms hydrogen bond interactions with neighboring amino acids (24). Proline lacks an amide proton, which inhibits hydrogen bond interactions. As a result, substituting 588N with a proline could disrupt hydrogen bond interactions with residues that may be involved in main chain hydrogen bonding and destabilize the protein. In addition, the pyrrolidine ring of proline is extremely rigid and can constrain the main chain, which may restrict the conformation of the residue preceding it in the protein sequence (43).

The variation between inferred landscape topographies increases dramatically for the 360 diallelic, 6-locus sublandscapes (Fig. 4C). Whereas all sublandscapes are largely compatible with an RMF landscape, the decay of landscape-wide epistasis with mutational distance (as measured by ${\gamma }_d$) shows a large variance, suggesting large differences in the degree of additivity. Interestingly, various sublandscapes, typically carrying mutation *588P, show a relaxation of epistatic constraint with increasing mutational distance (i.e., increasing ${\gamma }_d$) that is not captured by any of the proposed theoretical fitness landscape models, suggestive of systematic compensatory interactions (but see the egg-box model for an explicit example featuring nonmonotonicity in ${\gamma }_d$). The variation in the shape of the fitness (sub)landscapes is also reflected in the corresponding roughness-to-slope ratio (inset of Fig. 4C and D), further emphasizing heterogeneity of the fitness landscape with local epistatic hotspots.

Finally, the 1,570 di-allelic four-locus landscapes containing the parental genotype, although highly correlated genetically, reflect a variety of possible landscape topographies (Fig. 4D), ranging from almost additive to egg-box shapes, accompanied by an extensive range of roughness-to-slope ratios. The three focal landscapes discussed above are not strongly different compared with the overall variation and yet show diverse patterns of epistasis between substitutions (Fig. 5).

Thus, predicting fitness landscapes is difficult indeed. Extrapolation of the landscape, even across only a single mutation, may fail due to the existence of local epistatic hotspot mutations. Although the integration of biophysical properties into landscape models is an important step forward (e.g., ref. 44), we demonstrate that such models need to be mutation-specific. Considering a site-specific model [e.g., BLOSUM matrix (45)] is not sufficient. Newer models such as DeepAlign may provide the opportunity to allow integration of mutation-specific effects via aligning two protein structures based on spatial proximity of equivalent residues, evolutionary relationship, and hydrogen bonding similarity (46).

Conclusion

Originally introduced as a metaphor to describe adaptive evolution, fitness landscapes promise to become a powerful tool in biology to address complex questions regarding the predictability of evolution and the prevalence of epistasis within and between genomic regions. Due to the high-dimensional nature of fitness landscapes, however, the ability to extrapolate will be paramount to progress in this area, and the optimal quantitative and qualitative approaches to achieve this goal are yet to be determined.

Here, we have taken an important step toward addressing this question via the creation and analysis of a landscape comprising 640 engineered mutants of the Hsp90 protein in yeast. The unprecedented size of the fitness landscape, along with the multiallelic nature, allows us to test whether global features could be extrapolated from subsets of the data. Although the global pattern indicates a rather homogeneous landscape, smaller sublandscapes are a poor predictor of the overall global pattern because of “epistatic hotspots.”

In combination, our results highlight the inherent difficulty imposed by the duality of epistasis for predicting evolution. In the absence of epistasis (i.e., in a purely additive landscape), evolution is globally highly predictable because the population will eventually reach the single-fitness optimum, but the path taken is locally entirely unpredictable. Conversely, in the presence of (sign and reciprocal sign) epistasis evolution is globally unpredictable, because there are multiple optima and the probability to reach any one of them depends strongly on the starting genotype. At the same time, evolution may become locally predictable with the population following obligatory adaptive paths that are a direct result of the creation of fitness valleys owing to epistatic interactions.

The empirical fitness landscape studied here appears to be intermediate between these extremes. Although the global peak is within reach from almost any starting point, there is a local optimum that will be reached with appreciable probability, particular when starting from the parental genotype. From a practical standpoint, these results thus highlight the danger inherent to the common practice of constructing fitness landscapes from ascertained mutational combinations. However, this work also suggests that one promising way forward for increasing predictive power will be the utilization of multiple small landscapes used to gather information about the properties of individual mutations, combined with the integration of site-specific biophysical properties.

Materials and Methods

Here, we briefly outline the materials and methods used. A more detailed treatment of the theoretical work is presented in SI Appendix.

Data Generation.

Codon substitution libraries consisting of 640 combinations (single up to sextuplet mutants) of 13 previously isolated individual mutants within the 582-to-590 region of yeast Hsp90 were generated from optimized cassette-ligation strategies, as previously described (24) and cloned into the p417GPD plasmid that constitutively expresses Hsp90.

Constitutively expressed libraries of Hsp90 mutation combinations were introduced into the S. cerevisiae shutoff strain DBY288 (can1-100 ade2-1 his3-11,15 leu2-3,12 trp1-1 ura3-1 hsp82: :leu2 hsc82: :leu2 ho: : :pgals-hsp82-his3) using the lithium acetate method (47). Following transformation, the library was amplified for 12 h at 30 °C under nonselective conditions using galactose (Gal) medium with 100 $\mu$g/mL ampicillin (1.7 g/L yeast nitrogen base without amino acids, 5 g/L ammonium sulfate, 0.1 g/L aspartic acid, 0.02 g/L arginine, 0.03 g/L valine, 0.1 g/L glutamic acid, 0.4 g/L serine, 0.2 g/L threonine, 0.03 g/L isoleucine, 0.05 g/L phenylalanine, 0.03 g/L tyrosine, 0.04 g/L adenine hemisulfate, 0.02 g/L methionine, 0.1 g/L leucine, 0.03 g/L lysine, and 0.01 g/L uracil with 1% raffinose and 1% Gal). After amplification, the library culture was transferred to selective medium similar to Gal medium but raffinose and Gal are replaced with 2% (wt/vol) dextrose. The culture was grown for 8 h at 30 °C to allow shutoff of the wild-type copy of Hsp90 and then shifted to selective medium containing 0.5 M NaCl for 12 generations. Samples were taken at specific time points and stored at −80 °C.

Yeast lysis, DNA isolation, and preparation for Illumina sequencing were performed as previously described (25). Sequencing was performed by Elim Biopharmaceuticals and produced $\approx$30 million reads of 99% confidence at each read position based on PHRED scoring (48, 49). Analysis of sequencing data were performed as previously described (26).

Estimation of Growth Rates.

Individual growth rates were estimated according to the approach described in ref. 20 using a Bayesian MCMC approach proposed in ref. 27. Nucleotide sequences coding for the same amino acid sequence were interpreted as replicates with equal growth rates. The resulting MCMC output consisted of 10,000 posterior estimates for each amino acid mutation corresponding to an average effective samples size of 7,419 (minimum 725). Convergence was assessed using the Hellinger distance approach (50) combined with visual inspection of the resulting trace files.

Adaptive Walks.

In the strong selection weak mutation limit (51), adaptation can be modeled as a Markov process only consisting of subsequent fitness-increasing, one-step substitutions that continue until an optimum is reached (so-called adaptive walks). This process is characterized by an absorbing Markov chain with a total of $n$ different states (i.e., mutants), consisting of $k$ absorbing (i.e., optima) and $n-k$ transient states (i.e., nonoptima). Defining $w(g)$ as the fitness of genotype $g$, and $g_{\left[i\right]}$ as the genotype $g$ carrying a mutant allele at locus $i$, the selection coefficient is denoted by $s_j(g)=w(g_{[j]})-w(g)$, such that the transition probabilities $p_{g,g_{\left[i\right]}}$ for going from any mutant $g$ to any mutant $g_{\left[i\right]}$ are given by the fixation probability (52, 53) normalized by the sum over all adaptive, one-mutant neighbors of the current genotype $g$. If $g$ is a (local) optimum, $p_{g,g}=1$. Putting the transition matrix $𝐏$ (54) in its canonical form and computing the fundamental matrix then allows to determine the expectation and the variance in the number of steps before reaching any optimum and to calculate the probability to reach optimum $g$ when starting from genotype $g\prime$ (55). Robustness of the results and the influence of specific mutations were assessed by deleting the corresponding columns and rows in $𝐏$ (i.e., by essentially treating the corresponding mutation as unobserved) and recalculating and comparing all statistics to those obtained from the full dataset.

Correlation of Fitness Effects of Mutations.

Strength and type of epistasis were assessed by calculating the correlation of fitness effects of mutations $\gamma$ (14), which quantifies how the selective effect of a focal mutation is altered when put onto a different genetic background, averaged over all genotypes of the fitness landscape. Extending recent theory (14), we calculated the matrix of epistatic effects between different pairs of alleles $(A_i,B_i)$ and $(A_j,B_j)$ termed ${\gamma }_{(A_i,B_i)\to (A_j,B_j)}$ (SI Appendix, Eq. S1_8), the vector of epistatic effects between a specific pair of alleles $(A_i,B_i)$ on all other pairs of alleles ${\gamma }_{(A_i,B_i)\to }$ (SI Appendix, Eq. S1_9), the vector of epistatic effects between all pairs of alleles on a specific allele pair $(A_j,B_j)$ termed ${\gamma }_{\to (A_j,B_j)}$ (SI Appendix, Eq. S1_12), and the decay of correlation of fitness effects ${\gamma }_d$ (SI Appendix, Eq. S1_15) with Hamming distance $d$ averaged over all genotypes $g$ of the fitness landscape.

Fraction of Epistasis.

Following refs. 35 and 56, we quantified whether specific pairs of alleles between two loci interact epistatically and, if so, whether these display magnitude epistasis [i.e., fitness effects are nonadditive (57), but fitness increases with the number of mutations], sign epistasis (i.e., one of the two mutations considered has an opposite effect in both backgrounds) or reciprocal sign epistasis (i.e., if both mutations show sign epistasis). In particular, we calculated the type of epistatic interaction between mutations $g_{\left[i\right]}$ and $g_{[j]}$ (with $i\ne j$) with respect to a given reference genotype $g$ over the entire fitness landscape. There was no epistatic interaction if $|s_i(g_{\left[j\right]})-s_i(g)|<\epsilon ={10}^{-6}$, magnitude epistasis if $s_j(g)s_j(g_{\left[i\right]})\ge 0$ and $s_i(g)s_i(g_{[j]})\ge 0$, reciprocal sign epistasis if $s_j(g)s_j(g_{\left[i\right]})<0$ and $s_i(g)s_i(g_{[j]})<0$, and sign epistasis in all other cases (58).

Roughness-to-Slope Ratio.

Following ref. 11, we calculated the roughness-to-slope ratio $\rho$ by fitting the fitness landscape to a multidimensional linear model using the least-squares method. The slope of the linear model corresponds to the average additive fitness effect (10, 23), whereas the roughness is given by the variance of the residuals. Generally, the better the linear model fit, the smaller the variance in residuals such that the roughness-to-slope ratio approaches 0 in a perfectly additive model. Conversely, a very rugged fitness landscape would have a large residual variance and, thus, a very large roughness-to-slope ratio (as in the HoC model). In addition, we calculated a test statistic $Z_{\rho }$ by randomly shuffling fitness values in the sequence space to evaluate the statistical significance of the obtained roughness-to-slope ratio from the dataset ${\rho }_{\text{data}}$ given by $Z_{\rho }=\frac{{\rho }_{\text{data}}-\mathrm{E}\left[{\rho }_{\text{RSL}}\right]}{\sqrt{\mathrm{Var}\left[{\rho }_{\text{RSL}}\right]}}$.