Regional glucose metabolism and glutamatergic neurotransmission in rat brain in vivo

Abstract

Multivolume ¹H-[¹³C] NMR spectroscopy in combination with i.v. [1,6-¹³C₂]glucose infusion was used to detect regional glucose metabolism and glutamatergic neurotransmission in the halothane-anesthetized rat brain at 7 T. The regional information was decomposed into pure cerebral gray matter, white matter, and subcortical structures by means of tissue segmentation based on quantitative T₁ relaxation mapping. The ¹³C turnover curves of [4-¹³C]glutamate, [4-¹³C]glutamine, and [3-¹³C]glutamate + glutamine were fitted with a two-compartment neuronal-astroglial metabolic model. The neuronal tricarboxylic acid cycle fluxes in cerebral gray matter, white matter, and subcortex were 0.79 ± 0.15, 0.20 ± 0.11, and 0.42 ± 0.09 μmol/min per g, respectively. The glutamate-glutamine neurotransmitter cycle fluxes in cerebral gray matter, white matter, and subcortex were 0.31 ± 0.07, 0.02 ± 0.04, and 0.18 ± 0.12 μmol/min per g, respectively. The exchange rate between the mitochondrial and cytosolic metabolite pools was fast relative to the neuronal tricarboxylic acid cycle flux for all cerebral tissue types.

Carbon-13 NMR spectroscopy is a powerful technique to measure metabolic fluxes noninvasively in vivo. The flux through the neuronal tricarboxylic acid (TCA) cycle in human (1-3) and animal (4, 5) brain has been determined by following the isotopic ¹³C-label flow from [1-¹³C]glucose to [4-¹³C]glutamate. The subsequent labeling of [4-¹³C]glutamine has been measured in animal (4, 5) brain, and more recently in human brain (1, 2), and is indicative of a glutamate (Glu)/glutamine (Gln) neurotransmitter cycling flux between glutamatergic neurons and surrounding astroglia. Although ¹³C NMR spectroscopy offers a high spectral resolution (1), it suffers from an inherently low sensitivity, thereby limiting the detection to relatively large volumes. As an alternative to direct ¹³C NMR spectroscopy, the protons bound to ¹³C atoms can be detected by proton-observed, carbon-edited ¹H-[¹³C] NMR spectroscopy (6, 7). The high sensitivity of ¹H-[¹³C] NMR spectroscopy has opened the way for the detection of TCA cycle activity in different cerebral tissue types (8, 9) and during functional activation (10, 11) in human and animal brain at high magnetic fields. Pfeuffer et al. (12), and more recently de Graaf et al. (13), have demonstrated the reliable detection of a wide range of metabolites, including [4-¹³C]Glu and [4-¹³C]Gln.

Here we use the improved sensitivity of ¹H-[¹³C] NMR spectroscopy to increase the spatial resolution (25 μl) to measure regional metabolic fluxes in the anesthetized rat brain in vivo. In particular the turnover of [4-¹³C]Glu, [4-¹³C]Gln, and [3-¹³C]Glx (Glx = Glu + Gln) is measured in volumes that span the cerebral cortex, corpus callosum, hippocampus, and thalamus. In combination with quantitative tissue segmentation by T₁ relaxation mapping and multicompartment metabolic modeling, the rates of the neuronal TCA cycle and the Glu/Gln neurotransmitter cycle can be calculated in pure cerebral gray matter and white matter.

Methods

Animal Preparation. Six male Sprague-Dawley rats (140 ± 12 g, mean ± SD) were studied in accordance with the guidelines established by the Yale Animal Care and Use Committee. After an overnight fast (12-16 h), the animals were tracheotomized and ventilated with a mixture of 70% nitrous oxide and 28.5% oxygen under 1.5% halothane anesthesia. A femoral artery was cannulated for monitoring of blood gases (pO₂ and pCO₂), pH, and blood pressure. Physiological variables were maintained within normal limits by small adjustments in ventilation [pCO₂ = 33-42 mmHg; pO₂ > 120 mmHg; pH = 7.30-7.58; blood pressure = 95-110 mmHg (1 mmHg = 133 Pa)]. A femoral vein was cannulated for infusion of [1,6-¹³C₂]glucose. After all of the surgeries were completed, anesthesia was maintained by 0.3-0.8% halothane in combination with 70% nitrous oxide. During NMR experiments animals were restrained in a head holder, and additional immobilization was achieved with d-tubocurarine chloride (0.5 mg/kg every 40 min, i.p.). The core body temperature was measured with a rectal thermosensor and was maintained at 37 ± 1°C by means of a heated water pad. The animals were infused with [1,6-¹³C₂]glucose (Cambridge Isotope Laboratories, Cambridge, MA) according to a protocol described in ref. 13. Blood samples were taken before infusion and every 25 min after the start of infusion. The plasma glucose fractional ¹³C enrichments were measured by GC-MS.

In Vivo¹H NMR Spectroscopy. Experiments were performed on a 7.05-T Bruker magnet and console (Billerica, MA) equipped with a 12-cm-diameter actively shielded gradient coil insert (190 mT/m in 200 μs). Radiofrequency pulse transmission and NMR signal reception for protons (300.3 MHz) were performed with a 14-mm-diameter surface coil. Radiofrequency pulse transmission on carbon-13 (75.5 MHz) was achieved with two orthogonal 21-mm-diameter surface coils driven in quadrature. The magnetic field homogeneity over the volume-of-interest was optimized with the fastmap algorithm (14), which resulted in signal linewidths of 10-13 Hz for water and 8-9 Hz for metabolites in a volume of 100 μl.

Localized ¹H and ¹H-[¹³C] NMR spectra were obtained with an NMR pulse sequence described in ref. 13. Briefly, water suppression was achieved with SWAMP (Sequence for Water Suppression with Adiabatic-Modulated Pulses) (15), an adiabatic sequence employing frequency-selective excitation. Three-dimensional localization of a 5 × 4 × 5 mm (x × y × z) volume was achieved with a combination of outer volume suppression, image-selected in vivo spectroscopy, and slice-selective excitation (13). Multiple volumes were acquired by replacing the image-selected in vivo spectroscopy localization in the Y (top/bottom) direction by a four-step longitudinal Hadamard-encoding technique (16). Specifically, two 25-μl (5 × 1 × 5 mm) volumes were positioned in the cerebral cortex and around the corpus callosum, respectively. A third, 38-μl (5 × 1.5 × 5 mm) volume was placed in the “subcortex” encompassing areas of the hippocampus, thalamus, and several other subcortical areas. Inherent to the longitudinal Hadamard-encoding technique, the fourth volume encompasses all structures in between and around the three described volumes and was discarded in further data processing and analysis. The exact volume composition of the localized volumes was determined from quantitative T₁ relaxation maps. Images were acquired with an adiabatic rapid acquisition with relaxation enhancement sequence (17) from five 1.0-mm slices covering the spectroscopic volumes (data matrix = 128 × 128 over a 25.6 × 25.6-mm field-of-view). T₁ weighting was introduced by a nonselective adiabatic inversion pulse, and images were acquired at 10, 50, 100, 200, 400, 800, 1,500, 3,000, and 5,000 ms after inversion. Data processing consisted of pixel-by-pixel single-exponential fitting. Absolute T₁ maps were segmented into noncerebral tissue and white matter (T₁ < 1,600 ms), gray matter (1,600 ms ≤ T₁ < 1,900 ms), and cerebrospinal fluid (CSF) (1,900 ms ≤ T₁). The segmentation maps were then multiplied with the spatial profiles of the localized volumes to obtain the exact tissue composition of each voxel. The assignment of tissue compartments included cortical gray matter, corpus callosum (white matter), CSF, and subcortical tissue, which includes gray matter such as hippocampus, caudate putamen, and thalamus but also subcortical white matter. Because of severe partial volume effects, no efforts were made to subdivide the subcortical tissues.

Data Acquisition and Processing. The free induction decays were acquired with a 64-s time resolution (four image-selected in vivo spectroscopy increments × four Hadamard permutations with repetition time = 4.0 s). After a complete experiment of 25.6-min continuous signal acquisition, the free induction decays were zero-filled to 8,192 data points, apodized (1.0 Hz Gaussian), Fourier transformed, and phase-corrected. The spectra were frequency-shifted to account for drift in the main magnetic field, but no amplitude or phase corrections were allowed on individual spectra. Next, NMR spectra acquired over 6.4 min were added to increase the signal-to-noise ratio and were used for subsequent quantification of metabolite concentrations and fractional ¹³C enrichments by the lcmodel algorithm (18). Details of the precise implementation of lcmodel can be found in ref. 13.

Metabolic Modeling. The [4-¹³C]Glu, [4-¹³C]Gln, and [3-¹³C]Glx time courses were analyzed by using a two-compartment metabolic model comprising neuronal and astroglial compartments. Briefly, glucose is transported across the blood-brain barrier by specific glucose transporters that are characterized by Michaelis-Menten constants K_m = 12.9 mM and (V_max/CMR_Glc) = 5.8 (19), where V_max represents the maximum glucose transport rate and CMR_Glc is the cerebral metabolic rate of glucose consumption. The brain glucose is converted to pyruvate/lactate, which enters either the neuronal or astroglial TCA cycle. The ¹³C label of [1,6-¹³C₂]glucose is incorporated into the TCA cycle intermediate 2-oxo[4-¹³C]glutarate, which is in exchange with [4-¹³C]Glu. The 2-oxoglutarate (2-OG)/Glu exchange rate, V_x, is modeled by comparing the [4-¹³C]Glu and [3-¹³C]Glu curves. Because the spectral resolution did not allow the discrimination between [3-¹³C]Glu and [3-¹³C]Gln, the metabolic model was extended with a combination metabolic pool, [3-¹³C]Glx, which could be reliably determined by the lcmodel quantification method. The combination pool is treated as any other metabolite pool, taking into account the concentration difference between glutamate and glutamine. The [4-¹³C]Gln position is ultimately labeled by the action of a glutamatergic neurotransmitter cycle between the two compartments. In this metabolic model, a set of coupled differential equations (by using mass and isotope balance) was used within the cwave 2.0 software package (20) to describe the behavior of [4-¹³C]Glu, [4-¹³C]Gln, and [3-¹³C]Glx in response to the infusion of [1,6-¹³C₂]glucose. Because the infusion of [1,6-¹³C₂]glucose did not allow an accurate determination of the astroglial TCA cycle flux V_TCA,A, this metabolic pathway was fixed at 5% of the neuronal TCA cycle flux V_TCA,N (21). The impact of V_TCA,A on V_TCA,N and V_cycle was confirmed to be small (<5% for a 2-fold change). Anaplerotic flow was assumed to be 0.096 μmol/min per g (21), and dilutional fluxes were directed through lactate and glutamine. All multivolume ¹³C turnover data were fitted simultaneously by extending the described metabolic model with three macroscopic tissue compartments. The composition of the spectroscopic volumes in terms of the three tissue compartments was obtained from the quantitative T₁ segmentation results. The lactate, glutamate, and glutamine concentrations were determined in each volume on each individual animal from the nonedited ¹H-[¹³C] NMR spectra (no ¹³C inversion) with lcmodel and assuming the internal concentration standard total creatine to be 9 and 7.5 mM in pure gray and white matter, respectively. With the described prior knowledge and restrictions, the metabolic model was used to determine the neuronal TCA cycle flux V_TCA,N, the glutamatergic neurotransmitter cycle flux V_cycle, the mitochondrial/cytosolic exchange rate V_x, and the dilutional fluxes through lactate and glutamine, V_dil,Lac and V_dil,Gln, in cerebral gray matter, white matter, and subcortical structures.

Results

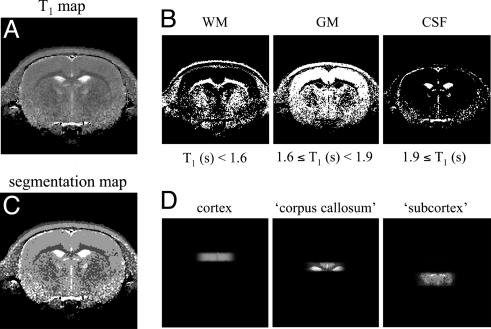
Fig. 1 illustrates the process of obtaining the volume fractions of gray matter, white matter, and CSF in the multiple volumes. Fig. 1 A represents a quantitative T₁ relaxation map of a rat brain. The T₁ relaxation maps are segmented by assigning a range of T₁ relaxation times to a particular tissue type (Fig. 1B). The tissue segmentation maps (Fig. 1C) are then multiplied with the spatial profiles of the localized volumes to yield the tissue composition in each of the spectroscopic volumes (Fig. 1D). The tissue composition of the “cortex” volume in this particular animal was 96% gray matter, 2% white matter, and 2% CSF. The “corpus callosum” volume was segmented into 26% gray matter, 42% white matter, 24% CSF, and 8% subcortical structures. The subcortex was not segmented and was considered a single tissue compartment. The contribution of CSF to the metabolic composition of the spectroscopic volumes was ignored for all metabolites, except for glutamine (0.3 mM) (22) and glucose (1.2 mM) (23).

Fig. 1.

Procedure for the generation of T₁-relaxation-based segmentation maps of rat brain. (A) A quantitative T₁ relaxation map, which was generated from multiple T₁-weighted MR images after a nonselective inversion pulse. See Introduction for more details. (B) By using the indicated T₁ relaxation constant boundaries, the T₁ map of (A) can be segmented into white matter (WM), gray matter (GM), and CSF. The WM map also contains noncerebral tissue such as muscle, skull, and fat. (C) The combined segmentation maps of (B) can be overlaid on the experimentally measured sensitivity profile of the three Hadamard-encoded volumes to obtain the exact tissue composition within each volume (D).

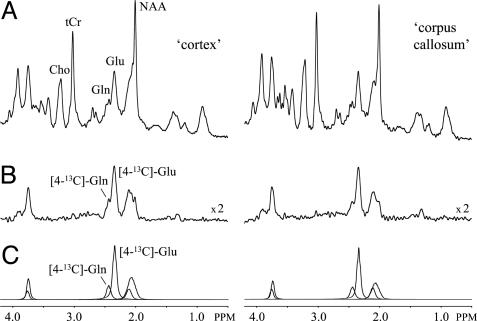
Fig. 2 A and B shows ¹H and ¹H-[¹³C] NMR spectra, respectively, from 25-μl volumes positioned in the cortex (Left) and corpus callosum (Right), as acquired between 95 and 120 min after the start of [1,6-¹³C₂]glucose infusion. The increased sensitivity in conjunction with optimal spectral resolution readily allows the separate detection of [4-¹³C]Glu at 2.34 ppm, [4-¹³C]Gln at 2.44 ppm, and [3-¹³C]Glx between 2.03 and 2.12 ppm (Fig. 2C) by using the lcmodel approach.

Fig. 2.

¹H and ¹H-[¹³C] NMR spectra from rat brain in vivo. Representative ¹H (A) and ¹H-[¹³C] (B) NMR spectra from 25-μl volumes encompassing cerebral cortex (Left) and corpus callosum (Right) are shown. The NMR spectra are acquired between 95 and 120 min after the start of [1,6-¹³C₂]glucose infusion. By using quantitative tissue segmentation as outlined in Fig. 1, the volumes can be decomposed into 92% GM and 8% WM for the cortex volume and 23% GM, 47% WM, and 30% subcortex for the corpus callosum volume. The excellent spectral resolution at 7.05 T readily allows the separate detection of [4-¹³C]Glu and [4-¹³C]Gln, as can also be seen from the glutamate and glutamine contributions to the best lcmodel fits shown in C. ¹H and ¹H-[¹³C] NMR spectra of similar quality were obtained for the subcortex volume (data not shown).

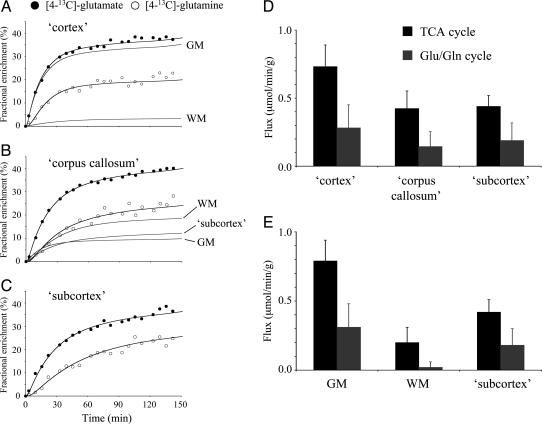
Fig. 3 A-C shows the [4-¹³C]Glu and [4-¹³C]Gln turnover curves for the three spectroscopic volumes after the infusion of [1,6-¹³C₂]glucose. The [3-¹³C]Glx turnover curves are not shown but were of similar quality as the [4-¹³C]Gln turnover curves and were included in all metabolic modeling. The position of [4-¹³C]Glu is labeled first, followed by [4-¹³C]Gln, in accordance with previous observations (4, 13, 21). Using the described metabolic model allows the determination of the rates of the neuronal TCA cycle and the Glu/Gln neurotransmitter cycle. Ignoring tissue heterogeneity (i.e., using a single macroscopic compartment per spectroscopic volume) gives rates for the three spectroscopic volumes (Fig. 3D). Specifically, the neuronal TCA cycle rates in the cortex, corpus callosum, and subcortex are 0.73 ± 0.16, 0.42 ± 0.13, and 0.44 ± 0.08 μmol/min per g (mean ± SD for five animals), respectively. The Glu/Gln neurotransmitter cycle rates are 0.28 ± 0.17, 0.14 ± 0.11, and 0.19 ± 0.13 μmol/min per g (mean ± SD for five animals) for the three tissue types, respectively. The metabolic rates in the corpus callosum and subcortex appear very similar because of severe partial volume effects. When an extended metabolic model with three macroscopic compartments per spectroscopic volume [i.e., gray matter (GM), white matter (WM), and subcortex] is used in combination with the quantitative tissue segmentation, the metabolic rates can be obtained for pure tissue types (Fig. 3E) despite the presence of severe tissue heterogeneity and partial volume effects. The neuronal TCA cycle rates in pure gray matter, white matter, and subcortex are given by 0.79 ± 0.15, 0.20 ± 0.11, and 0.42 ± 0.09 μmol/min per g, respectively, and the glutamatergic neurotransmitter cycle rates equal 0.31 ± 0.17, 0.02 ± 0.04, and 0.18 ± 0.12 μmol/min per g, respectively. The inclusion of tissue heterogeneity in the metabolic model now reveals the large differences in metabolic rates between the three tissue types. The mitochondrial/cytosolic V_x for gray matter, white matter, and subcortex were 12.4 ± 4.5, 6.1 ± 3.3, and 8.8 ± 5.1 μmol/min per g, respectively. Note that the quality of the fits in Fig. 3 A-C is nearly identical with or without prior knowledge of tissue heterogeneity. This result indicates that the turnover curves alone have insufficient sensitivity to detect metabolism from multiple compartments. Only when partial volume effects are completely eliminated or other independent prior knowledge on tissue composition is included can heterogeneity in regional metabolism be revealed.

Fig. 3.

Multicompartment metabolic modeling to obtain regional metabolic fluxes in the presence of partial-volume effects. (A-C) [4-¹³C]Glu and [4-¹³C]Gln turnover in volumes encompassing mainly cerebral cortex (A), corpus callosum with contributions from cerebral cortex and subcortex (B), and subcortex (C). The black filled lines are the best fits to the data obtained by using a two-compartment metabolic model. The inclusion or exclusion of tissue heterogeneity has no appreciable effect on the goodness-of-fit. The gray filled lines are the contributions of GM, WM, and subcortex to the overall turnover curves when tissue heterogeneity is included in the metabolic modeling. [3-¹³C]Glx turnover curves are not shown but were included in the metabolic modeling. Metabolic rates for the TCA cycle (black) and Glu/Gln neurotransmitter cycle (gray) when ignoring tissue heterogeneity (i.e., one macroscopic compartment) (D) or considering tissue heterogeneity through quantitative tissue segmentation (i.e., three macroscopic compartments) (E). See Methods and Results for more details.

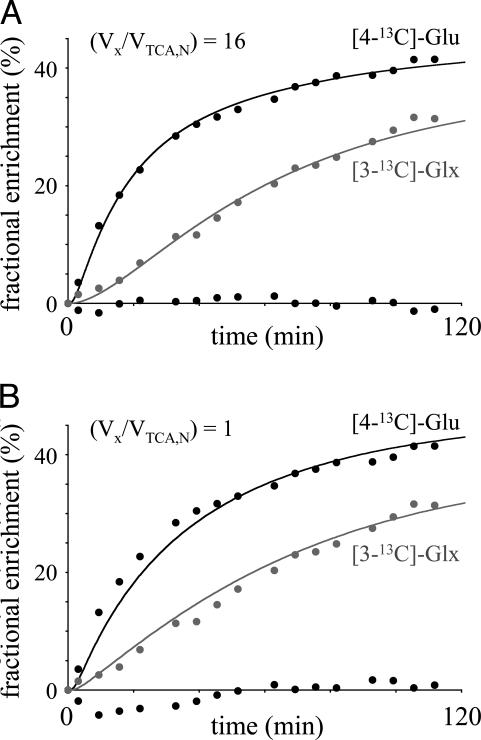
In recent reports on cerebral metabolism of [¹³C]glucose there has been some controversy concerning the magnitude of V_x between the mitochondrial pool of the TCA cycle intermediate 2-OG and the large cytosolic glutamate pool detected by NMR relative to the neuronal TCA cycle rate, V_TCA,N. The excellent quality of the spectroscopic data allowed a validation of the 2-OG/Glu exchange rate by simultaneously fitting the [4-¹³C]Glu and [3-¹³C]Glu turnover curves. Fig. 4 shows the [4-¹³C]Glu and [3-¹³C]Glx turnover curves for a composite voxel obtained by an intensity-weighted sum of the three acquired voxels. Fig. 4 A and B shows the best mathematical fits to the metabolic model for slow (V_x = V_TCA,N as described by ref. 2) and fast (V_x = 16 × V_TCA,N) mitochondrial/cytosolic exchange rates, respectively. It follows that the metabolic model does not accurately describe the experimental data when V_x is slow relative to V_TCA,N. The first half of the [4-¹³C]Glu turnover curve is underestimated, and the second half and most of the [3-¹³C]Glx turnover curve is overestimated. Interestingly, the specific value for V_TCA,N is relatively insensitive to V_x when the [4-¹³C] and [3-¹³C]Glu positions are fitted simultaneously [V_TCA,N = 0.68 ± 0.14 μmol/min per g for (V_x/V_TCA,N) = 1 and V_TCA,N = 0.63 ± 0.12 μmol/min per g for (V_x/V_TCA,N) = 16]. Similar results were obtained for the different tissue compartments. Monte Carlo simulations (200 repeats) yielded V_x = 9.6 ± 6.9, 6.4 ± 3.8, and 6.7 ± 4.1 μmol/min per g (mean ± SD) for gray matter, white matter, and subcortical structures, respectively. The single volume encompassing all tissues (Fig. 4) gave V_x = 8.2 ± 4.3 μmol/min per g. Note that the V_x distribution for all tissues was non-Gaussian and highly skewed toward higher V_x values. Ninety-five percent confidence intervals are given by 2.3-31.2, 1.1-16.3, 1.6-17.8, and 1.7-22.5 μmol/min per g for gray matter, white matter, subcortical structures, and the single volume shown in Fig. 4. Simulations showed that the goodness-of-fit did not improve appreciably for V_x > 10 × V_TCA,N, indicating that the sensitivity toward V_x is minimal for high (V_x/V_TCA,N).

Fig. 4.

Evaluating the effect of the 2-OG/Glu exchange rate V_x on the goodness-of-fit of the [4-¹³C]Glu and [3-¹³C]Glx turnover curves from a volume combining all tissues. (A) When V_x is fast relative to V_TCA, the quality of the fit is excellent, as can also be judged from the residual between the experimental and fitted [4-¹³C]Glu turnover curves (randomly scattered round a fractional enrichment of 0%). For a V_x-to-V_TCA ratio of 1, the initial data points of the [4-¹³C]Glu turnover curve are clearly underestimated, and the overall quality of the fit, as can be judged from the residual χ², is roughly twice that of A. Extensive simulations demonstrate that the goodness-of-fit (residual χ²) does not improve any further for V_x > 10 × V_TCA. Monte Carlo simulations give V_x = 8.2 ± 4.3 μmol/min per g with 95% confidence intervals of 1.7-22.5 μmol/min per g.

Discussion

Here we have used multivolume ¹H-[¹³C] NMR spectroscopy to study regional glucose metabolism and glutamatergic neurotransmitter cycling in rat brain in vivo. The optimal sensitivity of the ¹H-[¹³C] NMR method described in ref. 13 allowed signal detection at a spatial resolution of 25 μl. Although partial volume effects due to tissue heterogeneity still dominate, the increased spatial resolution in combination with quantitative tissue segmentation and multicompartment metabolic modeling allowed the detection of metabolic rates in pure tissue compartments, in particular, cerebral gray matter and white matter.

Tissue segmentation based on quantitative T₁ relaxation mapping is particularly effective for discrimination of cerebral gray matter, white matter, and CSF and is now routinely used for human brain applications (24, 25). This segmentation is equally effective on rat brain, although T₁-based tissue contrast is insufficient to discriminate between different subcortical tissues. As a result, the subcortical spectroscopic volume was not further segmented and considered a single tissue compartment in all metabolic modeling. However, quantitative tissue segmentation is not limited to T₁ relaxation, and a wide range of variables like T₂ relaxation, diffusion, magnetization transfer, and combinations thereof may be used to achieve a more specific tissue segmentation.

The results presented here for the TCA cycle rate are in good agreement with previous NMR, positron-emission tomography, and autoradiography results. For halothane-anesthetized rats, de Graaf et al. (13) found V_TCA = 0.52 μmol/min per g for a large volume encompassing both gray and white matter. Others reported rates of 0.5-0.8 μmol/min per g (5, 26) for similar experimental conditions but different anesthetics (isoflurane or α-chloralose). Reports on NMR detection of regional metabolism are fewer, mainly because of sensitivity limitations. Nevertheless, on human brain, Pan et al. (9) used spectroscopic imaging to obtain metabolic rates from 6-ml volumes and found a ≈3-fold difference in TCA cycle activity between gray (0.88 μmol/min per g) and white matter (0.28 μmol/min per g). Even larger differences (5-fold) were reported by Mason et al. (8). In rat brain Hyder et al. (27) used ultrafast spectroscopic imaging to detect [3,4-¹³CH₂]Glx turnover and demonstrated a 2.4-fold difference in V_TCA between gray and white matter, in good agreement with the present results. In the seminal paper on the [¹⁴C]deoxyglucose autoradiography method, Sokoloff et al. (28) presented local cerebral glucose utilization values for normal conscious rat brain. Although the absolute values for V_TCA are significantly higher, mainly because of the absence of anesthetics, the overall distribution is in excellent agreement with the present NMR results, with V_TCA (assuming 2CMR_Glc = V_TCA) in white matter and hippocampus being 3 and 1.5 times lower, respectively, than gray matter of the somatosensory cortex.

No information is available on the regional distribution of the Glu/Gln neurotransmitter cycle. In larger volumes encompassing multiple tissues, de Graaf et al. (13) found V_cycle = 0.25 μmol/min per g for halothane-anaesthetized rat brain, whereas Patel et al. (29) reported V_cycle = 0.22 μmol/min per g. Although other techniques cannot measure V_cycle directly, some indications can be obtained from enzyme distributions and activities. Berl (30) studied the activity of glutamine synthetase in different regions of cat brain. The relative activity of glutamine synthetase in gray matter of the somatosensory cortex, hippocampus, thalamus, and corpus callosum were 100%, 58%, 53%, and 28%, respectively, providing good support for the results presented here. Furthermore, Boulland et al. (31) demonstrated that glutamine transporters are highly concentrated in astroglia surrounding the synapses of glutamatergic and GABAergic neurons but absent in oligodendrocytes. Oligodendrocytes are rich in glutamine but are located far from synapses and, hence, are not directly involved in neurotransmission.

Glucose is transported across the blood-brain barrier by specific glucose transporters (GLUT) that are characterized by Michaelis-Menten kinetics. In this study we used published kinetic constants by Mason et al. (19) that were obtained for whole rat brain. Ignoring differences in glucose transport kinetics between different tissue types can potentially give erroneous results. However, de Graaf et al. (25) found no significant differences in glucose transport kinetic constants (V_max/CMR_Glc and K_m) between cerebral gray matter and white matter in human brain. Given the similarities between human and rat whole-brain glucose transport kinetics (19, 25), it is reasonable to assume that rat brain does not exhibit significant regional variations in glucose transport. Any assumptions regarding glucose transport can be eliminated by directly measuring brain glucose levels, as has been shown for the αH1-glucose resonance (5.23 ppm) at high magnetic field strengths (25).

The relationship between neuronal energy metabolism and neurotransmitter cycling was initially investigated by Sibson et al. (5) and was later extended by Patel et al. (29, 32). For cortical activities ranging from isoelectricity to bicuculline-induced seizures, they found a linear relationship between the cerebral metabolic rate of neuronal glucose oxidation, CMR_Glc(ox)N, and the Glu/Gln neurotransmitter cycle, V_cycle, with a slope of ≈1 and an intercept of ≈0.1 μmol/min per g (at V_cycle = 0). The proportionality of changes in CMR_Glc(ox)N and V_cycle has been explained theoretically on the basis of the energetic requirements of ion flows (sodium and potassium pumps) associated with glutamatergic neurotransmission (33). The regional metabolic fluxes presented in this paper provide further evidence for the linear relationship between neuronal glucose oxidation and Glu/Gln neurotransmitter cycling. The data points of all three tissue types fall directly on the previously observed line. The data for cerebral gray matter and subcortical tissues fall above and below the data for whole brain, as expected. The data for cerebral white matter are very close to those for isoelectricity (5): both are characterized by the absence of glutamatergic neurotransmission activity and both have low energetic requirements because of the absence of large ion flows.

The correlation between neuronal CMR_Glc(ox)N and V_cycle, as reported by Sibson et al. (5), may have been complicated by the use of different anesthetics to achieve different levels of cortical activity. However, the current results, together with the results by Patel et al. (29, 32), establish an identical relationship for halothane anesthesia that holds for cortical activities across the complete physiological range (i.e., from white matter at rest to whole-brain seizures).

The 2-OG pool is generated inside the mitochondria during TCA cycle activity, whereas the large glutamate pool resides in the cytosol. The 2-OG and glutamate pools are in exchange by means of the transaminases and transporter associated with the malate-aspartate shuttle and glutamate dehydrogenase. Mason et al. (34, 35) found that the mitochondrial/cytosolic exchange, as characterized by the rate V_x, is much faster (>60×) than the neuronal TCA cycle rate V_TCA,N, an observation that has recently been confirmed by Patel et al. (29, 32). However, recent reports, largely from the same research group (2, 26, 36), claim that the exchange rate V_x is comparable with V_TCA. A similar ratio between V_x and V_TCA has also been reported in other organs, particularly the heart (37, 38), although the ratio can be severalfold greater than 1, depending on the substrate and activity level. Given the large metabolic differences between brain and heart, this result may not be surprising. The heart has a very active aerobic metabolism, leading to a TCA cycle flux that can be almost an order of magnitude larger than that of the brain. Furthermore, the brain relies almost exclusively on glucose metabolism with a more active malate-aspartate shuttle, whereas under normal conditions, the heart utilizes very little, if any, glucose for oxidative energy production (39). Thus, the lower TCA cycle flux together with the higher malate-asparate shuttle activity lead to the expectation that V_x/V_TCA could be very different in the brain than in the heart.

Because shuttle activity and TCA cycle activity have a similar effect on the labeling of [4-¹³C]Glu, an independent measure of V_x and V_TCA requires additional information; for example, the turnover of [3-¹³C]Glu, [2-¹³C]Glu, [2-¹³C]aspartate, or [3-¹³C]aspartate. Although the sensitivity in the current study was insufficient to observe aspartate turnover, the high spectral resolution allowed the separation of [4-¹³C]Glu and [3-¹³C]Glx turnover. Using brain extracts after [¹³C]glucose infusion, Patel et al. (29) showed that V_x can be reliably estimated from [3-¹³C]Glx, provided that the contribution from [3-¹³C]Gln is included in the modeling. Using this approach, we found that the 2-OG/Glu exchange V_x rate for all three tissue types, as well as for the larger volume encompassing all tissue types, is on average ≈20 times faster than the neuronal TCA cycle rate. However, the 95% confidence intervals are large because the metabolic model becomes insensitive to V_x for large values of V_x relative to V_TCA,N. Nevertheless, although a high V_x-to-V_TCA ratio inherently has a large uncertainty, the results in Fig. 4 clearly show that our data do not support a V_x-to-V_TCA ratio of unity because this result clearly diminishes the goodness-of-fit.

One possible explanation for the variation in quantitative numbers for V_x among different research groups may be given by the goodness-of-fit and the relative importance that is given to each point in a turnover curve. From the results in Fig. 4A, it follows that the goodness-of-fit is high when V_x is ≫V_TCA, as can be judged from the residual between the experimental data and the best fit. However, for V_x = V_TCA, the initial data points of the [4-¹³C]Glu turnover curve are underestimated, whereas most of the [3-¹³C]Glx turnover curve is overestimated, leading to a significantly reduced goodness-of-fit. In several of the studies reporting a V_x-to-V_TCA ratio close to unity (2, 36), this finding is exactly the observed behavior, i.e., the initial data points of the [4-¹³C]Glu turnover curve are systematically underestimated. Although this observation can potentially provide a unifying explanation for the discrepancies reported for the mitochondrial/cytosolic exchange in brain studies, only a reanalysis of all existing (high-quality) data or the acquisition of independent measures of V_x will resolve the controversy. From the standpoint of studying brain metabolism by in vivo NMR spectroscopy, the most important practical issue is whether the specific (V_x/V_TCA,N) value has an impact on the resulting V_TCA,N and V_cycle values. Our present results, as well as the recent results by Patel et al. (29), suggest that the impact is minimal when the [3-¹³C]Glu and Gln positions are included in the modeling.