Probing Lipid Bilayers under Ionic Imbalance

Abstract

Biological membranes are normally under a resting transmembrane potential (TMP), which originates from the ionic imbalance between extracellular fluids and cytosols, and serves as electric power storage for cells. In cell electroporation, the ionic imbalance builds up a high TMP, resulting in the poration of cell membranes. However, the relationship between ionic imbalance and TMP is not clearly understood, and little is known about the effect of ionic imbalance on the structure and dynamics of biological membranes. In this study, we used coarse-grained molecular dynamics to characterize a dipalmitoylphosphatidylcholine bilayer system under ionic imbalances ranging from 0 to ∼0.06 e charges per lipid (e/Lip). We found that the TMP displayed three distinct regimes: 1) a linear regime between 0 and 0.045 e/Lip, where the TMP increased linearly with ionic imbalance; 2) a yielding regime between ∼0.045 and 0.060 e/Lip, where the TMP displayed a plateau; and 3) a poration regime above ∼0.060 e/Lip, where we observed pore formation within the sampling time (80 ns). We found no structural changes in the linear regime, apart from a nonlinear increase in the area per lipid, whereas in the yielding regime the bilayer exhibited substantial thinning, leading to an excess of water and Na⁺ within the bilayer, as well as significant misalignment of the lipid tails. In the poration regime, lipid molecules diffused slightly faster. We also found that the fluid-to-gel phase transition temperature of the bilayer dropped below the normal value with increased ionic imbalances. Our results show that a high ionic imbalance can substantially alter the essential properties of the bilayer, making the bilayer more fluid like, or conversely, depolarization of a cell could in principle lead to membrane stiffening.

Introduction

Ionic imbalance exists across biological membranes of both excitable and nonexcitable animal cells. Ionic imbalance in a cell is achieved by ion transporters and ion channels on cell membranes, leading to a transmembrane potential (TMP) gradient known as the resting potential. Normally, the TMP across cell membranes ranges between −60 mV and ∼−80 mV (1). This resting potential functions primarily as a battery, providing power for different molecules embedded in the membrane, and is also an essential element in cell signaling processes (2).

Under certain scenarios, the TMP can increase above the cell resting potential. In neurons and muscle cells, the TMP can reach ∼130 mV during the propagation of action potentials, which is known as hyperpolarization (3). During electroporation, cells can experience TMPs of up to several volts (4, 5, 6, 7). Electroporation utilizes an external electric field to increase the permeability of the cell membrane, allowing the exchange of materials between the inside and outside of the cell. Electroporation has many different applications, including improving drug delivery efficiency (8, 9, 10), introducing plasmids into living cells for gene transfection (11, 12, 13), inserting proteins into cell membranes (14, 15), activating membrane transporters and enzymes (16), and facilitating cell fusion (17, 18, 19).

Both theoretical modeling (20, 21) and experiments (4) have revealed that the TMP varies at different locations of cell membranes when the cells are placed in an external electric field, as occurs in electroporation. Under these conditions, one polar end of the cell develops a large positive TMP and the other polar end develops a large negative TMP. The equator does not exhibit a considerable TMP. Temporally, the TMP gradually increases to its steady-state value over the course of tens of microseconds when an external electric field is turned on (5, 22). Although it is not emphasized in the literature, a key point of electroporation is that the TMP results from the redistribution of ions in cell membranes, which corresponds to a local ionic imbalance. It must be noted that this comes about because the membrane is closed and impermeable to ions (see Fig. 1). It is believed that in both living and artificial systems, ionic imbalances can reach values that either directly generate pores on cell membranes or facilitate pore formation by other means. Thus, understanding the changes that occur in the structural and electrical properties of membranes with an increasing ionic imbalance is of much interest. However, the response of cell membranes to an ionic imbalance is still poorly understood due to the complexity of the problem. This lack of understanding has limited the development of many biomedical applications in which cells are manipulated with electric fields.

Figure 1.

(A) Illustration of a cell in the electroporation setup. E is the external electric field, V is the transmembrane potential, and Vt is the threshold potential. (B) Double bilayer system. The system has two identical patches of DPPC bilayer filled with polarizable water and 150 mM monovalent salt. An ionic imbalance is induced between the two regions to generate a TMP. To see this figure in color, go online.

Different approaches have been used to investigate the behavior of cell membranes in response to a high ionic imbalance and TMP in electroporation, and it was found that lipid bilayers can only sustain up to a maximum TMP, known as the threshold potential. Above this potential, membranes become conductive due to significant pore formation (5, 23). The threshold potential is an intrinsic property of the membrane that is related to the composition of lipids and proteins in the membrane. Several theoretical models that estimate the probability of pore formation as a function of TMP have been proposed (20, 24, 25), but these models employ several approximations, in particular that the structure of the membrane or the pore is not affected by an ionic imbalance.

With the recent advance of computational approaches, researchers have investigated pore formation on membranes using Monte Carlo simulations and molecular dynamics (MD) simulations, which can reveal the molecular process of pore formation (26, 27, 28, 29, 30). In a number of MD simulation studies, the TMP was conveniently modeled by an external electric field across the membranes without any involvement of ions (26, 27). However, an electric-field-emulated TMP is different from an ionic-imbalance-generated TMP, and thus may lead to an erroneous prediction of membrane structure and electrostatics. A few studies that employed ionic imbalance to induce a TMP were carried out using atomistic MD simulations (31, 32, 33). However, these studies were limited by system size constraints and therefore the TMP could not be changed in a continuous fashion. In addition, previous studies focused mainly on pore formation on the membrane; how the TMP influences cell membranes below the electroporation threshold has not been investigated, and questions regarding key membrane properties, such as the gel-to-fluid phase transition, are still unanswered.

To address this issue, we used coarse-grained (CG) MD simulations to probe the structural and dynamic changes of a model cell membrane under a TMP generated by ionic imbalances. The TMP starts from zero and gradually rises to the threshold potential in an aqueous environment featuring a physiological concentration of salt, emulating the real scenario in electroporation. The CG model allows us to routinely simulate a system with a size of 20 nm × 20 nm × 80 nm, with double lipid bilayers. We use a second lipid bilayer to divide the system into an intracellular and an extracellular region to host the ionic imbalance (see Fig. 1 B). The MARTINI CG force field is not specifically designed for charged interactions; however, by using a polarizable water model and the particle mesh Ewald (PME) method, we can obtain a better description of the electrostatics of our bilayer system.

Materials and Methods

CG force fields with polarizable water

Due to the high computational cost of simulating a double bilayer system for multiple ionic imbalances in full atomistic models, we choose to use a CG force field known as MARTINI (34). The MARTINI CG force field maps four heavy atoms to one CG bead. Therefore, it can improve the computational efficiency by three orders of magnitude. The MARTINI force field was originally developed for lipid bilayers, but recently has included other biomolecules. Full details about this CG force field can be found elsewhere (35). The standard water model in MARTINI only has dispersion interactions, and because of the lack of Coulombic interactions it may not accurately represent the electrostatic interactions in a bilayer system. Therefore, we choose to use the MARTINI polarizable water model, known as PW-MARTINI (36). The PW-MARTINI model features a dipole that can change with the external electric field, which gives a realistic dielectric constant for water (∼80) and bilayers (∼2.5) in the context of the MARTINI force field. Although it was not originally included in the PW-MARTINI model, PME is used in all of the simulations to account for long-range electrostatics. The impact of PME on the performance of the PW-MARTINI model was described previously (36).

Double bilayer system

A double bilayer system is used to create a stable ionic imbalance in a box with periodic boundary conditions (31, 37). We use a dipalmitoylphosphatidylcholine (DPPC) bilayer to study the structural changes of the bilayer under such an ionic imbalance. A small piece of the DPPC bilayer is taken from the MARTINI force field homepage (http://md.chem.rug.nl/cgmartini/). The bilayer is duplicated several times and combined to form a large bilayer with xy dimensions of 18 nm × 18 nm, and equilibrated with water for 80 ns. The bilayer-water system is then duplicated vertically and equilibrated for another 80 ns. The final dimensions of the double bilayer system are 18 nm × 18 nm × 50 nm, with ∼370,000 CG beads. A physiological concentration of NaCl (150 mM) is added to the water as salt.

The system is divided by the bilayers into two regions, extracellular and intracellular (Fig. 1 A). An ionic imbalance is implemented in the system by moving one Na⁺ ion from the intracellular region to the extracellular region and simultaneously moving one Cl⁻ ion from the extracellular region to the intracellular region. This counts as one ionic imbalance. The increment of ionic imbalance is one, two, three, four, or five. Since each bilayer had 2064 lipids, one ionic imbalance in our double bilayer system equals 9.689 × 10⁻⁴ e per lipid (e/Lip) ionic imbalance. After each increment of the ionic imbalance, the system is equilibrated for 80 ns.

Bilayer dipole potential

The dipole potential of the bilayer is calculated by solving Poisson’s equation for electrostatics, which has the following expression:

$${\nabla }^2\phi =-\frac{{\rho }_f}{\epsilon },$$ (1)

where $\phi$ is the electric potential, ${\rho }_f$ is the free charge density, and $\epsilon$ is the permittivity of the medium. The numeric implementation of calculating the dipole potential is done by dividing the box into a number of slices in the z direction, summing the charge per slice, and then integrating twice the charge distribution. Therefore, the dipole potential is calculated along the z direction. Here, the number of slices is 1000 for all of the simulated systems. The potentials in the intra- and extracellular regions are also calculated by the above procedure and then averaged. The TMP is the difference between the extracellular potential and intracellular potential.

Simulation setup

The time step of the simulation is 20 fs for the PW-MARTINI CG. The cutoff for both van de Waals interactions and short-ranged electrostatic interactions is 1.2 nm. The PME method is used to account for long-range electrostatic interactions, with a Fourier spacing of 0.14 nm (38). The neighbor list is updated every 10 time steps. The dielectric constant is set to be 2.5. Periodic boundary conditions are applied. The temperature is controlled at 300 K by Berendsen temperature coupling with a time constant of 1.0 ps (39). The pressure is semi-isotropically coupled to the bilayer system at 1 atm in both vertical and lateral directions using Berendsen pressure coupling with a time constant of 4 ps. Polarizable water is constrained by means of the LINCS algorithm with a LINCS order of 4. All simulations are performed with the use of GROMACS 4.6.7 (40).

Results and Discussion

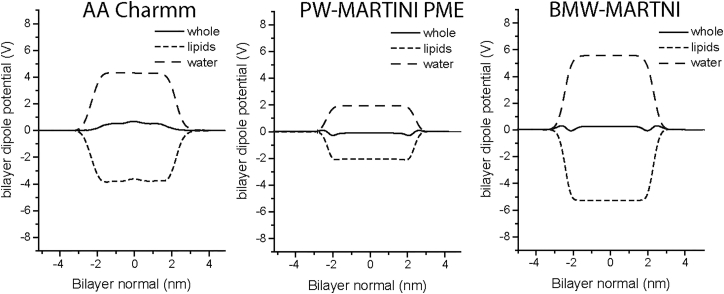
Since we are interested in the impact of an ionic imbalance on the bilayer structure, an accurate representation of the electrostatics of the bilayer-water system is essential. The bilayer dipole potential is one way to estimate the electrostatics predictability of the force field. The membrane dipole potential arises from the alignment of the water dipoles and the lipid headgroup dipoles at the bilayer-water interface. The experimental value of the dipole potential of fully saturated lipid membranes is in the range of 220–280 mV (41). Atomistic force fields always predict the dipole potential to be twice as large as experimental values (42). Fig. 2 gives the calculated dipole potential of a DPPC bilayer obtained using the all-atom (AA) CHARMM force field, the PW-MARTINI CG force field, and the big multipole water model in the frame of MARTINI, known as the BMW-MARTINI water model (43). The AA CHARMM force field gives a dipole potential of ∼500 mV. The dipole potentials of water and lipids are as large as ∼4 V in absolute values. The potentials of the two components cancel each other, resulting in a small total dipole potential of the bilayer. The PW-MARTINI model gives a smaller water dipole potential (∼2 V), and BMW-MARTINI gives a larger water dipole potential (∼5 V). At this point, it seems that BMW-MARTINI is a better choice since it gives a whole dipole potential closer to the atomistic value. However, BMW-MARTINI reproduces twice as much TMP as AA CHARMM at a given ionic imbalance (31). In the BMW-MARTINI setup, the bilayers can withstand ∼−3.7 V TMP and not break (within 100 ns), which is unacceptable. It has been demonstrated in multiple atomistic simulation studies that lipid bilayers will break at ∼−2 V TMP, and experiments have shown an even lower breakdown potential for lipid bilayers (<−1 V) (31, 44, 45, 46). On the other hand, the PW-MARTINI with PME reproduces a TMP nearly identical to that calculated by AA CHARMM at a given ionic imbalance. Given the fact that BMW-MARTINI reproduces unreasonable TMPs and is six times more computationally demanding than the original MARTINI with polarizable water, we choose to use PW-MARTINI PME for the setup of the force field in this study.

Figure 2.

Electric dipole potential of a DDPC bilayer calculated with the CHARMM AA force field, PW-MARTINI PME CG force field, and BMW-MARTINI CG force field. The size of the bilayer is 10 nm × 10 nm. No free ions are included. The dipole potential was averaged for 20 ns in both AA and CG simulations.

An ionic imbalance is created by exchanging ions between the intracellular region and the extracellular region in the double bilayer system. The charge density distribution and the potential profile of the double bilayer system with ∼40 ionic imbalances are shown in Fig. 3. The system has 40 ion imbalances, resulting in an imbalance of ∼0.04 ions per lipid (e/Lip). The extracellular region has zero electric potential, whereas the intracellular region features an ∼−1.5 V potential. The difference of the potential between the intra- and extracellular regions is the TMP. The fluctuation of the potential inside the bilayer is caused by the bilayer dipole potential. The dipole potential inside the bilayer is negligible compared with the TMP generated by ionic imbalance. The corresponding electric field E in the double bilayer system is consistent with the TMP. There are some fluctuations of E at the bilayer-water interface and there is a high plateau inside the bilayer. The value of E reaches ∼0.5 V/nm, or 5 × 10⁸ V/m, at the center of the bilayer, which is an enormous electric field strength. The distribution of Na⁺ and Cl⁻ in the double bilayer system is also given. The ion density is flat at the water region, whereas at the water-bilayer interface the density either increases or decreases depending on the type of ion. This indicates that there are either extra ions or fewer ions at the bilayer surface. The total charge density (including ions, lipid headgroups, and polarizable water) displays huge fluctuations at the water-bilayer interface, which should arise from the alignment of the water and headgroup dipole at the interface.

Figure 3.

Electric profile of the double bilayer system. Charge densities, electric field, and electric potentials are given as a function of the bilayer normal (z direction). Data were collected with an interval of 0.1 nm. To see this figure in color, go online.

One of our main goals in this work was to study the correlations between the TMP and a gradual increase in ionic imbalance. Since one bilayer has 2064 lipids, adding one ionic imbalance in this system equals 9.689 × 10⁻⁴ e ionic imbalance per lipid (e/Lip). After each ionic imbalance increment, the system is equilibrated for 80 ns to redistribute the ions. The ionic imbalance is added continuously in such a manner until the bilayer breaks. One might assume that the TMP increases linearly as we add up the ionic imbalance. However, this is not entirely true, as shown in Fig. 4. The TMP does increase proportionally with the ionic imbalance as it increases from 0 to 0.045 e/Lip, which we define as the linear region. However, a further increase in the ionic imbalance does not build up the TMP, as it stays at ∼−1.8 V when the ionic imbalance increases from 0.045 e/Lip to 0.06 e/Lip, which we define as the yielding region. When the ionic imbalance goes beyond 0.06 e/Lip, one of the bilayers spontaneously forms pores to reequilibrate the ionic imbalance. It has been reported that electroporation of cell membranes occurs around −1 V and electroporation of pure DMPC bilayers occurs around −2 V (7). Our simulation is consistent with those findings, and it further reveals details of how the TMP builds up in response to a gradually increasing ionic imbalance. Interestingly, a sudden increase of ionic imbalance (e.g., 0.005 e/Lip) in the system will result in instant pore formation on one of the bilayers even if the total ionic imbalance is below the pore-forming value (∼0.06).

Figure 4.

TMP on the upper bilayer as a function of ionic imbalance per lipid (e/Lip). One ionic imbalance in the studied bilayer system equals 9.689 × 10⁻⁴e/Lip. To see this figure in color, go online.

Changes in the size of the bilayer in response to an ionic imbalance buildup occur in the aforementioned three regions. Since the simulation system employs a semi-isotropic NPT ensemble, the lateral dimension and vertical dimension can change freely to maintain the designated pressure (1 atm). Fig. 5 A gives the area of the bilayer (area per lipid) as a function of ionic imbalance. When the ionic imbalance increases, the lateral dimension of the box also increases, stretching the bilayer laterally. When the ionic imbalance reaches the pore-forming imbalance (0.06 e/Lip), the surface area of the bilayer increases as much as ∼15%. In the linear region of TMP (<0.045 e/Lip), the area per lipid has a nonlinear relationship with the ionic imbalance. Interestingly, in the yielding region (0.045–0.06 e/Lip), the area per lipid still goes up while the TMP goes down slightly. Although in both regions the area per lipid has a tendency to increase, there is an obvious gap between the linear region and the yielding region, as shown in Fig. 5 A.

Figure 5.

(A) Area per lipid as a function of ionic imbalance per lipid. TMP is shown as a reference. (B) Imbalanced charge density as a function of ionic imbalance per lipid. TMP is shown as a reference.

Since the area of the lipid bilayer can change to adapt to the ionic imbalance increase, the ionic imbalance might not be the best way to describe the electric stress induced on the bilayer. Therefore, we looked at the imbalanced charge density. The imbalanced charge density is defined as the ionic imbalance divided by the surface area of the bilayer. Fig. 5 B shows the imbalanced charge density as a function of ionic imbalance per lipid. Surprisingly, we find that the imbalanced charge density is proportional to the ionic imbalance per lipid. This might due to the small change in the surface area that is not large enough to influence the charge density. Therefore, the ionic imbalance per lipid can be used to gauge the electric stress induced on the bilayer.

To identify the structural differences of the bilayer brought about by the ionic imbalances, we first plot the density profile of the components (including the phosphate group, water, and ions) in the bilayer system as a function of the bilayer normal at 0.00, 0.02, 0.04, and 0.06 e/Lip ionic imbalance. Phosphate groups are the center of the hydrophilic lipid heads, and their density peaks are usually an indicator of the thickness of the bilayer. The density of the phosphate group under zero ionic imbalance is typically two peaks located at each leaflet of the bilayer. At 0.02 e/Lip, which is a moderate increase of the ionic imbalance, the distribution of phosphate is similar to that of 0.00 e/Lip, except that the two peaks of each leaflet are slightly closer to each other. This is because the bilayer is squeezed by the attractions of ions on each side, resulting in a reduced thickness of the tail region. At 0.04 e/Lip, which is close to the yielding ionic imbalances, the density peaks on both leaflets continue to be closer together. At 0.06 e/Lip, where the imbalance is close to a pore-forming imbalance, the bilayer becomes substantially thinner, as indicated by the solid red line in Fig. 5 A. However, at this pore-forming imbalance, the width of the density peaks of the phosphate group does not appear to decrease correspondingly. Instead, the peaks are wider than they are at low imbalances. This indicates that the phosphate groups in each leaflet are distributed more widely around its equilibrated location.

For water molecules, there are no significant differences in the density distribution at each level of ionic imbalance. As shown in Fig. 6 B, the water density is gradually reduced at the hydrophilic layer and is completely eliminated at the headgroup-tail interface of the bilayer. As the ionic imbalance increases, the water density shifts into the bilayer center due the reduction of the bilayer thickness. At a 0.06 e/Lip ionic imbalance, there is water at the headgroup-tail interface of the upper leaflet of the bilayer (∼0.5 nm of the bilayer normal). This indicates that water can penetrate into the tail region of the upper leaflet of the bilayer at pore-forming imbalances.

Figure 6.

Density profile of each component of the double bilayer system under different ionic imbalances. (A) Phosphate group density as a function of the bilayer normal. (B) Water density as a function of the bilayer normal. (C) Na⁺ density as a function of the bilayer normal. Gray columns in the background show the phosphate group distribution. (D) Cl⁻ density as a function of the bilayer normal. Gray columns show the phosphate group distribution. Data were collected with an interval of 0.1 nm and averaged over 80 ns. To see this figure in color, go online.

The density profiles of Na⁺ and Cl⁻ exhibit more variability since there are only dozens of ions in the system (Fig. 6, C and D). At 0.00 e/Lip, both leaflets of the bilayer have some Na⁺ residing in the headgroup region (gray column). As the ionic imbalance increases, less Na⁺ stays at the intracellular leaflet and more resides in the extracellular leaflet of the bilayer. At 0.06 e/Lip, the concentration of Na⁺ in the upper leaflet is almost comparable to that in the water region, which has a physiological concentration of Na⁺ (150 mM). This high density of Na⁺ in the upper leaflet might be a significant contributor to pore formation on the bilayer. On the other hand, the density profile of Cl⁻ indicates that a chlorine ion does not partition into the headgroup region at all. Indeed, previous works have shown that the free-energy barrier of Na⁺ partitioning into the headgroup region of DPPC bilayers is substantially smaller than that of Cl⁻ (32). At higher imbalances, Cl⁻ gathers at the surface of the bilayer in the intracellular region. At 0.06 e/Lip, the density of Cl⁻ increases almost 50% compared with 0.00 e/Lip at the bilayer surface.

To characterize the degree of randomness of lipid molecules organized inside the bilayer, we show the second-order parameter of each bond on the lipid molecules at varying ionic imbalances in Fig. 7. The order parameter can give us a clue as to how the lipid headgroup and tails are aligned. The value of the order parameter can be interpreted as follows: 1.0 corresponds to perfect vertical alignment, 0.0 corresponds to completely random orientation, and −0.5 corresponds to perfect horizontal alignment. The hydrophilic lipid head region has an identical alignment for all ionic imbalances: the dipole (ammonium and phosphate) tends to slightly align horizontally, the bond between phosphate and the first glycerol group tends to align vertically, and the bond between the two glycerol groups tends to slightly align horizontally. The bonds in the tail region, on the other hand, show a different degree of alignment. At a 0.00 e/Lip ionic imbalance, the alkyl tails align vertically and the terminal bonds tend to become disordered, showing a typical lipid order parameter inside the bilayer. At a 0.04 e/Lip ionic imbalance, however, the order parameter of the tail bonds drops by ∼0.15, indicating a more disordered alignment. At 0.06 e/Lip, the ionic imbalance continues to drop another ∼0.05. Although phosphate groups have a much wider density distribution around their equilibrated position (Fig. 6 A), their dipole orientation with respect to amine groups is not disturbed. Therefore, the larger density distribution of the phosphate groups is mainly due to the randomness of the alkyl tail at higher ionic imbalances.

Figure 7.

Second-order parameter of lipid backbone bonds in the bilayer under varying ionic imbalances. Data were averaged over 80 ns.

Next, we probed the effect of ionic imbalance on the diffusivity of lipids within the bilayer. Lipid diffusion regulates protein transport, signaling, and lipid raft formation. Studying lipid diffusion under ionic imbalances may help to elucidate cell membrane functions in response to high electrical stress. Fig. 8 gives the averaged mean-square displacement (MSD) of the lipids in the bilayer as a function of time under different ionic imbalances. Generally, there are two regimes of lateral diffusion. There is a fast regime of diffusion that comes from the local fluctuation of the lipid around its equilibrated position, and there is a slow regime of diffusion that comes from the lateral migration of lipids inside the bilayer. We find that the MSDs of lipids are identical under 0.00, 0.02, and 0.04 e/Lip ionic imbalances, with a fast diffusivity of ∼1.1 × 10⁻⁶ cm² s⁻¹ and a slow diffusivity of ∼2.6 × 10⁻⁷ cm² s⁻¹. The MSD of lipids under a 0.06 e/Lip ionic imbalance, on the other hand, shows a slightly higher slope for both regimes, indicating higher diffusivities. This result indicates that the diffusion of lipids in the bilayer is not affected until the ionic imbalance reaches the pore-forming imbalance (0.06 e/Lip), at which point the lipids in the bilayer diffuse slightly faster.

Figure 8.

Lateral MSD of the lipids in the bilayer under varying ionic imbalances.

The above analysis shows that ionic imbalance can influence the structural and dynamical properties of lipid bilayers. Under high imbalances, the bilayer is vertically compressed by the attraction force between ions and therefore is stretched in the lateral dimensions. The lipid tails are disordered and the boundaries between headgroups and tails become blurry. Ions and waters can partition deeper into the bilayer, potentially reducing the barriers of lipid flip-flop and pore formation (Fig. 9). It should be noted that ions in the MARTINI CG force field include the first solvation shell, which results in a larger van der Waals radius. In an AA simulation, therefore, ions may penetrate even deeper into the bilayer. In future studies, it would be interesting to quantify the free-energy change of lipid flip-flop and ion permeation under ionic imbalances. We emphasize that the changes of the lipid bilayer caused by ionic imbalances are different from those caused by an external electric field, as the structural changes we observed, especially bilayer thinning, have not been reported in studies that applied an external electric field to bilayers.

Figure 9.

Schematic representation of the structural changes of lipid bilayers under low and high ionic imbalances. To see this figure in color, go online.

Phase transition is one of most fascinating properties of lipid bilayers. It is known that a DPPC bilayer will transit from the fluid phase to the gel phase below 283 K. Here, we controlled the temperature of the double bilayer system to drop from 300 K to 280 K under different ionic imbalances, to determine its effect on the phase transition. Snapshots of a cross-section view of the bilayer at the initial and final temperatures are shown in Fig. 10. At zero ionic imbalance, the lipid tails in the bilayer (shown as light purple sticks) change from a disordered alignment (300 K) to an ordered alignment (280 K), indicating a transition from the fluid phase to the crystalline phase. Under a 0.02 e/Lip ionic imbalance, the bilayer tail becomes slightly disordered at 280 K, showing an imperfect crystalline phase. At the yielding imbalance of 0.04 e/Lip, the difference in the bilayer tail alignment between 300 K and 280 K can barely be identified. At the pore-forming imbalance of ∼0.06 e/Lip, one cannot identify any change in the alignment after the temperature drop, indicating no phase transition between 300 K and 280 K. The phase transition temperature under such a high ionic imbalance may very well be below 280 K. Note that a decrease in the bilayer thickness can clearly be seen in the snapshot as the ionic imbalance increases.

Figure 10.

Fluid-to-gel phase transition of the bilayer under varying ionic imbalances. Snapshots were taken at 280 K and 300 K. The transition temperature of the DPPC bilayer under zero imbalance is ∼283 K. Black beads, ammonium; dark olive beads, phosphate; light green beads, glycerol; light purple sticks, lipid tails; blue transparent beads, water; large yellow beads, sodium ions; large violet beads, chlorine ions. To see this figure in color, go online.

The use of CG force fields has its limitations. The MARTINI CG force field has relatively smoother energy potentials compared with AA force fields, and thus the bilayer in MARTINI is more robust against disturbance. This will probably result in a higher imbalance threshold of pore formation on the bilayers. On the other hand, the electrostatic interactions in MARTINI are soundly represented using polarizable water and PME. Therefore, in general, bilayer structural changes due to electrical stress might be shifted from AA calculations. The results obtained from simulations thus should be considered to be more qualitative than quantitative; however, we expect the effects observed here to be important in determining the state of a membrane subjected to ionic imbalance.

The simulations show that a high ionic imbalance from the yielding regime to the pore-forming regime will soften the bilayer structure, making it more fluid like. Thus, it is possible to use a high ionic imbalance to control the fluidity of the lipid bilayer. In such a softened state, the bilayer is susceptible to any kind of perturbation that can easily trigger pore formation. In living cell membranes that have many proteins and lipid rafts embedded in the surface, the bilayer may break before it reaches the pore-forming imbalance or even the yielding imbalance.

Conclusions

In summary, we have investigated the impact of a gradual increase in ionic imbalance on the structural properties of phospholipid bilayers. We find that the ionic imbalance can reach a value of ∼0.06 e/Lip on a DPPC bilayer until pore formation occurs, whereas an abrupt increase of the ionic imbalance can only reach a value of ∼0.045 e/Lip. A linear regime and a yielding regime of the TMP can be identified as the ionic imbalance increases. In the linear regime, the bilayer is subject to minor structural changes, and the TMP increases linearly with respect to the ionic imbalance. In the yielding regime, the TMP stays at the same level and the bilayer experiences substantial structural changes, including bilayer thinning, a wider redistribution of lipid headgroups at the interface, and lipid tail disordering. The diffusivity of lipid molecules inside the bilayer also increases slightly at high ionic imbalances. In addition, the fluid-to-gel phase transition temperature drops well below 280 K at imbalances above the yielding regime. We conclude that moderate changes in the ionic imbalance at the physiological level do not disturb lipid bilayers, whereas high ionic imbalances can substantially alter the structures of the bilayer. Therefore, membrane functions may be fundamentally changed by the induction of high electrical stress on the cell membrane in applications such as electroporation.

Author Contributions

J.L. and A.A.-K. designed the research, analyzed the results, and wrote the manuscript. J.L. performed the simulations.

Editor: David Cafiso.