Sparse Multivariate Factor Analysis Regression Models and Its Applications to Integrative Genomics Analysis

Abstract

The multivariate regression model is a useful tool to explore complex associations between two kinds of molecular markers collected from same subjects, which enables the understanding of the biological pathways underlying disease etiology of scientific importance. For a set of correlated response variables are correlated, accounting for such dependency can increase statistical power in the data analysis. Motivated by integrative genomic data analyses, we propose a new methodology – sparse multivariate factor analysis regression model (smFARM), in which correlations of response variables are assumed to follow a factor analysis model with latent factors. This proposed method not only allows us to address the challenge that the number of association parameters is larger than the sample size, but also to adjust for unobserved genetic and/or non-genetic factors that potentially conceal the underlying response-predictor associations. The proposed smFARM is implemented by the EM algorithm and the blockwise coordinate descent algorithm. The proposed methodology is evaluated and compared to the existing methods through extensive simulation studies. Our results show that accounting for latent factors through the proposed smFARM can improve sensitivity of signal detection and accuracy of sparse association map estimation. We illustrate smFARM by two integrative genomics analysis examples, a breast cancer dataset and an ovarian cancer dataset, to assess the relationship between DNA copy numbers and gene expression arrays to understand genetic regulatory patterns relevant to the disease. We identify two trans-hub regions: one in cytoband 17q12 whose amplification influences the RNA expression levels of important breast cancer genes, and the other in cytoband 9q21.32-33, which is associated with chemoresistance in ovarian cancer.

1. Introduction

Unveiling regulatory patterns between genetic variants and gene expressions is of great importance to a broad range of biological studies, in the hope to improve our understanding of complex disease pathogenesis. As reported in many recent genetic studies, high-throughput gene expression array experiments and genotype or DNA copy number array experiments are carried out on the same set of subjects. This provides the unique opportunity to assess regulatory relationships among DNAs and RNAs via an integrative genomic analysis. Copy number alterations (CNAs), including both germline variants and somatic copy number aberrations, are found to be largely associated with disease mechanisms in many studies; see for example, Pollack et al. (1999). In particular, somatic aberrations are discovered to be important for tumorigenesis. For instance, oncogene activation by gene amplification or the loss of a tumor suppressor by gene deletion can cause transcriptional errors, which contributes to cancer pathogenesis (Yuan et al., 2012). On the other hand, gene expression can be related to copy number alterations in proximal genes within a a window of several megabase pairs (cis-acting), as well as remote alterations throughout the genome (trans-acting). It has been regarded as a difficult task to detect genomewide cis- and trans-acting effects simultaneously due to the fact that numerous passenger genes amidst the limited set of drivers may contribute to tumor progression. Recent studies (Horlings et al., 2010; Lahti et al., 2013; Pollack et al., 2002) have focused on the cis-acting effects of copy number on gene expressions and there are few studies that have considered trans-acting effects on a genomewide scale. To address these challenges require new analytic tools suitable for well-powered genomic studies.

The construction of genome-wide regulatory map by exploiting genomic and transcriptomic data typically involves in a large number of gene expressions as response variables and high-dimensional genetic variants (e.g. DNA copy number alterations) as predictors. This analytic task can be primarily formulated by a multivariate regression analysis (e.g. Bedrick and Tsai (1994); Lutz and Buhlmann (2006)). Usually, the genetic regulatory relationships are intrinsically sparse, in the sense that one genetic variant may regulate only a small proportion of gene expressions, rather than the majority of them. It is also reported that some genetic variants, known as master regulators, play more important roles than other variants in the regulatory network, in terms of their ability of influencing many gene expressions simultaneously (Gardner et al., 2003; Jeong et al., 2001). Thus, it is of great interest to develop proper multivariate regression models that account for both the sparsity in the regulatory relationships and the existence of master regulators in the mapping of genetic associations. Towards this goal, sparse penalty functions such as LASSO (Tibshirani, 1996), elastic net (Zou and Hastie, 2005), and group LASSO (Yuan and Lin, 2006) have been introduced to the multivariate regression framework (e.g. Lutz and Buhlmann (2006), Turlach et al. (2005) and Yuan et al. (2012)). Readers can find more details about the comparison of our work with the existing methods in Section 5.

Some researchers have pointed out (e.g. Gibson (2008) and Leek and Storey (2007)) that gene expressions are influenced by many biological and non-biological factors. Biological factors could include, for example, genotype polymorphisms/mutations, DNA copy number variations, DNA methylation, microRNA regulations, protein regulations and others. Non-biological factors include sample collection noise, instrumental errors, and batch effects. In addition, population admixtures or kinships in a study population may also influence data generation mechanism of gene expression profiles. Because of these complications, quite often only a small portion of variations in gene expressions can be explained by one type of genetic markers under investigation. Moreover, it is reported that gene expression heterogeneity is presented strongly in many studies but it is not yet properly taken into account in statistical analysis. For example, Leek and Storey (2007) and Stegle et al. (2008) have showed that gene expression heterogeneity not only leads to the reduction of statistical power but also produces spurious association signals when studying the regulatory relationships between genotypes and gene expressions. This motivates us to develop a new method that employs the factor analysis model to account for such heterogeneity attributed to some unobserved genetic and/or non-genetic variabilities. As a result, we can improve both statistical power and accuracy of identifying significant associations between genes and genetic markers.

In this article, we plan to achieve three objectives via a sparse multivariate factor analysis regression model (smFARM): (i) to identify both trans-acting and cis-acting effects in one modeling framework; (ii) to regularize the association map by encouraging the selection of important predictors (or regulators); and (iii) to estimate the covariance matrix of the response variables via the means of multivariate factor analysis. The smFARM is specified in a similar spirit of the seemingly unrelated regression (SUR) model (Zellner, 1962), which aims to improve the estimation efficiency of association in the detection of important signals by utilizing the residual correlations of gene expressions among genes. The factor analysis model enables us to understand and interpret additional association features beyond what expression-genetic variant associations describe. The mean model component of smFARM is parameterized by a matrix of regression coefficients that are supposed to contain many zeros because of sparse genetic regulatory relationships. This part of modeling relates closely to the remMap method proposed by Peng et al. (2010) for the identification of genetic regulatory relationships and master predictors using a regularized multivariate regression model. Compared to remMap, our proposed smFARM further extends their model and is able to capture residual correlations of the responses using latent factors. As discussed earlier, when studying the regulatory relationships between gene expressions and DNA copy numbers, gene expression levels could be often confounded by unobserved genetic and/or non-genetic factors. Thus, incorporating latent factors in smFARM leads to a more efficient method to extract important features of the regulatory network than remMap. This advantage is shown in both the analysis of breast cancer data set and the analysis of ovarian cancer data set. As shown, smFARM identifies several new novel regulatory relationships between gene expressions and copy number alternation intervals (CNAIs).

2. Model

2.1 Multivariate regression model

Multivariate regression model plays an important role in multivariate data analysis. Such model extends the classical one-dimensional regression model, which is widely used to deal with correlated response variables. Following the common notations in multivariate regression model, for subject i, we assume that the conditional distribution of a Q × 1 random vector y_i = (y_i1, … , y_iQ)^T given P-element explanatory vector x_i = (x_i1, … , x_iP)^T is a multivariate normal distribution. And its expectation is specified by the following linear equations:

$$E({\text{y}}_i\mid {\text{x}}_i)=ϴ{\text{x}}_i,i=1,\dots ,N,$$ (1)

where Θ = {θ_qp} is a Q × P matrix of unknown regression coefficients, and its covariance is Var(y_i|x_i) = Σ, which is an unknown Q × Q positive definite covariance matrix independent of x_i. Obviously, if Q = 1, model (1) becomes the classical one-dimensional regression model, where Θ is a P-dimensional regression coefficient vector. In matrix Θ, the q-th row represents the vector of regression coefficients corresponding to the q-th regression model, i.e. $E(y_{iq}\mid {\text{x}}_i)={\sum }_{p=1}^P{\theta }_{qp}{x}_{ip}$, which is a linear model of the q-th response variable y_iq on all P predictors. Clearly, the ordinary least square method (or equivalently the maximum likelihood method under the normally distributed errors) yields an estimator of Θ as ${\widehat{ϴ}}^T={\left({\text{X}}^T\text{X}\right)}^{-1}{\text{X}}^T\text{Y}$. This implies that each row of Θ can be estimated separately by regressing each of Q responses on the P predictors without accounting for any dependence across the Q responses. This is because in this estimation there are no common coefficients and/or common parameters in Σ shared across Q individual one-dimensional regression models. In contrast, when some common features are present in the mean models and/or covariance matrices, borrowing data information across different margins will be beneficial to improve statistical power, and consequently, joint estimation involving all Q rows is the focus of methodology development in this paper.

2.2 Factor analysis model

In this paper, we propose to model the covariance Σ by the following factor analysis model:

$$\sum ={\text{BB}}^T+\Psi ,$$ (2)

where B is a Q × K matrix of factor loadings pertinent to communalities for K (⩽ Q) latent factors and Ψ is a Q × Q diagonal matrix of uniqueness. Clearly, the mean model (1) does not involve the K latent factors, while the covariance model (2) is determined by loadings B and uniqueness Ψ. Factor analysis is one of the popular dimension reduction techniques that represents variations of correlated variables by a low number of latent factors. See for example, Blum et al. (2010), Friguet et al. (2009), Kustra et al. (2006) and Stegle et al. (2008), among others, in which the factor analysis model has been employed to deal with heterogeneity in functional gene expression profiles.

2.3 Multivariate factor analysis regression model

Combining models (1) and (2), with P predictors x_i and K unobserved latent factors z_i = (z_i1, … , z_iK)^T , we propose the following multivariate factor analysis regression model (mFARM):

$${\text{y}}_i=ϴ{\text{x}}_i+{\text{Bz}}_i+{ϵ}_i,i=1,\dots ,N,$$ (3)

where z_i’s are i.i.d. K-variate vectors of latent factors following multivariate normal distribution MVN_K (0, I), and ∊_i’s are i.i.d. measurement errors with MVN_Q(0, Ψ) and are independent of the latent factors z_i1, … , z_iK. In matrix notation, model (3) may be rewritten as follows:

$$\text{Y}=\text{X}{ϴ}^T+{\text{ZB}}^T+\text{E},$$ (4)

where ${\text{Y}}_{Q\times N}^T=({\text{y}}_1,\dots ,{\text{y}}_N),{\text{X}}_{P\times N}^T=({\text{x}}_1,\dots ,{\text{x}}_N),{\text{Z}}_{K\times N}^T=({\text{z}}_1,\dots ,{\text{z}}_N)$ and ${\text{E}}_{Q\times N}^T=({ϵ}_1,\dots ,{ϵ}_N)$. For simplicity, we assume that all Q responses and all P predictors are standardized to have zero mean and thus the intercept terms are removed from (4).

Our proposed mFARM model (4) will improve the capacity of statistical analysis for the construction of genetic regulatory maps with high-throughput array data, because it accounts for unobserved factors that better capture variabilities in the residuals.

3. Regularized Estimation

To achieve sparsity in the estimation of parameter matrix Θ, which characterizes the association map of interest, and to encourage the detection of master predictors (i.e. master regulators) in a similar spirit to the remMap method (Peng et al., 2010), we propose the following doubly penalized loss function:

$$\begin{array}{cc}\hfill L(ϴ,\Psi ,\text{B})& =\frac{1}{2N}\sum _{i=1}^N{({\text{y}}_i-ϴ{\text{x}}_i)}^T{({\text{BB}}^T+\Psi )}^{-1}({\text{y}}_i-ϴ{\text{x}}_i)\hfill \\ \hfill & +{\lambda }_1\sum _{q=1}^Q\sum _{p=1}^P\mid {\theta }_{qp}\mid +{\lambda }_2\sum _{p=1}^P\sqrt{{\theta }_{1p}^2+\cdots +{\theta }_{Qp}^2,}\hfill \end{array}$$ (5)

where λ₁ and λ₂ are two nonnegative tuning parameters. The first penalty term in (5) is the L₁ norm penalty that controls the overall sparsity in Θ by tuning parameter λ₁, while the second penalty is the L₂ norm penalty that controls the column sparsity in Θ via tuning parameter λ₂. The use of the two penalties facilitates the selection of important predictors, at both individual and group levels, that affect multiple responses simultaneously.

If there is some a priori knowledge about the known relationship between a predictor X_p and a response Y_q, such information may be incorporated into the estimation procedure via (5) in a similar way suggested in Peng et al. (2010). That is, consider a pre-specified Q × P matrix C^∗ whose (q, p)-th element is given by:

$$C_{qp}^{\ast }=\{\begin{array}{c}2,\text{if}{X}_p\text{is independent of}{Y}_q;\hfill \\ 0,\text{if}{X}_p\text{is associated with}{Y}_q;\hfill \\ 1,\text{if}\text{there is no prior information}.\hfill \end{array}\phantom{\}}$$ (6)

According to (5), given an unknown matrix Θ^∗, the (q, p)-th entry ${\theta }_{qp}^{\ast }$ will be set as 0 in advance if $C_{qp}^{\ast }=2$; otherwise, ${\theta }_{qp}^{\ast }$ will or will not be penalized by a flag value $C_{qp}^{\ast }=1$ or $C_{qp}^{\ast }=0$. After setting matrix Θ = Θ^∗ according to C^∗, the modified objective function is given by

$$\begin{array}{cc}\hfill L(ϴ,\Psi ,\text{B})& =\frac{1}{2N}\sum _{i=1}^N{({\text{y}}_i-ϴ{\text{x}}_i)}^T{({\text{BB}}^T+\Psi )}^{-1}({\text{y}}_i-ϴ{\text{x}}_i)\hfill \\ \hfill & +{\lambda }_1\sum _{q=1}^Q\sum _{p=1}^P\mid C_{qp}{\theta }_{qp}\mid +{\lambda }_2\sum _{p=1}^P\sqrt{C_{1p}{\theta }_{1p}^2+\cdots +C_{Qp}{ϴ}_{Qp}^2},\hfill \end{array}$$ (7)

where a Q × P matrix C = {C_qp} is defined as $C_{qp}=1\{C_{qp}^{\ast }=1\}$.

Without loss of generality, we assume that both λ₁ and λ₂ are positive, and if one of them is zero, we can modify our methodology with little effort. Also, the proposed smFARM may be used to deal with the case of high-dimensional measurements with $min(P,Q)⪢N$, which is pervasive in biological studies, such as microarray data that contain thousands of biological markers measured from typically dozens to hundreds of subjects.

4. Algorithm

4.1 EM-blockwise coordinate descent algorithm

In this paper, we estimate three unknown parameter matrices, (Θ, B, Ψ), through minimizing the doubly penalized loss function (7), where Θ and (B, Ψ) are involved in the mean model and the covariance model, respectively. A two-step iterative approach is used to estimate these three matrices. Given the current estimates of the factor model terms, (B^(t), Ψ^(t)), updating the association matrix, Θ^(t+1), is done by minimizing the doubly penalized loss function (7) by the blockwise coordinate descent algorithm proposed bySimon et al. (2013), while updating the factor model terms (B^(t+1), Ψ^(t+1)) is carried out through the EM algorithm after Θ^(t+1) being given. Repeating these two-step procedures iteratively till algorithmic convergence, we obtain estimates $(\widehat{ϴ},\widehat{\mathrm{B}},\widehat{\Psi })$ at the end of the algorithm operation. The computational complexity of the above algorithm may be assessed separately for the operation of the EM algorithm to estimate the loading coefficients B and the uniqueness Ψ = σ²I, and the operation of blockwise coordinate descent algorithm to obtain sparse group lasso estimation for the association matrix Θ. The computational complexity of the former is in the order of O(NQK) per iteration, and that of the latter is in the order of O(NPQ). Refer to the Supplementary Material where actual computation times in simulation studies are reported.

4.2 Tuning parameter selection

We consider the selection of the tuning parameters (λ₁, λ₂) with a given K = K₀. Following Peng et al. (2010), we adopt the M-fold cross-validation method to choose the tuning parameters (λ₁, λ₂). Since the true model is believed to be sparse, as suggested by Peng et al. (2010) we utilize the ordinary least squares (OLS) estimates instead of the shrunken estimates to calculate the cross-validation score. This is because, when there are many potential poor predictors, the cross-validation score based on shrunken estimates often leads to severe false positive rates (Peng et al., 2010; Efron et al., 2004). In contrast, using the OLS estimates seems to make a reasonable remedy for such a problem, which is also observed in our simulation studies. It is worth pointing out that Bayesian information criterion (BIC), another popular tuning selection method, is not considered here, mainly because estimating the degrees of freedom required by the BIC is difficult under a nonorthogonal design matrix of predictors.

In this paper smFARM is run at a prespecified number of latent factors K. In practice, K may be estimated from the data, and there exists a large amount of the literature concerning consistent estimation of K, including the widely used AIC Akaike (1992) and BIC Schwarz (1978), as well as other methods proposed by Bai and Ng (2002), Onatski (2009), and Ahn and Horenstein (2013), among others.

5. Simulation

5.1 Simulation Setup

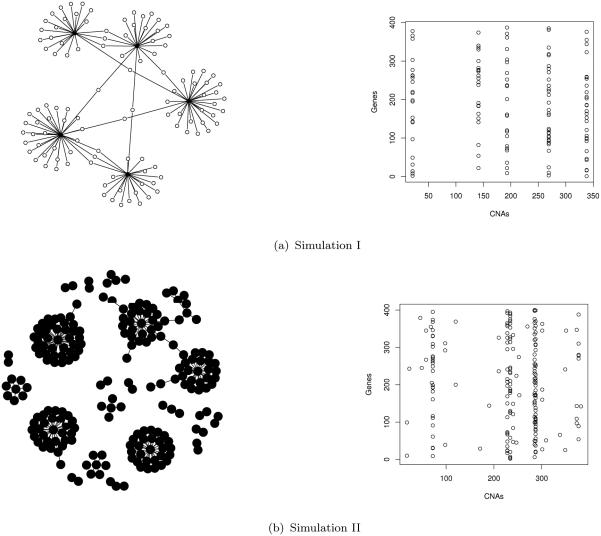
We conduct two simulation experiments to assess the performance of the proposed model and optimization method. To specify simulation settings, we mimic a microarray dataset with N = 200 subjects, Q = 400 gene expressions and P = 400 variables of copy number alterations (CNAs). For each simulation, we consider a specific association map between genes and CNAs, which is specified as being sparse in groups. The graphic presentations of the association maps are given, respectively, in panels (a) and (b) of Figure 1. In simulation experiment I, we begin with a simple association map shown in Figure 1(a), in which 5 CNAs (i.e. black nodes) are set as master regulators (or hubs). These master CNAs are designed to so strong that they link to a total of 114 genes (i.e. circles), on average each CNA regulating 20 to 30 gene expressions. The total number of nonzero associations in this map is 125. Simulation experiment II concerns a more practical situation, where the topology of the given association map appears to be neither group dominated nor individual dominated. As shown in Figure 1(b), such association map includes 5 strong master CNAI regulators, each influencing 24 to 37 genes, 5 weak master CNAI regulators, each influencing 3 to 7 genes, and 20 CNAIs linking to only 1 or 2 genes. The total number of nonzero associations is 192.

Figure 1.

True association maps of Θ (connectivity vs. heatmap) for Simulation I, and II. (LHS: connectivity maps of Θ between genes (white) and biomarkers (black); RHS: corresponding heatmap of Θ.)

In the first simulation experiment, P categorical CNAs x = (x₁, … , x_P)^T are generated as predictors from x_p ~ Binomial(2, 0.2) − 1, with values −1, 0, or 1, representing copy number deletion, normal and amplification. In the second simulation study, continuous copy number alternation intervals (CNAIs) are generated to mimic the true predictor characteristics discussed in Section 6. Based on the real breast cancer data and ovarian cancer data, we find that there exits the heterogeneity within CNAIs, characterized by certain chromosome-specific structures, occurring in the forms of both within-chromosome and between-chromosome differences. Here we assume that these P continuous CNAIs belong to 23 distinct chromosomes, where the number of CNAIs on the i-th chromosome (i.e. P_i, i = 1, … , 23) is proportional to the size of that chromosome obtained from the real data. Within the i-th chromosome, any pair of CNAIs, say, CNAI_m and CNAI_n, is set to be positively correlated and such correlation decreases when their genetic distance increases according to 0.9^|m−n|/2 for m, n = 1, … , P_i. If two CNAIs come from different chromosomes, a much weaker correlation is randomly drawn from {0.25, 0.25², … , 0.25²³} together with a randomly generated positive or negative sign. Finally we compute the nearest positive definite symmetric matrix Ξ based on the above correlations using the algorithm in Higham (1988), and P continuous CNAs are generated from x ~ MVN_P (0, Ξ).

To specify the Q × P association map of Θ = {θ_qp}, we first specify a sparse indicator matrix Δ = {δ_qp} which defines the connectivity in a genetic association mapping between Q genes and P CNAs. If δ_qp = 1, we generate θ_qp from $\text{Unif}([-5,-1]\bigcup [1,5])$; otherwise, θ_qp = 0. To specify the Q × K factor loadings matrix B, we start with an initial matrix ${\text{B}}^{\ast }=\left\{b_{qk}^{\ast }\right\}$, with $b_{qk}^{\ast }\stackrel{i,i,d.}{~}\text{Unif}\left([0,\tau ]\right)$ and τ is a given positive constant. Then, we specify a matrix B as of the form $\text{B}={\text{UV}}^{\frac{1}{2}}$, where V is a diagonal matrix with diagonal entries being the eigenvalues of B^∗B^∗T , and the column vectors of U are the orthonormal eigenvectors of B^∗B^∗T . In other words, matrix B is specified by an orthogonal rotation of the initial matrix B^∗. Note that the factor loadings have an “indeterminacy” problem, which means both B and BT give rise to the same covariance matrix Σ = BB^T + Ψ, where T is an arbitrary orthogonal matrix. To ensure a unique solution, we impose a constraint on B, according to Anderson and Rubin (1956), to enforce that B^T B is a diagonal matrix , which is accounted for in our procedure of generating the values of factor loadings for matrix B. Given Θ and B, for each subject, we generate K latent factors z = (z₁, … , z_K)^T by z_k ~ Normal(0, 1) and Q measurement errors ∊ = (∊₁, … , ∊_Q)^T ~ MVN_Q(0, Ψ), where the uniqueness Ψ is set as Ψ = σ²I_Q in the simulation studies. Recall that τ and σ² are two variance parameters that control the size of communality and that of uniqueness, respectively. The choice of τ and σ² is based on a pre-specified scale of signal-to-noise ratio, according to SNR₁ of regression mean effects and SNR₂ of latent factor’s effects; they are, ${\text{SNR}}_1=\text{avg}\left[\frac{\text{diag}\left(\text{Cov}(ϴx)\right)}{\text{diag}\left(\text{Cov}\left(ϵ\right)\right)}\right]$ and ${\text{SNR}}_2=\text{avg}\left[\frac{\text{diag}\left(\text{Cov}\left(\text{B}z\right)\right)}{\text{diag}\left(\text{Cov}\left(ϵ\right)\right)}\right]$, respectively. Finally, Q gene expressions y = (y₁, … , y_Q)^T are generated from model (3) by $\text{y}\mid \text{x},\text{z}~{\text{MVN}}_Q(ϴ\text{x}+\text{Bz},\Psi )$. Hereafter, a dataset of N i.i.d. (y, x) pairs is generated for each simulation round.

For convenience, the response variables and predictors are all centered to have mean zero, and the prior knowledge matrix C = {C_qp} is set as all entries being 1; in this case, all predictors are subject to shrinkage. Our primary evaluation criterion is the total number of false discoveries, TF = FP + FN, where FP and FN are the respective numbers of false positives and false negatives. Here, a “positive” (or a “negative”) refers to a nonzero (or a zero) entry of Θ. Following Fan et al. (2009), additional criteria used in the evaluation include sensitivity (Sen), and Matthews correlation coefficient (MCC) score defined respectively, by $\text{Sen}=\text{TP}∕(\text{TP}+\text{FN})$, and $\text{MCC}=\frac{(\text{TP}\times \text{TN}-\text{FP}\times \text{FN})}{\sqrt{(\text{TP}+\text{FP})(\text{TP}+\text{FN})(\text{TN}+\text{FP})(\text{TN}+\text{FN})}}$.

To assess the performance of our smFARM, we mainly compare it with remMap (K = 0) by varying SNR₁, SNR₂ and K. It is worth noting that Peng et al.’s (Peng et al., 2010) remMap approach, which is established for the classic multivariate regression models (i.e. K_true = 0), has been compared with two popular existing methods, single lasso penalty (i.e. λ₂ = 0) and Q separate individual lasso regressions, and its superiority has been showed in Peng et al. (2010). So the comparisons to the latter two methods are not reported in our comparison. Here we set the true number of latent factors as K_true = 2, and focus on comparing three scenarios with K = 0 (i.e. remMap), K = K_true (i.e. 2), and K = 3. The tuning parameters (λ₁, λ₂) are determined through 5-fold cross validation. And a total of 50 independently replicated datasets is used in the evaluation of our method. Results of method comparisons are summarized in Table 1. Additional simulation results may be found in the Supplementary Material.

Table 1.

Impact of different number of latent factors K and different SNR levels on Regulator Selection and Group Selection

			Regulator Selection			Group Selection
SNR	K true	Method	TF	Sen	MCC	TF	Sen	MCC
Simulation I.1
1:0:3	0	smFARMK=0	18.90(6.02)	0.89(0.04)	0.92(0.02)	0.06(0.24)	1(0)	0.99(0.02)
		remMap	21.88(6.61)	0.93(0.02)	0.92(0.02)	0.02(0.14)	1(0)	1(0.01)
1:0:5	0	smFARMK=0	27.24(3.51)	0.81(0.03)	0.88(0.01)	0(0)	1(0)	1(0)
		remMap	34.10(5.17)	0.88(0.03)	0.87(0.02)	0(0)	1(0)	1(0)
Simulation I.2
1:1:3	2	smFARMK=2	18.24(3.46)	0.87(0.03)	0.92(0.01)	0(0)	1(0)	1(0)
		remMap	25.68(11.32)	0.83(0.04)	0.89(0.04)	0.02(0.14)	1(0)	1(0.01)
1:1:5	2	smFARMK=2	28.51(4.26)	0.80(0.03)	0.88(0.02)	0(0)	1(0)	1(0)
		remMap	33.40(4.92)	0.76(0.04)	0.86(0.02)	0(0)	1(0)	1(0)
Simulation II
1:3:5	2	smFARMK=2	48.89(11.54)	0.82(0.05)	0.87(0.03)	10.89(2.53)	0.66(0.06)	0.79(0.05)
		smFARMK=0	79.80(16.76)	0.77(0.02)	0.79(0.04)	12.10(1.25)	0.62(0.04)	0.76(0.03)
		remMap	87.46(20.67)	0.79(0.03)	0.77(0.05)	12.46(1.35)	0.62(0.05)	0.75(0.03)

Note:For each Total False (TF), Sensitivity (Sen), or Matthews correlation coefficient (MCC) measurement, we report mean values together with their standard errors on 50 replicates. smFARM_K=K0 represents fitting the smFARM on a given number of latent factors K₀.

5.2 Findings from Simulation Studies

The results given in Table 1 concern simulation studies I and II. These results show that the proposed smFARM performs very well in all key aspects of regulator detection and group selection. Let us first focus on simulation study I, including two cases I.1 and I.2, with the corresponding numerical results being reported in the top part of Table 1. In Simulation I.1, when the true model contains no latent factors, subject to rounding errors, the proposed smFARM and the existing remMap perform equally well in terms of MCC. With no surprise, we find that, in both smFARM and remMap, larger SNR₁ leads to better performance in terms of lower TF, higher sensitivity and higher MCC in the comparison between SNR=1:0:3 and SNR=1:0:5. This outperformance of the smFARM repeats in the comparison between SNR=1:1:3 and SNR=1:1:5 with K_true = 2 in Simulation I.2. When the ratio of SNR₁ to SNR₂ is fixed at 1:1, smaller variation in the measurement errors (i.e. larger SNR₁) will lead to better performances. Moreover, an encouraging finding in Simulation I.2 is that, comparing our method accounting for the latent factors to the remMap that ignores latent factors, the smFARM approach is clearly more effective to identify true signals than the remMap when the data are from a multivariate model with correlated residuals or K_true ≠ 0. With fixed SNR₁, in a comparison of (SNR, K_true) = (1:0:3, 0) in Simulation I.1 with (SNR, K_true) = (1:1:3, 2) in Simulation I.2, or in another comparison of (SNR, K_true) = (1:0:5, 0) in Simulation I.1 with (SNR, K_true) = (1:1:5, 2) in Simulation I.2, very similar findings are obtained from the smFARM that accounts for latent factors. We also find that SNR₂ has a strong influence on the reconstruction of the association map, when the dependency of latent factors is ignored in the analysis.

It is interesting to note that results of group selection in simulation study I are rather stable and accurate across the four cases in the top part of Table 1. This is probably because identifying clusters in these settings is not hard due to group-dominant topology designed in the association maps (see Figure 1(a)). In other words, relative to the L₁-penalty, the L₂-penalty is more effective to remove irrelevant groups or clusters.

In addition, all the above conclusions have repeated consistently in the more realistic simulation study II with continuous predictors. To examine the robustness of the proposed method, we simulated 50 replicates under the Simulation II setup from a model y_i = Θx_i + u_i, i = 1, … , N, where the errors u_i are drawn directly from a multivariate normal distribution MVN_Q(0, BB^T + Ψ) with a certain non-diagonal covariance matrix used in the data simulation. In this case, we again found that the proposed smFARM model with K = 2 performed better in identifying the true signals than the remMap (or smFARM model with K = 0). The detail of this simulation is included in the Supplementary Material. To sum up, our proposed method has demonstrated clearly as being a very effective tool to achieve desirable statistical power by accounting for latent factors in the regulatory map reconstruction with high-dimensional complex data.

6. Application

In this section we apply the proposed smFARM to analyze TCGA (The Cancer Genome Atlas) breast and ovarian cancer data sets. We are interested in detecting DNA copy number alterations (CNA) that have large impact on transcript activities (i.e. trans-regulate many RNA expressions). Such trans-hub CNAs often play important roles in tumor initiation and progression. Information on the regulatory pattern between these trans-hub CNAs and their downstream genes deems to shed important light on disease etiology.

6.1 Data preparation

Level-three RNAseq data and level-three segmented DNA copy number data of breast and ovarian cancer tumor samples were obtained from the TCGA website. We focus on subsets of samples (77 breast tumors and 71 ovarian tumors), which are also subjected to deep protein-profiling by CPTAC (Clinical Proteomic Tumor Analysis Consortium). Thus findings from our analysis may lead to a further investigation and knowledge generation through the corresponding protein profiles in the future.

We preprocess the breast and ovarian cancer data separately. For breast cancer data, based on level-three segmented DNA copy number profiles, we first break the genome using the union of the break-points detected in all tumor samples and filter the small regions with less than 10k base pairs. This result in 17482 regions. Then for each region of each sample, we record its copy number based on the inferred DNA copy number of the corresponding segment in the sample, with tail values truncated at ±1.5. Due to the high spatial correlation in DNA copy number profiles, we further condense these 17482 regions into 1730 copy number alteration intervals (CNAI) by applying the fixed order clustering (FOC) (Wang, 2010), so that DNAs in the same interval tend to have similar CNA patterns in one sample. The copy number of one CNAI in a given sample is then calculated as the mean of the copy number of all regions within the interval in that sample. We exclude CNAI with no variation across the 77 samples, which results in 1571 CNAIs. For RNAseq data, we first set zeros to be missing values and take log transformation. We then standardize each sample to have median 0 and MAD (median absolute deviance) 1. We exclude genes with more than 10% missing, and select the top 15% genes with largest interquartile ranges across samples. The resulting data matrix consists of 1466 gene expressions.

We preprocess the ovarian cancer data set in the same manner as described above. Specifically, we derive 1617 CNAIs by applying FOC on merged level-three segmented DNA copy number profiles. By further eliminating CNAIs with little variation, we end up with 1300 CNAIs that are actually used in the analyses in this paper. For RNAseq data, we select 2437 genes after applying the same normalization and filtering criteria as those applied in the breast cancer data above.

6.2 smFARM analysis

We apply smFARM to analyze the preprocessed breast cancer data and ovarian cancer data, separately. Our primary goal is to construct the regulatory map between copy number alterations and RNA expressions in each cancer dataset, adjusting for potential latent factors. Specifically, for each cancer type, we fit the following model:

$${\text{Y}}_{\text{RNA}}={\text{X}}_{\text{CNAI}}{ϴ}^T+{\text{ZB}}^T+\text{E},$$ (8)

where Y_RNA is the RNA expression matrix, X_CNAI is the CNAIs copy number matrix, Θ is the regression coefficient matrix with respect to CNAIs. In the above model, Q responses (Y_RNA) and P predictors (X_CNAI) are all standardized to have mean 0 and standard deviation 1. Note that Q = 1466, P = 1571 in the breast cancer data, while Q = 2437, P = 1300 in the ovarian cancer data. The estimated latent factors (B) help to account for additional genetic and/or non-genetic features beyond the observed CNAI genetic markers, X_CNAI.

In addition, we classify a CNAI×RNA pair to be a cis pair, if the RNA gene falls in the genome region of the CNAI; or otherwise the pair is referred to as a trans pair. There are in total 1172 cis pairs in the breast and 1862 cis pairs in the ovarian cancer data set, respectively. Since we are particularly interested in identifying trans-hub CNAIs, we do not impose shrinkage on the coefficients of these cis pairs. As pointed above, this choice can be managed by setting C_qp = 0 given that the p-th CNAI and the q-th gene form a cis pair; and C_qp = 1, otherwise in equation (7). We apply the proposed model fitting procedure and select the tuning parameters (λ₁, λ₂) using 10-fold cross validation on a 25 × 25 grid. We vary the number of latent factors K from 0 to 20, and explore how the regulatory map varies accordingly as K increases.

6.3 Results

Some interesting trans-hub CNAIs are revealed by the application of smFARM for both the breast cancer and the ovarian cancer.

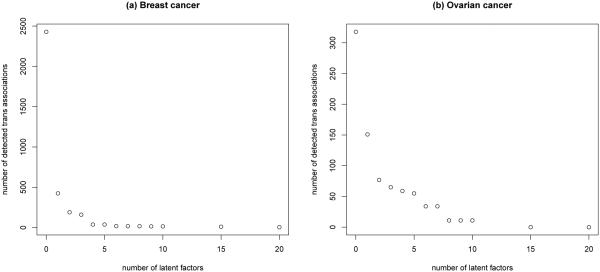
Figure 2 shows that with an increase in the number of latent factors, the detected number of tran edges decreases. When fully ignoring latent factors in the analysis, we detect a total of 2429 trans edges from the breast cancer data and a total of 318 trans edges from the ovarian cancer data. However, most of these detected edges are deemed false positive and are not biologically meaningful. Note that in either the breast cancer dataset or the ovarian dataset only about 70 subjects are measured, each being observed with thousands of genes and CNAIs. Indeed, both give rise to an ultra high-dimensional estimation problem, for which it is not easy to select the optimal number of latent factors. In this analysis, we choose K = 2, because this choice leads to the association maps that achieve a desirable balance between sparsity and discovery of important biological signals.

Figure 2.

The number of detected trans edges under different K.

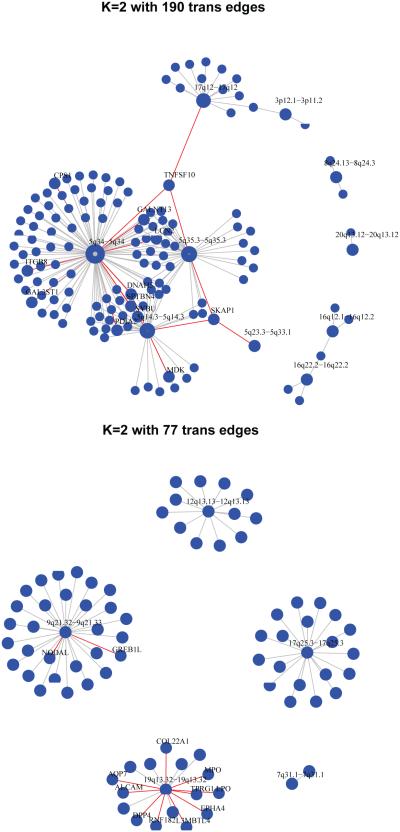
For the breast cancer data, at K = 2, the proposed smFARM detected 190 trans-regulation edges between 10 CNAIs and 134 transcripts. The detailed CNAI-RNA regulatory map is illustrated in Figure 3. The biggest trans-hub CNAIs are all from chromosome arm 5q. Deletions on chromosome arm 5q are key characteristics for basal-like breast cancer. Our findings that the DNA copy number alterations in 5q have big impact on a large number of transcripts is consistent with previous observations in the literature (Curtis et al., 2012). Besides the tran-hub CNAIs on 5q, another major trans-hub is from 17q12. This CNAI is known as the harbor of the famous oncogene ERBB2, whose amplification is a trigger event for HER2 subtype of breast cancer (Bergamaschi et al., 2006). In addition to ERBB2, the 17q12 amplicon also harbors many other important cancer genes and transcript factors (Lamy et al., 2011), thus it is expected that this region serves as a tran-hub in the CNAI-RNA regulatory map. Among the transcripts regulated by these major trans-hub CNAIs, one transcript, TNFSF10, is regulated by all CNAIs in 17q12, 5q34, and 5q35.3. TNFSF10 is a member of the tumor necrosis factor superfamily. It has been shown to mediate p53-dependent cell death (Kuribayashi et al., 2008) and can be used as therapeutic targets to improve the treatment of triple-negative breast cancer patients (Hunter et al., 2014). Our analysis suggests that the DNA copy number alterations in ERBB2 amplicon and 5q34-35.3 region could act as upper-stream regulator for TNFSF10 during tumor initiation and progression. These intriguing results help to cast light on the regulatory mechanism of these important disease genes.

Figure 3.

Detected association maps under K = 2. (Top: Breast cancer; Bottom: Ovarian cancer.

On the other hand, the analysis of the ovarian cancer data reveals a different set of CNAIs trans-hubs, suggesting these two types of cancers are driven by distinct tumor mechanisms. Specifically, we find that the CNAI-RNA regulatory map consists 77 trans-regulation edges between 5 CNAIs and 77 transcripts. The CNAI with the largest number of trans-edges locates in 9q21.32-33. Copy number gain in this region is reported to be associated with chemoresistance in ovarian cancer patients (Österberg et al., 2010). The transcripts regulated by this CNAI include two known cancer genes, GREB1 and NODAL. Gene GREB1 regulated by estrogen in breast cancer 1 was first identified as a hormone-responsive gene in the breast cancer cell line. Recently, this gene has also been found to be up-regulated by E2 (Exogenous 17β-estradiol) in ovarian tumors, and thus could serve as a novel gene target for therapeutic intervention (Laviolette et al., 2014). Gene NODAL encodes a protein belonging to the TGF-beta superfamily, which is an important regulator of embryonic stem cell and possibly cancer stem cells (Lonardo et al., 2011). The signaling of NODAL promotes a tumorigenic phenotype in human breast cancer through activating MAPK signaling pathway and could serve as a promising target for treating triple-negative breast cancer (Kirsammer et al., 2014). Our analyses suggest potential regulatory relationships among these known cancer related alterations and genes in the current literature. Such findings could lead to useful biological hypotheses to be tested in future studies.

7. Discussion

We developed a new methodology, sparse multivariate factor analysis regression model, to reconstruct a sparse genetic association map. The proposed smFARM extended the classic multivariate regression model, allowing a low-dimensional set of latent factors to account for the dependence among response variables instead of assuming residuals being independent noise. We developed an effective and flexible EM-blockwise coordinate descent algorithm to obtain regularized estimation and variable selection in the smFARM.

We have shown that by accounting for latent factors, the proposed smFARM can effectively identify response-predictor associations from high dimensional data with improved sensitivity and accuracy. The numerical results have indicated that the proposed smFARM works well to derive the underlying sparse association relationship. Furthermore, both real breast cancer data and ovarian cancer examples have also shown that our proposed smFARM provides richer and biologically relevant discoveries to facilitate transcriptomic analyses. The sparse genetic association map between CNAIs and gene expressions helped us understand and interpret genetic regulation mechanisms and generate useful biological hypotheses on those detected signals given in this paper.

To our knowledge, there are some other methods that can characterize the variability in the gene expressions such as singular value decomposition (SVD) or principle component analysis (PCA). There is a direct relationship between PCA and SVD in the case where principal components are calculated from the covariance (Wall et al., 2003). Furthermore, the essential difference between SVD/PCA and factor analysis lies whether or not a covariance model is used for the residuals. Refer to Schneeweiss and Mathes (1995), Tipping and Bishop (1999) and Van Wieringen and Van De Wiel (2011) for more details. We find that unlike PCA/SVD using superficial labeling such as “eigengenes”, “supergenes”, or “meta-genes” without clear biological entity (Alter et al., 2000), the number of latent factors can provide a biologically relevant parameter in the reconstruction of association map, which is appealing in practice.

Besides the gene-CNA association analysis illustrated in this paper, our proposed method may be applied in a broad range of problems. For instance, it may be applied to systematically explore the relationship between gene expression levels and genotypes as to, for example, whether a gene is differentially expressed with different genotypes (or alleles) at a specific locus. The loci that are associated with gene expression levels are known as expression quantitative loci (eQTL). For a given gene, an eQTL data analysis aims to identify genetic loci or single nucleotide polymorphisms (SNPs) that are linked or associated with expression levels of a common gene. Moreover, in eQTL analysis, SNPs may be naturally grouped according to their functionality or biological pathways based on some prior knowledge. When we are interested in associations of multiple SNPs simultaneously within a biological pathway, incorporating genetic or non-genetic latent factors would help us to achieve a more powerful and richer analysis, leading to better understanding of the underlying biological mechanisms.