A method for integrating neuroimaging into genetic models of learning performance

Abstract

Specific learning disorders (SLD) are an archetypal example of how clinical neuropsychological traits can differ from underlying genetic and neurobiological risk factors. Disparate environmental influences and pathologies impact learning performance assessed through cognitive exams and clinical evaluations, the primary diagnostic tools for SLD. We propose a neurobiological risk for SLD with neuroimaging biomarkers which is integrated into a genomewide association study (GWAS) of learning performance in a cohort of 479 European individuals between 8 and 21 years of age. We first identified six regions of interest (ROIs) in temporal and anterior cingulate regions where the group diagnosed with learning disability has the least overall variation, relative to the other group, in thickness, area, and volume measurements. Although we used the three imaging measures, the thickness was the leading contributor. Hence, we calculated the Euclidean distances between any two individuals based on their thickness measures in the six ROIs. Then, we defined the relative similarity of one individual according to the averaged ranking of pairwise distances from the individuals to those in the SLD group. The inverse of this relative similarity is called the neurobiological risk for the individual. Single nucleotide polymorphisms in the AGBL1 gene on chromosome 15 had a significant association with learning performance at a genomewide level. This finding was supported in an independent cohort of 2,327 individuals of the same demographic profile. Our statistical approach for integrating genetic and neuroimaging biomarkers can be extended into studying the biological basis of other neuropsychological traits.

1 Introduction

Individuals with learning problems often suffer from diminished socioeconomic status and reduced emotional well-being (American Psychiatric Association, 2013), and treating them is an important public health priority (Castle, 2002). Five to fifteen percent of school children in the United States have a specific learning disorder (SLD) (Altarac & Saroha, 2007). The Diagnostic and Statistical Manual of Mental Disorders V (DSM-V) defines a SLD as a distinct diagnosis for cognitive deficits in perceiving and processing information that has a biological origin and that cannot be better explained by developmental, neuropsychological, or physical disorders (American Psychiatric Association, 2013). Learning disorders are, however, a latent construct manifesting along a continuous risk spectrum (Fletcher, Lyon, Fuchs, & Barnes, 2007).

The primary tools used for diagnosing a SLD are reading, writing and mathematical performance assessments. Many unrelated factors, including quality of instruction received, personal motivation, socioeconomic status, and the presence of emotional or attention disorders, also influence test performance (American Psychiatric Association, 2013; Fletcher et al., 2007). At the same time, there is considerable evidence that genetic factors influence cognitive traits related to learning performance such as reading, working memory, and episodic memory (Ando, Ono, & Wright, 2001; Donohoe, Deary, Glahn, Malhotra, & Burdick, 2013; Fletcher et al., 2007; Glahn et al., 2012; Hansell et al., 2015; Harlaar, Spinath, Dale, & Plomin, 2005; Panizzon et al., 2011).

There are many challenges in mapping genetic variants to learning performance because cognitive traits and neuropsychological (NP) traits, more generally, have a complex genetic basis (Lee et al., 2013; Okbay et al., 2016; Ripke et al., 2014). Missing heritability is endemic in genetic studies of NP traits and may be complicated by copy number variations and rare variants (Eichler et al., 2010). These issues raise considerable hurdles in genomewide association studies (GWAS) to detect single nucleotide polymorphisms (SNP) having significant relationships with NP traits (Visscher, Brown, McCarthy, & Yang, 2012).

Emerging evidence suggests that neuroimaging can offer insight into improving genomic studies of NP traits (Meyer-Lindenberg, 2012). Neuroimaging biomarkers, obtained using modalities such as magnetic resonance imaging or positron emission tomography, are heritable and have significant associations with NP traits such as depressed mood, schizophrenia, and cognitive deficits (Glahn et al., 2012; Meyer-Lindenberg & Weinberger, 2006). Since brain function has a closer biological relationship to clinical traits than genetic risk factors, neuroimaging biomarkers are suitable endophenotypes, or intermediaries, in genomic studies of cognitive and NP phenotypes (Donohoe et al., 2013; Glahn et al., 2012).

With this view in mind, several recent large-scale research initiatives performed neuroimaging scans with one goal being to improve genomic studies of NP traits. Integrating multimodal data collected by these initiatives into a single inferential framework requires statistical methods that account for large numbers of observed biomarkers and traits. Complex and multivariate relationships between genetics, neurobiology, and clinical assessments are not well characterized and thus handicap inference in this field called imaging genetics (J. Liu & Calhoun, 2014). Developing effective statistical frameworks for imaging genetics offers a promising avenue for better inferring sources of genetic and neurobiological risk affecting NP traits (Meyer-Lindenberg, 2012).

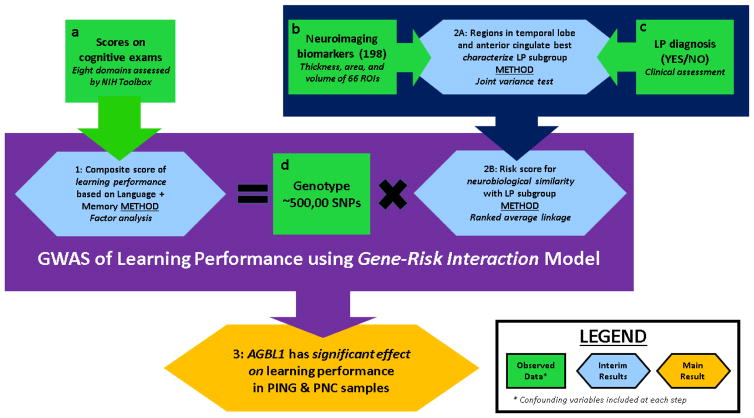
We sought to develop an integrated framework for studying the genomic basis of learning ability from neuroimaging, cognitive, and genetic data collected by the Pediatric Imaging, Neurocognition, and Genomics Study (PING) (Jernigan et al., 2015). To this end we proceed in three steps as outlined in Figure 1. First, we use principal component analysis to generate a quantitative learning performance score based on cognitive assessments in the NIH Toolbox used in the PING. In this approach, an ideal score would reflect cognitive domains relevant for perceiving and processing information, while deemphasizing others such as attention or executive function. Next, we use neuroimaging biomarkers to generate a neuroimaging risk score for learning problems that takes into account functional specialization of relevant brain regions. We developed novel, robust, and computationally efficient methods using variance-based methods to develop both of these scores. Finally, we integrate the combined learning performance and neuroimaging risks into a gene-environment interaction of learning performance that accounts for population heterogeneity.

Figure 1. Overview of inferential procedure applied to PING study.

Data: Cognitive assessments were taken from eight exams within the NIH Toolbox. Learning problem (LP) status is a binary variable corresponding to a yes/no answer in response to the question whether a subject was ever diagnosed with a learning problem. There are 198 neuroimaging biomarkers corresponding to average thickness, area, and volume measurements for 66 cortical regions of interest (ROI) obtained from structural MRI scans. Approximately 500,000 SNPs were genotyped for each subject in the sample. Results: (1) A composite learning performance score was derived from exams assessing memory (working and episodic) and language (reading and vocabulary). (2A) The joint variance test was performed to determine how well each ROI discriminated subjects with a LP diagnosis from others in the sample using thickness, area, and volume measurements. Of the 10 most significant regions, seven were in the temporal lobe and two were in the anterior cingulate on either the left or right hemispheres. (2B) With neuroimaging biomarkers best discriminating the LP subgroup, rank-based average linkage (similarity) clustering was applied to evaluate continuous risk scores for each subjects’ neuroimaging similarity to those in the LP subgroup. The similarities were with respect to the neuroimaging biomarkers identified as being most significant under the joint variance test. (3) A GWAS of the learning performance score was conducted using models including effects from interactions between genomic markers and the neuroimaging risk score. Six SNPs on the AGBL1 gene were observed to have significant associations with learning performance score at a genomewide level.

2 MATERIALS AND METHODS

2.1 PING Cohort

The primary results are from data collected by the PING Study, which examined a cohort of 1,492 typically developing children from the United States, 3 years through 21 years of age. Subjects were genotyped with the Illumina Human660W-Quad Beadchip and underwent structural MRI scans with one of 13 devices at multiple sites (see Table S1 for scanner parameters). Subjects were also accessed with age-appropriate exams from the NIH Toolbox to evaluate neuropsychological performance across several cognitive domains (Weintraub et al., 2013). The cognitive attributes evaluated by the respective exams are listed in Table S2. Protocols for data collection, informed consent, and quality assurance are described in Jernigan, et al. (2015). Non-genetic data was obtained from PING’s web portal, while genetic data was obtained from the study’s principal investigators. All statistical procedures were evaluated in R unless otherwise noted. Script and custom functions for duplicating all results presented here may be obtained from the corresponding author.

Our analysis was restricted to 479 PING participants of European genetic ancestry (EGA), ages 8 years through 21 years. Restrictions were placed to reduce nonlinear effects on exam scores (Akshoomoff et al., 2014) and neuroimaging biomarkers due to age and population heterogeneity. See Table S3 and Table S4 for demographic summaries and inclusion criteria, respectively, for the sample of 479 subjects considered here.

EGA was determined by principal component analysis (PCA) of the genotype data from the PING. Participants were designated as having EGA if their scores on the first two principal components were below the extreme 1^st percentile of participants with self-reported European ancestry (see Figure S1 for details). The sample was also restricted to include only the elder of any pair of participants having high genetic-relatedness, which was defined as having an identity-by-descent (IBD) value greater than 0.20. There were 97 such pairs in the entire PING cohort. EGA and IBD restrictions were placed to avoid inflated test statistics that often arise in samples that are highly stratified or contain cryptic relatedness. PCA and IBD analysis were both performed with PLINK version 1.9 (Purcell et al., 2007).

Variables for household income and highest level of parental education were used as covariates in the analysis. Missing values for either variable were imputed with the missForest package in R (Stekhoven & Bühlmann, 2012; Stekhoven, 2013) (see Table S5 for details).

2.2 Cognitive exam scores

Covariate effects of age, sex, household income, parents’ education, and first two PCs of genotype were removed from scores on each cognitive exam through multivariate linear regression over the PING sample (n=479). Exam scores were then each scaled to zero mean and unit variance. A learning performance score was defined as the equal-weighted average of the List Sorting, Picture Sequence Memory, Picture Vocabulary, and Oral Reading Recognition exams. Executive function scores are defined as the equal-weighted average of the Attention, Flanker Inhibitory Control, Dimensional Change Card Sort, and Pattern Comparison Processing Speed exams.

2.3 Neuroimaging data

Common measures of brain morphometry for cortical and subcortical regions of interest (ROI), as well as white matter tracts associated with diffusion tensor imaging, were estimated from structural MRI scans with Freesurfer. We considered 198 neuroimaging biomarkers obtained from PING that we denote by { $v_{\mathit{ijk}}^{\text{OBS}}$} with i = 1,…,479 representing the subject, j= 1,…,66 the cortical ROI, and k = 1,2,3 the measurements of average thickness, total area, and volume respectively. Throughout our analysis, we worked with residuals from the multivariate linear regression models

$$v_{\mathit{ijk}}^{\text{OBS}}=a_{jk}^{(0)}+\sum _{q=1}^7{a}_{jk}^{(q)}·w_{iq}+a_{jk}^{(8)}·w_{i;(k)}$$

for each j= 1, …, 66 and k = 1,2,3 over the PING sample (n=479), to control for eight covariates. These covariates include age, sex, handedness, the first two principal components of the genotype data, and two dummy variables used to represent the three sets of scanner device settings, given in Table S1, used in obtaining the subjects’ neuroimaging biomarkers. Finally, the eighth covariance w_i;(k) represents either the whole brain average thickness, total area, or volume for k = 1,2,3 respectively. We denote {v_ijk} to be residuals from these regressions after being standardized to zero mean and unit variance for each j= 1, …,66 and k = 1,2,3.

Since there is evidence that household income and parental education account for variance in cortical surface area (Noble et al., 2015), we also covaried for them in the area measurements but found there was no material effect on our results.

2.4 Joint Variance test

Throughout, we use S⁺ to represent 37 subjects in the PING sample (n=479) that provided an affirmative answer to whether they were ever diagnosed with a learning problem (LP). The remaining 442 subjects are represented by S⁻.

The Joint Variance (JVAR) test is a method for assessing the importance of each ROI in discriminating the brain morphologies of S⁺ (positive LP diagnosis) from S⁻ (no LP diagnosis) subgroups. Its main assumption is that the j^th ROI is important if ${\mathrm{\sigma }}_{\text{jk}+}^2<{\mathrm{\sigma }}_{\text{jk}-}^2$ for every k = 1,2,3, where ${\mathrm{\sigma }}_{\text{jk}+}^2$ and ${\mathrm{\sigma }}_{\text{jk}-}^2$ respectively represent the population variances of {v_ijk :i ∈ S⁺} and {v_ijk :i∈ S⁻}. The idea behind this is that subjects in S⁺ have greater intra-class similarity, and thus lower variance, than those in S⁻ along all three measurements of an important ROI.

We determined the importance of the j^th ROI by testing the null hypothesis

$${\mathcal{H}}_{0;j}:min\left(\frac{{\sigma }_{j1+}^2}{{\sigma }_{j1-}^2},\frac{{\sigma }_{j2+}^2}{{\sigma }_{j2-}^2},\frac{{\sigma }_{j3+}^2}{{\sigma }_{j3-}^2}\right)\ge 1.$$

Under ℋ_0;j, variances of all three measurements of ROI j for individuals in S⁺ are simultaneously greater than or equal to the respective variances for S⁻. We evaluated its significance with the statistic

$$T_j:=1-{\prod }_{k=1}^3(1-p_{jk}),$$

where p_jk is the observed p-value from a one-sided ratio of variances F-test of ${\sigma }_{jk+}^2\ge {\sigma }_{jk-}^2$ with 36 and 441 degrees of freedom. Lower values of p_jk provide greater evidence that ${\sigma }_{jk+}^2<{\sigma }_{jk-}^2$ and imply lower T_j. The JVAR test thus rejects ℋ_0;j for lower values of T_j.

The JVAR test statistic T_j serves as a proxy for the probability of the alternative to ℋ_0;j

$$T_j\approx P\left\{min\left(\frac{{\sigma }_{j1+}^2}{{\sigma }_{j1-}^2},\frac{{\sigma }_{j2+}^2}{{\sigma }_{j2-}^2},\frac{{\sigma }_{j3+}^2}{{\sigma }_{j3-}^2}\right)<1\right\}$$

under its null distribution. In fact, T_j is an unbiased estimate of it when v_ij1, v_ij2, and v_ij3 are mutually independent. If the three variables are correlated, the approximation breaks down and is difficult to evaluate. Permutation tests were conducted to obtain the null distribution of the T_j’s. First, Q=10⁶ permuted samples were produced by randomly assigning 37 subjects to S⁺ and the remaining 442 to S⁻. The JVAR statistic $T_j^q$ was evaluated from each randomly permuted sample. We defined $p_j:=Q^{-1}{\sum }_{q=1}^{Q}I\{T_j\le T_j^q\}$ to be the p-value for the JVAR test of ℋ_0;j.

Our primary reason for taking the similarity approach is that it characterizes differences in brain morphology between S⁺ and S⁻ in a multivariate setting to evaluate a notion of neurobiological risk in a way that is robust against non-linear relationships between neuroimaging variables. This requires selecting a manageable number of important neuroimaging biomarkers on which to place our focus. The JVAR test is ultimately a tool for performing this task in a way that is consistent with the similarity approach.

2.5 Neuroimaging similarity risk score

In the results section, we describe why we chose measure of thickness for six ROIs as being important. Denoting these variables by $v_{i1}^{\ast },\dots ,v_{i6}^{\ast }$, with order being arbitrary, we measure “neuroimaging similarity” between each pair of subjects in the PING sample as being the Euclidean distances between these six variables. Similarity between subjects i and r is

$$D_{ir}:=\sqrt{{\sum }_q^6{(v_{iq}^{\ast }-v_{rq}^{\ast })}^2}$$

with D_ir = D_ri. Relative similarities of subject i to others are the rankings R_i1, …, R_in of D_i1, …, D_in from least to greatest with n =479 the sample size. Lower values of D_ir and R_ir indicate greater similarity between subjects i and r, with D_ii =0 and R_ii =1 for every i.

The risk score we seek to evaluate for each is subject is their average relative similarity to subjects in S⁺ (LP diagnosis). Clinical criteria for LP diagnoses however do not reflect neuroanatomical risk. As such, we considered average relative similarity to subjects in a subset of S⁺ formed after identifying and removing neuroanatomical outliers.

Subject i ∈ S⁺ was designated as an outlier by comparing their average distances to the group of individuals in S⁺ and S⁻, that is, the means of { D_ir : r ∈ S⁺} and {D_ir : r ∈ S⁻ } respectively. Letting ${\mu }_i^{+}$ and ${\mu }_i^{-}$ denote the average distances, we quantified a level of “outlyingness” of each subject i ∈ S⁺ through the p-value q_i from the Wilcoxon rank sum test of the null hypothesis ${\mu }_i^{+}\le {\mu }_i^{-}$. Lower values of q_i mean subject i ∈ S⁺ has a lower level of outlyingness within S⁺ because there is increasing evidence that ${\mu }_i^{+}>{\mu }_i^{-}$, that is, their average distance to S⁻ is lower than their average distance to S⁺.

We controlled for the number of outliers through a threshold v used to define the subsets by

$$S_{\nu }^{\times }=\{i\in S^{+}:q_i>\nu \}\text{and}{S}_{\nu }^{+}=\{i\in S^{+}:q_i\le \nu \},$$

which respectively contain outliers and non-outliers in the LP diagnosed subgroup S⁺. Selecting outliers reflects clinical LP diagnoses that do not necessarily represent neurobiological risk (American Psychiatric Association, 2013; Fletcher et al., 2007).

Each subject’s rank-based average similarity with $S_{\nu }^{+}$is

$$Z_i^{\nu }=c·{\left(\sum _{r\in S_{\nu }^{+}}{R}_{ir}\right)}^{-1}$$

where c > 0 is an arbitrary scaling value and can be set so that $\underset{i}{min}{Z}_i^{\nu }=1$. We term $Z_i^{\nu }$ as a risk score of “neuroimaging similarity with learning problem diagnoses” (NS-LP). Throughout our analysis, we set v=0.01. It is easy to see that subject i will have a higher risk score for lower values of { $R_{ir}:r\in S_{\nu }^{+}$}, that is, for greater relative similarity to individuals in $S_{\nu }^{+}$.

2.6 Genetic studies

We performed a genomewide association study (GWAS) of the learning performance scores over the PING sample (n=479). Marginal association tests were for performed for 488,200 SNPs on autosomal chromosomes having minor allele frequency and Hardy-Weinberg equilibrium p-value greater than 0.05 and 10⁻⁴, respectively, in that sample. The genotype call rate was at least 0.99 for every subject.

Tests for the effect of each SNP were performed in two models of the learning performance score Y_i, which by construction was uncorrelated with age, sex, household income, and parental education. We included in both models the covariate effects of a learning problem diagnosis and the first two principal components of the genotype data that, along with an intercept, are represented by b^TW_i.

We first tested the null hypothesis that there was no genetic effect in the gene-risk interaction (G×R) model for the g^th SNP, given by

$$Y_i={\mathit{b}}^T{\mathit{W}}_i+{\alpha }_g{Z}_i+{\beta }_g{X}_{ig}+{\gamma }_g(Z_i\times X_{ig})$$

where X_ig is the number of risk alleles and $Z_i:=Z_i^{\nu }$ is the NS-LP risk score for v = 0.01. There is no genetic effect in this model only if β_g + γ_g · Z_i = 0 for all values of Z_i, which is possible only under the joint null hypothesis ${\mathcal{J}}_0^{(g)}:{\beta }_g=0$, γ_g = 0. We performed a F-test with 2 and 472 df for each ${\mathcal{J}}_0^{(g)}$. For comparison we also performed a F-test, with 1 and 474 df, of the null hypothesis ${\mathcal{M}}_0^{(g)}:{\theta }_g=0$ in the main effect model Y_i = b^TW_i + θ_gX_ig for each SNP.

All estimates were obtained using ordinary least squares (OLS). In the G×R model, the estimated effect from one additional risk allele is E(z; β, γ ) = β+γ · z with standard error being $SE(z;\beta ,\gamma )=\sqrt{d_z^T{\mathit{\sum }}_D{d}_z}$, where d_z = (1, z)^T is a vector of size two and Σ_D is the 2×2 matrix of the covariance for the β and γ estimates.

In our GWAS, we performed tests of the null hypotheses ${\mathcal{M}}_0^{(g)}$ and ${\mathcal{J}}_0^{(g)}$ for each of 488,200 SNPs. To correct for multiple testing, we evaluated false discovery rates over the Q=976,400 tests performed in the GWAS. We also evaluated permutation-based family-wide error rates (p-FWER) to account for correlations between SNPs and control for finite sample size.

The steps for evaluating p-FWER are as follows. Let $p_1^0,\dots ,p_Q^0$ denote the Bonferroni-adjusted p-values, sorted from least to greatest, observed in the GWAS with Q tests. In p-FWER, the Q tests are performed again, except after randomly permuting the responses over the sample. This was repeated for a total of R times. For each permutation r =1, …, R, we denote $p_1^r,\dots ,p_Q^r$ as the Bonferroni-adjusted p-values, ordered from least to greatest.

$$\text{For}q=1,\dots Q,\text{let}\stackrel{\sim }{p_q}:=\frac{1}{R}{\sum }_{r=1}^{R}I\{p_q^0<q_q^r\}$$

denote the average number of times that $p_q^0$ is less than $p_q^1,\dots ,p_q^R$. Defining the integer $s_{\alpha }:=max\{s:\stackrel{\sim }{p_s}\le \alpha \}$ for α > 0, the s_α tests with the lowest observed p-values are designated as having genomewide significance at level α. The p-FWER thus examines the joint distribution of extreme test statistics under null distributions.

2.7 Power analysis

In the JVAR test for ROI j, we compared the ratio of variances along the respective three measurements between S⁺ (n=37) and S⁻ (n=442) subgroups in the PING sample. Through simulation experiments, we determined that the JVAR tests of size 0.05 have 80% power when $max\left(\frac{{\sigma }_{j1+}^2}{{\sigma }_{j1-}^2},\frac{{\sigma }_{j2+}^2}{{\sigma }_{j2-}^2},\frac{{\sigma }_{j3+}^2}{{\sigma }_{j3-}^2}\right)\le 0.85$ for case and control groups of these sizes.

The GWAS was conducted over the PING sample (n=479). We performed power analysis for minimum effect size needed for a sample of this size for tests of level 5 × 10⁻⁸ that achieve 80% power. For tests of ${\mathcal{J}}_0^{(g)}$, parameters β_g and γ_g in the GxR effect model for a SNP with minor allele frequency p must satisfy

$$\frac{2p(1-p)({\beta }_g^2+{\gamma }_g^2)}{\widehat{{\sigma }_{\epsilon }^2}}\ge 0.094,$$

where $\widehat{{\sigma }_{\epsilon }^2}$ is the variance of residuals from the model fit using NS-LP scores that are first standardized to zero mean and unit variance. We verified this relationship through numerical experiments. For tests of ${\mathcal{M}}_0^{(g)}$, the parameter θ_g in the main effect model must satisfy

$$\frac{2p(1-p){\theta }_g^2}{\widehat{{\sigma }_{\epsilon }^2}}\ge \mathrm{0.086.}$$

2.8 PNC study

We found support for the significant genetic results from the GWAS of the PING sample with participants of 8 through 21 years of age and possessing EGA from the Philadelphia Neurodevelopmental Cohort (PNC) study (Satterthwaite et al., 2014). The PNC study genotyped participants with one of six platforms, of which the Illumina Human610-Quad or Human550 (v1 and v3) platforms included six SNPs we sought to validate. Subjects were included in the PNC sample if they were genotyped with those platforms, had no major developmental problems, and possessed EGA. The latter was determined by performing PCA on the three platforms separately. Subjects were designated as having EGA if their scores on the first two PCs were both greater than the respective extreme third percentile of subjects with self-reported European ancestry.

The PNC sample had n=2,327 subjects with valid scores on the Wide Range Achievement Test (WRAT) (Wilkinson & Robertson, 2006) that was taken to be cognitive response for assessing learning performance. The WRAT is a comprehensive IQ-achievement exam commonly used in diagnosing learning disorders. Table S3 and Table S6 respectively provide demographics and inclusion criteria for the PNC sample.

We performed a F-test with 1 and 2321 df, on the null hypothesis ${\mathcal{M}}_{0;\text{PNC}}^{(\mathrm{g})}:{\mathrm{\theta }}_{\mathrm{g}}=0$ in the main effect model for the six most significant SNPs in the PING GWAS. Covariates included age, sex, two dummy variables for chip platform, and an indicator whether the subject had a reading problem. Household income and parental education data was not available on dbGAP. Neuroimaging data at the region of interest level from the PNC study was also not available on dbGAP. As a result, NS-LP scores could not be evaluated and, in turn, tests of the G×R model could not be performed.

3 RESULTS

3.1 Memory and language exams best predict learning problem diagnoses

We first sought a composite measure of learning performance, which refers throughout here to the cognitive measures associated with reading, writing, or mathematics deficits in the DSM-V model of SLDs as opposed to others like attention or executive function. To achieve this goal, we performed principal component analysis (PCA) on scores from the eight exams in the NIH Toolbox. Because exam scores were highly associated with subjects’ age, sex, level of household income, highest level of parents’ education, and genetic ancestry (Akshoomoff et al., 2014) we removed their effects from each exam through multivariate regression prior to PCA in order to reduce these common sources of variation.

The exam loadings on the first PC, shown in Table S7, all had the same sign, which indicates it represents a latent factor for overall cognition, along with other confounding effects, common to all eight exams. Loadings on the second PC gave more insight into achieving our goal. Four exams evaluating episodic memory, working memory, reading, and vocabulary had negative loadings. These cognitive domains define learning performance as being distinct from executive control and attention. Indeed, there were positive loadings on the remaining four exams, which evaluated executive function, attention, and processing speed.

Our composite learning performance score, as described in the Methods section, was an equal-weighted average of language and memory exams and was, by construction, uncorrelated with age, sex, household income, highest level of parents’ education, and first two PCs of genotype data. The mean and standard deviation of the learning performance scores were μ = 0 and σ = 0.67 respectively.

The learning performance score discriminated between subjects with and without a learning diagnosis. As shown in Figure S2, the learning performance score distribution for S⁺ (diagnosed with LP) subgroup was markedly lower than that of S⁻ subgroup (KS-test: D = 0.39, p < 10⁻⁴). For comparison, we also derived a composite executive function score in the same way using the four exams assessing executive function, attention, and processing speed. There was no significant difference (KS-test: D = 0.17, p = 0.26 ) in the distributions of that composite score between S⁺ and S⁻, which indicates those domains are less relevant for diagnosis of learning problems.

3.2 Thickness of ROIs in temporal lobes best characterize neurobiological risk for learning problems

We next sought to quantify neurobiological risk related to learning performance using neuroimaging biomarkers. To decouple this risk from cognitive assessments, we used the subgroup S⁺ (diagnosed with LP) as a surrogate measure. Indeed, Figure S2 shows there is a large overlap in the distributions of learning performance scores of S⁺ and S⁻ (no LP diagnosis), which indicates the LP diagnosis status does not directly reflect cognitive evaluations.

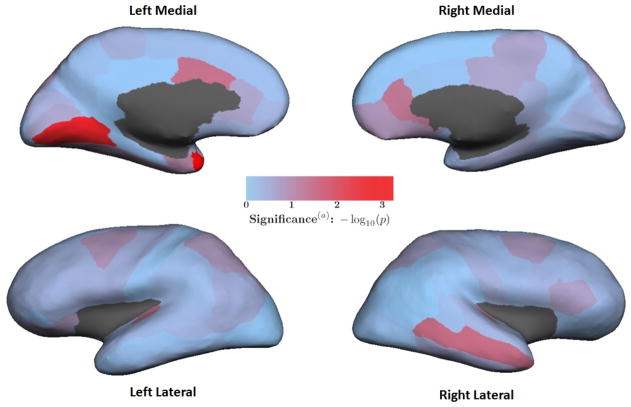
We identified neuroimaging biomarkers that best characterized S⁺ as being distinct from S⁻ using the joint variance (JVAR) test described in the Methods section. The heat map in Figure 2 illustrates p-values for the respective ROIs from the JVAR test, where significance was assessed from a null distribution generated by permutations. Lower p-values indicate the ROI better characterizes the brain morphology of S⁺ relative to S⁻. Most regions did not characterize S⁺ well under the JVAR test over the PING sample. See Table S12 for p-values for all 66 ROIs.

Figure 2. Heat map of each ROI’s significance under JVAR test.

Colors represent p-values from the JVAR test for each ROI comparing subjects with a learning problem diagnosis (n=37) and without a LP diagnosis (n=442) in the PING sample (n=479). Red indicates greater significance. (a) The p-values are not adjusted for multiple comparisons. The p-values from the JVAR tests for all 66 ROIs are listed in Table S9.

Table 1 lists the ten most significant ROIs among the JVAR test results. Only the left temporal pole had a Bonferroni-adjusted p-value less than 0.05. Six ROIs with unadjusted p-values less than 0.054 were in the temporal lobes and anterior cingulate gyri on either hemisphere. The thickness component of the JVAR statistic contributes to the significance of all six ROIs, whereas area and volume components are less consistent. We quantified neurobiological risk for learning problems with the thickness of these six ROIs. We chose a cut-off for this number of ROIs because there was a marked decrease in significance for the right transverse temporal gyrus, which was the seventh most significant ROI.

Table 1. Ten most significant ROIs under joint variance (JVAR) test.

Greater significance and lower p-values under JVAR test implies that a ROI better characterizes S⁺ (n=37) as a group relative to S⁻ (n=442) in thickness, area, and volume measurements simultaneously. (a) One-sided F-tests for ratio of variances, with 36 and 441 degrees of freedom, between the groups were performed for thickness, area, and volume variables of each respective ROI. (b) The p-values for the JVAR test statistic $T_j=1-{\mathrm{\Pi }}_{k=1}^3(1-p_{jk})$ were generated through permutation distributions, as described in the Methods section. Significance of all 66 ROIs is provided in Supplementary Table 9. (c) FDR-adjusted p-values are over JVAR tests for 66 ROIs. (d) The left temporal pole had a FDR-adjusted p-value less than 0.05.

Rank	Region of Interest	Ratio of Variances F-testa: pjk			Joint variance testb of ℋ0;j
		Thickness	Area	Volume	Statistic Tj	p-value	FDRc
1	Left Temporal Pole d	0.044	0.014	0.002	0.0582	0.0005	0.035
2	Left Lingual	0.002	0.033	0.006	0.0403	0.0016	0.052
3	Right Middle Temporal	0.080	0.228	0.093	0.3558	0.0266	0.524
4	Left Caudal Anterior Cingulate	0.028	0.235	0.109	0.3381	0.0318	0.524
5	Right Rostral Anterior Cingulate	0.029	0.074	0.285	0.3576	0.0427	0.563
6	Left Transverse Temporal	0.031	0.053	0.385	0.4352	0.0533	0.586
7	Right Transverse Temporal	0.047	0.286	0.220	0.4686	0.0797	0.703
8	Left Entorhinal	0.065	0.063	0.372	0.4499	0.0852	0.703
9	Left Fusiform	0.286	0.256	0.244	0.5979	0.1211	0.802
10	Right Medial Orbitofrontal	0.016	0.460	0.284	0.6193	0.1409	0.802

3.3 NS-LP scores predict learning performance scores

There were 7 outliers among the 37 subjects having a positive LP diagnosis with respect to these variables for outlyingness threshold v = 0.01. Also using these six variables, we evaluated NS-LP risk scores, denoted $Z_i:=Z_i^{\nu }$ for v = 0.01, in the PING sample (n=479).

The distribution of the NS-LP risk scores had a high positive skew (ξ = 0.84). Along with the covariates used for the neuroimaging variables, NS-LP scores also had insignificant correlations with either household income (ρ̂ = 0.04 ; p=0.37 ) or parental education (ρ̂ =0.006; p=0.89).

To understand the relationship between the NS-LP and the learning performance scores Y_i described above, we fit three models to the PING sample (n=479). Model A is Y_i = a₀ + a_zZ_i, model B is Y_i = b₀ + b_LL_i, and model C is Y_i = c₀ + c_LL_i + c_zZ_i with L_i = 1 for positive LP diagnosis and L_i = 0 otherwise. Learning performance scores are, by construction, uncorrelated with age, sex, household income, parents’ education (highest level), and genetic ancestry. Summaries of the three model fits are given in Table 2.

Table 2. Models of learning performance for LP status and NS-LP score.

Model A: Y_i = a₀ + a_zZ_i. Model B: Y_i = b₀ + b_LL_i. Model C: Y_i = c₀ + c_LL_i + c_zZ_i. Learning performance score Y_i is average of working memory, episodic memory, vocabulary, and reading exams. Each exam score was scaled to zero mean and unit variance after controlling for age, sex, household income, parents’ education, and first two PCs of genotype. Indicator L_i=1 for positive LP diagnosis and L_i=0 otherwise. NS-LP score $Z_i:=Z_i^v$ for v = 0.01. (a) F-test for respective models; degrees of freedom (df) are 1 and 477 for Models A and B, and df are 2 and 476 for Model C. (b) F-test for respective coefficients with 1 and 477 df’s. (c) Model C’s fit is 44% better than Model B as determined by percentage increase in adjusted R².

	Summary of model fits
	Adjusted R2	R2	p-value a
Model A	0.024	0.026	3.7E-04
Model B c	0.036	0.038	1.6E-05
Model C c	0.052	0.056	9.7E-07

	Model estimates
	beta	T	p-value b
Model A
a0	0.57	3.50	5.1E-04
aZ	−0.36	−3.56	4.1E-04
Model B
b0	0.04	1.21	0.23
bL	−0.49	−4.37	2.0E-05
Model C
c0	0.51	3.18	1.5E-03
cL	−0.44	−3.85	1.3E-04
cZ	−0.31	−3.01	2.8E-03

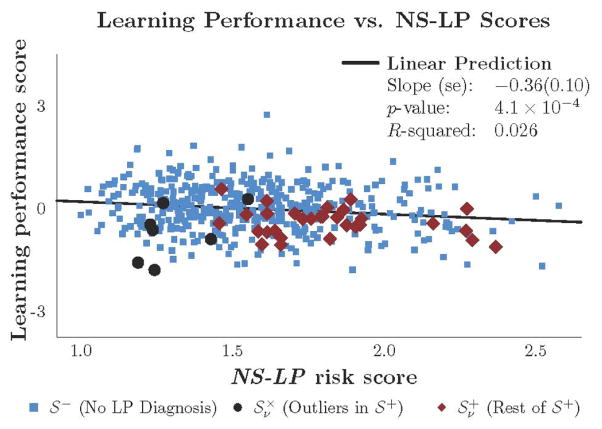
Figure 3 shows there was a significant negative relationship between the NS-LP and the learning performance scores in model A (ẑ_z = −0.36, p = 3.7×10⁻⁴). It was not surprising that LP diagnosis status had a significant negative relationship to learning performance in Model B, given what was observed in Figure S2. It was surprising, however, that Model C fit learning performance better than Model B by 44% based on adjusted R². A F-test of the null hypothesis for Model B against the alternative of Model C yielded a significance of p = 2.8×10⁻³ over the PING sample. The significant negative marginal relationship between the two scores in Model C (ĉ_z = 0.31, p =2.8×10⁻³) suggests that neuroimaging variables enabled NS-LP to predict learning performance.

Figure 3. Learning performance scores versus NS-LP scores.

The blue, black, and red markers represent subjects in subgroups denoted by S⁻ (n=442), $S_{\nu }^{\times }(\mathrm{n}=7)$, and $S_{\nu }^{+}(\mathrm{n}=30)$ respectively. The $S_{\nu }^{\times }$ and $S_{\nu }^{+}$ subgroups respectively contain outliers and non-outliers in S⁺ (n=37) based on outlyingness of subjects, with respect to neuroanatomical measurements, threshold v = 0.01. Methods section describes how outliers are identified. Regression results are over the PING sample (n=479) and based on Model (A) specified in Table 2.

In post-hoc analysis, we performed marginal association tests between learning performance Y_i and {v_ijk} for each respective j =1, …, 66 and k = 1,2,3 over the PING sample. Among the 198 tests, there was no p-value less than 0.006; see Table S10. This lends evidence to the hypothesis that multivariate approaches to neuroimaging are more favorable than univariate ones (J. Liu & Calhoun, 2014; Meyer-Lindenberg, 2012; Norman, Polyn, Detre, & Haxby, 2006).

3.4 Genetic results

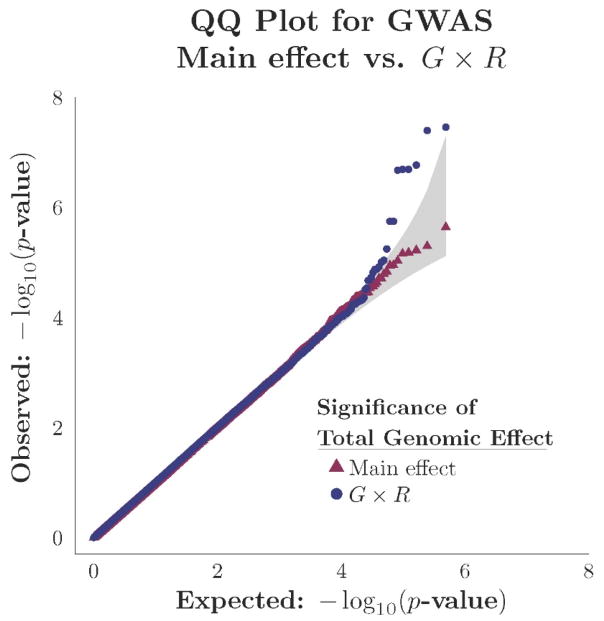
We performed a GWAS of the learning performance scores under the G×R and main effect models for each of the 488,200 SNPs genotyped from the PING sample (n=479). The significances from the GWAS of ${\mathcal{M}}_0^{(\mathrm{g})}$ and ${\mathcal{J}}_0^{(\mathrm{g})}$ tests are compared in the QQ-plots shown in Figure 4. The horizontal axis represents the theoretical null distribution of p-values over the G =488,200 tests, with values given by $-{\mathit{log}}_{10}\left(\frac{G-g}{G+1}\right)$ for g=1, …, G. The vertical axis corresponds to the ordered p-values, on a −log₁₀ scale, observed in the GWAS of the two hypotheses. Tests of ${\mathcal{J}}_0^{(\mathrm{g})}$ detected two significant SNPs whereas those of ${\mathcal{M}}_0^{(\mathrm{g})}$ failed to detect any under theoretical asymptotic null distributions.

Figure 4. QQ-plot of GWAS of learning performance score in PING sample (n=479).

Tests were performed for genomic effects G×R and Main effect models of learning performance scores for each of 488,200 SNPs. Observed p-values in the GWAS of each model were sorted and then plotted on a −log₁₀ scale against expected values in theoretical null distributions. The shaded region indicates a 95% confidence interval. Blue dots correspond to tests of ${\mathcal{J}}_0^{(g)}$ in the G×R model. Red triangles correspond to tests of ${\mathcal{M}}_0^{(g)}$ in the main effect model. The genomic inflation factors for the GWAS of the G×R and Main effect models were 1.012 and 1.002, respectively.

Among tests of ${\mathcal{J}}_0^{(\mathrm{g})}$ and ${\mathcal{M}}_0^{(\mathrm{g})}$ performed for G SNPs, the six tests having greatest significance were of ${\mathcal{J}}_0^{(\mathrm{g})}$ for SNPs all on the same linkage disequilibrium block within the AGBL1 gene on chromosome 15. Table 3 provides their respective significances and model estimates. They all have FDR less than 0.05 over the 976,400 tests performed. We verified the significance with p-FWER.

Table 3.

Six SNPs on AGBL1 gene (chromosome 15) significant in GWAS of learning performance. Tests of ${\mathcal{J}}_0^{(g)}$ and ${\mathcal{M}}_0^{(g)}$ were performed for G×R and Main effect models, respectively, for 488,200 SNPs of the learning performance scores over the PING sample (n=479). Both models included covariates for status of learning problem diagnosis and the first two PCs of genotype data. Learning performance scores were, by construction, uncorrelated with age, sex, household income, and parental education. Tests of ${\mathcal{M}}_{0;\mathit{PNC}}^{(g)}$ were performed for main effect models of WRAT scores over the PNC sample (n=2,327). Covariates there included age, sex, status of learning problem diagnosis, and genotyping platform (see Methods section). (a) F-tests of ${\mathcal{J}}_0^{(g)}$ were performed with statistic having 2 and 472 df. F-tests of ${\mathcal{M}}_0^{(g)}$ were performed with statistic having 1 and 474 df. F-tests of ${\mathcal{M}}_{0;\mathit{PNC}}^{(g)}$ were performed with statistic having 1 and 2,322 df. (b) FDR-adjustments were made to the p-values from 976,400 tests performed in the PING sample (n=479). (c) Information gain are for respective G×R and Main effect models over the PING sample (n=479). It represents the increase in adjusted R² for the respective model fit over that of the non-genetic base model including only the covariates. (e) Minor allele frequency is over the PING sample (n=479). (f) SNPs were genotyped with the Illumina Human660W-Quad Beadchip array and their positions correspond to HG build 19. See Supplementary Table 11 for minor alleles for the respective SNPs.

SNP	MAFe (Positionf)	p-valuea (FDRb)			Information gain c		Parameter estimates (standard error)
					Model		G×R model			Main effect model
		${\mathcal{J}}_0^{(g)}$	${\mathcal{M}}_0^{(g)}$	${\mathcal{M}}_{0;\mathit{PNC}}^{(g)}$	G×R	Main	αg	βg	γg	θg	θg;PNC
rs11633708	0.47 (87050708)	3.5E-08 (0.020)	2.3E-06 (0.24)	7.0E-04	7.89	4.27	−0.81 (0.18)	−0.90 (0.22)	0.44 (0.14)	−0.20 (0.04)	−0.100 (0.030)
rs4243100	0.45 (87037559)	4.0E-08 (0.020)	6.5E-05 (0.90)	4.6E-04	7.84	3.01	0.24 (0.17)	1.03 (0.21)	−0.54 (0.13)	0.17 (0.04)	0.102 (0.029)
rs11853362	0.44 (87057124)	1.7E-07 (0.034)	7.7E-05 (0.90)	6.9E-04	7.29	2.95	−0.90 (0.18)	−1.00 (0.22)	0.51 (0.14)	−0.15 (0.04)	−0.100 (0.029)
rs11632104	0.45 (87049894)	2.0E-07 (0.034)	3.0E-04 (0.97)	3.0E-04	7.23	2.44	0.24 (0.17)	1.00 (0.22)	−0.53 (0.13)	0.15 (0.04)	0.105 (0.029)
rs4887473	0.45 (87053206)	2.0E-07 (0.034)	3.0E-04 (0.97)	3.0E-04	7.23	2.44	0.24 (0.17)	1.00 (0.22)	−0.53 (0.13)	0.15 (0.04)	0.106 (0.029)
rs2011905	0.45 (87053846)	2.1E-07 (0.034)	3.1E-04 (0.97)	3.3E-04	7.21	2.42	0.24 (0.17)	1.00 (0.22)	−0.53 (0.13)	0.15 (0.04)	0.105 (0.029)

The most significant SNP in both the G×R and main effect models of the 488,200 SNPs tests was rs11633708. In the G×R model, its p-value was less than 5×10⁻⁸, a threshold commonly accepted for designating a SNP with genomewide significance in a GWAS. Table 3 also shows tests of the main effect model for these six SNPs over the PNC sample (n=2,327) were all significant with p-values all less than or equal to 7×10⁻⁴. Table S11 provides minor allele frequencies, minor allele, and positions for these SNPs along with those of the 50 most significant SNPs in the GWAS under both the G×R and main effect models.

For these SNPs, tests of ${\mathcal{J}}_0^{(\mathrm{g})}$ had greater significance than tests of ${\mathcal{M}}_0^{(\mathrm{g})}$ suggesting that the gene-risk interaction model had greater information gain than the respective main effect model. Information gain here is the increase in adjusted R² of the fitted model (main effect or G×R) over that of the fitted base model, given by Y_i =b^TW_i. For these six SNPs, the gene-risk interaction model had higher information gain despite being penalized for having two extra parameters.

In Figure 5, the change in estimated effect from one additional allele of rs11633708, given everything else equal, on the learning performance score in the G×R model is plotted as a function of NS-LP scores (red line). A 95% confidence interval band is also shown where the upper and lower 2.5% percentiles are

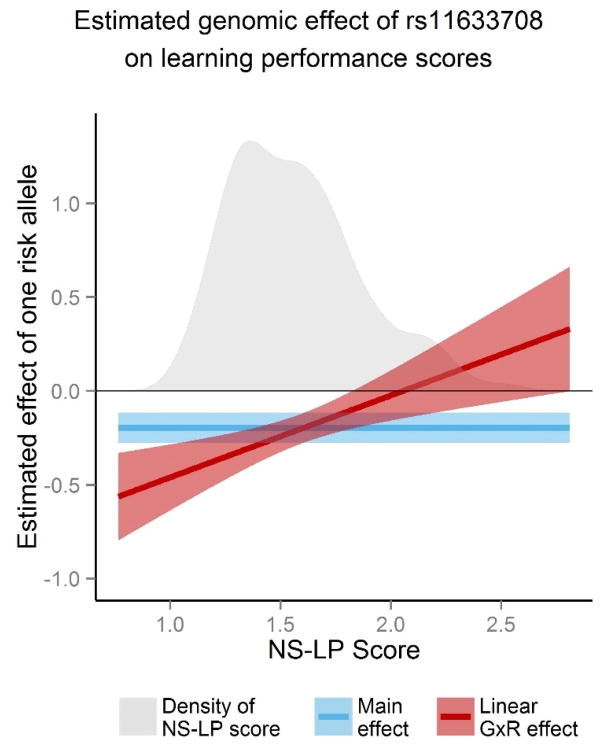
Figure 5. Estimated effect of rs11633708 on learning performance as function of NS-LP risk score.

The SNP rs11633708 on AGBL1 (chromosome 15) was the most significant in a GWAS of learning performance scores over the PING sample (n=479). The vertical axes represents estimated effect one additional risk allele of rs11633708 on learning performance scores (μ= 0, σ= 0.67). Lines and shaded regions represent estimated effects and their 95% confidence intervals in three models. Blue represents the main effect model, which does not rely on NS-LP risk scores. Red represents the G×R model presented in the genomic results section. Estimates and standard errors in the G×R model are a function of NS-LP scores. Standard errors there were evaluated from the covariance matrix of estimates in the respective linear regression models. The gray region in both plots is the empirical density of NS-LP scores and is at scale with the vertical axis.

$${CI}_{\mathit{Upper}/\mathit{Lower}}(Z;\beta ,\gamma )=E(z;\beta ,\gamma )\pm 1.96·SE(z;\beta ,\gamma )$$

with derivations of E(z; β, γ) and SE(z; β, γ) given in the methods section. The significance of the estimated effect is greatest for subjects in the sample with low NS-LP scores and is negligible for subjects scoring at the higher range of NS-LP, as indicated by the widening confidence interval that crosses 0.0 (blue line). In contrast, the main effect model (red line) does not account for differences in estimated genetic effects on learning performance, with respect to NS-LP risk, over the sample. Therefore, testing genetic effect in the main effect model suffers from diminished power.

To confirm these findings, we performed a gene-based analysis for the set of 150 SNPs on AGBL1 included in our GWAS. The combined significance from the respective tests of ${\mathcal{J}}_0^{(\mathrm{g})}$ for these SNPs was 1.99×10⁻⁶ when using the VEGAS method (J. Z. Liu et al., 2010). The Bonferroni-corrected p-value is 0.04 if the same SNP-set analysis was conducted for 20,000 genes.

Finally, we performed post-hoc analysis to determine whether we could arrive at similar results using, for interaction variables in the GxR model, any of the neuroimaging biomarkers identified as being important with the JVAR test. To do this, we tested the genetic effect in G×R models for rs11633708 where the thickness measurement of the six most significant ROIs in the JVAR test are the interaction variables. The results are reported in Table S12 and show that the significance of genetic effect for these models was far lower than in the GxR model with the NS-LP score.

3.5 Sensitivity Analysis

We detected a significant association between SNPs in AGBL1 and learning performance in the PING sample through the G×R model, which required evaluating NS-LP scores. These scores represent within-sample risk as they are constructed from pairwise similarities between subjects’ neuroimaging measurements. This inherently heightens sample dependence of the genetic results.

We performed a sensitivity analysis to assess the stability of the NS-LP scores and their effect on the genetic results. To do this, we fit the main effect and G×R models for rs11633708 to a random subset of 407 subjects (85%) from the PING sample. The G×R model used NS-LP scores which were reevaluated over that subset. Figure S3 compares the information gain of the two models over 100 different random subsets. It shows that the G×R model for rs11633708 yielded more information gain than the main effect model over the random subsets.

4 DISCUSSION

We observed several SNPs in the AGBL gene that were significantly associated with learning performance at genomewide levels in our GWAS. AGBL1 encodes an enzyme regulating protein deglutamylation in the cytosolic carboxypeptidase (CCP) family of catalysts. This enzyme and others in the CCP family have been observed to effect neuronal survival (Rogowski et al., 2010; Wang, Parris, Li, & Morgan, 2006). To the best of our knowledge, there are no findings linking AGBL1 to any cognitive traits through either neurochemistry or genetic association studies.

On the other hand, AGBL1 has been linked to schizophrenia in two separate GWAS with independent samples (Ikeda et al., 2013; Sullivan et al., 2008). Both GWAS identified SNPs in AGBL1 as being the most significant among approximately 500,000 tested, albeit not at genomewide levels, with p-values less than 4×10⁻⁶. Schizophrenic patients suffer from several cognitive deficits (Barch, 2005) including ones related to working memory (Forbes, Carrick, McIntosh, & Lawrie, 2009; Lett, Voineskos, Kennedy, Levine, & Daskalakis, 2014), episodic memory (Leavitt & Goldberg, 2009; Lepage, Sergerie, Pelletier, & Harvey, 2007), and language (Bhati, 2005; Covington et al., 2005; Robbins, 2002). Taken together, these results suggest a pleiotropic effect of AGBL1 on both schizophrenia and certain cognitive traits related to learning performance.

In the PING sample, the SNPs in AGBL1 had significant association with learning performance at the genomewide level in the gene-risk interaction model. Within this model, the magnitude and direction of genetic effect depends on the NS-LP risk. The interaction term in the model mitigated the impact of this heterogeneity might have had on detecting genetic variants in AGBL1.

Indeed, many disparate environmental and non-genetic biological risk factors, in conjunction with genetic risk, influence how neuropsychological traits manifest (Hardy & Singleton, 2009). For example, early environmental stressors, substance abuse, hormones, and immunological factors are related to the onset of psychosis-spectrum disorders in individuals with a genetic predisposition (Agid et al., 1999; Ikeda et al., 2013; Kirkbride et al., 2006; Kulkarni, Hayes, & Gavrilidis, 2012). Identifying significant risk factors stands to dramatically improve power in statistical inference of NP traits (Agid et al., 1999). As our results demonstrate, neuroimaging biomarkers can be used to quantify neurobiological risk.

Neurobiological risk is, however, neither observable nor well-defined. Furthermore, many influences on brain plasticity and function, such as socioeconomic status (Noble et al., 2015), stress (McEwen, 1999), and cardiovascular fitness (Colcombe et al., 2004), among others (Ellingson, Fleming, Vergés, Bartholow, & Sher, 2014), are confounders present in neuroimaging studies. Here, we describe a new multivariate method that defines neurobiological risk in a sample by similarity in brain morphology for a given diagnosis (see Figure 6 for an illustration). This approach assumes only that individuals in a high diagnosis risk subgroup are clustered in a multivariate space of a few important neuroimaging biomarkers. Any given individual’s risk is then their average similarity in that space to those in the diagnosed subgroup.

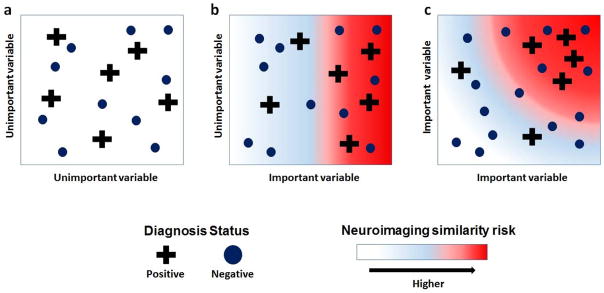
Figure 6. Illustration of neuroimaging similarity for a diagnosis.

Two subgroups of subjects are formed on the basis of observed diagnosis. Plus signs represent S⁺ (positive diagnosis) and dots represent S⁻ (negative diagnosis). Along important variables, S⁺ has greater level of within-group similarity (homogeneity) relative to S^-. Along unimportant variables, the level of within-group similarity for S⁺ and S⁻ are roughly equal. Background colors represent subjects’ continuous level of along respective axes. Each figure represents bivariate comparisons between variables. Background color represent continuous level to neuroimaging similarity with S⁺ in bivariate setting. (a) Axes represent two unimportant variables where neuroimaging similarity risk cannot be detected. (b) Respective axes are important and unimportant variables. Neuroimaging similarity risk increases only along axis for important variable. (c) Axes represent two important variables, where neuroimaging similarity to S⁺ is with respect to multivariate distances.

The clustering will remain persistent when projecting onto a single important variable and will disappear when projecting onto a single unimportant variable any individual’s risk. The JVAR test identifies neuroimaging biomarkers that distinguish subjects at high risk for learning problems. The rank-based average similarity then allows for quantifying risk in a multivariate setting without the need to specify complicated parametric models of multivariate neuroimaging data. That this approach requires no additional assumptions about environmental exposures suggests that it is robust and potentially generalizable to other phenotypes and domains.

The similarity framework is also robust against “mislabeling” if the high-risk subgroup is initialized as being those with clinical diagnoses. Mislabeling here means that the diagnosis status of individuals may not match up with their neurobiological risk. Outliers in the diagnosed group can be identified through their neuroimaging biomarkers.

We used the JVAR test here to determine how well ROIs characterize the LP diagnosis group as being distinct from rest of the PING sample. As listed in Table 1, seven of the ten most significant regions are in the temporal lobes in either hemisphere. This is consistent with well-established neuroimaging findings in learning performance. The temporal lobes contain networks vital to memory formation, recall and language comprehension (Brockway et al., 1998; Hoenig & Scheef, 2005; Leritz, Grande, & Bauer, 2006). Two other regions with high significance are in the anterior cingulate gyrus, which plays a key role in motivation through rewards-based learning (Shenhav, Botvinick, & Cohen, 2013).

Finally, the genetic results also depend on the learning performance phenotype. Here, we conditioned association on a composite of four memory and language assessments. This improves power for detecting genetic markers having significant association with latent factors common to all four assessments by reducing idiosyncratic noise and amplifying signal-to-noise ratio in the genetic model. Table S8 shows that rs11633708 had associations with the composite learning performance score with far greater significance than with any of the eight individual exams under both ${\mathcal{J}}_0^{(\mathrm{g})}$ and ${\mathcal{M}}_0^{(\mathrm{g})}$ hypotheses.

Our approach for integrating genetics, neuroimaging, and clinical data into a single statistical framework can be readily extended to other phenotypes for symptom severity, such as attention exams or psychotic symptom ratings, using risk scores of neuroimaging similarity to clinical diagnoses of attention or psychosis disorders. A major advantage to this framework is that, by summarizing neuroimaging risk with a single variable, it presents a massive reduction in tests for interactions between genetic and neuroimaging biomarkers.

When defined appropriately, neurobiological risk can better control for population heterogeneity in the study of any NP trait. Controlling for heterogeneity enables detecting genetic risk factors important for individuals at any given level of neurobiological risk. A direct consequence here is identifying targets for actionable personalized treatments of NP disorders, which is an important priority in current psychiatric and neuropsychological research missions (Insel & Cuthbert, 2015).

Supplementary Material

Supp Table S10

Table S1: Scanner Models and Parameters. Taken from Supplementary Table 4 of Noble, et al. (2015). (a) All four scanner models have T3 strength. (b) Number of subjects in the PING sample (n=479) imaged with respective MRI scanner. (c) Scanner parameters correspond to T1-weighted MPRage scans.

Table S2: Description of exams in NIH Toolbox. Taken from Table 3 in Akshoomoff, et al (2014).

Table S3: Sample demographics. Subjects in both of the samples studied here were restricted to being 8 through 21 years ago age and having European genetic ancestry (EGA). Inclusion criteria for the PING (n=479) and PNC (n=2,327) samples studied here are given in Supplementary Tables 5 and 8 respectively.

Table S4: Inclusion Criteria for PING sample. (a) Only the elder of any pair of participants with IBD > 0.20 were retained in the final sample. (b) See Figure S1 for illustration on how European genetic ancestry was determined.

Table S5: Summary of socioeconomic status in PING sample (n=479). The PING study asked participants, or their parents, to report level of household income and highest level of education completed by parents. (a) Household income (HI) and parents’ education (PE) were reported at 12 and 7 discrete levels. (b) Number of subjects within the PING sample (n=479) reporting respective level. (c) There were 17 subjects with no HI reported and 12 subjects with no PE reported. These missing values were imputed simultaneously using a nonparametric method with the missForest package in R over PING subjects prior to placing sample restrictions and performing analysis. The imputation incorporated level of parents’ occupation and first PC of genotype, which were highly correlated with HI and PE.

Table S6: PNC sample inclusion criteria. Genotype and cognitive exam data was available for 8,719 participants of the Philadelphia Neurodevelopmental Cohort (PNC) study. Three of the six genotyping platforms used by PNC included SNPs having high significance in the genomewide association study of learning performance in the PING sample. Subjects in the PNC sample were restricted to being genotyped by these three platforms (P4,P5,P6), having no major neurodevelopmental problems (medical rating of 0, 1, or 2), and had valid scores on the Wide Range Achievement exam. The 4,482 subjects meeting this sample inclusion criteria were further restricted to having European genetic ancestry (EGA). The first two PCs of genotypes on P4, P5, and P6 were used to determine EGA. Subjects with scores falling within the extreme quantiles, on each PC, for self-reported whites.

Table S7: Loadings from principal component analysis performed on scores on eight exams. Exam scores were for n=479 subjects in PING sample. Prior to performing PCA, covariate effects of age, sex, household income (level), parents’ education (highest level), and genetic ancestry were removed from scores for each exam through multivariate regression. (a) There are two groupings of exams based on sign of loadings on PC2. (b) Learning performance scores was average of PSTM, List Sorting, Vocabulary, and Oral Reading scores, after they were controlled for covariates listed above and then standardized to zero mean and unit variance.

Table S8: Effect of rs11633708 on eight individual exam scores. The SNP rs11633708 on AGBL1 (chromosome 15) was the most significant in a GWAS of learning performance scores over the PING sample (n=479). Results are tests of genomic effect in the $\mathrm{G}\times \mathrm{R}({\mathcal{J}}_0^{(\mathrm{g})})$ and main effect ( ${\mathcal{M}}_0^{(\mathrm{g})}$) models of the respective eight exam performances. Covariates included in each model were age, sex, household income, highest level of parents’ education, status of learning problem diagnosis, and first two PCs of genotype data. F-tests of ${\mathcal{J}}_0^{(\mathrm{g})}$ were performed with statistic having 2 and 472 df. F-tests of ${\mathcal{M}}_0^{(\mathrm{g})}$ were performed with statistic having 1 and 474 df.

Table S12: Tests of genetic effect in GxR models with various neuroimaging risk factors. Thickness measurements for six most important ROIs were considered as interaction variables in a GxR model for rs11633708 on AGBL1. Tests for null hypotheses of no genetic effect were performed over the PING sample (n=479). (a) Significance was evaluated under ${\mathcal{J}}_0^{(g)}$ for G×R models for the respective risk variable through F-tests using statistics having 2 and 472 df. Significance in the main effect model was evaluated under ${\mathcal{M}}_0^{(g)}$ using a F-test with statistic having 1 and 474 df.

Figure S1: Assessing European genetic ancestry (EGA). There were 623 participants in the PING study 8 through 21 years of age and for whom MRI, genetic, and cognitive exam data was available. In this pool of participants, no pair of subjects had identity-by-descent greater than 0.20. Each subject had available scores on first two principal components of genotype data (PCA performed over 1036 PING participants for whom genotype was available). (a) Plot of first two PCs with blue (circle) and red (triangle) marks corresponding to self-reported whites and remainder of subjects within pool of N=623 subjects. (b) Three clusters in bivariate space of first two PCs were identified with K-means algorithm. (c) K-means cluster corresponding to self-reported whites was extended to include all subjects with PC1 < 0.04 and PC2 > 0.05, which percentiles 1 and 99 respectively of PC1 and PC2 for subjects with self-reported white ancestry. A total of 479 subjects in this group were designated as having EGA through thresholds on principal components of genotype.

Figure S2: Empirical distributions of composite cognitive scores by diagnosis status for a learning problem. (a) Learning performance is the average of PSMT, List Sorting, Vocabulary, and Reading exams. (b) Executive function scores are an average of PSPAC, Attention, Flanker, and DCCS exams. Prior to taking average, covariates for age, sex, household income, parental education, and first two PCs of genotype were removed through multivariate regression. Both learning performance and executive function exams are uncorrelated with each of those covariates. The blue lines represent subjects without a LP diagnosis (n=442) and red lines subjects with a LP diagnosis (n=37). The Kolmogorov-Smirnov tests compares empirical distributions of respective scores between the two groups in the PING sample (n=479).

Figure S3: Sensitivity analysis for results’ dependence on sample. G×R and main effect models of learning performance scores for rs11633708 were fit to 100 random subsamples of size 407 (85%) of the PING sample (n=479) considered here. The N=100 red dots represent information gain under the two models for each subsample. For comparison, the blue dot represents the information gains for the models fit over the PING sample (n=479). The SNP rs11633708 on AGBL1 (chromosome 15) was the most significant in a GWAS of learning performance scores over the PING sample (n=479). Information gain from either the G×R or main effect models are their respective adjusted R² less that of the adjusted R² in the base model.