Skip to main content
PMC home page
Nature Communications logoLink to Nature Communications
. 2016 Dec 9;7:13552. doi: 10.1038/ncomms13552

Raman signatures of inversion symmetry breaking and structural phase transition in type-II Weyl semimetal MoTe2

Kenan Zhang 1, Changhua Bao 1, Qiangqiang Gu 2, Xiao Ren 2, Haoxiong Zhang 1, Ke Deng 1, Yang Wu 1,3,a, Yuan Li 2,4, Ji Feng 2,4, Shuyun Zhou 1,4,b
PMCID: PMC5155143  PMID: 27934874

Abstract

Transition metal dichalcogenide MoTe2 is an important candidate for realizing the newly predicted type-II Weyl fermions, for which the breaking of the inversion symmetry is a prerequisite. Here we present direct spectroscopic evidence for the inversion symmetry breaking in the low-temperature phase of MoTe2 by systematic Raman experiments and first-principles calculations. We identify five lattice vibrational modes that are Raman-active only in the low-temperature noncentrosymmetric structure. A hysteresis is also observed in the peak intensity of inversion symmetry-activated Raman modes, confirming a temperature-induced structural phase transition with a concomitant change in the inversion symmetry. Our results provide definitive evidence for the low-temperature noncentrosymmetric Td phase from vibrational spectroscopy, and suggest MoTe2 as an ideal candidate for investigating the temperature-induced topological phase transition.

To experimentally confirm the predicted type-II Weyl fermions in transition metal dichalcogenide, the evidence of inversion symmetry breaking is required. Here, Zhang et al. report Raman spectroscopic evidence for the inversion symmetry breaking in MoTe2.

Layered transition metal dichalcogenides (TMDs) have attracted extensive research interests because of their intriguing physical properties for both fundamental research and potential applications in electronics, optoelectronics, spintronics and valleytronics1,2. So far, most of the research has been focused on semiconducting TMDs with hexagonal or trigonal (2H or 1T) structures, which show strong quantum confinement effects in atomically thin films. In recent years, TMDs with monoclinic 1T′ and orthorhombic Td phase have been proposed to be important host materials for realizing novel topological quantum phenomena, for example, quantum spin Hall effect3,4 and Weyl fermions5. Weyl fermions were originally introduced in high-energy physics by Weyl6, and their condensed matter physics counterparts have not been realized until recently in Weyl semimetals in the TaAs family7,8,9. Weyl fermions can be realized by breaking either the time-reversal symmetry or inversion symmetry of a three-dimensional Dirac fermion such that a pair of degenerate Dirac points separate into two bulk Weyl points with opposite chiralities, which are connected by topological Fermi arcs when projected on the surface. Recently, it has been predicted that a new type of Weyl fermions can be realized in TMDs. Different from type-I Weyl fermions, which have point-like Fermi surface and obey Lorentz invariance, the newly predicted type-II Weyl fermions emerge at the topological protected touching points of an electron and a hole pocket with strongly tilted Weyl cones5. Such type-II Weyl fermions break Lorentz invariance and therefore do not have counterparts in high-energy physics.

Type-II Weyl fermions have been first predicted in the orthorhombic (Td) phase of WTe2 with space group Pmn21 (ref. 5). However, it is challenging to observe the extremely small Fermi arcs in WTe2 because of the small separation of the Weyl points (0.7% of the Brillouin zone). Weyl fermions have also been predicted in the low-temperature phase of MoTe2 with much larger Fermi arcs10,11, and signatures of the Fermi arcs have been suggested in a combined angle-resolved photoemission spectroscopy (ARPES) and scanning tunnelling spectroscopy study12 and other ARPES studies13,14,15,16,17. The existence of Weyl fermions has been relied on the assumption that the low-temperature phase of MoTe2 is isostructural to the noncentrosymmetric Td phase of WTe2 (refs 10, 11). The high-temperature monoclinic 1T′ phase with an inclined staking angle of ∼93.9° has a centrosymmetric P21/m space group. Although a temperature-induced structural transition with a change in the stacking angle from ∼93.9° to 90° has been reported both crystallographically18,19 and computationally20, there are two possible space groups can be assigned to the low-temperature orthorhombic phase—noncentrosymmetric Pmn21 and centrosymmetric Pnmm18. Previous X-ray diffraction study was limited to resolve the subtle differences between these two space groups to provide conclusive evidence on the inversion symmetry18. Recent ARPES studies have detected Fermi arcs at the low-temperature phase12; however, the absence of Fermi arcs at high-temperature 1T′ phase is difficult to be observed because of the thermal broadening. Since the noncentrosymmetry is a prerequisite for realizing Weyl fermions for non-magnetic materials, it is critical to reveal the inversion symmetry breaking from Raman spectroscopic measurements, which are directly sensitive to the crystal symmetry.

Results

Polarized Raman spectra

In this paper, we provide direct experimental evidence for the inversion symmetry-breaking in the low-temperature phase of MoTe2 and study its evolution across the temperature-induced structural phase transition using Raman vibrational spectroscopy. Our Raman measurements reveal the emergence of five Raman- and infrared-active modes in the low-temperature phase, and they are in good agreement with first-principles calculations and symmetry analysis of the Td phase. These peaks are, however, absent in the high-temperature centrosymmetric 1T′ phase, suggesting that they are Raman signatures for the breaking of the inversion symmetry. A clear hysteresis is observed in the peak intensity of two A1 modes—the shear mode at ≈13 cm−1 and the out-of-plane vibration mode at ≈130 cm−1. Our results provide clear evidence for the lack of inversion symmetry in the low-temperature Td phase from a lattice dynamics point of view, and indicate that MoTe2 can be a good candidate for studying the temperature-induced topological phase transition.

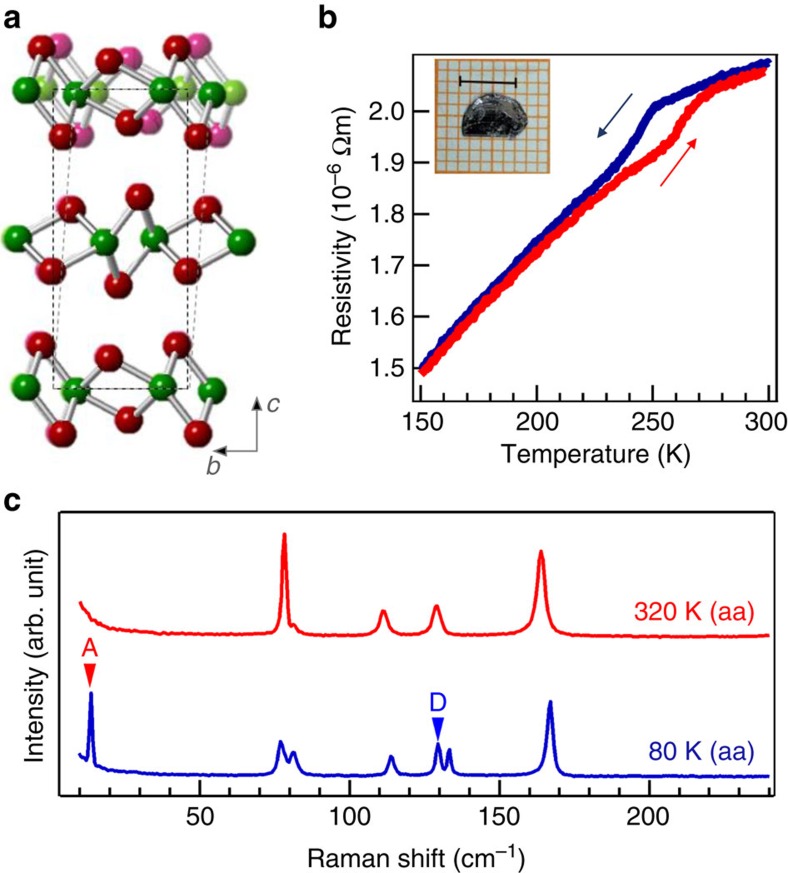
Figure 1a shows a comparison of the low-temperature (solid) and high-temperature (shadow) phases with corresponding space groups of Pmn21 and P21/m, respectively. They share almost the same in-plane crystal structure with zigzag Mo metal chains and distorted Te octahedra. The structural phase transition is revealed by an anomaly in the temperature-dependent resistivity21, which occurs at ≈260 K upon warming and ≈250 K upon cooling (Fig. 1b). Figure 1c shows the Raman spectra at 320 and 80 K on cleaved bulk single crystals. The polarizations for incident and scattered photons are denoted by two letters representing the crystal axes. For example, aa shows that both the incident and scattered photons are polarized along the a axis direction. Here we used the crystal axes of the Td phase to denote the polarization directions and all single-crystal samples were oriented using Laue diffraction patterns (see Supplementary Fig. 1 and Supplementary Note 1) before performing Raman characterizations. The comparison of Raman spectra reveals two new peaks labelled by A and D only in the low-temperature Td phase, suggesting that these Raman peaks may signal the structural phase transition.

Figure 1. Temperature-induced phase transition in MoTe2.

Figure 1

Open in a new tab

(a) Crystal structures of 1T′ (shadow) and Td (solid) phases. (b) Resistivity measurement shows a temperature-induced phase transition. The inset shows a photograph of the high-quality single crystal; scale bar, 5 mm. (c) Raman spectra at 320 and 80 K. The letters inside the parenthesis indicate the polarization directions for incident and scattering lights.

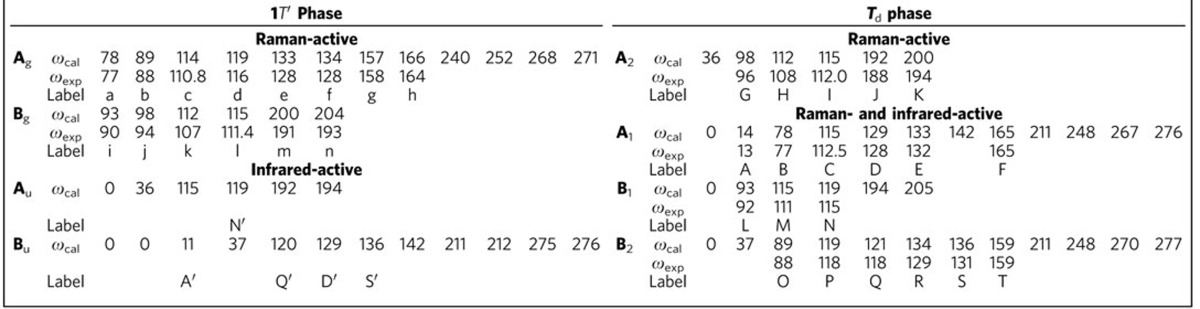
To understand the Raman modes, we first perform group theory analysis. Both the 1T′ and Td phases have 12 atoms in one unit cell and, correspondingly, there are a total of 36 phonon modes. The vibrational modes in the 1T′ phase decompose into 36 irreducible representations: [12Ag+6Bg]+[5Au+10Bu]+[Au+2Bu], where the first, second and third groups of irreducible representations correspond to the Raman-active, infrared-active and the acoustic modes, respectively. Since the infrared-active and Raman-active modes are exclusive of each other in centrosymmetric structures, the infrared-active modes Au and Bu cannot be observed in Raman measurements. In the Td phase, the vibration modes decompose into 36 irreducible representations: [11A1+6A2+5B1+11B2]+[11A1+5B1+11B2]+[A1+B1+B2], where A1, B1 and B2 modes are both infrared- and Raman-active, while A2 modes are only Raman-active.

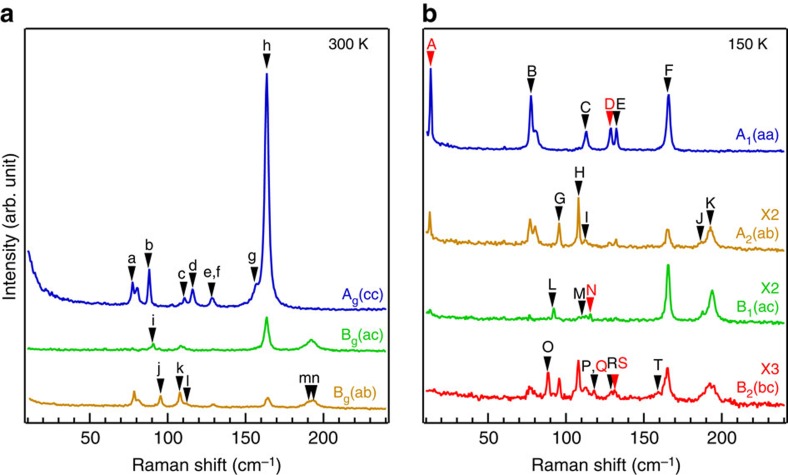
Figure 2 shows an overview of the polarized Raman spectra measured at 300 and 150 K. Raman selection rules for the 1T′ phase (see Supplementary Table 1) and for the Td phase (see Supplementary Table 2) indicate that the Ag modes in the 1T′ phase can be observed in the aa, bb, cc and bc configurations, whereas the Bg modes can be observed in the ac and ab configurations (see Supplementary Note 2). To obtain all possible phonon modes at low wave number in the 1T′ phase, we performed Raman measurements in the cc, ac and ab configurations at 300 K. The azimuthal dependence of the Raman peak intensities for Ag and Bg modes (see Supplementary Fig. 2 and Supplementary Note 3) further confirm the good alignment22,23. Eight sharp peaks of pure Ag modes are detected in the cc configuration and all the six Bg modes are found in the ac and ab configurations. The sharp peaks observed are because of improved sample quality and more peaks can be resolved clearly. In the Td phase, the A1 modes can be observed in the aa, bb and cc configurations, whereas the A2, B1 and B2 modes can only be observed in the ab, ac and bc configurations, respectively. The signal leakage of A1 in other polarization configurations is likely due to the imperfect cleavage of ac and bc surfaces from plate-like samples; however, this does not change the conclusion. In the low-temperature phase, we observe six pure A1 modes in the aa configuration, five A2 modes in the ab configuration, three B1 modes in the ac configuration and six B2 modes in the bc configuration.

Figure 2. Polarized Raman spectra measured in the high- and low-temperature phases.

Figure 2

Open in a new tab

(a,b) Polarized Raman spectra measured at 300 K (a) and 150 K (b). The identified Raman peaks are labelled by lowercase (high-temperature phase) and capital (low-temperature phase) letters. The red labels A, D, N, Q and S mark the Raman modes that are directly sensitive to the inversion symmetry breaking. The small peak at 83 cm−1 is from the instrument and not intrinsic to the sample.

Signature of phase transition and symmetry breaking

The comparison of Raman modes between experimental results and theoretical calculations in Table 1 shows a good agreement. Here we focus on Raman-active modes that are sensitive to the breaking of the inversion symmetry across the phase transition. Since the crystal structure changes only slightly across the phase transition, we can track each phonon mode by comparing their vibrational pattern in these two phases. Due to the breaking of inversion centre, some Raman in-active modes that belong to the Au or Bu representations in the 1T′ phase evolve to A1, B1 or B2 representations that are both infrared- and Raman-active in the Td phase. Thus, the presence of these Raman modes reflects the transition into the noncentrosymmetric phase. Similarly, a nonlinear optical method was employed to reveal the lack of inversion symmetry in few-layer MoS2 and h-BN24,25.

Table 1. Comparison of the calculated and experimental Raman modes in the 1T′ and T d phases in units of cm−1.

graphic file with name ncomms13552-t1.jpg

Open in a new tab

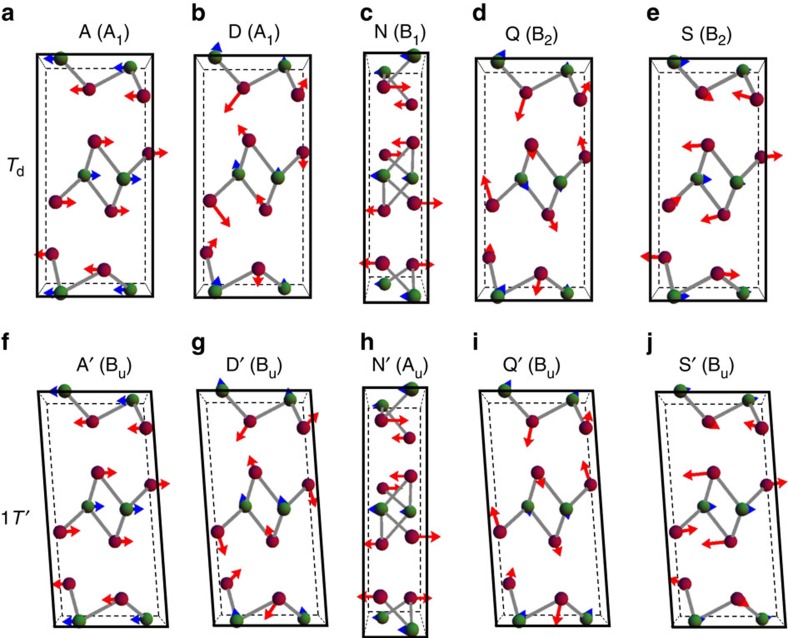
Figure 3 compiles the calculated vibrational patterns for such phonons that are directly sensitive to the inversion symmetry breaking, where the arrows scale the atomic displacements. The upper panels show the vibration modes labelled by A, D, N, Q and S, which are indicated by red arrows in Fig. 2b, where the irreducible representations in the Td phase are given in parenthesis. The lower panels show the corresponding vibration modes labelled by A′, D′, N′, Q′ and S′ that belong to the Au and Bu irreducible representations in the 1T′ phase. These phonons have almost identical vibrational patterns as A, D, N, Q and S, respectively, but no Raman activity due to the centrosymmetry. The A and A′ denote interlayer shear modes along the b axis and the A peak is also observed in a previous report26. Compared with previous work, here we present a systematic Raman characterization of the low-temperature phase by distinguishing all modes that reflect the breaking of the centrosymmetry. The strongest Raman signals that distinguished these two phases are the interlayer shear mode A at ≈13 cm−1 and another out-of-plane vibration mode D at ≈130 cm−1. Similar vibrational modes have been reported in many 2D materials, such as multilayer graphene27,28,29 and TMDs, for example, MoS2 and WSe2 (refs 30, 31, 32, 33). The low-frequancy interlayer shear modes are sensitive to the stacking sequence, layer number and symmetry, and can be used as a measure of interlayer coupling. For in-plane shear modes, all atoms in the same layer all vibrate along the same direction, while atoms in two adjacent layers vibrate toward opposite directions. If there is an inversion centre that lies in the layer, such shear modes have odd parity with respect to the inversion symmetry and therefore are Raman-inactive. This is the reason why A mode is invisible in 1T′ MoTe2, opposite to high symmetric 2H-MoS2, MoSe2, WSe2 and 2H-MoTe2. However, when the crystal structure does not hold inversion symmetry, these modes are both Raman- and infrared-active and visible in Raman spectroscopy, providing direct evidence on the breaking of centrosymmetry in the orthorhombic Td structure.

Figure 3. Calculated vibrational patterns for Raman modes that are directly sensitive to the inversion symmetry breaking.

Figure 3

Open in a new tab

Calculated vibrational patterns in the Td phase (a–e) and corresponding Bu and Au modes in the 1T′ phases (f–j). A, D, Q and S modes vibrate in the bc plane and N mode in the ac plane.

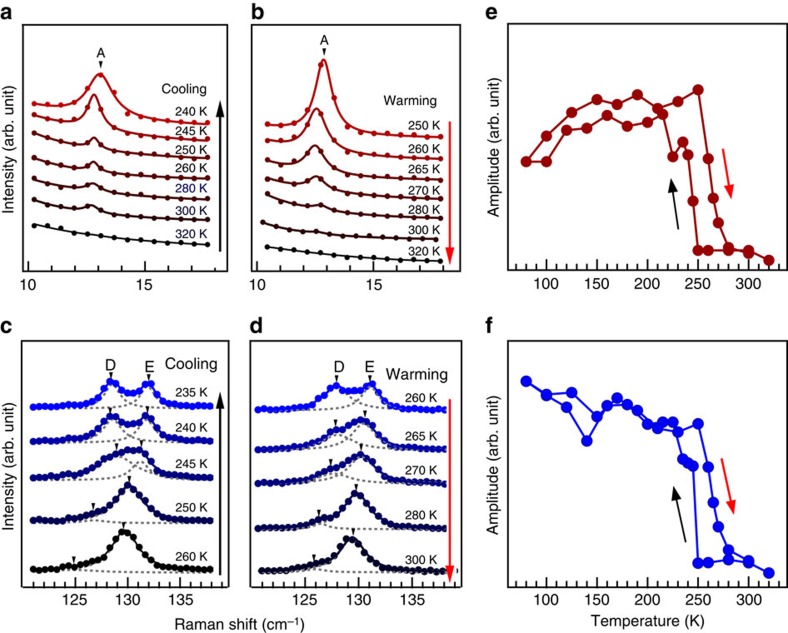
We further track the evolution of peaks A and D that signal the inversion symmetry breaking across the phase transition. The evolution of the A peak at 12.5 cm−1 and D peak at 128.3 cm−1 are displayed in Fig. 4a–d. Upon warming, the intensity of the A and D peaks decreases with the sharpest decrease at ≈260 K and eventually disappears above 300 K. Upon cooling, the A and D peaks appear at a lower temperature, and their intensities sharply increase at ≈250 K, and reach the maximum below 200 K. The intensity of the A and D peaks as a function of temperature is shown in Fig. 4e,f. The temperature-dependent peak position and full-width at half-maximum are shown in Supplementary Fig. 3 and Supplementary Note 4. A discontinuity in the temperature-dependent peak position can be regarded another signature of the structural phase transition of MoTe2. The thermal hysteresis effect in the peak intensity is consistent with our transport measurement, confirming that these peaks directly indicate the structural phase transition from high-temperature 1T′ to low-temperature Td phase.

Figure 4. Temperature dependence of the Raman spectra for peaks A and D in the aa configuration.

Figure 4

Open in a new tab

(a–d) Selected Raman spectra across the phase transition for peaks A (a,b) and D (c,d) upon cooling (a,c) and warming (b,d). (e,f) Temperature dependence of the Raman intensity for peaks A and D.

Discussion

To summarize, by performing a systematic Raman study using polarization selection rules combined with theoretical calculation, we reveal the Raman signatures of structural phase transition across the 1T′ to Td phase transition and provided unambiguous evidence on the absence of inversion symmetry of the Td phase. Our work demonstrates that the Td phase of MoTe2 is a strong candidate for both type-II Weyl semimetal and investigating the temperature-induced topological phase transition.

Methods

Sample growth and Raman measurement

Single crystals of MoTe2 were grown by chemical vapour transport method as reported previously12. Raman scattering experiments were performed in a confocal back-scattering geometry on freshly cleaved single-crystal surfaces along the ab, ac and bc planes. Parallel and cross-polarizations between the incident and scattered lights were used. Raman spectra were measured using a Horiba Jobin Yvon LabRAM HR Evolution spectrometer with the λ=514 nm excitation source from an Ar laser and a 1,800 gr mm−1 grating. A liquid-nitrogen-cooled charge-coupled device detector and BragGrate notch filters allow for measurements at low wave numbers. The temperature of the sample was controlled by a liquid-nitrogen flow cryostat and a heater in a chamber with a vacuum better than 5 × 10−7 Torr.

First-principles calculations

To determine the phonon frequencies, we performed first-principles calculations of the phonon modes at the zone centre using the Vienna ab initio simulation package34 with the local density approximation35 and the projector-augmented wave potentials36. We set a 4 × 8 × 2 Monkhorst-Pack k-point mesh and 400 eV cutoff for plane waves. The coordinates and the cell shape in ref. 19 have been fully relaxed until the forces acting on the atoms are all smaller than 10−4 eV Å−1. We use the phonopy package37 that implements the small displacement method to obtain the phonon frequencies and vibration modes at the Γ point.

Data availability

The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.

Additional information

How to cite this article: Zhang, K. et al. Raman signatures of inversion symmetry breaking and structural phase transition in type-II Weyl semimetal MoTe2. Nat. Commun. 7, 13552 doi: 10.1038/ncomms13552 (2016).

Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Material

Supplementary Information

Supplementary Figures 1-3, Supplementary Tables 1-2, Supplementary Notes 1-4 and Supplementary Reference

ncomms13552-s1.pdf (426.7KB, pdf)
Peer Review File
ncomms13552-s2.pdf (562.5KB, pdf)

Acknowledgments

This work is supported by the National Natural Science Foundation of China (grant Nos 11274191 and 11334006), Ministry of Science and Technology of China (Nos 2015CB921001 and 2012CB932301).

Footnotes

Author contributions S.Z. and Y.W. conceived the research project. K.Z., H.Z. and K.D. grew and characterized the samples under supervision of Y.W., K.Z., C.B., X.R. and Y.L. performed the Raman measurements and analysed the data. Q.G. and J.F. performed the first-principle calculations. K.Z., C.B., Q.G., Y.W. and S.Z. wrote the manuscript, and all authors commented on the manuscript.

References

  1. Wang Q. H., Kalantar-Zadeh K., Kis A., Coleman J. N. & Strano M. S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotechnol. 7, 699–712 (2012). [DOI] [PubMed] [Google Scholar]
  2. Chhowalla M. et al. The chemistry of two-dimensional layered transition metal dichalcogenide nanosheets. Nat. Chem. 5, 263–275 (2013). [DOI] [PubMed] [Google Scholar]
  3. Qian X., Liu J., Fu L. & Li J. Quantum spin hall effect in two-dimensional transition metal dichalcogenides. Science 346, 1344–1347 (2014). [DOI] [PubMed] [Google Scholar]
  4. Zheng F. et al. On the quantum spin hall gap of monolayer 1T′-WTe2. Adv. Mater. 28, 4845–4851 (2016). [DOI] [PubMed] [Google Scholar]
  5. Soluyanov A. A. et al. Type-II weyl semimetals. Nature 527, 495–498 (2015). [DOI] [PubMed] [Google Scholar]
  6. Weyl H. Gravitation and the electron. PNAS 15, 323–334 (1929). [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Xu S. Y. et al. Topological matter. discovery of a weyl fermion semimetal and topological fermi arcs. Science 349, 613–617 (2015). [DOI] [PubMed] [Google Scholar]
  8. Lv B. Q. et al. Observation of weyl nodes in TaAs. Nat. Phys. 11, 724–727 (2015). [Google Scholar]
  9. Lv B. Q. et al. Experimental discovery of weyl semimetal TaAs. Phys. Rev. X 5, 031013 (2015). [Google Scholar]
  10. Sun Y., Wu S.-C., Ali M. N., Felser C. & Yan B. Prediction of weyl semimetal in orthorhombic MoTe2. Phys. Rev. B 92, 161107 (2015). [Google Scholar]
  11. Wang Z. et al. Mote2: a type-II weyl topological metal. Phys. Rev. Lett. 117, 056805 (2016). [DOI] [PubMed] [Google Scholar]
  12. Deng K. et al. Experimental observation of topological Fermi arcs in type-II Weyl semimetal MoTe2. Nat. Phys http://dx.doi.org/10.1038/nphys3871 (2016). [Google Scholar]
  13. Huang L. et al. Spectroscopic evidence for a type II weyl semimetallic state in MoTe2. Nat. Mater. 15, 1155–1160 (2016). [DOI] [PubMed] [Google Scholar]
  14. Jiang J. et al. Observation of the Type-II Weyl Semimetal Phase in MoTe2. Preprint at http://arxiv.org/abs/1604.00139 (2016).
  15. Xu N. et al. Discovery of Weyl semimetal state violating Lorentz invariance in MoTe2. Preprint at http://arxiv.org/abs/1604.02116 (2016).
  16. Liang A. et al. Electronic evidence for type II Weyl semimetal state in MoTe2. Preprint at http://arxiv.org/abs/1604.01706 (2016).
  17. Tamai A. et al. Fermi arcs and their topological character in the candidate type-II Weyl semimetal MoTe2. Preprint at http://arxiv.org/abs/1604.08228 (2016).
  18. Clarke R., Marseglia E. & Hughes H. P. A low-temperature structural phase transition in β-MoTe2. Phil. Mag. B 38, 121–126 (1978). [Google Scholar]
  19. Dawson W. G. & Bullett D. W. Electronic structure and crystallography of MoTe2 and WTe2. J. Phys. C Solid State Phys. 20, 6159–6174 (1987). [Google Scholar]
  20. Chang T.-R. et al. Prediction of an arc-tunable Weyl Fermion metallic state in MoxW1−xTe2. Nat. Commun. 7, 10639 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Hughes H. P. & Friend R. H. Electrical resistivity anomaly in β-MoTe2 (metallic behaviour). J. Phys. C Solid State Phys. 11, L103–L105 (1978). [Google Scholar]
  22. Ribeiro H. B. et al. Unusual angular dependence of the raman response in black phosphorus. ACS Nano 9, 4270–4276 (2015). [DOI] [PubMed] [Google Scholar]
  23. He R. et al. Coupling and stacking order of ReS2 atomic layers revealed by ultralow-frequency raman spectroscopy. Nano Lett. 16, 1404–1409 (2016). [DOI] [PubMed] [Google Scholar]
  24. Kumar N. et al. Second harmonic microscopy of monolayer MoS2. Phys. Rev. B 87, 161403 (2013). [Google Scholar]
  25. Li Y. et al. Probing symmetry properties of few-layer MoS2 and h-BN by optical second-harmonic generation. Nano Lett. 13, 3329–3333 (2013). [DOI] [PubMed] [Google Scholar]
  26. Chen S.-Y., Goldstein T., Venkataraman D., Ramasubramaniam A. & Yan J. Activation of new Raman modes by inversion symmetry breaking in type II Weyl semimetal candidate T′-MoTe2. Nano Lett. 16, 5852–5860 (2016). [DOI] [PubMed] [Google Scholar]
  27. Tan P. et al. The shear mode of multilayer graphene. Nat. Mater. 11, 294 (2012). [DOI] [PubMed] [Google Scholar]
  28. Lui C. H. et al. Observation of layer-breathing mode vibrations in few-layer graphene through combination raman scattering. Nano Lett. 12, 5539–5544 (2012). [DOI] [PubMed] [Google Scholar]
  29. Lui C. H. & Heinz T. F. Measurement of layer breathing mode vibrations in few-layer graphene. Phys. Rev. B 87, 1504–1509 (2013). [Google Scholar]
  30. Zhou X. et al. Phonon and raman scattering of two-dimensional transition metal dichalcogenides from monolayer, multilayer to bulk material. Chem. Soc. Rev. 44, 2757 (2015). [DOI] [PubMed] [Google Scholar]
  31. Zhao Y. et al. Interlayer breathing and shear modes in few-trilayer MoS2 and WSe2. Nano Lett. 13, 1007–1015 (2013). [DOI] [PubMed] [Google Scholar]
  32. Zhao W. et al. Lattice dynamics in mono- and few-layer sheets of WS2 and WSe2. Nanoscale 5, 9677–9683 (2013). [DOI] [PubMed] [Google Scholar]
  33. Zhang X. et al. Raman spectroscopy of shear and layer breathing modes in multilayer MoS2. Phys. Rev. B 87, 1504–1509 (2013). [Google Scholar]
  34. Kresse G. & Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996). [DOI] [PubMed] [Google Scholar]
  35. Perdew J. P. & Zunger A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 23, 5048–5079 (1981). [Google Scholar]
  36. Kresse G. & Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999). [Google Scholar]
  37. Togo A. & Tanaka I. First principles phonon calculations in materials science. Script. Mater. 108, 1–5 (2015). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Figures 1-3, Supplementary Tables 1-2, Supplementary Notes 1-4 and Supplementary Reference

ncomms13552-s1.pdf (426.7KB, pdf)
Peer Review File
ncomms13552-s2.pdf (562.5KB, pdf)

Data Availability Statement

The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.

Articles from Nature Communications are provided here courtesy of Nature Publishing Group

RESOURCES