Abstract
Interfacial spin-orbit torques (SOTs) enable the manipulation of the magnetization through in-plane charge currents, which has drawn increasing attention for spintronic applications. The search for material systems providing efficient SOTs, has been focused on polycrystalline ferromagnetic metal/non-magnetic metal bilayers. In these systems, currents flowing in the non-magnetic layer generate—due to strong spin–orbit interaction—spin currents via the spin Hall effect and induce a torque at the interface to the ferromagnet. Here we report the observation of robust SOT occuring at a single crystalline Fe/GaAs (001) interface at room temperature. We find that the magnitude of the interfacial SOT, caused by the reduced symmetry at the interface, is comparably strong as in ferromagnetic metal/non-magnetic metal systems. The large spin-orbit fields at the interface also enable spin-to-charge current conversion at the interface, known as spin-galvanic effect. The results suggest that single crystalline Fe/GaAs interfaces may enable efficient electrical magnetization manipulation.
Interfacial spin-orbit torque allows electrical manipulation of magnetization, but this has been shown mostly in polycrystalline metal bilayers. Here the authors show robust spin-orbit torque in single crystalline Fe/GaAs interface at room temperature, observing conversion between spin and charge current.
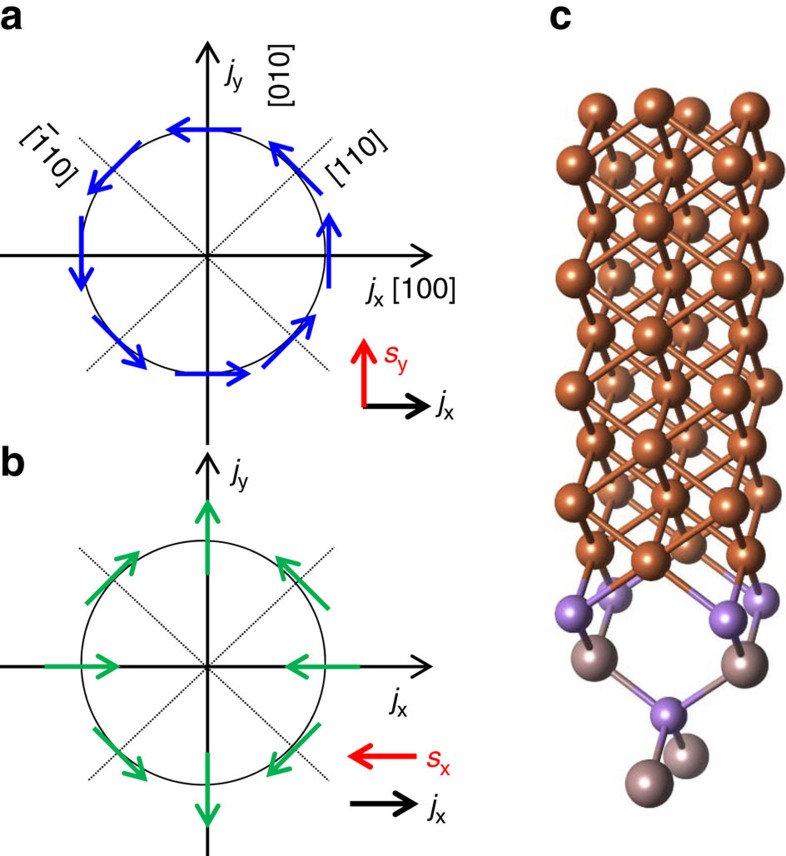
In solids with space-inversion asymmetry intrinsic spin-orbit fields (SOFs) emerge. These SOFs can arise from Dresselhaus spin–orbit interaction (SOI) which originates from bulk inversion asymmetry1, and/or from Bychkov-Rashba SOI which originates from structure inversion asymmetry2. In the limit of small wave vector k near the Γ point, both SOIs can be expressed by k-linear terms in the Hamilton operator; that is, HD=β(σxkx−σyky) in case of Dresselhaus SOI and HR=α(σxky−σykx) in case of Bychkov-Rashba SOI. Here σx,y are Pauli spin matrices and α and β characterize the strength of Rashba and Dresselhaus spin-orbit coupling. Figure 1a,b show the SOFs due to Rashba and Dresselhaus SOI. The most striking property of these SOIs is that spin and carrier momentum are coupled, meaning that a charge current is accompanied by a non-equilibrium spin accumulation3,4,5. The magnitude and orientation of this spin accumulation is controlled by the charge current. It is convenient to quantify this spin accumulation by an effective SOF (eSOF). On the other hand, the inverse process is also applicable: a non-equilibrium spin accumulation drives a charge current6. Making use of SOI is thus a promising pathway for future spintronic applications7. In fact, it has been demonstrated that SOI can be used to manipulate the magnetization direction by a local current8,9,10,11. Thus, establishing a new material system with strong SOI at room temperature is of utmost importance for the realization of practical spin-orbit torque (SOT) devices. Motivated by early work on strained low-temperature (Ga,Mn)As10,11,12,13, it has been shown recently that there is sizeable Dresselhaus dominated SOT in the Heusler alloy NiMnSb14. Furthermore, electric switching in the antiferromagnet CuMnAs by an internal SOT has been demonstrated at room temperature15.
Figure 1. Spin-orbit coupling at the Fe/GaAs interface.
Schematic of Rashba (a) Dresselhaus (b) spin-orbit fields (SOFs) for different crystallographic orientations. Red arrows in a,b denote the direction of spin accumulation induced by a current flow jx. (c) Atomic structure of the Fe/GaAs (001) spin–orbit interface. Zincblende GaAs exhibits bulk inversion asymmetry (BIA) with D2d symmetry and adding a single crystalline Fe on top of GaAs further lowers the D2d symmetry to C2v. The C2v symmetry results in the Rashba and Dresselhaus SOFs at the Fe/GaAs (001) interface.
It is well established that single crystalline Fe thin films grow epitaxially on GaAs (001) due to the small lattice mismatch between twice the lattice constant of Fe (2.87 Å) and GaAs (5.65 Å). The Fe/GaAs interface has C2v symmetry. For this particular interface it has been shown that near the Fermi energy and in the vicinity of the Γ-point the SOFs arising from C2v symmetry can be expressed as a combination of Dresselhaus- and Bychkov-Rashba-like SOFs16, causing, for example, an anisotropic tunneling magnetoresistance17 and a crystalline anisotropic magnetoresistance (AMR) with two-fold symmetry, when the Fe layer is only a few monolayers thick18.
Here we demonstrate that a robust SOT exists at the Fe/GaAs interface at room temperature. We find that the dominating eSOF contribution stems from Bychkov-Rashba-like SOI, and importantly, that the magnitude of the eSOF is comparable to the ones in ferromagnetic metal/non-magnetic metal systems19,20,21,22. Moreover, we show that the strong SOI at the interface converts a pure spin current, generated by spin pumping23,24,25, into a charge current. This is due to the spin-galvanic effect (SGE)6 also called inverse Rashba-Edelstein effect26, which is similar to the inverse spin Hall effect (ISHE) in a three dimensional material7. Apart from semiconductors it has only been observed at an Ag/Bi interface26 and in the three dimensional Rashba-metal GeTe27. The simple structure of Fe/GaAs used here excludes any bulk contribution via ISHE since the conducting non-magnetic layer is absent. Our results indicate that a single crystalline Fe/GaAs interface is sufficient for electrical magnetization manipulation.
Results
Quantifying eSOFs by spin-orbit ferromagnetic resonance
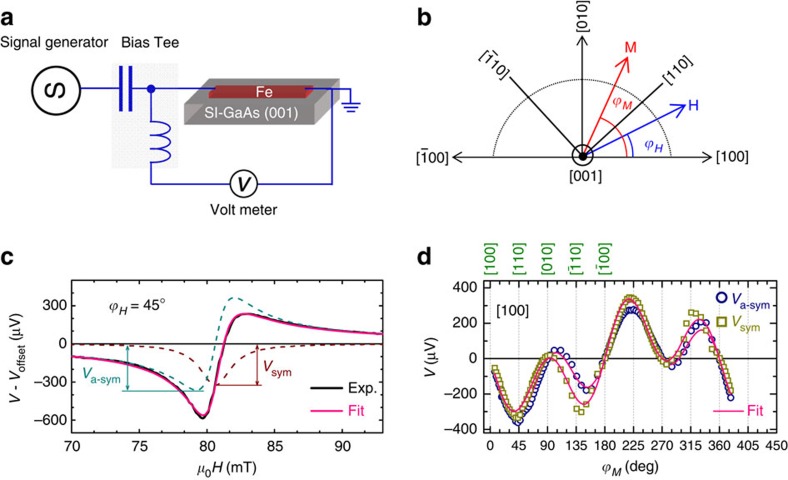
We determine the strength of the interfacial SOFs by using spin-orbit ferromagnetic resonance (SO-FMR) developed previously to quantify SOFs in the ferromagnetic semiconductor (Ga,Mn)As12,13. SO-FMR is similar to the spin-torque ferromagnetic resonance (FMR) technique which is used to quantify the spin Hall effect in ferromagnetic metal/non-magnetic metal bilayers9. The mechanism is illustrated in Fig. 2a. An alternating in-plane current j(t) flowing in the Fe stripe generates, due to SOI, a time dependent non-equilibrium spin accumulation at the Fe/GaAs interface. This spin accumulation exerts a torque on the magnetization of the Fe film and can be viewed as a time varying interfacial magnetic field hSO, which excites the magnetization dynamics. The precessing magnetization causes a resistance variation R(t) via the AMR of Fe. Due to mixing of the alternating current and the oscillating resistance, a dc voltage V results28. Thus, by measuring this dc voltage for different crystallographic directions we can quantitatively determine the effective spin-orbit fields at the Fe/GaAs interface.
Figure 2. Spin-orbit ferromagnetic resonance measurements.
(a) Depiction of sample structure and experimental set-up. A microwave current passes through the Bias Tee and to the sample to drive the magnetization dynamics in the Fe film. A rectified dc voltage is detected across the Fe stripe. (b) Definition of magnetic-field angle ϕH and magnetization angle ϕM. (c) Typical spectrum of the dc voltage V obtained at a magnetic-field angle of ϕH=45°, microwaves frequency of 12 GHz, and temperature of 300 K, where the offset voltage Voffset is subtracted. (d) Dependence of Va-sym and Vsym on the magnetization angle ϕM for a [100]-orientated device. The solid lines are fits to equation (1).
The sample used in our study is a 5-nm thick single crystalline Fe film grown by molecular-beam epitaxy (MBE; see Fig. 1c and Methods) on top of a 100 nm thick undoped GaAs buffer layer on a semi-insulating GaAs (001) substrate. Additionally, we grew a polycrystalline Fe reference film on an amorphous SiOx substrate. Devices of size, 6.4 × 100.0 μm, oriented along different crystallographic directions, are defined by employing electron-beam lithography and ion beam etching. Figure 2c shows a typical V trace (where an offset voltage Voffset, due to thermo-electric effect, has been subtracted) of a [100]-orientated stripe measured at room temperature. To fit the characteristic line shape, we introduce a symmetric (Lsym=ΔH2/[4(H−HR)2+ΔH2]) and an anti-symmetric Lorentzian (La-sym=−4ΔH(H−HR)/[4(H−HR)2+ΔH2]), where HR is the magnetic field H at FMR, ΔH the line width (full width at half maximum: FWHM). V−Voffset is fitted by a combination of Lsym and La-sym, VsymLsym+Va-symLa-sym, with Vsym (Va-sym) the magnitude of the symmetric (anti-symmetric) component of the dc voltage. By fitting we obtain values for HR, ΔH, Vsym and Va-sym. These parameters have been extracted as a function of ϕH and for Fe stripes along different crystallographic directions (see Supplementary Figs 3 and 5). The ϕH-dependence of HR and ΔH can be well explained by conventional FMR analysis29,30, from which we obtain the Landé g factor (g=2.12), the effective demagnetization field (μ0HK=1,750 mT), the biaxial magnetic anisotropy field (μ0HB=40 mT), the uniaxial magnetic anisotropy field (μ0HU=48 mT), and the damping constant (α=0.0036) (see Supplementary Note 3).
For comparison, we also tried to measure dc voltages on polycrystalline Fe films deposited on thermally oxidized Si substrates; however, no characteristic dc voltages can be observed at FMR using the same excitation conditions as for single crystalline films of Fe/GaAs, indicating that the driving force for magnetization dynamics originates from the eSOFs at the interface of single crystalline Fe/GaAs and not from any current induced Oersted field (see Supplementary Note 1).
To quantify the magnitude of the eSOFs, it is necessary to understand the dependence of the dc voltage on ϕM. By taking a [100]-orientated stripe as an example, the anti-symmetric and symmetric components can be expressed as (for the derivation of other orientations see Supplementary Note 2 and 3)
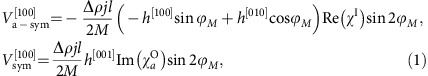 |
where h[100], h[010], h[001] are the eSOFs along the [100], [010] and [001] directions, Δρ is the magnitude of AMR, j the microwave current density, l the length of the device, M the magnetization of the Fe film, Im(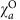 ) the imaginary part of the off-diagonal component of the magnetic susceptibility due to out-of-plane excitation (h[001]), and Re(χI) the real part of the diagonal component due to in-plane excitation (h[100] and h[010]). Since the dc voltage is induced by FMR, the magnitude of Im(
) the imaginary part of the off-diagonal component of the magnetic susceptibility due to out-of-plane excitation (h[001]), and Re(χI) the real part of the diagonal component due to in-plane excitation (h[100] and h[010]). Since the dc voltage is induced by FMR, the magnitude of Im(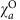 ) and Re(χI) can be calculated by solving the Landau–Lifshits–Gilbert equation31, which is anisotropic due to the in-plane magnetic anisotropy as well as the angular variation of the linewidth30 (see Supplementary Note 3).
) and Re(χI) can be calculated by solving the Landau–Lifshits–Gilbert equation31, which is anisotropic due to the in-plane magnetic anisotropy as well as the angular variation of the linewidth30 (see Supplementary Note 3).
In-plane effective spin-orbit fields
Figure 2d shows the dependence of Va-sym on the magnetization angle ϕM for the stripes oriented along the [100] direction. The results can be fitted by a superposition of sin2ϕM sinϕM and sin2ϕM cosϕM, indicating that the driving field contains both Dresselhaus and Bychkov-Rashba contributions (see equation (1)). The magnitude of μ0h[100] (Dresselhaus) and μ0h[010] (Bychkov-Rashba) is determined to be −0.15 and 0.28 mT by using μ0M=1.63 T, Δρ=7.0 × 10−10 Ωm, l=100.0 μm and j=1.91 × 1011 Am−2. Here M and Δρ have been determined by separate magnetization and dc transport measurements, and the microwave current j is calibrated by thermally shifting the resonance field (see Supplementary Note 5).
For an independent crosscheck, we also show in the Supplementary Note 7 that the Dresselhaus field can be alternatively verified by varying HR via a dc current.
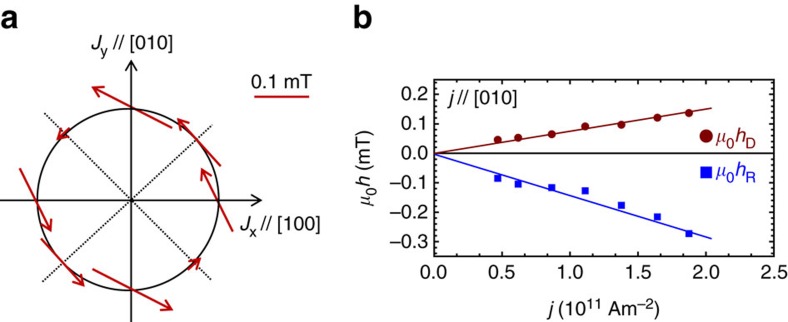
In Fig. 3a, we show direction and magnitude of the in-plane effective spin-orbit fields obtained for a current density of 1011 Am−2 in a polar plot for devices with different orientations. Figure 3a indicates that Bychkov-Rashba is the dominating contribution since the field vectors along [100] and [010] directions align mainly perpendicular to the current direction. For [110] and [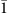 10] directions, the spin-orbit fields are perpendicular to the current as expected for both Rashba and Dresselhaus contribution (Fig. 1a,b). Although the current induced Oersted field may also cause a field contribution perpendicular to the current directions, this effect is expected to be small for two reasons: First, the magnitude of the SOF for the [
10] directions, the spin-orbit fields are perpendicular to the current as expected for both Rashba and Dresselhaus contribution (Fig. 1a,b). Although the current induced Oersted field may also cause a field contribution perpendicular to the current directions, this effect is expected to be small for two reasons: First, the magnitude of the SOF for the [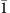 10] direction is ∼5 times smaller than that for the [110] direction for a similar current density (Fig. 3a and Supplementary Fig. 5b), which indicates that the effect is intrinsically related to SOI. Second, the non-detectable dc voltage in Fe/SiOx further excludes a sizeable influence of any Oersted field. The different magnitudes of the eSOFs along the [110] and [
10] direction is ∼5 times smaller than that for the [110] direction for a similar current density (Fig. 3a and Supplementary Fig. 5b), which indicates that the effect is intrinsically related to SOI. Second, the non-detectable dc voltage in Fe/SiOx further excludes a sizeable influence of any Oersted field. The different magnitudes of the eSOFs along the [110] and [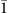 10] directions stem from constructive and destructive superposition of Dresselhaus and Bychkov-Rashba fields (see Fig. 1a,b). In Fig. 3b, we show that the amplitudes of μ0hR and μ0hD in the [010] stripe increase linearly with the current density, indicating that reduction of M and Δρ due to Joule heating is negligibly small in the device. From the slope of hR and hD, the ratio of α and β, (α/β )in-plane, is determined to be ∼2. We have repeated these measurements for two more sets of devices (eight devices); each set shows similar behaviour.
10] directions stem from constructive and destructive superposition of Dresselhaus and Bychkov-Rashba fields (see Fig. 1a,b). In Fig. 3b, we show that the amplitudes of μ0hR and μ0hD in the [010] stripe increase linearly with the current density, indicating that reduction of M and Δρ due to Joule heating is negligibly small in the device. From the slope of hR and hD, the ratio of α and β, (α/β )in-plane, is determined to be ∼2. We have repeated these measurements for two more sets of devices (eight devices); each set shows similar behaviour.
Figure 3. In-plane spin-orbit fields.
(a) Experimentally determined magnitude and direction of the in-plane spin-orbit fields, which are normalized by a unit current density of 1011 Am−2. (b) Current density dependence of the magnitudes of μ0hR and μ0hD obtained from a [010]-orientated device. From the slope of μ0hR and μ0hD, the ratio of α and β, (α/β)in-plane, is determined to ∼2.0.
Out-of-plane effective spin-orbit fields
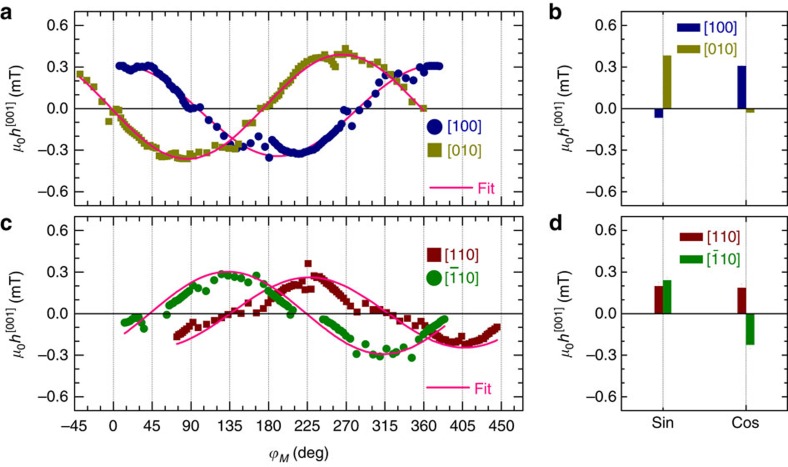
The presence of the component Vsym displayed in Fig. 2c implies a sizeable out-of-plane effective spin-orbit field (see equation (1)). Figure 2d shows the dependence of Vsym on ϕM for a current flowing along the [100] direction. The results cannot simply be fitted by sin2ϕM indicating that h[001] depends on ϕM. Figure 4a,c show the ϕM dependence of h[001] for four crystallographic orientations. Here one can see that h[001] strongly depends on ϕM and reaches a value as large as 0.35 mT for a current density of 1011 Am−2. We estimate that the magnitude of the SOT in our system is comparable to that observed in ferromagnetic metal/non-magnetic metal bi-layer systems19,20,21,22 (see Supplementary Note 9). Note that an additional contribution to the symmetric part of the dc voltage can in principle arise from spin pumping together with the spin galvanic effect. However, we calculate that this effect is two orders of magnitude smaller than the detected spin-orbit voltage.
Figure 4. Out-of-plane spin-orbit fields.
(a) Magnetization angle ϕM dependences of the out-of-plane spin-orbit field μ0h[001] for [100] and [010]-orientated devices; the solid lines are fits by equation (2), from which (α/β)out-of-plane is obtained (see Supplementary Note 8). The fitting coefficients of sinϕM and cosϕM are shown in (b). (c) ϕM dependences of μ0hz for [110] and [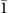 10] orientated devices. (d) Fitting coefficients of sinϕM and cosϕM. The error bar in b,d is the s.d. obtained from the fit. All the fields are normalized by a unit current density of 1011 Am−2.
10] orientated devices. (d) Fitting coefficients of sinϕM and cosϕM. The error bar in b,d is the s.d. obtained from the fit. All the fields are normalized by a unit current density of 1011 Am−2.
To gain insight into the microscopic origin of the interfacial out-of-plane spin-orbit field, we show in Supplementary Note 8 that, within a two-dimensional spin-orbit ferromagnet model32, h[001] is given by
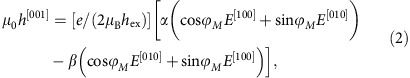 |
where E[100], E[010] is the electric field along the [100] and [010] directions, e the electronic charge, μβ the Bohr magneton, and hex the exchange field. First, we estimate from this equation that the expected magnitude of h[001] agrees well with the experiment (Supplementary Note 8). According to equation (2), the ϕM dependence of h[001] can be explained by a combination of sinϕM and cosϕM terms depending on the symmetry of the SOI. The fitting coefficients of the sinϕM and cosϕM terms are shown in Fig. 4b,d (Supplementary Note 8). For the [100] and [010] directions, the cosϕM and sinϕM terms dominate, respectively. This indicates again that the Bychkov-Rashba SOI is the dominating SOI at the Fe/GaAs interface13. Moreover, the fitting coefficients for [110] and [ 10] directions also agree well with the theoretical model of Bychkov-Rashba dominated SOI. From the fitting coefficients, the ratio of α and β, (α/β)out-of-plane, is determined. The value of (α/β)out-of-plane for each device is larger than that of (α/β)in-plane (see Supplementary Note 8). This is due to the different origins between in-plane and out-of-plane induced spin polarization. The in-plane spin polarization is created only at the Fermi level, while the out-of-plane spin polarization is due to the electrical polarization (intrinsic effect) of the whole bands32. Previous work on the ferromagnetic semiconductor (Ga,Mn)As13,33 explains an emerging h[001] by the Kubo formalism, taking into account the presence of Dresselhaus dominated SOI and p-d exchange coupling. However, for our system of Fe/GaAs, h[001] results from the broken symmetry at the interface and interfacial exchange coupling, a scenario which is distinctly different from the (Ga,Mn)As case.
10] directions also agree well with the theoretical model of Bychkov-Rashba dominated SOI. From the fitting coefficients, the ratio of α and β, (α/β)out-of-plane, is determined. The value of (α/β)out-of-plane for each device is larger than that of (α/β)in-plane (see Supplementary Note 8). This is due to the different origins between in-plane and out-of-plane induced spin polarization. The in-plane spin polarization is created only at the Fermi level, while the out-of-plane spin polarization is due to the electrical polarization (intrinsic effect) of the whole bands32. Previous work on the ferromagnetic semiconductor (Ga,Mn)As13,33 explains an emerging h[001] by the Kubo formalism, taking into account the presence of Dresselhaus dominated SOI and p-d exchange coupling. However, for our system of Fe/GaAs, h[001] results from the broken symmetry at the interface and interfacial exchange coupling, a scenario which is distinctly different from the (Ga,Mn)As case.
Measurement of the SGE
The effective spin-orbit fields stem from charge-to-spin conversion. In the following we demonstrate the inverse process, i.e., spin-to-charge conversion. In ferromagnetic metal/non-magnetic bilayers, spin pumping generates pure spin currents in the ferromagnetic layer. The pure spin current flows within the spin diffusion length into the non-magnetic layer and generates a transverse electrical current due to SOI, which is called ISHE23,24,25.
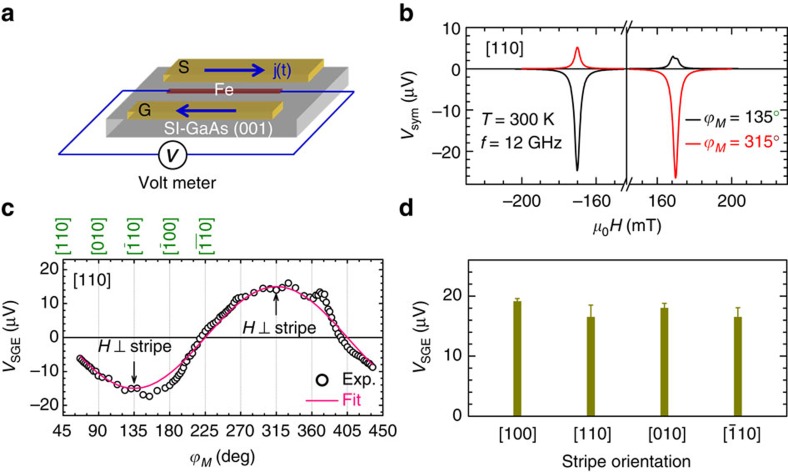
Figure 5a shows the schematic of the device used in our experiments. Fe/GaAs stripes with different orientations are integrated in the gap between the signal line and the ground plane of a coplanar waveguide. The stripe experiences an out-of-plane Oersted field excitation, which has been demonstrated to be an ideal configuration to study spin pumping and ISHE34,35. Figure 5b shows the measured voltage when the external magnetic field is in the plane but perpendicular to the stripe. For ϕM=135°, the voltage has the opposite polarity at ±HR but differs in magnitude, |V(−HR)|>|V(+HR)|. When the external magnetic field is rotated by 180°, the polarity reverses and |V(−HR)|<|V(+HR)| holds. This behaviour36 evidences the ISHE in ferromagnetic/non-magnetic layers and, in our case without the non-magnetic conducting layer, the presence of the SGE. The difference in the absolute magnitude at ±HR indicates that a symmetric thermo-electric background37 coexists with the SGE, so that the magnitude of the spin-galvanic voltage VSGE can be obtained by VSGE=[V(−HR)−V(HR)]/2 (see Supplementary Note 10). The ϕM dependence of VSGE, presented in Fig. 5c, can be fitted by cos(ϕM+45°), concordant with the SGE6. Due to the C2v symmetry of the system, the electric current flows always perpendicular to the spin polarization (magnetization)6. The angular dependence suggests that the Rashba SOI dominates the spin-to-charge conversion process. As shown in Fig. 5d, the SGE occurs in each orientations and the magnitude of VSGE takes similar values for different orientations, indicating a similar strength of the Rashba SOI. An anisotropy in VSGE could, in principle, be expected due to anisotropic scattering. However, according to the measurements of anisotropic tunnelling magnetoresistance17 and crystalline AMR18, the anisotropy is smaller than 1%. This should also be case for VSGE, which is beyond our detection limit.
Figure 5. Spin-galvanic effect in Fe/GaAs.
(a) Schematic of the device for spin pumping and spin-galvanic effect SGE. The [110]-orientated Fe/GaAs stripe is integrated between the signal (S) and ground (G) lines of the coplanar waveguide (CWG). (b) Magnetic-field μ0H dependent voltage measured at 300 K for ϕM=135° and 315°. This is the ideal configuration for the study of SGE since the parasitic AMR of Fe is absent when H is perpendicular to the stripe. (c) Magnetization angle ϕM dependence of VSGE, the solid line is a fit to cos(ϕM+45°). (d) Crystallographic orientation dependence of the magnitude of VSGE. The error bar is the s.d. obtained by fitting the ϕM dependence of VSGE for different stripe orientations.
Discussion
We notice that in our system consisting of single crystalline Fe/GaAs, it is difficult to determine the magnitude of the spin current JS injected into the interface by comparing the damping enhancement as commonly done for ferromagnetic/non-magnetic bilayers38,39 (for example, for Py/Pt bilayers, the damping constant is usually compared with that of Py/SiOx. The enhancement of damping is used to determine the spin mixing conductance and then JS). Recent experiments26 and microscopic theory40 suggest that the magnitude of JS can be estimated by JS=JC/λSGE, where JC=IC/w (IC is the charge current density and w the width of the stripe) is an areal current density and λSGE the ‘effective thickness' of the spin-orbit layer. Our previous magneto-transport measurements18 show that the symmetry of AMR changes when the Fe layer reaches a characteristic thickness of ∼4 monolayers (0.57 nm). This is evidence for the presence of interfacial SOFs, which gives an upper limit of λSGE. By using an average JC of 6.7 × 10−4 Am−1, the lower bound of JS is determined to be 1.2 × 106 Am−2. This value is in good agreement with that in ferromagnetic/non-magnetic bilayers26,34,41 for a similar excitation. It should also be noted that at the Fe/GaAs interface both ferromagnetic exchange exists and SOI emerges. The generation of pure spin currents by spin pumping is due to the Fe exchange interaction and the spin-to-charge conversion occurs at the interfacial Fe layer due to SOI. The whole process occurs in one system. This is significantly different from any ferromagnet/non-magnetic bi-layer ever studied25,26,27,30,34,35,36,37,38,39,41, where the ferromagnetic and non-magnetic layer is separated and decoupled.
In summary, we have observed mutual conversion between charge and spin current, which is known as the SGE and inverse SGE, at an epitaxial Fe/GaAs interface by SO-FMR and spin pumping at room temperature. The magnitudes of the interfacial SOT in this single crystalline ferromagnetic metal/semiconductor system are found to be comparable to those at ferromagnetic metal metal/non-magnetic metal interfaces, which could be useful for future spintronic applications. Our findings open a pathway in search for efficient SOT in various single crystalline ferromagnetic metal/semiconductor interfaces.
Methods
Sample preparation
To guarantee high quality of the interfaces, Fe/GaAs samples are grown by MBE in a MBE cluster with in-situ transfer. First, an undoped GaAs buffer layer (100 nm) is deposited on top of a GaAs (001) semi-insulating substrate at 560 °C. Clear (2 × 4) surface construction pattern has been observed, indicating an As-terminated flat surface. Then, without breaking the vacuum, the sample is transferred to another MBE chamber, where a 5-nm Fe film is deposited on GaAs at a substrate temperature of 75 °C. Reflection high-energy electron diffraction oscillations have been observed during growth, indicating the epitaxial growth mode as well as the flat interface between Fe/GaAs. Finally, a 3-nm thick Al capping layer is deposited onto the Fe film to avoid oxidation. The high quality of the Fe films is evidenced by the small damping constant of 0.0036 (see Supplementary Note 3).
Device
For the SO-FMR measurements, 6.4 × 100.0 μm stripes with different orientations are defined by electron-beam lithography and ion beam etching. The contacts are made from 15 nm Ti and 150 nm Au. All stripes have a resistance of ∼1.6 kΩ. For spin pumping measurements, 10.0 × 400.0 μm stripes with different orientations are integrated in the gap of the signal and ground lines of a coplanar wave guide. The resistances of the stripes are ∼2.6 kΩ. The width of the signal and ground line, which are also made from 15 nm Ti and 150 nm Au, is 50 and 30 μm, respectively.
Measurements
For both SO-FMR and spin pumping measurements, microwave currents with a frequency of 12 GHz are used and the input microwave power is 22 dBm (∼158 mW). For SO-FMR measurements, a Bias Tee is used to separate the dc voltage from microwave background, and the driving power acting on the sample is estimated to be 65 mW. Since the skin depth at 12 GHz (∼145 nm) is much larger than the Fe thickness (5 nm), the current density in Fe is expected to be spatially uniform. Thus, the Oersted field should not produce torque on Fe itself. All measurements are performed at room temperature.
Data availability
The data that support the findings of this study are available from the corresponding author on request.
Additional information
How to cite this article: Chen, L. et al. Robust spin-orbit torque and spin-galvanic effect at the Fe/GaAs (001) interface at room temperature. Nat. Commun. 7, 13802 doi: 10.1038/ncomms13802 (2016).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Material
Supplementary Figures 1-12, Supplementary Tables 1-3, Supplementary Notes 1-10 and Supplementary References.
Acknowledgments
L.C. is grateful for the support from Alexander von Humboldt Foundation. This work is support by the German Science Foundation (DFG) via SFB 689 and SPP 1538.
Footnotes
Author contributions L.C., C.H.B and D.W. planned the study and wrote the manuscript. M.K., D.S., D.B. did the MBE growth; L.C., R.I. and M.D. fabricated the devices. L.C. collected and analysed the experimental data. J.F. and M.G. developed the theory. All authors discussed the results.
References
- Dresselhaus G. Spin-orbit coupling effects in zincblende structures. Phys. Rev. 100, 580–586 (1955). [Google Scholar]
- Bychkov Y. A. & Rashba E. I. Oscillatory effects and the magnetic susceptibility of carriers in inversion layers. J. Phys. C: Solid State Phys. 17, 6039–6045 (1984). [Google Scholar]
- Aronov A. G., Lyanda-Geller Y. B. & Pikus G. E. Spin polarization of electrons by an electric current. Sov. Phys. JETP 73, 537–541 (1991). [Google Scholar]
- Edelstein V. M. Spin polarization of conduction electrons induced by electric current in two-dimentional asymmetric electron systems. Solid State Commun. 73, 233–235 (1990). [Google Scholar]
- Sinova J. et al. Universal intrinsic spin Hall effect. Phys. Rev. Lett. 92, 126603 (2004). [DOI] [PubMed] [Google Scholar]
- Ganichev S. D. et al. Spin-galvanic effect. Nature 417, 153–156 (2002). [DOI] [PubMed] [Google Scholar]
- Sinova J., Valenzuela S. O., Wunderlich J., Back C. H. & Jungwirth T. Spin Hall effects. Rev. Mod. Phys. 87, 1213–1259 (2015). [Google Scholar]
- Miron I. M. et al. Perpendicular switching of a single ferromagnetic layer induced by in-plane current injection. Nature 476, 189–193 (2011). [DOI] [PubMed] [Google Scholar]
- Liu L. Q. et al. Spin-torque switching with the giant spin Hall effect of Tantalum. Science 336, 555–558 (2012). [DOI] [PubMed] [Google Scholar]
- Chernyshov A. et al. Evidence for reversible control of magnetization in a ferromagnetic material by means of spin-orbit magnetic field. Nat. Phys. 5, 656–659 (2009). [Google Scholar]
- Endo M., Matsukura F. & Ohno H. Current induced effective magnetic field and magnetization reversal in uniaxial anisotropy (Ga,Mn)As. Appl. Phys. Lett. 97, 222501 (2010). [Google Scholar]
- Fang D. et al. Spin-orbit-driven ferromagnetic resonance. Nat. Nanotech. 6, 413–417 (2011). [DOI] [PubMed] [Google Scholar]
- Kurebayashi H. et al. An antidamping spin-orbit torque originating from the Berry curvature. Nat. Nanotech. 9, 211–217 (2014). [DOI] [PubMed] [Google Scholar]
- Ciccarelli C. et al. Room-temperature spin-orbit torque in NiMnSb. Nat. Phys. 12, 855–860 (2016). [Google Scholar]
- Wadley P. et al. Electrical switching of an antiferromagnet. Science 351, 587–590 (2016). [DOI] [PubMed] [Google Scholar]
- Gmitra M., Matos-Abiague A., Draxl C. & Fabian J. Magnetic control of spin-orbit fields: a first-principle study of Fe/GaAs junctions. Phys. Rev. Lett. 111, 036603 (2013). [DOI] [PubMed] [Google Scholar]
- Moser J. et al. Tunneling anisotropic magnetoresistance and spin-orbit coupling in Fe/GaAs/Au tunnel junctions. Phys. Rev. Lett. 99, 056601 (2007). [DOI] [PubMed] [Google Scholar]
- Hupfauer T. et al. Emergence of spin-orbit fields in magnetotransport of quasi-two-dimensional iron on gallium arsenide. Nat. Commun. 6, 7374 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garello K. et al. Symmetry and magnitude of spin-orbit torques in ferromagnetic heterostructures. Nat. Nanotech. 8, 587–593 (2013). [DOI] [PubMed] [Google Scholar]
- Fan X. et al. Quantifying interface and bulk contributions to spin-orbit torque in magnetic bilayers. Nat. Commun. 5, 3042 (2014). [DOI] [PubMed] [Google Scholar]
- Kim J. et al. Layer thickness dependence of the current-induced effective field vector in Ta |CoFeB| MgO. Nat. Mater. 12, 240–245 (2013). [DOI] [PubMed] [Google Scholar]
- Skinner T. D. et al. Complementary spin-Hall and inverse spin-galvanic effect torques in a ferromagnet/semiconductor bilayer. Nat. Commun. 6, 6730 (2015). [DOI] [PubMed] [Google Scholar]
- Tserkovyak Y. et al. Enhanced Gilbert damping in thin ferromagnetic films. Phys. Rev. Lett. 88, 117601 (2002). [DOI] [PubMed] [Google Scholar]
- Mizukami S., Ando Y. & Miyazaki T. Effect of spin diffusion on Gilbert damping for a very thin permalloy layer in Cu/permalloy/Cu/Pt films. Phys. Rev. B 66, 104413 (2002). [Google Scholar]
- Saitoh E., Ueda M., Miyajima H. & Tatara G. Conversion of spin current into charge current at room temperature: inverse spin-Hall effect. Appl. Phys. Lett. 88, 182509 (2006). [Google Scholar]
- Rojas Sánchez J. C. et al. Spin-to-charge conversion using Rashba coupling at the interface between non-magnetic materials. Nat. Commun. 4, 2944 (2013). [DOI] [PubMed] [Google Scholar]
- Rinaldi C. et al. Evidence for spin to charge conversion in GeTe(111). APL Mater. 4, 032501 (2016). [Google Scholar]
- Juretschke H. J. Electromagnetic theory of dc effects in ferromagnetic resonance. J. Appl. Phys. 31, 1401–1406 (1960). [Google Scholar]
- Liu X. & Furdyna J. K. Ferromagnetic resonance in Ga1-xMnxAs dilute magnetic semiconductors. J. Phys. Condens. Matter 18, R245–R279 (2006). [Google Scholar]
- Chen L., Matsukura F. & Ohno H. Direct-current voltages in (Ga,Mn)As structures induced by ferromagnetic resonance. Nat. Commun. 4, 2055 (2013). [DOI] [PubMed] [Google Scholar]
- Gilbert T. L. A phenomenological theory of damping in ferromagnetic materials. IEEE Trans. Magn. 40, 3443–3449 (2004). [Google Scholar]
- Qaiumzadeh A., Duine R. A. & Titov M. Spin-orbit torques in two-dimentional Rashba ferromagnets.. Phys. Rev. B 92, 014402 (2015). [Google Scholar]
- Li H. et al. Intraband and interband spin-orbit torques in noncentrosymmetric ferromagnets.. Phys. Rev. B 91, 134403 (2015). [Google Scholar]
- Obstbaum M. et al. Inverse spin Hall effect in Ni81Fe19/normal-metal bilayers. Phys. Rev. B 89, 060407 (R) (2014). [Google Scholar]
- Bai L. H., Feng Z., Hyde P., Ding H. F. & Hu C. M. Distinguishing spin pumping from spin rectification in a Pt/Py bilayer through angle dependence line shape analysis. Appl. Phys. Lett. 102, 242402 (2013). [Google Scholar]
- Bai L. H. et al. Universal method for separating spin pumping from spin rectification voltage of ferromagnetic resonance. Phys. Rev. Lett. 111, 217602 (2013). [DOI] [PubMed] [Google Scholar]
- Shiomi Y. et al. Spin-electricity conversion induced by spin injection into topological insulators. Phys. Rev. Lett. 113, 196601 (2014). [DOI] [PubMed] [Google Scholar]
- Urban R., Woltersdorf G. & Heinrich B. Gilbert damping in single and multilayer ultrathin films: Role of interfaces in nonlocal spin dynamics. Phys. Rev. Lett. 87, 217204 (2001). [DOI] [PubMed] [Google Scholar]
- Mosendz O. et al. Quantifying spin Hall angles from spin pumping: experiments and theory. Phys. Rev. Lett. 104, 046601 (2010). [DOI] [PubMed] [Google Scholar]
- Shen K., Vignale G. & Raimondi R. Microscopic theory of the inverse Edelstein effect. Phys. Rev. Lett. 112, 096601 (2014). [DOI] [PubMed] [Google Scholar]
- Wei D. H., Obstbaum M., Ribow M., Back C. H. & Woltersdorf G. Spin Hall voltages from a.c. and d.c. spin currents. Nat. Commun. 5, 3768 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Figures 1-12, Supplementary Tables 1-3, Supplementary Notes 1-10 and Supplementary References.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author on request.