Simultaneous atomic force microscope and fluorescence measurements of protein unfolding using a calibrated evanescent wave

Abstract

Fluorescence techniques for monitoring single-molecule dynamics in the vertical dimension currently do not exist. Here we use an atomic force microscope to calibrate the distance-dependent intensity decay of an evanescent wave. The measured evanescent wave transfer function was then used to convert the vertical motions of a fluorescent particle into displacement (SD = <1 nm). We demonstrate the use of the calibrated evanescent wave to resolve the 20.1 ± 0.5-nm step increases in the length of the small protein ubiquitin during forced unfolding. The experiments that we report here make an important contribution to fluorescence microscopy by demonstrating the unambiguous optical tracking of a single molecule with a resolution comparable to that of an atomic force microscope.

Measuring changes in the length or position of a single molecule with nanometer resolution has become the method of choice for tracking the activity and conformational changes of a wide variety of molecules (1–6). Among the available techniques, the versatility of optical detection has made it widespread in tracking the activity of single molecules (1, 3, 7–11). Through the optical detection of fluorophores, it is now possible to resolve the displacement of a single molecule in the x–y plane with a resolution of 1.5 nm (1). However, resolution in the z axis remains well below that of the x–y plane, at best resolving ≈10 nm at a low time resolution (5). Here we demonstrate a technique that can detect the changes in length or position of a single molecule moving along the z axis of an optical microscope, with subnanometer and millisecond time resolution. We call this technique evanescent nanometery, and we use it to track the unfolding of a single ubiquitin protein in real time. Our approach uses a nanometer-scale-calibrated evanescent wave to measure the position of a fluorescent particle moving along the z axis. We make use of a total internal reflection fluorescence (TIRF)-generated evanescent wave with an intensity that decays exponentially as a function of vertical distance (Fig. 1A) (12, 13). Our measuring system exploits the distance-dependent evanescent wave as a “ruler” to deconvolve fluorescent intensity into length. To calibrate the evanescent wave, we built a combined atomic force microscope (AFM)–TIRF instrument consisting of an AFM head mounted on top of a TIRF microscope equipped with an electron-multiplying charge-coupled device (EMCCD) (Fig. 1B).

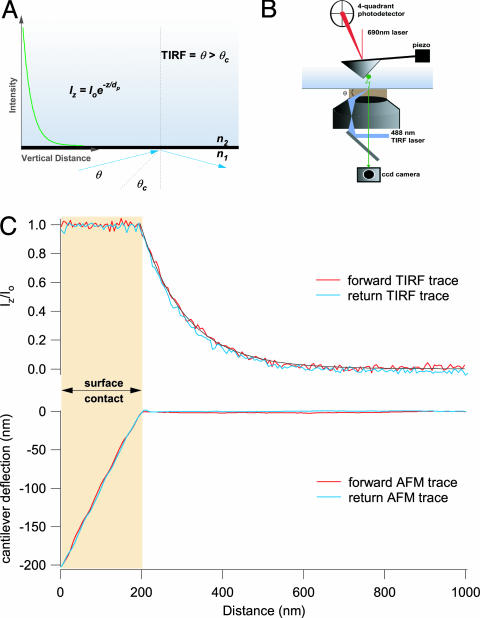
Fig. 1.

Simultaneous measurements of the position of a fluorescent particle by using AFM and TIRF microcopy. (A) An exponentially decaying evanescent wave field results when a laser beam is reflected at an angle (θ > critical angle, θ_c) across the boundary between two media with different refractive indexes (n₁ > n₂). The evanescent wave transfer function that relates fluorescence intensity and distance is given by I_z = I_o·e^–z/d_p, where I_z is the fluorescence intensity measured at a vertical distance z from the interface, I_o is the intensity measured at the interface, and d_p is the penetration depth. (B) We use an AFM head (Dimension 3100, Veeco Metrology Group) mounted on top of a through-the-lens TIRF microscope (IX71, Olympus) equipped with an EMCCD camera (iXon DV887, Andor Technology) to confirm the exponential relationship between intensity and distance and to directly measure d_p. (C) Simultaneous measurements of fluorescence intensity (upper trace) and cantilever deflection (lower trace) as a fluorescently labeled AFM cantilever is driven in and out of the evanescent wave field. Fluorescence was recorded with an exposure time of 30 ms.

Materials and Methods

Fluorescent Modification of AFM Cantilever Tips. Simultaneous force and fluorescence studies were carried out by using Si₃N₄ cantilevers (Nanoprobe, Digital Instruments, Santa Barbara, CA) that were modified with either quantum dots or a single fluorescent bead. Cantilevers could be made fluorescent by affixing a single 200-nm yellow-green fluorescent microsphere (FluoSphere, no. F8764, Molecular Probes) to the cantilever tip through nonspecific interactions (Fig. 1C). However, most of our experiments were done with quantum-dot-modified cantilevers. Cantilever tips were covered with quantum dots after either of two procedures. In the first procedure, cantilevers were soaked in a solution of 0.5 mg/ml biotinylated BSA (Sigma) overnight in a humidified chamber at 4°C. After several rinses in PBS, the biotinylated BSA-coated tips were then coupled to quantum dot–streptavidin conjugates (Qdot 525, Quantum Dot, Hayward, CA) through biotin–streptavidin affinity. These cantilevers were used to obtain the data in Fig. 2. In the second approach, CdSe/hexane quantum dots (a gift from Irvin Herman, Department of Applied Physics, Columbia University, New York) were dissolved in a solution of butyl acetate/isopropyl alcohol/ethyl acetate/nitrocellulose/tosylamide formaldehyde resin (clear nail polish) and dry cast onto cantilever tips (spring constant ≈15 pN/nm). This last approach produced a durable cantilever fluorescence (Fig. 3) that could be used in the combined fluorescence/single-molecule unfolding studies (Fig. 4).

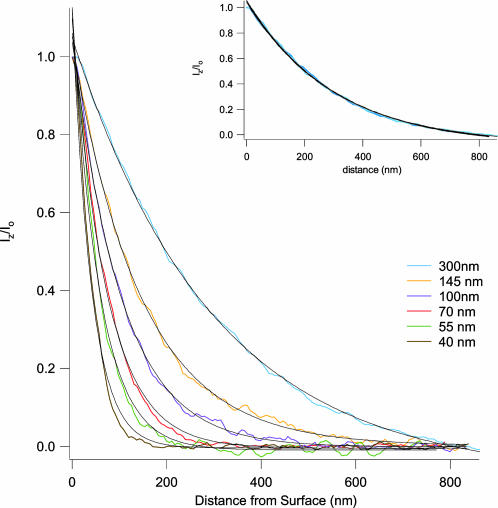
Fig. 2.

Fluorescent measurements of evanescent wave intensities reveal single exponential decays that are stable over time. The penetration depth (d_p) is determined by the angle of incidence (θ) of the reflecting laser beam (Eq. 2). Starting from just beyond the critical angle, θ was increased five times, resulting in decreasing values of d_p. At each new angle, the fluorescence intensity vs. distance curve was measured and then fitted with a single exponential decay function (Eq. 1; see text): blue trace, d_p = 300 nm, θ = 48.7°; orange trace, d_p = 145 nm, θ = 49.7°; purple trace, d_p = 100 nm, θ = 51.1°; red trace, d_p = 70 nm, θ = 53.9°; green trace, d_p = 55 nm, θ = 57.8°; brown trace, d_p = 40 nm, θ = 66.5°. (Inset) Repeated measurements of an evanescent field are highly reproducible over time. An evanescent wave was maintained for 2 h and measured at the times t = 0, 60, and 120 min. The black lines represent single exponential decay fits of the data corresponding to d_p = 300 nm (t = 0 min), d_p = 299 nm (t = 60 min), and d_p = 302 nm (t = 120 min). Fluorescence was recorded with an exposure time of 10 ms for all measurements.

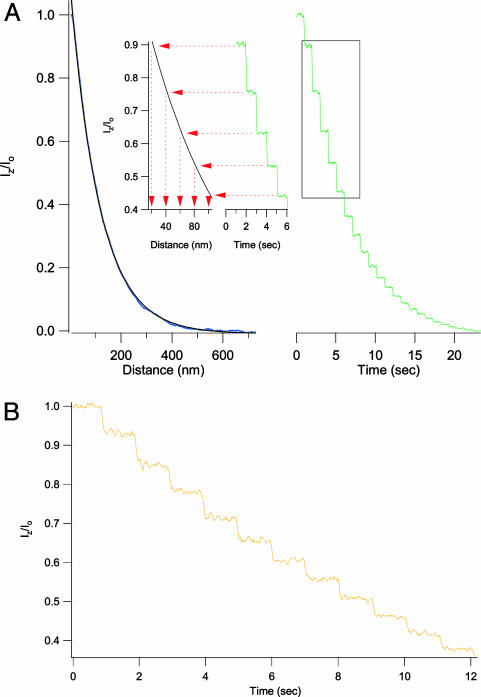
Fig. 3.

Use of a calibrated evanescent field measures the vertical displacement of a fluorescent cantilever with subnanometer resolution. (A) The evanescent wave transfer function in this experiment (Left, blue trace) was fit with a single exponential (black trace) (d_p = 115 nm). The green trace (Right) shows the fluorescent intensity that results when a fluorescently labeled cantilever tip is retracted from the surface in 20-nm steps at 1-s intervals. The observed fluorescence staircase shows the largest steps to be near the surface and becoming smaller as the cantilever moves away, in agreement with the shape of the evanescent transfer function. We use the transfer function to convert the fluorescence trace into a measure of vertical distance (Inset). Using this procedure, we recovered step sizes of 20 ± 0.4 nm for the first 10 steps taken from the surface, in agreement with the programmed stepwise movement of the AFM cantilever. Fluorescence was recorded with an exposure time of 10 ms. (B) This trace shows that when the same cantilever is retracted in steps of 5 nm (1-s intervals, d_p = 55 nm), the resulting fluorescent intensity staircase is well resolved. Fluorescence was recorded with an exposure time of 10 ms.

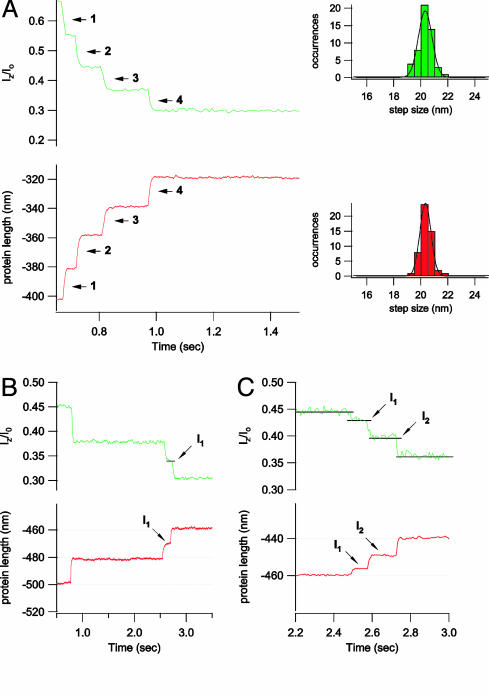
Fig. 4.

Optical detection of the unfolding of a single protein by using evanescent nanometry. (A) Simultaneous measurements of fluorescence intensity and protein length from a single ubiquitin polyprotein unfolding under a constant stretching force (100 pN). The force-clamp AFM trace (red) shows that the length of the ubiquitin polyprotein, as it unfolds, increases in steps of 20.1 ± 0.4 nm (n = 52; Lower Right, red histogram). A simultaneous recording of the fluorescence intensity of the labeled cantilever shows a decreasing staircase. By using the evanescent wave transfer function (d_p = 103 nm), the fluorescence step sizes were converted to length, giving 20.1 ± 0.5 nm (n = 52; Upper Right, green histogram), in excellent agreement with the AFM data. B and C show two examples where ubiquitin unfolds through intermediates. The AFM recordings of the length of the polyubiquitin protein (red traces) show that unfolding can occur through well marked intermediates (I₁ in B; I₁ and I₂ in C). These intermediates are easily distinguished in the corresponding fluorescent intensity traces (green). For example, in the recordings shown in C, we observe a ubiquitin-unfolding event that lengthens the molecule through two intermediate steps of 3.2 nm (I₁) and a second intermediate elongation by 7.4 nm (I₂) before its complete unfolding with a final step of 9.5 nm. This sequence of intermediate steps is readily measured by the evanescent nanometry technique where even the smallest event is well resolved (e.g., 3.2-nm transition to I₁, which has a lifetime of only 85 ms). Fluorescence was recorded with an exposure time of 1 ms for all experiments presented in this figure.

Evanescent nanometry is not limited to tracking the motions of a fluorescent cantilever. Any fluorescently labeled particle will work well inside a calibrated evanescent field. However, it is advantageous to use relatively large fluorescent particles to cut down on the exposure time necessary to make a recording. This can be done with ease by using fluorescently labeled beads. For example, we have found that 200-nm fluorescent beads provide enough fluorescence intensity to track nanometer-scale motions at 30 ms. Larger, 500-nm diameter beads are routinely attached to motor proteins such as kinesin for manipulations by using optical tweezers (2). It is then quite possible to use relatively large fluorescent particles to track the molecules of interest allowing for a time-resolved record that is not photon-limited. For instance, in an evanescent field with a d_p of 103 nm, ≈2,000–2,300 photons were recorded from a quantum-dot-tipped cantilever with an exposure of 1 ms and the cantilever tip at the surface. When the tip was moved 100 nm from the surface, we collected ≈800 photons per ms. A 200-nm fluorescent bead typically generated 1/10th to 1/15th fewer photons under the similar conditions.

Combined AFM and TIRF Microscope. The dual-force and fluorescence microscope (Fig. 1) was built around three commercially available devices, namely a Digital Instruments Dimension 3100 AFM head (Veeco Metrology Group, Santa Barbara, CA), an IX71 TIRF microscope (Olympus, Melville, NY), and an iXon EMCCD (Andor Technology, Belfast, Northern Ireland). The AFM head was mounted onto a 30-mm-thick steel base plate via a z translator (Spectra-Physics) bolted onto an aluminum tower, which was attached to the steel base by using a large tunable magnet (Newport, Fountain Valley, CA). Data acquisition and control of the Dimension 3100 AFM head were done by means of data acquisition cards (6052E and 6703, National Instruments, Austin, TX) controlled by software written in igor pro (WaveMetrics, Lake Oswego, OR). The EMCCD camera was controlled by custom-made external operation (XOP) functions that were called by the main igor pro program.

In addition to being a physical mount for the AFM, the base plate is also the stage for our TIRF microscope and contains a cutout for the Olympus APO100×/1.65 oil immersion lens. All TIRF studies were carried out by generating an evanescent wave with a 488-nm argon ion laser (IMA 100, Melles Griot, Irvine, CA), using the “through-the-lens” method. We used refractive index-matched immersion oil (series M, refractive index = 1.78; Certified Refractive Index Liquids R. P., Cargille Laboratories, Cedar Grove, NJ) and cover glass (APO100×/OHR-CG, Olympus).

The emitted light was passed through a green filter set consisting of a 505-nm dichroic mirror, a 510-nm long-pass filter (Chroma Technology, Rockingham, VT), and, finally, a 600-nm short-pass filter (Optical, Oxnard, CA). Fluorescent light was collected by an iXon DV887 back-illuminated EMCCD (512 × 512 pixels, 16 × 16 μm per pixel, with 95% quantal efficiency) operated at –70°C with a 5-MHz readout rate. All fluorescence data were normalized to their maximum value.

During our experiments, the cantilever tip was initially held ≈800 nm above the cover-glass surface, the velocity of the piezo was set to 100 nm/sec, and the piezo excursion toward the surface was set to 1,000 nm to ensure surface contact of the fluorescent tip. To maximize the camera's acquisition rate, we sampled from a 20 × 20 pixel subregion of the EMCCD with background subtraction. The camera was cooled to –70°C for all acquisition sequences. During all combined AFM–TIRF measurements, the camera fan was turned off to eliminate its mechanical vibrations, which severely degrade the AFM recordings.

For the dual-force and fluorescence monitoring of polyubiquitin unfolding (Fig. 4), the ubiquitin polyproteins were prepared as described in refs. 6 and 14, and standard single-molecule force-clamp conditions were established with a constant pulling force of 100 pN (6, 14).

Results and Discussion

Calibration of the Evanescent Wave with an AFM. The piezoelectric actuator of the AFM head provides z positioning with nanometer accuracy. High-precision mapping of the TIRF evanescent field relies on using the z piezo to drive a fluorescent AFM cantilever tip through a TIRF field as a reporter of evanescent wave intensity. The top graph of Fig. 1C corresponds to the fluorescence–distance curves measured as the fluorescent cantilever penetrates the evanescent field; the bottom graph shows the corresponding force–extension curves reported by the cantilever. The experiment begins with the cantilever positioned ≈800 nm vertically above the surface. At this position, there is no force upon the cantilever and no evanescent wave to excite the fluorescence at the cantilever tip. As the cantilever progressively enters the TIRF field, its fluorescence increases. The forward AFM trace continues to register no force until the cantilever touches the surface (downward inflection of the AFM trace). This position also corresponds with the beginning of the plateau of the fluorescence intensity trace. As the piezoelectric actuator is set to travel 1,000 nm, it continues to drive the cantilever forward (Fig. 1C, shaded box region in the force and fluorescence traces). The continued forward transit of the piezo causes a linear deflection of the cantilever that equals the displacement of the piezo (slope = 1) seen on the AFM trace. Because the cantilever's further forward progress is impeded by the surface, the position of the fluorescent reporter does not change during contact; consequently, the forward fluorescence trace continues to record a plateau of maximal fluorescence. The return path of the cantilever mirrors that of the forward travel, overlapping the forward records. A single exponential decay fits the fluorescence–distance curves.

Setting and Measuring the Penetration Depth of the Evanescent Wave. The experimentally observed single exponential decay of the evanescent wave (Fig. 1C) matches that predicted from theory (12). The equation

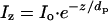[1]

describes the behavior of the distance-dependent intensity, where z is the vertical distance from the surface, I_z and I_o are the intensities at a distance z above the surface and at surface, respectively, and d_p is the penetration depth (Fig. 1 A). The penetration depth can also be calculated from

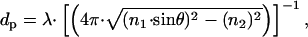[2]

where λ and θ are the wavelength and the angle of incidence of the laser beam and n₁ and n₂ are the indices of refraction for the high- and low-index media, respectively (Fig. 1 A). Hence, changing the angle of incidence (θ) changes the value of the penetration depth of the TIRF field. Although the prismless TIRF setup that we employ does not allow direct measure of the angle of incidence of the beam, relative changes in this angle are possible. The graph in Fig. 2 depicts measured TIRF maps at various laser angles. Starting with the maximal TIRF setting, the angle of the TIRF laser was incrementally adjusted to obtain progressively shallower TIRF fields. At each new angle, the penetration depth (d_p) of the evanescent wave was directly measured by fitting a single exponential decay (Eq. 1) to the measured fluorescence–distance curve. The first curve (blue) was obtained just above the critical angle. From Eq. 2, the measured value of d_p = 300 nm corresponds to an angle of 48.7°. Four successive increases in the incident angle generated the next set of curves (orange, purple, red, and green) with measured penetration depths of 145 nm (orange, 49.7°), 100 nm (purple, 51.1°), 70 nm (red, 53.9°), and 55 nm (green, 57.8°). The final measurement (brown) was made at the maximal angle setting and produced the shallowest TIRF with a d_p of 40 nm (θ = 66.5°). As expected, the calculated angles are within the boundaries of the critical angle (θ = 48.4°) and the maximal aperture angle of the lens (θ = 68°), covering a range of penetration depth between 40 and 300 nm. For a given value of θ, repeated measurements of the intensity–distance relationship yielded traces that, over a 2-h period, varied from d_p = 300 nm at the start of the experiment to d_p = 302 nm at the end, demonstrating the stability and low drift of our experimental system (Fig. 2 Inset).

Deconvolution of Fluorescence into Distance with Subnanometer Resolution. The stability and high spatial sensitivity of the evanescent field makes it an ideal tool to measure displacement in the z-axis direction, with subnanometer resolution. Fig. 3 illustrates our method. We first measure the normalized fluorescence intensity vs. distance relationship (Fig. 3A Left, blue trace). An exponential fit with Eq. 1, produces the precise relationship between the normalized fluorescence and the position along the z axis (black trace, I_z/I_o = e^–z/dp, d_p = 115 nm). We can now use this relationship to convert a change in intensity into a change in distance along the z axis. The green staircase in Fig. 3A Right represents the intensity changes recorded from a fluorescently modified cantilever retracted through the evanescent wave field in steps of 20 nm, with pauses of 1 s. Although the AFM-driven cantilever was always moved in steps of 20 nm, the fluorescence intensity steps measured decay in amplitude as the cantilever moves further away from the surface. Nonetheless, fluorescent intensity can be readily deconvolved into distance by using Eq. 1 (d_p = 115 nm). Fig. 3A Inset shows four consecutive steps and projects the average value of each step against the decay function of the evanescent field measured in Fig. 3A, readily recovering step sizes of 20 ± 0.5 nm (red arrows). A more stringent test is shown in Fig. 3B where the AFM was programmed to move the fluorescent cantilever in steps of only 5 nm in amplitude; steps of this size are easily resolved (d_p = 55 nm). This resolution is unprecedented in the optical detection of position.

To get a quantitative estimate of the positional resolution obtained by the procedures illustrated in Fig. 3, we measured the standard deviation (σ) of the position of a fluorescent cantilever calculated from normalized fluorescence intensities. For an evanescent field (d_p = 103 nm) and a fluorescent cantilever held 7.5 nm away from the surface, we measured σ = 0.53 nm after sampling for 210 ms (30 intensity data points). As expected, the standard deviation increased as we moved away from the surface (at 50 nm, σ = 0.63 nm; and at 100 nm, σ = 0.82 nm). Clearly, being closest to the surface provides the greatest resolution where the standard deviation is subnanometer and the standard error of the mean is subangstrom (at 7.5 nm, SEM = 0.95 Å).

Simultaneous Fluorescence and AFM Detection of Single Protein Unfolding Events. To demonstrate the ability of evanescent nanometry to capture the conformations of a single molecule, we have combined evanescent nanometry with force-clamp AFM techniques to track the unfolding of the small protein ubiquitin stretched by a constant force (6). AFM pulling causes the ubiquitin polyprotein to align with the z axis of the optical microscope, fulfilling the principal requirement for detection by evanescent nanometry. Furthermore, any unfolding of ubiquitin would cause an elongation of the molecule by 20.3 ± 0.9 nm in the z axis (14), which, as our results in Fig. 3 showed, can be easily resolved by evanescent nanometry. Our preference for using polyproteins (15) stems from their characteristic unfolding pattern corresponding to a staircase of equally sized steps that can be readily recognized and distinguished, unambiguously, from background nonspecific interactions (14). Hence, the conditions of our experiment are well defined.

The combined AFM and evanescent nanometry recordings are shown in Fig. 4. In these experiments, we used a fluorescent cantilever, similar to those used in the experiments of Fig. 3, and a calibrated evanescent field (d_p = 103 nm). The experiment consists of tethering a single polyubiquitin between the surface and the cantilever tip and applying a constant pulling force of 100 pN (14). Unfolding events are recorded by the AFM as a series of stepwise elongations of the end-to-end length of the protein (Fig. 4A Lower Left, red trace). Simultaneously, we measure the fluorescence intensity changes of the AFM cantilever as it moves away from the surface as the polyprotein unfolds (Fig. 4A Upper Left, green trace). The fluorescence intensity was also recorded as a staircase of diminishing amplitude that mirrors the unfolding events observed with the AFM. We have observed 52 ubiquitin unfolding events recorded simultaneously with force-clamp AFM and evanescent nanometry. An accumulated histogram of the unfolding step sizes captured by force-clamp AFM gives 20.1 ± 0.4 nm (Fig. 4A Lower Right). We used the measured transfer function of the calibrated evanescent wave to convert the step decreases of fluorescence shown in Fig. 4A into actual distance. A histogram of the fluorescence–intensity step sizes converted into distance gives 20.1 ± 0.5 nm, in agreement with the simultaneously recorded AFM data. Ubiquitin unfolding under a stretching force is stochastic, and the time interval between unfolding events varies widely (6, 14). Indeed, the dwell time between some unfolding events is shown to be 30 ms, yet evanescent nanometry readily resolves them (Fig. 4A). Some ubiquitins unfold via intermediates (Fig. 4 B and C) that appear as these steps increase in length that are smaller than 20.1 nm, yet their combined length adds up to the size of a full unfolding event (14). These events are well resolved by the force-clamp AFM recordings (Fig. 4 B and C, red traces), as well as by the fluorescence signal from evanescent nanometry (Fig. 4 B and C, green traces). The smallest-sized unfolding intermediate observed by force-clamp AFM (3.2 nm, I₁) (Fig. 4C), which shows a dwell time of only 85 ms, can be easily resolved in the fluorescence trace (Fig. 4C, green trace).

Conclusion

These results demonstrate that evanescent nanometry can measure the length of a single molecule in the z axis with a length and time resolution comparable to that of an AFM. However, evanescent nanometry is not limited to tracking the motions of an AFM cantilever. The technique is of general applicability to any fluorescent particle (see Materials and Methods). We anticipate that our technique will be of wide use in cellular biology, i.e., in monitoring displacements and conformations of molecules inside a living cell, where an AFM cannot reach. Evanescent nanometry can effectively replace AFM as a means of accurately measuring length in the z axis, provided that other means are used to ensure a vertical displacement of the molecule. This can be done by using magnetic tweezers (5) or a variety of other nanofabricated substrates that can provide a template in the z-axis direction (16). These approaches can be used to vertically align actin filaments or microtubules to observe the z-axis movement of fluorescently labeled molecular motors at a much higher resolution than currently possible. Furthermore, evanescent nanometry has the potential of tracking the activity of many single molecules simultaneously.

As a measuring tool, evanescent nanometry prompts a comparison with fluorescence imaging with 1-nm accuracy (FIONA) (1, 17). FIONA can observe length changes and displacement of a single Cy3 dye in the x–y plane with 1.5-nm resolution. This was done by fitting the point-spread function of the microscope to the fluorescence image of a single dye molecule. Evanescent nanometry complements FIONA by adding nanometer resolution in the z axis. Hence, it now becomes possible to optically track molecules with nanometer resolution in all three axes of an optical microscope. Förster resonance energy transfer (FRET) is also a powerful and widely used technique to measure length changes in single molecules (3, 10, 11, 18, 19). However, it is always a challenge to convert the FRET signal into an absolute distance. The assignment of the dipole–dipole energy transfer orientation factor between fluorophores (K²) and the rapid drop of energy transfer as a function of distance limit the range and precision of FRET (17). The short range of distances covered by FRET (1–10 nm) (17, 20) would make it difficult to capture even a single ubiquitin forced unfolding event, which extends the protein by 20.1 nm. By contrast, many successive ubiquitin unfolding events can be easily resolved by evanescent nanometry. For example, in a calibrated evanescent field (d_p = 103 nm), it is possible to measure step changes in length in a range of up to 300 nm while still retaining a high resolution (σ = 1.9 nm measured at 300 nm).

Although prior studies have also recognized the utility of the evanescent wave transfer function to measure vertical displacement (21–23), we demonstrate the use of an AFM to precisely calibrate the evanescent wave with subnanometer resolution. The high spatial resolution of the AFM was the key to providing an accurate transfer function for converting fluorescence intensity into distance without invoking any assumptions. In addition, the AFM provided simultaneous confirmation of forced unfolding of single ubiquitin polyproteins monitored by evanescent nanometry, demonstrating the ability of a calibrated evanescent wave to track the variations in length of a single molecule.

A potential limitation of evanescent nanometry is that it requires that the fluorescence is changed only by distance. Errors arising from fluctuations in the emission intensity due to photobleaching would reduce the effectiveness of the technique. However, as demonstrated here, this problem easily can be addressed by using relatively large fluorescent reporters. Given that the resolution of evanescent nanometry does not depend on the point-spread function of the microscope, larger fluorescent reporters can be used without detriment, greatly enhancing the resolution and stability of the fluorescence measurements. Furthermore, a 0.5- to 300-nm distance detection range makes evanescent nanometry an ideal technique to capture the full range of conformational changes of most known biological molecules.