Skip to main content
PMC home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 2004 Aug 26;101(36):13138–13141. doi: 10.1073/pnas.0405086101

Colossal kinetic isotope effects in proton-coupled electron transfer

My Hang V Huynh †, Thomas J Meyer ‡,§
PMCID: PMC516537  PMID: 15331783

Abstract

The kinetics of reduction of benzoquinone (Q) to hydroquinone (H2Q) by the Os(IV) hydrazido (trans-[OsIV(tpy)(Cl)2(N(H)N(CH2)4O)]-PF6 = [1]PF6, tpy = 2,2′:6′,2″-terpyridine), sulfilimido (trans-[OsIV-(tpy)(Cl)2(NS(H)-4-C6H4Me)]PF6 = [2]PF6), and phosphoraniminato (trans-[OsIV(Tp)(Cl)2(NP(H)(Et)2)] = [3], Tp– = tris(pyrazolyl)-borate) complexes have been studied in 1:1 (vol/vol) CH3CN/H2O and CH3CN/D2O (1.0 M in NH4PF6/KNO3 at 25.0 ± 0.1°C). The reactions are first order in both [Q] and Os(IV) complex and occur by parallel pH-independent (k1) and pH-dependent (k2) pathways that can be separated by pH-dependent measurements. Saturation kinetics are observed for the acid-independent pathway, consistent with formation of a H-bonded intermediate (KA) followed by a redox step (kred). For the pH-independent pathway, k1(H2O)/k1(D2O) kinetic isotope effects are 455 ± 8 for [1+], 198 ± 6 for [2+], and 178 ± 5 for [3]. These results provide an example of colossal kinetic isotope effects for proton-coupled electron transfer reactions involving nitrogen, sulfur, and phosphorus as proton-donor atoms.

Proton-coupled electron transfer (PCET) reactions are at the heart of important biological processes, including photosynthesis and respiration (1–4). These reactions avoid high-energy intermediates through the concerted transfer of an electron and a proton. PCET is distinguished from H-atom transfer (HAT) in that the transferring electron and proton come from different sites in the reducing agent rather than from a single chemical bond (5–10). Nuclear quantum effects often play an important role, as evidenced experimentally by the kinetic isotope effect (KIE), the ratio of rate constants for the hydrogen and deuterium forms of the reducing agent. Large kH/kD KIEs have been observed in other reactions, including H-abstraction by methyl radicals in low-temperature glasses (11), the photoenolization of ortho-methyl aryl ketones in rigid media (12), and in certain enzymatic reactions (13–15). For PCET reactions, values of up to 30 have been observed in solution (16) and >70 on an oxide surface (17).

In earlier work, we described a PCET reaction with a k1(H2O)/k1(D2O) KIE of 175 at room temperature based on the reduction of benzoquinone (Q) by an osmium complex containing a phosphorus–hydrogen bond (18). We report here values of 198 and 455 for PCET reactions from sulfur and nitrogen–hydrogen bonds based on an extended analysis of reactions reported earlier in preliminary accounts.

Methods

UV–visible kinetic traces were acquired by use of Hewlett–Packard 8452A and 8453 diode array spectrophotometers interfaced with an IBM-compatible personal computer. The measurements were made in standard quartz 1-cm pathlength cuvettes. All kinetics were studied by conventional mixing and UV–visible monitoring in 1:1 (vol/vol) mixtures of H2O or D2O and CH3CN at 25.0 ± 0.1°C with a pseudo-first-order excess of Q. The concentration of Os(IV) reductant was varied from 3.0 × 10–6 M to 5.0 × 10–5 M, and [Q] was varied from 1.5 × 10–4 M to 1.0 × 10–2 M. The concentration of Os(V) oxidant was varied from 2.0 × 10–5 M to 2.0 × 10–4 M, and [H2Q] was varied from 3.0 × 10–4 M to 8.0 × 10–2 M. The temperature of solutions during the kinetic studies was maintained to within ±0.1°C with use of Lauda RM6 and Thermo Neslab RTE 7 circulating water baths and monitored with an Omega HH-51 thermocouple probe. All rate constants cited in this work are reported as the averages of at least three or more independent experiments.

Cyclic voltammetric experiments were measured with the use of Princeton Applied Research (PAR) models 263A and 273 potentiostats, and bulk electrolyses were performed with a PAR model 173 potentiostat/galvanostat. All measurements were conducted in a three-compartment cell in 1:1 (vol/vol) CH3CN/H2O with 1.0 M NH4PF6 as the supporting electrolyte. A glassy carbon working electrode was used for aqueous measurements. All potentials are referenced to the saturated sodium chloride/calomel electrode (SSCE, 0.236 V vs. the normal hydrogen electrode) at room temperature and are uncorrected for junction potentials. In all cases, the auxiliary electrode was a platinum wire. The solution in the working compartment was deoxygenated by N2 or argon bubbling. All redox couple potentials are the average of four independent measurements and are ±2 mV.

Results and Discussion

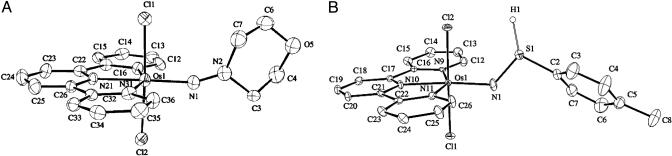
The kinetics of the reactions shown in Eqs. 1–3 were studied in 1:1 (vol/vol) CH3CN/H2O mixtures at 25.0 ± 0.1°C in 1.0 M NH4PF6/HPF6 mixtures. The details of the reaction in Eq. 2 with phosphorus as the proton-donor atom were reported in ref. 18, and preliminary accounts with S and N were reported in refs. 19 and 20. The structures of the Os(V) nitrogen-based electron–proton acceptor and Os(IV) sulfur-based electron–proton donor are shown in Fig. 1.

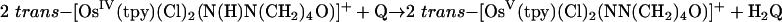graphic file with name M1.gif [1]
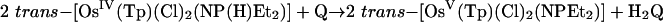graphic file with name M2.gif [2]
graphic file with name M3.gif [3]

tpy = 2,2′:6′,2″-terpyridine and Tp– = tris(pyrazol-1-yl)borate.

Fig. 1.

Fig. 1.

Open in a new tab

Structures of osmium complexes. (A) trans-[OsV(tpy)(Cl)2(NN(CH2)4O)]+. (B) trans-[OsIV(tpy)(Cl)2(NS(H)C6H4Me)]+

All three reactions in Eqs. 1–3 occur with small driving forces with ΔG° =–0.05, +0.08, and +0.06 eV, respectively, based on electrochemical measurements. Kinetic studies with UV–visible monitoring under conditions where the reactions essentially go to completion as written in Eqs. 1–3 reveal that over the pH range 0.0–2.9, all three are first-order in Os complex and first-order in Q in the forward direction. All three reactions are pH-dependent in this pH range, with the dependence consistent with the rate law in Eq. 4 and contributions from acid-dependent and acid-independent pathways (18–20).

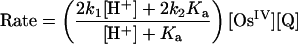graphic file with name M4.gif [4]

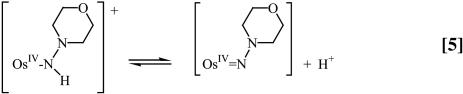
Using the reaction in Eq. 1 as the example, the acid-independent pathway (k1) involves initial deprotonation with Ka = 6.3 × 10–4 M, to give trans-[OsIV(tpy)(Cl)2(NN(CH2)4O)], followed by outer-sphere electron transfer. The initial electron transfer products are trans-[OsV(tpy)(Cl)2(NN(CH2)4O)]+ and Q•–, Eqs. 5 and 6.

graphic file with name zpq03504581500e5.jpg
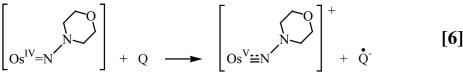graphic file with name zpq03504581500e6.jpg

Electron transfer is followed by a series of rapid electron/proton transfer steps to give the final products, Eq. 7.

graphic file with name zpq03504581500e7.jpg

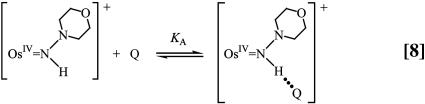
The pH-independent pathway is far more interesting for all three cases because it occurs with a high H2O/D2O kinetic isotope effect. A detectable intermediate (presumably H-bonded) intervenes in these reactions as shown by spectral measurements and the appearance of saturation kinetics in added Q, Eq. 12.

graphic file with name zpq03504581500e8.jpg
graphic file with name zpq03504581500e9.jpg
graphic file with name zpq0350458150e10.jpg
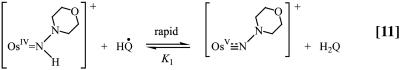graphic file with name zpq0350458150e11.jpg

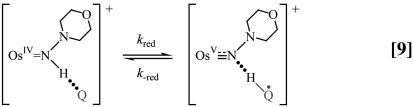
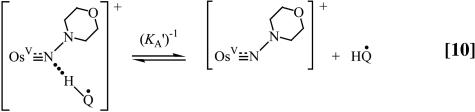
A proposed mechanism is shown in Eqs. 8–11 for the nitrogen proton-donor case. The key steps are intermediate formation followed by electron transfer. The association constant, KA, and the rate constant for the redox step, kred, were separated by analysis of the dependence of k1 on [Q] according to Eq. 12 (18). Similar mechanisms were identified for the acid-independent pathways for PCET-P and PCET-S.

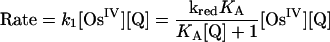graphic file with name M5.gif [12]

Because ΔG° ≈ 0, it is possible to study the kinetics of these reactions in both the forward and reverse directions. Concentration-dependence studies reveal the rate law for the reverse reaction, shown in Eq. 13, for the nitrogen-donor case. Saturation kinetics were observed, and spectroscopic evidence for an intermediate, illustrated in Eqs. 9 and 10 as the semiquinone adduct Inline graphic.

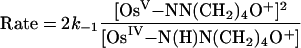graphic file with name M7.gif [13]
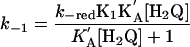graphic file with name M8.gif [14]

All of these observations are consistent with the mechanism in Eqs. 8–11. In the reverse direction, k–red is the rate-limiting step and K1 = 3.6 × 107 from redox potential measurements. Analysis of the kinetics data in 1:1 (vol/vol) CH3CN/H2O in both directions gave kred = (6.19 ± 0.05) × 10–3 s–1, KA = (4.43 ± 0.18) × 103 M–1 for the forward reaction and k–red = (1.03 ± 0.02) × 10–3 s–1, K′A = (2.06 ± 0.06) × 103 M–1 for the reverse reaction, all for the N proton-donor case.

The free energy change for the proton-coupled electron transfer step in Eq. 9, ΔG°(PCET), is available by using electrochemical measurements to determine ΔG° for the reaction in Eq. 15,

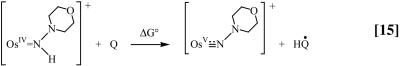graphic file with name zpq0350458150e15.jpg

and KA and K′A by using the relationship

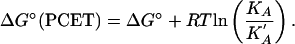graphic file with name M9.gif [16]

From the experimental data for PCET-N, the correction factor RT ln(KA/K′A) is negligible. Assuming this to be the case for the other two reactions, ΔG°(PCET) = 18 kcal/mol for PCET-N, 22 kcal/mol for PCET-P, and 21 kcal/mol for PCET-S under the conditions of the kinetics experiments.

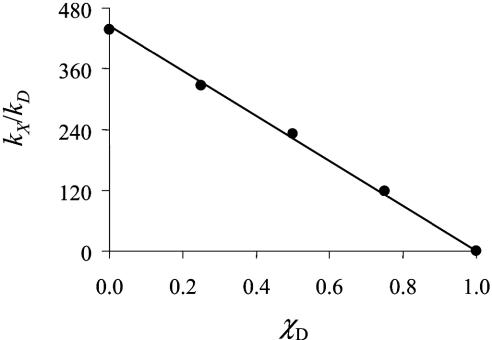
Kinetic studies for all three reactions in the forward direction were extended to CH3CN/D2O–H2O mixtures varying from pure H2O to “pure” D2O with the actual mole fraction of protium in the latter determined by 1H NMR. Rate constants k1 and k2 in Eq. 4 were separated by acid-dependent measurements and kred and KA by concentration-dependent measurements and Eq. 12. In Fig. 2 is shown a plot of the rate constant ratio kX/kD versus mole fraction χD with k = kred for the N-proton donor with χD varied from 0 to 0.996. The linearity of these plots for all three reactions points to a solvent isotope effect dominated by transfer of a single proton. It also suggests that a single pathway dominates reactivity over the entire mole fraction range.

Fig. 2.

Fig. 2.

Open in a new tab

Plot of kX/kD versus χD for the reaction between Q and trans-[OsIV(tpy)(Cl)2(N(H)N(CH2)4O)]PF6 in 1:1 (vol/vol) CH3CN/H2O–D2O mixtures at 25.0 ± 0.1°Cat[Q] < 2.80 × 10–3 M.

Rate constants and KA values for the three reactions involving N, S, and P proton donors in both 1:1 (vol/vol) CH3CN/H2O and CH3CN/D2O are given in Table 1. They were obtained by using the kinetic analysis described above with kD obtained by extrapolation of plots of kX/kD versus χD. As shown by the data in Table 1, all three reactions occur with colossal H/D kinetic isotope effects in the forward direction. Within experimental error, the isotope effect appears solely in the redox step. To put the magnitudes of the isotope effects in perspective, the ratios k2(H2O)/k2(D2O) for the outer-sphere electron transfer reactions illustrated by the reaction in Eqs. 1, 3, and 2 are 2.8, 2.0, and 3.4 for the N, S, and P-based complexes, respectively.

Table 1. Isotope effects.

Reaction*
Rate constant PCET-N PCET-P PCET-S
kredKA(H2O), M-1·s-1 (2.74 ± 0.04) × 101 (1.48 ± 0.01) × 101 (6.77 ± 0.01) × 10-1
kredKA(D2O), M-1·s-1† (6.02 ± 0.03) × 10-2 (8.30 ± 0.07) × 10-2 (3.42 ± 0.05) × 10-2
KA(H2O), M-1 (4.43 ± 0.18) × 103 (2.15 ± 0.02) × 103 (1.33 ± 0.10) × 103
KA(D2O), M-1 (4.28 ± 0.04) × 103 (2.10 ± 0.02) × 103 (1.27 ± 0.08) × 103
kred(H2O), s-1 (6.19 ± 0.05) × 10-3 (6.94 ± 0.06) × 10-3 (5.09 ± 0.02) × 10-3
kred(D2O), s-1 (1.41 ± 0.04) × 10-5 (3.97 ± 0.05) × 10-5 (2.69 ± 0.02) × 10-5
kred(H2O)/kred(D2O) 439 ± 8 175 ± 5 189 ± 6
Open in a new tab
*

Conditions: 25.0 ± 0.1°C in 1:1 (vol/vol) CH3CN/H2O or 1:1 (vol/vol) CH3CN/D2O.

†

Obtained by extrapolation of plots of kH/kχ versus χD to χD = 1.

Electron transfer from Os(IV) to Q in these reactions is coupled to transfer of the N–H, S–H, or P–H protons. These are proton-coupled electron transfer reactions with electron transfer occurring from a largely dπ orbital on Os(IV) to the lowest π* acceptor orbital on Q and proton transfer occurring from a σ(N–H), σ(S–H), or σ(P–H) molecular orbital to a σ(sp2) acceptor orbital on Q. Hydrogen atom transfer from the N–H, S–H, or P–H bonds would result in high-energy intermediates containing ligand-based radicals such as trans-[OsIV(tpy)(Cl)2(•NN(CH2)4O)]+. Although the three reactions are closely related microscopically, it is worth noting that the proton-donor atom is directly bonded to Os(IV) in the N case and is one atom removed in the other two.

Coupled electron–proton transfer has been treated theoretically by a number of authors (21–28). The reactions studied here have been examined theoretically by use of a multistate continuum theory that treats the transferring H-atom quantum mechanically (29), developed by Hammes-Schiffer and coworkers (25–28). Important elements in this theory are the extent of electronic coupling between the electron transfer donor and acceptor, coupling with the solvent, and the extent of vibrational overlap for the transferring proton between the largely νN-H, νS-H, and νP-H vibrational levels in the initial state to νO-H levels in the final state; note the reaction in Eq. 9. Based on the results in ref. 29, the colossal kH/kD KIEs result from a relatively small overlap between the reactant and product H or D vibrational wavefunctions arising from large hydrogen transfer distances. The pattern of isotope effects within the N–H, S–H, and P–H series is a balance of factors: (i) the proton transfer distance, which increases in the order NH < SH < PH decreasing overlap; (ii) the ν(X–H) frequency, which increases in the order PH < SH < NH also decreasing overlap; (iii) Boltzmann population of levels above ν = 0 in the reactants where overlap is greater, the importance of which increases in the order PH > SH > NH; and (iv) the driving force ΔG°. Even though the proton transfer distance is longest for PH, it has the lowest KIE because of a favorable thermal population above ν = 0 in ν(P–H)/ν(P–D).

Acknowledgments

We acknowledge greatly useful conversations with Sharon Hammes-Schiffer. We are grateful to the National Science Foundation and the Los Alamos National Laboratory Directed Research and Development Program for support of this research.

Abbreviations: PCET-X, proton-coupled electron transfer involving X as the donor atom; KIE, kinetic isotope effect; Q, benzoquinone; tpy, 2,2′:6′,2″-terpyridine; Tp–, tris(pyrazol-1-yl)borate.

Footnotes

The free energy changes were calculated from the reduction potentials for the OsV/OsIV and Q/HQ• couples by the relationship
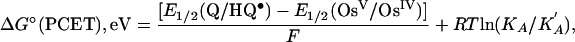graphic file with name M10.gif
with F the Faraday constant.

References

  • 1.Kohen, A. & Klinman, J. P. (1998) Acc. Chem. Res. 31, 397–404. [Google Scholar]
  • 2.Paddock, M. L., Feher, G. & Okamura, M. Y (2000) Proc. Natl. Acad. Sci. USA 97, 1548–1553. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Rucker, J. & Klinman, J. P. (1997) J. Am. Chem. Soc. 121, 1997–2006. [Google Scholar]
  • 4.Feher, G. (1998) Photosynth. Res. 55, 3–40. [Google Scholar]
  • 5.Binstead, R. A., Moyer, B. A., Samuels, G. J. & Meyer T. J (1981) J. Am. Chem. Soc. 103, 2897–2899. [Google Scholar]
  • 6.Thorp, H. H., Sarneski, J. E., Brudvig, G. W. & Crabtree, R. H (1989) J. Am. Chem. Soc. 111, 9249–9250. [Google Scholar]
  • 7.Che, C. M., Lau, K., Lau, T. C. & Poon, C. K. (1990) J. Am. Chem. Soc. 112, 5176–5181. [Google Scholar]
  • 8.Cukier, R. I. & Nocera, D. G (1998) Annu. Rev. Phys. Chem. 49, 337–369. [DOI] [PubMed] [Google Scholar]
  • 9.Roth, J. P., Yoder, J. C., Won, T. J. & Mayer, J. M (2001) Science 294, 2524–2526. [DOI] [PubMed] [Google Scholar]
  • 10.Hammes-Schiffer, S. (2001) Acc. Chem. Res. 34, 273–281. [DOI] [PubMed] [Google Scholar]
  • 11.Le Roy, R. G., Murai, H. & Williams, F. F (1980) J. Am. Chem. Soc. 102, 2325–2334. [Google Scholar]
  • 12.Garcia-Garibay, M. A., Gamarnik, A., Pang, L., Jenks, W. S. (1995) J. Am. Chem. Soc. 117, 10264–10275. [Google Scholar]
  • 13.Reinhardt, L. A., Svedruzic, D., Chang, C. H., Cleland, W. W. & Richards, N. G. J. (2003) J. Am. Chem. Soc. 125, 1244–1252. [DOI] [PubMed] [Google Scholar]
  • 14.Whittaker, M. M. & Whittaker, J. W. (2001) Biochemistry 40, 7140–7148. [DOI] [PubMed] [Google Scholar]
  • 15.Su, Q. J. & Klinman, J. P. (1998) Biochemistry 37, 12513–12525. [DOI] [PubMed] [Google Scholar]
  • 16.Binstead, R. A., McGuire, M. E., Dovletoglou, A., Seok, W. K., Roecker, L. E. & Meyer, T. J. (1992) J. Am. Chem. Soc. 114, 173–186. [Google Scholar]
  • 17.Trammell, S. A., Wimbish, J. C., Odobel, F., Gallagher, L. A., Narula, P. M. & Meyer, T. J. (1998) J. Am. Chem. Soc. 120, 13248–13249. [Google Scholar]
  • 18.Huynh, M. H. V. & Meyer, T. J. (2002) Angew. Chem. Int. Ed. 41, 1395–1398. [DOI] [PubMed] [Google Scholar]
  • 19.Huynh, M. H. V., White, P. S. & Meyer, T. J. (2000) Angew. Chem. Int. Ed. 39, 4101–4104. [DOI] [PubMed] [Google Scholar]
  • 20.Huynh, M. H. V., White, P. S. & Meyer, T. J. (1999) J. Am. Chem. Soc. 121, 4530–4531. [Google Scholar]
  • 21.Zhao, X. G. & Cukier, R. I. (1995) J. Phys. Chem. 99, 945–954. [Google Scholar]
  • 22.Cukier, R. I. (2002) J. Phys. Chem. B 106, 1746–1757. [Google Scholar]
  • 23.Shin, S. & Choi, S.-I. (2000) Chem. Phys. 259, 27–38. [Google Scholar]
  • 24.Georgierskii, Y. & Stuchebrukhov, A. A. (2000) J. Chem. Phys. 113, 10438–10450. [Google Scholar]
  • 25.Soudackov, A. & Hammes-Schiffer, S. (1999) J. Chem. Phys. 111, 4672–4687. [Google Scholar]
  • 26.Soudackov, A. & Hammes-Schiffer, S. (2000) J. Chem. Phys. 113, 2385–2396. [Google Scholar]
  • 27.Iordanova, N. & Hammes-Schiffer, S. (2002) J. Am. Chem. Soc. 124, 4848–4856. [DOI] [PubMed] [Google Scholar]
  • 28.Decornez, H. & Hammes-Schiffer, S. (2000) J. Phys. Chem. A 104, 9370–9384. [Google Scholar]
  • 29.Iordanova, N. (2003) Ph.D. dissertation (Pennsylvania State Univ., University Park).

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES