Abstract
Mediation analysis requires a number of strong assumptions be met in order to make valid causal inferences. Failing to account for violations of these assumptions, such as not modeling measurement error or omitting a common cause of the effects in the model, can bias the parameter estimates of the mediated effect. When the independent variable is perfectly reliable, for example when participants are randomly assigned to levels of treatment, measurement error in the mediator tends to underestimate the mediated effect, while the omission of a confounding variable of the mediator to outcome relation tends to overestimate the mediated effect. Violations of these two assumptions often co-occur, however, in which case the mediated effect could be overestimated, underestimated, or even, in very rare circumstances, unbiased. In order to explore the combined effect of measurement error and omitted confounders in the same model, the impact of each violation on the single-mediator model is first examined individually. Then the combined effect of having measurement error and omitted confounders in the same model is discussed. Throughout, an empirical example is provided to illustrate the effect of violating these assumptions on the mediated effect.
Keywords: Mediation, Measurement Error, Confounding, Sensitivity Analysis
Mediating variables are central to theoretical and applied research in psychology (Baron & Kenny, 1986; James & Brett, 1984; MacKinnon, 2008) and other disciplines because they provide information on the process by which one variable affects another variable. For example, mediating variables are used to explain how social norms and knowledge mediate the effect of an intervention to decrease the self-reported use of steroids and diet pills in female student athletes (Ranby et al., 2009). Other examples include how assignment to an intensive case management condition increases the number of contacts with housing agencies which in turn increases the number of days stably housed per month for homeless individuals (Morse, Calsyn, Allen, & Kenny, 1994) and how posttraumatic stress symptoms mediate the relation between childhood sexual abuse and self-injury (Weierich & Nock, 2008).
Recent developments in statistical mediation analysis have focused on the strong assumptions required to make causal inferences (e.g., Imai, Keele, & Tingley, 2010; MacKinnon, 2008; Pearl, 2011; Valeri & VanderWeele, 2013). Though not an exhaustive list of assumptions for the single-mediator model, four of the most discussed assumptions are: correct causal ordering of the variables in the model, variables are measured when exerting their influence on other variables (i.e., temporal precedence states that causes proceed effects in time such that changes in X must occur before changes in M which must occur before changes in Y), ensuring no variables that cause the relations between X, M, and Y are omitted from the model, and ensuring that X, M, and Y are measured without error. For more information on assumptions see MacKinnon (2008), Maxwell and Cole (2007), McDonald (1997), and VanderWeele (2015). Worries about whether these assumptions are reasonable in all situations has led many researchers (e.g., Bullock, Green, & Ha, 2010) to be critical of using statistical methods alone for mediation analysis, especially in situations where the mediator is not randomly assigned.
Testing of assumptions is an important, too often ignored, component of statistical mediation analysis. When any of the assumptions of the single-mediator model are violated, the parameter estimates from the mediation analysis may be biased and lead to incorrect conclusions regarding the presence and magnitude of a mediated effect. In general, the greater the degree of violation, the greater the bias. When two or more assumptions are violated, however, the pattern is more complicated. It might be the case that the violation of the second assumption increases the bias in the estimates, but it might also be the case that violation of the second assumption offsets the violation of the first assumption to a degree. The current paper explores this idea by considering the violation of two assumptions in the single-mediator case: omitting one or more confounding variables and measurement error. We first discuss each individually and then consider their combined effects on the estimates of the parameters in the single-mediator model. Throughout, we illustrate our results using an empirical example.
The Single-Mediator Model
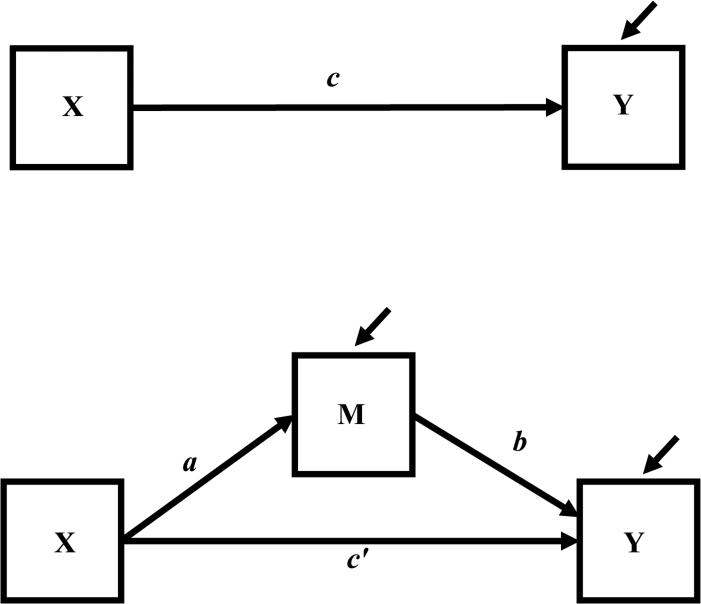
The single-mediator model is illustrated in Figure 1 where the arrows directed at M and Y represent residual errors. The indirect or mediated effect is equal to the product ab where a is the effect of the independent variable X on the mediator M and b is the effect of M on the dependent variable Y after controlling for X. The direct effect of X on Y that is not mediated is c′. The total effect, c, is equal to the sum of the indirect and direct effects
| (1) |
The relation in Equation 1 does not hold when M or Y is not continuous and may not apply to more complex models. The effects in Figure 1 can be estimated using a variety of strategies including finding the estimates separately using three ordinary-least-squares (OLS) regression equations
| (2) |
| (3) |
| (4) |
or simultaneously using structural equation modeling (SEM).
Figure 1.
The single-mediator model.
Empirical Example
In order to illustrate the single-mediator model we present a re-analysis of data originally presented by Morse et al. (1994) that is be used throughout our discussion of confounding and measurement error. As cited in the original study, up to 40% of the American homeless population has a mental illness. In addition to help with housing, income, and other social services, these individuals need mental health services, but often reject outpatient and other traditional treatments. They may, however, accept help in the form of day treatments, case management, and housing assistance (Morse et al., 1986). For this reason, Morse and colleagues compared the number of days a sample of mentally ill homeless individuals were stably housed after being randomly assigned to receive intensive case management or to a control group. Individuals in the intensive case management condition were assigned to a continuous treatment team clinical case manager, while individuals in the control condition were assigned to either a drop-in center or outpatient therapy, representing treatment-as-usual. For more information see Morse et al. (1994).
For the current example, the X variable (M = 0.42, SD = 0.494) represents random assignment to a treatment program of intensive case management (X = 1) or to a treatment-as-usual condition (X = 0).1 The mediator M (M = 10.39, SD = 11.473) is the number of contacts with agencies providing housing during the nine months after the intervention was initiated. The outcome Y (M = 15.55, SD = 13.047) is the number of days per month stably housed for a seven-month period that starts nine months after initiation of the intervention (i.e., Y is measured seven months after M was measured and 16 months after assignment to X). There are 109 cases and the observed correlations are: rXY = .248, rXM = .237, and rMY = .446. To put these in context, these correlations are slightly smaller than the medium and large effects, .3 and .5, described by Cohen (1988). All analyses were conducted using Mplus (Muthén & Muthén, 2015).2 The dataset and the setup and output files for all examples for Mplus and AMOS (IBM Corp, 2015) are available at (Link removed for review).
Table 1 contains the results for the single-mediator model in Figure 1, labeled Model 1. All of the estimates are positive and significant at the .05 level, except for c′. Based on these results, there is evidence to support the hypothesis that intensive case management increases the number of contacts with housing agencies which in turn increases the number of days per month stably housed. It is possible, however, that the relation between number of contacts and days stably housed is due, partially or completely, to an omitted variable that causes both. The impact of omitting such a variable on the estimate of the mediated effect is now considered.
Table 1.
Mediation parameter estimates and confidence intervals for the empirical example when there are one or more confounders of the M to Y relation.
| Model 1: | Model 2A: | Model 2B: | Model 2C: | Model 2D: | Model 2E: |
|---|---|---|---|---|---|
| Omitted | |||||
| Confounder (OC) | |||||
| cOC = 6.558 (0.248) [1.501, 11.367] | cT = 6.558 (0.248) [1.501, 11.367] | 6.558 (0.248) [1.501, 11.367] | 6.558 (0.248) [1.501, 11.367] | 6.558 (0.248) [1.501, 11.367] | 6.558 (0.248) [1.501, 11.367] |
| aOC = 5.502 (0.237) [1.179, 10.043] | aT = 5.502 (0.237) [1.179, 10.043] | 5.502 (0.237) [1.179, 10.043] | 5.502 (0.237) [1.179, 10.043] | 5.502 (0.237) [1.179, 10.043] | 5.502 (0.237) [1.179, 10.043] |
| bOC = 0.466 (0.410‡) [0.318, 0.675] | bT = 0.343† (0.302) [0.191, 0.505] | 0.239 (0.210) [0.065, 0.377] | 0.590 (0.519) [0.433, 0.860] | 0.287 (0.252) [0.128, 0.438] | 0.367 (0.322) [0.214, 0.537] |
| abOC = 2.566 (0.097) [0.505, 4.859] | abT = 1.887 (0.071) [0.394, 3.582] | 1.315 (0.050) [0.178, 2.543] | 3.245 (0.123) [0.670, 6.353] | 1.579 (0.060) [0.285, 2.989] | 2.017 (0.076) [0.412, 3.810] |
| c′OC = 3.992 (0.151) [−1.144, 8.869] | c′T = 4.671 (0.177) [−0.207, 9.602] | 5.243 (0.198) [0.432, 10.221] | 3.313 (0.125) [−1.938, 8.135] | 4.979 (0.188) [0.133, 9.898] | 4.541 (0.172) [−0.341, 9.462] |
Note. The estimates of b and c′ for Model 1 represent the biased estimates due to the omitted confounder(s), bOC and c′OC. The estimates of b and c′ for Models 2A – 2E represent the true values for that particular model, bT and c′T. Unstandardized estimates are presented first, followed by standardized estimates in parentheses. The 95% confidence intervals for the unstandardized estimates are in square brackets and are based on the percentile bootstrap with 1000 bootstrap samples. sC1 = 1, sX = 0.494, sM = 11.473, sY = 13.047, rXM = .237, and rC1M = .32
Bias: , where
Sensitivity analyses: .
When , then , so .
When , then , so .
Confounding of M and Y
A primary assumption of the single-mediator model estimated in Model 1 is that no variables that explain the relations between X, M, and Y, often called confounders, have been omitted from the model. Problems with omitted variables causing biased parameter estimates in the single-mediator model have been described by many others (see for example: Bullock et al., 2010; Clark, 2005; Cornfield et al., 1959/2009; Greenland & Morgenstern, 2001; Hafeman, 2011; Imai, Keele, & Yamamoto, 2010; Imai & Yamamoto, 2013; James, 1980; Judd & Kenny, 1981, 2010; Li, Bienias, & Bennett, 2007; Liu, Kuramoto, & Stuart, 2013; MacKinnon, 2008; MacKinnon, Krull, & Lockwood, 2000; Mauro, 1990; McDonald, 1997; Pearl, 2009; VanderWeele, 2008, 2013, 2015; VanderWeele, Valeri, & Ogburn, 2012). Recent work has provided a more formal treatment of the influence of confounding variables in general (Imai, Keele, & Yamamoto, 2010; VanderWeele, 2010). Multiple methods to adjust for confounding when measures of confounders are available including principal stratification (Jo, 2008) and inverse probability weighting (Coffman & Zhong, 2012). In addition, multiple authors have explored methods to investigate the sensitivity of results to confounding (Cox, Kisbu-Sakarya, Miočević, & MacKinnon, 2014; Imai, Keele, & Yamamoto, 2010; Imai & Yamamoto, 2013; Liu et al., 2013; MacKinnon & Pirlott, 2015; VanderWeele, 2008, 2010, 2013).
Consider the case in the empirical example presented here where X represents random assignment to levels of treatment. Judd and Kenny (2010; Holland, 1988; MacKinnon, 2008 and others) state that when X is a manipulated variable, such as random assignment, it can safely be assumed that no confounders of the X to M or X to Y relations exist provided all potential confounders are balanced across levels of X. A manipulated X variable does not remove potential confounders of the M to Y relation, however. If there exists a set of q confounders (C1, C2, ... Cq) of the M to Y relation, then Equation 4 becomes
| (5) |
Adapting work by Clarke (2005; see also Greene, 2003; Hanushek & Jackson, 1977) from the general OLS regression case, the biased estimates that would result from omitting the q confounders of the M to Y relation (i.e., estimating Equation 4 instead of Equation 5), bOC and c′OC, are equal to
| (6) |
| (7) |
Here bT and c′T are the true values, ek is the coefficient for the kth confounder, Ck, from Equation 5, fCkM.X is the partial regression coefficient for Ck regressed on M partialling out X, and fCkX.M is the partial regression coefficient for Ck regressed on X partialling out M.
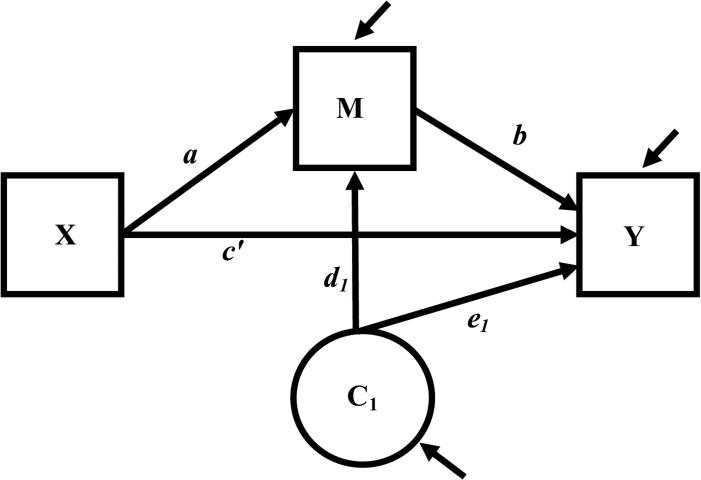
When there is a single confounder of the M to Y relation, C1, that is uncorrelated with X, as would occur when X is random assignment (Judd & Kenny, 2010) and illustrated in Figure 2, then Equations 6 and 7 can be rewritten as
| (8) |
| (9) |
where sX, sM, and sC1 are standard deviations. Equations 8 and 9 show that when bT and e1rC1M have the same sign, bOC is biased in the direction of bT (i.e., overestimated) while c′OC is biased in the opposite direction of c′T. The case where bT and e1rC1M have the same sign can be thought of as a case of consistent confounding because the relation of C1 to M and C1 to Y are consistent with the relation between M and Y. As described by Bullock et al. (2010), the consistent confounding case leads to an overestimate of b and in turn the mediated effect. This makes sense because when rC1X = 0, a and c are unaffected by omitting the confounder, but b is overestimated, so c′ must change in the opposite direction in order for Equation 1 to remain true. Note that Equations 8 and 9 are the same for standardized estimates and when X is continuous as long as X and C1 remain uncorrelated.
Figure 2.
The single-mediator model with a confounder C1 of the mediator to outcome relation.
Overestimating b is not the only possible result of omitting a confounder of the M to Y relation. First, it is possible for bT and e1rC1M to be opposite in sign, which can be thought of as inconsistent confounding. The bias in b and c′ due to omitting an inconsistent confounder is opposite to the bias due to an omitted consistent confounder. That is, c′OC is now biased in the direction of c′T, but bOC is biased in the opposite direction of bT leading to an underestimate or even a change in sign of the mediated effect. Second, it is possible for C1 to be correlated with X, even when X is a manipulated variable, if despite randomization sampling error creates groups unbalanced on pre-randomization levels of C1 (Judd & Kenny, 1981). Third, the values of C1 may change across time. If the randomization to levels of X created groups that were balanced on the pre-randomization levels of C1, but the groups differed in their values of C1 at some point after randomization, then it can be concluded that X caused a change in C1. This would mean that while C1 is a confounder of the M to Y relation, it is also a mediator of the X to M and X to Y relations. Though a variable that explains the M to Y relation and is caused by X is sometimes referred to as a post-treatment confounder, these variables are considered mediators for our purposes, not confounders. Regardless of the reason, when C1 and X are correlated, then a and c are biased when C1 is also omitted from Equations 2 and 3. In turn, the bias in bOC and c′OC reflects the bias in a and c in order to maintain the relation in Equation 1.
Finally, while discussing a single confounder of the M to Y relation provides a simple example to explore, it is much more likely that multiple confounders of the M to Y relation exist. As Clarke (2005) points out, when multiple variables are omitted from a model, the bias can increase, decrease, or remain the same compared to the bias caused by the first omitted variable, depending on the size and signs of relations between all variables. For the single-mediator model this can be seen by rewriting Equations 8 and 9 for the case where there is a second confounder, C2, that is also uncorrelated with X such that
| (10) |
| (11) |
When bT, e1rC1M, and e2rC2M, have the same sign, the effect of the second confounder is to increase the bias in bOC in the same direction as the first confounder. When e1rC1M and e2rC2M are opposite in sign, each confounder mitigates the bias caused by the other confounder. In rare situations, the bias caused by the two confounders could even cancel out exactly and result in unbiased estimates when both confounders are omitted such that bOC = bT and c′OC = c′T.
Omitted Confounder Example
To illustrate this existing work on how omitting confounders of the M to Y relation biases the parameter estimates from the single-mediator model, we return to Table 1 and the Morse et al. (1994) example. As a reminder, X is random assignment to a treatment program of intensive case management, M is the number of contacts with agencies providing housing during the nine months after the intervention was initiated, and Y is the number of days per month stably housed for a seven-month period that starts nine months after initiation of the intervention. Model 1 (i.e., Figure 1) includes only X, M, and Y, so the estimates of b and c′ from Model 1 are only unbiased with regards to confounders if no confounders of the M to Y relation exist. When this assumption is violated, then the estimates of b and c′ from Model 1 are biased and instead equal to bOC and c′OC. In order to determine the amount of bias caused by omitting one or more confounders from Model 1, bOC and c′OC must be compared to the unbiased estimates bT and c′T from models that include these confounders. Models 2A-2E (i.e., Figure 2) provide the unbiased estimates for five different combinations of confounders to which bOC and c′OC are compared. Note that this is somewhat counterintuitive as the incorrect model (Model 1) remains the same while the correct model (Models 2A-2E) changes.
The unbiased values of all coefficients for Models 2A-2E can be calculated directly using SEM by adding a latent variable for each omitted confounder and specifying the values of the relations between the confounders and the measured variables, as well as between the confounders. A confounder of the X to M or X to Y relation could be added to the model in a similar manner. For the model in Figure 2 with a single confounder the structural equation is
| (12) |
where d1, e1, and the variance of C1 need to be set to specific values. This approach differs from previous work in confounding that focuses on correlations between error terms rather than introducing the confounder as an explicit variable. For example, Imai, Keele, and Yamamoto (2010) emphasize the correlation of the residuals ρ of M and Y, which equals standardized d1e1.
For Model 2A the standardized values and (denoted by *) are both assumed to be equal to 0.32 to represent the case where the confounder has slightly less than medium partial effects on M and Y (MacKinnon, Lockwood, Hoffman, West, & Sheets, 2002).3 The unstandardized values of d1 and e1 are by multiplying, and by (SM / SC1) and (SY / SC1), respectively (Cohen, Cohen, West, & Aiken, 2003). Since sM = 11.473 and sY = 13.047, if the variance of C1 is set to one, the unstandardized values of d1 and e1 are equal to 3.671 and 4.175. From Model 2A in Table 1, bT = 0.343 and c′T = 4.671. Here rC1X = 0, so rC1M = .32. With rXM = .237, we have all of the values needed to compute bOC and c′OC directly using Equations 8 and 9, such that bOC = 0.466 (as shown in the note for Table 1) and c′OC = 3.992, which are the estimates found for Model 1. As expected for a single consistent confounder where all of the effects are positive and rC1X = 0, the values of a and c are unchanged. The value of bOC in Model 1 is positively biased (0.123 = 0.466 – 0.343) compared to the true value in Model 2A, whereas c′OC is negatively biased (−0.679 = 3.992 – 4.671). This results in a positively biased estimate of the mediated effect in Model 1, though ab is statistically significant in both models. Note that the same relation is seen for the standardized estimates of bOC and c′OC which can be calculated in the same manner as the unstandardized estimates by using the standardized values of bT and c′T in Model 2A and setting sY = sM = sC1 =1.
Equations 8 and 9 show that as the magnitude of the effect of the confounder on M and/or Y is increased, the amount of bias increases as well. This increase in bias is illustrated by Model 2B, which is identical to Model 2A except that is set to correspond to a large partial effect of 0.59 (MacKinnon et al., 2002) so that e1 = 7.697. As e1 increases from Model 2A to Model 2B, the positive bias in bOC increases from 0.123 to 0.227 (0.466 – 0.239), while c′OC becomes more negatively biased. This leads to a more positively biased estimate of the mediated effect in Model 1 as well, though ab is statistically significant in both models.
As described previously, an omitted confounder does not always result in this pattern of bias. Model 2C represents the inconsistent confounding case where , but . Using the new negative value of e1 (−4.175) to get the true values from Model 2C, bT = 0.590 and c′T = 3.313, Equations 8 and 9 again give the values of bOC and c′OC in Model 1. Unlike in the consistent confounding case in Models 2A and 2B, bOC is now negatively biased (−0124 = 0.466 – 0.590) compared to bT, though still significant, and c′OC is positively biased (0.679 = 3.992 – 3.313), resulting in ab now being negatively biased in Model 1.
Models 2D and 2E illustrate the impact of adding a second confounder, C2, of the M to Y relation to the model in Figure 2 that is also uncorrelated with X. This requires adding a second latent variable to the model and specifying values for the variance of C2, the effects of C2 on M and Y, d2 and e2, and the correlation between C1 and C2. In Model 2D, C1 is a consistent confounder with as in Model 2A, while C2 is a consistent confounder with small partial effects such that (MacKinnon et al., 2002). The variance of C2 is set to one, so the unstandardized values for d2 and e2 are 1.606 and 1.827, respectively. In addition, the correlation between C1 and C2 is set equal to .3, as it would be expected that the confounders were related, so rC1M and rC2M are .362 and .236, respectively.4 Table 1 shows the true values for Model 2D are bT = 0.287 and c′T = 4.797. When these values are compared to the biased estimates in Model 1, it can be seen that the positive bias in b increased from 0.123 (Model 1 vs. Model 2A) to 0.179 (Model 1 vs. Model 2D) when C2 was added to the model, while the negative bias in c′ also increased. As all of the relations are positive in Model 2D, Equations 10 and 11 show that the effects of C1 and C2 combine to create more bias in the estimates.
Model 2E is identical to Model 2D except that to represent the situation where C2 is an inconsistent confounder while C1 is a consistent confounder.5 The true values for Model 2E in Table 1 are bT = 0.367 and c′T = 4.541. As in Model 2D, rC1M = .362 and rC2M = .236, so Equations 10 and 11 can be used to compute bOC and c′OC in Model 1. When the true values are compared to the biased estimates, it can be seen that the positive bias in b decreased from 0.123 (Model 1 vs. Model 2A) to 0.099 (Model 1 vs. Model 2E) when C2, an inconsistent confounder, is added to the model containing C1, a consistent confounder. Equation 10 shows that the effects of C1 and C2 are now creating bias in opposite directions, so the two effects combine to create less biased estimates than when C1 is the only omitted confounder.
Sensitivity to an Omitted Confounder
Liu et al. (2013) describe two types of sensitivity analyses. Sensitivity analyses from the epidemiological perspective focus on the extent to which a significant relation between two variables can be explained by an omitted variable. The results presented in Table 1 represent epidemiological sensitivity analyses because they illustrate how the confounder explains part of the relation between M and Y (i.e., the difference between bT and bOC). In contrast, sensitivity analyses from the statistical perspective focus on how large the effect of an omitted variable needs to be in order to make a statistically significant effect zero or nonsignificant. Because X is assumed to be measured without error and uncorrelated with C1 here, the estimate of a is unaffected by an omitted confounder. Therefore, a statistical sensitivity analysis to determine how large the effect of an omitted confounder must be for the mediated effect to be zero in the Morse et al. (1994) data must focus on b.
Using standardized values to ease interpretation, Equation 8 can be used to show that when = 0.387; see the note for Table 1 for more details. If , then both effects are equal to .622. While these effects are both large (Cohen, 1988; MacKinnon et al., 2002), it may be plausible for a confounder with effects of this size to exist for this set of variables. Mauro (1990) discusses the difference between the limits of possibility (i.e., the largest possible value of rC1M is 1.0, which results in ) for omitted variables versus the limits of plausibility based upon theory or the effects found in prior research (e.g., if the largest plausible value of rC1M we would expect to see in these data is .800, the smallest value could be is 0.484). This means that rather than just reporting the possible values from a sensitivity analysis, considerable attention needs to be given to the plausibility of a confounder with effects of this size existing for a specific set of variables. Examining the situation where shows that not all possible combinations of effects are equally plausible for these data. Consider the case where rC1M = .5, a large correlation, which results in , a very large, though potentially plausible, partial effect. If rC1M = 3, however, then , an extremely large partial effect which may not be plausible for these data. Note that here it is assumed that b and are both positive because only a consistent confounder could cause b to become zero. An inconsistent confounder would cause the estimate of b to increase if it were added to the model as shown in Table 1. If multiple confounders were omitted, some consistent, others inconsistent, the combined effect of these multiple confounders would need to be known in order determine the effect on the significance of the mediated effect.
Equation 8 could also be used to determine how large the effect of a confounder would need to be in order for b to become nonsignificant.6 For a Type I error rate of .05, the two-tailed critical values for in the example are t(106) = ±1.987. The standard error for is 0.077, so using this value, must be 0.153 (= 1.987 * .077) or larger to be statistically significant. When , then as illustrated in the note for Table 1. If , then both effects must be .493 or larger for the effect to no longer be significant. When rC1M is .3 or .1, then must be 0.810 and 2.430 (or larger), respectively. While 0.810 is a very large partial effect, it may still be plausible for these data. A partial effect of 2.430 is so large, however, that an omitted confounder with such a large effect on Y seems implausible for these data.
Measurement Error in M and Y
In addition to the no omitted confounder assumption, another commonly violated assumption of the single-mediator model is that X, M, and Y must be perfectly reliable to ensure the observed estimates of relations among variables are not biased by measurement error (Baron & Kenny, 1986; Hoyle & Kenny, 1999; VanderWeele et al., 2012). Measurement error refers to any irrelevant factors that cause a score on a variable besides the theoretical construct of interest. When a variable M is measured with error, the observed variance, , is overestimated such that the true variance, , is equal to
| (13) |
where rMM is the reliability of M (Kenny, 1979). While measurement error affects the variances of variables that are not perfectly reliable, measurement error does not affect the covariances provided the errors themselves are independent. In OLS regression, the unstandardized parameter estimates are a function of the covariances between all variables in the model and the variances of the predictors, but not the variance of the outcome variable (Cohen et al., 2003). Therefore, only measurement error in the predictors, not the outcome variable, affects the unstandardized estimates.
When X represents random assignment to treatment, X can safely be assumed to be measured without error (Judd & Kenny, 2010), but the same assumption cannot reasonably be made for M and Y in most situations. A perfectly reliable X leads to unbiased unstandardized estimates of a and c, regardless of the amount of measurement error in M or Y. The unstandardized estimates of b and c′ are biased by measurement error in M, but not Y. Kenny (1979) shows that when rXX = 1, the unstandardized estimates of b and c′ that are biased due to measurement error in M, bME and c′ME, are equal to
| (14) |
| (15) |
where ω is the reliability of M after partialling out X
| (16) |
and rXM is the observed correlation between X and M. It should be noted that Equations 14, 15, and 16 are the same when X is a perfectly reliable continuous variable.
Because ω is less than one whenever rMM is less than one, bME would be biased in the opposite direction from bT, resulting in attenuation of bME when . When ab and c′ have the same sign, the effect is referred to as consistent mediation because the effect of X on Y is consistent regardless of whether the effect is direct or indirect through M. In the consistent mediation case, c′ME is biased in the same direction as c′T, overestimating the effect. This can also be seen from Equation 1 because if c and a remain constant, when b is attenuated, c′ must be overestimated in order to maintain the relationship between c and the other parameters. Inconsistent mediation occurs when ab and c′ are opposite in sign (MacKinnon, Krull, & Lockwood, 2000). In inconsistent mediation, bME is again attenuated when , but c′ME is biased in the opposite direction as c′T, either underestimating c′T or even changing the sign.
Unlike the unstandardized estimates, the standardized parameter estimates in the single-mediator model are based on correlations and therefore are biased by measurement error in both the predictors and the outcome. The effect of measurement error on the correlation between two variables M and Y is equal to
| (17) |
where rMY is the observed correlation between M and Y, rMM is the reliability of M, rYY is the reliability of Y, and rMTYT is the true correlation between M and Y. Because the reliability of a variable measured with error is less than one, Equation 17 shows that the observed correlation becomes more attenuated compared to the true correlation, regardless of sign, as one or both of the variables’ reliabilities decline. The standardized estimate for an OLS regression model with a single predictor is equal to the correlation between the predictor and the outcome (Cohen et al., 2003). Hence, the standardized estimates of a and c (denoted by *) that are biased due to measurement error, and , when X is perfectly reliable are equal to
| (18) |
| (19) |
The true standardized values are equal to the true correlations, and . As rMM and rYY are less than one when M and Y are not perfectly reliable, the effect of measurement error in M and Y is to attenuate and in comparison to their true values.
When X is perfectly reliable, the standardized estimates of b and c′ that are biased due to measurement error,7 and , are equal to
| (20) |
| (21) |
In the standardized case, the bias in b and c′ is now dependent on the reliabilities of M and Y. When rMM > rYY, is more attenuated compared to , but when rMM < rYY, is less attenuated than . The value of could therefore be positively biased, negatively biased, or even unbiased.
Measurement Error Example
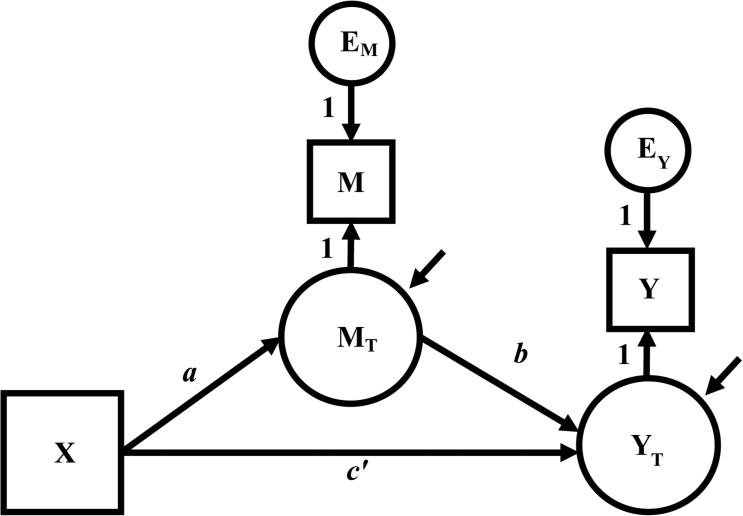
To illustrate the existing work on the effect of measurement error on the parameter estimates from the single-mediator model, we again return to the Morse et al. (1994) example. In Table 2, Model 1 (i.e., Figure 1) assumes that X, M, and Y are all measured without error. When M and/or Y are measured with error, then the estimates b and c′ from Model 1 are biased and instead equal to bME and c′ME. Determining the amount of bias requires comparing these values to the unbiased estimates from models that account for the measurement error. Models 3A-3C (i.e., Figure 3) provide the unbiased estimates bT and c′T for three different combinations of measurement error to which bME and c′ME are compared. Again, note that the incorrect model (Model 1) remains the same while the correct model (Models 3A-3C) changes.
Table 2.
Mediation parameter estimates and confidence intervals for the empirical example for different reliabilities of M and Y when X is perfectly reliable.
| Model 1: | Model 3A: | Model 3B: | Model 3C: | Model 1–IM:† | Model 3A–IM: |
|---|---|---|---|---|---|
| Measurement | rMM = .8 | rMM = .8 | rMM = .6 | Measurement | rMM = .8 |
| Error (ME) | rYY = 1.0 | rYY = .8 | rYY = .8 | Error (ME) | rYY = 1.0 |
| cME = 6.558 (0.248) [1.501, 11.367] | cT = 6.558 (0.248) [1.501, 11.367] | 6.558 (0.278) [1.501, 11.367] | 6.558 (0.278) [1.501, 11.367] | cME = 6.557 (0.248) [−0.169, 13.623] | cT = 6.557 (0.248) [−0.169, 13.623] |
| aME = 5.502 (0.237) [1.179, 10.043] | aT = 5.502 (0.265) [1.179, 10.043] | 5.502 (0.265) [1.179, 10.043] | 5.502 (0.306) [1.179, 10.043] | aME = −5.500 (−0.237) [−11.061, −0.184] | aT = −5.500 (−0.265) [−11.060, −0.184] |
| bME = 0.466 (0.410) [0.318, 0.675] | bT = 0.592† (0.465) [0.401, 1.000] | 0.592 (0.520) [0.401, 1.000] | 0.809 (0.616) [0.514, 2.186] | bME = 0.608 (0.535) [0.400, 0.812] | bT = 0.773 (0.608) [0.512, 1.047] |
| abME = 2.566 (0.097) [0.505, 4.859] | abT = 3.256 (0.123) [0.664, 7.168] | 3.256 (0.138) [0.664, 7.168] | 4.453 (0.188) [0.867, 13.796] | abME = −3.344 (−0.127) [−7.015, −0.076] | abT = −4.254 (−0.161) [−9.069, −0.096] |
| c′ME = 3.992 (0.151) [−1.144, 8.869] | c′T = 3.302 (0.125) [−2.042, 8.053] | 3.302 (0.140) [−2.042, 8.053] | 2.105 (0.089) [−7.139, 7.282] | c′ME = 9.902 (0.375) [3.859, 15.886] | c′T = 10.811 (0.409) [4.666, 17.185] |
Note. The estimates of b and c′ for Models 1 and 1–IM represent the biased estimates due to measurement error, bME and c′ME. The estimates of b and c′ for Models 3A – 3C and 3A–IM represent the true values for that particular model, bT and c′T. Unstandardized estimates are presented first, followed by standardized estimates in parentheses. The 95% confidence intervals for the unstandardized estimates are in square brackets and are based on the percentile bootstrap with 1000 bootstrap samples. Regular bootstrap confidence intervals are not available in Mplus when the individual data are not used, so the 95% confidence intervals for Models 1-IM and 3A-IM were created using the MONTECARLO command in Mplus with 1000 replications. rXM = .237.
Bias: bME = ωbT = .788*.592 = .466, where
Figure 3.
Modeling measurement error in the mediator and outcome variable in the single-mediator model.
The unbiased values of all coefficients for Models 3A-3C can be calculated directly using SEM if the reliabilities are known. The structural model for Figure 3 is
| (22) |
and assumes X is perfectly reliable because it represents random assignment to levels of treatment. The model accounts for measurement error in M and Y by adding the latent variables MT, YT, EM, and EY based on classical test theory. Here MT and YT are the true values of M and Y, and EM and EY are error terms such that M = MT + EM and Y = YT + EY (McDonald, 1999). It follows that since M and Y are the only measures of MT and YT, the paths from M to MT and Y to YT are set to one as illustrated in the measurement model for M and Y
| (23) |
The only remaining quantities needed are the variances of MT and YT. From Equation 13, the variance of MT equals which is achieved by setting the variance of EM to . This procedure is repeated for Y by setting the variance of EY to . The mediation parameters now involve MT and YT, so the estimates equal the true values. The same strategy is used to account for measurement error in X when necessary.
Model 3A represents the case where rYY = 1.0 and rMM = .8. As rXX = 1.0, the unstandardized estimates of a and c are the same in Model 1 and Model 3A. Using Equation 16 with rMM = .8 and rXY = .237, ω = 0.788. Inputting ω and the true values from Model 3A into Equations 14 and 15 gives bME = 0.466 (as shown in the note for Table 2) and c′ME = 3.992, which are the measurement error biased estimates in Model 1. Since all of the effects are positive here, when X is perfectly reliable, the effect of measurement error in M is to negatively bias bME (−0.126 = 0.466 – 0.592) and positively bias c′ME (0.690 = 3.992 – 3.302) compared to the true values. Hence, the mediated effect in Model 1 is underestimated. The same pattern is seen when comparing the standardized estimates of b and c′, from Model 3A to those in Model 1, which can be calculated using Equations 20 and 21. In addition, the standardized estimate of a is attenuated.
Model 3B keeps rMM = .8, but adds measurement error to Y such that rYY = .8. Because in our model Y is only an outcome and never a predictor, measurement error in Y has no effect on the unstandardized estimates. Thus, the unstandardized values are the same for Models 3A and 3B, so the bias in bME and c′ME is also the same for Model 3A and 3B. The standardized estimates are affected by the measurement error in Y, however. Equations 18 and 19 can be used to compute and in Model 1, which are attenuated compared to the true values in Model 3B. Unlike the unstandardized estimates, the negative bias in increases from Model 3A (−0.055 = 0.410 – 0.465) to Model 3B (−0.110 = 0.410 – 0.520), while the positive bias in decreases from 0.026 (0.151 – 0.125) to 0.011 (0.151 – 0.140).
Model 3C illustrates how the amount of bias in b and c′ is directly related to the amount of measurement error in M. Decreasing rMM from .8 to .6 in Model 3C decreases ω from 0.788 to 0.576. Equations 14 and 15 show that decreasing ω increases the bias in bME and c′ME from Model 1 compared to their true values. Here the negative bias in bME increases from −0.126 (0.466 – 0.592) in Model 3B to −0.343 (0.466 – 0.809) in Model 3C, as the positive bias in c′ME increases from 0.690 (3.992 – 3.302) to 1.887 (3.992 – 2.105). This also increases the bias in all of the standardized estimates, except for c*.
The values for a, b, and c′ are all positive for the Morse et al. (2004) data, which is an example of consistent mediation. In order to illustrate the effect of measurement error in the inconsistent mediation case, the observed covariance matrix for the Morse et al. data was altered so that the sign of the covariance between X and M is negative, while all of the other covariance values remained positive. Note that we are not simply reversing the scale of a variable here, but are instead artificially altering the covariance matrix to produce inconsistent mediation for illustration purposes only. Hence, the results based on the altered covariance matrix should not be interpreted substantively. Two models, Model 1–IM and 3A–IM, are fit to the altered covariance matrix. Model 3A-IM is identical to Model 3A with rMM = .8 and rYY = 1.0, and contains the true values for the estimates in the inconsistent mediation case. Model 1–IM is identical to Model 1 so it does not correct for measurement error in M or Y and now provides the measurement biased estimates for the inconsistent mediation case. As shown in Table 2, the values for cME and aME in Model 1–IM are the same magnitude as in the consistent mediation case in Model 1, except that a is now negative. The values for bME and and c′ME in Model 1–IM both remain positive, but have changed from Model 1. As in the consistent mediation case, bME is negatively biased (−0.165 = 0.608 – 0.773) compared to the true value in Model 3A–IM, but unlike the consistent mediation case, c′ME is now also negatively biased (−0.909 = 9.902 – 10.811). The same pattern is seen for the standardized estimates.
Sensitivity to Measurement Error
Table 2 illustrates how different amounts of measurement error in M affect the measurement error biased b coefficient (bME), which are sensitivity analyses from the epidemiological perspective (Liu et al, 2013). Because bT is always larger than bME for the Morse et al. (1994) data, measurement error can never cause a significant bME to become nonsignificant or a nonzero bME to become zero for the example presented here. Hence, there is no need here to conduct a statistical sensitivity analysis for the mediated effect for the effect of measurement error.
Measurement Error and Confounding in the Same Model
The effects of omitting a confounder of the M to Y relation or measuring these variables with error have been examined separately up to this point. Violations of these two assumptions are likely to co-occur, however. The effect of simultaneously violating both assumptions has not been investigated previously in the mediation literature, so the effect of violating both assumptions simultaneously is now discussed. Consider again the model in Equation 5 where there are q confounders of the M to Y relation. When M, Y, or any of the confounders are measured with error, the unstandardized estimates of b and c′ when a set of q confounders of the M to Y relation are omitted from the model and any of the variables are measured with error, bOCME and c′OCME, are
| (24) |
| (25) |
Here bME.C and c′ME.C are the estimates of b and c′ that partial out the effect of the confounders but are biased due to measured error. And ekME, fCkX.MME, and fCkM.XME have the same interpretations as in Equations 6 and 7 except that these values are biased due to measurement error.
When examined separately, the effects of measurement error and omitted confounders on the magnitude and direction of the bias in the parameter estimates for the single-mediator model have been shown to depend on the pattern of correlations, the reliabilities, and the number of confounders. As illustrated in Equations 24 and 25, describing the combined bias in bOCME and c′OCME in the general case is difficult without knowing at least some of these quantities. To simplify the discussion, consider the example previously described where X is perfectly reliable, but M and Y are measured with error, and there is a single confounder of the M to Y relation that is uncorrelated with X, C1. In this case, Equations 8 and 9 can be combined with Equations 14 and 15 to give the joint effect for unstandardized b and c′ as
| (26) |
| (27) |
Note that rC1M and rXM are the observed correlations that are biased due to measurement error in M, not the true, unbiased correlations. And as before, a and c are unaffected by measurement error in M or Y, or omitted confounders of the M to Y relation.
As shown in Table 1, when b is positive and the mediation is consistent, measurement error negatively biases b. Table 2 shows that a consistent omitted confounder positively biases b. Therefore, in the consistent mediation, consistent confounding case, measurement error and an omitted confounder have opposing effects on bOCME. Therefore, the overall bias in bOCME depends on whether measurement error or the omitted confounder has a stronger effect. That is, when the effect of measurement error is larger than the effect of the confounder, bOCME is negatively biased. However, when the effect of the omitted confounder is larger than the effect of measurement error, bOCME would be positively biased. These opposing effects are easier to see for c′OCME as the effect of measurement error [aTbT(1 – ω)] and the effect of the omitted confounder have opposite signs, such that measurement error opposes the bias caused by the omitted confounder and vice versa. This also means that when
| (28) |
the effects are exactly equal in magnitude but opposite in sign, resulting in perfectly unbiased estimates of b and c′. While it may be nearly impossible in practice to find an empirical situation that satisfies the relation in Equation 28, if the magnitude of one of the individual effects is known, the magnitude of the other effect necessary to perfectly oppose the first effect can be calculated.
Even in the rare circumstances where the combined effect produces unbiased unstandardized estimates, the standardized coefficients are still usually biased because they are also affected by measurement error in Y. In the combined condition, the omitted confounder does not affect a* or c*, but these values are attenuated due to measurement error in M and Y as shown in Equations 18 and 19. The equations for and are equal to
| (29) |
| (30) |
and show that when the unstandardized estimates are unbiased, is only unbiased when rMM = rYY and is unbiased only when rYY = 1.0.
Measurement Error and Omitted Confounder Example
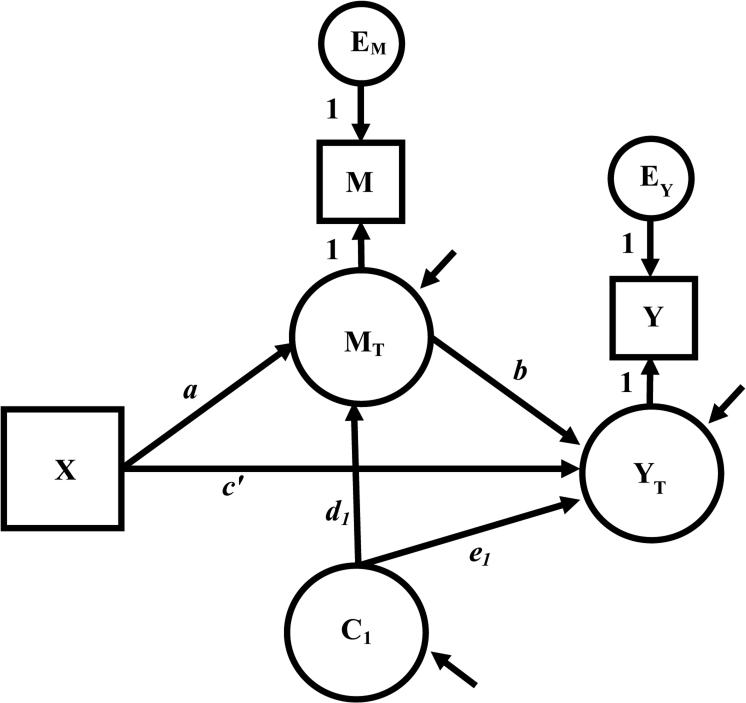
To illustrate the combined effect of measurement error and omitting a confounder in the same single-mediator model, we return a final time to the Morse et al. (1994) example. The unbiased values for all parameter estimates in the model that includes measurement error and confounding can be estimated simultaneously by combining the confounder model in Figure 2 with the measurement error model in Figure 3, the result of which is shown in Figure 4. The model in Figure 4 is specified in the same manner as the previous models with the exception that d1 and e1 now are directed to MT and YT rather than M and Y. As a result, d*1 and e*1 must be multiplied by (sMT / sC1), and (sYT / sC1), where and , to find the unstandardized values.
Figure 4.
The single-mediator model with measurement error in M and Y, and a confounder C1 of the M to Y relation.
As the effects of measurement error and an omitted confounder are opposing in the consistent case, the joint effect of measurement error and an omitted confounder on the parameter estimates in the empirical example is determined by which effect is larger. That is, when the effect of measurement error is larger, then bOCME is negatively biased and c′OCME is positively biased, though less so than if there were no confounders. Alternatively, when the effect of the omitted confounder is larger, then bOCME is positively biased and c′OCME is negatively biased, though again less so than if all of the variables are perfectly reliable. It is also possible in very specific and likely rare situations for the individual effects to perfectly cancel one another out, resulting in bOCME and c′OCME being unbiased.
To illustrate these three possible joint effects, Table 3 contains the results for four models, labeled Models 4A-4D. Each of these models accounts for measurement error in M and Y, as well as a single omitted confounder of the M to Y relation. These combined models can now be thought of as the unbiased models with the models in Table 1 only accounting for the omitted confounders and the models in Table 2 only accounting for measurement error. As a result, the effects of the confounders for Models 2A – 2E now represent the effects of the confounders biased due to measurement error (i.e., d1ME and e1ME). The estimates from the single-mediator model that omits all confounders and does not account for measurement error (i.e., Figure 1) is labeled Model 1 and provides the biased estimates aOCME, bOCME, and c′OCME to which all other models are compared.
Table 3.
Mediation parameter estimates and confidence intervals for the empirical example for different reliabilities of M and Y when X is perfectly reliable and there are one or more confounders of the M to Y relation.
| Model 1: | Model 4A: | Model 4B: | Model 4C: | Model 4D: | Model 4A-IM: |
|---|---|---|---|---|---|
| Omitted Confounder and Measurement | |||||
| Error (OCME) | rMM = .6, rYY = .8 | rMM = .9, rYY = .8 | rMM = .75, rYY = .8 | rMM =.6, rYY =.8 | rMM =.6, rYY =1 |
| cOCME = 6.558 (0.248) [1.501, 11.367] | cT = 6.558 (0.278) [1.501, 11.367] | 6.558 (0.278) [1.501, 11.367] | 6.588 (0.278) [1.501, 11.367] | 6.588 (0.278) [1.501, 11.367] | 6.557 (0.248) [−0.169, 13.623] |
| aOCME = 5.502 (0.237) [1.179, 10.043] | aT = 5.502 (0.306) [1.179, 10.043] | 5.502 (0.250) [1.179, 10.043] | 5.502 (0.273) [1.179, 10.043] | 5.502 (0.306) [1.179, 10.043] | −5.500 (−0.307) [−11.060, −0.184] |
| bOCME = 0.466 (0.410‡) [0.318, 0.675] | bT = 0.595† (0.453) [0.338, 1.470] | 0.384 (0.358) [0.212, 0.583] | 0.467 (0.397) [0.268, 0.818] | 1.023 (0.779) [0.645, 2.900] | 0.845 (0.574) [0.488, 1.267] |
| abOCME = 2.566 (0.097) [0.505, 4.859] | abT = 3.275 (0.139) [0.642, 9.373] | 2.111 (0.089) [0.423, 4.141] | 2.567 (0.109) [0.489, 5.585] | 5.631 (0.238) [1.078, 18.465] | −4.647 (−0.176) [−10.481, −0.099] |
| c′OCME = 3.992 (0.151) [−1.144, 8.869] | c′T = 3.283 (0.139) [−3.385, 8.202] | 4.447 (0.188) [−0.531, 9.358] | 3.991 (0.169) [−1.288, 8.877] | 0.927 (0.039) [−11.502, 6.318] | 11.204 (0.424) [4.713, 18.028] |
Note. The estimates of b and c′ for Model 1 represent the biased estimates due to measurement error and the omitted confounder, bOCME and c′OCME. The estimates of b and c′ for Models 4A – 4D and 4A–IM represent the true values for that particular model, bT and c′T. Unstandardized estimates are presented first, followed by standardized estimates in parentheses. The 95% confidence intervals for the unstandardized estimates are in square brackets and are based on the percentile bootstrap with 1000 bootstrap samples. Regular bootstrap confidence intervals are not available in Mplus when the individual data are not used, so the 95% confidence interval for Model 4A-IM was created using the MONTECARLO command in Mplus with 1000 replications.
Bias: , where and
Sensitivity analyses: For rMM = .6 and rYY = .8, ,
When , then , so .
When , then , so
Model 4A combines Models 2A and 3C such that rXX = 1.0, rMM = .6, and rYY = .8 with . In order to calculate the true values of the unstandardized mediation parameters, and must be multiplied by sM and sY, not sMT and sYT, even though they are still directed towards MT and YT, such that d1ME = 3.671 and e1ME = 4.175. With ω = 0.576 and rC1M = .32, the true values in Model 4A can be entered into Equations 26 and 27 to compute the combined bias estimates in Model 1 as bOCME = 0.466 (as shown in the note for Table 3) and c′OCME = 3.992. Here bOCME is negatively biased (−0.129 = 0.466 – 0.595) and c′OCME is positively biased (0.709 = 3.992 – 3.283) compared to Model 4A. Hence, the effect of measurement error is larger here than that of the confounder and the mediated effect is underestimated in Model 1. The same effect is seen for the standardized estimates. Note, however, that the negative bias of −0.129 in bOCME between Model 1 and Model 4A is less than the negative bias of −0.343 (0.466 – 0.809) between bOCME in Model 1 and the estimate of b in Model 3C in Table 2 that is corrected for measurement error but not for the opposing effect of the omitted confounder.
Model 4B is identical to Model 4A except that rMM = .9, decreasing the effect of measurement error. Compared to the true values in Model 4B, bOCME and c′OCME from Model 1 are now positively biased (0.082 = 0.466 – 0.384) and negatively biased (−0.455 = 3.992 – 4.447), respectively. As a result, the effect of the omitted confounder is larger than that of measurement error and the mediated effect is overestimated in Model 1; the same effect is seen for the standardized estimates. But again, the positive bias of 0.082 in bOCME between Model 1 and Model 4B is less than the positive bias of 0.123 (0.466 – 0.343) in bOCME between Model 1 and bME.C in Model 2A that is corrected for the omitted confounder but not the opposing effect of measurement error.
In Models 4A and 4B, the effects of measurement error and confounding were unbalanced. The value of rMM that would exactly balance the effect of confounding and produce unbiased unstandardized estimates can be computed using Equations 16 and 26. First, we solve for ω in Equation 26 using the following values: e1ME = 4.175 rXM = .237, rC1M = .32 sM = 11.473, aT = 5.502, and bT = 0.466. Next, the computed value for ω, 0.735, is used in Equation 16 to solve for rMM, which is equal to .75. We can verify this value by fitting Model 4C which is identical to Models 4A and 4B except that rMM = .75. As shown in Table 3, the uncorrected unstandardized estimates in Model 1 are equal to the true values in Model 4C, within rounding. Hence, in Model 4C the individual effects of measurement error and omitting the confounder are exactly equal, but opposite, such that the estimate of the mediated effect in Model 1 is unbiased. Alternatively, if rMM is known, the magnitude of a confounder that would cancel out the effect of the measurement error can be computed. Note that since rMM and rYY are less than one and not equal, none of the standardized estimates are unbiased.
While measurement error and a single consistent confounder have opposite effects, Table 1 also shows that for the empirical example, a single inconsistent confounder positively biases b, while negatively biasing c′, which is the same as the bias caused by measurement error. Model 4D is identical to Model 4A except for in order to illustrate the combined effect of an inconsistent confounder and measurement error. The results show that the negative bias in bOCME in Model 1 is much higher when the confounder is inconsistent in Model 4D (−0.557 = 0.466 – 1.023) than when the confounder is consistent in Model 4A (−0.129). The negative bias in bOCME of −0.557 between Model 1 and Model 4D is also much higher than the negative bias of −0.124 (0.466 – 0.590) between Model 1 and Model 2C in Table 1 when there was only an inconsistent confounder and no additive effect of measurement error.
Finally, Model 4A–IM illustrates the effect of inconsistent mediation with a consistent confounder and measurement error. Model 4A–IM is identical to Model 3A–IM except an omitted confounder C1 was added with . As before, Model 1–IM in Table 2 serves as the completely uncorrected model. The effect of measurement error on the inconsistent mediation model (Model 1–IM vs. Model 3A–IM) was to negatively bias b (−0.165 = 0.608 – 0.773) and c′ (−0.909 = 9.902 – 10.811). Adding the consistent confounder increases the negative bias in b (−0.237 = 0.608 – 0.845) and c′ (−1.302 = 9.902 – 11.204) between Model 1–IM and Model 4A–IM.
Sensitivity to a Confounder and Measurement Error
Determining the size of the effect of a confounder needed to exactly cancel out the bias caused by measurement error, as illustrated by Model 4C in Table 3, is a form of epidemiological sensitivity analysis. A statistical sensitivity analysis to determine how large the effect of a confounder is needed for to be zero that includes the effect of measurement error can be conducted using Equation 29. As illustrated in the note for Table 3, when rMM = .6 and rYY = .8 as in Model 4A, when . This is the same value as found for the statistical sensitivity analysis with no measurement error because when , Equation 29 simplifies to Equation 8.
Measurement error in M does play a role in how large the effect of a confounder is needed to make nonsignificant, however. Using the same critical values (t(106) = ±1.987) and standard error (0.077) as before, the effect is again nonsignificant when . When rMM = .6 and rYY = .8, then only when . This value is larger than for the case where all variables were perfectly reliable (i.e., ) because is attenuated compared to . Correcting for this attenuation requires a larger effect of the omitted confounder in order make the effect nonsignificant. Therefore, statistical sensitivity analyses that ignore the role of measurement error are likely to underestimate the size of the effect of an omitted confounder needed to change a significant effect to a nonsignificant effect.
Discussion
Most users of tests of statistical mediation have assumed the best-case scenario where all assumptions of the model are met, including all variables measured without error and no confounders omitted from the model. When any assumption of the single-mediator model is violated, the usual result is a biased estimate of the mediated effect. In general, the greater the violation, the greater the bias. When the bias comes from two different sources, the combined effect can result in an estimate of the mediated effect that is more biased, less biased, or, in very rare situations, unbiased. As described here and shown in the empirical example, the bias in the mediated effect due to measurement error is often in the opposite direction as the bias due to confounding. This can lead to the situation where correcting for only one source of bias can produce more biased estimates when both sources of bias are present. In most situations, however, failing to correct for measurement error, a confounding variable, or both still likely result in more biased parameter estimates.
Our primary goal here is to raise awareness of the importance of measurement error and confounding in mediation analysis by describing how violating these assumptions affect mediation analysis, illustrated by an applied mediation example. As the magnitude and direction of the bias is not always predictable beforehand, researchers should strive to develop and use the most reliable measures of M that are possible to reduce bias. Latent variable models can then be used to remove any remaining bias due to measurement error (Ledgerwood & Shrout, 2011; MacKinnon, 2008). Researchers should also routinely identify and measure potential confounders when possible so these variables can be included in the model. Sensitivity analyses can be used to determine how large of an omitted confounder is needed for a significant effect to become nonsignificant or zero when the mediator is measured with error. The plausibility of such confounders existing for a specific study can then be discussed. Note that while sample size is an important factor when considering statistical significance in a sensitivity analysis, the bias in the estimates of the mediated effect described here is unaffected by sample size.
The equations presented in this article provide a way for researchers to investigate the extent to which measurement error and omitted confounders may alter estimates in the single-mediator model. Given that there may be multiple omitted confounders that exert their influences at different times and the true effects of each confounder are likely unknown, values to be used in these equations can be chosen based upon many different criteria. For example, values can be found by using the theoretical relation between a specific omitted variable and the included variables, by using prior research where the confounder was measured and included in a similar model, or by selecting values to examine the amount of bias in b and c′ that would result from omitting a confounder with specific effects (e.g., positive medium effects) on M and Y (see also Cox et al., 2014). Values of reliability used in the equations to assess how measurement error affects mediation analysis can be obtained from published studies and other prior information or by assessing how different hypothetical reliability values affect results. Perhaps a first goal for applied researchers who use mediation models is to obtain information about possible confounder effects and reliability of measures for their variables of interest. Routinely reporting information about reliability, suspected omitted confounders, and sensitivity analyses as part of all statistical mediation analysis results would go a long way towards providing information about the magnitude and direction of bias found in different research areas.
We wish to emphasize that researchers should not use the results presented here to justify ignoring measurement error and confounders. In order to cancel out completely, the effects of measurement error and the omitted variable need to be approximately equal. As shown in Table 3, as the reliability of M decreases, the size of the effect of the omitted variable needed to exactly cancel the effect of measurement error can become quite large. For very low reliabilities, the effects of the presumed omitted variable needed to cancel out the effect of measurement error are so large that it may not even be possible to find an effect that large in the social sciences. In turn, for omitted confounders with very large effects, in order to exactly cancel out the effect the reliability of the mediator would need to be so low that the measure of M would be essentially useless.
Additionally, the discussion of confounders was necessarily simplified here to one very specific scenario in order to clearly illustrate the potential impact of the single-mediator model simultaneously containing measurement error and omitted confounders. When cases are randomly assigned to levels of X, as assumed in the examples presented, then in most cases it can be assumed there are no confounders of the X to M or X to Y relation (Holland, 1988; Judd & Kenny, 2010; MacKinnon, 2008). There are exceptions to this, however, including a failure of the random assignment to create groups balanced on the pre-randomization level of the confounder, a post-treatment confounder that is actually a mediator, and attrition. Besides causing X and the confounder to be related, attrition represents another possible source of bias not considered here. If the data are missing due to M or Y, the data are missing not at random. If the data are missing due to the treatment or the confounder, then the data are missing at random (MAR). Because models for MAR data, such as full information maximum likelihood and multiple imputation, require the source of the missingness to be included in the model to obtain unbiased estimates (Enders, 2010), data missing due to treatment should be ignorable in the example presented here. Data missing due to the confounder, however, are nonignorable because the omitted confounder is by definition not included in the model, resulting in further bias to the mediated effect.
Regardless of the reason for the relation, when a confounder that is related to X is omitted from the single-mediator model, then the estimates of a and c are biased and the bias in the estimates of b and c′ changes. If the confounder exerts its influence after the cases are randomly assigned to levels of X or if X is not a manipulated variable, such as in a purely observational study, then it is more likely that X and the confounder are related. When X and the confounder are related, consideration must be given to whether the confounder is only a confounder of the M to Y relation or is directly caused by X, which means the confounder is actually a mediator of the X to M and X to Y relations. As noted by numerous authors (e.g., Baron & Kenny, 1986), it is unlikely in the social and behavioral sciences for a single variable to completely mediate the relation between two other variables. Instead, single-mediator models represent a small portion of a much larger process consisting of numerous variables that are all interrelated, some causally, others noncausally. What complicates this further is that a single construct may have multiple roles depending on when it exerts its influence on the other variables in the model (e.g., is it time-varying or time-invariant) and when these effects are measured.
For example, consider the role of employment status, as suggested by one reviewer, on the Morse et al. (1994) data used in the empirical example. Employment status prior to random assignment of individuals to the intensive case management and treatment-as-usual groups, C1,t=0, is likely to be unrelated to X. In addition, pre-treatment employment status cannot be a mediator of the relation between treatment and number of housing agency contacts or days stably housed, since this variable is measured prior to treatment (i.e., temporal precedence states that an effect cannot exist prior to a cause). But pre-randomization employment status could be a confounder of the M to Y relation, reducing or completely removing the relation between M and Y when added to the model. It is highly unlikely that employment status would remain constant for all individuals across the sixteen months of the study, however. Therefore, employment status one month after assignment to treatment, C1,t=1, could also be a confounder of the M to Y relation and is more likely to be related to treatment than C1,t=0. But if the treatment was believed to take at least three months to have a measureable effect on any mediators, then C1,t=1 could not be a mediator of X. If employment status nine months after treatment began, C1,t=9, (i.e., at the same time as M is measured) is a confounder of the M to Y relation and was directly affected by treatment, then C1,t=9 would not be a confounder in the conventional sense. Instead it would be an additional mediator between intensive case management and days housed that could also reduce or completely remove the relation between agency contacts and days housed when added to the model. Finally, employment status sixteen months after assignment to treatment, C1,t=16, (i.e., at the same time Y is measured) is likely to be related to X, M, and Y, but cannot be a mediator or a confounder of the M to Y relation. That is four potential roles for employment status depending on when the effect of employment status is considered! This illustrates two important points. First, the timing of effects is as important as the variables themselves when identifying the role (e.g., mediator, outcome, confounder, and so on) of a specific variable and estimating mediated effects. And second, adding any variables to the single-mediator model, regardless of their role, can have a large impact the mediated effect and any conclusions based upon it.
Although many researchers understand that estimating mediation effects using cross-sectional data often results in biased estimates of longitudinal mediation effects (Maxwell & Cole, 2007), longitudinal data alone do not guarantee unbiased results. For example, the variables in the Morse et al. (1990) data presented here were each measured once at a different point in time (i.e., 0, 9, and 16 months), but that does not guarantee that the mediation results presented here are unbiased. Mitchell and Maxwell (2013) call this a sequential design and found that the estimates of the mediated effect from a sequential design are not necessarily less biased than those from cross-sectional designs. If the Morse et al. data had repeated measurements of the variables, as recommended by Mitchell and Maxwell, there would be a greater opportunity to explore the timing of effects, including whether a previous measure of M or Y served as a confounder of the M to Y relation. Even repeated measurements are not a guarantee of unbiased effects because the repeated measures must have the correct elapsed time between the first and last measurement, as well as the number and spacing of the repeated measurements, collectively known as the temporal design of the study (Collins & Graham, 2002).
What this means for researchers applying mediation models is that in most social and behavioral science studies, the assumptions that all variables are measured without error and that all relevant variables have been included in the model at the correct points in time are always violated. Rather than let the almost certain violation of these assumptions prevent us from using these models completely, we can recognize that even the best mediation models contain only the variables that were measured at specific times in that study and represent only a small part of what is probably a much larger causal process that may change over time. Thinking of every mediation model as a smaller piece of a larger longitudinal process forces us to consider how the effects in our estimated model would change if we were able to include these additional variables from the larger process or change based on when we measured the variables. And it is within this context that the results presented here should be considered. The information provided here should not be used as a reference that can be cited to justify ignoring measurement error and omitted confounders since in very specific situations the effects can cancel out, but as a tool to examine how the effects in an incomplete model may change if additional variables could be added to make a less incomplete model.
Acknowledgments
The ideas and opinions expressed herein are those of the authors alone, and endorsement by the author's institutions the National Institute on Drug Abuse is not intended and should not be inferred.
Funding: This work was supported by Grant DA009758 from the National Institute on Drug Abuse.
This research was supported in part by a grant from the National Institute on Drug Abuse (DA 009757).
Role of the Funders/Sponsors: None of the funders or sponsors of this research had any role in the design and conduct of the study; collection, management, analysis, and interpretation of data; preparation, review, or approval of the manuscript; or decision to submit the manuscript for publication.
Footnotes
The mean of 0.42 is a result of an unbalanced initial design (n = 52 for the intensive case management group and n = 126 for the control group) and unequal attrition in the two groups (13% for the intensive case management group and almost 50% in the control group), though the attrition was not found to be related to scores on the variables used here. See Morse et al. (1994) for more information.
Note that Mplus does not apply the finite sample correction when calculating variances. The standard deviations for X, M, and Y presented here were calculated using n rather than n – 1 so these values may be used later. Therefore, other programs that use the finite sample correction will provide slightly different variance values.
A standardized partial effect of 0.32 represents a partial effect that is 82% the size of a medium partial effect of 0.39 (MacKinnon et al., 2002) which is the same percentage the observed correlation between X and Y (.237) is to a medium correlation (.3, Cohen, 1988) resulting in a confounder with an approximately equal effect on M and Y relative to the variables in the model, but not larger than the overall effect between X and Y.
Here the values for rC1M and rC1M were computed directly in Mplus using the TECH4 command.
This situation may seem contrived since all of the relations in Model 2E are positive except e2, but the correlation matrix for Model 2E still contains all positive correlations when e2 is negative.
For simplicity's sake, the joint significance test is used. While one of the bootstrap tests would likely be preferred in practice, Fritz, Taylor, and MacKinnon (2012) recommend the percentile bootstrap over the bias-corrected bootstrap when the sample size is less than 500, as is the case here, and Fritz and MacKinnon (2007) showed the joint significance test has approximately the same statistical power as the percentile bootstrap when c′≠ 0, which also occurs here, so the results should be approximately equal for the percentile bootstrap.
In order to move from the unstandardized estimates to the standardized estimates, bT and bME are multiplied by (SMT/SYT) and (SM / SY), respectively, to obtain and (Cohen et al., 2003). From Equation 12, and , so the scales and are off by a factor of . As Equation 19 solves for , multiplying by puts the right side of the equation in the same scale as . This is also the purpose of the term in Equation 20.
Conflict of Interest Disclosures: Each author signed a form for disclosure of potential conflicts of interest. No authors reported any financial or other conflicts of interest in relation to the work described.
Ethical Principles: The authors affirm having followed professional ethical guidelines in preparing this work. These guidelines include obtaining informed consent from human participants, maintaining ethical treatment and respect for the rights of human or animal participants, and ensuring the privacy of participants and their data, such as ensuring that individual participants cannot be identified in reported results or from publicly available original or archival data.
Contributor Information
Matthew S. Fritz, Department of Educational Psychology, University of Nebraska - Lincoln
David A. Kenny, Department of Psychology, University of Connecticut
David P. MacKinnon, Department of Psychology, Arizona State University
References
- Baron RM, Kenny DA. The moderator-mediation variable distinction in social psychological research: Conceptual, strategic, and statistical considerations. Journal of Personality and Social Psychology. 1986;51:1173–1182. doi: 10.1037//0022-3514.51.6.1173. doi: 10.1037/0022-3514.51.6.1173. [DOI] [PubMed] [Google Scholar]
- Bullock JG, Green DP, Ha SE. Yes, but what's the mechanism? (Don't expect an easy answer). Journal of Personality and Social Psychology. 2010;98:550–558. doi: 10.1037/a0018933. doi: 10.1037/a0018933. [DOI] [PubMed] [Google Scholar]
- Clark KA. The phantom menace: Omitted variable bias in econometric research. Conflict Management and Peace Science. 2005;22:341–352. doi: 10.1080/07388940500339183. [Google Scholar]
- Cohen J. Statistical power analyses for the behavioral sciences. 2nd ed. Lawrence Erlbaum Associates; Mahwah, NJ: 1988. [Google Scholar]
- Cohen J, Cohen P, West SG, Aiken LS. Applied multiple regression/correlation analysis for the behavioral sciences. 3rd ed. Lawrence Erlbaum Associates; Mahwah, NJ: 2003. [Google Scholar]
- Coffman DK, Zhong W. Assessing mediation using marginal structural models in the presence of confounding and moderation. Psychological Methods. 2012;17:642–664. doi: 10.1037/a0029311. doi: 10.1037/a0029311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collins LM, Graham JW. The effect of the timing and spacing of observations in longitudinal studies of tobacco and other drug use: Temporal design considerations. Drug and Alcohol Dependence. 2002;68:S85–S96. doi: 10.1016/s0376-8716(02)00217-x. [DOI] [PubMed] [Google Scholar]
- Cornfield J, Haenszel W, Hammond EC, Lilienfeld AM, Shimkin MB, Wynder EL. Smoking and lung cancer: Recent evidence and a discussion of some questions. 1959. International Journal of Epidemiology. 2009;38:1175–1191. doi: 10.1093/ije/dyp289. doi: 10.1093/ije/dyp289. [DOI] [PubMed] [Google Scholar]
- Cox MG, Kisbu-Sakarya Y, Miočević M, MacKinnon DP. Sensitivity plots for confounder bias in the single mediator model. Evaluation Review. 2014;37:405–431. doi: 10.1177/0193841X14524576. doi: 10.1177/019384X14524576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Enders CK. Applied missing data analysis. Guilford; New York: 2010. [Google Scholar]
- Fritz MS, MacKinnon DP. Required sample size to detect the mediated effect. Psychological Science. 2007;18:233–239. doi: 10.1111/j.1467-9280.2007.01882.x. doi:10.1111/j.1467-9280.2007.01882.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fritz MS, Taylor AB, MacKinnon DP. Explanation of two anomalous results in statistical mediation analysis. Multivariate Behavioral Research. 2012;47:61–87. doi: 10.1080/00273171.2012.640596. doi:10.1080/00273171.2012.640596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greene WH. Econometric analysis. 5th ed. Prentice Hall; Upper Saddle River, NJ: 2003. [Google Scholar]
- Greenland S, Morgenstern H. Confounding in health research. Annual Review of Public Health. 2001;22:189–212. doi: 10.1146/annurev.publhealth.22.1.189. doi: 10.1146/annurev.publhealth.22.1.189. [DOI] [PubMed] [Google Scholar]
- Hafeman DM. Confounding of indirect effects: A sensitivity analysis exploring the range of bias due to a cause common to both the mediator and the outcome. American Journal of Epidemiology. 2011;174:710–717. doi: 10.1093/aje/kwr173. doi: 10.1093/aje/kwr173. [DOI] [PubMed] [Google Scholar]
- Hanushek EA, Jackson JE. Statistical methods for social scientists. Academic Press; New York: 1977. [Google Scholar]
- Holland PW. Causal inference, path analysis, and recursive structural equation models. Sociological Methodology. 1988;18:449–484. [Google Scholar]
- Hoyle RH, Kenny DA. Sample size, reliability, and tests of statistical mediation. In: Hoyle RH, editor. Statistical strategies for small sample research. Sage; Thousand Oaks, CA: 1999. pp. 195–222. [Google Scholar]
- IBM Corp. IBM SPSS Amos [v. 22] IBM Corp.; Armonk, NU: 2015. [Google Scholar]
- Imai K, Keele L, Tingley D. A general approach to causal mediation analysis. Psychological Methods. 2010;15:309–334. doi: 10.1037/a0020761. doi: 10.1037/a0020761. [DOI] [PubMed] [Google Scholar]
- Imai K, Keele L, Yamamoto T. Identification, inference, and sensitivity analysis for causal mediation effects. Statistical Science. 2010;25:51–71. [Google Scholar]
- Imai K, Yamamoto T. Identification and sensitivity analysis for multiple causal mechanisms: Revisiting evidence from framing experiments. Political Analysis. 2013;21:141–171. doi: 10.1093/pan/mps040. [Google Scholar]
- James LR. The unmeasured variables problem in path analysis. Journal of Applied Psychology. 1980;65:415–421. doi : 10.1037/0021-9010.65.4.415. [Google Scholar]
- James LR, Brett JM. Mediators, moderators, and tests for mediation. Journal of Applied Psychology. 1984;69:307–321. doi: 10.1037/0021-9010.69.2.307. [Google Scholar]
- Jo B. Causal inference in randomized experiments with mediational processes. Psychological Methods. 2008;13:314–336. doi: 10.1037/a0014207. doi: 10.1037/a0014207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Judd CM, Kenny DA. Process analysis: Estimating mediation in treatment evaluations. Evaluation Review. 1981;5:602–619. doi: 10.1177/0193841X8100500502. [Google Scholar]
- Judd CM, Kenny DA. Data analysis in social psychology: Recent and recurring issues. In: Fiske ST, Gilbert DT, Lindzey G, editors. Handbook of Social Psychology. 5th ed. Vol. 1. Wiley; New York: 2010. pp. 115–139. [Google Scholar]
- Kenny DA. Correlation & causality. John Wiley & Sons; New York: 1979. [Google Scholar]
- Ledgerwood A, Shrout PE. The trade-off between accuracy and precision in latent variable models of mediation processes. Journal of Personality and Social Psychology. 2011;101:1174–1188. doi: 10.1037/a0024776. doi: 10.1037/a0024776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y, Bienias JL, Bennett DA. Confounding in the estimation of mediation effects. Computational Statistics & Data Analysis. 2007;51:3173–3186. doi: 10.1016/j.csda.2006.10.016. doi: 10.1016/j.csda.2006.10.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu W, Kuramoto SJ, Stuart EA. An introduction to sensitivity analysis for unobserved confounding in non-experimental prevention research. Prevention Science. 2013;14:570–580. doi: 10.1007/s11121-012-0339-5. doi: 10.007/s11121-012-0339-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP. Introduction to statistical mediation analysis. Lawrence Erlbaum Associates; New York: 2008. [Google Scholar]
- MacKinnon DP, Krull JL, Lockwood CM. Equivalence of the mediation, confounding, and suppression effect. Prevention Science. 2000;1:173–181. doi: 10.1023/a:1026595011371. doi: 10.1023/A:1026595011371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Lockwood CM, Hoffman JM, West SG, Sheets V. A comparison of methods to test mediation and other intervening variable effects. Psychological Methods. 2002;7:83–104. doi: 10.1037/1082-989x.7.1.83. doi: 10.1037/1082-989X.7.1.83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Pirlott A. Statistical approaches for enhancing causal interpretation of the M to Y relation in mediation. Personality and Social Psychology Review. 2015;19:30–43. doi: 10.1177/1088868314542878. doi: 10.1177/1088868314542878. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mauro R. Understand L.O.V.E. (Left Out Variables Error): A method for estimating the effects of omitted variables. Psychological Bulletin. 1990;108(2):314–329. doi: 10.1037/0033-2909.108.2.314. [Google Scholar]
- Maxwell SE, Cole DA. Bias in cross-sectional analyses of longitudinal mediation. Psychological Methods. 2007;12:23–44. doi: 10.1037/1082-989X.12.1.23. doi: 10.1037/1082-989X.12.1.23. [DOI] [PubMed] [Google Scholar]
- McDonald RP. Haldane's lungs: A case study in path analysis. Multivariate Behavioral Research. 1997;32:1–38. doi: 10.1207/s15327906mbr3201_1. doi: 10.1207/s15327906mbr3201_1. [DOI] [PubMed] [Google Scholar]
- McDonald RP. Test theory: A unified treatment. Lawrence Erlbaum Associates; Mahwah, NJ: 1999. [Google Scholar]
- Mitchell MA, Maxwell SE. A comparison of the cross-sectional and sequential designs when assessing longitudinal mediation. Multivariate Behavioral Research. 2013;48:301–339. doi: 10.1080/00273171.2013.784696. doi: 10.1080/00273171.2013.784696. [DOI] [PubMed] [Google Scholar]
- Morse GA, Calsyn RJ, Allen G, Kenny DA. Helping homeless mentally ill people: What variables mediate and moderate program effects. American Journal of Community Psychology. 1994;22:661–683. doi: 10.1007/BF02506898. doi: 10.1007/BF02506898. [DOI] [PubMed] [Google Scholar]
- Morse G, Shields N, Hanneke C, Calsyn R, Burger R, Nelson B. St. Louis’ homeless: Mental health needs, services, and policy implications. Psychological Rehabilitation Journal. 1986;9:39–50. doi: 10.1037/h0099150. [Google Scholar]
- Muthén BO, Muthén L. Mplus user's guide. 7th ed. Muthen & Muthen; Los Angeles, CA: 2015. [Google Scholar]
- Pearl J. Causality: Models, reasoning, and inference. 2nd ed. Cambridge University Press; Cambridge: 2009. [Google Scholar]
- Pearl J. The causal mediation formula – A guide to pathways and mechanisms. Prevention Science. 2011;13:426–436. doi: 10.1007/s11121-011-0270-1. doi: : 10.1007/s11121-011-0270-1. [DOI] [PubMed] [Google Scholar]
- Ranby KW, Aiken LS, MacKinnon DP, Elliot DL, Moe EL, McGinnis W, Goldberg L. A mediation analysis of the ATHENA intervention for female athletes: Prevention of athletic-enhancing substance use and unhealthy weight loss behaviors. Journal of Pediatric Psychology. 2009;34:1069–1083. doi: 10.1093/jpepsy/jsp025. doi: 10.1093/jpepsy/jsp025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valeri L, VanderWeele TJ. Mediation analysis allowing for exposure-mediator interactions and causal interpretations: Theoretical assumptions and implementations with SAS and SPSS macros. Psychological Methods. 2013;18:137–150. doi: 10.1037/a0031034. doi: 10.1037/a0031034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanderWeele TJ. Sensitivity analysis: distributional assumptions and confounding assumptions. Biometrics. 2008;64:645–649. doi: 10.1111/j.1541-0420.2008.01024.x. doi: 10.1111/j.1541-0420.2008.01024.x. [DOI] [PubMed] [Google Scholar]
- VanderWeele TJ. Bias formulas for sensitivity analysis for direct and indirect effects. Epidemiology. 2010;21:540–551. doi: 10.1097/EDE.0b013e3181df191c. doi: 10.1097/EDE.0b013e3181df191c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanderWeele TJ. Unmeasured confounding and hazard scales: sensitivity analysis for total, direct, and indirect effects. European Journal of Epidemiology. 2013;28:113–117. doi: 10.1007/s10654-013-9770-6. doi: 10.1007/s10654-013-9770-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanderWeele TJ. Explanation in causal inference: Methods for mediation and interaction. Oxford University Press; Oxford, UK: 2015. [Google Scholar]
- VanderWeele TJ, Valeri L, Ogburn EL. The role of measurement error and misclassification in mediation analysis. Epidemiology. 2012;23:561–564. doi: 10.1097/EDE.0b013e318258f5e4. doi:10.1097/EDE.0b013e318258f5e4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weierich MR, Nock MK. Posttraumatic stress symptoms mediate the relation between childhood sexual abuse and non-suicidal self-injury. Journal of Consulting and Clinical Psychology. 2008;76:39–44. doi: 10.1037/0022-006X.76.1.39. doi: 10.1037/0022-006X.76.1.39. [DOI] [PubMed] [Google Scholar]