Abstract
We consider a phenomenological continuum theory for an extensile, overdamped active nematic liquid crystal, applicable in the dense regime. Constructed from general principles, the theory is universal, with parameters independent of any particular microscopic realization. We show that it exhibits two distinct instabilities, one of which arises due to shear forces, and the other due to active torques. Both lead to the proliferation of defects. We focus on the active torque bend instability and find three distinct nonequilibrium steady states including a defect-ordered nematic in which disclinations develop polar ordering. We characterize the phenomenology of these phases and identify the relationship of this theoretical description to experimental realizations and other theoretical models of active nematics.
Introduction
Liquid crystals are anisotropic fluid mesophases that exhibit broken rotational symmetry and have been extensively studied for many years1. The study of topological defects in the orientational order in these systems, which typically occur under driving, has had a central role in developing our understanding of the material properties of these systems2,3. Active liquid crystals are driven at the scale of the microscopic nematogen, and the microscale internal forces give rise to spontaneous nucleation of defects and novel defect dynamics4–7.
One system, composed of cytoskeletal filaments driven by motor proteins4–6 confined to a fluid interface, has inspired much theoretical effort to understand its dynamics6,8–19. These theories show how fluid mediation, in the form of active and passive backflow, can lead to the formation and propulsion of defects. However, these nonequilibrium phenomena also arise in active nematic systems in which fluid mediation plays little or no part, such as vibrated monolayers of granular rods20, epithelial cell monolayers21, and elongated fibroblasts22. It must therefore be possible to describe these systems with overdamped dynamics, in which activity is transmitted directly, rather than through the mediation of a fluid.
In this work we develop a phenomenological continuum theory that describes the dynamics of an overdamped active nematic in two dimensions, and is applicable to all systems in this symmetry class. This theory contains two mechanisms through which the active forces give rise to instabilities in the homogeneous nematic state in the dense regime. One is analogous to the instability due to flow alignment in fluid-mediated theories11,13,23, in that it arises due to reorientation of the director under shear. The other is an instability that arises due to rotation of the director by internal forces in an active nematic.
We unfold the rich phenomenology that emerges due to the active torque instability in the numerical investigation, focusing on extensile systems in the dense regime. The nonequilibrium steady-states that we find are (i) a defect-ordered nematic that exhibits emergent polar ordering of defects, (ii) a defect-free undulating nematic (see Fig. 1 and ESI†), and (iii) a defective, turbulent nematic (see Fig. 2).
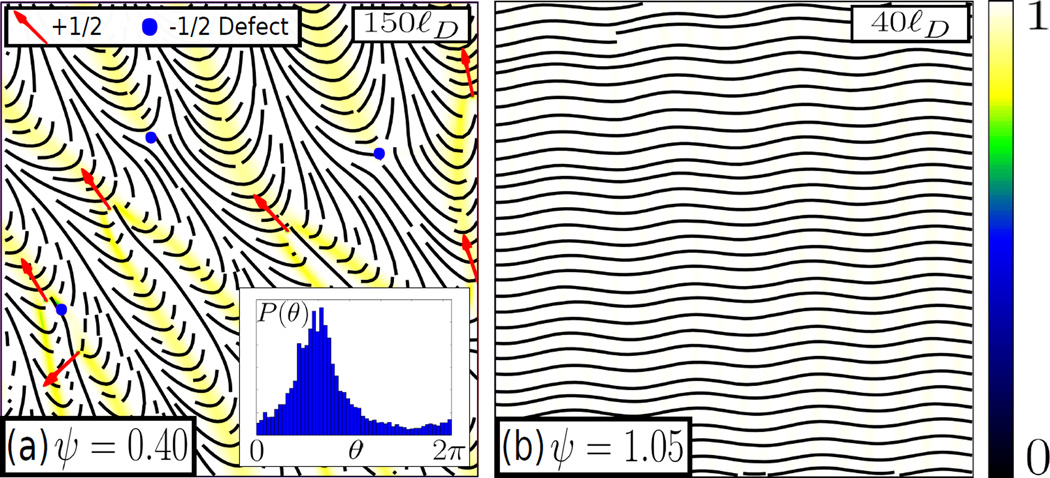
Fig. 1.
Heatmaps of the degree of order (S/S0, colorbar on the right) showing the nonequilibrium steady-states. (a) The defect-ordered state, with a histogram inset showing the sharp polar ordering in the orientation of defects. The lines, showing the direction of order, highlight the extended trails left by the motion of these defects. (b) The undulating nematic state is highly ordered (S ≃ S0) but the direction of order undulates. Scale bars are in the top right corners.
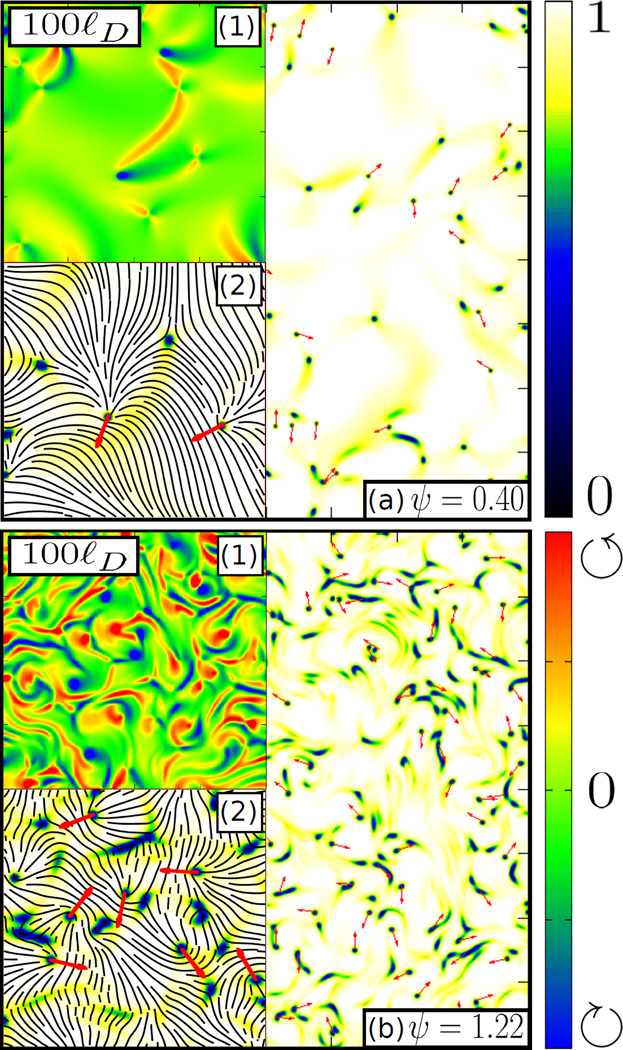
Fig. 2.
Heatmaps of the degree of order (S/S0, colorbar on the upper-right) showing the defective states (a) at low activity (ψ < 1) and (b) at high activity (ψ > 1). Insets on each heatmap include (1) a heatmap of the vorticity (colorbar on the lower-right), and (2) 2×-magnified region with lines showing the direction of order. Scale bars are in the top left corners.
The appearance of a defect-ordered state is of particular interest, as defect-ordering was recently discovered in layers of active cytoskeletal filaments and in simulations of overdamped extensile rigid rods6. While the long-range ordering of defects in these states is reminiscent of blue phases24 and twist-grain-boundary phases25 in equilibrium liquid crystals, the defect-ordered states in the active systems differ in that the defects themselves are motile and transient rather than existing in a static lattice.
The defect ordering in the experiment had nematic symmetry, while simulations displayed the same polar symmetry that we observe. We show that polar ordering of defects is a metastable state that occurs below the threshold for any instability of the homogeneous nematic state and depends on the breaking of Galilean invariance in the overdamped limit. Further, we identify the relationship of our approach to other theories in the literature.
Theoretical Framework
An equilibrium nematic is described by the well-known Landaude Gennes free energy ℱ that is a functional of the density ρ(r⃗, t) and the nematic order tensor, Q(r⃗, t), associated with rotational symmetry breaking1,26. Its dynamics is given by gradient descent on this free energy landscape: ‘Model A’ dynamics for the director, , and ‘Model B’ dynamics for the conserved density field, . For an active nematic, however, microscopic forces exerted by the constituent particles can give rise to dynamics that are not integrable, and are therefore inherently nonequilibrium.
We shall consider the dynamics of systems of extensile particles, which push along their long axes, acting as force dipoles. The forces exerted by the particles cause a stress σ = fQ§. In a flat nematic these forces are locally balanced and the stress is exerted only on the boundary. When there is a local distortion of the order, however, there is a net force F ∝ − ∇⃗ · Q from this stress. This force can lead to a flow of particles ρu⃗ = −F⃗/ξ (where ξ is a friction coefficient). We postulate that an active liquid crystal undergoes gradient descent dynamics in the local rest frame of a self-generated flow arising from the activity.
The flows which we consider are the motions of particles which reside near some surface, and in which neighboring particles are pushing on each other. We will therefore use a generalized form of the Beris-Edwards equations26, which describe how flow modifies the gradient descent dynamics of particles which are suspended in fluid when they interact solely through stresses in the fluid.
| (1) |
| (2) |
where is the vorticity tensor, is the strain-rate tensor associated with the flow, λ1 and λ2 are the first and second-order flow-alignment parameters, and (A)𝒯 denotes the traceless version of A (e.g. ).
The dynamical equations above are a generalization of the Beris-Edwards dynamical equations in that the equations above are not coupled to the flow of an incompressible medium, and in that these equations allow for broken Galilean invariance through the inclusion of coefficients in front of the convective and rotational terms, λ̄C and λ̄R respectively. It is relevant to consider an effectively compressible flow on a two-dimensional surface, as fluid can be pushed out into the third dimension. Also, in an overdamped system which is moving with respect to a fixed substrate, Galilean invariance may be broken, as that surface provides a reference frame. This generalization is also logical in the case of particles which are in direct contact, rather than suspended and interacting purely through a fluid. Broken Galilean invariance has been shown to make a significant difference in the dynamics of active polar fluids27–31, but its consequence for a fluid of nematic symmetry has not been considered in existing literature.
When the flow from the active forces is replaced in Eqs. 1 and 2, the dynamical equations for an active nematic take the form
| (3) |
| (4) |
where A : B = AijBij, and 𝒮 denotes symmetrization (i.e. )
The self-generated flow enters through the curvature induced density flux (CIDF), controlled by DQ in the dynamics of the density, and through the coefficients λx in the dynamics of the order parameter. , and control the strength of active convection and active torque, and flow-alignment due to active shearing respectively. The term with coefficient also comes from the flow-alignment, and appears as the Laplacian of the nematic order tensor. This term, therefore, acts as a negative Frank elasticity in the dynamics.
Before we proceed with the analysis of our theory, we make the following observations in order to place this model in the context of other the existing literature in this field:
The CIDF, introduced by Ramaswamy et. al.32,33, is the only active contribution to the dynamics which is first order in Q and therefore gives a universal description of the behavior of active nematics near the critical density, where Q is small. This term gives rise to striking phenomena, such as giant number fluctuations, phase separation, and band formation near the critical density20,34–45. In this work we will focus on the dynamics of a system which is well above the critical density and highly ordered, away from this well-studied regime.
Existing theories of active nematics that account for the novel defect dynamics seen in these systems consider nematohydrodynamic equations coupled to a Stokes equation for the activity-induced flow (such as8–14,18). In the presence of a screening mechanism such as confinement to 2D, the flow field can be eliminated in terms of the active stress yields Eqs. (3–4), but with DQ = λC = λR i.e., a Galilean invariant version of our theory18,46–48.
The approach taken here is one which can be generalized to other active systems. We consider gradient descent on a free energy, in an imposed flow, and allow for broken Galilean invariance. We then replace the general flow with one which depends on the local order parameter, and arises due to the active forces. The same prescription can be applied to polar systems to get the dynamical equations of Toner and Tu27–29. The difference being that, in a polar system, the flow from the active forces is u⃗ ∝ P⃗ where P⃗ is the polar order parameter. In both cases the gradient descent dynamics are purely smoothing and allow for a homogeneous solution, but the flow which arises due to the motion of those particles, or the forces that they exert, can lead to instabilities in that homogeneous solution, and inhomogeneous dynamical steady states.
Parameters of the Theory
The relaxational contributions to the dynamics of the order parameter arising from a free energy take the form
where α = (ρ − 1) and , Dr is the rotational diffusion constant and Dρ is a kinetic term also seen in prior works36,37,41. There are three elastic terms. D̄E is the mean elasticity, and it competes with the active term with coefficient λE. We will therefore work with an effective mean-elastic relaxation term with coefficient DE = D̄E − λE. Dδ is a differential elasticity, measuring the difference between bend and splay energies. Finally, a fourth-order gradient term (with coefficient K) is included to ensure smoothness and numerical stability.
The relevant parameters for the phenomenology discussed are: the active force and torque (λC,R) and the effective mean and the differential elastic constants DE and Dδ. The active shear (with coefficient λS) does not affect the linear stability or the phenomenology considered here. In the following, we nondimensionalize our equations by setting our time scale to be the rotational diffusion time, , and our length-scale to be the diffusion length, . In all of the subsequent sections we will work in these dimensionless variables.
Instabilities of the Nematic State
In the homogeneous limit, Eqs. (4) and (3) admit a uni-axial nematic solution with average density ρ0 > 1, and the order parameter , with degree of ordering . Let us consider spatial fluctuations about this state.
Phase Separation Instability
There is an instability which occurs near the critical density for the onset of ordering, and leads to phase separation. It occurs when fluctuations perpendicular to the director cause an instability in the degree of ordering, which occurs for . This instability causes phase separation into bands of dense ordered regions coexisting with dilute disordered regions when the material is near the critical density (ρc = 1). This has been discussed in previous work by us45 and others39–41,43,44,49,50. The nonlinear active terms (λC, λR and λS) do not significantly alter the phenomenology discussed in previous work.
Splay and Bend Instabilities
Let us also consider fluctuations in the direction of order δQxy. The Fourier transform (X̃ = ∫ dr⃗eik⃗·r⃗X(r⃗, t)) of the linearized equation for this mode can be expressed as
where we consider only pure bend fluctuations which are parallel to the director (k⃗ = kx̂, upper sign) or pure splay fluctuations which are perpendicular (k⃗ · x̂ = 0, lower sign). Pure bend and splay decouple fluctuations in the direction of order from those in the degree of order (δQ̃xy) and the density (δρ̃) which enables a clear identification of mechanisms at play. This equation reveals two instabilities in the direction of order which come from the activity. Both grow as k2, and the fourth-order gradient term with coefficient K guarantees that, when there is an instability in this mode, the ordered solution will restabilize at finite wavelength.
The generic instability
This instability occurs when DE = D̄E − λE < 0, and it comes from the first order flow-alignment term . This instability in the homogeneous nematic occurs for suspensions of extensile rods (f,λ1 > 0), which we consider here¶. It is a bend (splay) instability when λR > 2Dδ (λR < 2Dδ). The analogous instability has been identified and discussed in detail (in the Dδ = 0 limit) in existing active nematic theories for suspensions11,13,23,51 and for flows with damping18.
This instability has also been discussed in the overdamped limit, where it results in a Swift-Hohenberg-type dynamical equation, which can lead to pattern formation, or a turbulent steady-state19. The systems with a negative effective elastic constant form steady-state patterns in the modulation of the director for the case of active systems18,19. This result is reminiscent of the patterns seen in equilibrium phases of liquid crystals which have a negative elastic constant due to their shape52–54. As this instability and its consequences have been the topic of previous theoretical and numerical investigation, we shall forgo further discussion of them here.
Active Torque Instability
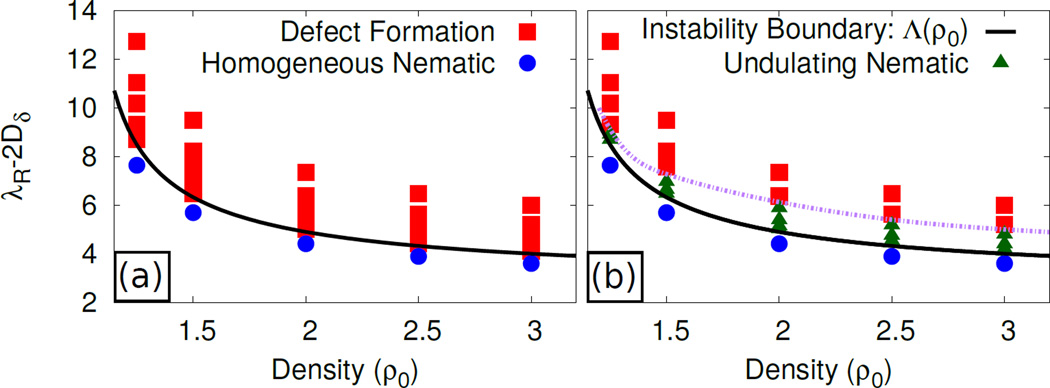
Of primary interest here is a bend instability which arises from the active torque. This occurs when a ‘bend instability parameter’ where (Fig. 3). This parameter reflects a competition between the active torque λR and the differential elasticity Dδ, which is positive if bend distortions are more energetically expensive than splay. This bend instability is also a mechanism for defect generation and formation of inhomogeneous steady states in this active system. Note that if the nematic was contractile, λR is negative and hence there exists a splay instability, which occurs when ψ < − 1. We have, however, focused on extensile systems for this study of the overdamped dynamics, and left the study of the contractile, overdamped dynamics to future work.
Fig. 3.
Plots showing the end state which forms from nematic initial conditions. (a) At Dδ = 1.0, the homogeneous nematic state transitions into a defective nematic above the instability boundary. (b) At Dδ = −0.50 we find an undulating state at intermediate activities.
Consequences of the Active Torque
In order to elucidate the consequence of the active torque instability, we numerically explored the dynamics using a semi-implicit finite difference method, with periodic boundary conditions‖. Integrating from nematic initial conditions with small amplitude Gaussian noise, two states were found above the threshold for the bend instability (ψ > 1). These were (I) an undulating nematic state where the system is strongly ordered but the director undulates along the broken symmetry direction (see Fig. 1, and (II) a turbulent state (see Fig. 3,2) in which charge disclinations continually form and annihilate and the defects are self-propelled as seen in4–6,8–10,10–15,51,55.
The structure of the undulating nematic state is reminiscent of twist-bend and splay-bend modulated structures found in equilibrium nematics52,56,57. This state present when active convection was large (λC > 1.0) or and it was small (λC << 1) and Dδ ≤ 0 (see ESI† for details). In other regions of parameter space the system transitioned directly into the defective nematic state.
The above analysis focused on the instabilities of the homogeneous nematic state. Next we consider isotropic initial conditions and vary parameters which control the bend instability (λR, Dδ, and ρ0) and the strength of active convection (λC) while keeping the other parameters fixed.
Defect-ordered state
When the strength of active torque is dominant over the strength of active convection (λR > λC), and Dδ > 0 there is a steady-state with finite defect density below the bend instability (ψ < 1). This is where the defect-ordered state occurs (see Fig. 4). The properties of this state are as follows: (i) Defects are point-like and the background is a (locally) well-ordered nematic (see Fig. 2). (ii) Defining the orientation of defects to be opposite the “comet tail” (along the direction of propulsion), we find that these defects exhibit significant polar ordering. (iii) The degree of polar ordering decreases as ψ increases. (iv) The high degree of polar ordering corresponds with long splay distortions which are left by defects as they travel (see Fig. 1). Other defects tend to reorient rather than cross these distortion-trails, leading to long parallel structures which are visible in the states with a large degree of polar ordering.
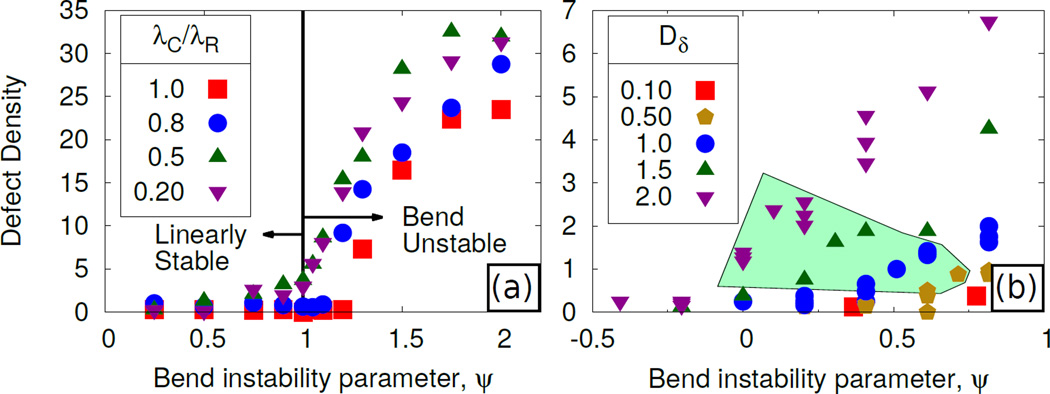
Fig. 4.
Plots of the defect density (defects per (100ℓD)2) as a function of ψ, for ρ0 = 2.0. (a) Curves with fixed Dδ = 1.0, for a range of λC/λR, show that when the strength of active convection is comparable to active torque, defects vanish near the bend instability. When λC < λR the defect density can be nonzero for ψ < 1, in which case it increases sharply when ψ crosses 1, and then saturates. (b) Fixed λC = 1.0 (less than λR), and a range of Dδ, for ψ < 1. Defect density is greater for larger Dδ, and it vanishes as Dδ goes to 0. The shaded region indicates where there was statistically significant polar ordering of defects.
Turbulent nematic state
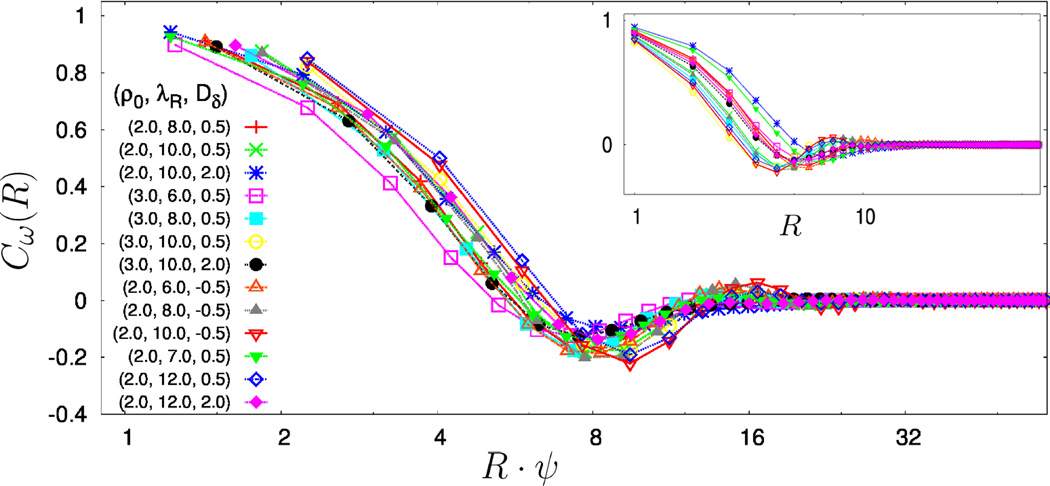
The turbulent, defective nematic state occurs above the bend instability when the defect density and vorticity increase sharply (Fig 4). The defects, which were small and circular near ψ = 1, become spatially extended and the average degree of ordering decreases. This turbulent nematic state appears distinct from the one arising through the generic bend instability through correlation function Cω(R) = 〈ω(0)ω(R)〉/〈ω2〉, where ρω⃗= λR∇⃗ × (∇ · Q). It scales with the bend instability parameter ψ (see Fig. 5), which is linear in the strength of the active torque λR. This differs from what was found in a recent study13 where vorticity scaled as the strength of the activity to the 1/4th power. Further, if the length scale for defect separation ℓd scales with the vorticity , then the defect density should scale as ψ2. This is compatible with the trend seen near the critical value of the bend instability parameter, but the range is not large enough for a conclusive comparison.
Fig. 5.
Log-linear plot of vorticity correlation functions, Cω(R) for fixed parameters (λR, Dδ and ρ0) above the bend instability (ψ > 1.10). The length is scaled by ψ, which gives a data collapse for a large range of parameters.
Summary
We have introduced a universal theory of an overdamped active nematic in which activity enters through self-induced flows. This theory encompasses the physics already identified in previous work and identifies additional phenomena particularly relevant for rigid rod extensile systems. We have identified three nonequilibrium steady states admitted by this theory. The first is a defect-ordered nematic state where polar ordering of +1/2 disclinations emerges from the underlying apolar theory. The theory provides robust predictions about when polar defect ordering will be found. The ordering occurs below any bend instability, i.e., ψ < 1 and DE > 0 and when Dδ > 0 and λR > λC. This result implies that an polar ordered fluid phase of defects may not occur in theories which have Galilean invariance (λC = λR). Other steady states found include an undulating nematic state which is reminiscent of the “walls” of distortion in the order parameter seen before the onset of defective states11,13, or the distortion of the director which happens during relaxation oscillations51,58. Finally we find a turbulent nematic state similar to that which occurs in theories of active nematic suspensions8–14.
Supplementary Material
Acknowledgments
We thank Mike Hagan, Zvonimir Dogic, and Stephen DeCamp for sharing information and ideas. EFP and AB acknowledge support from NSF-DMR-1149266, the Brandeis-MRSEC through NSF DMR-0820492 and NSF MRSEC-1206146, NSF PHY11-25915 through KITP, and the HPC cluster at Brandeis for computing time. EFP also acknowledges support through NIH-5T32EB009419 and IGERT DGE-1068620.
Footnotes
Electronic Supplementary Information (ESI) available: See DOI: 10.1039/b000000x/
f is positive (negative) if the particles are extensile (contractile)
The generic instability can also occur for contractile discs (f,λ1 < 0)
The spatial resolutions (h, units of ℓD) used were 0.1 ≤ h ≤ 0.4, temporal resolutions were diffusion times, and system sizes were between 400 and 1200 ℓD
References
- 1.De Gennes P-G, Prost J. The physics of liquid crystals. Vol. 23. Clarendon press Oxford; 1993. [Google Scholar]
- 2.Chaikin PM, Lubensky TC. Principles of condensed matter physics. Cambridge Univ Press; 2000. [Google Scholar]
- 3.Laverntovich OD. Soft matter physics: an introduction. Springer; 2003. [Google Scholar]
- 4.Sanchez T, Chen DTN, DeCamp SJ, Heymann M, Dogic Z. Nature. 2012;491:431–434. doi: 10.1038/nature11591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Keber FC, Loiseau E, Sanchez T, DeCamp SJ, Giomi L, Bowick MJ, Marchetti MC, Dogic Z, Bausch AR. Science. 2014;345:1135–1139. doi: 10.1126/science.1254784. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.DeCamp SJ, Redner GS, Baskaran A, Hagan MF, Dogic Z. Nature Materials. 2015;14:1110–1115. doi: 10.1038/nmat4387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Zhou S, Sokolov A, Lavrentovich OD, Aranson IS. Proc. Nat. Acad. Sci. U.S.A. 2014;111:1265–1270. doi: 10.1073/pnas.1321926111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Giomi L, Bowick MJ, Ma X, Marchetti MC. Phys. Rev. Lett. 2013;110:228101. doi: 10.1103/PhysRevLett.110.228101. [DOI] [PubMed] [Google Scholar]
- 9.Thampi SP, Golestanian R, Yeomans JM. Phys. Rev. Lett. 2013;111:118101. doi: 10.1103/PhysRevLett.111.118101. [DOI] [PubMed] [Google Scholar]
- 10.Blow ML, Thampi SP, Yeomans JM. Phys. Rev. Lett. 2014;113:248303. doi: 10.1103/PhysRevLett.113.248303. [DOI] [PubMed] [Google Scholar]
- 11.Giomi L, Bowick MJ, Mishra P, Sknepnek R, Marchetti MC. Phil. Trans. R. Soc. A. 2014;372:20130365. doi: 10.1098/rsta.2013.0365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Thampi SP, Golestanian R, Yeomans JM. Phys. Rev. E. 2014;90:062307. doi: 10.1103/PhysRevE.90.062307. [DOI] [PubMed] [Google Scholar]
- 13.Thampi SP, Golestanian R, Yeomans JM. Phil. Trans. R. Soc. A. 2014;372:20130366. doi: 10.1098/rsta.2013.0366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Thampi SP, Golestanian R, Yeomans JM. Europhys. Lett. 2014;105:18001. [Google Scholar]
- 15.Shi X-q, Ma Y-q. Nat. Commun. 2013;4:3013. doi: 10.1038/ncomms4013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Saintillan D, Shelley MJ. Phys. Rev. Lett. 2007;99:058102. doi: 10.1103/PhysRevLett.99.058102. [DOI] [PubMed] [Google Scholar]
- 17.Saintillan D, Shelley MJ. Phys. Rev. Lett. 2008;100:178103. doi: 10.1103/PhysRevLett.100.178103. [DOI] [PubMed] [Google Scholar]
- 18.Doostmohammadi A, Adamer MF, Thampi SP, Yeomans JM. Nat. Commun. 2016;7:10557. doi: 10.1038/ncomms10557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Oza AU, Dunkel J. eprint arXiv:1507.01055. 2015 [Google Scholar]
- 20.Narayan V, Ramaswamy S, Menon N. Science. 2007;317:105–108. doi: 10.1126/science.1140414. [DOI] [PubMed] [Google Scholar]
- 21.Kemkemer R, Kling D, Kaufmann D, Gruler H. Eur. Phys. J. E. 2000;1:215–225. [Google Scholar]
- 22.Duclos G, Garcia S, Yevick HG, Silberzan P. Soft Matter. 2014;10:2346–2353. doi: 10.1039/c3sm52323c. [DOI] [PubMed] [Google Scholar]
- 23.Ramaswamy S, Rao M. New J. Phys. 2007;9:423. [Google Scholar]
- 24.Lavrentovich O, Kleman M. Chirality in Liquid Crystals. Springer; 2001. pp. 115–158. [Google Scholar]
- 25.Renn SR, Lubensky TC. Phys. Rev. A. 1988;38:2132. doi: 10.1103/physreva.38.2132. [DOI] [PubMed] [Google Scholar]
- 26.Beris AN, Edwards BJ. Thermodynamics of flowing systems: with internal microstructure. Oxford University Press; 1994. [Google Scholar]
- 27.Toner J, Tu Y. Phys. Rev. Lett. 1995;75:4326–4329. doi: 10.1103/PhysRevLett.75.4326. [DOI] [PubMed] [Google Scholar]
- 28.Toner J, Tu Y. Phys. Rev. E. 1998;58:4828–4858. [Google Scholar]
- 29.Toner J, Tu Y, Ramaswamy S. Annals of Physics. 2005;318:170–244. [Google Scholar]
- 30.Farrell FDC, Marchetti M, Marenduzzo D, Tailleur J. Phys. Rev. Lett. 2012;108:248101. doi: 10.1103/PhysRevLett.108.248101. [DOI] [PubMed] [Google Scholar]
- 31.Gopinath A, Hagan MF, Marchetti MC, Baskaran A. Physical Review E. 2012;85:061903. doi: 10.1103/PhysRevE.85.061903. [DOI] [PubMed] [Google Scholar]
- 32.Simha R, Ramaswamy S. Physica A. 2002;306:262–269. [Google Scholar]
- 33.Ramaswamy S, Simha RA, Toner J. Europhys. Lett. 2003;62:196–202. [Google Scholar]
- 34.Mishra S, Ramaswamy S. Physical Review Letters. 2006;97:090602. doi: 10.1103/PhysRevLett.97.090602. [DOI] [PubMed] [Google Scholar]
- 35.Chaté H, Ginelli F, Montagne R. Phys. Rev. Lett. 2006;96:180602. doi: 10.1103/PhysRevLett.96.180602. [DOI] [PubMed] [Google Scholar]
- 36.Baskaran A, Marchetti MC. Phys. Rev. E. 2008;77:011920. doi: 10.1103/PhysRevE.77.011920. [DOI] [PubMed] [Google Scholar]
- 37.Baskaran A, Marchetti M. Phys. Rev. Lett. 2008;101:268101. doi: 10.1103/PhysRevLett.101.268101. [DOI] [PubMed] [Google Scholar]
- 38.Mishra S, Aditi Simha R, Ramaswamy S. J Stat. Mech. Theory Exp. 2010;2010:P02003. [Google Scholar]
- 39.Peruani F, Ginelli F, Bär M, Chaté H. J. Phys. Conf. Ser. 2011;297:012014. [Google Scholar]
- 40.Peshkov A, Ngo S, Bertin E, Chaté H, Ginelli F. Phys. Rev. Lett. 2012;109:098101. doi: 10.1103/PhysRevLett.109.098101. [DOI] [PubMed] [Google Scholar]
- 41.Peshkov A, Aranson IS, Bertin E, Chaté H, Ginelli F. Phys. Rev. Lett. 2012;109:268701. doi: 10.1103/PhysRevLett.109.268701. [DOI] [PubMed] [Google Scholar]
- 42.Baskaran A, Marchetti MC. Eur. Phys. J. E. 2012;35:95. doi: 10.1140/epje/i2012-12095-8. [DOI] [PubMed] [Google Scholar]
- 43.Bertin E, Chaté H, Ginelli F, Mishra S, Peshkov A, Ramaswamy S. New J. Phys. 2013;15:085032. [Google Scholar]
- 44.Ngo S, Peshkov A, Aranson IS, Bertin E, Ginelli F, Chaté H. Phys. Rev. Lett. 2013;113:038302. doi: 10.1103/PhysRevLett.113.038302. [DOI] [PubMed] [Google Scholar]
- 45.Putzig E, Baskaran A. Phys. Rev. E. 2014;90:042304. doi: 10.1103/PhysRevE.90.042304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Pismen LM. Phys. Rev. E. 2013;88:050502. doi: 10.1103/PhysRevE.88.050502. [DOI] [PubMed] [Google Scholar]
- 47.Srivastava P, Marchetti MC. Private Commnication. 2015 [Google Scholar]
- 48.Srivastava P, Marchetti MC. Instabilities and patterns in an active nematic film. APS March Meeting; 2015. [Google Scholar]
- 49.Ginelli F, Peruani F, Bär M, Chaté H. Phys. Rev. Lett. 2010;104:184502. doi: 10.1103/PhysRevLett.104.184502. [DOI] [PubMed] [Google Scholar]
- 50.Ngo S, Ginelli F, Chaté H. Phys. Rev. E. 2012;86:4–8. doi: 10.1103/PhysRevE.86.050101. [DOI] [PubMed] [Google Scholar]
- 51.Giomi L, Mahadevan L, Chakraborty B, Hagan MF. Nonlinearity. 2012;25:2245. [Google Scholar]
- 52.Dozov I. Europhys. Lett. 2007;56:247–253. [Google Scholar]
- 53.Panov VP, Nagaraj M, Vij JK, Panarin YP, Kohlmeier A, Tamba MG, Lewis RA, Mehl GH. Phys. Rev. Lett. 2010;105:15–18. doi: 10.1103/PhysRevLett.105.167801. [DOI] [PubMed] [Google Scholar]
- 54.Ponti S, Freire FCM, Dias JC, Evangelista LR. Phys. Lett. A. 2008;372:6521–6526. [Google Scholar]
- 55.Gao T, Blackwell R, Glaser MA, Betterton M, Shelley MJ. Phys. Rev. Lett. 2015;114:048101. doi: 10.1103/PhysRevLett.114.048101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Meyer R. Les Houches summer school in theoretical physics. 1973:273–373. [Google Scholar]
- 57.Shamid SM, Dhakal S, Selinger JV. Phys. Rev. E. 2013;87:1–11. doi: 10.1103/PhysRevE.87.052503. [DOI] [PubMed] [Google Scholar]
- 58.Giomi L, Mahadevan L, Chakraborty B, Hagan MF. Phys. Rev. Lett. 2011;106:218101. doi: 10.1103/PhysRevLett.106.218101. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.