Significance
In this work, we investigate the role of defects on the electronic and photocatalytic properties of In2O3-x(OH)y nanoparticles that have been shown to effectively reduce CO2 to CO via the reverse water–gas shift reaction under light. To understand how such defects affect photogenerated electrons and holes in these materials, we studied the relaxation dynamics of these nanoparticles with varying concentration of defects. This analysis showed that higher defect concentrations result in longer excited-state lifetimes, which are attributed to improved charge separation and correlate well with the observed trends in the photocatalytic activity.
Keywords: indium oxide, solar fuels, CO2 hydrogenation, transient absorption, surface defects
Abstract
In2O3-x(OH)y nanoparticles have been shown to function as an effective gas-phase photocatalyst for the reduction of CO2 to CO via the reverse water–gas shift reaction. Their photocatalytic activity is strongly correlated to the number of oxygen vacancy and hydroxide defects present in the system. To better understand how such defects interact with photogenerated electrons and holes in these materials, we have studied the relaxation dynamics of In2O3-x(OH)y nanoparticles with varying concentration of defects using two different excitation energies corresponding to above-band-gap (318-nm) and near-band-gap (405-nm) excitations. Our results demonstrate that defects play a significant role in the excited-state, charge relaxation pathways. Higher defect concentrations result in longer excited-state lifetimes, which are attributed to improved charge separation. This correlates well with the observed trends in the photocatalytic activity. These results are further supported by density-functional theory calculations, which confirm the positions of oxygen vacancy and hydroxide defect states within the optical band gap of indium oxide. This enhanced understanding of the role these defects play in determining the optoelectronic properties and charge carrier dynamics can provide valuable insight toward the rational development of more efficient photocatalytic materials for CO2 reduction.
Concerns over climate change and the projected rise in global energy demand have motivated researchers to develop alternative, more sustainable ways to generate energy from naturally abundant and renewable sources (1–3). An important challenge associated with using renewable energy sources, such as solar, is their inherent intermittent nature (4–6). The emerging field of solar fuels seeks to address this issue by storing radiant solar energy in chemical bonds, which can then be released on demand and act as a drop-in replacement for traditional fossil fuels (7–11). By using the greenhouse gas, CO2, currently regarded as a waste product, as a feedstock and converting it into valuable products such as solar fuels or platform chemicals, we could simultaneously address concerns over climate change and energy security while creating significant economic benefits (12–14). However, despite recent advances in the development of active materials that can drive the photocatalytic reduction of CO2 into useful chemical species, much remains unknown about the fundamental physical properties that control the activity of a photocatalyst. To facilitate the rational development and improvement of photocatalytic materials, a detailed understanding of the complex interplay between chemical, optical, and electronic processes is needed.
Indium oxide has many favorable optical, electronic, and surface properties that make it a compelling choice as a photocatalyst for CO2 reduction. It has a relatively high conduction band, and common defects such as oxygen vacancies (Ov) have been shown to cause electron accumulation on its surfaces (15), both of which could aid in facilitating electron transfer to adsorbed molecules such as CO2. Additionally, indium oxide is also very stable under illumination, unlike other similarly promising semiconductors such as metal sulfides, which can degrade under illumination, particularly in the presence of water (6, 16).
Previously, our group has demonstrated that highly defected nanostructured In2O3-x(OH)y functions as an effective gas-phase photocatalyst for the reduction of CO2 to CO via the reverse water–gas shift reaction (RWGS) (17–20). Notably, the photocatalytic activity was found to be strongly correlated to the number and the type of defects present in the material. In particular, a combination of both Ov and hydroxides (OH) appeared to be necessary to facilitate efficient CO2 reduction at the surface of indium oxide. To gain insight into how the efficiency of this photocatalyst could be improved and extended to other more earth-abundant materials, we sought to probe more deeply into the optoelectronic properties of defected In2O3-x(OH)y. The goal of this study is to improve our understanding of how photogenerated electrons and holes, which are essential to photocatalytic activity, are impacted by the presence of defects in these materials.
Defects such as vacancies and hydroxyl groups, in particular, have been shown to have a substantial impact on the carrier relaxation dynamics (21–26). Generally, defects are associated with the creation of mid-band-gap states. These defect states can function as electron or hole traps that facilitate charge separation, thereby prolonging excited-state lifetimes. Conversely, they can also act as charge recombination centers that facilitate the rapid recombination of photoexcited electrons and holes, reducing excited-state lifetimes. Their chemical nature and location within the band gap largely determine their role in the relaxation pathway (21–24, 27). In metal oxides, both bulk and surface oxygen vacancies can act as traps for excited-state electrons (27–29), whereas surface hydroxyl groups typically function as hole traps (21, 27). Transient absorption (TA) spectroscopy has been used extensively to understand the processes that govern the relaxation dynamics of photoexcited electrons and holes and has been successfully applied to the study of midgap states in metal oxides (21, 22, 26, 27, 30–34). By studying highly defected materials and modeling the TA decay as a function of defect concentration, time, and excitation wavelength, a more detailed understanding of the dominant charge carrier relaxation processes can be obtained (22–24).
Although the optoelectronic properties of indium oxide have been widely studied in relation to its use as a transparent conductive oxide material (29, 35, 36), to our knowledge only Tsokkou et al. have looked at these processes in detail using TA spectroscopy (37, 38). They investigated excited-state lifetimes in In2O3 nanoparticles (37) and gold-decorated In2O3 nanorods (38) and their dependence on the pump fluence, and indicated that both shallow and deep trap states played a significant role in the carrier dynamics. However, these In2O3 samples were prepared at very high temperatures (1,000 °C and 700 °C, respectively) and are essentially stoichiometric, containing a minimal numbers of defects and in our experience photocatalytically inactive. To understand how these processes proceed in photocatalytically relevant samples with much higher defect densities, a detailed understanding of the charge carrier relaxation dynamics in highly defected indium oxide In2O3-x(OH)y samples is necessary.
In this work, we have used TA spectroscopy to study the relaxation dynamics of three photocatalytically active In2O3-x(OH)y samples prepared with varying concentrations of surface OH and Oy defects. We use two different excitation energies corresponding to above-band-gap (318-nm) and near-band-gap (405-nm) excitation to better understand how excited-state charge carriers with different potential energies interact with the different defect states available within the samples. By studying these two photocatalytically relevant excitation regimes, we can gain a better understanding of how In2O3-x(OH)y might behave under broadband solar irradiation. We also examine the most active photocatalyst under several relevant atmospheres––Ar, H2, and CO2––to better understand how the presence or absence of interacting surface species affects charge carrier relaxation dynamics. Using multiexponential functions to fit the data, we are able to extract information on various relaxation processes occurring within the sample at both short and long time scales. We then use hybrid density-functional theory to calculate both the density of states (DOS) and partial density of states (PDOS) for pristine and defected indium oxide (111) surfaces to gain a deeper understanding of how the presence of defects alters the electronic structure of our indium oxide samples. Finally, we discuss the role the defect states play in determining photoexcited, charge carrier localization, excited-state lifetimes, and ultimately the resultant photocatalytic activity. Our results demonstrate that defects play a significant role in the excited-state charge carrier relaxation pathways, which ultimately determine the photocatalytic activity occurring on longer time scales. This enhanced understanding of the interplay between the optoelectronic properties and photocatalytic activity of defected In2O3-x(OH)y can help to facilitate the rational design and synthesis of efficient photocatalytic materials.
Results and Discussion
Physical Characterization of the In2O3-x(OH)y Nanoparticles.
To gain a better understanding of the role that surface and bulk defects have in determining the optoelectronic properties of indium oxide nanoparticles, we prepared indium oxide samples with different concentrations of Ov and surface OH groups, which was achieved by controlling the calcination temperature during the thermal dehydroxylation reaction of the precursor indium hydroxide. The atomic rearrangement and associated loss of water from the lattice during the conversion of cubic indium hydroxide to cubic bixbyite indium oxide require significant thermal energy and will not occur below 210 °C (39). As the calcination temperature is increased, there is more thermal energy available to allow atomic rearrangement that minimizes the surface energy (40). This affords significant control over the nature and density of defects present in the final material. Indium oxide samples, prepared at temperatures close to this transition temperature, do not have sufficient thermal energy to enable the passivation of many of the defects formed. As a result, they contain a higher proportion of defects such as residual surface hydroxide groups and coordinatively unsaturated indium sites (oxygen vacancies), which could play a significant role in determining the optoelectronic properties responsible for driving the photocatalytic reduction of CO2. To this end, we prepared indium oxide samples calcined at three different temperatures: 250 °C, 350 °C, and 450 °C. For clarity, these samples will be henceforth referred to as I-250, I-350, and I-450, respectively.
Fig. 1 shows the high-angle angular dark field (HAADF) scanning transmission electron microscope (STEM) images of the three samples. The high-resolution images (Fig. 1, Right) indicate that all three In2O3-x(OH)y samples are highly crystalline. After carefully surveying STEM data, we found no evidence of preferred facets for any of the samples. We consider our samples to be isotropic, with many different exposed crystal surfaces. The lower-resolution images (Fig. 1, Left) show that, as expected, the sample morphology changes with increasing temperature. The I-250 sample exhibits the smallest particle size and highest porosity with a Brunauer–Emmett–Teller (BET) surface area of 125 m2/g. I-350 has slightly larger particles and exhibits more faceting than the I-250 sample; however, the morphology is still relatively similar to the I-250 sample, and the BET surface area is also 125 m2/g. The morphology of the I-450 sample comprises much larger particles and reduced porosity relative to the other two samples, as is also reflected in its BET surface area of 89 m2/g. This can be attributed to the minimization of surface energy at higher calcination temperatures, resulting in increased particle size, passivation of defects, and reduction in dangling surface bonds.
Fig. 1.
HAADF STEM images of the In2O3-x(OH)y samples. (A and B) I-250, (C and D) I-350, (E and F) I-450. In the high-resolution images (B, D, and F) the zone axis labels of [110], [001], and [112] indicate the zone axes of the viewing direction.
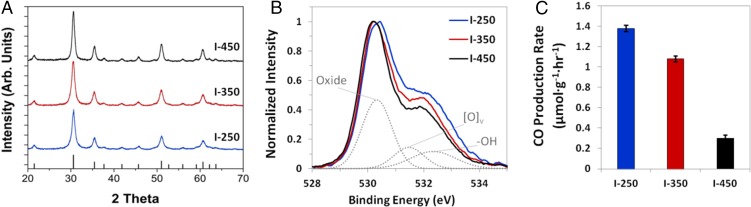
The powder X-ray diffraction (PXRD) patterns shown in Fig. 2A further confirm the crystalline nature of the In2O3-x(OH)y samples. All three samples are composed of pure crystalline bixbyite indium oxide with no evidence of other phases. The FWHM of the PXRD peaks decreases with increasing calcination temperature (see also SI Appendix, Fig. S1), indicating an increase in crystallite size, correlating well with the STEM data presented in Fig. 1. Fig. 2B shows the X-ray photoelectron spectroscopy (XPS) O1s core-level spectra for the three samples. The main portion of the peak is centered around 530 eV and is associated with indium oxide. The shoulder peak at higher binding energies, which decreases with decreasing calcination temperature, is commonly attributed to a combination of defects with contribution from both oxygen vacancies, with a peak centered around 531 eV, and hydroxides, with a peak centered around 532 eV (35, 41). The light-gray curves in Fig. 2B represent a qualitative deconvolution, scaled by 60%, of the O1s spectrum of the I-250 sample, and are intended for illustrative purposes only. These data provide further evidence that the amount of defects present in the three samples decreases with increasing calcination temperature.
Fig. 2.
Physical characterization of the In2O3-x(OH)y samples. (A) PXRD; (B) O 1s X-ray photoemission spectra; and (C) photocatalytic activity of the In2O3-x(OH)y samples under 800-W m−2 (0.8 suns) illumination at 150 °C and confirmed using 13C isotope tracing.
Despite this change in morphology and defect concentration, the diffuse reflectance spectra and band-offset diagrams (shown in SI Appendix, Fig. S2) indicate that the steady-state absorption properties of the three samples are remarkably similar. All three samples show an absorption onset around 425 nm, which corresponds to a band gap of around 2.9 eV, consistent with other reports in the literature (35). This would suggest that defects and surface morphology do not significantly affect the photonic properties in the steady-state regime.
Photocatalytic Activity Correlates with Defect Concentration.
The non–steady-state nature of photoexcitation is clearly evident from photocatalytic activity measurements. Fig. 2C demonstrates that the photocatalytic activity of the In2O3-x(OH)y samples decreases with increasing calcination temperature. Even when normalized to surface area (SI Appendix, Fig. S3), this trend in photocatalytic activity remains. We attribute this effect to a decrease in the number of active defect sites, specifically surface hydroxides and oxygen vacancies, within the material (18). In a separate study, which combined theoretical simulations and kinetics experiments, we have confirmed that both hydroxides and oxygen vacancies are needed at the active site to facilitate the reduction of CO2 to CO (17). Significantly, we were able to demonstrate that there is a 20-kJ/mol reduction in the apparent activation energy for the light-driven reaction relative to the dark reaction, indicating that light plays an important role in activating this defected In2O3-x(OH)y material to facilitate photocatalysis on its surface. This indicates the inherent role of defects is in modifying the excited-state properties of the photocatalytic surface as analyzed below in detail.
Excited-State Charge Carrier Dynamics in In2O3-x(OH)y.
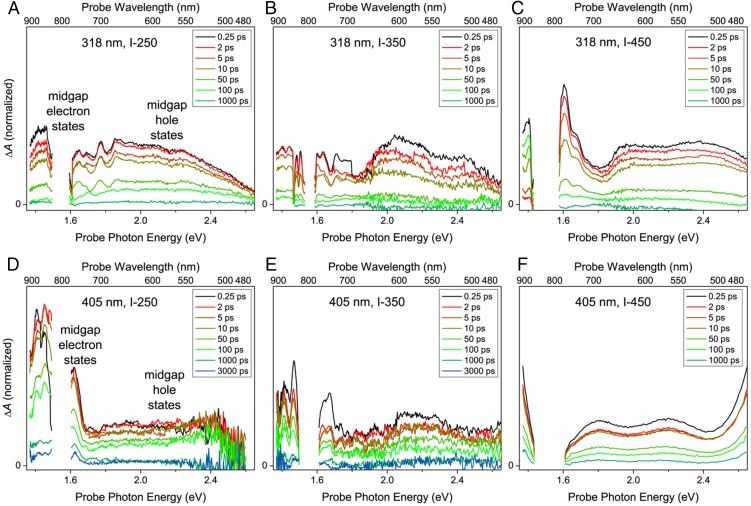
TA spectroscopy was conducted to study the excited-state carrier dynamics of In2O3-x(OH)y and understand how photogenerated electrons and holes interact with these catalytically relevant defects. In TA spectroscopy, an ultrafast, single-wavelength laser “pump” pulse is used to put the sample into an excited state. It is then followed by a second broadband laser “probe” pulse, which measures the excited-state absorption spectra of the sample at different time delays after the initial excitation. Fig. 3 shows the TA spectra of the three In2O3-x(OH)y samples measured in air at different time delays between pump and probe pulses. Both higher-energy above-band-gap (318-nm, 3.90-eV) and lower-energy near-band-gap (405-nm, 3.06-eV) pump pulses were used to excite the samples. These two excitation wavelengths allow a comparison between the different valence-band regions in In2O3, with near-band-gap transitions being optically forbidden in a pure, defect-free In2O3 crystal (36). The signal-to-noise ratio varies with the thickness of the irradiated area of the sample, which is not well controlled in the drop-cast films. Excitation wavelengths above 405 nm were not used, as the relatively low absorbance of the material falls rapidly with increasing wavelength in this region (SI Appendix, Fig. S1).
Fig. 3.
TA spectra at different time delays between pump and probe pulses of the In2O3-x(OH)y samples excited with above-band-gap (318-nm, 0.241-mJ cm–2 incident fluence) light (A–C) and near-band-gap (405-nm, 0.657-mJ cm–2 incident fluence) light (D–F). The data gap centered at ∼1.53 eV (809 nm) is due to the strong residual laser fundamental in the probe beam, which led to poor data within this region.
Above-band-gap excitation (318 nm) leads to distribution of excited-state absorption with similar intensity throughout the visible and near-IR regions of the spectra (Fig. 3 A–C). There does not appear to be any significant difference in the spectral shapes between the samples, indicating that the relaxation processes are similar for all three samples when excited with above-band-gap light energy (318 nm). On the other hand, near-band-gap excitation (405 nm) results in substantial differences in the transient absorption spectra when comparing between samples (Fig. 3 D–F). The same broad, featureless absorption in the visible region is observed for all samples; however, I-250 shows a significantly higher absorbance in the near-IR, which does not decay down to the baseline even at long delay times (>3 ns) when measured in air. The broad, featureless absorption in the visible region observed in all spectra is indicative of the formation of coulombically bound excitons (22, 27, 42). The presence of enhanced near-IR absorption is attributed to charge carriers in shallow trap states created by defects within the material, such as oxygen vacancies and surface hydroxyl groups (21, 22, 26). Both trapped electrons and trapped holes may contribute to this near-IR signal. Under 405-nm excitation, this near-IR signal decreases with increasing sample calcination temperature which is consistent with the loss of oxygen vacancies and surface hydroxyl groups due to surface defect passivation at higher temperatures.
Because the excitation wavelength determines the initial potential energy of the excited-state charge carriers, it is possible to generate different distributions of populated states. Using near-band-gap excitation, trap states and shallow donor (acceptor) states near the conduction (valence) band edge can be directly excited (27). The lower potential energy of the photogenerated charge carriers means they are more likely to be trapped at these localized surface states, leading to longer-lived excited states. Because the population of these oxygen vacancy and surface hydroxyl donor and acceptor states is highest in I-250 and decreases with increasing calcination temperature; this could explain the difference in near-IR signal. On the other hand, 318-nm excitation produces higher-energy charge carriers, which are more mobile and able to access many different relaxation pathways, resulting in shorter excited-state lifetimes. The absence of a substantial near-IR signal likely indicates that this above-band-gap excitation does not relax via the same localized surface trap pathway as with the 405-nm excitation.
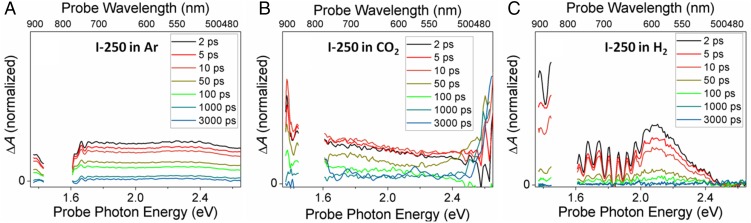
Because the presence or absence of atmospheric gases can have a significant effect on the dynamics of carriers trapped at a metal oxide surface (43), we also examined our most photocatalytically active sample, I-250, under several relevant gas atmospheres. Fig. 4 shows the TA spectra under 405-nm excitation of I-250 films, which were grown inside of a quartz photochemical cell, and subsequently purged with either Ar, H2, or CO2 gas and then sealed (see SI Appendix, Fig. S4 for a comparison of all three atmospheres with air after a time delay of 2 ps). As these results show, the dynamics in these three atmospheres are somewhat distinct from experiments performed in air, which we attribute to the ability of the different gases to interact with the indium oxide surface. Indium oxide has an electron-rich surface, so gases such as O2, which are good electron acceptors, can interact with the surface and influence the electron density, making charge recombination less likely (44). A noninteracting gas such as Ar does not exhibit such an effect, as the lack of adsorbates to serve as scavengers or additional trap sites facilitates more rapid electron–hole recombination, resulting in faster decay processes and the noticeably flat TA spectra shown in Fig. 4A. Under CO2, a stronger effect on the relaxation dynamics is observed than under Ar, exhibiting weak signals in the near-IR and in the visible (Fig. 4B). Our previous work with these materials has shown that CO2 binds weakly to the surface of defected indium oxide, generally as carbonate, bicarbonate, and formate species (17, 18). These weakly adsorbed species could impact the relaxation dynamics by altering the energetics of the surface. Indeed, it is interesting to note that at longer times, the near-IR signal has decayed back to the baseline while the visible signal, which is generally associated with trapped holes, remains. CO2 is a weak electron acceptor, so it is possible that some electron density has been removed from the sample through interaction with surface-bound CO2 species, leaving behind excess holes. H2, on the other hand, interacts strongly with the indium oxide surface, exhibiting a substantial effect on the charge carrier relaxation dynamics, both in the near-IR and the visible regions of the spectra. Previously we have demonstrated that H2 dissociates heterolytically at defect sites created by an oxygen vacancy having low In coordination adjacent to a surface hydroxide group (17). This produces an indium hydride at the indium atom that was previously adjacent to the oxygen vacancy (and therefore coordinatively unsaturated) as well as a protonated surface hydroxyl group, which now more closely resembles a surface-bound water. It is clear that this type of interaction results in substantially altered relaxation dynamics, as shown in Fig. 4C. Note that on the short time scales (femtosecond–nanosecond) examined in Figs. 3 and 4, charge scavenging by interacting gases, which typically occurs on the nanosecond–microsecond time scale, is not expected to dominate. Instead, the majority of the transient signal decay in this time regime (<500 ps) is likely due to recombination and relaxation of charge carriers into deeper trap states (45).
Fig. 4.
Transient absorption spectra at different time delays between pump and probe pulses of the In2O3-x(OH)y samples excited with near-band-gap (405-nm) light: (A) in Ar, 0.657-mJ cm−2 incident fluence; (B) in CO2, 0.445-mJ cm−2 incident fluence; (C) in H2, 0.643-mJ cm−2 incident fluence The data gap centered at ∼1.53 eV (809 nm) is due to the strong residual laser fundamental in the probe beam, which led to poor data within this region.
Modeling Excited-State Charge Carrier Relaxation in In2O3-x(OH)y.
To better understand the complex processes apparent in the TA spectra, we used a multiexponential decay function to model the different charge carrier relaxation dynamics in the material. Each data set, collected with a single pump wavelength, incident pump fluence, and a series of probe wavelengths (λ), was fit to a sum of exponentials
| [1] |
where An and τn are the amplitudes and time constants for the exponential decays, respectively, A0 is a constant term (for signal not decaying over the maximum time scale measured by the experiment, which is 2–3 ns), f is the instrument-response function (a Gaussian of width 240 fs, empirically measured using blanks), and the “*” operator represents convolution (27). We did not constrain the fitting to a specific number of decay processes, but rather let it vary as needed to obtain the best fit of the data, using up to a maximum of four exponential terms. This is indicative of the many different relaxation pathways and associated trap states that can occur in such highly defected metal oxides (24, 27, 37). Analyzing the exponential decay processes in this manner across the entire spectral region gives us a more comprehensive picture of the different relaxation pathways present within the In2O3-x(OH)y samples. Representative fits are shown in SI Appendix, Fig. S5.
The samples have multiple decay pathways extending over multiple time scales, including those which have time constants much longer than can be measured with a translation stage for pump–probe delay. Therefore, we have divided the discussion into the fraction of the signal whose decay can be followed (amplitudes and time constants A1–4 and τ1–4, respectively) and the longer-lived fraction (A0). For the picosecond–nanosecond decays, we define the amplitude-weighted average time constant
| [2] |
SI Appendix, Figs. S6–S15 summarize time constants extracted from fitting the exponential decay curves at various wavelengths and pump fluences for I-250, measured in air (SI Appendix, Figs. S6, S10, and S11), Ar (SI Appendix, Fig. S7), CO2 (SI Appendix, Fig. S8), and H2 (SI Appendix, Fig. S9) atmospheres. The average decay times in all cases vary little as a function of probe wavelength throughout the visible midgap region. This confirms that electrons and holes within the material do not relax independently of one another on short time scales and instead behave as coulombically bound excitons, as discussed above (27).
The fastest time constants (SI Appendix, Figs. S6 C and D, S7B, S8B, and S9B) can be attributed to several relaxation pathways. One is the redistribution of charge carriers among shallow states close in energy to the initial excited state, which typically occurs within the first few picoseconds after photoexcitation (24, 27), although this process is often much faster. For example, initial trapping of free carriers in anatase TiO2 was reported to occur in less than ∼200 fs (27). The behavior is modified by the presence or absence of adsorbates at the surface. The fastest time constants under air and CO2 (SI Appendix, Figs. S6C and S8B), can be as much as two orders of magnitude larger than that in Ar (SI Appendix, Fig. S7B), which is likely related to the effect surface adsorbed O2 and CO2 have on the number and distribution of trap states in I-250. Interestingly, under H2, the fastest time constant is 1–2 orders of magnitude smaller than that in air or CO2 (SI Appendix, Fig. S9B) and only slightly larger than in Ar, which may be related to the type of trap states created by the heterolytic dissociation of H2 on the surface of I-250. Because, as we demonstrate herein, the effect of different gas atmospheres can have a substantial effect on the relaxation dynamics, to simplify the number of variables and because of the substantial literature precedent for using air (21, 22, 27, 45) we carried out the most extensive comparison of samples and excitation conditions in air as discussed below.
Decay processes occurring on these short time scales can also be attributed to the second-order relaxation dynamics, such as Auger recombination, which involves nonradiative energy transfer between multiple charge carriers. Tsokkou et al. have demonstrated that Auger recombination processes occur in In2O3 within the first ∼10 ps and become a significant relaxation pathway at pump fluences above 3 µJ cm–2 (37, 38). Auger recombination tends to dominate the short relaxation processes at higher pump intensities when more excited-state charge carriers are present (23, 24, 27). In general, both the amplitude-weighted time constant and the fastest time constant become smaller at higher incident pump fluences (SI Appendix, Fig. S6); this means that, at the lowest incident fluences used, a significant population of the carriers are not relaxing via Auger recombination despite fluences 1–2 orders of magnitude higher than 3 µJ cm–2. A plausible explanation for the 318-nm results, which are the most similar to literature values (37, 38), is the heterogeneity of the I-250 film causing a distribution in the number of photons absorbed per nanocrystal.
Unlike the highly pure In2O3 nanocrystals and nanowires with minimal numbers of oxygen vacancy and hydroxide defects, which have been previously measured with TA, near-band-gap excitation of I-250 creates enough electron–hole pairs to yield observable photoinduced absorption. With 405-nm excitation, much higher fluences are required for Auger recombination to dominate (SI Appendix, Fig. S6 B and D) than when 318-nm excitation is used (SI Appendix, Fig. S6 A and C). Finally, the amplitude-weighted lifetimes for I-250 excited with 405 nm (SI Appendix, Fig. S6B) are 2–10× longer than those measured with 318-nm excitation (SI Appendix, Fig. S6A). These observations are consistent with a band structure modified by defect states. However, the absorbance at 405 nm is extremely weak (SI Appendix, Fig. S2A). Thus, with a lower probability of creating an electron–hole pair with a 405-nm photon, a much higher photon flux is required to create multiple excitons in close enough spatial proximity, such as within the same nanocrystal, for Auger recombination to be observed. The weak near-UV absorbance is balanced by the longer lifetime of carriers trapped at defects, as will be discussed in more detail below, making the defect states relevant for photocatalysis.
An estimation of the Auger time constant can be obtained by examining the time constants at the highest pump fluences, where Auger recombination is expected to dominate in the absence of photodegradation (as confirmed in SI Appendix, Fig. S16). Using this method, we have found Auger constants between 5 and 11 ps (SI Appendix, Figs. S6–S15), depending on the sample and excitation wavelength, which is consistent with the data reported by Tsokkou et al. (38).
SI Appendix, Figs. S11–S13 illustrate the different time constants extracted from fitting the exponential decay curves at various wavelengths and pump intensities for I-250, I-350, and I-450 in air. The time constants have been roughly grouped into four categories based on the types of processes they represent. The first, indicated by the green squares, corresponds to fast processes occurring within the first 20 ps (as discussed above). The next grouping of time constants, represented by the blue squares, is associated with further relaxation into shallow surface-defect states and deeper trap states at lower energies. These processes generally dominate the relaxation dynamics at time delays of ∼20–100 ps (24, 27, 38). The final two groups of time constants, represented by red (100–500 ps) and black (>500 ps) squares, are related to the recombination and ultimate relaxation back to the ground state of long-lived trapped charge carriers. The broad time scale over which this occurs (from ∼100 ps to >10,000 ps) is indicative of the many different relaxation pathways and associated trap states that can occur (24, 27, 37).
When comparing the distribution of time constants in SI Appendix, Fig. S6 to those for I-350 (SI Appendix, Figs. S12 and S14) and I-450 (SI Appendix, Figs. S13 and S15) on short time scales, the relaxation dynamics in I-350 and I-450 are relatively similar to I-250 (SI Appendix, Figs. S6 and S11). The primary difference between the three In2O3-x(OH)y samples is on the longest time scale (>500 ps). Although there is a substantial contribution to this long-lived signal in nearly all of the I-250 results, almost no time constants greater than 500 ps are observed for I-450. I-350 falls in the middle of these two samples, exhibiting some longer-lived components, particularly when excited with 405 nm; however, their contribution is significantly lower than in I-250. This trend correlates with increasing number of intentional defects on passing from I-450 to I-350 to I-250 samples, indicating that these longer-lived excited states may be due to trapped excited-state charge carriers localized in these extrinsic OH and Ov defects.
Estimation of Long-Lived Excited-State Component in In2O3-x(OH)y.
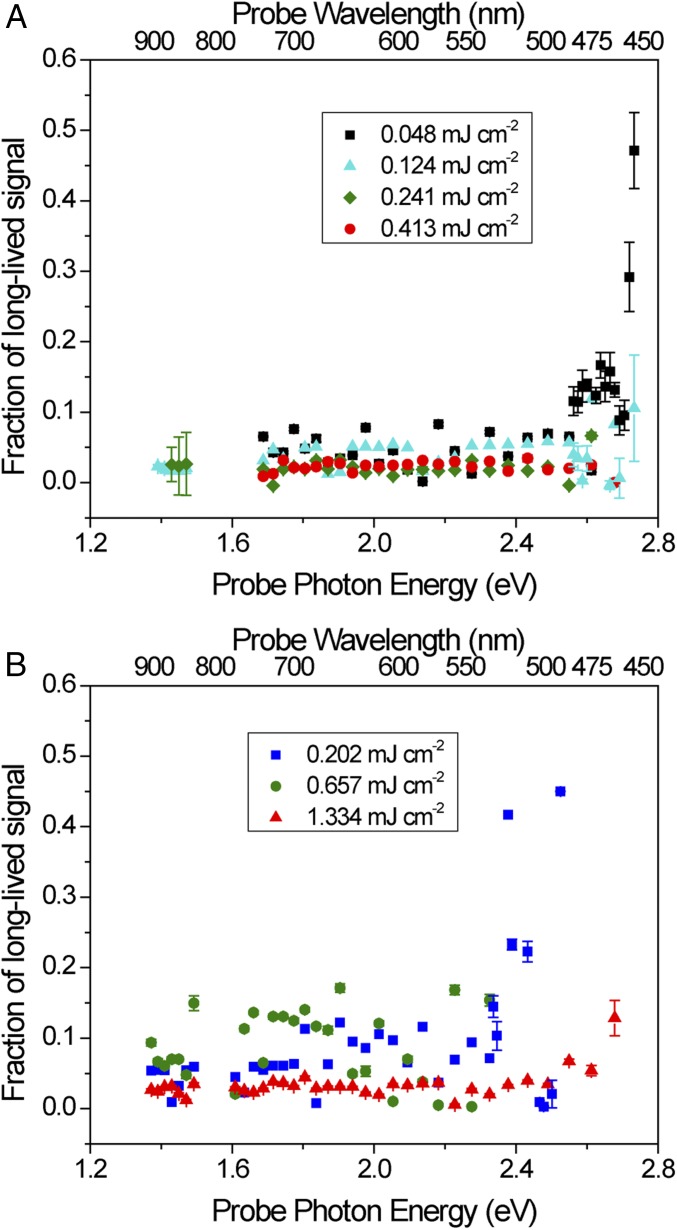
Long-lived excited states have been identified as an important attribute in an effective photocatalyst, with longer lifetimes typically associated with higher photocatalytic performance (21, 27, 46, 47). Whereas the measurement window in this study was restricted to 3 ns due to instrument limitations, it is possible to estimate long-lived components using the model described in the previous section. The constant term A0 represents this long-lived signal which, if representing the absorption of excited carriers, would possess a lifetime of at least ∼10 ns (27). Values of A0 <0 can occur at wavelengths where the signal is weak and are interpreted as the absence of long-lived carriers combined with experimental noise and possibly other effects, such as transient heating, and will not be discussed here. The long-lived component for I-250 in air under 318-nm and 405-nm excitation is shown in Fig. 5 A and B, respectively. Whereas on short time scales the relaxation is largely independent of probe photon energy, at longer time scales the behavior is more complex. A high fraction of long-lived excited states is observed for I-250 at higher probe energy, beginning near 2.6 eV or 2.4 eV under 318-nm or 405-nm excitation, respectively. This signal decreases with increasing pump fluence, likely as a result of enhanced Auger recombination at higher light intensities, which facilitates faster relaxation. In metal oxides, positive TA signals in this region of the spectrum are typically associated with trapped holes (21, 22, 27). It has been demonstrated that surface hydroxyl groups are very efficient hole traps in these materials (21, 22), and in some cases have been attributed to helping to enhance the overall excited-state lifetime of charge carriers in the material. For example, Wang et al. reported an increase in charge carrier relaxation rates upon vacuum heat treatment, which removed surface hydroxyl groups on anatase TiO2 (21).
Fig. 5.
Fraction of long-lived signal (τ >∼10 ns), equal to A0, at different pump fluences for I-250 excited with (A) 318-nm light and (B) 405-nm light.
Although there is a clear wavelength dependence of the long-lived component of the I-250 spectra in air, there is no such dependence observed for I-350 (SI Appendix, Fig. S17) or I-450 (SI Appendix, Fig. S18). This could be due to the reduced concentration of surface hydroxyl groups in these samples, which would reduce the amount of available hole traps in the material. All three samples using a 405-nm excitation source produce a higher signal from the long-lived component than 318-nm excitation. One possible explanation of this, as discussed above, could be the direct excitation of trap states, producing less mobile, more localized charge carriers. In I-250 it is significant that both 318- and 405-nm excitation produce a pronounced signal in the same region of the spectrum. This indicates that the generation of trapped holes in this long-lived charge-separated state is a property of the material, likely resulting from high concentrations of surface hydroxyl groups, and not an effect of the excitation source.
The fact that we do not observe a peak associated with trapped electrons, which in TiO2 occurs at probe energies of 1.2–2.1 eV, suggests that the electrons were somehow removed (22). Because these measurements were performed in air, it is likely that electron scavenging by O2, which typically occurs on the nanosecond–microsecond time scale, is responsible for this long-lived charge-separated state (22, 48). This is consistent with the lack of any long-lived component for I-250 measured in Ar (SI Appendix, Fig. S7C), as the lack of electron transfer to O2 facilitates rapid electron–hole recombination. Under both H2 and CO2, there is a very faint long-lived signal remaining (SI Appendix, Figs. S8C and S9C), indicating that in the absence of a strong electron or hole scavenger, charge recombination is much faster. In H2 this is largely flat across the entire near-IR and visible spectrum, but under CO2, there is a slight increase beginning around 2.3 eV, which is the region typically associated with trapped holes. This is consistent with the enhanced signal observed in this region at 3,000 ps (Fig. 4B), indicating that a very small amount of photogenerated electrons at the surface of indium oxide are able to react with CO2.
Examining the Impact of Ov and OH Defects on the Electronic Band Structure.
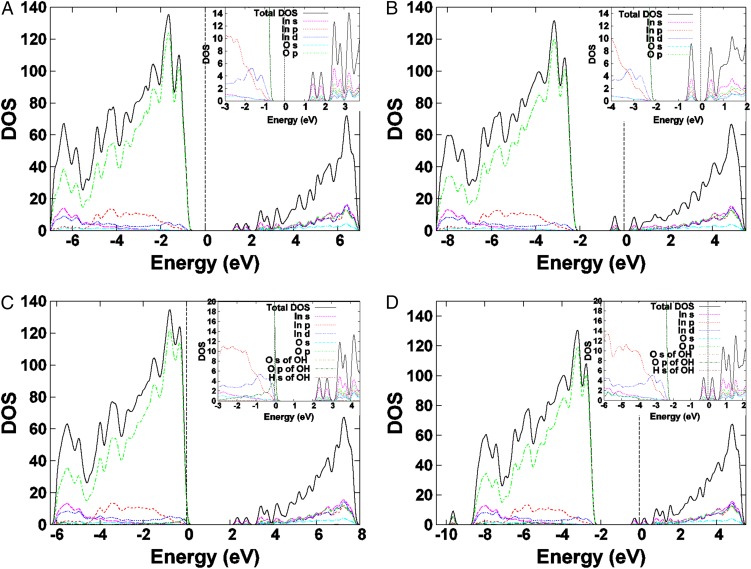
Our experimentally prepared In2O3-x(OH)y nanoparticles, which are heterogeneous in nature, are likely to contain four types of defected surfaces within the same sample: surface with an isolated OH [In2O3(OH)y], surface with O vacancy defects (In2O3-x), surface with both OH and O vacancy defects [In2O3-x(OH)y], and the surface with no defects at all (In2O3). To gain a deeper understanding of how these surfaces impact the electronic band structure of our samples, we calculated the total DOS and PDOS of the bulk material (SI Appendix, Fig. S19) and all four types of surfaces (shown in SI Appendix, Fig. S20) using hybrid DFT calculations (see SI Appendix, Experimental, Computational Details). By examining the electronic character and effects of each of these defected surfaces individually, we gained a deeper understanding of different contributions within the sample and how this may affect the relaxation processes for photoexcited electrons and holes.
Fig. 6 shows DOS and PDOS calculated for the four different surfaces. Comparing the DOS of bulk In2O3 (SI Appendix, Fig. S19B) with the DOS of pristine, defect-free In2O3 surface (Fig. 6A) indicates that the introduction of surface states reduces the bulk band gap by ∼1.1 eV. This occurs through both a lowering of the conduction band (CB) states and a raising of the valence band (VB) states, resulting in a band gap estimate of 2.0 eV, which is consistent with other reports in the literature (43). As in the bulk In2O3 structure, the Fermi level (EF) for this surface is approximately centered within the optical band gap.
Fig. 6.
Effect of Ov and OH defects on the total and PDOS for various indium oxide (111) surfaces. (A) Pristine, defect-free In2O3 surface. (B) In2O3-x surface containing only an oxygen vacancy (Ov) defect. (C) In2O3(OH)y surface containing only an OH defect. (D) In2O3-x(OH)y surface containing both Ov and OH defects. The zero-energy value is set at the Fermi level, represented by the vertical dashed line. (Insets) An expanded view of the states at the band edges.
The oxygen vacancy-only In2O3-x surface (Fig. 6B) produces deeper states at the surface. They are found to be 1.5 eV above the VB minimum for the In2O3-x surface. Further, the position of the Fermi level shows that these states are fully occupied. Because oxygen vacancies act as donors, an increase in electron surface charge develops. The increased donor concentration toward the surface layer should effectively lead to an electron accumulation in this material. However, when only a hydroxide defect is present on the (111) surface (Fig. 6C), the band gap does not change as dramatically as in the case of the vacancy-only, remaining almost identical to the pristine, defect-free In2O3 surface. The key difference between this surface and the other three surfaces studied is the accumulation of p electrons from the O atom of the surface OH group at the VB edge, as illustrated in the Fig. 6C (Inset). Additionally, the Fermi level for this surface has shifted to the VB edge, providing further support that the surface hydroxides act as acceptors.
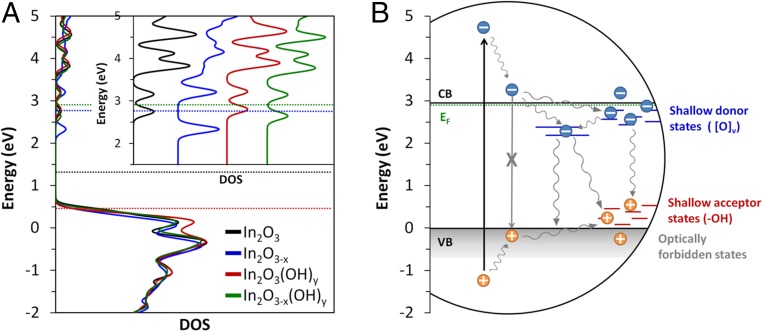
When both Oy and OH defects are present (Fig. 6D), an overall reduction in the band gap of 0.1 eV is observed relative to the pristine surface, indicating that the effect of the Ov is moderated by the addition of the OH group to the surface. However, the Fermi level of the In2O3-x(OH)y surface indicates that some states near the CB edge will be occupied in contrast to the pristine surface. Fig. 7A provides a comparison of the total DOS for each of the four surfaces, clearly illustrating how the presence of OH and Ov defects on the indium oxide surface impacts the electronic band structure. The combination of both OH and Ov defects in the In2O3-x(OH)y surface produces a band structure that is closer to the pristine surface, however with the key distinction of having the highest Fermi energy of all of the surfaces we examined herein.
Fig. 7.
Comparison between calculated total DOS for pristine and defected (111) indium oxide surfaces and a schematic diagram illustrating the different charge carrier relaxation processes in In2O3-x(OH)y. Both diagrams are plotted on the same energy scale and aligned using the Fermi level of the In2O3-x(OH)y surface and the experimentally measured Fermi level of I-250. (A) The total DOS for (111) In2O3, In2O3-x, In2O3(OH)y, and the In2O3-x(OH)y surfaces. The horizontal dashed lines indicate the position of the Fermi level for each surface. (Inset) Expanded view of the DOS in the conduction band region. (B) A schematic illustration of charge carrier recombination pathways in In2O3-x(OH)y nanoparticles. The vertical black arrow indicates initial excitation from the pump pulse. The wavy gray arrows illustrate different nonradiative relaxation processes. Blue and red lines indicate midgap states created by oxygen vacancy and surface hydroxyl groups, respectively.
Previously, several TA studies have demonstrated that, in metal oxides, oxygen vacancies and surface hydroxyl groups create midgap states that act as electron and hole traps, respectively (21, 27–29). It is generally believed that oxygen vacancies create donor states just below the CB edge, whereas surface hydroxyl groups create acceptor states just above the VB edge. From both our TA experiments and DFT calculations, it is clear that this is also the case for defected indium oxide materials. This is represented schematically in Fig. 7B, in which a simplified illustration of the various charge carrier recombination pathways involving Ov and OH defects in In2O3-x(OH)y nanoparticles is placed on the same energy scale as the total DOS of the pristine and defected In2O3 surfaces in Fig. 7A. The two plots were aligned using the experimentally measured Fermi level from XPS (SI Appendix, Fig. S2) of I-250 and the calculated Fermi level of the In2O3-x(OH)y surface from DFT. When comparing the experimentally measured positions of the CBs and VBs based on the optical band gap, the predicted locations of Ov and OH defects based on our TA observations, and the calculated electronic states created by the introduction of these defects, it is evident that there is a strong correlation and support for our assignments of the TA signals in the previous sections.
Correlation of Charge Carrier Relaxation Dynamics to Photocatalytic Activity in In2O3-x(OH)y.
The excited-state charge carrier relaxation dynamics have significant implications for photocatalysis, determining the population of electrons and holes available with sufficient energy to facilitate charge transfer to surface adsorbed reactant molecules, such as H2 and CO2. As indicated in Fig. 7B, the relaxation processes involving such a large number of defect states is highly complex and it is therefore very difficult to draw conclusions about the specific relaxation pathways the charge carriers travel on their route toward the ground state in these materials. However, several key trends have emerged in this study that can help to explain the observed trends in photocatalytic activity. Our results indicate that for In2O3-x(OH)y nanocrystals, a higher concentration of defects corresponds to both longer lifetimes and higher photocatalytic rates. This suggests that intentionally engineering defects in these photocatalysts would not only facilitate the photocatalytic reduction of CO2 by creating active surface sites, but could also positively impact the optoelectronic properties, by enhancing the population of available photogenerated charge carriers to facilitate light-driven catalytic reactions. On short time scales (<3 ns), we have observed an increase in TA signal in the near-IR region, indicative of transitions from photogenerated charge carriers populating shallow traps such as oxygen vacancy states near the CB edge or surface hydroxyl group states near the VB edge (21, 22, 26). This signal intensity is highest for I-250, indicating a higher population of charge carriers in these states, which is likely due to the greater number of vacancy and hydroxide states available. This is further supported by the DOS calculations, which indicate that the addition of oxygen vacancy within indium oxide does indeed create populated states near the CB edge and the addition of surface OH group increases the number of states near the VB edge. On longer time scales (>10 ns) we demonstrate a significant enhancement in the signal for I-250 in air at 2.4–2.6 eV, which is attributed to holes trapped in surface hydroxyl groups after the electrons have been scavenged by O2 (21). This is supported by the lack of long-lived signal in Ar and H2 atmospheres. In the absence of a strong electron scavenger such as O2, charge recombination is much faster. Under CO2, the long-lived component was equally weak; however, there is a slightly enhanced signal in the region attributed to holes trapped in surface hydroxyl groups, indicating that a very small amount of photogenerated electrons at the surface of indium oxide may be able to react with CO2. The localization of electrons in oxygen vacancies and holes in surface hydroxyl groups has significant implications for the surface-mediated, light-driven RWGS reaction mechanism. This trapping of photoexcited electrons and holes at these surface sites is proposed to increase their basicity and acidity, respectively. This could explain the 20-kJ·mol−1 lower apparent activation energy for the light-driven reaction at the surface of defected In2O3-x(OH)y relative to the dark, thermally driven reaction. Although the interaction of light with defected In2O3-x(OH)y materials is very complex, a clearer picture is beginning to emerge regarding the role defect states play in determining both the excited-state lifetimes of photogenerated charge carriers as well as their localization in catalytically relevant defects, which ultimately determines the photocatalytic activity of the material.
In a broader context, the results reported herein suggest that in the design of a photocatalyst one must think beyond the more commonly considered parameters, such as band-gap size, positions of the CBs and VBs, Fermi energy, and so forth. In particular, researchers seeking to design an effective CO2 reduction photocatalyst must also consider both the surface properties of the material as well as how the surface states affect the lifetime of the photogenerated electrons and holes. Further, because of the demonstrated effectiveness of Ov and OH defects in facilitating electron and hole trapping, respectively, as well as the key role they play in the reaction mechanism (17, 19), it is anticipated that the controlled, intentional incorporation of these defects into other metal oxides may help to improve their photocatalytic activity.
Conclusions
In this study, three photocatalytically active In2O3-x(OH)y samples were prepared with varying concentrations of oxygen vacancies and surface hydroxyl groups. Femtosecond TA measurements demonstrate that these defects play a significant role in the excited-state charge relaxation pathways, which strongly correlates to photocatalytic activity. Higher defect concentrations result in longer excited-state lifetimes, which is attributed to electron- and hole trapping in oxygen vacancies and surface hydroxyl groups, respectively, and which have been shown to play a central role in the photocatalytic reaction mechanism. We then used computational modeling to better understand how the introduction of these intentional defects changes the density of states and charge localization in In2O3-x(OH)y materials, confirming our assignment of these electron- and hole-trap states. A deeper understanding of how intentional defects, such as oxygen vacancies and surface hydroxyl groups, impact the optoelectronic properties of photocatalytically active materials like indium oxide can provide valuable insight into how to rationally tune these defects through materials engineering to optimize the photocatalytic performance, facilitating efficient solar fuel production.
Materials and Methods
The In2O3-x(OH)y nanoparticles were prepared via a previously published procedure (18), which is described in detail in the SI Appendix. PXRD was performed on a Bruker D2-Phaser X-ray diffractometer, using Cu Kα radiation at 30 kV. Sample morphology was determined using the aberration-corrected JEOL JEM-ARM200CF STEM operated at 200 kV. Diffuse reflectance of the samples was measured using a Lambda 1050 UV/VIS/NIR spectrometer from Perkin-Elmer and an integrating sphere with a diameter of 150 mm. XPS was performed using a Perkin-Elmer Phi 5500 ESCA spectrometer in an ultrahigh vacuum chamber with base pressure of 1 × 10−9 torr. The spectrometer uses an Al Kα X-ray source operating at 15 kV and 27 A. The samples used in XPS analyses were prepared by drop-casting aqueous dispersions onto p-doped Si(100) wafers. Gas-phase photocatalytic rate measurements were conducted via a previously published procedure (18), which is described in detail in the SI Appendix. Transient absorption measurements were carried out under air, Ar (99.999%, Airgas), H2 (99.999%, Airgas), or bone-dry CO2 (99.999%, Airgas) atmospheres using a Helios UV-visible spectrometer (Ultrafast Systems). Data were analyzed in MATLAB (Mathworks) software using the Nelder–Mead simplex algorithm for fitting (49). Further details are given in the SI Appendix.
The model of In2O3 (111) surface used in this study is a 3-layer periodic slab model having 120 atoms and a vacuum layer of size >20 Å. The modeled system was a continuous layer, roughly 8.5 Å in thickness, which represents a nanofilm, and captures the behavior of nonedge nanocrystal regions, which form the majority of surface area. The computational approaches based on hybrid functionals have demonstrated success in describing the electronic, optical, and defect properties of transition metal oxides and metal oxides (50–54). Therefore, in this study, plane-wave DFT implemented in Quantum ESPRESSO code (55) along with the hybrid HSE06 approach (56, 57) is used for calculating the electronic properties of pristine and defected surfaces. The details of the computational model and technique used for DFT calculations are given in the SI Appendix, including the optimized DFT models (SI Appendix, Figs. S19 and S20).
Supplementary Material
Acknowledgments
C.V.S. gratefully acknowledges SciNet (58) and Calcul Quebec consortia under the auspices of Compute Canada for computational resources. G.A.O. is a Government of Canada Research Chair in Materials Chemistry and Nanochemistry. Financial support for this work was provided by the Ontario Ministry of Research Innovation; Ministry of Economic Development, Employment and Infrastructure; Ministry of the Environment and Climate Change; Connaught Innovation Fund; Connaught Global Challenge Fund; and the Natural Sciences and Engineering Research Council of Canada. P.S. and M.A.E.-S. acknowledge the funding from the US National Science Foundation, Division of Chemistry (Grant 1608801). Q.Q. was supported by the Center for the Computational Design of Functional Layered Materials (CCDM), an Energy Frontier Research Center (EFRC) funded by the US Department of Energy - Basic Energy Sciences (US DOE-BES) (DE-SC0012575) for her TEM work, and Y.Z. was supported by DOE-BES, Materials Science and Engineering Division (DE-SC0012704).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1609374113/-/DCSupplemental.
References
- 1.Tahir M, Amin NS. Recycling of carbon dioxide to renewable fuels by photocatalysis: Prospects and challenges. Renew Sustain Energy Rev. 2013;25:560–579. [Google Scholar]
- 2.Thomas JM. Heterogeneous catalysis and the challenges of powering the planet, securing chemicals for civilised life, and clean efficient utilization of renewable feedstocks. ChemSusChem. 2014;7(7):1801–1832. doi: 10.1002/cssc.201301202. [DOI] [PubMed] [Google Scholar]
- 3.Tachibana Y, Vayssieres L, Durrant JR. Artificial photosynthesis for solar water-splitting. Nat Photonics. 2012;6:511–518. [Google Scholar]
- 4.Kim D, Sakimoto KK, Hong D, Yang P. Artificial photosynthesis for sustainable fuel and chemical production. Angew Chem Int Ed. 2015;54:3259–3266. doi: 10.1002/anie.201409116. [DOI] [PubMed] [Google Scholar]
- 5.Centi G, Quadrelli EA, Perathoner S. Catalysis for CO2 conversion: A key technology for rapid introduction of renewable energy in the value chain of chemical industries. Energy Environ Sci. 2013;6(6):1711. [Google Scholar]
- 6.Habisreutinger SN, Schmidt-Mende L, Stolarczyk JK. Photocatalytic reduction of CO2 on TiO2 and other semiconductors. Angew Chem Int Ed Engl. 2013;52(29):7372–7408. doi: 10.1002/anie.201207199. [DOI] [PubMed] [Google Scholar]
- 7.Olah GA, Prakash GKS, Goeppert A. Anthropogenic chemical carbon cycle for a sustainable future. J Am Chem Soc. 2011;133(33):12881–12898. doi: 10.1021/ja202642y. [DOI] [PubMed] [Google Scholar]
- 8.Bensaid S, Centi G, Garrone E, Perathoner S, Saracco G. Towards artificial leaves for solar hydrogen and fuels from carbon dioxide. ChemSusChem. 2012;5(3):500–521. doi: 10.1002/cssc.201100661. [DOI] [PubMed] [Google Scholar]
- 9.Liu G, Hoivik N, Wang K, Jakobsen H. Engineering TiO2 nanomaterials for CO2 conversion/solar fuels. Sol Energy Mater Sol Cells. 2012;105:53–68. [Google Scholar]
- 10.Tran PD, Wong LH, Barber J, Loo JSC. Recent advances in hybrid photocatalysts for solar fuel production. Energy Environ Sci. 2012;5(3):5902. [Google Scholar]
- 11.van der Giesen C, Kleijn R, Kramer GJ. Energy and climate impacts of producing synthetic hydrocarbon fuels from CO2. Environ Sci Technol. 2014;48(12):7111–7121. doi: 10.1021/es500191g. [DOI] [PubMed] [Google Scholar]
- 12.Zhou H, Fan T, Zhang D. An insight into artificial leaves for sustainable energy inspired by natural photosynthesis. ChemCatChem. 2011;3(3):513–528. [Google Scholar]
- 13.Liu A, Gao J, He L. New and Future Developments in Catalysis: Activation of Carbon Dioxide. Elsevier; Amsterdam: 2013. pp. 81–147. [Google Scholar]
- 14.Kumar B, et al. Photochemical and photoelectrochemical reduction of CO2. Annu Rev Phys Chem. 2012;63:541–569. doi: 10.1146/annurev-physchem-032511-143759. [DOI] [PubMed] [Google Scholar]
- 15.King PDC, et al. Band gap, electronic structure, and surface electron accumulation of cubic and rhombohedral In2O3. Phys Rev B. 2009;79(20):1–10. [Google Scholar]
- 16.Meissner D, Lauermann I, Memming R, Kastening B. Photoelectrochemistry of cadmium sulfide. 2. Influence of surface-state charging. J Phys Chem. 1988;92:3484–3488. [Google Scholar]
- 17.Ghuman KK, et al. Illuminating CO2 reduction on frustrated Lewis pair surfaces: Investigating the role of surface hydroxides and oxygen vacancies on nanocrystalline In2O3-x(OH)y. Phys Chem Chem Phys. 2015;17(22):14623–14635. doi: 10.1039/c5cp02613j. [DOI] [PubMed] [Google Scholar]
- 18.Hoch LB, et al. The rational design of a single-component photocatalyst for gas-phase CO2 reduction using both UV and visible light. Adv Sci. 2014;1(1):1400013. doi: 10.1002/advs.201400013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kaur Ghuman K, et al. Photoexcited surface frustrated Lewis pairs for heterogeneous photocatalytic CO2 reduction. J Am Chem Soc. 2016;138(4):1206–1214. doi: 10.1021/jacs.5b10179. [DOI] [PubMed] [Google Scholar]
- 20.He L, et al. Spatial separation of charge carriers in In2O3-x(OH)y nanocrystal superstructures for enhanced gas-phase photocatalytic activity. ACS Nano. 2016;10(5):5578–5586. doi: 10.1021/acsnano.6b02346. [DOI] [PubMed] [Google Scholar]
- 21.Wang X, et al. Trap states and carrier dynamics of TiO2 studied by photoluminescence spectroscopy under weak excitation condition. Phys Chem Chem Phys. 2010;12(26):7083–7090. doi: 10.1039/b925277k. [DOI] [PubMed] [Google Scholar]
- 22.Yoshihara T, et al. Identification of reactive species in photoexcited nanocrystalline TiO2 films by wide-wavelength-range (400−2500 nm) transient absorption spectroscopy. J Phys Chem B. 2004;108(12):3817–3823. [Google Scholar]
- 23.Klimov VI, McBranch DW, Leatherdale CA, Bawendi MG. Electron and hole relaxation pathways in semiconductor quantum dots. Phys Rev B. 1999;60(19):13740–13749. [Google Scholar]
- 24.Zhang JZ. Interfacial charge carrier dynamics of colloidal semiconductor nanoparticles. J Phys Chem B. 2000;104(31):7239–7253. [Google Scholar]
- 25.Hwang GW, et al. Identifying and eliminating emissive sub-bandgap states in thin films of PbS nanocrystals. Adv Mater. 2015;27(30):4481–4486. doi: 10.1002/adma.201501156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ahmed SM, Szymanski P, El-Nadi LM, El-Sayed MA. Energy-transfer efficiency in Eu-doped ZnO thin films: The effects of oxidative annealing on the dynamics and the intermediate defect states. ACS Appl Mater Interfaces. 2014;6(3):1765–1772. doi: 10.1021/am404662k. [DOI] [PubMed] [Google Scholar]
- 27.Triggiani L, et al. Excitation-dependent ultrafast carrier dynamics of colloidal TiO2 nanorods in organic solvent. J Phys Chem C. 2014;118:25215–25222. [Google Scholar]
- 28.Zhang KHL, et al. Microscopic origin of electron accumulation in In2O3. Phys Rev Lett. 2013;110(5):056803. doi: 10.1103/PhysRevLett.110.056803. [DOI] [PubMed] [Google Scholar]
- 29.Lany S, et al. Surface origin of high conductivities in undoped In2O3 thin films. Phys Rev Lett. 2012;108(1):016802. doi: 10.1103/PhysRevLett.108.016802. [DOI] [PubMed] [Google Scholar]
- 30.Berera R, van Grondelle R, Kennis JTM. Ultrafast transient absorption spectroscopy: Principles and application to photosynthetic systems. Photosynth Res. 2009;101(2-3):105–118. doi: 10.1007/s11120-009-9454-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Bonneau R, Wirz J, Zuberbuhler AD. Methods for the analysis of transient absorption data. Pure Appl Chem. 1997;69(5):979–992. [Google Scholar]
- 32.Forster M, et al. Oxygen deficient α-Fe2O3 photoelectrodes: A balance between enhanced electrical properties and trap-mediated losses. Chem Sci (Camb) 2015;6:4009–4016. doi: 10.1039/c5sc00423c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ghuman KK, Singh CV. Effect of doping on electronic structure and photocatalytic behavior of amorphous TiO2. J Phys Condens Matter. 2013;25(47):475501. doi: 10.1088/0953-8984/25/47/475501. [DOI] [PubMed] [Google Scholar]
- 34.Yamakata A, Vequizo JJM, Matsunaga HJ. Behavior and energy state of photogenerated charge carriers in single-crystalline and polycrystalline powder SrTiO3 studied by time-resolved absorption spectroscopy in the visible to mid-infrared region. J Phys Chem C. 2015;119:24538–24545. [Google Scholar]
- 35.Janowitz C, et al. Experimental electronic structure of In2O3 and Ga2O3. New J Phys. 2011;13(8):85014. [Google Scholar]
- 36.Walsh A, et al. Nature of the band gap of In2O3 revealed by first-principles calculations and x-ray spectroscopy. Phys Rev Lett. 2008;100(16):167402. doi: 10.1103/PhysRevLett.100.167402. [DOI] [PubMed] [Google Scholar]
- 37.Othonos A, Zervos M, Tsokkou D. Femtosecond carrier dynamics in In2O3 nanocrystals. Nanoscale Res Lett. 2009;4(6):526–531. doi: 10.1007/s11671-009-9275-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Tsokkou D, Othonos A, Zervos M. Ultrafast time-resolved spectroscopy of In2O3 nanowires. J Appl Phys. 2009;106(8):84307. [Google Scholar]
- 39.Koga N, Kimizu T. Thermal decomposition of indium(III) hydroxide prepared by the microwave-assisted hydrothermal method. J Am Ceram Soc. 2008;91(12):4052–4058. [Google Scholar]
- 40.Chorkendorff I, Niemantsverdriet JW. Concepts of Modern Catalysis and Kinetics. Wiley-VCH; Weinheim, Germany: 2003. [Google Scholar]
- 41.Chang W-C, et al. Sn-doped In2O3 nanowires: Enhancement of electrical field emission by a selective area growth. Nanoscale Res Lett. 2012;7(1):684. doi: 10.1186/1556-276X-7-684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Yang X, Tamai N. How fast is interfacial hole transfer? In situ monitoring of carrier dynamics in anatase TiO2 nanoparticles by femtosecond laser spectroscopy. Phys Chem Chem Phys. 2001;3(16):3393–3398. [Google Scholar]
- 43.Baldoví HG, et al. Understanding the origin of the photocatalytic CO2 reduction by Au- and Cu-loaded TiO2: A microsecond transient absorption spectroscopy study. J Phys Chem C. 2015;119(12):6819–6827. [Google Scholar]
- 44.Henderson MA, Epling WS, Peden CHF, Perkins CL. Insights into photoexcited electron scavenging processes on TiO2 obtained from studies of the reaction of O2 with OH groups adsorbed at electronic defects on TiO2(110) J Phys Chem B. 2003;107(2):534–545. [Google Scholar]
- 45.Tamaki Y, et al. Dynamics of efficient electron-hole separation in TiO2 nanoparticles revealed by femtosecond transient absorption spectroscopy under the weak-excitation condition. Phys Chem Chem Phys. 2007;9(12):1453–1460. doi: 10.1039/b617552j. [DOI] [PubMed] [Google Scholar]
- 46.Green ANM, Palomares E, Haque SA, Kroon JM, Durrant JR. Charge transport versus recombination in dye-sensitized solar cells employing nanocrystalline TiO2 and SnO2 films. J Phys Chem B. 2005;109(25):12525–12533. doi: 10.1021/jp050145y. [DOI] [PubMed] [Google Scholar]
- 47.Chen Y, Pu Y, Hsu Y. Interfacial charge carrier dynamics of the three-component In2O3−TiO2−Pt heterojunction system. J Phys Chem C. 2012;116:2967–2975. [Google Scholar]
- 48.Peiró AM, et al. Photochemical reduction of oxygen adsorbed to nanocrystalline TiO2 films: A transient absorption and oxygen scavenging study of different TiO2 preparations. J Phys Chem B. 2006;110(46):23255–23263. doi: 10.1021/jp064591c. [DOI] [PubMed] [Google Scholar]
- 49.Press WH, Teukolsky SA, Vetterling WT, Flannery BP. Numerical Recipes in C: The Art of Scientific Computing. 2nd Ed Cambridge Univ Press; New York: 1992. [Google Scholar]
- 50.Muscat J, Wander A, Harrison NM. On the prediction of band gaps from hybrid functional theory. Chem Phys Lett. 2001;342:397–401. [Google Scholar]
- 51.Moreira I de PR, Illas F, Martin RL. Effect of Fock exchange on the electronic structure and magnetic coupling in NiO. Phys Rev B. 2002;65:155102. [Google Scholar]
- 52.Walsh A, Da Silva JLF, Yan Y, Al-Jassim MM, Wei S-H. Origin of electronic and optical trends in ternary In2O3(ZnO)n transparent conducting oxides (n=1,3,5): Hybrid density functional theory calculations. Phys Rev B. 2009;79:73105. [Google Scholar]
- 53.Scanlon DO, Morgan BJ, Watson GW, Walsh A. Acceptor levels in p-type Cu2O: Rationalizing theory and experiment. Phys Rev Lett. 2009;103(9):096405. doi: 10.1103/PhysRevLett.103.096405. [DOI] [PubMed] [Google Scholar]
- 54.Vidal J, Trani F, Bruneval F, Marques MAL, Botti S. Effects of electronic and lattice polarization on the band structure of delafossite transparent conductive oxides. Phys Rev Lett. 2010;104(13):136401. doi: 10.1103/PhysRevLett.104.136401. [DOI] [PubMed] [Google Scholar]
- 55.Giannozzi P, et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J Phys Condens Matter. 2009;21(39):395502. doi: 10.1088/0953-8984/21/39/395502. [DOI] [PubMed] [Google Scholar]
- 56.Heyd J, Scuseria GE, Ernzerhof M. Hybrid functionals based on a screened Coulomb potential. J Chem Phys. 2003;118:8207–8215. [Google Scholar]
- 57.Heyd J, Scuseria GE, Ernzerhof M. 2006. Erratum: "Hybrid functionals based on a screened Coulomb potential." J Chem Phys 124(21):219906.
- 58.Loken C, et al. SciNet: Lessons learned from building a power-efficient top-20 system and data centre. J Phys Conf Ser. 2010;256:12026. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.