Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2017 Oct 3.
Published in final edited form as: J Biomech. 2016 Aug 6;49(14):3244–3251. doi: 10.1016/j.jbiomech.2016.08.004

THE FUNCTIONAL ROLES OF MUSCLES DURING SLOPED WALKING

Nathaniel T Pickle 1, Alena M Grabowski 2,3, Arick G Auyang 4, Anne K Silverman 1
PMCID: PMC5167499  NIHMSID: NIHMS812012  PMID: 27553849

Abstract

Sloped walking is biomechanically different from level-ground walking, as evidenced by changes in joint kinematics and kinetics. However, the changes in muscle functional roles underlying these altered movement patterns have not been established. In this study, we developed a total of 273 muscle-actuated simulations to assess muscle functional roles, quantified by induced body center-of-mass accelerations and trunk and leg power, during walking on slopes of 0°, ±3°, ±6°, and ±9° at 1.25 m/s. The soleus and gastrocnemius both provided greater forward acceleration of the body parallel to the slope at +9° compared to level ground (+126% and +66%, respectively). However, while the power delivered to the trunk by the soleus varied with slope, the magnitude of net power delivered to the trunk and ipsilateral leg by the biarticular gastrocnemius was similar across all slopes. At +9°, the hip extensors absorbed more power from the trunk (230% hamstrings, 140% gluteus maximus) and generated more power to both legs (200% hamstrings, 160% gluteus maximus) compared to level ground. At −9°, the knee extensors (rectus femoris and vasti) accelerated the body upward perpendicular to the slope at least 50% more and backward parallel to the slope twice as much as on level ground. In addition, the knee extensors absorbed greater amounts of power from the ipsilateral leg on greater declines to control descent. Future studies can use these results to develop targeted rehabilitation programs and assistive devices aimed at restoring sloped walking ability in impaired populations.

Keywords: biomechanics, incline, decline, gait, modeling and simulation

1. INTRODUCTION

Sloped surfaces are encountered in both man-made and natural environments. When walking on slopes, the muscles raise or lower the body center-of-mass (COM) while maintaining balance. The altered biomechanical demands of sloped walking, particularly with large slope angles, require greater activity from lower-limb muscles, such as the gluteus maximus on inclines and rectus femoris and vasti on declines (Lay et al., 2007). On inclines, metabolic power is increased compared to level-ground walking (Jeffers et al., 2015). These results suggest that sloped walking is a more difficult biomechanical task than level-ground walking.

Previous sloped walking studies have established how joint kinematics and kinetics change compared to level-ground walking. For example, when walking on a 24% grade (13.5°) the hip and ankle ranges-of-motion increase by 20% and 59%, respectively, compared to level ground (Lange et al., 1996). In addition, when walking on a 39% grade (21.3°) the peak hip extension moment during early stance is nearly four times larger than on level ground and the peak ankle plantarflexion moment during late stance is 19% greater than on level ground (Lay et al., 2006). On declines, the knee joint mechanical power can be up to six times larger than on level ground (Kuster et al., 1995). However, the contributions of individual muscles to these altered biomechanics have not been established.

Musculoskeletal modeling and simulation allow for investigation of the functional roles of individual muscles during movement (Piazza, 2006). Muscles can accelerate all body segments (Zajac et al., 2002) and their functional roles can be difficult to predict based solely on anatomical classification (Hernández et al., 2008; Neptune et al., 2001). For example, the soleus generates power to the trunk while the gastrocnemius generates power to the ipsilateral leg for swing initiation during level-ground walking (Neptune et al., 2001). The hamstrings absorb power from the trunk and generate power to the ipsilateral leg during level-ground walking (Neptune et al., 2004; Silverman and Neptune, 2012), and the knee extensors provide braking acceleration of the COM (Pandy et al., 2010) while absorbing power from the ipsilateral leg and generating power to the trunk (Neptune et al., 2004; Silverman and Neptune, 2012). While these results provide an understanding of level-ground walking, muscle functional roles likely change in response to the biomechanical demands of sloped walking.

Our goal was to characterize the functional roles of the major lower-limb muscle groups in unimpaired adults during sloped walking using musculoskeletal modeling and simulation. We quantified muscle functional roles with induced COM acceleration and mechanical power delivered to the trunk and legs, and refer to each muscle’s contribution to the net COM acceleration and segment mechanical power. Based on previous kinematic, kinetic, and musculoskeletal simulation results, we hypothesized that on inclines the ankle plantarflexors and hip extensors would accelerate the COM and generate power to the trunk and ipsilateral leg to a greater extent than in level-ground walking. We also hypothesized that during decline walking the knee extensors would provide greater braking acceleration and absorb more power from the ipsilateral leg relative to level-ground walking.

2. METHODS

2.1. Experimental Data Collection

Thirteen healthy adults (4 female/9 male, 67±10 kg, 173±9 cm, 28±7 years) provided written informed consent to participate in the protocol approved by the Department of Veterans Affairs’ Human Subjects Institutional Review Board. Participants walked at 1.25 m/s on an instrumented dual-belt treadmill (Bertec Corp., Columbus, OH) on slopes of 0°, ±3°, ±6°, and ±9° in randomized order while we measured bilateral ground reaction forces (GRFs, 1500 Hz), whole-body kinematics (100 Hz, Vicon Inc., Centennial, CO) and electromyographic (EMG) signals (1500 Hz, Noraxon Corp., Scottsdale, AZ) from eight muscles of each leg (Table 1). For each person (13 total participants), three gait cycles were analyzed for each slope (7 total slopes), for a total of 273 simulations.

Table 1.

Muscle group definitions and abbreviations. Muscles for which EMG was measured experimentally are denoted by ‘E’, and muscles in the group which were constrained based on EMG are denoted by ‘C’.

Abbreviation Muscles in group
SOL SoleusEC
GAS Lateral gastrocnemiusEC
Medial gastrocnemiusC
TA Tibialis anteriorEC
Extensor digitorum longus
Extensor hallucis longus
Peroneus tertius
VAS Vastus lateralisEC
Vastus medialisC
Vastus intermediusC
RF Rectus femorisEC
HAMS Biceps femoris long headEC
Gracilis
Semimembranosus
Semitendinosus
GMAX Gluteus maximus (superior, middle, and inferior compartments)EC
IL Iliacus
Psoas
GMED Gluteus medius (anterior, middle, and posterior compartments)EC
Gluteus minimus (anterior, middle, and posterior compartments)
Piriformis
Open in a new tab

2.2. Simulation Development

Kinematic marker trajectories were low-pass filtered with a cutoff frequency of 6 Hz using a 4th-order bidirectional Butterworth filter in Visual3D (C-Motion, Inc., Germantown, MD). An inverse kinematics solution was computed using a least squares optimization approach (Lu and O’Connor, 1999), and the resulting joint angles were low-pass filtered with a 6 Hz cutoff frequency. Force data were also low-pass filtered with a 6 Hz cutoff to eliminate noise caused by treadmill vibrations (Antonsson and Mann, 1985; Kram et al., 1998; Riley et al., 2007) and maintain consistency between data types (Bisseling and Hof, 2006; Kristianslund et al., 2012). Musculoskeletal models were developed in OpenSim 3.1 (Delp et al., 2007) by scaling a generic model (Anderson and Pandy, 1999; Delp et al., 1990) with 21 degrees-of-freedom (DOF) and 92 Hill-type musculotendon actuators with force-length-velocity properties (Zajac, 1989). Scale factors for each segment were computed from a static trial in Visual3D. Passive structures were represented by torques applied to each rotational DOF as an exponential function of joint angle (Anderson, 1999; Davy and Audu, 1987). A residual reduction algorithm (RRA) was used to ensure dynamic consistency between the inverse kinematics solution, model and GRFs by adjusting the total model mass and torso COM location (Delp et al., 2007). After making model adjustments, we used a custom optimization algorithm to adjust the inverse kinematics solution and minimize a multi-objective cost function based on the root-mean-squared residual forces and kinematic tracking errors for each trial. We then used a computed muscle control (CMC) algorithm to determine muscle forces that reproduced the kinematic solution from RRA while minimizing the sum of squared muscle excitations. Measured EMG signal timing was used to constrain the minimum and maximum excitations of the corresponding muscles in the model (Table 1). The EMG signals were processed by subtracting the mean, rectifying the signal, and applying a bidirectional moving average filter with a window of 100 milliseconds. For each muscle, the processed signal for each trial was normalized by the peak value across all trials. Simulated muscles were constrained to be “on” (excitation≥0.5) if the normalized EMG was greater than 0.5 for more than 0.01 seconds, and “off” (excitation≤0.1) if the normalized EMG was less than 0.05 for more than 0.01 seconds. Otherwise the minimum and maximum excitation bounds were 0.02 and 1.0, respectively.

2.3. Induced Acceleration and Segment Power Analyses

An induced acceleration analysis (IAA) was performed to determine muscle contributions to net COM acceleration. We used a “rolling without slipping” kinematic constraint between the foot and ground during stance (Hamner et al., 2010) and solved the equations of motion to compute accelerations due to each force acting on the model. Accelerations were reported in the directions parallel to the treadmill (braking [−]/propulsion [+]), perpendicular to the treadmill (normal [+]), and mediolateral (lateral [−]/medial [+]). The treadmill reference frame was chosen instead of the global reference frame because it describes the accelerations parallel and perpendicular to the direction of progression during sloped walking.

We calculated the instantaneous power delivered to the body segments by each force in the model (Fregly and Zajac, 1996). The power delivered to the trunk (pelvis and torso) and legs (toes, calcaneus, talus, tibia, and femur in each leg) was calculated by summing the power delivered to each segment. The power in each segment was normalized by that segment’s mass. Because participants were unimpaired, we assumed symmetry between legs and reported left leg muscle contributions to induced COM acceleration and segment power.

2.4. Statistical Comparisons

A linear mixed effects ANOVA (Pinheiro et al., 2015) with slope as a fixed effect and participant as a random effect was used to assess changes in muscle results across slopes. The mean induced COM acceleration and power delivered to the trunk and legs from each left leg muscle group (Table 1) during stance (defined as 0–60% of the gait cycle) were compared. When a significant slope effect was found, post-hoc comparisons were performed between each slope and level ground using least squares means and Dunnett’s method for p-value adjustments (Lenth and Hervé, 2015).

3. RESULTS

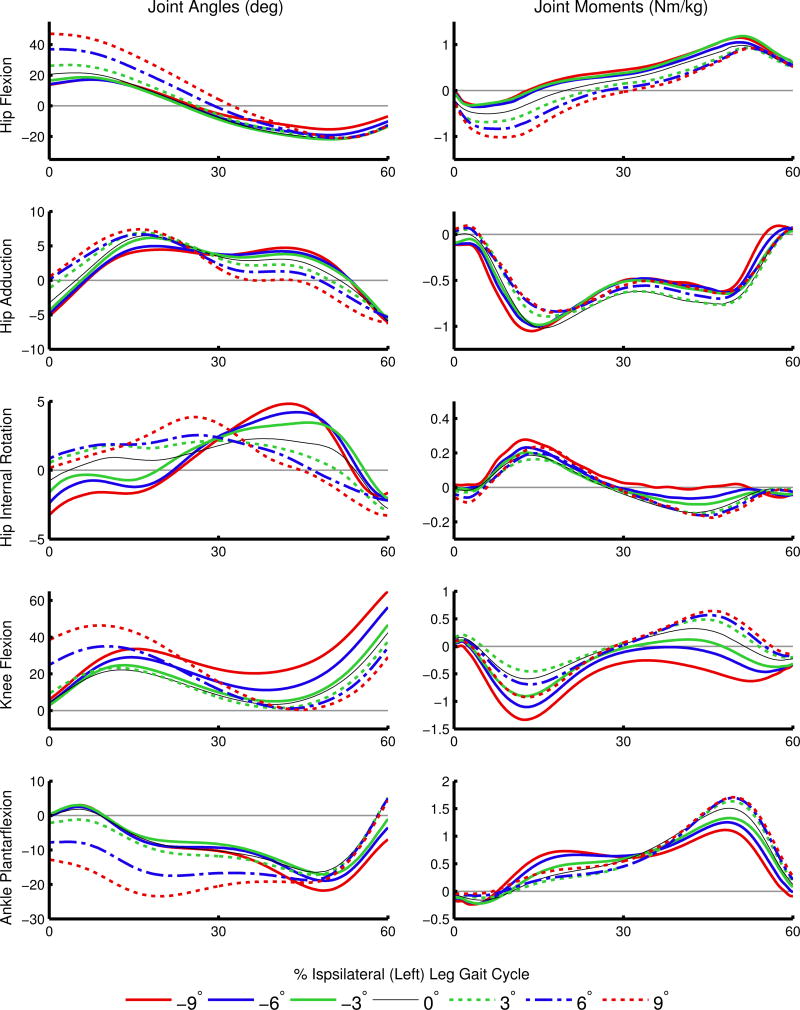
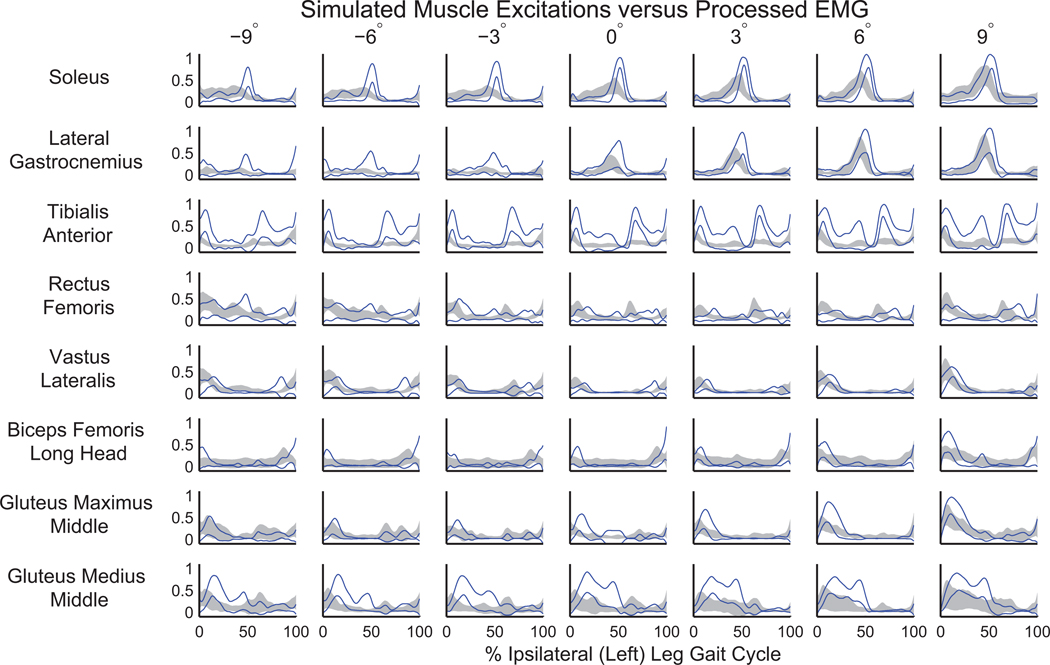
Overall, the experimental joint angles and net joint moments from RRA (Figure 1) were consistent with the literature (Fradet et al., 2010; Lay et al., 2006; Silverman et al., 2012). The model changes were within acceptable bounds for measurement error in model mass properties, with an average mass change of 1.00±0.76 kg and torso COM change of 6.84±2.70 cm. The simulations had similar muscle excitations to the collected EMG signals (Figure 2), low residuals (Supplementary Table 1), and low tracking errors (Supplementary Table 2).

Figure 1.

Figure 1

Open in a new tab

Average joint angles (left column) and joint moments (right column) during stance. Net joint moments were calculated from the residual reduction algorithm (RRA) and are normalized by body mass. Positive angles and moments represent hip flexion, hip adduction, hip internal rotation, knee flexion, and ankle plantarflexion.

Figure 2.

Figure 2

Open in a new tab

Comparison of mean (±SD) processed electromyographic (EMG) signals (gray shaded area) with the similarly processed mean of computed muscle control excitations (±SD shown in solid blue). The relative timing and magnitude of excitations in the simulations compared well with EMG as slope varied.

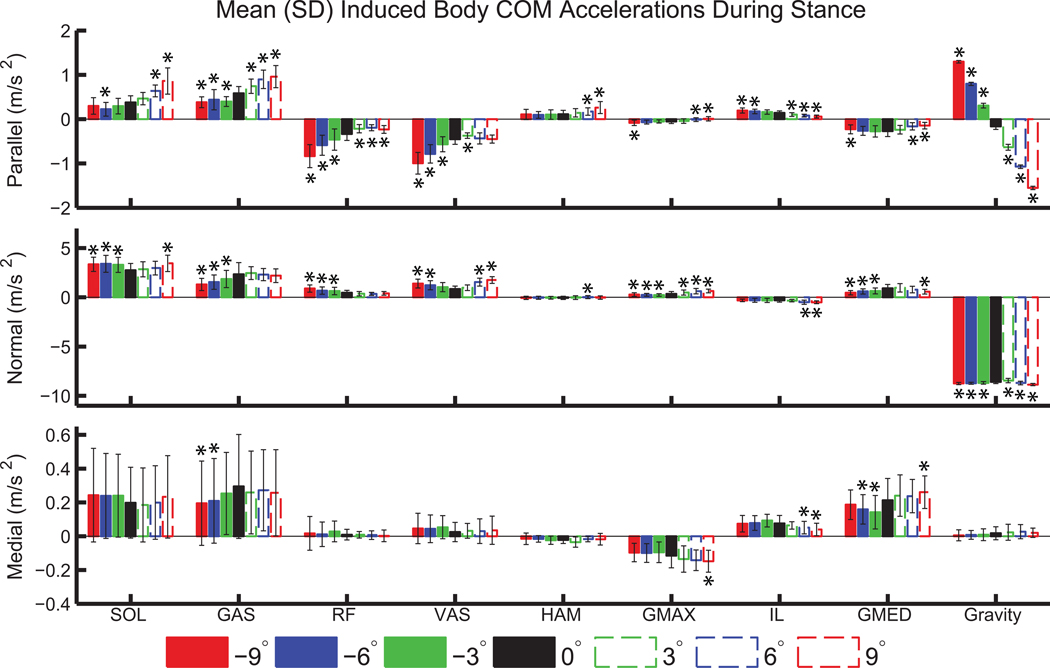
3.1. Induced Body COM Acceleration

SOL and GAS had increased contributions to propulsion (positive acceleration parallel to the treadmill) on inclines relative to level ground, with a 126% increase in SOL (p<0.001) and a 66% increase in GAS (p<0.001) contributions at +9° compared to 0° (Figure 3). RF and VAS provided greater braking (negative acceleration parallel to the treadmill) on declines compared to level ground, with more than 100% increase in both muscles at −9° compared to 0° (p<0.001). SOL had increased positive normal acceleration on all declines and at +9° relative to level ground. GAS had decreased normal acceleration on all declines relative to level ground, with a decrease of 44% at −9° relative to 0° (p<0.001). RF and VAS had increased normal acceleration on declines relative to level ground, with an 89% increase in RF and a 62% increase in VAS at −9° relative to 0° (p<0.001). SOL and GAS contributed to medial COM acceleration, but had large variability. GMED accelerated the COM medially on all slopes.

Figure 3.

Figure 3

Open in a new tab

Mean body COM acceleration (±SD) induced by left leg muscle groups and gravity during left leg stance. Significant differences relative to level-ground are indicated by ‘*’.

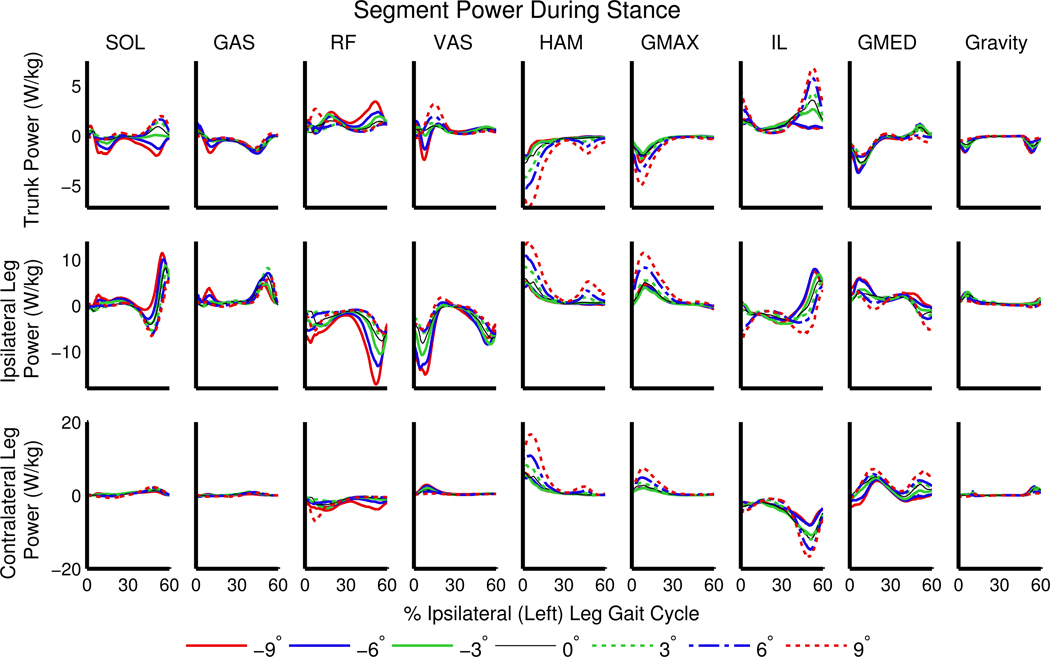
3.2. Segment Power

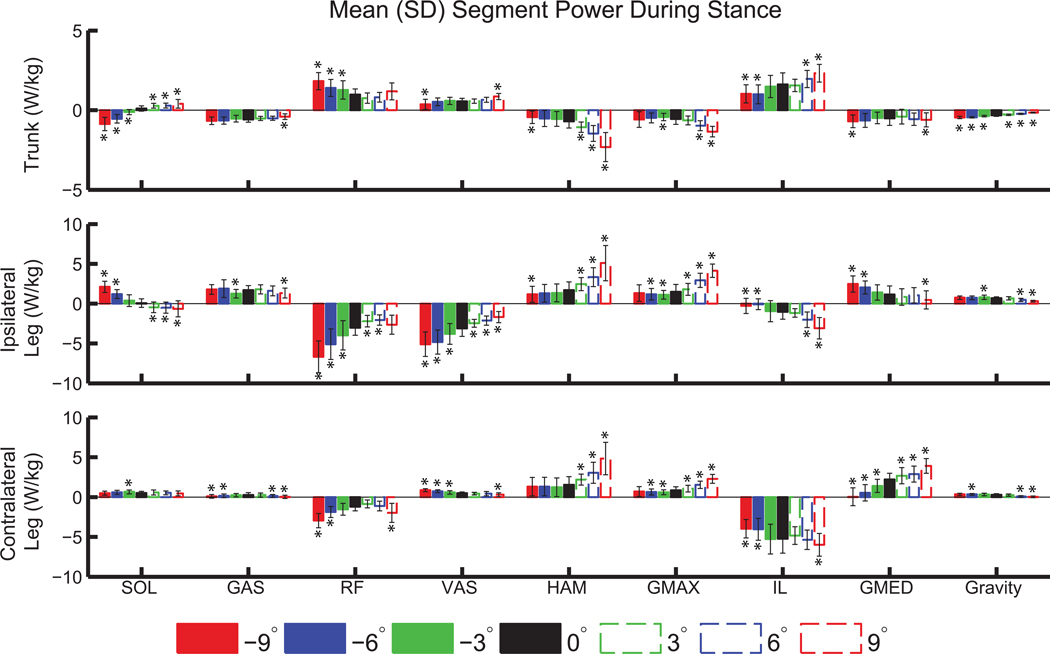
SOL generated power to the trunk on level ground and inclines (Figures 4 and 5), with an increase in the mean power generation during stance of 300% at +9° compared to 0° (p<0.001; Figure 5). On declines SOL absorbed power from the trunk, and with seven times more mean power absorbed at −9° compared to −3° (Figure 5). GAS transferred power from the trunk to the ipsilateral leg on all slopes (Figure 4). RF and VAS absorbed more power from the ipsilateral leg on declines than on level ground and inclines, with an increase in mean power absorption during stance of more than 160% in both muscles at −9° compared to 0° (Figure 5). HAM and GMAX transferred more power from the trunk to the legs on inclines than on level ground or declines (Figure 4). At +9° compared to 0°, HAM absorbed 230% more power from the trunk, generated 200% more power to the ipsilateral leg, and generated 210% more power to the contralateral leg during stance (all p<0.001, Figure 5). Also at +9° compared to 0°, GMAX absorbed 140% more power from the trunk, generated 175% more power to the ipsilateral leg, and generated 165% more power to the contralateral leg during stance (all p<0.001, Figure 5).

Figure 4.

Figure 4

Open in a new tab

Net power delivered to the trunk (pelvis and torso; top row) and legs (toes, calcaneus, talus, tibia, and femur; middle and bottom rows) during stance by the ipsilateral (left) leg muscles, normalized by segment mass and averaged across participants.

Figure 5.

Figure 5

Open in a new tab

Mean (±SD) segment power delivered to the trunk and legs during left leg stance, normalized by segment mass. Significant differences relative to level ground are indicated by ‘*’.

4. DISCUSSION

Our goal was to quantify the muscle action underlying kinematic and kinetic changes for sloped compared to level-ground walking. The results showed that muscle functional roles vary with slope, and our hypotheses for specific muscle groups were largely supported.

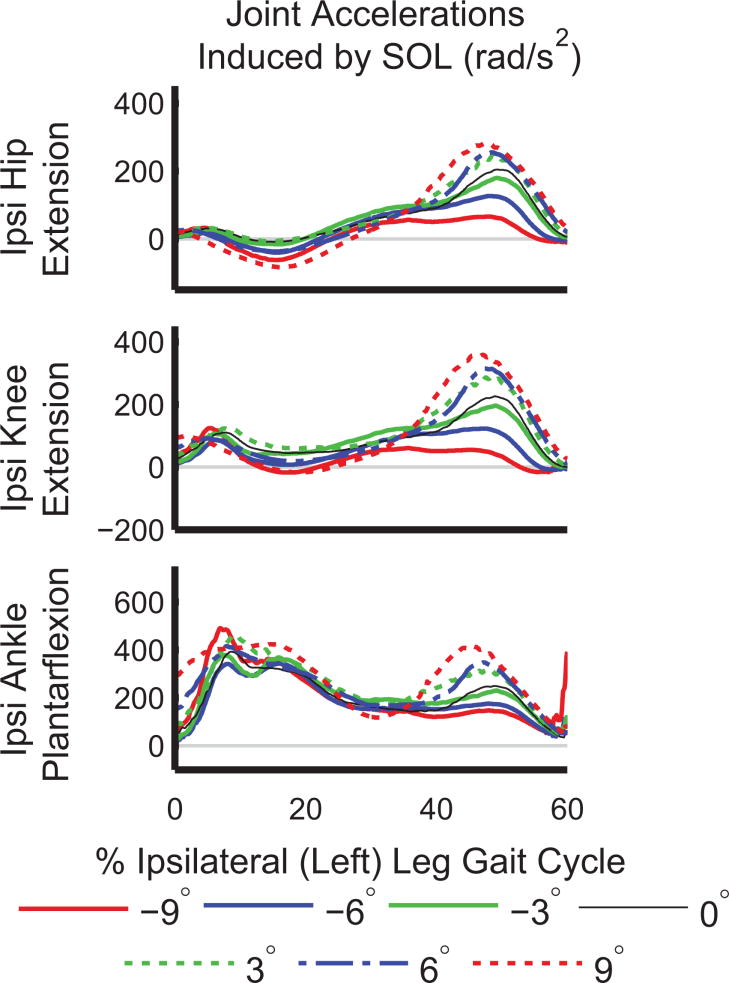
Our first hypothesis, that SOL and GAS would have increased contributions to COM acceleration and trunk and ipsilateral leg power on inclines, was supported for COM acceleration and partially supported for trunk and ipsilateral leg power. SOL generated power to the trunk on level ground and inclines (Figure 5), which was consistent with its functional role in level-ground walking (Neptune et al., 2001). However, SOL absorbed power from the trunk during decline walking (Figure 5). A post-hoc analysis of induced joint accelerations and joint angles showed that while SOL accelerated the ipsilateral hip, knee, and ankle into extension/plantarflexion during late stance (30–60% ipsilateral leg gait cycle) on all slopes (Figure 6), the mean magnitudes were reduced by 75% (hip), 83% (knee), and 46% (ankle), at −9° compared to +9° (p<0.001 for all three joints). The knee was more flexed during late stance on declines compared to inclines, with a mean flexion angle of 31.6±8.4° at −9° compared to 7.75±5.4° at +9° (p<0.001). Also, the mean lumbar joint angle over the gait cycle was more flexed on inclines, with 0.8±6.0° of flexion at −9° compared to 9.2±5.6° of flexion at +9° (p<0.001). Prior work has also found that leaning forward is a key postural adaptation to uphill walking (Leroux et al., 2002). Changes in kinematics affect the direction and magnitude of COM acceleration a muscle can induce, as demonstrated in crouch gait (Steele et al., 2013). Therefore, kinematic changes at the knee and lumbar joint likely contributed to SOL absorbing power from, rather than generating power to, the trunk when walking downhill.

Figure 6.

Figure 6

Open in a new tab

Average joint accelerations induced in the ipsilateral (Ipsi) leg joints by SOL during stance. Acceleration into extension is defined positively for all three joints.

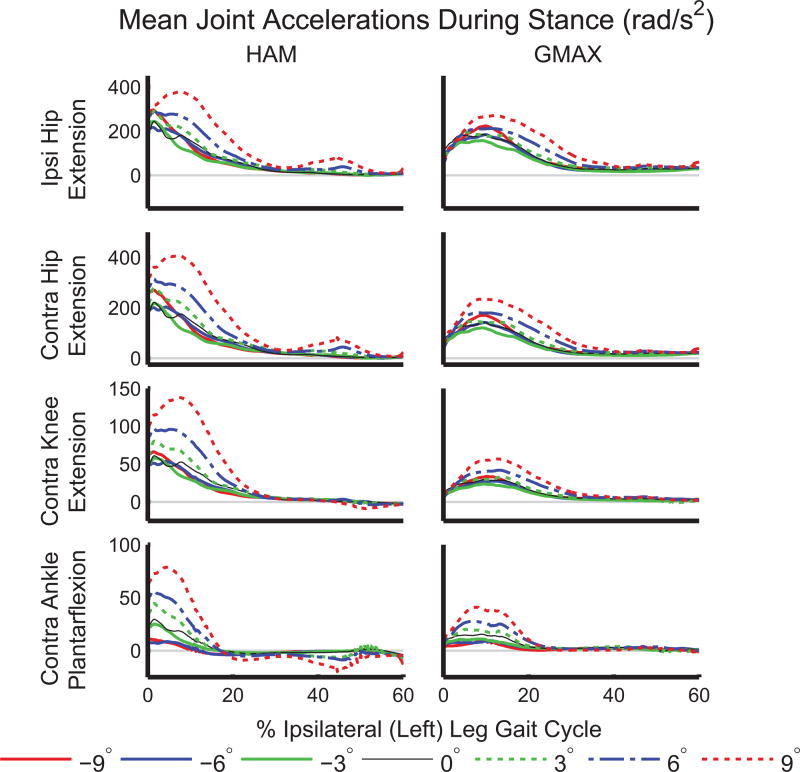
We expected that GAS would generate greater power to the ipsilateral leg on inclines because GAS initiates leg swing during level-ground walking (Neptune et al., 2001) and the need to raise the leg against gravity is greater during incline walking than on level ground. However, GAS did not provide greater power to the ipsilateral leg on inclines relative to level ground (Figure 5). While the biarticular GAS provided power to the ipsilateral leg on all slopes, the magnitude was not strongly affected by slope. Instead, the hip extensors (HAM and GMAX) generated power to the contralateral leg (Figure 4, bottom row) during 0–30% of the ipsilateral leg gait cycle, corresponding to pre- and early-swing in the contralateral leg. The hip extensors accelerated both hips as well as the contralateral knee and ankle into extension during early ipsilateral stance (Figure 7).

Figure 7.

Figure 7

Open in a new tab

Accelerations induced in the ipsilateral (Ipsi) hip and all contralateral (Contra) leg joints by HAM and GMAX during stance. Acceleration into extension is defined positively for all joints.

Our second hypothesis, that the hip extensors would provide greater acceleration of the COM and generate more power to the trunk and ipsilateral leg on inclines, was also partially supported. HAM and GMAX transferred power from the trunk to both legs (Figures 4 and 5) on all slopes in early stance, consistent with the role of HAM during level-ground walking (Neptune et al., 2004; Silverman and Neptune, 2012). The amount of power absorbed from the trunk and generated in both the ipsilateral and contralateral legs by HAM and GMAX approximately doubled from 0° to +9° (Figure 5). The hip flexors (IL), which were not included in our initial hypotheses, generated power to the ipsilateral leg in late stance (Figure 4). Thus, the contralateral HAM and GMAX, in combination with the ipsilateral IL and GAS, are important for generating energy to the ipsilateral leg during its pre-swing phase (50–60% ipsilateral gait cycle). Greater power transfer from HAM and GMAX is consistent with the observed increased hip extensor moment on inclines relative to level ground (Figure 1), also shown in previous work (Lay et al., 2006). The contributions of HAM and GMAX to COM acceleration in the parallel and normal directions were small compared to those of other muscle groups (Figure 3). The small COM acceleration induced by HAM and GMAX highlight that interpretation of muscle functional roles is aided by segment power analyses that reveal power transfer between body segments.

Our final hypothesis, that RF and VAS would provide more braking acceleration and absorb more power from the ipsilateral leg on declines, was largely supported. Both muscles accelerated the COM backward and absorbed power from the ipsilateral leg on declines. RF delivered more power to the trunk on declines than level ground. Overall, these muscle results are consistent with the greater knee extension moment (Figure 1; Lay et al., 2006), greater mean and peak VAS activity (Lange et al., 1996) and longer duration of RF and VAS activity (Lay et al., 2007) during decline compared to level-ground walking. In addition, these results are supported by greater knee power on declines compared to level ground (Kuster et al., 1995), suggesting that the knee muscles are largely responsible for lowering the body (Redfern and Dipasquale, 1997).

The mediolateral COM accelerations were smaller than in the other directions, and muscles like GMED that contributed mediolaterally (Pandy et al., 2010; Silverman and Neptune, 2012) did not have many differences across slopes. The ankle plantarflexors contributed to medial COM acceleration, contrary to previous results (Pandy et al., 2010) but consistent with other studies that used a “rolling without slipping” ground contact model (Dorn et al., 2012). However, there was large variability in the mediolateral COM acceleration induced by the plantarflexors (Figure 3), and their regulation of mediolateral balance has been shown to be sensitive to foot placement (Silverman and Neptune, 2012).

A potential limitation of this study is the sensitivity of IAA to the ground contact model. Our muscle-level IAA results are similar to other studies that used the “rolling without slipping” constraint (Dorn et al., 2012; Hamner and Delp, 2013; Steele et al., 2013), but have some differences from other studies that used five time-varying kinematic constraints (Lin et al., 2015; Pandy et al., 2010) and GRF decomposition using viscoelastic elements with Coulomb friction (Neptune et al., 2001; Silverman and Neptune, 2012) to model ground contact. For example, the contact model affects whether SOL provides braking or propulsion in early to mid-stance and the medial versus lateral contributions of GAS, SOL, and VAS to COM acceleration (Supplementary Figure 1). These differences have been previously documented (Dorn et al., 2012), and should be noted when interpreting the results of this study. We elected to use the “rolling without slipping” constraint for its computational efficiency, which facilitated analyzing a large number of simulations. Our results of the ankle plantarflexors in late stance, hip extensors in early stance, and vasti in early stance in the sagittal plane are supported by multiple studies that have used different contact models; thus we do not expect these to change with ground contact model selection (Neptune et al., 2001; Pandy et al., 2010; Steele et al., 2013, 2010).

This study analyzed incline and decline walking performed on treadmill. The biomechanics of treadmill walking may differ from overground ramp walking. However, differences in joint angles and moments between level walking overground and on a treadmill are within the variability inherent in these quantities (Riley et al., 2007). In addition, the joint angles and moments in this study were similar to those reported in previous studies of ramp walking (Fradet et al., 2010; Lay et al., 2006; Silverman et al., 2012). Because joint angles and moments were used in the estimation of muscle forces, we do not expect our results to change between ramp and treadmill walking.

In addition, this study is limited by the assumption that the CMC cost function (i.e., minimizing the sum of muscle excitations squared) is appropriate for simulating sloped walking, and may require further investigation. For example, muscle co-contraction may be more common on greater slopes as balance becomes more difficult to maintain, and may be underestimated with this cost function. However, our simulated muscle controls were similar to EMG signals, providing confidence in our results. There was some discrepancy in the timing and magnitude of muscle controls relative to EMG, notably in SOL on declines (Figure 2), suggesting that our simulations may differ from muscle behavior. The burst in simulated SOL excitation at approximately 50% of the gait cycle may exaggerate the amount of power absorbed from the trunk by SOL during decline walking.

This work provides a baseline for investigating many populations. For example, individuals with unilateral transtibial amputation using passive prostheses compensate for lost ankle muscle function by increasing work from the hip extensors in the affected leg (Silverman et al. 2008). Our results suggest that non-amputees rely heavily on the hip extensors to transfer power on inclines. Thus, using a hip compensation strategy may place unrealistic demands on HAM and GMAX on extreme slopes of +9° and make these walking conditions difficult for people with leg amputations. In addition, traditional leg prostheses do not span the knee like the biarticular GAS. GAS contributes to leg swing initiation during level-ground walking (Neptune et al., 2001), and our results suggest that this contribution may not be increased on inclines. Thus, if an assistive device can replicate the functional role of GAS on level ground, it may also perform well on inclines. Gait deviations in impaired populations are also frequently attributed to muscle weakness, such as plantarflexor weakness in individuals with hemiparesis (Nadeau et al., 1999) or knee extensor weakness in individuals with transtibial amputation (Langlois et al., 2014; Schmalz et al., 2001) or total knee arthroplasty (Mizner and Snyder-Mackler, 2005). Sloped walking is likely especially challenging for these populations because of greater power requirements on extreme inclines and declines.

CONCLUSION

We quantified the functional roles of lower-limb muscle groups for sloped walking by developing 273 simulations. We found that SOL and GAS were critical for generating power to the trunk and leg during incline walking, similar to level ground. However, while SOL provided more trunk power on greater inclines, the power generated to the leg from GAS had few significant differences from level-ground walking. HAM and GMAX delivered more power to both legs on inclines than on level ground. During decline walking, RF and VAS absorbed more power from the ipsilateral leg and provided more backward (braking) acceleration of the COM, which helped control descent. The COM mediolateral induced accelerations had large variability and were not affected by slope. The results of this study provide a baseline of unimpaired muscle functional roles during sloped walking, which can be used to develop rehabilitation programs that target specific muscle groups as well as to evaluate and design assistive devices that restore lost function in impaired populations.

Supplementary Material

1
2

Acknowledgments

This work was supported by VA Career Development Award VA RR&D A7972-W (awarded to A.M.G.) and by NIH NICHD Award Number R03HD007946 (awarded to A.K.S.). The content is solely the responsibility of the authors and does not represent the official views of the Department of Veterans Affairs or the National Institutes of Health.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Anderson FC. (Ph.D. Thesis. The University of Texas at Austin) 1999. A Dynamic Optimization Solution for a Complete Cycle of Normal Gait. [Google Scholar]
  2. Anderson FC, Pandy MG. A Dynamic Optimization Solution for Vertical Jumping in Three Dimensions. Comput Methods Biomech Biomed Engin. 1999;2:201–231. doi: 10.1080/10255849908907988. [DOI] [PubMed] [Google Scholar]
  3. Antonsson E, Mann R. The frequency content of gait. J Biomech. 1985;18:39–47. doi: 10.1016/0021-9290(85)90043-0. [DOI] [PubMed] [Google Scholar]
  4. Bisseling RW, Hof AL. Handling of impact forces in inverse dynamics. J Biomech. 2006;39:2438–44. doi: 10.1016/j.jbiomech.2005.07.021. [DOI] [PubMed] [Google Scholar]
  5. Davy DT, Audu ML. A dynamic optimization technique for predicting muscle forces in the swing phase of gait. J Biomech. 1987;20:187–201. doi: 10.1016/0021-9290(87)90310-1. [DOI] [PubMed] [Google Scholar]
  6. Delp SL, Loan J, Hoy M, Zajac F, Topp E, Rosen J. An interactive graphics-based model of the lower extremity to study orthopaedic surgical procedures. IEEE Trans Biomed Eng. 1990;37:757–767. doi: 10.1109/10.102791. [DOI] [PubMed] [Google Scholar]
  7. Delp SL, Anderson FC, Arnold AS, Loan P, Habib A, John CT, Guendelman E, Thelen DG. OpenSim: open-source software to create and analyze dynamic simulations of movement. IEEE Trans Biomed Eng. 2007;54:1940–50. doi: 10.1109/TBME.2007.901024. [DOI] [PubMed] [Google Scholar]
  8. Dorn TW, Lin Y, Pandy MG. Estimates of muscle function in human gait depend on how foot-ground contact is modelled. Comput Methods Biomech Biomed Engin. 2012;15:657–668. doi: 10.1080/10255842.2011.554413. [DOI] [PubMed] [Google Scholar]
  9. Fradet L, Alimusaj M, Braatz F, Wolf SI. Biomechanical analysis of ramp ambulation of transtibial amputees with an adaptive ankle foot system. Gait Posture. 2010;32:191–8. doi: 10.1016/j.gaitpost.2010.04.011. [DOI] [PubMed] [Google Scholar]
  10. Fregly B, Zajac F. A state-space analysis of mechanical energy generation, absorption, and transfer during pedaling. J Biomech. 1996;29:81–90. doi: 10.1016/0021-9290(95)00011-9. [DOI] [PubMed] [Google Scholar]
  11. Hamner SR, Delp SL. Muscle contributions to fore-aft and vertical body mass center accelerations over a range of running speeds. J Biomech. 2013;46:780–7. doi: 10.1016/j.jbiomech.2012.11.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Hamner SR, Seth A, Delp SL. Muscle contributions to propulsion and support during running. J Biomech. 2010;43:2709–16. doi: 10.1016/j.jbiomech.2010.06.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Hernández A, Dhaher Y, Thelen D. In vivo measurement of dynamic rectus femoris function at postures representative of early swing phase. J Biomech. 2008;41:137–144. doi: 10.1016/j.jbiomech.2007.07.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Jeffers JR, Auyang AG, Grabowski AM. The correlation between metabolic and individual leg mechanical power during walking at different slopes and velocities. J Biomech. 2015;48:1–6. doi: 10.1016/j.jbiomech.2015.04.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Kram R, Griffin TM, Donelan JM, Chang YH. Force treadmill for measuring vertical and horizontal ground reaction forces. J Appl Physiol. 1998;85:764–769. doi: 10.1152/jappl.1998.85.2.764. [DOI] [PubMed] [Google Scholar]
  16. Kristianslund E, Krosshaug T, van den Bogert AJ. Effect of low pass filtering on joint moments from inverse dynamics: implications for injury prevention. J Biomech. 2012;45:666–71. doi: 10.1016/j.jbiomech.2011.12.011. [DOI] [PubMed] [Google Scholar]
  17. Kuster M, Sakurai S, Wood GA. Kinematic and kinetic comparison of downhill and level walking. Clin Biomech. 1995;10:79–84. doi: 10.1016/0268-0033(95)92043-l. [DOI] [PubMed] [Google Scholar]
  18. Lange GW, Hintermeister RA, Schlegel T, Dillman CJ, Steadman JR. Electromyographic and kinematic analysis of graded treadmill walking and the implications for knee rehabilitation. J Orthop Sports Phys Ther. 1996;23:294–301. doi: 10.2519/jospt.1996.23.5.294. [DOI] [PubMed] [Google Scholar]
  19. Langlois K, Villa C, Bonnet X, Lavaste F, Fodé P, Martinet N, Pillet H. Influence of physical capacities of males with transtibial amputation on gait adjustments on sloped surfaces. J Rehabil Res Dev. 2014;51:193–200. doi: 10.1682/JRRD.2013.05.0118. [DOI] [PubMed] [Google Scholar]
  20. Lay AN, Hass CJ, Gregor RJ. The effects of sloped surfaces on locomotion: a kinematic and kinetic analysis. J Biomech. 2006;39:1621–8. doi: 10.1016/j.jbiomech.2005.05.005. [DOI] [PubMed] [Google Scholar]
  21. Lay AN, Hass CJ, Richard Nichols T, Gregor RJ. The effects of sloped surfaces on locomotion: an electromyographic analysis. J Biomech. 2007;40:1276–85. doi: 10.1016/j.jbiomech.2006.05.023. [DOI] [PubMed] [Google Scholar]
  22. Lenth R, Hervé M. lsmeans: Least-Squares Means [WWW Document] R Packag. version 2.16. 2015 http://cran.r-project.org/package=lsmeans.
  23. Leroux A, Fung J, Barbeau H. Postural adaptation to walking on inclined surfaces: I. Normal Strategies. Gait Posture. 2002;15:64–74. doi: 10.1016/s0966-6362(01)00181-3. [DOI] [PubMed] [Google Scholar]
  24. Lin Y, Fok LA, Schache AG, Pandy MG. Muscle coordination of support, progression and balance during stair ambulation. J Biomech. 2015;48:340–347. doi: 10.1016/j.jbiomech.2014.11.019. [DOI] [PubMed] [Google Scholar]
  25. Lu TW, O’Connor JJ. Bone position estimation from skin marker co-ordinates using global optimisation with joint constraints. J Biomech. 1999;32:129–34. doi: 10.1016/s0021-9290(98)00158-4. [DOI] [PubMed] [Google Scholar]
  26. Mizner RL, Snyder-Mackler L. Altered loading during walking and sit-to-stand is affected by quadriceps weakness after total knee arthroplasty. J Orthop Res. 2005;23:1083–1090. doi: 10.1016/j.orthres.2005.01.021. [DOI] [PubMed] [Google Scholar]
  27. Nadeau S, Gravel D, Arsenault AB, Bourbonnais D. Plantarflexor weakness as a limiting factor of gait speed in stroke subjects and the compensating role of hip flexors. Clin Biomech. 1999;14:125–135. doi: 10.1016/s0268-0033(98)00062-x. [DOI] [PubMed] [Google Scholar]
  28. Neptune RR, Kautz SA, Zajac FE. Contributions of the individual ankle plantar flexors to support, forward progression and swing initiation during walking. J Biomech. 2001;34:1387–98. doi: 10.1016/s0021-9290(01)00105-1. [DOI] [PubMed] [Google Scholar]
  29. Neptune RR, Zajac FE, Kautz SA. Muscle force redistributes segmental power for body progression during walking. Gait Posture. 2004;19:194–205. doi: 10.1016/S0966-6362(03)00062-6. [DOI] [PubMed] [Google Scholar]
  30. Pandy MG, Lin YC, Kim HJ. Muscle coordination of mediolateral balance in normal walking. J Biomech. 2010;43:2055–64. doi: 10.1016/j.jbiomech.2010.04.010. [DOI] [PubMed] [Google Scholar]
  31. Piazza SJ. Muscle-driven forward dynamic simulations for the study of normal and pathological gait. J Neuroeng Rehabil. 2006:3. doi: 10.1186/1743-0003-3-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Pinheiro J, Bates D, DebRoy S, Sarkar D R Core Team. nlme: Linear and Nonlinear Mixed Effects Models 2015 [Google Scholar]
  33. Redfern MS, Dipasquale J. Biomechanics of descending ramps. Gait Posture. 1997;6:119–125. [Google Scholar]
  34. Riley PO, Paolini G, Della Croce U, Paylo KW, Kerrigan DC. A kinematic and kinetic comparison of overground and treadmill walking in healthy subjects. Gait Posture. 2007;26:17–24. doi: 10.1016/j.gaitpost.2006.07.003. [DOI] [PubMed] [Google Scholar]
  35. Schmalz T, Blumentritt S, Reimers CD. Selective thigh muscle atrophy in trans-tibial amputees: an ultrasonographic study. Arch Orthop Trauma Surg. 2001;121:307–12. doi: 10.1007/s004020000227. [DOI] [PubMed] [Google Scholar]
  36. Silverman AK, Fey NP, Portillo A, Walden JG, Bosker G, Neptune RR. Compensatory mechanisms in below-knee amputee gait in response to increasing steady-state walking speeds. Gait & Posture. 2008;28(4):602–609. doi: 10.1016/j.gaitpost.2008.04.005. http://dx.doi.org/10.1016/j.gaitpost.2008.04.005. [DOI] [PubMed] [Google Scholar]
  37. Silverman AK, Neptune RR. Muscle and prosthesis contributions to amputee walking mechanics: a modeling study. J Biomech. 2012;45:2271–8. doi: 10.1016/j.jbiomech.2012.06.008. [DOI] [PubMed] [Google Scholar]
  38. Silverman AK, Wilken JM, Sinitski EH, Neptune RR. Whole-body angular momentum in incline and decline walking. J Biomech. 2012;45:965–71. doi: 10.1016/j.jbiomech.2012.01.012. [DOI] [PubMed] [Google Scholar]
  39. Steele KM, Seth A, Hicks JL, Schwartz MH, Delp SL. Muscle contributions to vertical and fore-aft accelerations are altered in subjects with crouch gait. Gait Posture. 2013;38:86–91. doi: 10.1016/j.gaitpost.2012.10.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Steele KM, Seth A, Hicks JL, Schwartz MS, Delp SL. Muscle contributions to support and progression during single-limb stance in crouch gait. J Biomech. 2010;43:2099–105. doi: 10.1016/j.jbiomech.2010.04.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Zajac F. Muscle and Tendon: Properties, Models, Scaling, and Application to biomechanics and motor control. Crit Rev Biomed Eng. 1989;17:359–411. [PubMed] [Google Scholar]
  42. Zajac FE, Neptune RR, Kautz SA. Biomechanics and muscle coordination of human walking, Part 1: Introduction to concepts, power transfer, dynamics and simulations. Gait Posture. 2002;16:215–232. doi: 10.1016/s0966-6362(02)00068-1. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

1
NIHMS812012-supplement-1.docx (37.1KB, docx)
2
NIHMS812012-supplement-2.eps (1.1MB, eps)

RESOURCES