Abstract
Case-control association studies often collect from their subjects information on secondary phenotypes. Reusing the data and studying the association between genes and secondary phenotypes provide an attractive and cost effective approach that can lead to discovery of new genetic associations. A number of approaches have been proposed, including simple and computationally efficient ad hoc methods that ignore ascertainment or stratify on case-control status. Justification for these approaches relies on the assumption of no covariates and the correct specification of the primary disease model as a logistic model. Both might not be true in practice, for example, in the presence of population stratification or the primary disease model following a probit model. In this paper, we investigate the validity of ad hoc methods in the presence of covariates and possible disease model misspecification. We show that in taking an ad hoc approach, it may be desirable to include covariates that affect the primary disease in the secondary phenotype model, even though these covariates are not necessarily associated with the secondary phenotype. We also show that when the disease is rare, ad hoc methods can lead to severely biased estimation and inference if the true disease model follows a probit model instead of a logistic model. Our results are justified theoretically and via simulations. Applied to real data analysis of genetic associations with cigarette smoking, ad hoc methods collectively identified as highly significant (p < 10−5) single nucleotide polymorphisms from over ten genes, genes that were identified in previous studies of smoking cessation.
Keywords: Case-control sampling, Genome-wide association studies, Linear regression, Logistic regression, Secondary phenotypes, SNPs
Introduction
Genome-wide association studies (GWAS) examine associations between genetic variants and disease status, often by employing a case-control design. Many of these studies also collect a variety of secondary traits—quantitative and qualitative traits besides the case-control status. In view of high genotyping costs, the resulting data provide a cost-effective way to identify genetic associations with secondary traits. For example, in a lung cancer GWAS conducted at the Massachusetts General Hospital (MGH), detailed smoking histories were collected from each study participant. It is of interest to reuse the data to identify single nucleotide polymorphisms (SNPs) associated with smoking behavior [Schifano et al., 2012].
A number of methods have been proposed for the analysis of a binary or continuous secondary trait. They include: (a) the naïve method which analyzes the combined sample of cases and controls, ignoring case-control ascertainment [Nagelkerke et al., 1995]; (b) the case-only or control-only analysis [Nagelkerke et al., 1995]; (c) the “adjusted” analysis where the case-control status is included as a covariate in the fitted model [Jiang et al., 2006]; (d) meta-analytic methods [Li et al., 2010]; (e) the inverse probability weighted (IPW) method [Richardson et al., 2007; Wang and Shete, 2011]; and (f) the semiparametric likelihood method that explicitly accounts for the case-control sampling scheme [Jiang et al., 2006; Lin and Zeng, 2009; Wang and Shete, 2011; He et al., 2012; Tchetgen Tchetgen, 2014].
We focus here on studying the validity of using the simple and computationally efficient methods (a)-(c), commonly referred to as the “ad hoc” or “standard” methods. Though these methods are widely popular, a deeper understanding of when they are valid is required for proper analysis of secondary traits. It has been argued previously that ad hoc methods can lead to biased estimates of marker-secondary trait associations, except under special conditions [Nagelkerke et al., 1995; Lin and Zeng, 2009; Monsees et al., 2009]:
If the disease is not associated with the secondary trait given the genotype, then ad hoc methods are valid.
For a binary secondary trait, if the disease is not associated with the genotype given the secondary trait, then ad hoc methods are valid. For a continuous secondary trait, the same is true if, in addition, the null hypothesis of no marker-secondary trait association holds.
If the disease is rare, then methods (b)-(c) are approximately valid.
Consequently, other methods such as (e) and (f) have been proposed as general solutions to secondary trait analysis.
In spite of their limitations and the emergence of other approaches, ad hoc methods have remained popular. Recent years have seen a steady stream of publications on genetic variants influencing human quantitative traits such as body mass index [Speliotes et al., 2010; Wen et al., 2012; Monda et al., 2013]. It is common practice to obtain data from multiple case-control association studies of complex diseases (e.g., diabetes, cancer, and hypertension), analyze the data from each study separately using an ad hoc approach, and combine the study-specific results via meta-analysis.
There are several reasons why ad hoc methods have remained popular. First, considering the majority of tested markers in a GWAS are unlikely to be associated with disease risk, and diseases of interest are usually rare, conditions (ii) and (iii) are often met in practice, making ad hoc methods a seemingly valid option. Second, ad hoc methods are straightforward to apply. They require little model building and can be easily performed using linear or logistic regression. In contrast, methods (e)-(f) are more complex. (e) requires that the disease prevalence in a population is known and weighting the sampled subjects in such a way that the weighted subjects approximate the underlying population, which itself might not be well defined. (f) accounts for the case-control sampling by modeling certain nuisance terms in the retrospective likelihood, such as the distribution of the disease given the genotype and secondary trait in the underlying population, which might not be known in practice and requires the knowledge of the population prevalence. In addition, methods (e)-(f), despite their added complexity, may not necessarily be more efficient or robust than ad hoc methods when the assumptions under which the ad hoc methods are valid are met. It has been shown that the weighted approach generally has less power than ad hoc methods that use the entire case-control sample when the ad hoc methods are valid [Monsees et al., 2009]. If any of the assumed nuisance models in a semiparametric likelihood are misspecified, then inference may be invalid [Jiang et al., 2006].
Here, we revisit the problem of when ad hoc methods can and cannot be used. This problem is of practical interest because previous discussions leading to (ii) and (iii) make two limiting assumptions: that there are no covariates in the regression models for the disease and secondary trait, and that the disease follows a correctly specified logistic regression model. These assumptions may not be true in practice. Indeed, there may be confounders that need to be adjusted for in order to protect against spurious associations in GWAS. A familiar example of such confounders in GWAS is the presence of population structure, which can be correlated with both the disease and the tested genetic markers [Rosenberg et al., 2002; Price et al., 2006]. On the other hand, researchers often assume a logistic model for the disease model in case-control studies. In some cases, the logistic model that is used for analysis might be misspecified, e.g., the probit model for the disease status instead of the logistic model might be true.
Therefore, the purpose of this article is to study the performance of ad hoc methods on estimation and inference for the genetic effect on a secondary trait in the presence of covariates and possible disease model misspecification. Our first key contribution is that we show theoretically and with simulations that the presence of covariates confounding the effect of a genetic marker on the disease can lead to spurious genetic associations even when condition (ii) is met. We identify conditions under which the ad hoc methods are valid in the presence of confounders. We show that the spurious associations can be easily and effectively avoided by including the covariates into the fitted regression model for secondary phenotypes. Our second key contribution is that when the disease is rare, we show that the case-only and adjusted analyses can lead to severely biased estimation and incorrect inference if the true disease model is a probit model instead of a logistic model.
The remainder of this article is organized as follows. In the next section, we describe in more detail the study setting, notation, and ad hoc methods. In the Results section, we provide conditions for valid ad hoc analysis in the presence of covariates. Theoretical justification for the conditions are relegated to the Appendix and Web Appendix. We present simulation results to examine the conditions in finite samples and to compare existing methods. We also illustrate various methods by applying them to a GWAS of smoking behavior in a sample of lung cancer cases and controls. Finally, we discuss the implications of our results for the design and analysis of GWAS of secondary traits using samples ascertained on the basis of another trait.
Methods
Study Setting and Notation
Consider a case-control study with n1 cases and n0 controls. Let D denote the disease status (1=case, 0=control), Y a binary or continuous secondary trait, G the genotypes, and Z and X the covariates associated with D and Y, respectively. We assume that in the population, disease and secondary trait are distributed with conditional means μD(Y) = E(D|Z, G, Y) and μY = E(Y|X, G), which follow the generalized linear models:
| (1) |
| (2) |
where gD(·) is the link function for the primary phenotype (disease) D model; gY(·) is the link function for the secondary phenotype Y model; (β0, βZ, βG, βY) are the regression coefficients in the D model; and (α0, αX, αG) are the regression coefficients in the Y model.
For binary Y, we assume gy(·) = logit. For continuous Y, we assume gY(·) is the identity link function and Y follows a normal distribution with the conditional population mean μY = E(Y|X, G) and variance σ2. Our main interest is in estimating and making inference on αG, the population parameter capturing the genetic marker-secondary trait association.
As discussed in the Introduction, existing literature regarding the validity of ad hoc methods often assume a logistic disease model. This is not so much because the logistic model is believed to best model the data, but more so because if the disease in fact follows a logistic model in the population, then valid point estimators of the population odds ratio parameters—including estimators of genetic associations with the disease—can be obtained by fitting the prospective logistic model to the retrospective case-control data [Prentice and Pyke, 1979]. Here, we allow gD(·) to be any smooth link function. For a rare disease, we consider more closely the choice between the logistic model and the probit model in order to show that misspecification of the disease model by using a misspecified link function can be consequential for the secondary phenotype analysis, which is of primary interest. It is natural to compare the logistic disease model to the probit disease model, because the probit model is arguably the most popular alternative to the logistic model for analyzing binary response data. Also, there is increasing interest to use the probit model (also known as the liability threshold model) in studies of genetic association, heritability, and risk prediction [Wray et al., 2010; So and Sham, 2010; Lee et al., 2011; Zaitlen et al., 2012].
Ad Hoc Methods
The typical ad hoc approach in the presence of covariates is to regress Y on X, G, and perhaps D, using only the n1 cases, the n0 controls, or all n = n1 +n0 subjects. However, we have found that such a simple ad hoc approach may be invalid in the presence of confounders under the previously established conditions where the ad hoc methods are valid in the absence of covariates. We will show in the next section that including a linear effect of disease-related confounders Z in the regression model for Y can correct for bias under suitable conditions similar to the existing conditions. Therefore, in the presence of covariates, there are two types of ad hoc methods that one can consider applying. The first type, which we shall refer to as the ad hoc methods with Y -related covariates, takes the typical approach by regressing Y on X, G, and perhaps D. The second type regresses Y on X, G, perhaps D, and Z. Since this type includes both X and Z as covariates in the model for Y, we shall refer to them as the ad hoc methods with pooled covariates. Note that if Z ⊆ X, then the two types of ad hoc methods are equivalent. Furthermore, if an ad hoc method with Y -related covariates (e.g., control-only analysis with Y -related covariates) is valid, then its pooled counterpart (e.g., control-only analysis with pooled covariates) is also valid.
Results
Conditions for Valid Ad Hoc Analysis in the Presence of Covariates
We have conducted a thorough investigation into the properties of the ad hoc methods. We state here the main conclusions while relegating the theoretical details to the Appendix and Web Appendix. Ad hoc methods can lead to invalid estimation and inference of αG, except under special conditions:
(i) If the disease is not associated with the secondary trait (βY = 0), then ad hoc methods are valid.
(ii*) For binary Y, if the disease is not associated with the genotype (βG = 0), then ad hoc methods with pooled covariates (X, Z) are approximately valid. Ad hoc methods with only Y -related covariates X are also approximately valid if, in addition, the D-related covariates Z is not associated with G, i.e., are not confounders for gene-disease association. Similarly, for continuous Y, if neither the disease nor secondary trait are associated with the genotype (αG = βG = 0), then ad hoc methods with pooled covariates (X, Z) are approximately valid. Ad hoc methods with Y -related covariates are also approximately valid if, in addition, Z is not associated with G.
(iii*) If the disease is rare, then the control-only analysis is approximately valid. The case-only and adjusted analyses are also approximately valid if, in addition, gD(·) = logit; however, if gD(·) = Φ−1, then these two analyses can lead to biased estimation and incorrect inference.
Simulation Study
To quantify the type I error rate, bias, and power of ad hoc methods for secondary trait analysis, we simulated case-control association studies drawn from an underlying cohort of size N. Our simulation procedure extends that of Monsees et al. [2009] by allowing for covariates and a non-logistic disease model.
First, covariates Z1i and X1i for subjects i = 1, …, N were drawn from a standard normal distribution, and Z2i = X2i was sampled as a Bernoulli random variable with probability of success 0.5. Diallelic genotype Gi was sampled conditional on Z1i as a binomial random variable of size 2 with probability of success expit(γ0 + γ1Z1i). Continuous secondary trait Yi was drawn from a normal distribution with mean α0 + X1iαX1 + X2iαX2 + GiαG and variance 1. (In Web Appendix B, we consider a binary secondary trait.) Disease Di was sampled conditional on Zi = (Z1i, Z2i)′, Gi, and Yi as a Bernoulli random variable with . Finally, case-control samples were selected by randomly sampling n1 cases and n0 controls from the simulated cohort. Note that, depending on the values of γ1 and βZ1, Z1 was or was not a confounder of the effect of G on D.
We simulated a wide variety of scenarios, varying seven parameters: disease prevalence κ ∈ {0.01,0.10}; link function gD(·) ∈ {logit, Φ−1}; the increase in log odds of inheriting a minor allele from a specific parent per unit change in Z1 = γ1 ∈ {0, ln(1.7)/2, ln 1.7}; the percent of variance in Y explained by ; the association between Z1 and D = βZ1 ∈ {0, ln(1.7)/2, ln 1.7}; the association between Y and D = βY ∈ {0, ln(2)/2, ln 2}; and the association between G and D = βG ∈ {0, ln(1.7)/2, ln 1.7}.
We fixed (α0, αXj, βZ2) = (0, 0.2, log(1.7)/2). For gD(·) = logit, we set λ = 1 so that a non-intercept coefficient in the disease model could be interpreted as the increase in log odds of disease per unit change in the corresponding explanatory variable. For gD(·) = Φ−1, we set λ = √3/π so that the association between D and (Z, Y, G) were comparable between the logistic and probit disease model [Amemiya, 1981]. γ0 was chosen so that the genotype had a minor allele frequency of approximately 0.13. The mean change in Y per copy of the minor allele (αG) and the baseline odds parameter β0 were chosen to be consistent with and κ. We generated large cohorts and sampled from each n1 = 1,000 cases and n0 = 1,000 controls. In order to estimate type I error rate (power) accurately, a total of 108 (104) replicate data sets were simulated for each scenario.
For an example of a scenario with different confounders for the disease models and the secondary phenotype models, consider Crohn's disease (D) and lactase persistence (Y). Genetic lactase persistence has been linked to risk of Crohn's disease, lactase persistence has been shown to vary from northeast to southeast Europe (X1), and Jews of European descent (Z1) are at significantly higher risk of Crohn's disease [Nolan et al., 2010; Price et al., 2006; Kenny et al., 2012]. Another example is lung cancer (D) and smoking behavior (Y). It is well known that first and second hand smoking (Z1) causes lung cancer (U.S. Department of Health and Human Services, 2006). While there is no data to suggest that the two are themselves associated, the practice of smoking differs from culture to culture, so it is possible that first and second hand smoking are associated with certain genetic markers.
We conducted the following nine analyses for each simulated dataset:
Naïve analysis with Y -related covariates: regress Y on (X, G) in the case-control sample.
Control-only analysis with Y -related covariates: regress Y on (X, G) among controls.
Case-only analysis with Y -related covariates: regress Y on (X, G) among cases.
Adjusted analysis with Y -related covariates: regress Y on (X, G, D) in the case-control sample.
Naïve analysis with pooled covariates: regress Y on (X, Z, G) in the case-control sample.
Control-only analysis with pooled covariates: regress Y on (X, Z, G) among controls.
Case-only analysis with pooled covariates: regress Y on (X, Z, G) among cases.
Adjusted analysis with pooled covariates: regress Y on (X, Z, G, D) in the case-control sample.
IPW regression: regress Y on (X, G) using weights w1 = κ for cases and w0 = 1 − κ for controls.
We included Analysis 9 for the purpose of generalizing previous results by Monsees et al. [2009] comparing the performance of ad hoc methods to IPW regression. For each method and scenario, the probability of rejecting the null hypothesis H0: αG = 0 was estimated by applying a nominal significance threshold of α ∈ {10−4, 10−5, 10−6}. Bias was obtained by taking the average of α̂G − αG.
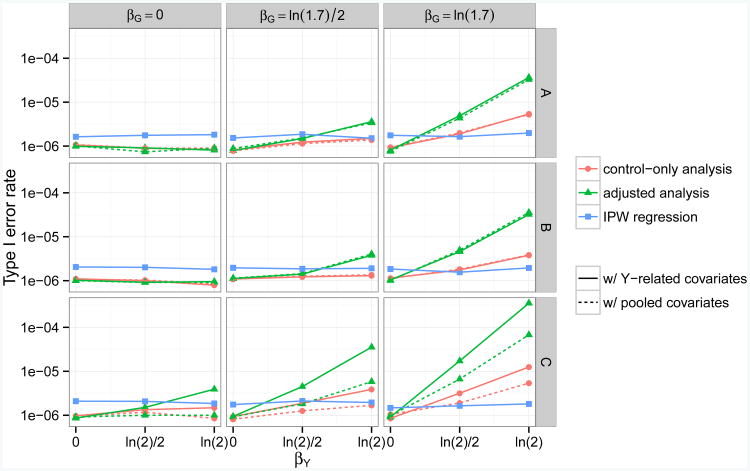
Figures 1–3 summarize the type I error rates and bias for the control-only adjusted, and IPW regression analyses across the null scenarios (αG = 0) that were considered. Results for the naïve and case-only analyses can be found in Appendix C. Results for α ∈ {10−4,10−5} are omitted but similar. As expected, IPW regression (Analysis 9) was unbiased for all of the scenarios considered. However, interestingly, its type I error rates were consistently slightly inflated due to the instability of the sandwich estimator. Increasing the sample size (n1, n0) improved type I error control (not shown). Ad hoc methods with pooled covariates (Analyses 5–8) had appropriate type I error rates and no perceptible bias whenever βY = 0 or βG = 0. Likewise, ad hoc methods with Y -related covariates (Analyses 1–4) were valid whenever βY = 0, or βG = 0 and Z is not a confounder for the effect of G on D (γ1 = 0 or βZ1 = 0).
Fig 1.
Empirical type I error rates for testing genetic associations with a continuous secondary trait, at genome-wide α = 10−6 level and across scenarios with different combinations of βY, βG, γ1 and βZ1. Five methods (Analysis 2,4,6,8,9) are compared here. Each method takes either a control-only, adjusted, or IPW approach, and adjusts for covariates related to Y or covariates related to (Y, D). The disease is assumed to be common (10% prevalence) and to follow a logistic model. In row A, covariate Z1 is assumed to be associated with G but not with D (γ1 = ln 1.7, βZ1 = 0). In row B, Z1 is associated with D but not with G (γ1 = 0, βZ1 = ln 1.7). In row C, Z1 is a confounder of the association between G and D (γ1 = βZ1 = ln 1.7).
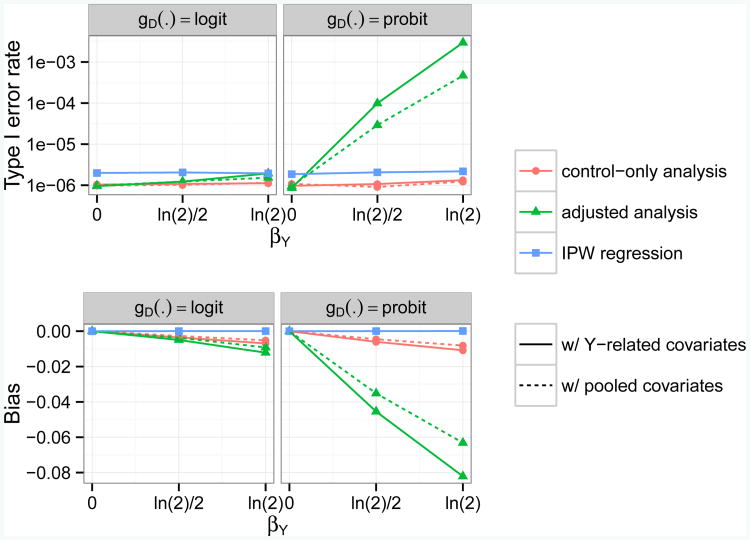
Fig 3.
Empirical type I error rates and bias for testing and estimating genetic associations with a continuous secondary trait, at genome-wide α = 10−6 level and across null scenarios (αG = 0) with different combinations of βY and link function gD(·) for the disease model. Five methods (Analysis 2,4,6,8,9) are compared here. Each method takes either a control-only, adjusted, or IPW approach, and adjusts for covariates related to Y or covariates related to (Y, D). The disease is assumed to be rare (1% prevalence) and to follow either a logistic or probit model (gD(·) = logit or Φ−1). G is assumed to be associated with D (βG = ln 1.7). Z1 is assumed to be a confounder of the association between G and D (γ1 = βZ1 = ln 1.7). The scenarios with a logistic disease model (left column) are the same as the scenarios in the bottom right plots of Figures 1 and 2, except here the disease is not common but rather rare.
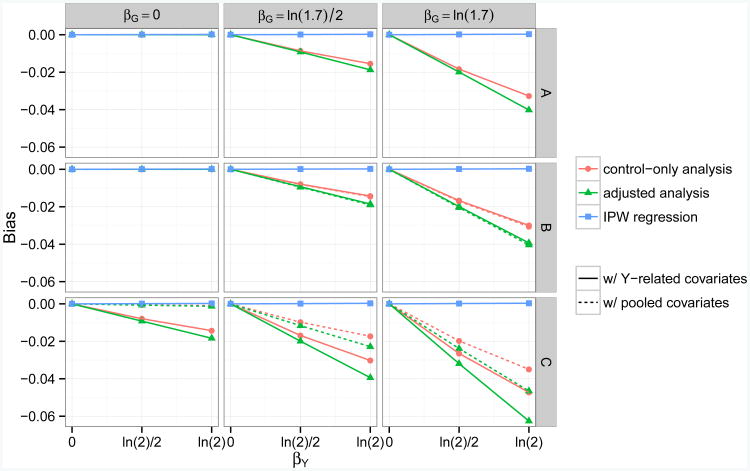
For common disease (κ = 0.10; Figures 1 and 2), we detected an inflation in type I error rates and bias for all eight ad hoc methods when βY ≠ 0 and βG ≠ 0. We also detected an inflation in type I error rates and bias for Analyses 1–4 when βY ≠ 0, βG = 0, and Z1 confounded the association between G and D (|γ1| > 0, |βZ1| > 0).
Fig 2.
Empirical bias for the estimated genetic effect α̂G on a continuous secondary trait, across null scenarios (αG = 0) with different combinations of βY, βG, γ1 and βZ1. Five methods (Analysis 2,4,6,8,9) are compared here. Each method takes either a control-only, adjusted, or IPW approach, and adjusts for covariates related to Y or covariates related to (Y, D). The disease is assumed to be common (10% prevalence) and to follow a logistic model (gD(·) = logit). In row A, covariate Z1 is assumed to be associated with G, but not with D (γ1 = ln 1.7, βZ1 = 0). In row B, Z1 is associated with D, but not with G (γ1 = 0, βZ1 = ln 1.7). In row C, Z1 is a confounder of the association between G and D (γ1 = βZ1 = ln 1.7).
For rare disease (κ = 0.01; Figure 3) with a logistic link function, all ad hoc methods that condition on case-control status (Analyses 2–4, 6–8) had little to no inflation in type I error rates and bias regardless of whether βY = 0 or βG =0. However, for rare disease with a probit link function, only the control-only analysis (Analyses 2 and 6) and IPW regression were approximately valid in general. All other ad hoc methods had highly inflated type I error rates and severe bias when βY ≠ 0 and βG ≠ 0.
We compared the power of Analyses 1–9 whenever the analyses were approximately valid by varying αG ∈ {0, ln(1.7)/2, ln(1.7)} (Web Appendix C). The naïve analyses (Analyses 1 and 5) tended to be the most powerful, followed by the adjusted analyses (Analyses 4 and 8), IPW regression (Analysis 9), and finally the ad hoc analyses restricted to cases or controls (Analyses 2, 3, 6, and 7). In addition, ad hoc methods with Y -related covariates were slightly more powerful than their corresponding ad hoc methods with pooled covariates.
Example: GWAS of Smoking Behavior
To demonstrate the application of ad hoc methods, we performed a genome-wide association analysis of smoking behavior using a set of 696 lung cancer cases and 730 controls.
Study population
Our study population was derived from a large ongoing case-control study of the molecular epidemiology of lung cancer at MGH, and has been described in detail elsewhere [Schifano et al., 2012]. Briefly, the controls were recruited from the friends or spouses of cancer patients or the friends or spouses of other surgery patients in the same hospital. To reduce confounding due to population structure, the study was limited to individuals of self-reported European descent.
Genotyping
Peripheral blood samples were obtained from all study participants at the time of enrollment. DNA was extracted from samples using the Puregene DNA Isolation Kit (Gentra Systems), and genoyping was performed with the Illumina Human610-Quad BeadChip. For quality control, SNPs that had call rate less than 95%, that failed the Hardy-Weinberg equilibrium test at 10−6, or that had minor allele frequency less than 5%, were excluded. Blood samples with genotyping call rates less than 95% were also excluded. There were 513,271 SNPs remaining after frequency and quality control. To further control for population structure, EIGENSTRAT was used to perform a principal components (PCs) analysis [Price et al., 2006]. We included the first four PCs, on the basis of significant Tracy-Widom tests (p < 0.05) and genomic control inflation factor, as covariates for all analyses. Of the remaining six out of ten top PCs, we decided to also include the ninth PC as a covariate in our secondary linear regression models because we found this PC to be significantly associated with lifetime smoking exposure (p < 0.05).
Covariate and phenotypic data collection
Interviewer-administered questionnaires collected information on sociodemographic variables from each subject, including age (years; continuous), gender, education history (college degree or more; yes/no), and smoking intensity (cigarettes/day and number of years smoked). Subjects were classified as either never smokers (less than 100 cigarettes in their lifetime), former smokers (quit smoking at least 1 year prior to interview date), or current smokers (at time of interview). Only ever-smokers (former and current) were used in our data analysis, as we were interested in studying the genetic effects on smoking intensity measured by pack-years.
We used square root pack-years (number of packs of cigarettes smoked daily times the number of years smoked) as our secondary outcome measure of smoking behavior. The square root transformation was applied to better satisfy assumptions of normality.
We performed the naïve, control-only, case-only, adjusted, and IPW analyses for each SNP by regressing square root of pack-years on genotype (number of minor alleles), age, gender, college education, and PCs 1–4 and 9. For the adjusted analysis, lung cancer status was included in the regression model. For IPW regression, we estimated the prevalence of lung cancer amongst ever-smokers in Massachusetts to be 0.00148, and used this prevalence to calculate the inverse probability weight for each study individual (see Web Appendix D for more details).
On conditions (i)-(iii*)
Since conditions (i)-(iii*) play an important role in determining which results from a genome-wide ad hoc analysis of a secondary trait are credible, we sought to verify these conditions in our dataset.
For condition (i), we found that smoking intensity is significantly associated with lung cancer risk (OR = 1.45, p < 10−15). For condition (ii*), we fitted for each SNP a logistic regression model to test for genetic associations with lung cancer, adjusting for square root pack-years, age, gender, college education, and the first four PCs. For condition (iii*), given an estimated prevalence of 0.00148, lung cancer can be considered a rare disease within the at-risk population of ever-smokers in Massachusetts. We looked at diagnostic plots to investigate whether a logistic model for (1) is a reasonable fit for lung cancer risk (Figure 4). Under such a model, one would expect case- and control-only estimates to be unbiased and uninfluenced by marker-disease associations. However, we see from Figure 4 that for our dataset the case- and control-only analyses were generally estimating different quantities, and that the difference between their estimates (α̂G,case — α̂G,ctrl) tended to increase as the log odds ratio of SNPs and lung cancer (β̂G) increased. It was only when a SNP was weakly associated with lung cancer (β̂G ≈ 0) that the expected difference between case- and control-only estimates equalled 0.
Fig 4.
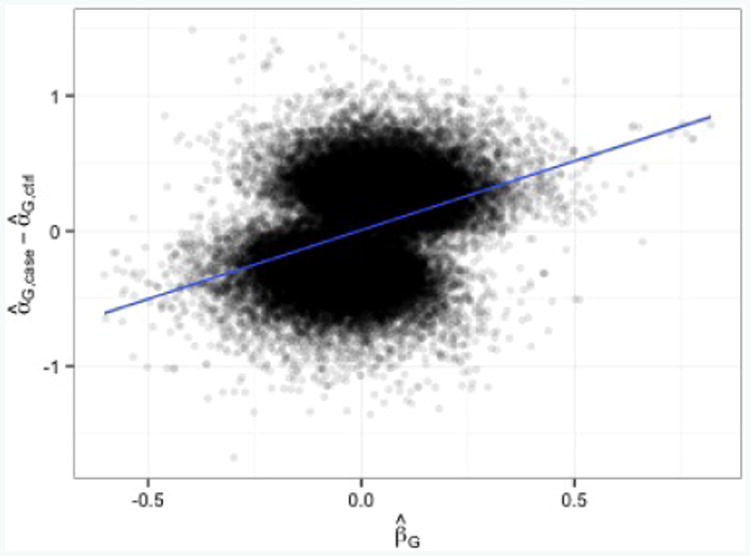
Top 50k SNPs from IPW regression. Observed difference between case-only and control-only estimates has a significant tendency to increase as the log odds-ratio of a genetic marker and lung cancer increases (slope of best fit line = 1.02, p < 10−15). Under the assumption of a rare disease with a logistic model, one would expect the best fit line to be y = 0.
These observations led us to conclude that for our purpose of analyzing genome-wide associations with smoking behavior, condition (i) does not hold, the disease is rare, and the disease model (1) with gD (·) = logit is somehow misspecified. Consequently, we may prefer results from IPW regression, the control-only analysis (because the disease is rare), and the adjusted analysis of SNPs with weak evidence of an association with lung cancer risk (because the adjusted analysis is one of the more powerful valid ad hoc approaches under condition (ii*). Yet, when condition (ii*) is not satisfied, it is not as severely biased as the naïve analysis.)
Results
Manhattan plots for the naïve, control-only, case-only, adjusted, and IPW analyses can be found in Web Appendix D. In total, 1130 SNPs were identified as nominally significant at p < 10−3 by the control-only, adjusted, or IPW analysis (see Figure 5). Comparing the control-only analysis to IPW regression, SNPs identified as nominally significant by the control-only analysis were roughly a subset of the SNPs identified by IPW regression. Indeed, 429 of the 468 (91.7%) SNPs identified by the control-only analysis were also identified by IPW regression. Meanwhile, IPW regression identified 185 other SNPs. Of the 429 SNPs identified by both analyses, the majority (328, 76.5%) were more significant when analyzed by IPW regression than by the control-only analysis.
Fig 5.
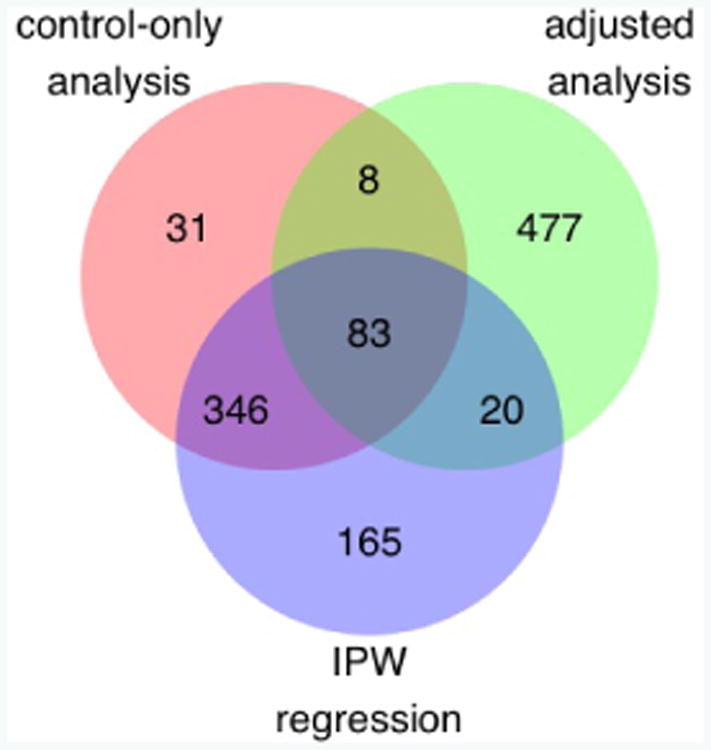
Number of nominally significant SNPs (p < 10−3) from the control-only, adjusted, and IPW analysis of . p values from a 1-DF Wald test assuming an additive genetic model.
The adjusted analysis generally identified different SNPs as nominally significant than the control-only and adjusted analyses. Specifically, the adjusted analysis identified 477 novel SNPs, novel in the sense that they were nominally significant (p < 10−3) when analyzed by the adjusted analysis, but nominally insignificant (p ≥ 10−3) when analyzed by the control-only and IPW analyses. Likewise, the control-only and IPW analyses identified 31 and 165 novel SNPs. However, taken together, the control-only and IPW analyses collectively identified 542 SNPs that were nominally insignificant when analyzed by the adjusted analysis (Figure 5).
A large number of the novel SNPs identified by adjusted analysis had weak evidence of an association with lung cancer risk; when tested for H0: βG = 0, 139 (29.1%), 220 (46.1%), and 118 (24.7%) SNPs had p value in the range [0.0, 0.1), [0.1, 0.5), and [0.5, 1.0], and odds ratio in the range [0.63, 1.62], [0.74, 1.35], and [0.92, 1.09], respectively. Therefore, applying condition (ii*), the adjusted analysis of many of these SNPs are likely to be valid.
Table I displays the top ten SNPs for the control-only analysis. (The top ten SNPs for the naïve, case-only, adjusted, and IPW analyses are included in Web Appendix D. Also included are the top ten novel SNPs for the adjusted, control-only, and IPW analyses.) Looking at the top SNPs and the top ten novel SNPs for the control-only, adjusted, and IPW analyses, we found SNPs from several genes identified in previous GWASs of smoking cessation: ARHGAP24, C1orf95, CDH18, CDYL2, DOK6, FAM189A1, HSD17B2, KSR1, NBEA, PDE10A, SLC9A2 (a paralog of SLC9A9), and TACR1 [Rose et al., 2010; Uhl et al., 2010; Tang et al., 2014].
Table I.
Top 10 SNPs from the genome-wide control-only analysis of . Estimates of the additive genetic effect on smoking behavior (α̂G) and their p values from a 1-DF Wald test for the naïve, control-only, case-only, adjusted, and IPW analysis. Marker-lung cancer effect estimates ( ) and their p values from a 1-DF Wald test are also provided.
| Lung cancer | Smoking behavior | ||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|
|
||||||||
| SNP | Chr. | Gene |
|
Naïve | Control-only | Case-only | Adjusted | IPW | |
| rs7588326 | 2 | TACR1 | 1.16 (8.41×10−2) | -0.40 (9.82×10−6) | -0.51 (2.02×10−5) | -0.30 (9.97×10−3) | -0.40 (2.02×10−6) | -0.51 (8.82×10−6) | |
| rs4461636 | 5 | CDH18 | 1.25 (1.44×10−1) | -0.44 (5.57×10−3) | -0.98 (5.78×10−6) | 0.01 (9.49×10−1) | -0.46 (1.65×10−3) | -0.98 (7.78×10−6) | |
| rs4242066 | 5 | CDH18 | 1.28 (1.08×10−1) | -0.40 (1.13×10−2) | -0.99 (6.02×10−6) | 0.06 (7.65×10−1) | -0.44 (2.93×10−3) | -0.99 (7.26×10−6) | |
| rs1391429 | 5 | CDH18 | 1.22 (1.73×10−1) | -0.43 (5.80×10−3) | -0.90 (2.00×10−5) | -0.03 (8.95×10−1) | -0.45 (1.99×10−3) | -0.90 (2.50×10−5) | |
| rs7842063 | 8 | N/A | 0.91 (3.79×10−1) | 0.44 (8.69×10−5) | 0.64 (1.29×10−5) | 0.17 (2.52×10−1) | 0.41 (7.77×10−5) | 0.64 (4.41×10−5) | |
| rs4404875 | 8 | RP1L1 | 0.86 (1.53×10−1) | 0.35 (2.19×10−3) | 0.66 (1.89×10−5) | 0.05 (7.23×10−1) | 0.36 (6.89×10−4) | 0.66 (1.74×10−5) | |
| rs1655645 | 15 | FAM189A1 | 0.95 (5.89×10−1) | 0.28 (1.99×10−3) | 0.55 (8.48×10−6) | -0.03 (8.05×10−1) | 0.26 (2.17×10−3) | 0.55 (2.080×10−5) | |
| rs1893213 | 18 | N/A | 0.89 (1.68×10−1) | 0.28 (2.30×10−3) | 0.54 (1.03×10−5) | 0.00 (9.91×10−1) | 0.28 (1.04×10−3) | 0.54 (5.98×10−6) | |
| rs4805573 | 19 | ZNF536 | 1.36 (6.63×10−2) | -0.65 (1.77×10−4) | -1.06 (4.52×10−6) | -0.27 (2.38×10−1) | -0.67 (2.91×10−5) | -1.06 (1.29×10−6) | |
| rs4805574 | 19 | ZNF536 | 1.34 (8.40×10−2) | -0.65 (1.84×10−4) | -1.02 (1.13×10−5) | -0.30 (1.85×10−1) | -0.67 (3.51×10−5) | -1.02 (3.99×10−6) | |
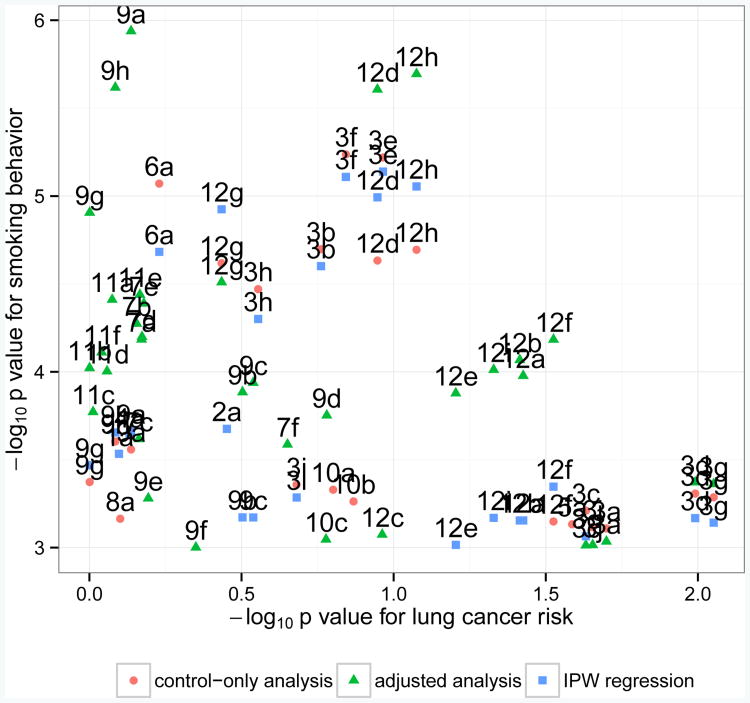
In Figure 6, we see that the control-only analysis and IPW regression performed similarly for nominally significant SNPs from the previously known genes. Meanwhile, for some SNPs their association with smoking behavior were much more significant when analyzed by the adjusted analysis than by the control-only or IPW analysis (e.g., SNPs from HSD17B2, NBEA, SLC9A2), and vice versa (e.g., SNPs from CDH18). This is consistent with simulation results that the adjusted analysis is more powerful than the control-only analysis and the IPW analysis in the situations when they are valid. Only TACR1 had similar results across the three methods. We note that SNPs which were nominally significant only when analyzed by the adjusted analysis had weak evidence of an association with lung cancer risk.
Fig 6.
p values from the genome-wide association analysis of and lung cancer risk for nominally significant SNPs (p < 10−3) from twelve selected genes: (1) ARHGAP24, (2) C1orf95, (3) CDH18, (4) CDYL2, (5) DOK6, (6) FAM189A1, (7) HSD17B2, (8) KSR1, (9) NBEA, (10) PDE10A, (11) SLC9A2, and (12) TACR1. All genes have been identified in previous studies of smoking cessation. Here, we compare the results from the control-only, adjusted, and IPW analyses of . Results can be distinguished by gene (number), SNP (letter), and the secondary analysis applied (shape and color).
Discussion
In this paper, we have given new conditions for using ad hoc methods. Our findings extend previous work by demonstrating that if there are covariates confounding the effect of a genetic marker on the disease but that are not adjusted for in the secondary trait analysis, then ad hoc analysis can lead to spurious associations even when the genetic marker is not associated with the disease. Futhermore, for a rare disease, the case-only and adjusted analyses can lead to severely biased estimation and incorrect inference if the true disease model is not strictly logistic.
The conditions set forth in this paper apply to the setting where there are no gene-environment interactions in the disease. We now briefly discuss the validity of the ad hoc methods for G-E interaction models. It is easy to show that if there is an interaction between gene and covariates, but no interaction between gene and secondary trait, then conditions (i) and (iii*) hold, but not condition (ii*). On the other hand, if there is an interaction between gene and secondary trait on disease risk, then (i) and (ii*) do not hold, and the only valid analysis for a rare disease is the control-only analysis. The fact that the case-only and adjusted analyses lead to incorrect estimation and inference has been discussed previously by Li et al. [2012]. As a solution, the authors proposed an adaptively weighted method that combines the case-only and control-only estimates, while reducing to the control-only analysis if there is strong evidence of a marker-secondary trait interaction. Another approach proposed by Wang and Shete [2011] has been shown to accurately estimate association between marker and binary secondary traits in the presence of interactions [Wang and Shete, 2012].
We considered the possibility of interaction between SNPs and smoking behavior for lung cancer risk in our data analysis. We found that SNPs identified as nominally significant by the adjusted analysis tended not to modify the effect of smoking behavior on lung cancer risk, but SNPs identified by the control-only or IPW analysis had moderate to strong evidence of G-E interaction (Web Appendix D). This difference explains why we observed relatively little overlap in Figure 5, and why some previously known genes were identified by only the adjusted analysis, or by the control-only and IPW analyses but not the adjusted analysis (Figure 6).
The results in this paper have several important implications for secondary trait analysis. First, when applying ad hoc methods, one should consider including potential confounders of the association between the genetic marker and the disease, even if these covariates are not predictors of the secondary trait. For example, one might adjust for population structure associated with the secondary trait and population structure associated with the disease. However, one should be aware that when including additional covariates, power may be reduced if the secondary trait is binary and the covariates are not actually confounders [Pirinen et al., 2012].
Second, for a rare disease, it is crucial to verify disease model assumptions or to perform sensitivity analysis. A potential pitfall is misspecifying the link function of the disease model (e.g., logit vs probit). Another is ignoring gene-environment interactions in the linear predictor. One may test whether a probit or logistic model better describes the disease by fitting the null models (i.e. disease models with covariates but no SNPs) using IPW probit and IPW logistic regression, then comparing the Bayesian information criterions [Schwarz, 1978]. One may also look at diagnostic plots like Figure 4 to determine whether a logistic disease model is a reasonable assumption; however, constructing such diagnostic plots requires one to perform beforehand primary and secondary trait analyses across the genome. The importance of having a robust analysis applies not only to ad hoc methods, but also to complex approaches. For instance, the approaches proposed by Lin and Zeng [2009], Wang and Shete [2011], and Li et al. [2012]all assume that the disease follows a logistic model. Lin and Zeng's semiparametric approach further assumes that there are no G-E interactions. It is important when applying either of these methods to verify their assumptions.
Finally, researchers may benefit from applying multiple methods rather than a one-size-fits-all solution. In our data analysis of smoking behavior, the adjusted analysis identified a large number of promising SNPs that were otherwise missed by the control-only analysis and IPW regression, and vice versa. Meanwhile, the control-only analysis and IPW regression performed similarly when analyzing SNPs from previously known genes. However, the control-only analysis was easier and computationally much faster to perform, while IPW regression was slightly more powerful because it used both the lung cancer cases and controls. Therefore, whether it is to save computational time or to improve the identification of promising genetic markers, researchers would do well to apply several ad hoc and complex methods.
Supplementary Material
Acknowledgments
This research was supported by grants from the National Institutes of Health (R37 CA076404 and P01 CA134294 to Lin X.).
Appendix
Theoretical Justification for Conditions (i)-(iii*)
Let P(·) denote the population-based probability, κ = P(D = 1) denote the disease prevalence, S indicate with the values 1 versus 0 whether or not an individual from the population is sampled in the case-control study, and π(D) = P(S = 1|D) be the probability of being sampled in the case-control study for an individual with disease status D. Also, let P̃(·) = P(·|S = 1), μ̃Y = E(Y|X, G, Z, S = 1), μ̃Y|D = E(Y|X, G, Z, D, S = 1), σ̃2 = Var(Y|X, G, Z, S = 1), and denote the case-control probability, conditional means of Y, and conditional variances of Y, all observed under the case-control design.
Common Disease, Binary Secondary Trait
When the secondary phenotype Y is binary, we can show that the conditional means of Y in case-control samples satisfy
| (3) |
| (4) |
where
and d = 0, 1. Equivalent expressions for (3) and (4) were derived by Lin and Zeng [2009] and Tchetgen Tchetgen [2014]. From (3) and (4), it is easy to see that differences between the mean models for the secondary phenotype in case-control studies and in the population (2) are given by r(Z, G) and rd(Z, G). Therefore, validity of ad hoc methods depends on the value of these extra terms and whether the methods properly adjust for them. It should be noted that the true means of the secondary phenotypes Y in case-control studies not only depend on the Y -related covariates X but also the D-related covariates Z.
If βY = 0, i.e., the secondary phenotype Y is not associated with the disease D, then μD(1) = μD(0) and r(Z, G) = rd(Z, G) = 0. It follows that (3) and (4) reduce to (2), and ad hoc methods with only Y -related covariates X can be used as a valid tool to estimate and perform inference on all the population parameters α0, αX, and αG.
Alternatively, if βG = 0, i.e., when a SNP is not associated with disease, then r(Z, G) = r(Z) and rd(Z, G) = rd(Z) are functions of Z but not of G. In this situation, validity of ad hoc methods depends on whether Z and G are associated, whether r(·) and rd(·) are linear in Z, and whether r1(·) and r0(·) differ by a constant. When Z and G are independent, i.e., when Z is not a confounder for the genetic association with disease, it is not necessary to adjust for r(·) and rd(·) in the secondary phenotype regression in order to obtain valid estimation and inference of αG. Hence the ad hoc methods with only Y -related covariates X can be used. When Z and G are correlated, i.e., Z is a confounder for the genetic association with disease, failure to adjust for r(·) and rd(·) can lead to spurious associations between G and Y, because an estimate of the association between G and Y may also capture the association between Z and Y induced by r(·) and rd(·). This leads us to consider ad hoc methods with pooled covariates (X, Z).
Suppose, in addition to βG =0, that r(·) and rd(·) are linear in Z, and r0(·) and r1(·) differ by a constant. Then we can write and , from which it is easy to see that ad hoc methods with pooled covariates are valid. In Web Appendix A and B, we generalize this result by first showing theoretically that for any smooth link function gD(·), r(·) and rd(·) are approximately linear in Z as long as |βY| and |βZ| are not exceedingly large. We then show for several choices of link function (logit, probit, complementary log-log) that r0(·) and r1(·) differ by approximately, if not exactly, a constant. These theoretical results, confirmed by our simulation studies, show that for typical values of βY and βZ, ad hoc methods with pooled covariates lead to approximately unbiased estimates of αG and nominal type I error rates. We conclude that for practical purposes, if βG = 0, then ad hoc methods with pooled covariates can be used and provide approximately correct inference.
Common Disease, Continuous Secondary Trait
In the case that Y is continuous, we have for the case-control conditional distributions,
| (5) |
| (6) |
If βY = 0, then factors cancel in the numerators and denominators so that P̃(Y|X, G, Z) = P̃(Y|X, G, Z, D) = P(Y|X, G) and ad hoc methods with only Y -related covariates X can be used to estimate and perform inference on all the population parameters α0, αX, and αG. On the other hand, if βY ≠ 0, then calculations of the case-control conditional means and variances of Y, such as μ̃Y|D = ∫yP̃(y|X, G, Z, D)dy, are generally intractable. There is however one exception. When gD(·) = Φ−1, it can be shown that
| (7) |
| (8) |
where
Derivations for (7) and (8) as well as closed form expressions for μ̃Y and σ̃2 can be found in Web Appendix A. Given that the logit and probit functions are very close in the mid-range [Amemiya, 1981], we can also find approximate expressions for gD(·) = logit. Together, these expressions can be useful for investigating what happens when βY ≠ 0 and ad hoc methods are applied.
If αG = βG = 0, then r(·) and rd(·) are functions of Z and X but not of G. In this situation, validity of ad hoc methods depends on whether Z is associated with G, whether r(·) and rd(·) are linear functions of (Z′, X′)′, whether r0(·) and r1(·) differ by a constant, and whether s(·) and sd(·) are constants. For example, if r0(·) and r1(·) are linear functions of (Z′, X′)′ that differ by a constant, and sd(·) are constants, then we can write and . It follows that for large samples, ad hoc method (b) with pooled covariates (X, Z) provides valid estimation and inference of αG. The adjusted analysis (c) with pooled covariates can be used too if .
In Web Appendix A, we show theoretically that r(·) and rd(·) are approximately linear in (Z′, X′)′ and s(·) and sd(·) are approximately constants as long as |βY| and are not exceedingly large. In the Results section of the main article, we show with simulations that for typical values of βY and , ad hoc methods (a) and (b) with pooled covariates lead to approximately unbiased estimates of αG and nominal type I error rates. Therefore, we conclude that for practical purposes, if αG = βG = 0, then ad hoc methods (a) and (b) with pooled covariates are approximately valid.
As mentioned, the adjusted analysis with pooled covariates is valid if, in addition, r1(·) − r0(·) is a constant and . While it is easy to show that the first condition is approximately true for common disease (Web Appendix A), is generally not equal to . Nevertheless, the difference between the sample variance of the case-only and control-only analyses with pooled covariates seemed to be small enough for inference to be approximately correct in our simulations.
Rare Disease
For rare disease, P(D = 0|Z, G, Y) and P(D = 0|Z, G) in (6) are approximately equal to 1, so P̃(Y|X, G, Z, D = 0) ≈ P(Y|X, G). It follows that a control-only analysis is approximately valid for binary and continuous secondary traits. Intuitively when the disease is rare, the controls closely resemble the general population. Therefore, any conclusion about the population based on the controls will be approximately correct.
As for ad hoc methods that use cases, these methods may or may not be valid depending on the underlying disease model. If gD(·) = logit, then we have for binary Y that r1(Z, G) ≈ βY, and for continuous Y that r1(Z, G, X) ≈ βY σ2 and s1(Z, G, X) ≈ 0. In fact, for continuous Y, P̃(Y|X, G, Z, D = 1) is approximately proportional to exp {− [Y − μY − βYσ2]/2σ2} [Lin and Zeng, 2009]. Thus, for both binary and continuous secondary traits, ad hoc methods (b)-(c) with only Y -related covariates X yield approximately valid estimation and inference for αX and αG.
If instead, gD(·) = Φ−1, then we have for binary Y that r1(Z, G) ≈ constant − βY (Φ−1(μD(0)), and for continuous Y that and s1(Z, G, X) ≈ −c2. Derivations are available in Web Appendix A. Note that in both cases, r1 involves G. These results are substantially different from those obtained under gD(·) = logit, where we saw r1 are constants. They imply that an estimate of αG from the case-only analysis with pooled covariates is generally biased:
By extension, the adjusted analysis is also invalid. Finally, one might consider extending the adjusted analysis with pooled variates to include D-Z, D-G, and D-X interactions. In doing so, the main effect of G will encode the marginal association of interest αg. However, if Z and X include large numbers of possibly confounding covariates for population stratification, it is unlikely that adding a large number of interactions will lead to an increase in power compared to the control-only analysis.
References
- Amemiya T. Qualitative response models: a survey. J Econ Lit. 1981;19:1483–1536. [Google Scholar]
- He J, Li H, Edmondson AC, Rader DJ, Li M. A gaussian copula approach for the analysis of secondary phenotypes in casecontrol genetic association studies. Biostatistics. 2012;13:497–508. doi: 10.1093/biostatistics/kxr025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang Y, Scott AJ, Wild CJ. Secondary analysis of case-control data. Stat Med. 2006;25:1323–1339. doi: 10.1002/sim.2283. [DOI] [PubMed] [Google Scholar]
- Kenny EE, Pe'er I, Karban A, Ozelius L, Mitchell AA, Ng SM, Erazo M, Ostrer H, Abraham C, Abreu MT, et al. A genome-wide scan of Ashkenazi Jewish Crohns Disease suggests novel susceptibility loci. PLoS Genet. 2012;8 doi: 10.1371/journal.pgen.1002559. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee SH, Wray NR, Goddard ME, Visscher PM. Estimating missing heritability for disease from geneome-wide association studies. Am J Hum Genet. 2011;88:294–305. doi: 10.1016/j.ajhg.2011.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H, Gail MH, Berndt S, Chatterjee N. Using cases to strengthen inference on the association between single nucleotide polymorphisms and a secondary phenotype in genome-wide association studies. Genet Epidemiol. 2010;34:427–433. doi: 10.1002/gepi.20495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin DY, Zeng D. Proper analysis of secondary phenotype data in case-control association studies. Genet Epidemiol. 2009;33:256–265. doi: 10.1002/gepi.20377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monda KL, Chen GK, Taylor KC, Palmer C, Edwards TL, Lange LA, Ng MC, Adeyemo AA, Allison MA, Bielak LF, et al. A meta-analysis identifies new loci associated with body mass index in individuals of African ancestry. Nat Genet. 2013;45:690–696. doi: 10.1038/ng.2608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monsees GM, Tamimi RM, Kraft P. Genome-wide association scans for secondary traits using case-control samples. Genet Epidemiol. 2009;33:717–728. doi: 10.1002/gepi.20424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagelkerke NJD, Moses S, Plummer FA, Brunham RC, Fish D. Logistic regression in case-control studies: the effect of using independent as dependent variables. Stat Med. 1995;14:769–775. doi: 10.1002/sim.4780140806. [DOI] [PubMed] [Google Scholar]
- Nolan DJ, Han DY, Lam WJ, Morgan AR, Fraser AG, Tapsell LC, Ferguson LR. Genetic adult lactase persistence is associated with risk of Crohns Disease in a New Zealand population. PMC Research Notes. 2010;3 doi: 10.1186/1756-0500-3-339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pirinen M, Donnelly P, Spencer CCA. Including known covariates can reduce power to detect genetic effects in case-control studies. Nat Genet. 2012;44:848–851. doi: 10.1038/ng.2346. [DOI] [PubMed] [Google Scholar]
- Price AL, Patterson NJ, Plenge RM, Weinblatt ME, Shadick NA, Reich D. Principal components analysis corrects for stratification in genome-wide association studies. Nat Genet. 2006;38:904–909. doi: 10.1038/ng1847. [DOI] [PubMed] [Google Scholar]
- Prentice RL, Pyke R. Logistic disease incidence models and case-control studies. Biometrika. 1979;66:403–411. [Google Scholar]
- Rose JE, Behm FM, Drgon T, Johnson C, Uhl GR. Personalized Smoking Cessation:Interactions between Nicotine Dose, Dependence and Quit-Success Genotype Score. Mol Med. 2012;16:247–253. doi: 10.2119/molmed.2009.00159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenberg NA, Pritchard JK, Weber JL, Can HM, Kidd KK, Zhivotovsky LA, Feldman MW. Genetic structure of human populations. Science. 2002;298:2381–2385. doi: 10.1126/science.1078311. [DOI] [PubMed] [Google Scholar]
- Schifano ED, Li L, Christiani D, Lin X. Genome-wide association analysis for multiple continuous secondary phenotypes. Am J Hum Genet. 2013;92:1–16. doi: 10.1016/j.ajhg.2013.04.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwarz G. Estimating the dimension of a model. Ann Stat. 1978;6:461–464. [Google Scholar]
- So HC, Sham PC. A unifying framework for evaluating the predictive power of genetic variants based on the level of heritability explained. PLoS Genet. 2010;6 doi: 10.1371/journal.pgen.1001230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Speliotes EK, Willer CJ, Berndt SI, Monda KL, Thorleifsson G, Jackson AU, Lango Allen H, Lindgren CM, Luan J, Mägi R, et al. Association analyses of 249,796 individuals reveal 18 new loci associated with body mass index. Nat Genet. 2010;42:937–948. doi: 10.1038/ng.686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang H, Wei P, Duell EJ, Risch HA, Olson SH, Bueno-de-Mesquita HB. Axonal guidance signaling pathway interacting with smoking in modifying the risk of pancreatic cancer: a gene- and pathway-based interaction analysis of GWAS data. Carcinogenesis. 2014;33:1039–1045. doi: 10.1093/carcin/bgu010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tchetgen Tchetgen EJ. A general regression framework for a secondary outcome in case-control studies. Biostatistics. 2014;15:117–128. doi: 10.1093/biostatistics/kxt041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uhl GR, Drgon T, Johnson C, Ramoni MF, Behm FM, Rose JE. Genome-wide association for smoking cessation success in a trial of precessation nicotine replacement. Mol Med. 2010;16:513–526. doi: 10.2119/molmed.2010.00052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J, Shete S. Estimation of odds ratios of genetic variants for the secondary phenotypes associated with primary diseases. Genet Epidemiol. 2011;35:190–200. doi: 10.1002/gepi.20568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J, Shete S. Analysis of secondary phenotype involving the interactive effect of the secondary phenotype and genetic variants on the primary disease. Ann Hum Genet. 2012;76:484–499. doi: 10.1111/j.1469-1809.2012.00725.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wen W, Cho YS, Zheng W, Dorajoo R, Kato N, Qi L, Chen CH, Delahanty RJ, Okada Y, Tabara Y, et al. Meta-analysis identifies common variants associated with body mass index in east Asians. Nat Genet. 2012;44:307–311. doi: 10.1038/ng.1087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wray NR, Yang J, Goddard ME, Visscher PM. The genetic interpretation of area under the ROC curve in genomic profiling. PLoS Genet. 2010;6 doi: 10.1371/journal.pgen.1000864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zaitlen N, 1, Lindström S, Pasaniuc B, Cornelis M, Genovese G, Pollack S, Barton A, Bickeböller H, Bowden DW, Eyre S, et al. Informed conditioning on clinical covariates increases power in case-control association studies. PLoS Genet. 2012;8 doi: 10.1371/journal.pgen.1003032. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.