Translational PK/PD of Anti-Infective Therapeutics

Abstract

Translational PK/PD modeling has emerged as a critical technique for quantitative analysis of the relationship between dose, exposure and response of antibiotics. By combining model components for pharmacokinetics, bacterial growth kinetics and concentration-dependent drug effects, these models are able to quantitatively capture and simulate the complex interplay between antibiotic, bacterium and host organism. Fine-tuning of these basic model structures allows to further account for complicating factors such as resistance development, combination therapy, or host responses. With this tool set at hand, mechanism-based PK/PD modeling and simulation allows to develop optimal dosing regimens for novel and established antibiotics for maximum efficacy and minimal resistance development.

Introduction

The treatment options available to combat infectious diseases are becoming increasingly limited due to a rising incidence of resistance among bacteria against the currently used antibiotics. Additionally, the discovery and development of new antibiotics has slowed down because of limited incentives for the pharmaceutical industry in this therapeutic area and a high benefit-risk ratio of existing antibiotics [1]. This necessitates prudent use of the currently clinically available as well as newly developed antibiotics. One of the key requirements for preserving clinical efficacy of antibiotics and avoiding tolerance development is to identify the optimum dosing schedule for maximum bacterial kill and minimal emergence of resistance [2]. Although standard PK/PD indices have been used for this purpose with some clinical success, this approach is associated with several drawbacks. One of them is the high dependence upon the minimum inhibitory concentration (MIC), which is limited to a single efficacy endpoint that does not take into account the entire time course of effect and may vary between treated individuals and bacterial strains [3].

Translational PK/PD modeling and simulation has emerged as an alternative strategy to characterize the relationship between dose, exposure and response for identifying the most suitable dosing regimen. For example, infections with Mycobacterium tuberculosis are usually characterized by the presence of both multiplying and non-multiplying bacteria, and most antibiotics are usually more effective in killing multiplying rather than non-multiplying microorganisms. Mechanistic PK/PD models have successfully been applied to delineate the independent drug effects associated with killing of the multiplying and the non-multiplying bacterial populations [4]. In another example, different dosing regimens with similar exposure to colistin resulted in greater emergence of resistance with longer dosing intervals. Based on this observation, PK/PD models have subsequently been used for simulating untested dosing scenarios and developing an optimum dosing regimen for colistin [5].

It is the purpose of this review to provide an overview on the mechanism-based PK/PD models applied in translational PK/PD modelling for antibiotics.

PK/PD indices

For decades, the PK/PD relationships of antibiotics have been categorized with three different PK/PD indices, which rely on a summary measurement of in vivo drug exposure relative to the MIC, determined in vitro using serial dilution steps [6]. Usually, only free rather than total drug concentrations are considered as only free drug which is not bound to plasma proteins exerts the pharmacological activity. Standardized notations for these PK/PD indices are AUC/MIC, C_max/MIC and T>MIC. AUC/MIC is the ratio of area under the free plasma concentration-time curve relative to MIC, C_max/MIC is the ratio of free peak plasma concentration relative to MIC, and T>MIC is the cumulative percentage of a time period that the free concentration is above MIC. Antibiotics that are classified as having their efficacy driven by T>MIC show time-dependent killing which suggests that the antibacterial effect is at its maximum with concentrations just above the MIC and no further improvement in killing is obtained by further increasing the concentrations. C_max/MIC best describes antibiotics which follow concentration-dependent killing and require maximum peak antibiotic concentration for maximum efficacy, whereas AUC/MIC is representative of the antibiotics which elicit both time- and concentration-dependent killing [3]. Although the MIC based approach has been widely used by clinicians for designing dosing regimens and can be useful to predict the effect of dose fractionation on antibacterial activity, this approach is associated with several limitations.

PK/PD indices rely heavily on MIC. Measurement of MIC is associated with substantial uncertainty and variability because of the two-fold dilution technique used for its assessment and the interpretation as implied binary response, which considers efficacy only above MIC and no killing below MIC. Furthermore, MIC varies across patient populations and bacterial strains, and may change with time in the same patient [7]. Thus, MIC-based approaches ignore the dynamics of bacterial killing with time. It is typically assumed that a PK/PD index determined in a preclinical species or population can be extrapolated to another patient population. However, PK/PD indices have been found to vary among different patient populations, species, and disease conditions, and one of the reasons is associated with differences in the pharmacokinetics of the antibiotic in these groups [8,9]. For example, in case of β-lactam antibiotics, the PK/PD index has been observed to change from T>MIC to AUC/MIC as the half-life increases in renally impaired patients. Similarly, decreases in half-life will shift the PK/PD index from AUC/MIC to T>MIC [10]. Thus, the value for PK/PD indices as guiding tool for dosage regimen design seems questionable.

One approach to overcome these drawbacks is the use of mechanism-based PK/PD modeling. Rather than relying on point estimates that integrate PK and PD factors of the host, the drug and the microorganism into one index, a mechanism-based PK/PD model has sufficient granularity to allow adjustment to changes in one of several of the PK and PD parameters as needed by changing clinical situations. In addition, PK/PD models reflect the graduate killing effect on bacteria with changing drug exposure rather than dichotomous all-or-nothing effects as implied by MIC values. Finally, PK/PD models consider the time-courses of bacterial growth and killing in relation to time courses of drug concentrations rather than time-integrated measures as used for the indices. Overall, these advantages allow for a more flexible, realistic and dynamic interplay of drug, host and microorganism-related factors that are ultimately predictive of bacterial killing and therapeutic efficacy.

Mechanism based PK/PD modeling

Mechanism based PK/PD models take into consideration the time course of bacterial count based on in vitro, in vivo and clinical information. These models are composed of three basic components: (i) a component that describes the bacterial growth kinetics, (ii) a component that describes the pharmacokinetics of the drug, and (iii) a component that integrates the effect of the drug concentration on bacterial turnover.

Bacterial Growth Kinetics

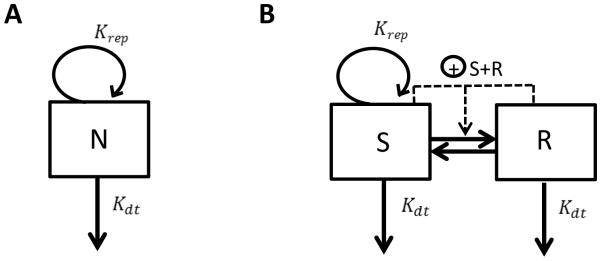
The simplest model component used for describing the bacterial growth kinetics consists of a single bacterial compartment with a first-order rate constant for bacterial replication (K_rep) and a first order rate constant for death of the bacteria (K_dt). Eq. 1 and Fig. 1A describe the mono-exponential increase in microbial number seen in the absence of drug treatment [11], where N is the number of bacteria.

Figure 1.

Models for bacterial growth kinetics: A) One cell population model, B) Two cell population model with different cell growth status. N Number of bacteria; K_rep, first-order replication rate constant; K_dt, first-order death rate constant; S, Number of bacteria in growing state; R, Number of bacteria in resting state.

$$\frac{\mathit{dN}}{\mathit{dt}}={\mathit{K}}_{\mathit{rep}}\times \mathit{N}-{\mathit{K}}_{\mathit{dt}}\times \mathit{N}$$ (1)

Quite often only the net process between bacterial growth and kill is quantified, with a first-order rate constant K_growth = K_rep − K_dt, also called K_net, since it is difficult to separately estimate both the replication and death rate constants with limited data [12]. The underlying assumption of this model is that the microbial population is homogenous having the same turnover rate constants, which is an oversimplification of the real scenario as microbial populations are usually known to be heterogeneous with multiple subpopulations with distinct metabolic states and drug resistance profiles [7].

In the absence of antibiotics, the bacterial number N eventually approaches a maximum N_max when limitation in nutrients and bacterial density limit further growth. In this steady-state condition there is no net change in the microbial population. There are three ways to describe these capacity limited growth curves:

• a) Using a logistic growth function [13,14]:

  $$\frac{\mathit{dN}}{\mathit{dt}}={\mathit{K}}_{\mathit{growth}}\times \left(1-\frac{\mathit{N}}{{\mathit{N}}_{\mathit{max}}}\right)\times \mathit{N}$$ (2)
• b) Using a saturable, non-linear function [15]:

  $$\frac{\mathit{dN}}{\mathit{dt}}=\left(\frac{{\mathit{VG}}_{\mathit{max}}}{{\mathit{N}}_{50}+\mathit{N}}\right)\times \mathit{N}$$ (3)

  where VG_max is the bacterial maximum growth in bacterial count per time, and N₅₀ is N at which the bacterial growth is half-maximal.

• c) Using a model where transformation from the growing (S) to the resting stage (R) occurs when the total microbial count approaches the stationary phase [16] (Fig. 1B).

  $$\frac{\mathit{dS}}{\mathit{dt}}=={\mathit{K}}_{\mathit{rep}}\times \mathit{S}-{\mathit{K}}_{\mathit{dt}}\times \mathit{S}-({\mathit{K}}_{\mathit{rep}}-{\mathit{K}}_{\mathit{dt}})\times \left(\frac{\mathit{S}+\mathit{R}}{{\mathit{N}}_{\mathit{max}}}\right)\times \mathit{S}+{\mathit{K}}_{\mathit{rs}}\times \mathit{R}$$ (4)
  $$\begin{gathered} \frac{\mathit{dR}}{\mathit{dt}}=({\mathit{K}}_{\mathit{rep}}-{\mathit{K}}_{\mathit{dt}})\times \left(\frac{\mathit{S}+\mathit{R}}{{\mathit{N}}_{\mathit{max}}}\right) \\ \times \mathit{S}-{\mathit{K}}_{\mathit{rs}}\times \mathit{R}-{\mathit{K}}_{\mathit{dt}}\times \mathit{R} \end{gathered}$$ (5)

  where S and R are the number of growing and resting bacteria, respectively. A high total bacterial load is assumed to potentiate the transformation from S to R. The transfer back to the growing stage (K_rs) is usually assumed to be negligible during in vitro time-kill experiments and therefore in those cases fixed to 0.

In some instances, additional delay functions have been introduced to characterize the growth delay observed during the first hours after the initiation of growth experiments when the microbes have not yet reached the logarithmic growth phase. For example, inverse mono-exponential functions with asymptotic increase such as 1 − e^−δ×t have been used as multiplier for K_rep or K_growth, where δ is a first-order rate constant characterizing the dissipation of the delay [17,18].

Pharmacokinetics

The pharmacokinetic model component is used for characterizing the concentration profile of a drug over a time period. Traditional compartmental modeling approaches are generally used to describe the pharmacokinetics with one- or multi-compartment systems. For example, in an in vitro chemostat-based PK/PD model system [18], the drug concentration can be described with a one-compartment model with mono-exponential decrease with time according to

$$\frac{\mathit{dC}}{\mathit{dt}}=-{\mathit{K}}_{\mathit{e}}\times \mathit{C}$$ (6)

where C is the concentration of the K_e drug and is the first-order elimination rate constant of the drug.

The pharmacokinetic profile of a new drug is usually established in healthy subjects during the initial clinical phase of drug development. The pharmacokinetics may however be altered under pathophysiologic conditions in a diseased population. For example, drugs which are primarily renally cleared may reach higher systemic exposure in patients with renal impairment compared to healthy individuals. In these cases, creatinine clearance is typically found to be a significant covariate and can be used to guide patient customized dosing [19]. Disease conditions can also cause changes in the body fluids and protein binding which may ultimately affect tissue distribution and the free fraction of the drug [20], and may thus need to be considered in the pharmacokinetic model component of mechanism based PK/PD models.

Many microbial infections are localized in extravascular tissues rather than blood or plasma [21]. The concentration at the site of infection may in these cases be different from plasma concentrations due to drug distribution processes and may thereby complicate the accurate assessment of optimal dosing regimens [22]. For example, concentration-time profiles of antibiotics in epithelial lining fluid in the lungs was found to be different from plasma with concentration ratios ranging from <0.1 to 3 [23]. In addition to efficacy, organ or tissue concentrations may also be of interest with regard to toxicity [24]. Techniques like microdialysis have been used for measurement of drug concentrations in tissue/organs [25]. Tissue distribution of antibiotics may be predicted using physiologically-based pharmacokinetic (PBPK) modelling [26,27]. Recently, a PBPK model incorporating a multi-compartment permeability-limited lung model was used to simulate the pharmacokinetics of anti-tuberculosis agents in plasma, lungs and its sub-compartments where the mycobacteria reside in the host [28]. This model also provides a framework for predicting the lung concentrations of novel anti-tuberculosis agents.

Pharmacodynamics

The drug effect E can be modeled to either inhibit bacterial replication or potentiate bacterial killing. The relationship between drug concentration and its antimicrobial effect is usually described using an ordinary (γ = 1) or a sigmoidal (γ≠1) inhibitory E_max model. The general expression for the bacterial growth kinetics is then modified to Eq. 7:

$$\frac{\mathit{dN}}{\mathit{dt}}={\mathit{E}}_{\mathit{rep}}\times {\mathit{K}}_{\mathit{rep}}\times \mathit{N}-{\mathit{E}}_{\mathit{dt}}\times {\mathit{K}}_{\mathit{dt}}\times \mathit{N}$$ (7)

Drug effect decreasing the replication rate can then be modeled as

$${\mathit{E}}_{\mathit{rep}}=1-\frac{{\mathit{I}}_{\mathit{max}}\times {\mathit{C}}^{{\gamma }^1}}{{\mathit{IC}}_{50}^{{\gamma }^1}+{\mathit{C}}^{{\gamma }^1}}$$ (8)

Drug effect increasing the death rate can be modeled as

$${\mathit{E}}_{\mathit{dt}}=1+\frac{{\mathit{E}}_{\mathit{max}}\times {\mathit{C}}^{{\gamma }^2}}{{\mathit{EC}}_{50}^{{\gamma }^2}+\mathit{C}{\gamma }^2}$$ (9)

Here E_max and I_max represent the maximum increase or decrease in effect, EC₅₀ and IC₅₀ represent the concentrations of drug that produce half of E_max and I_max , and γ₁ and γ₂ are the sigmoidicity coefficients. In Eq. 8 and 9, the effect corresponds to a unitless fractional change in the rate constant with E_max and I_max representing the maximum achievable fractional change.

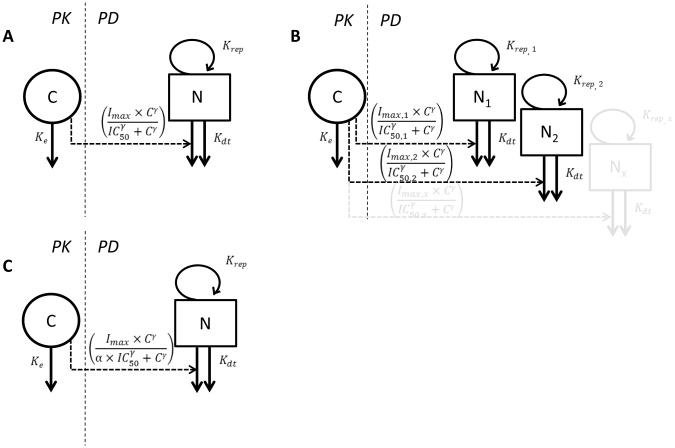
Alternatively to these proportional effect models, the increase in the death rate can also be modeled as an additive effect (Fig. 2A):

$$\frac{\mathit{dN}}{\mathit{dt}}={\mathit{K}}_{\mathit{rep}}\times \mathit{N}-{\mathit{K}}_{\mathit{dt}}\times \mathit{N}-\frac{{\mathit{I}}_{\mathit{max}}\times {\mathit{C}}^{\gamma }}{{\mathit{IC}}_{50}^{\gamma }+{\mathit{C}}^{\gamma }}\times \mathit{N}$$ (10)

In Eq. 10, the effect corresponds to an additional kill-rate constant contributed by the drug with I_max representing the maximum achievable drug-imposed kill-rate constant having the unit 1/time.

Figure 2.

PK/PD models consisting of PK component, bacterial growth model, and PD link: A) One bacterial population with additive effect on death rate. B) Subpopulation approach for antibiotic resistance with two or more bacterial populations each having different drug sensitivity. C ) Adaptation approach for drug resistance with adaptation factor modulating drug sensitivity.

C, drug concentration; N/N₁/N₂/N_x, number of bacteria in different bacterial populations; K_e, first order drug elimination rate constant; K_rep, first-order replication rate constant; K_dt, first-order death rate constant; I_max, maximum achievable effect (subscripts indicate different values for different bacterial populations); IC₅₀, drug concentration producing 50% of I_max (subscripts indicate different values for different bacterial populations); γ, is the sigmoidicity factor; α, adaptation factor.

Combination Therapy

Combination therapy of antibiotics has been found to be useful as it may improve efficacy, increase patient compliance by optimizing dosing schedules, reduce toxicity, and suppress the emergence of resistance [29]. There is high potential for pharmacodynamic drug-drug interactions when antibiotics of a combination therapy act on the same or different molecular targets (serial or parallel) in the same pathogen, resulting in additive, synergistic or antagonistic interaction [30]. The concentration-effect relationship for two-drug combinations results in a three dimensional response surface which is usually characterized quantitatively using the response surface analysis as described by Eq. 11 [31,32]:

$$1=\frac{{\mathit{C}}_1}{{\mathit{IC}}_{50,1}\times {\left(\frac{\mathit{I}}{{\mathit{I}}_{\mathit{max}}-\mathit{I}}\right)}^{\frac{1}{{\gamma }_1}}}+\frac{{\mathit{C}}_2}{{\mathit{IC}}_{50,2}\times {\left(\frac{\mathit{I}}{{\mathit{I}}_{\mathit{max}}-\mathit{I}}\right)}^{\frac{1}{{\gamma }_2}}}+\frac{\omega \times {\mathit{C}}_1\times {\mathit{C}}_2}{{\mathit{IC}}_{50,1}\times {\mathit{IC}}_{50,2}\times {\left(\frac{\mathit{I}}{{\mathit{I}}_{\mathit{max}}-\mathit{I}}\right)}^{\frac{1}{2{\gamma }_1}+\frac{1}{2{\gamma }_2}}}$$ (11)

where C₁ and C₂ are the concentrations of drug 1 and drug 2 in the combination therapy; IC_50,1 is the concentration for which the effect is half maximal for drug 1 when present alone; IC_50,2 is the concentration for which the effect is half maximal for drug 2 when present alone; γ₁ and γ₂ are the sigmoidicity coefficients for drug 1 and drug 2, respectively; I_max is the maximum bacterial killing rate constant; ω is the interaction parameter; and I is the killing rate constant resulting from the combination therapy. The summation of the first and second term on the right side of the equation defines the additive effect whereas the third term is the drug interaction term. The combination effect is additive when ω = 0, is synergistic when ω >> 0, and is antagonistic when ω << 0.

The kinetics of bacterial killing for the combination therapy can then be described using Eq. 12 with modification of the drug effect term by taking a similar approach as described above for the response surface analysis [33].

$$\begin{gathered} \frac{\mathit{dN}}{\mathit{dt}}={\mathit{K}}_{\mathit{rep}}\times \mathit{N}-{\mathit{K}}_{\mathit{dt}}\times \mathit{N} \\ -\left(\frac{{\mathit{I}}_{\mathit{max}}\times {\left(\frac{{\mathit{C}}_1}{{\mathit{IC}}_{50,1}}+\frac{{\mathit{C}}_2}{{\mathit{IC}}_{50,2}}+\omega \times \frac{{\mathit{C}}_1\times {\mathit{C}}_2}{{\mathit{IC}}_{50,1}\times {\mathit{IC}}_{50,2}}\right)}^{\gamma }}{1+{\left(\frac{{\mathit{C}}_1}{{\mathit{IC}}_{50,1}}+\frac{{\mathit{C}}_2}{{\mathit{IC}}_{50,2}}+\omega \times \frac{{\mathit{C}}_1\times {\mathit{C}}_2}{{\mathit{IC}}_{50,1}\times {\mathit{IC}}_{50,2}}\right)}^{\gamma }}\right)\times \mathit{N} \end{gathered}$$ (12)

ω is the interaction parameter; and γ is the sigmoidicity coefficient for the combination therapy, under the assumption that in the response surface analysis, γ₁ = γ₂.

Antibiotic resistance

Antibiotic resistance can be mathematically explained either by an increase in IC₅₀ or decrease in I_max. Prior knowledge about the mechanism of resistance can be used as a rationale for choosing the appropriate model. When reduced drug sensitivity can completely be overcome with a higher dose, an increase in IC₅₀ is suggested as the probable mechanism for resistance. If even high doses are unable to achieve the maximum effect, however, then a decrease in I_max might be the more appropriate mechanism [12].

A variety of PK/PD models have been proposed for describing antibiotic resistance. These models can be broadly categorized into subpopulation approaches and adaptation approaches.

Subpopulation Approaches

The more commonly used subpopulation approaches assume that the total bacterial population is composed of several discrete subpopulations with different drug susceptibility as shown in Fig. 2B. These subpopulations are considered to be present even in the initial inoculum. Subsequent treatment with antibiotic leads to predominant killing of susceptible subpopulations along with selective replication of the less susceptible subpopulations resulting overall in regrowth. More than one differential equation is used simultaneously with each equation representing one bacterial subpopulation (often with different drug susceptibilities) [34]. A variation of the subpopulation model is one in which new drug resistant mutants are formed from the growing subpopulation with a first-order mutation rate during the experiment resulting in regrowth [35].

A modification of the sub-population approach could potentially be used to facilitate development of new generation anti-infectives which do not necessarily kill the bacteria. For example, Bezlotoxumab, a fully human monoclonal antibody, was found to decrease the rate of recurrence of Clostridium difficile infection in patients treated with standard-of-care antibiotics [36]. Bezlotoxumab acts by neutralizing the exotoxin B thereby averting its interaction with colonic cells and the associated inflammation. One of the possible approaches to characterize the PK/PD in this scenario could be a modified subpopulation model where the Bezlotoxumab induced toxin neutralization is modeled in parallel with the killing effect imposed by the standard-of-care treatment on the susceptible Clostridium difficile population.

Adaptation Approaches

An alternative to the subpopulation model in which the total bacteria are assumed to be a mixture of different populations is the adaptive resistance mechanism in which the initial drug susceptible population is gradually considered to evolve into a drug resistant population as shown in Fig. 2C. Only one differential equation is used to describe the rate of change of the total bacterial population. An adaptation factor (α) is introduced which may be dependent on time and concentration:

$$\alpha =1+\beta \times (1-{\mathit{e}}^{\mathit{C}\times \mathit{t}\times \tau })$$ (13)

where β describes the maximum adaptation factor and τ represents the rate of adaptation. Dependent on how the adaptation function is implemented in the PK/PD model, a gradual increase in time and concentration may result in an increase in IC₅₀, decrease in I_max, or decrease in bacterial replication rate [37].

Identification of the true resistance mechanism based only on total bacterial counts and statistical modelling criteria have failed in majority of cases. Quantification of resistant populations will help in distinguishing between competing models and support the selection of the most appropriate model for bacterial resistance [38].

Inoculum Effect

The phenomenon that when a higher bacterial density of initial inoculum in an experiment leads to a reduced antibacterial effect is referred to as inoculum effect [39]. Some of the potential mechanisms for this phenomenon are (i) enzymatic inactivation of the drug, (ii) non-specific binding to the bacteria, and (iii) increased likelihood of the preexistence of subpopulations of resistant bacteria if the density of the inoculum is higher than the natural mutation rate of the bacteria. For example, the pharmacodynamic effect of ceftazidime, a β-lactam antibiotic, changed from time-dependent killing to concentration-dependent killing when inoculum density was increased [40]. This conversion in the PK/PD-index has been linked to the distribution and accumulation of β-lactamase in the biofilm of high density inocula which can hydrolyze β-lactam antibiotics.

Bacterial burden shows a wide variation in patients and therefore a PK/PD model which incorporates an inoculum effect might be more predictive in clinical scenarios. One of the models proposed to describe inoculum effects is based on the concept of quorum sensing. It assumes that all bacteria release signal molecules to communicate with each other which consequently results in reduced drug sensitivity [41].

Host Responses

In vivo models of bacterial infection are oftentimes established in immuno-compromised animals as they allow for proper estimation of antibiotic efficacy without any interference from the immune system. In many cases, the PK/PD indices needed to be achieved for efficacy in these models are higher compared to those obtained in immuno-competent animals [42]. In vivo infection models in animals with functional immune system, although less common, have also been used for assessing the efficacy of antibiotics. As the immune system of immunocompetent animals has the ability to kill bacteria, it is important to study the time course of this effect independently from antibiotic therapy in order to be able to delineate the intrinsic activity of the drug from that of the immune system.

The immune system effect can be assessed by three different approaches:

• a) Modulation of bacterial challenge: In this approach inocula with different initial density were used in the same type of animal infection model to quantify the antimicrobial effect associated with the immune system [43]. The immune system was successful in reducing the bacterial load when the initial inoculum was low; at higher initial inocula, however, the immune system’s capacity was overwhelmed resulting in net bacterial growth. This impact of immune system has been described quantitatively using mathematical models where the rate of change in bacterial count is equal to the difference between the growth rate of bacteria and the kill rate contributed by the antibacterial effect of the immune system [43]:

  $$\begin{gathered} \frac{\mathit{dN}}{\mathit{dt}}={\mathit{K}}_{\mathit{growth}}\times \left(1-\frac{\mathit{N}}{{\mathit{N}}_{\mathit{max}}}\right) \\ \times \mathit{N}-\left(\frac{{\mathit{K}}_{\mathit{tr}}\times \mathit{N}}{{\mathit{N}}_{50}+\mathit{N}}\right)\times \mathit{N} \end{gathered}$$ (14)

  Here, K_ir is the maximal kill rate induced by the immune system and N₅₀ is the number of bacteria per g of tissue at which the immune-system mediated kill rate is half-maximal.
• b) Modulation of immune reactivity: An alternative strategy to quantify the contribution of the immune system towards bacterial reduction is to use animal infection models with different levels of immunosuppression [44]. A pneumonia mouse model with functional immune system was treated with different escalating doses of the immunosuppressant cyclophosphamide, thereby reducing the neutrophil counts by 20, 70 and 90%, respectively. The rate of change in the bacterial count was equal to the difference between the first order growth rate of bacteria and the saturable kill rate attributed to the number of available neutrophils:

  $$\begin{gathered} \frac{\mathit{dN}}{\mathit{dt}}={\mathit{K}}_{\mathit{growth}}\times \left(1-\frac{\mathit{N}}{{\mathit{N}}_{\mathit{max}}}\right) \\ \times \mathit{N}-\left(\frac{{\mathit{K}}_{\mathit{tr}}\times \mathit{ANC}}{{\mathit{ANC}}_{50}+\mathit{ANC}}\right)\times \mathit{N} \end{gathered}$$ (15)

  ANC is the absolute neutrophil count and ANC₅₀ is the ANC required to achieve 50% of maximal kill rate.
• c) Natural progression of disease: The effect of the immune system can also be included as a time-dependent first-order kill rate, in addition to the natural death rate as described by Eq.16, for example when immunocompetent animals are treated with vehicle control and establish adaptive immunity over time. This assessment may result in a slight overestimation of the impact of the immune system, however, if comparative data in immunocompetent and immune-compromised animals are not available to delineate the real immune system effect from natural bacterial death:

  $$\begin{gathered} \frac{\mathit{dN}}{\mathit{dt}}={\mathit{K}}_{\mathit{rep}}\times \left(1-\frac{\mathit{N}}{{\mathit{N}}_{\mathit{max}}}\right) \\ \times \mathit{N}-\left(\frac{{\mathit{K}}_{\mathit{ir}}\times {\mathit{t}}^{\gamma }}{{{\mathit{t}}_{50}}^{\gamma }+{\mathit{t}}^{\gamma }}\mathit{t}\right)\times \mathit{N}-{\mathit{K}}_{\mathit{dt}}\times \mathit{N} \end{gathered}$$ (16)

  Here K_ir is the maximum death rate constant induced by the immune system, t is the time, t₅₀ is the time when the death rate constant is half of its maximum value, and γ is the sigmoidicity factor that determines the shape of the curve. The effect of the immune system is thus modeled as a gradual, time-dependent increase of the death rate constant until it reaches its maximum K_ir.

Bench to Bedside Translation of PK/PD Models for Anti-Infectives

The current paradigm for translation of antibacterial PK/PD from preclinical species to humans requires integration of the PK/PD index determined in animal models with human pharmacokinetics [45]. Stochastic simulation of human drug exposure using population pharmacokinetic models generates concentration-time profiles which are then used to compute the PK/PD index for each simulated subject. Based on the proportion of subjects with the desired value of the PK/PD index, probability of attaining the therapeutic target is predicted. This approach helps in making decisions regarding the choice of dosing regimens to be implemented in the clinic.

The use of mechanistic PK/PD models for translation from preclinical to clinical scenarios has been limited. PK/PD models based on in vitro static and dynamic kill curves have been successful in the prediction of in vivo effects in animal models [8]. However, there is still a knowledge gap regarding translation of PK/PD parameters from preclinical to clinical settings. For example, recently a multistate tuberculosis pharmacometric model describing different bacterial states of Mycobacterium tuberculosis was developed based on in vitro data [4]. For clinical implementation of this model [46], most of the parameters pertaining to the natural bacterial growth were fixed to the in vitro estimates; however the exposure-response parameters related to drug effect had to be estimated from clinical data and were different from the in vitro drug effect parameters. More research efforts are needed in this area to better facilitate the quantitative translation of mechanistic PK/PD models to clinical situations.

Development of a Translational PK/PD model for Antibiotics

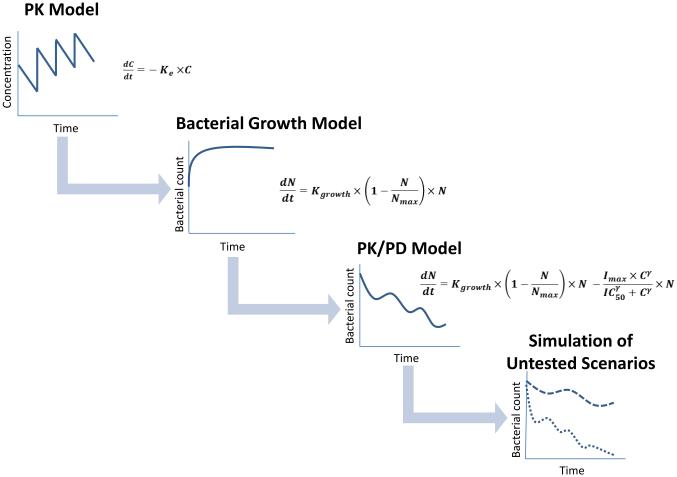
Mechanism-based models for antibiotics are usually established in a stepwise fashion, in which the different model components are individually developed and integrated (Fig. 3). The typical steps include the following:

1. Development of a pharmacokinetic model in the studied population (animal models or humans), that captures the time course of free, pharmacologically active concentrations of the antibiotic, preferably in the relevant target tissue.

2. Development of a bacterial growth model that captures the bacterial growth kinetics and potential host response effects.

3. Integration of the bacterial growth model and the pharmacokinetic model component into a PK/PD model with a pharmacodynamic model component that links the dynamics of drug concentrations to bacterial turnover. This may include drug combination models, inocula effects, and resistance development.

Figure 3.

Steps involved in the development and application of a translational PK/PD model for antibiotics.

Once the model has been established, it can be used for simulations to interpolate and extrapolate the observed experimental data to other, untested scenarios, such as different dosing regimens, or different patient populations [3,47]. It can also be used for quantitative comparisons of multiple drug candidates to identify lead candidates and support go-no go decisions [7].

Conclusions

Mechanism-based PK/PD models are increasingly been used in developing dosing strategies for antibiotics in drug development and clinical application. Although these models are simplified depictions of rather complex interactions of drug, microbe and host physiologic processes, they are able to capture the time course and magnitude of antibacterial effect in relation to bacterial growth, the pharmacokinetic and pharmacodynamic properties of the drug, and the chosen dosing regimen. Complicating factors such as resistance development, combination therapy, or host responses can be incorporated in the modeling approach. In situations where only limited data are available, system specific parameters describing for example growth characteristics may also be implemented based on prior knowledge [4]. With these tools at hand, translational PK/PD modelling and simulation may play a pivotal role in identifying the right balance between bacterial killing, adverse effects, and appearance of resistance, and may help identifying and optimizing dosing regimens for novel and established antibacterial agents.