Bayesian Nonparametric Estimation for Dynamic Treatment Regimes with Sequential Transition Times

Abstract

We analyze a dataset arising from a clinical trial involving multi-stage chemotherapy regimes for acute leukemia. The trial design was a 2 × 2 factorial for frontline therapies only. Motivated by the idea that subsequent salvage treatments affect survival time, we model therapy as a dynamic treatment regime (DTR), that is, an alternating sequence of adaptive treatments or other actions and transition times between disease states. These sequences may vary substantially between patients, depending on how the regime plays out. To evaluate the regimes, mean overall survival time is expressed as a weighted average of the means of all possible sums of successive transitions times. We assume a Bayesian nonparametric survival regression model for each transition time, with a dependent Dirichlet process prior and Gaussian process base measure (DDP-GP). Posterior simulation is implemented by Markov chain Monte Carlo (MCMC) sampling. We provide general guidelines for constructing a prior using empirical Bayes methods. The proposed approach is compared with inverse probability of treatment weighting, including a doubly robust augmented version of this approach, for both single-stage and multi-stage regimes with treatment assignment depending on baseline covariates. The simulations show that the proposed nonparametric Bayesian approach can substantially improve inference compared to existing methods. An R program for implementing the DDP-GP-based Bayesian nonparametric analysis is freely available at https://www.ma.utexas.edu/users/yxu/.

1 Introduction

We analyze a dataset arising from a clinical trial involving multi-stage chemotherapy regimes for acute leukemia. The trial design was a 2×2 factorial for frontline therapies only. However, motivated by the idea that subsequent salvage therapies affect survival time, Wahed and Thall (2013) modeled and analyzed treatments in the trial as a dynamic treatment regime (DTR), that is, an alternating sequence of treatments or other actions and transition times between disease states. We propose a Bayesian nonparametric (BNP) approach for evaluating such DTRs in which the outcome at each stage is a random transition time between two disease states. The final overall survival (OS) time outcome of primary interest is the sum, T, of a sequence of transition times. The actually observed sequence is determined by the way that a patient’s treatment regime plays out, and the mean of T may be expressed as an appropriately weighted average over all possible sequences of event times. Our proposed BNP methodology for estimating the mean of T is based on the idea of Robins’ G-computation (Robins, 1986, 1987).

An algorithm commonly used by oncologists in chemotherapy of solid tumors is to choose the patient’s initial (frontline) treatment based on his/her baseline covariates, continue as long as the patient’s disease is stable, switch to a different chemotherapy (salvage) if progressive disease (P) occurs, stop chemotherapy if the tumor is brought into complete or partial remission (C), and begin salvage if P occurs at some time after C. There are many elaborations of this in oncology, including multiple attempts at salvage therapy, use of consolidation therapy for patients in remission, suspension of therapy if severe toxicity is observed, or inclusion of radiation therapy or surgery in the regime. Another important application of this general adaptive structure occurs in treatment regimes for psychological disorders or drug addiction. For example, in treatment of schizophrenia one may replace P by a psychotic episode or other worsening of the subject’s psychological status, C by a specified improvement in mental status, and death by a psychological breakdown severe enough to require hospitalization.

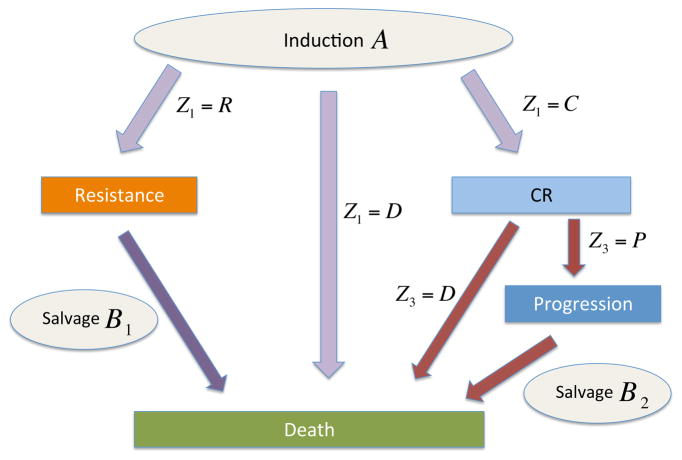
Denote the action at stage ℓ of the DTR by Z^ℓ, which may be a treatment or a decision to delay or terminate therapy. Here, stage refers to the decision point in the DTR – that is, the choice of frontline and possible salvage therapies. At each stage one observes a disease state s_ℓ, such as P, C or death (D). Let T^(j,r) denote the transition time from disease state j to state r, with j = 0 the patient’s initial disease status. See Figure 1 for an example (details of which will be provided later) with up to n_stage = 3 stages, n_state = 4 disease states, and a total of n_T = 7 different transition times. Because the actions are adaptive, the actual number of stages and observed transition times vary between patients depending on how the specific treatment-outcome sequence plays out.

Figure 1.

The scheme

Formally, a DTR is the sequence Z = (Z¹, Z², ⋯), where each Z^ℓ is an adaptive action based on the patient’s history ℋ^ℓ−1 of previous treatments and transition times, and ℋ⁰ is the patient’s baseline covariate vector. One possible treatment-outcome sequence is (ℋ⁰, Z¹, T ^(0,C), Z², T ^(C,D)), in which the initial chemotherapy Z¹ was chosen based on ℋ⁰, complete remission (C) was achieved, Z² was chosen based on ℋ¹ = (ℋ⁰, Z¹, T^(0,C)). In this case, Z² would be consolidation therapy given to keep the patients in remission, that is, prevent relapse, although consolidation treatments were not included in the dataset that we will analyze. OS time is T = T^(0,C) + T^(C,D). In this case, s₁ = C and s₂ = D. Similarly, a patient brought into remission who later suffers progressive disease has sequence (ℋ⁰, Z¹, T^(0,C), T^(C,P), Z², T^(P,D)) and T = T^(0,C) +T^(C,P) +T^(P,D). We will apply BNP methods to estimate the conditional distributions of the transition times given the most recent histories, with the goal to estimate the mean of T for each possible DTR. This also will include estimates given specific baseline covariates, for so called “individualized” therapy. Key elements of our proposed approach are quantification of all sources of uncertainty and prediction of T under a reasonable set of viable counterfactual DTRs (Wang et al., 2012). BNP methods have been used in estimating regime effects by Hill (2011) and Karabatsos and Walker (2012). Hill (2011) focused on modeling outcomes flexibly using Bayesian additive regression trees (BART), which required less assumptions in model fitting. However, the uncertainty of BART increases dramatically when there is complete treatment-subgroup confounding, and hence limited empirical counterfactuals, which often occurs in causal inference. Karabatsos and Walker (2012) proposed a nonparametric mixture model with a stick-breaking prior for the probability of treatment assignment to provide a more accurately estimated propensity score in the inverse probability of treatment weighting (IPTW) method.

Since all elements of a DTR may affect T, the clinically relevant problem is optimizing the entire regime, rather than the treatment at one particular stage. Most clinical trials or data analyses attempt to reduce variability by focusing on one stage of the actual DTR, usually frontline or first salvage treatment, or by combining stages in some manner. This often misrepresents actual clinical practice, and consequently conclusions may be very misleading. For example, an aggressive frontline cancer chemotherapy may maximize the probability of C, but it may cause so much immunologic damage that any salvage treatment given after rapid relapse, i.e. short T^(C,P), may be unlikely to achieve a second remission. In contrast, a milder induction treatment may be suboptimal to eradicate the tumor, but it may debulk the tumor sufficiently to facilitate surgical resection. Such synergies may have profound implications for clinical practice, especially because effects of multi-stage treatment regimes often are not obvious and may seem counter-intuitive. Physicians who have not been provided with an evaluation of the composite effects of entire regimes on the final outcome may unknowingly set patients on pathways that include only inferior regimes.

A major practical advantage of BNP models is that they often provide better fits to complicated data structures than can be obtained using parametric model-based methods. In the case study that we analyze here, leukemia patients were randomized among initial chemotherapy treatments but not among later salvage therapies, and the BNP model provides a good fit for each transition time distribution conditional on previous history. Failure to randomize patients in treatment stages after the first is typical in clinical trials, most of which ignore all but the first stage of therapy. In contrast, sequential multi-arm randomized treatment (SMART) designs, wherein patients are re-randomized at stages after the first, have been used in oncology trials (Thall et al., 2000, 2007a,b; Wang et al., 2012), and are being used increasingly in trials to study multi-stage adaptive regimes for behavioral or psychological disorders (Dawson and Lavori, 2004; Murphy et al., 2007a,b; Connolly and Bernstein, 2007).

While re-randomization is desirable, it is not commonly done and inference has to adjust for this lack of randomization. A wide array of methods have been proposed for evaluating DTRs from observational data and longitudinal studies, beginning with the seminal papers by Robins (1986, 1987, 1989, 1997) on G-estimation of structural nested models. Additional references include applications to longitudinal data in AIDS (Hernán et al., 2000), inverse probability of treatment weighted (IPTW) estimation of marginal structural models (Murphy et al., 2001; van der Laan and Petersen, 2007; Robins et al., 2008), augmented IPTW (AIPTW) (Tsiatis, 2007; Zhao et al., 2015), G-estimation for optimal DTRs (Murphy, 2003; Robins, 2004), and a review by Moodie et al. (2007). A variety of methods have been developed to evaluate DTRs from clinical trials (Lavori and Dawson, 2000; Thall et al., 2002; Murphy, 2005; Goldberg and Kosorok, 2012; Zajonc, 2012). For survival analysis, Lunceford et al. (2002) introduced ad hoc estimators for the survival distribution and mean restricted survival time under different treatment policies. These estimators, although consistent, were inefficient and did not exploit information from auxiliary covariates. Wahed and Tsiatis (2006) derived more efficient, easy-to-compute estimators that included auxiliary covariates for the survival distribution and related quantities of DTRs. Their estimators compared DTRs using data from a two-stage randomized trial, in which two options were available for both stages and the second-stage treatment assignments were determined by randomization. However, these estimators must be adapted for more general or more complicated designs that permit various numbers of treatment options at each stage and involve the scenarios where second-stage treatment is not randomized, but rather is determined by the attending physicians.

For settings where the DTR’s final overall time, such as survival time, is the sum of a sequence of transition times, our proposed BNP approach employs a nonparametric survival regression model for each transition time conditional on the most recent history of actions and outcomes. We assume a dependent Dirichlet process prior with Gaussian process base measure (DDP-GP), and summarize a joint posterior by Markov chain Monte Carlo (MCMC) simulation. To address the important issue that Bayesian analyses depend on prior assumptions, we provide guidelines for using empirical Bayes methods to establish prior hyperparameters. Posterior analyses include estimation of posterior mean overall outcome times and credible intervals for each DTR.

The rest of the paper is organized as follows. In Section 2 we review the motivating study, and give a brief review of DTRs in settings with successive transition times in Section 3. We present the DDP-GP model in Section 4. A simulation study of the BNP approach in single-stage and multi-stage regimes, with comparison to frequentist IPTW and AIPTW, is summarized in Section 5. We re-analyze the leukemia trial data in Section 6, and close with brief discussion in Section 7.

2 A Study of Multi-Stage Chemotherapy Regimes for Acute Leukemia

Our case study was a clinical trial conducted at The University of Texas M.D. Anderson Cancer Center to evaluate chemotherapies for acute myelogenous leukemia (AML) or myelo-dysplastic syndrome (MDS). Patients were randomized fairly among four frontline combination chemotherapies for remission induction: fludarabine + cytosine arabinoside (ara-C) plus idarubicin (FAI), FAI + all-trans-retinoic acid (ATRA), FAI + granulocyte colony stimulating factor (GCSF), and FAI + ATRA + GCSF. The goal of induction therapy for AML/MDS was to achieve complete remission (C), a necessary but not sufficient condition for long-term survival. Patients who did not achieve C, or who achieved C but later relapsed, were given salvage treatments as another attempt to achieve C. Following conventional clinical practice, patients were not randomized among salvage therapies, which instead were chosen by the attending physicians based on clinical judgment. Since there were many types of salvage, these are broadly classified into two categories as either containing high dose ara-C (HDAC) or other. This dataset was analyzed initially using conventional methods (Estey et al., 1999), including logistic regression, Kaplan-Meier estimates, and Cox model regression, including comparisons of the induction therapies in terms of OS, that ignored possible effects of salvage therapies.

Figure 1 illustrates the actual possible therapeutic pathways and outcomes of the patients during the trial, which is typical of chemotherapy for AML/MDS. Death might occur (1) during induction therapy, (2) following salvage therapy if the disease was resistant to induction, (3) during C, or (4) following disease progression after C. Wahed and Thall (2013) re-analyzed the data from this trial by accounting for the structure in Figure 1, and identified 16 DTRs including both frontline and salvage therapies. To correct for bias due to the lack of randomization in estimating the mean OS times, they used both IPTW (Robins and Rotnitzky, 1992) and G-computation based on a frequentist likelihood. In the G-computation, for each transition time they first fit accelerated failure time (AFT) regression models using Weibull, exponential, log-logistic or lognormal distributions, and chose the distribution having smallest Bayes information criterion (BIC). They then performed likelihood-based G-computation by first fitting each conditional transition time distribution regressed on patient baseline covariates and previous transition times, and then averaging over the empirical covariate distribution.

Like Wahed and Thall, the primary goal of our analyses of the AML/MDS dataset is to estimate mean OS and determine the optimal regime. We build on their approach by replacing the parametric AFT models for transition times with the DDP-GP model. We also demonstrate the usefulness of the BNP regression model for G-computation in simulation studies of single-stage and multi-stage regimes in which treatment assignments depend on patient covariates.

3 Dynamic Regimes with Stochastic Transition Times

The case study involves more complicated structure than a stylized linear sequential study, as often is assumed in papers on DTRs that focus on basic methodology. We introduce the following notation to accommodate this more complex structure. Denote the set of possible disease states by {0, 1, ⋯, n_state}, with 0 denoting the patient’s initial state before receiving the first treatment. The pairs of states (s_ℓ−1, s_ℓ) for which a transition s_ℓ−1 → s_ℓ is possible at stage ℓ of the patient’s therapy depend on the particular regime. Here s₀ = 0 refers to the patient’s initial state, before start of therapy. We will identify specific states using letters such as P, C, etc., as in the earlier examples, to replace the generic integers. For example, in cancer therapy, s_ℓ−1 → C means that a patient’s disease has responded to treatment, P → D means a patient with progressive disease has died, and of course D → s_ℓ is impossible. We denote the transition time from state s_ℓ−1 to state s_ℓ in stage ℓ of treatment by T^{(s_ℓ−1,s_ℓ)}, for ℓ = 1, ⋯, n_stage, the maximum number of stages in the DTR. In general it might be necessary to add a third index to indicate the stage ℓ when the same transitions are possible in multiple stages. However, in our case study no ambiguity arises by simply writing T^(r,s). To simplify notation for the transition time distributions, we denote the history of all covariates, treatments, and previous transition times through ℓ stages, before observation of T^{(s_ℓ−1,s_ℓ)} but including the stage ℓ action Z^ℓ by x^ℓ = (ℋ^ℓ−1, Z^ℓ) = (x⁰, Z¹, T^(s₀,s₁), ⋯, T^{(s_ℓ−1,s_ℓ)}, Z^ℓ), with x⁰ = ℋ⁰. Thus, a DTR is Z = (Z¹, Z², . . .), a sequence of actions for all possible stages. For example, in the leukemia trial (Figure 1), Z¹ might be FAI+ATRA given as frontline therapy, followed by salvage therapies Z²=salvage with high dose ara-C if the disease is resistant to induction, and Z³= other salvage if the patient first achieves a complete remission (C) but he later suffers progressive disease (P).

In the leukemia trial, the three possible outcomes following induction chemotherapy, C, R, and D, are competing risks. Thus, only one of the transition times, T^(0,C), T^(0,R), or T^(0,D), is observed for each patient. The distribution of s₁ is determined by these three transition times. For example, the probability of C is

$$Pr(s_1=C\mid {\mathit{x}}^0,Z^1)=Pr[T^{(0,C)}<min\{T^{(0,R)},T^{(0,D)}\}\mid {\mathit{x}}^0,Z^1].$$

This could be made explicit by including the states in the notation for x^l. We chose not to do this for notational parsimony.

When no meaning is lost, we will further simplify notation and use a single running index on the transition times, and write T^{(s_ℓ−1,s_ℓ)} as T^k, where k = 1, . . . , n_T is a running index of all possible state transitions. For example, in Figure 1 we have up to n_stage = 3 stages and n_T = 7 possible transitions. Similarly, we will write x^k for the corresponding covariate vector. Our use of a single index to identify stage is a slight abuse of notation since, for example, the actual second stage of therapy might differ depending on the sequence of outcomes. For example, stage 2 treatment Z² of a patient with sequence (x⁰, Z¹, T^(0,R), Z²) is first salvage for resistant disease during induction with Z¹, while stage 3 treatment Z³ of a patient with sequence (x⁰, Z¹, T^(0,C), T^(C,P), Z³) is first salvage for progressive disease after achieving response initially with Z¹. This latter example could be elaborated if, under a different regime, consolidation therapy, Z², were given for patients who enter C, in which case the sequence would be (x⁰, Z¹, T^(0,C), Z², T^(C,P), Z³).

Below, we will develop a general BNP model for all possible conditional distributions p(T^k | x^k). For any transition index k, let ℛ^k denote the risk set, f^k the probability density function and F̄^k the survival function of the transition time, ${\delta }_i^k$ is a censoring indicator with ${\delta }_i^k=1$ if patient i is not censored and ${\delta }_i^k=0$ if censored, and $V_i^k$ the observed time to the next state or censoring for patient i in risk set ℛ^k. For example, in the leukemia trial consider the transition (0, R), corresponding to the single running index k = 1. The risk set is ℛ¹ = ℛ^(0,R) = {1, . . . , n}. Let U_i denote the time from the start of induction to last followup for patient i. Then ${\delta }_i^1=1$ if $T_i^1=min(U_i,T_i^1)$ and the observed time for patient i is $V_i^1=min(T_i^{(0,D)},T_i^{(0,R)},T_i^{(0,C)},U_i)$ since C, R, and D are competing risks. The likelihood for all possible sequences of treatments and transition times through n_T transitions is the product

$$\mathcal{L}=\prod _{k=1}^{n_T}\prod _{i\in {\mathcal{R}}^k}{f}^k{(V_i^k\mid {\mathit{x}}_i^k)}^{{\delta }_i^k}{\overline{F}}^k{(V_i^k\mid {\mathit{x}}_i^k)}^{1-{\delta }_i^k}.$$ (1)

The overall time for any counterfactual sequence of transition times is the sum $T={\sum }_{k=1}^{n_T}{T}^k$. Our goal is to estimate the mean of T for each possible Z. Specific details of the likelihood are given in the Appendix.

4 A Nonparametric Bayesian Model for DTR

4.1 DDP and Gaussian Process Prior

Our motivation for using the BNP model described in this section is that it is highly robust and has full support. To specify the BNP model, we denote Y^k = log(T^k) and write the distribution of [Y^k | x^k] as F^k(· | x^k). For convenience, we will refer to x^k as ‘covariates’. We construct a BNP survival regression model for F^k(· | x^k) by successive elaborations, starting with a model for a discrete random distribution G^k(·). We then use a Gaussian kernel to extend this to a prior for a continuous random distribution F^k(·), and finally endow the kernel means with a regression structure by expressing them as functions of x^k. The latter construction extends F^k to a family {F^k(· | x^k)}, indexed by x^k. The construction of G^k(·) and F^k(·) is outlined briefly below, by way of a brief review of BNP models. In the end we will only use the last model {F^k(· | x^k)}, which we use as a sampling model for Y^k. See, for example, Müller and Mitra (2013) and Müller and Rodriguez (2013) for more extensive reviews of BNP inference. In the following discussion we temporarily drop the superindex ^k.

The Dirichlet process (DP) prior was first proposed by Ferguson et al. (1973) as a probability distribution on a measurable space of probability measures. The DP is indexed by two hyperparameters, a base measure, G₀, and a precision parameter, α > 0. If a random distribution G follows a DP prior, we denote this by G ~ DP (α, G₀). Denoting a beta distribution by Be(a, b), if G ~ DP (α, G₀) then G(A) ~ Be{αG₀(A), α[1 − G₀(A)]} for any measurable set A, and in particular E{G(A)} = G₀(A). Let δ(θ) denote a point mass at θ. Sethuraman (1991) provided a useful representation of the DP as $G={\sum }_{h=0}^{\infty }{w}_h\delta ({\theta }_h)$, where ${\theta }_h\stackrel{\text{i.i.d}}{\sim }{G}_0$, and the weights w_h are generated sequentially from rescaled beta distributions as $w_h/(1-{\sum }_{r=1}^{h-1}{w}_r)~\text{Be}(1,\alpha )$, the so-called “stick-breaking” construction. The discrete nature of G is awkward in many applications. A DP mixture model extends the DP model by replacing each point mass δ(θ_h) with a continuous kernel centered at θ_h. Without loss of generality, we will use a normal kernel. Let N(·; μ, σ) denote a normal kernel with mean μ and standard deviation σ. The DP mixture model assumes

$$G=\sum _{h=0}^{\infty }{w}_{h}N(·;{\theta }_h,\sigma ).$$ (2)

The use and interpretation of (2) is very similar to that of a finite mixture of normal models. In practical applications, the sum in (2) is often truncated at a reasonable finite value. This model is useful for density estimation under i.i.d. sampling from an unknown distribution, and it provides good fits to a wide variety of datasets because a mixture of normals can closely approximate virtually any distribution (Ishwaran and James, 2001).

To include the regression on covariates that we will need for the survival model of each conditional transition time distribution, F^k(· | x^k), we extend the DP mixture to a dependent DP (DDP), which was first proposed by MacEachern (1999). The basic idea of a DDP is to endow each ${\theta }_h^k$ with additional structure that specifies how it varies as a function of covariates x^k. Writing this regression function as ${\theta }_h^k({\mathit{x}}^k)$ for the argument in each summand in (2), and returning to the conditional transition time distributions, we assume that

$$F^k(y\mid {\mathit{x}}^k)=\sum _{h=0}^{\infty }{w}_h^{k}N(y;{\theta }_h^k({\mathit{x}}^k),{\sigma }^k).$$ (3)

This form of the DDP, which includes both the convolution with a normal kernel and functional dependence on covariates, provides a very flexible regression model.

To complete our specification of the DDP, we will assume that the ${\theta }_h^k(·)$’s are independent realizations from a Gaussian process (GP) prior. The GP was first popularized by O’Hagan and Kingman (1978) in Bayesian inference for a random function (unrelated to the use in a DDP prior). For more recent discussions see, for example, Rasmussen and Williams (2006); Neal (1995); Shi et al. (2007). Temporarily suppressing the transition superindex ^k and running index _h in (3), a GP is a stochastic process θ(·) in which (θ(x₁), . . . , θ(x_n)) has a multivariate normal distribution with mean vector (μ(x₁), . . . , μ(x_n)) and (n × n) covariance matrix with (i, j) element C(x_i, x_j) for any set of n ≥ 1 covariate vectors x_i. We denote this by θ(x) ~ GP(μ, C).

We use the GP prior to define the dependence of ${\theta }_h^k({\mathit{x}}^k)$ as a function of x^k by assuming $\{{\theta }_h^k({\mathit{x}}_k)\}~GP({\mu }_h^k,C^k)$, as a function of x_k, for fixed h. That is, there is a separate GP for each term indexed by h in (3). We will refer to the DDP with a convolution using a normal kernel and a GP prior on the normal kernel means as a DDP-GP model. While the mean and covariance processes of the GP can be quite general, in practice, $C^k({\mathit{x}}_i^k,{\mathit{x}}_j^k)$ is often parameterized as a function $C({\mathit{x}}_i^k,{\mathit{x}}_j^k;{\xi }^k)$, where ξ^k is a vector of hyperparameters, and the mean function is indexed similarly by hyperparameters ${\mathit{\beta }}_h^k$ and written as ${\mu }_h^k({\mathit{x}}^k;{\mathit{\beta }}_h^k)$. In the DTR setting, since each covariate vector x^k is a history, its entries can include baseline covariates, transition times, and indicators of previous treatments or actions. To obtain numerically reasonable parameterizations of the GP functions C^k and ${\mu }_h^k$, we standardize numerical-valued covariates such as age. We now have

$$\{{\theta }_h^k({\mathit{x}}^k)\}~\text{GP}({\mu }_h^k(·),C^k(·,·))h=1,2,\dots$$

To specify the form of ${\mu }_h^k$and C^k, let i = 1, 2, ⋯ , index patients, so that ${\mathit{x}}_i^k$ is the history of patient i at transition k, and define the indicator δ_ij = I(i = j) = 1 if i = j and 0 otherwise. We model the mean function ${\mu }_h^k(·)$ as a linear regression, by assuming that

$${\mu }_h^k({\mathit{x}}_i^k;{\mathit{\beta }}_h^k)={\mathit{x}}_i^k{\mathit{\beta }}_h^k.$$ (4)

For patients i and j, we assume that the covariance process takes the form

$$C^k({\mathit{x}}_i^k,{\mathit{x}}_j^k)=exp\{-\sum _{m=1}^{M^k}{(x_{im}^k-x_{jm}^k)}^2\}+{\delta }_{ij}{J}^2,i,j=1,\dots ,n,$$ (5)

where M^k is the number of covariates at transition k and J is the variance on the diagonal reflecting the amount of jitter (Bernardo et al., 1999), which usually takes a small value (e.g, J = 0.1). There are no further hyperparameters ξ^k to index the covariance function. For binary covariates, the quadratic form in (5) reduces to counting the number of binary covariates in which two patients differ. If desired, additional hyperparameters could be introduced in (5) to obtain more flexible covariance functions. However, in practice this form of the covariance matrix yields a strong correlation for observations on patients with very similar x^k, and has been adopted widely (Williams, 1998).

Combining all of these structures, we denote the model for the conditional distribution of the k^th transition time as $F^k~\text{DDP-GP}\{\{{\mu }_h^k\},C^k;{\alpha }^k,\{{\mathit{\beta }}_h^k\},{\sigma }^k\}$, recalling that the weights of the DDP are generated sequentially as $w_h^k/(1-{\sum }_{r=1}^{h-1}{w}_r^k)~\text{Be}(1,{\alpha }^k)$. For later reference we state the full model. For k = 1, . . . , n_T

$$\begin{array}{c}p(y_i^k\mid {\mathit{x}}_i^k,F^k)=F^k(y_i^k\mid {\mathit{x}}_i^k)\\ F^k~\text{DDP-GP}\{\{{\mu }_h^k\},C^k;{\alpha }^k,\{{\mathit{\beta }}_h^k\},{\sigma }^k\}.\end{array}$$ (6)

4.2 Determining Prior Hyperparameters

As priors for ${\mathit{\beta }}_h^k$ in (6) we assume ${\mathit{\beta }}_h^k~N({\mathit{\beta }}_0^k,{\mathrm{\sum }}_0^k)$ for each transition k, h = 1, 2, . . . . For σ^k we assume ${({\sigma }^k)}^{-2}\stackrel{\text{i.i.d.}}{\sim }\text{Ga}({\lambda }_1,{\lambda }_2)$. Finally, ${\alpha }^k\stackrel{\text{i.i.d}.}{\sim }\text{Ga}({\lambda }_3,{\lambda }_4)$.

To apply the DDP-GP model, one must first determine numerical values for the fixed hyperparameters { ${\mathit{\beta }}_0^k,{\mathrm{\sum }}_0^k$, k = 1, 2, ...} and λ = (λ₁, λ₂, λ₃, λ₄). This is a critical step. These numerical hyperparameter values must facilitate posterior computation, and they should not introduce inappropriate information into the prior that would invalidate posterior inferences. With this in mind, the hyperparameters ( ${\mathit{\beta }}_0^k,{\mathrm{\sum }}_0^k$) for the k^th transition time covariate effect distribution may be obtained via empirical Bayes by doing preliminary fits of a lognormal distribution $Y^k=log(T^k)~N({\mathit{x}}^k{\mathit{\beta }}_0^k,{\sigma }_0^k)$ for each transition k. Similarly, we assume a diagonal matrix for ${\mathrm{\sum }}_0^k$ with the diagonal values also obtained from the preliminary fit of the lognormal distribution. Once an empirical estimate of σ^k is obtained, one can tune (λ₁, λ₂) so that the prior mean of σ^k matches the empirical estimate and the variance equals 1 or a suitably large value to ensure a vague prior. Finally, information about α^k typically is not available in practice. We use λ₃ = λ₄ = 1.

This approach works in practice because the parameter ${\mathit{\beta }}_0^k$ specifies the prior mean for the mean function of the GP prior, which in turn formalizes the regression of T^k on the covariates x^k, including treatment selection. The imputed treatment effects hinge on the predictive distribution under that regression. Excessive prior shrinkage could smooth away the treatment effect that is the main focus. The use of an empirical Bayes type prior in the present setting is similar to empirical Bayes priors in hierarchical models. This type of empirical Bayes approach for hyperparameter selection is commonly used when a full prior elicitation is either not possible or is impractical. Inference is not sensitive to values of the hyperparameters λ that determine the priors of σ^k and α^k for two reasons. First, the standard deviation σ^k is the scale of the kernel that is used to smooth the discrete random probability measure generated by the DDP prior. It is important for reporting a smooth fit, that is for display, but it is not critical for the imputed fits in our regression setting. Assuming some regularity of the posterior mean function, smoothing adds only minor corrections. Second, the total mass parameter α^k determines the number of unique clusters formed in the underlying Polya urn. However, because most clusters are small, changing the prior of α^k does not significantly change the posterior predictive values that are the basis for the proposed inference.

The conjugacy of the implied multivariate normal on { ${\theta }_h^k({\mathit{x}}_i^k)$, i = 0, . . . , n} and the normal kernel in (3) greatly simplify computations, since any Markov chain Monte Carlo (MCMC) scheme for DP mixture models can be used. MacEachern and Müller (1998) and Neal (2000) described specific algorithms to implement posterior MCMC simulation in DPM models. Ishwaran and James (2001) developed alternative computational algorithms based on finite DPs, which truncated (2) after a finite number of terms. We provide details of MCMC computations in the online supplement.

4.3 Computing Mean Survival Time

We apply the Bayesian nonparametric DDP-GP model to obtain posterior means and credible intervals of mean survival time for each DTR. In the motivated leukemia trial, recall that the disease states are D (death), R (resistant disease), C (complete remission), and P (progressive disease). In stage ℓ = 1 (induction chemotherapy), the three events D, R, and C are competing risks, so only one can be observed. For the i^th patient, the stage 1 outcome is denoted by s_1i ∈ {D, R, C}, with transition times $T_i^{(0,D)},T_i^{(0,R)}$ or $T_i^{(0,C)}$ (Figure 1). In stage 2, the transition time $T_i^{(R,D)}$ is defined only if (s_1i, s_2i) = (R, D), and similarly for $T_i^{(C,D)}$ and $T_i^{(C,P)}$. Finally, $T_i^{(P,D)}$ is defined if (s_1i, s_2i) = (C, P). We thus define seven counterfactual transition times $T_i^k$, where k indexes the transitions (0, D), (0, R), (0, C), (R, D), (C, D), (C, P) and (P, D). Figure 1 shows a flowchart of the possible outcome pathways. A dynamic treatment regime for this data may be expressed as Z = (Z¹, Z^2,1, Z^2,2) where Z¹ is the induction chemo, Z^2,1 is the salvage therapy given if s_1i = R, and Z^2,2 is the salvage therapy given if s_1i = C and s_2i = P.

Our primary goal is to estimate mean survival time for each DTR Z while accounting for baseline covariates and non-random treatment assignment. Under the DDP-GP model, we denote the mean survival time for a future patient under Z by

$$\eta (\mathit{Z})=E(T\mid \mathit{Z}).$$ (7)

In terms of the seven counterfactual transition times, the survival time for a future patient i = n + 1 is

$$T_i=I(s_{1i}=D)T_i^{(0,D)}+I(s_{1i}=R)(T_i^{(0,R)}+T_i^{(R,D)})+I(s_{1i}=C)\{I(s_{2i}=D)(T_i^{(0,C)}+T_i^{(C,D)})+I(s_{2i}=P)(T_i^{(0,C)}+T_i^{(C,P)}+T_i^{(P,D)})\}.$$ (8)

The expectation of (8) under the DDP-GP model is evaluated by applying the law of total probability, using the same steps as in Wahed and Thall (2013). We first condition on the four possible cases, (s_1i = D), (s_1i = R), (s_1i = C, s_2i = D) and (s_1i = C, s_2i = P), compute the conditional expectation in each case, and then average across the cases. This computation requires evaluating seven expressions for the conditional mean transition times η^k(Z, x^k) = E(T^k | Z, x^k) under F^k(· | x^k), for each k. For example, η^(P,D)(Z¹, Z^2,2, x⁰, T^(0,C), T^(C,P)) is the conditional mean remaining survival time, from P to D, given that C was achieved in stage 1 with frontline therapy Z¹, followed by P and salvage therapy Z^2,2 in stage 2. The DDP-GP models for F^k(· | x^k), k = 1, . . . , n_T = 7 define most of the marginalization for the expectation in η(Z), leaving only conditioning on the baseline covariates ${\mathit{x}}_i^0$. As Wahed and Thall (2013), we use the empirical covariate distribution p̂(x⁰) over the observed patients to define an overall mean survival time (7). Note that the DDP-GP model does not accommodate time-varying covariates. The described evaluation of η(Z) is an application of Robins’ G-computation (Robins, 1986; Robins et al., 2000). The complete expression is given as equation (14) in the Appendix. In the upcoming discussion, we will use η(Z) to evaluate the proposed approach.

5 Simulation Studies

We conducted four simulation studies to evaluate the performance of the proposed DDP-GP model as a tool for estimating the mean of T in survival regression settings. The simulations focused on estimation of survival regression (simulation 1); regime effects in a study with two treatment arms and single-stage regimes (simulation 2); and regime effects in two studies with multi-stage regimes (simulations 3 and 4). For each of the latter three studies, the treatment assignment probabilities depended on patient covariates. That is, we introduced treatment selection bias. In all four simulations, we implemented inference under DDP-GP models. In simulation 1, we used a single survival regression model F(Y_i | x_i) for a patient-specific baseline covariate vector x_i. For simulation 2 we still used a single DDP-GP model F(Y_i | x_i, Z_i), now adding a treatment indicator Z_i to the survival regression model to estimate the causal effect. In simulations 3 and 4, we used independent DDP-GP models $F^k(Y_i^k\mid {\mathit{x}}_i^k)$ for multiple transition times, k = 1, . . . , n_T , similar to the application in our case study. For all four simulation studies, the hyperprior parameters were determined using the empirical Bayes approach described earlier. For all posterior computations, the MCMC algorithm was implemented with an initial burn-in of 2,000 iterations and a total of 5,000 iterations, thinning out in batches of 10. This worked well in all cases, with convergence diagnostics using the R package coda showing no evidence of practical convergence problems. Traceplots and empirical autocorrelation plots (not shown) for the imputed parameters indicated a well mixing Markov chain.

5.1 Fitting a Survival Regression Model

In simulation 1, we considered four scenarios, with n = 50, 100, or 200 observations without censoring or n = 200 with 23% censoring. The details of simulation 1 are presented in Supplement B. Comparing the DDP-GP model with maximum likelihood estimates under the AFT model with Weibull, lognormal and exponential distributions, the estimates under the DDP-GP model reliably recovered the shape of the true survival function and avoided the excessive bias seen with the AFT models.

5.2 Estimating a Treatment Effect in Single-stage Regimes

Simulation 2 was designed to investigate inference under the DDP-GP model for the regime effect in a single-stage treatment setting. The simulated data represent what might be obtained in an observational setting where treatment is chosen by the attending physician based on patient covariates, rather than from a fairly randomized clinical trial. We simulated a binary treatment indicator Z_i ∈ {0=control, 1=experimental} that depended on two continuous covariates, x_i = (L_i, W_i), for n = 100 patients, i = 1, . . . , n. For example, L_i could be a patient’s creatinine to quantify kidney function, and W_i could be body weight. We generated L_i from a mixture of normals, $L_i~\frac{1}{2}N(40,{10}^2)+\frac{1}{2}N(20,{10}^2)$, which could correspond to a subgroup of patients having worse kidney function (higher creatinine level) due to damage from prior chemotherapy. We assumed that $W_i~\text{Unif}(-\sqrt{12},\sqrt{12})$, a uniform with zero mean and unit standard deviation, which could arise from standardizing a uniformly distributed raw variable. We generated the treatment indicators using the modified logistic regression model

$$\begin{gathered} p(Z_i=1\mid L_i,W_i) \\ =\{\begin{array}{ll}0.05\hfill & \text{if}{\{1+exp[-2(L_i-30)/10]\}}^{-1}\le 0.05\hfill \\ 0.95\hfill & \text{if}{\{1+exp[-2(L_i-30)/10]\}}^{-1}\ge 0.95\hfill \\ {\{1+exp[-2(L_i-30)/10]\}}^{-1}\hfill & \text{otherwise},\hfill \end{array} \end{gathered}$$

that is, a logistic regression model with intercept 30 and slope 1/5 truncated at 0.05 and 0.95. This produces a very unbalanced treatment assignment, for example, p(Z_i = 1 | L_i = 40) = 0.88 versus p(Z_i = 1 | L_i = 20) = 0.12. This could arise in a setting where standard therapy (the ‘control’), Z = 0, is known to be nephrotoxic, while it is believed by most of the treating physicians that the experimental therapy, Z_i = 1, is not, so patients with high creatinine are more likely to be given the experimental therapy. In this simulation study, the goal is to estimate the comparative effect on survival of the experimental therapy versus the control. In the two treatment arms, we generated patients’ responses from

$$Y(1)~\frac{1}{2}N(3-0.2L+\sqrt{L}-0.1W,\sigma )+\frac{1}{2}N(2-0.2L+\sqrt{L}-0.1W,\sigma )$$

and

$$Y(0)~N(-0.2L+\sqrt{L}-0.1W,\sigma ),$$

with σ = 0.4. We simulated 1,000 trials. Note that under the simulation truth the treatment effect, E[Y(1) − Y(0) | x = (L, W)] = 2.5, is constant across L, W.

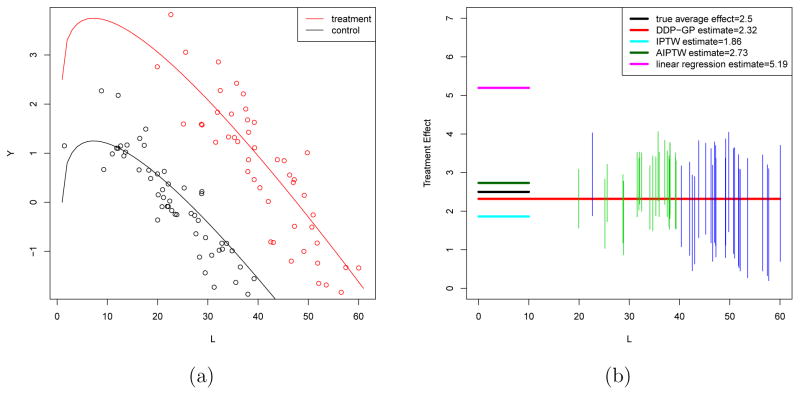
Figure 2(a) plots the simulation truth for the mean response curve under Z = 1 and Z = 0 versus L, with W ≡ 0, in one randomly selected trial. The upper red solid curve represents E[Y(1) | L, W = 0] and the lower black curve represents E[Y(0) | L, W = 0]. The red dots close to the upper curve are the observations for experimental arm patients and the black dots close to the lower curve are the observations for the control arm patients. We define an average treatment effect for the entire population under the simulation truth as ${\text{ATE}}^{★}=\frac{1}{n}{\sum }_{i=1}^{n}E[Y_i(1)-Y_i(0)]=2.5$.

Figure 2.

Simulation 2. (a) Simulated data for one (treatment, control) pair. The upper red solid curve represents E[Y(1) | X], the lower black curve represents E[Y(0) | X] given W = 0. The red dots close to the upper curve are the treated observations and the black dots close to the lower curve are the untreated. (b) Average treatment effect estimations ATE^★ (black solid line), ATE_DDP (red line), ATE_IPTW (turquoise blue), ATE_AIPTW (dark green), ATE_LR (heliotrope). The vertical line segments are marginal 90% posterior intervals for the treatment effect at each L value from treated observations (under the DDP-GP model).

We implemented inference for a survival regression F(Y_i | x_i, Z_i) using the proposed DDP-GP model (6). Figure 2(b) summarizes inference for the data from panel (a). Let Ŷ_i(z) = E(Y_n+1 | L_n+1 = L_i, W_n+1 = W_i, Z_n+1 = z, data) denote the posterior expected response for a future patient n + 1. We defined an estimated average treatment effect as ${\text{ATE}}_{\text{DDP}}=\frac{1}{n}{\sum }_{i=1}^n[{\widehat{Y}}_i(1)-{\widehat{Y}}_i(0)]$. Figure 2(b) shows the estimated average treatment effect (horizontal red line), and credible intervals for individual effects Ŷ_i(1) − Ŷ_i(0) (vertical line segments, located at L_i).

Inverse Probability of Treatment Weighting (IPTW)

For comparison, we also implemented inference using naive linear regression (LR), using an IPTW estimator, and an augmented IPTW (AIPTW) estimator for the average treatment effect. The LR estimator is based on a linear regression for log survival times, ignoring the lack of randomization. We use linear predictor functions Y_i(1) = β₁₀+β₁₁L_i+β₁₂W_i+ε_1i and Y_i(0) = β₀₀+β₀₁L_i+β₀₂W_i+ε_0i. Denoting the least squares estimates by β̂_zj for z = 0, 1 and j = 0, 1, 2, the estimated means are Ê{Y_i(z)} = β̂_z0 + β̂_z1L_i + β̂_z2W_i. We define an estimated average treatment effect based on the LR model as ${\text{ATE}}_{\text{LR}}=\frac{1}{n}{\sum }_i[\widehat{E}\{Y_i(1)\}-\widehat{E}\{Y_i(0)\}]$. Denote the propensity score π_i = pr(Z_i = 1 | x_i). The IPTW method corrects for bias due to lack of randomization by assigning each patient i a weight b_i equal to the inverse of an estimate of p(Z_i | x_i), the conditional probability of receiving his or her actual treatment (Robins et al., 2000). When Z_i = 1, b_i = 1/π_i; when Z_i = 0, b_i = 1/(1 − π_i). An estimate of π_i is obtained by fitting a logistic regression model. We define the IPTW mean outcome estimator

$$\text{IPTW}(Z=z)=\frac{{\sum }_{i}I(Z_i=z)b_i{Y}_i}{{\sum }_{i}I(Z_i=z)b_i},$$

and corresponding average treatment effect estimate ATE_IPTW = IPTW(Z = 1)−IPTW(Z = 0).

Augmented IPTW (AIPTW)

The AIPTW estimate (Robins, 2000) is a doubly robust generalization of the IPTW. It is consistent whenever the outcome regression model is correct and/or the propensity score model is correct. We evaluate the AIPTW estimator for average treatment effect (ATE):

$${\text{ATE}}_{\text{AIPTW}}=\frac{1}{n}\sum _{i=1}^n\left\{\left[\frac{I(Z_i=1)Y_i}{{\widehat{\pi }}_i}-\frac{I(Z_i=0)Y_i}{1-{\widehat{\pi }}_i}\right]-\frac{I(Z_i=1)-{\widehat{\pi }}_i}{{\widehat{\pi }}_i(1-{\widehat{\pi }}_i)}\left[(1-{\widehat{\pi }}_i)\widehat{E}(Y_i\mid Z_i=1,{\mathit{x}}_i)+{\widehat{\pi }}_i\widehat{E}(Y_i\mid Z_i=0,{\mathit{x}}_i)\right]\right\},$$ (9)

where π̂_i is the estimated propensity score using logistic regression and Ê(Y_i | Z_i, x_i) is estimated by a linear regression model, i = 0, 1.

Figure 2(b) shows ATE_DDP, ATE_LR, ATE_IPTW and ATE_AIPTW for one simulated dataset under this simuation setup. We found E(ATE_DDP | data) = 2.31, with 90% posterior credible interval (1.89, 2.96), compared with the simulation truth ATE^★ = 2.5. In contrast, ATE_LR = 4.13 overestimates, while the IPTW method underestimates, with ATE_IPTW = 1.11. The AIPTW method reports ATE_AIPTW = 2.73. In Figure 2(b), the vertical green and blue segments are marginal 90% posterior credible intervals for the treatment effect (under the DDP-GP model) at each observed L value. Lengths of posterior credible intervals larger than 2 are highlighted by blue segments. Note how the uncertainty bounds grow wider in the range where there is less overlap across treatment groups, that is, over a range of covariate values for which we do not observe reliable empirical counterfactuals for each data point (e.g. L > 50). Most of the credible intervals reasonably cover the true treatment effect.

Figure 2(b) reports inference for one hypothetical data set. For a comparison of average behavior, we carried out extensive simulations and report the distribution of estimated regime effects across these simulations. We compared the regime effect estimates obtained by DDP-GP, IPTW, AIPTW and LR based on data from 1,000 simulated trials. Figure 3 shows density plots of the distributions of estimated regime effects. Compared to the estimates obtained from DDP-GP or AIPTW, the IPTW estimates are much more variable, ranging from 1.14 to 7.13. The LR estimates are highly biased, and overestimate the true effects. The distribution of estimated regime effects under the DDP-GP model is highly concentrated around the simulation truth.

Figure 3.

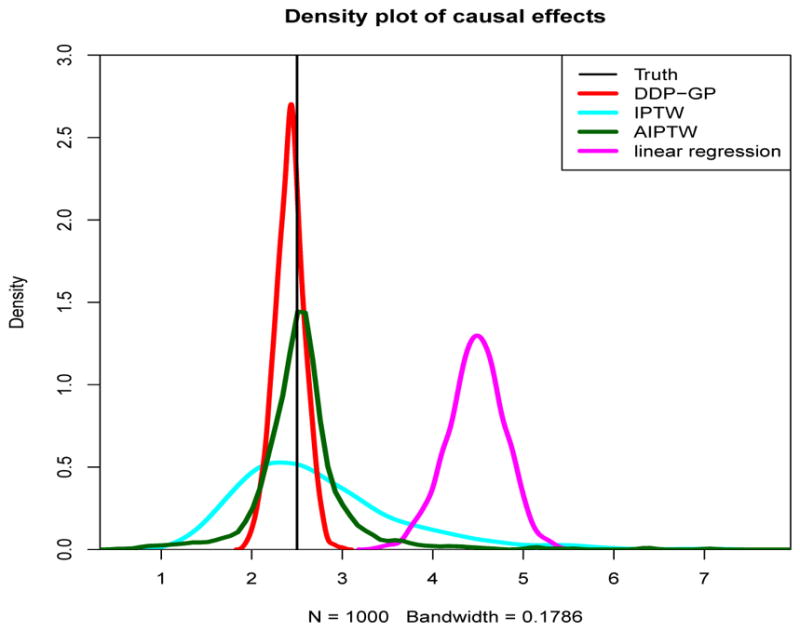
Simulation 2. The density plot of estimated regime effects by DDP-GP, IPTW, AIPTW and linear regression in 1,000 trials. The truth is indicated by a black vertical line.

5.3 Regime Effect for Multi-stage Regimes

Simulation 3 was designed to examine inference on strategy effects for multi-stage regimes with a general DTR setup. This simulation is similar to the scenario in Moodie et al. (2007). We simulated samples of size n = 200. Patients were randomized to initial induction therapy or not, coded as $Z_i^1=a_1$ and $Z_i^1=a_2$, with the randomization probabilities based on their baseline CD4 counts, which were simulated as L_i ~ N(450, 10²). For frontline therapy, we used the model $p(Z_i^1=a_1\mid L_i)=0.8I(L_i<450)+0.2I(L_i\ge 450)$. In order to focus on covariate-dependent induction and salvage therapies, we assumed for simplicity that all patients were resistant to the induction therapy. Let X ~ LN(m, s) denote a lognormal random variable with log(X) ~ N(m, s), we simulated the times $T_i^{(0,R)}~\text{LN}(2+0.005L_i,0.3)$. The salvage treatment for each patient $Z_i^2$ was assigned with probability $p(Z_i^2=1\mid Z_i^1,T_i^{(0,R)})=Z_i^1\text{expit}(1-0.003T_i^{(0,R)})+(1-Z_i^1)\text{expit}(-0.8-0.004T_i^{(0,R)})$ where expit(u) = e^u/(1 + e^u). For the first stage transition times, we generated transition times $T_i^{(R,D)}~\text{LN}({\mathit{\beta }}^{(R,D)}{\mathit{x}}_i^{(R,D)},0.3)$, where β^(R,D) = (−0.5, 0.03, 0.2, 0.5, 0.3) and ${\mathit{x}}_i^{(R,D)}=(1,L_i,Z_i^1,log(T_i^{(0,R)}),Z_i^2)$.

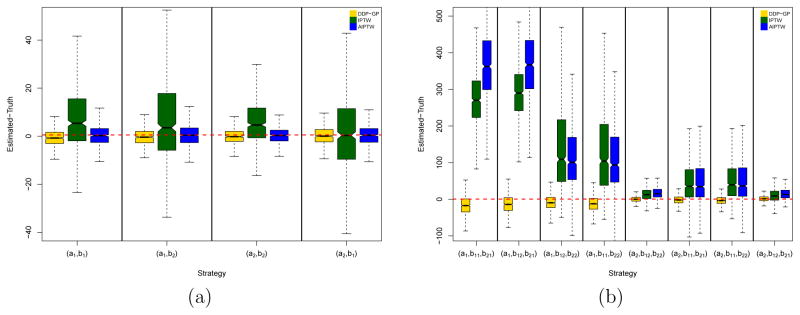
The goal is to estimate mean survival time for each DTR (Z¹, Z²). We have four possible DTRs in this simulation. We applied the Bayesian nonparametric DDP-GP model, IPTW and AIPTW (Zhang et al., 2013) to each simulated dataset to estimate mean survival for each of the four possible DTRs. When implementing IPTW and AIPTW, we estimated the propensity score using logistic regression and the outcome model using AFT regression models with a lognormal distribution. For the nonparametric Bayesian inference we defined independent DDP-GP models $F^k(Y_i^k\mid {\mathit{x}}_i^k)$ as in (6) for each of the n_T = 2 log transition times $Y_i^k=log{T}_i^k$. Figure 4(a) compares the mean survival estimates using boxplots of (Estimated mean survival - Simulation truth), based on 1,000 simulated datasets, arranged by inference method (DDP-GP, IPTW and AIPTW) and by the four possible DTRs (the four sub-plots). Note that the DDP-GP and the AIPTW estimates are on average closer to the truth and have much smaller variability, compared to the IPTW estimates, across all four strategies. Because we use the same outcome regression models as the simulation truth when implementing the AIPTW method, it performs well in this simulation study. In summary, both, the DDP-GP and the AIPTW methods show satisfactory performance in this example, although the DDP-GP estimates show slightly smaller variability than the AIPTW estimates.

Figure 4.

(a) Simulation 3 and (b) simulation 4. The yellow boxplots show posterior estimated mean OS using the DPP-GP model under each of the regimes as a difference with the simulation truth over 1,000 simulations. The green and blue boxes show the corresponding inferences under the IPTW and AIPTW approaches, respectively. In each notched box-whisker plot, the box shows the interquartile range (IQR) from 1st quantile (Q1) to 3rd quantile (Q3), and the mid-line is the median. The top whisker denotes Q3+1.5*IQR and the bottom whisker Q1-1.5*IQR. The notch displays a confidence interval for the median, that is $\text{median}\pm 1.57\ast \mathit{IQR}/\sqrt{1000}$.

Simulation 4 is a stylized version of the leukemia data that we will analyze in Section 6. We simulated samples of size n = 200 and patients’ blood glucose values L_i ~ N(100, 10²). Patients initially were randomized equally between two induction therapies Z¹ ∈ {a₁, a₂}. We then generated a response (see below). Patients who were resistant (R) to the assigned induction therapies were then assigned salvage treatment Z^2,1 ∈ {b₁₁, b₁₂}. Salvage treatments were randomized using the rule p(Z^2,1 = b₁₁ | L_i) = 0.8 I(L_i < 100) + 0.2 I(L_i ≥ 100). Patients who achieved C and subsequently suffered disease progression (P), were given salvage treatment Z^2,2 ∈{b₂₁, b₂₂}, using p(Z^2,2 = b₂₁ | L_i) = 0.2 I(L_i < 100) + 0.85 I(L_i ≥ 100). Finally, the survival time for each patient was evaluated as

$$T_i=\{\begin{array}{ll}{T}_i^{(0,R)}+T_i^{(R,D)}\hfill & \text{if}\text{patient}i\text{had}\text{sequence}(L,Z^1,T^{(0,R)},Z^{2,1})\hfill \\ T_i^{(0,C)}+T_i^{(C,P)},T_i^{(P,D)}\hfill & \text{if}\text{patient}i\text{had}\text{sequence}(L,Z^1,T^{(0,C)},T^{(C,P)},Z^{2,2}).\hfill \end{array}$$

We simulated the times of the two competing risks R and C as $T_i^{(0,R)}~\text{LN}({\mathit{\beta }}^{(0,R)}{\mathit{x}}_i^{(0,R)},{\sigma }^{(0,R)})$ and $T_i^{(0,C)}~\text{LN}({\mathit{\beta }}^{(0,C)}{\mathit{x}}_i^{(0,C)},{\sigma }^{(0,C)})$, where β^(0,R) = (2, 0.02, 0), β^(0,C) = (1.5, 0.03, −0.8), with ${\mathit{x}}_i^k=(1,L_i,Z_i^1)$ for k ∈{(0, R), (0, C)}. For the three possible second stage transitions k ∈{(R, D), (C, P), (P, D)}, we generated (competing) transition times $T_i^k~\text{LN}({\mathit{\beta }}^k{\mathit{x}}_i^k,{\sigma }^k)$, where β^(R,D) = (−0.5, 0.03, 0.2, 0.5, 0.3), β^(C,P) = (1, 0.05, 1, −0.6), β^(P,D) = (0.8, 0.04, 1.5, −1, 0.5, 0.5), with covariate vectors ${\mathit{x}}_i^{(R,D)}=(1,L_i,Z_i^1,log(T_i^{(0,R)}),Z_i^{2,1}),{\mathit{x}}_i^{(C,P)}=(1,L_i,Z_i^1,log(T_i^{(0,C)}))$ and ${\mathit{x}}_i^{(P,D)}=(1,L_i,Z_i^1,log(T_i^{(0,C)}),log(T_i^{(C,P)}),Z_i^{2,2})$. We simulated N = 1,000 trials with 15% censoring.

The goal is to estimate mean survival time for each DTR (Z¹, Z^2,1, Z^2,2). We performed inference under the Bayesian nonparametric DDP-GP model, IPTW, and AIPTW for each simulated dataset to estimate mean survival for each of the eight possible DTRs. When implementing IPTW and AIPTW, we estimated the propensity score using logistic regression and the outcome model using AFT regression models with a lognormal distribution. For the nonparametric Bayesian inference, we defined independent DDP-GP models $F^k(Y_i^k\mid {\mathit{x}}_i^k)$ for each of the n_T = 5 log transition times $Y_i^k=log{T}_i^k$. Figure 4(b) compares mean survival estimates using boxplots of (Estimated mean survival - Simulation truth), based on 1000 simulated datasets. The boxplots are arranged by inference method (DDP-GP, IPTW, AIPTW) and by all eight possible DTRs. In this simulation, both the propensity score model and the outcome model are incorrect when we implement the IPTW and AIPTW methods. In this case, the DDP-GP estimates on average are much closer to the truth and have much smaller variability, compared to the IPTW and AIPTW estimates, across all eight strategies as shown in Figure 4(b).

6 Evaluation of the Leukemia Trial Regimes

6.1 Leukemia Data – Inference for the Survival Regression

To analyze the AML-MDS trial data under the proposed DDP-GP model, we first implement posterior inference for six of the n_T = 7 transition times. The exception is T^(C,D). Due to the limited sample size – only 9 patients died after C without first suffering disease progression (P) – we do not implement the DDP-GP model, and instead use an intercept-only Weibull AFT model. Table 1 summarizes the data. The table reports the number of patients and median transition times for some selected transitions.

Table 1.

The sample median of each transition time is given, with lower 25% quantile and upper 75% quantile in the parenthesis next to each median .

Induction	Resistance		Die after resistance
	N	TR(days)	Salvage	N	T(R,D)(days)
All	39	59 (47,84)	All	37	76 (27,187)
FAI	17	63 (41,97)	HDAC	25	65 (21,154)
FAI+ATRA	13	59 (55,76)
FAI+GCSF	4	77 (43.5,106.75)	non HDAC	12	146 (79, 376.75)
FAI+ATRA+GCSF	5	51 (48, 65)

Induction	CR		Die after progression
	N	TC(days)	Salvage	N	T(P,D)(days)
All	102	32 (27,41)	All	83	120 (45,280)
FAI	20	31 (29, 44)	HDAC	47	106 (45,175.5)
FAI+ATRA	26	31 (25.25, 35)
FAI+GCSF	28	35.5 (28,42.75)	non HDAC	36	147.5 (42.75, 592.25)
FAI+ATRA+GCSF	28	32 (26,41)

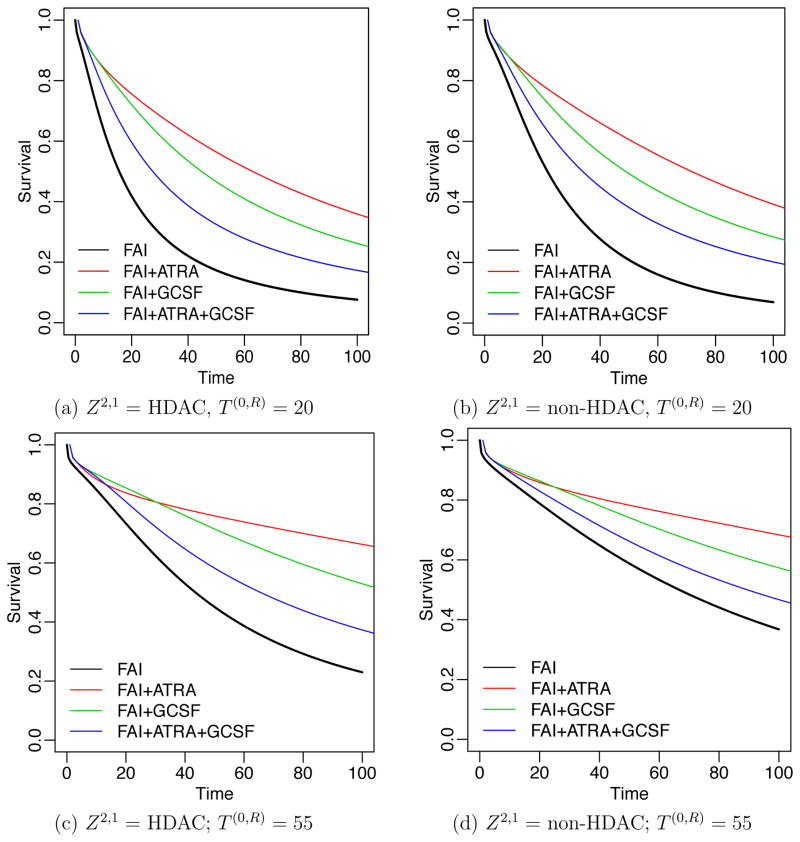
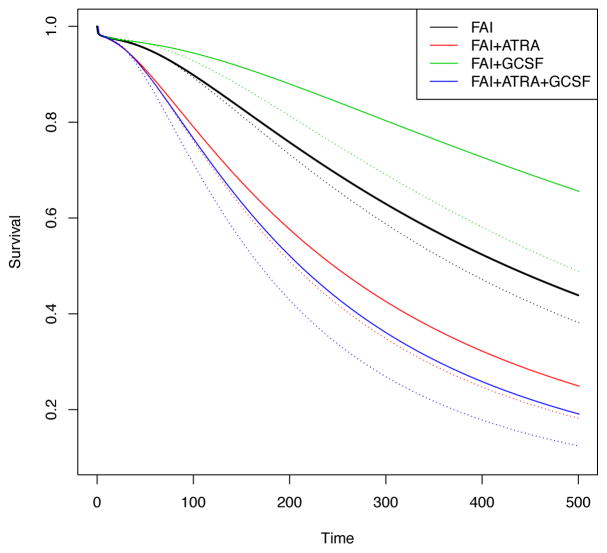
We first report results for T ^(R,D). Of 210 patients, 39 (18.57%) experienced resistance to their induction therapies. The rate of resistance varied across regimes, from 31% for patients receiving FAI, 24% for FAI plus ATRA, 7.8% for FAI plus GCSF, and 10% for FAI plus ATRA plus GCSF. The times to treatment resistance were longer, with greater variability in the FAI plus GCSF arm compared to the other three arms. Among the 39 patients who were resistant to induction therapies, 27 were given HDAC as salvage treatment, of whom 2 were censored before observing death. Figure 5 summarizes survival regression under the proposed DDP-GP model by plotting posterior predicted survival functions for a hypothetical future patient at age 61 with poor prognosis cytogenetic abnormality. The figure shows posterior predicted survival functions, arranged by different induction therapies Z¹ (the four curves in each panel), T ^(0,R) and Z^2,1 (as indicated in the subtitle). Figure 5 shows that patients with shorter T ^(0,R) had lower predicted survival once their cancer became resistant. Also, patients with s₁ = R who received Z^2,1 = HDAC as salvage had worse predicted survival than patients who received salvage treatment with non HDAC. Similar results can be obtained for other transition times.

Figure 5.

Survival regression for T ^(R,D) in the AML-MDS trial. Panels (a)–(d) show the posterior estimated survival functions for a future patient at age 61 with poor prognosis cytogenetic abnormality, with T ^(0,R) and Z^2,1 as indicated. Survival curves are shown for four induction therapies. Black, red, green and blue curves indicate Z¹ = FAI, FAI+ATRA, FAI+GCSF and FAI+ATRA+GCSF, respectively.

Next, we summarize results of the survival regression for T ^(C,P). Among the n = 210 patients, 102 (48.6%) achieved C, with C rates of 37%, 48%, 53% and 56% in the FAI, FAI plus ATRA, FAI plus GCSF and FAI plus GCSF plus ATRA arms, respectively. Of the 102 patients who achieved CR, 93 experienced disease progression before death or being lost to follow-up. Among these 93 relapsed patients, 53 received salvage treatment with HDAC. For a hypothetical future patient at age 61 with poor prognosis cytogenetic abnormality, Figure 6 summarizes survival regression functions for each of the four induction therapies, with solid lines representing T ^(0,C) = 20 and dotted lines representing T ^(0,C) = 30. The four dotted lines are below the four corresponding solid lines, indicating that T ^(0,C) was associated with T ^(C,P). This observation coincides with the well-known phenomenon in chemotherapy for AML or MDS that, regardless of induction therapy, the longer it takes to achieve C, the shorter the period that the patient remains in C.

Figure 6.

The effect of T ^(0,C) on T ^(C,P) at age 61 with poor cytogenetic abnormality. Black, red, green and blue curves represent induction treatments FAI, FAI+ATRA, FAI+GCSF and FAI+ATRA+GCSF, respectively. Solid lines and dotted lines represent T ^(0,C) = 20 and T ^(0,C) = 30, respectively. The longer it takes to achieve C, the shorter the period of time that the patient remained in C.

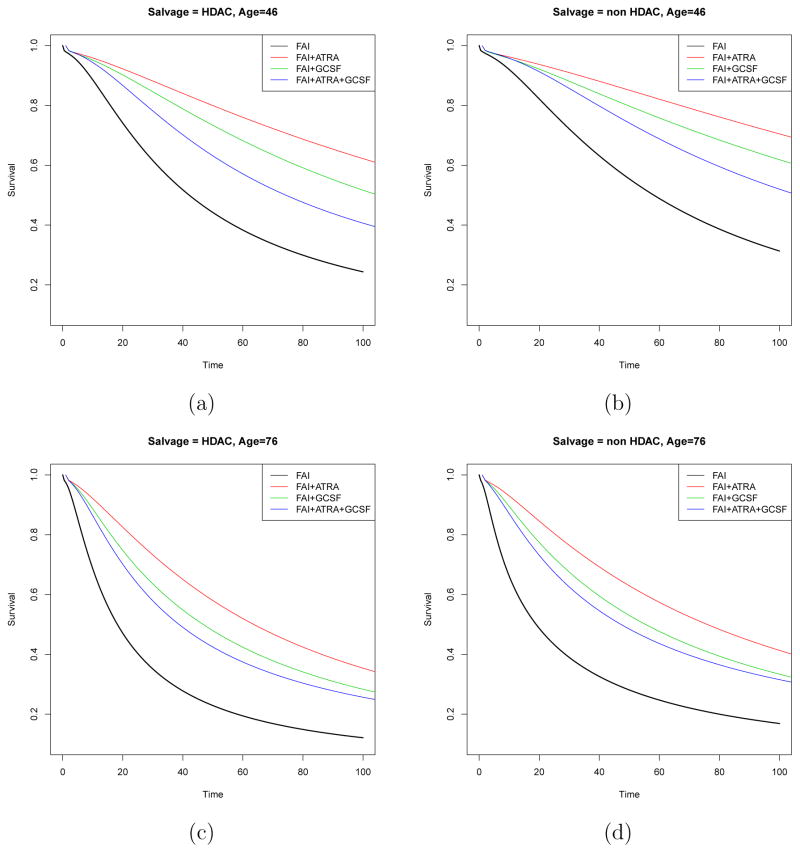
Similarly, we summarize results for the survival regression for T ^(P,D). For a patient with poor prognosis cytogenetic abnormality, Figure 7 shows the posterior predicted survival functions under different combinations of induction therapy and age. Panels (a) and (c) show the survival functions of a patient assigned salvage treatment HDAC with age 46 or 76, while panels (b) and (d) plot the corresponding survival functions for the patient assigned non HDAC as salvage. Four different colors represent the four induction therapies. Figure 7 shows that residual survival time after disease progression following C was associated with both age and salvage therapy. Older patients were more likely to have shorter residual life once their disease progressed, and patients given HDAC as salvage died more quickly than patients given non HDAC salvage.

Figure 7.

AML-MDS trial data in transition (P, D): Panels (a) and (c) show the posterior estimated survival functions of patient at age 46 and 76 with poor cytogenetic abnormality assigned to salvage treatment HDAC for four induction therapies respectively. Panels (b) and (d) show the posterior estimated survival functions of patient at age 46 and 76 with poor cytogenetic abnormality assigned to salvage treatment non HDAC for four induction therapies respectively. Black, red, green and blue curves represent induction treatments FAI, FAI+ATRA, FAI+GCSF and FAI+ATRA+GCSF, respectively.

6.2 Estimating the Regime Effects

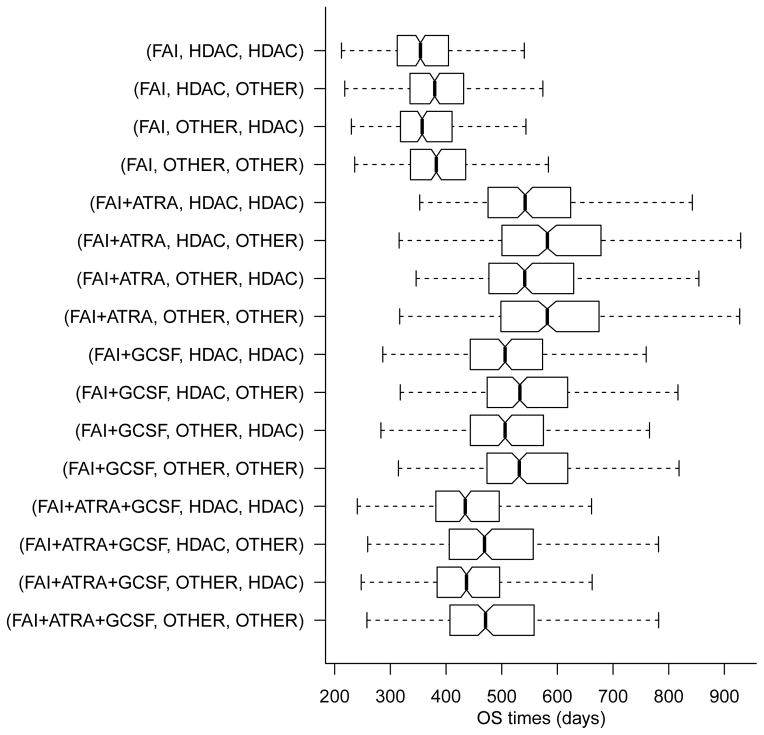
In the AML-MDS trial, the four induction therapies and two salvage therapies define a total of 16 regimes. Mean survival time estimates under each of the 16 regimes were calculated using posterior inference under independent DDP-GP models $F^k(Y_i^k\mid {\mathit{x}}_i^k)$ for each of the n_T = 7 transition times. For comparison, we also evaluated mean survival times using the IPTW method. See equation (16) in the Appendix for details. Table 2 summarizes the results using IPTW and the DDP-GP model, including 90% credible intervals. Figure (8) shows boxplots of the marginal posterior distributions of survival times under the DDP-GP model for the 16 regimes.

Table 2.

Mean overall survival time under the IPTW method and the posterior mean and 90% credible interval (CI) under the DDP-GP model.

Regime (A, B1, B2)	Estimated mean OS times (days)
	DDP-GP
	IPTW	Posterior mean	90% CI
(FAI, HDAC, HDAC)	191.67	390.35	(286.47 545.6)
(FAI, HDAC, other)	198.18	416.34	(295.84 581.73)
(FAI, other, HDAC)	216.59	394.2	(287.15 538.63)
(FAI, other, other)	222.42	420.19	(296.51 579.05)
(FAI+ATRA, HDAC, HDAC)	527.43	572.9	(416.63 829.12)
(FAI+ATRA, HDAC, other)	458.85	617.15	(434.4 905.82)
(FAI+ATRA, other, HDAC)	532.29	573.46	(413.59 830.39)
(FAI+ATRA, other, other)	464.39	617.71	(434.49 900.32)
(FAI+GCSF, HDAC, HDAC)	326.15	542.06	(393.49 725.23)
(FAI+GCSF, HDAC, other)	281.78	578.24	(419.69 781.05)
(FAI+GCSF, other, HDAC)	327.66	542.5	(392.77 726.08)
(FAI+GCSF, other, other)	283.36	578.68	(421.46 781.26)
(FAI+ATRA+GCSF, HDAC, HDAC)	337.44	458.34	(327.91 651.21)
(FAI+ATRA+GCSF, HDAC, other)	285.64	502.48	(360.29 727.44)
(FAI+ATRA+GCSF, other, HDAC)	362.56	459.42	(328.09 651.61)
(FAI+ATRA+GCSF, other, other)	309.62	503.56	(358.84 726.88)

Figure 8.

Marginal posterior distributions of overall survival time under the DDP-GP model for all 16 regimes.

The two methods give very different estimates for mean survival time, with the DDP-GP likelihood-based estimator much larger than the corresponding IPTW estimator for most regimes. The differences are expected due to the distinct properties of these two methods. The IPTW estimator uses the covariates to estimate the regime probability weights. In contrast, the DDP-GP likelihood-based method computes mean survival time, using G-computation, accounting for patients’ covariates and previous transition times in addition to treatment followed by marginalizing over the empirical covariate distribution to obtain η(Z). Additionally, the IPTW estimate is calculated from the overall samples, whereas the likelihood-based DDP-GP method models each transition time distribution separately, which reduces the effective sample size for each model fit and thus increases the overall variability even though they share the same prior for the β^k’s.

For both methods, the estimates were smallest for the four regimes with FAI as induction therapy regardless of salvage treatment, and the 90% credible intervals were relatively small for these inferior regimes. Under the IPTW method, the estimates were largest for the four regimes with FAI plus ATRA as induction therapy, and the best regime is (FAI+ATRA, other, HDAC). With the DDP-GP likelihood-based approach, FAI plus ATRA as induction also gave the largest estimates, except for the regimes (FAI+GCSF, HDAC, other) and (FAI+GCSF, other, other), while the best regime is (FAI+ATRA, other, other). Most importantly, the DDP-GP likelihood-based approach showed that (FAI + ATRA, Z^2,1, other) was superior to (FAI + ATRA, Z^2,1, HDAC) regardless of Z^2,1. Therefore, our results suggest that (1) FAI plus ATRA was the best induction therapy, (2) if the patient’s disease was resistant to FAI plus ATRA, then it was irrelevant whether the salvage therapy contained HDAC, and (3) if patients experienced progression after achieving C with FAI plus ATRA, then salvage therapy with non HDAC was superior.

These conclusions, although not confirmatory, contradict those given by Estey et al. (1999), who concluded that none of the three adjuvant combinations FAI plus ATRA, FAI plus GCSF, or FAI plus ATRA plus GCSF were significantly different from FAI alone with respect to either survival or event-free survival time, based on consideration of only the frontline therapies by applying conventional Cox regression and hypothesis testing.

7 Conclusions

We have proposed a Bayesian nonparametric DDP-GP model for analyzing survival data and evaluating joint effects of induction-salvage therapies in clinical trials, using the posterior estimates, to predict survival for future patients. The Bayesian paradigm works very well, and the simulation studies suggest that our DDP-GP method yields more reliable estimates than IPTW and AIPTW. The DDP-GP model can be extended easily to multivariate outcomes. In equation (2), this could be done by replacing the normal distribution with a multivariate normal distribution as the base measure. A referee has noted that, in settings where interpretability is important, our proposed BNP approach could be applied in the context of a policy search algorithm (Orellana et al., 2010; Zhang et al., 2012a,b, 2013; Zhao et al., 2012, 2014, 2015).

We employed two different methods to evaluate the 16 possible two-stage regimes for choosing induction and salvage therapies in the leukemia trial data. The IPTW method estimates the regime effect by using covariates only to compute the assignment probabilities of salvage therapies to correct for bias. In contrast, likelihood-based G-computation under the DDP-GP model accounts for all possible outcome paths, the transition times between successive states, and effects of covariates and previous outcomes, on each transition time. Although the two methods gave different numerical estimates of mean survival time, they both reached the conclusion that FAI plus ATRA was the best induction therapy and FAI was the worst induction therapy. Although our current models are set up for two-stage treatment regimes, they easily can be extended to other applications with multi-stage regimes.

Appendix

Likelihood

The following structure is adapted from Wahed and Thall (2013), and is included here for completeness. The risk sets of the seven transition times in the leukemia trial are defined as follows. Let ℛ⁰ = {1, . . . , n} denote the initial risk set at the start of induction chemotherapy, and ℛ^(0,r) = {i : s_1i = r} for r = D, C, R, so ℛ⁰ = ℛ^(0,D) ∪ ℛ^(0,C) ∪ ℛ^(0,R). Similarly, ℛ^(C,P) = {i : s_1i = C, s_2i = P } is the later risk set for T^(P,D).

To record right censoring, let U_i denote the time from the start of induction to last followup for patient i. We assume that U_i is conditionally independent of the transition time given prior transition times and other covariates. Censoring of event times occurs by competing risk and/or loss to follow up. For patient i in the risk set for transition time $T_i^k$, let ${\delta }_i^k=1$ if patient i is not censored and 0 if patient i is right censored. For example, ${\delta }_i^{(0,D)}=1$ for i ∈ ℛ⁰ if $T_i^{(0,D)}=min(U_i,T_i^{(0,D)},T_i^{(0,C)},T_i^{(0,R)})$. Similarly, ${\delta }_i^{(R,D)}=1$ for i ∈ ℛ^(0,R) if $T_i^{(0,R)}+T_i^{(R,D)}<U_i$ and ${\delta }_i^{(P,D)}=1$ for i ∈ ℛ^(C,P) if $T_i^{(0,C)}+T_i^{(C,P)}+T_i^{(P,D)}<U_i$.

For i ∈ ℛ⁰, let $V_i^0=min(T_i^{(0,D)},T_i^{(0,R)},T_i^{(0,C)},U_i)$ denote the observed time for the stage 1 event or censoring. For i ∈ ℛ^(0,C) let $V_i^C=min(T_i^{(C,D)},T_i^{(C,P)},U_i-T_i^{(0,C)})$ denote the observed event time for the competing risks D and P and loss to followup. Similarly, for i ∈ ℛ^(0,R) , let $V_i^R=min(T_i^{(R,D)},U_i-T_i^{(0,R)})$ and for i ∈ ℛ^(C,P) let $V_i^{(C,P)}=min(T_i^{(P,D)},U_i-T_i^{(0,C)}-T_i^{(C,P)})$.

The joint likelihood function is the product ℒ= ℒ₁ℒ₂ℒ₃ℒ₄. The first factor ℒ₁ corresponds to response to induction therapy,

$${\mathcal{L}}_1=\prod _{i\in {\mathcal{R}}^0}\prod _{r\in \{D,R,C\}}{f}^{(0,r)}{(V_i^0\mid {\mathit{x}}_i^{(0,r)})}^{{\delta }_i^{(0,r)}}{\overline{F}}^{(0,r)}{(V_i^0\mid {\mathit{x}}_i^{(0,r)})}^{1-{\delta }_i^{(0,r)}}.$$ (10)

where F̄^k = 1 − F^k. The second factor ℒ₂ corresponds to patients i ∈ R^(0,R) who experience resistance to induction and receive salvage Z^2,1,

$${\mathcal{L}}_2=\prod _{i\in {\mathcal{R}}^{(0,R)}}{f}^{(R,D)}{(V_i^R\mid {\mathit{x}}_i^{(R,D)})}^{{\delta }_i^{(R,D)}}{\overline{F}}^{(R,D)}{(V_i^R\mid {\mathit{x}}_i^{(R,D)})}^{1-{\delta }_i^{(R,D)}}.$$ (11)

The third factor ℒ₃ is the likelihood contribution from patients achieving C,

$${\mathcal{L}}_3=\prod _{i\in {\mathcal{R}}^{(0,C)}}\prod _{k=(C,D),(C,P)}{f}^k{(V_i^C\mid {\mathit{x}}_i^k)}^{{\delta }_i^k}{\overline{F}}^k{(V_i^C\mid {\mathit{x}}_i^k)}^{1-{\delta }_i^k}.$$ (12)

The fourth factor ℒ₄ is the contribution from patients who experience tumor progression after C,

$${\mathcal{L}}_4=\prod _{i\in {\mathcal{R}}^{(C,P)}}{f}^{(P,D)}{(V_i^{(C,P)}\mid {\mathit{x}}_i^{(P,D)})}^{{\delta }_i^{(P,D)}}{\overline{F}}^{(P,D)}{(V_i^{(C,P)}\mid {\mathit{x}}_i^{(P,D)})}^{1-{\delta }_i^{(P,D)}}.$$ (13)

The mean survival time of a patient treated with regime Z = (Z¹, Z^2,1, Z^2,2) is

$$\begin{array}{l}\eta (\mathbf{Z})=\int \left[p(s_1=D\mid {\mathit{x}}^0,Z^1){\eta }^{(0,D)}({\mathit{x}}^0,Z^1)\right]d\widehat{p}({\mathit{x}}^0)\\ +\int \left\{p(s_1=R\mid {\mathit{x}}^0,Z^1)\left[{\eta }^R({\mathit{x}}^0,Z^1)+\int {\eta }^{(R,D)}({\mathit{x}}^0,Z^1,Z^{2,1},T^{(0,R)})d\mu (T^{(0,R)})\right]\right\}d\widehat{p}({\mathit{x}}^0)\\ +\int p(s_1=C\mid {\mathit{x}}^0,Z^1)[{\eta }^C({\mathit{x}}^0,Z^1)+\int [p(s_2=D\mid s_1=C,{\mathit{x}}^0,Z^1,T^{(0,C)}){\eta }^{(C,D)}({\mathit{x}}^0,Z^1,T^C)\\ +p(s_2=P\mid s_1=C,{\mathit{x}}^0,Z^1,T^{(0,C)})[{\eta }^{(C,P)}({\mathit{x}}^0,Z^1,T^{(0,C)})\\ +\int {\eta }^{(P,D)}({\mathit{x}}^0,Z^1,Z^{2,2}{T}^{(0,C)},T^{(C,P)})d\mu (T^{(C,P)})]d\mu (T^{(0,C)})]d\widehat{p}({\mathit{x}}^0).\end{array}$$ (14)

IPTW

We compute the IPTW estimates for overall mean survival with regime Z as

$$\mathit{IPTW}(\mathbf{Z})=\sum _{i=1}^n{w}_i(\mathbf{Z})T_i/\sum _{i=1}^n{w}_i(\mathbf{Z}),$$ (15)

where

$$\begin{array}{l}{w}_i(\mathbf{Z})=\frac{I(\mathbf{Z}={\mathbf{Z}}_i){\delta }_i}{\widehat{K}(U_i)}[I(s_{1i}=D)+I(s_{1i}=R)I_i(Z^{2,1})/\widehat{Pr}(Z^{2,1}\mid s_{1i}=R,Z^1,{\mathit{x}}_i^0,T_i^{(0,R)})\\ +I(s_{1i}=C,s_{2i}=D)\\ +I(s_{1i}=C,s_{2i}=P)I_i(Z^{2,2})/\widehat{Pr}(Z^{2,2}\mid s_{1i}=C,s_{2i}=P,Z^1,{\mathit{x}}_i^0,T_i^{(0,C)},T_i^{(C,P)})].\end{array}$$ (16)

In (16), K̂ is the Kaplan-Meier estimator of the censoring survival distribution K(u) = P (U ≥ t) at time t. I_i(Z) is is an indictor of treatment Z and 0 otherwise, and $\widehat{Pr}(Z^{2,1}\mid s_{1i}=C,Z^1,{\mathit{x}}_i^0,T_i^{(0,R)})$ is the probability of receiving salvage treatment Z^2,1 estimated using logistic regression, and similarly for $\widehat{Pr}(Z^{2,2}\mid s_{1i}=C,s_{2i}=P,Z^1,{\mathit{x}}_i^0,T_i^{(0,C)},T_i^{(C,P)})$. The above estimator has been shown to be consistent under suitable assumptions (Wahed and Thall, 2013; Scharfstein et al., 1999).