Abstract
Motivation: Genomic studies often involve estimation of variances of thousands of genes (or other genomic units) from just a few measurements on each. For example, variance estimation is an important step in gene expression analyses aimed at identifying differentially expressed genes. A common approach to this problem is to use an Empirical Bayes (EB) method that assumes the variances among genes follow an inverse-gamma distribution. This distributional assumption is relatively inflexible; for example, it may not capture ‘outlying’ genes whose variances are considerably bigger than usual. Here we describe a more flexible EB method, capable of capturing a much wider range of distributions. Indeed, the main assumption is that the distribution of the variances is unimodal (or, as an alternative, that the distribution of the precisions is unimodal). We argue that the unimodal assumption provides an attractive compromise between flexibility, computational tractability and statistical efficiency.
Results: We show that this more flexible approach provides competitive performance with existing methods when the variances truly come from an inverse-gamma distribution, and can outperform them when the distribution of the variances is more complex. In analyses of several human gene expression datasets from the Genotype Tissues Expression consortium, we find that our more flexible model often fits the data appreciably better than the single inverse gamma distribution. At the same time we find that in these data this improved model fit leads to only small improvements in variance estimates and detection of differentially expressed genes.
Availability and Implementation: Our methods are implemented in an R package vashr available from http://github.com/mengyin/vashr.
Contact: mstephens@uchicago.edu
Supplementary information: Supplementary data are available at Bioinformatics online.
1 Introduction
Genomic studies often involve estimation of variances of thousands of genes (or other genomic units) from just a few measurements on each. For example, variance estimation is an important step in gene expression analyses aimed at identifying differentially expressed genes. The small number of measurements on each gene mean that simple estimates of the variance at each gene (e.g. the sample variance) can be quite unreliable. A common solution to this problem is the use of Empirical Bayes (EB) methods, which combine information across all genes to improve estimates at each gene. In particular they have the effect of ‘shrinking’ the variance estimates towards a common mean value, which has a stabilizing effect, avoiding unusually large or small outlying estimates that may have high error. A key question is, of course, how much to shrink. While all EB methods aim to learn the appropriate shrinkage from the data, existing EB approaches make relatively inflexible modelling assumptions that could limit their effectiveness. Here we propose a new, more flexible, EB approach, which can improve variance estimation accuracy in some settings.
Perhaps the most commonly encountered example of the use of EB methods is in gene expression analyses that aim to identify differences in gene expression among conditions. A typical pipeline for identifying differentially expressed genes computes a P-value for each gene using a t-test (two condition experiments) or F-test (multiple condition experiments), both of which require an estimate of the variance in expression of each gene among samples. In the classical t-test or F-test, sample variances are used as plug-in estimates of gene-specific variances. However, when the sample size is small, sample variances can be inaccurate, resulting in loss of power (Murie et al., 2009). Hence, many methods have been proposed to improve variance estimation. For example, several papers (Broberg et al., 2003; Efron et al., 2001; Tusher et al., 2001) suggested adding an offset standard deviation to stabilize small variance estimates. A more sophisticated approach (Baldi and Long, 2001) used parametric hierarchical models to combine information across genes, using an inverse gamma prior distribution for the variances, and a Gamma likelihood to model the observed sample variances. This idea was further developed by Lönnstedt and Speed (2002) and Smyth (2004) into an Empirical Bayes (EB) approach that estimates the parameters of the prior distribution from the data. This improves performance by making the method more adaptive to the data. Smyth (2004) also introduces the ‘moderated t-test’, which modifies the classical t-test by replacing the gene-specific sample variances with estimates based on their posterior distribution. This pipeline, implemented in the software limma, is widely used in genomics thanks to its adaptivity, computational efficiency and ease of use.
While assuming an inverse-gamma distribution for the variances yields simple procedures, the actual distribution of variances may be more complex. Motivated by this, Phipson et al. (2016) (limma with robust option, denoted by limmaR) modified the procedures from Smyth (2004) to allow for some small proportion of ‘outlier’ genes that have higher variability than expected under the inverse-gamma assumption. Specifically, the limmaR procedure changes the moderated t statistics from limma by decreasing their degrees of freedom (df) in a way that varies for each gene, depending on whether the gene looks like an outlier. Genes that look like an outlier have their df reduced appreciably, making them less significant, whereas other genes have their df unchanged or reduced very little. They showed that, in the presence of such outliers, this procedure could improve on the standard limma pipeline.
Here we consider a more formal EB approach to this problem, which generalizes previous EB methods by replacing the usual inverse gamma prior distribution with a substantially more flexible family of distributions. The main constraint we place on this prior is that the distribution of the variances (or, alternatively, the precisions) is unimodal. This unimodal assumption not only seems likely to be plausible in many settings, but also provides an attractive compromise between flexibility, statistical stability and computational convenience. Specifically it provides more flexibility and generality than many parametric models while avoiding potential over-fitting issues of fully non-parametric methods. (An alternative approach would be to use some kind of regularization to prevent over-fitting; see Efron (2016) for example.) We use a mixture of (possibly a large number of) inverse-gamma distributions to flexibly model this unimodal distribution, and provide simple computational procedures to fit this model by maximum likelihood of the mixture proportions.
Our procedure provides a posterior distribution on each variance or precision, as well as point estimates (posterior mean). The methods are an analogue of the ‘adaptive shrinkage’ methods for mean parameters introduced in Stephens (2016), and are implemented in the R package vashr (for ‘variance adaptive shrinkage in R’). We compare our method with both limma and limmaR in various simulation studies, and also assess its utility on real gene expression data.
2 Methods
2.1 Models
Suppose that we observe variance estimates that are estimates of underlying ‘true’ variances . Motivated by standard normal theory, we assume that
| (1) |
where the degrees of freedom dj depends on the sample size and we assume it to be known.
Empirical Bayes (EB) approaches to estimating (e.g. Smyth, 2004) are commonly used to improve accuracy, particularly when the degrees of freedom dj for each observation are modest. The EB approach typically assumes that the variances are independent and identically distributed from some underlying parametric distribution g:
| (2) |
where the parameters θ are to be estimated from the data. Equivalently, that the precisions (inverse variances), , are i.i.d. from some . A standard approach (Smyth, 2004) assumes that g is an inverse-gamma distribution (i.e. h is a gamma distribution) which simplifies inference because of conjugacy. Here we introduce more flexible assumptions for g or h: specifically that either g or h is unimodal. By using a mixture of inverse gamma distributions for g (i.e. a mixture of gamma distributions for h), we can flexibly capture a wide variety of unimodal distributions for g or h, while preserving many of the computational benefits of conjugacy.
2.2 A unimodal distribution for the variances
Let denote the density of an inverse-gamma distribution with shape a and rate b. This distribution is unimodal with mode at . To obtain a more flexible family of unimodal distributions with mode at c we consider a mixture of inverse-gamma distributions, each with mode at c:
| (3) |
where
| (4) |
and πk are mixture proportions. Each component in (3) has mode at c, and the variance about this mode is controlled by ak, with large ak corresponding to small variance. By setting to a large fixed dense grid of values that range from ‘small’ to ‘large’, we obtain a flexible family of distributions, with hyperparameters π, that are unimodal about c.
We emphasize that the representation (3) is simply a computationally convenient way to achieve a flexible family of unimodal distributions. Our goal is that K be sufficiently large, and the grid of values be sufficiently dense, that results would not change much by making the grid larger and denser. In practice modest values of K (e.g. 10–16) are sufficient to give reasonable performance (see below for specific details on choice of grid for ). Using a dense grid makes the hyperparameters π non-identifiable, because different values for π can lead to similar values for , but this is not a concern here because accurate EB inference requires only a good estimate for g and not πv. This approach is analogous to Stephens (2016), which uses mixtures of normal or uniform distributions, with a fixed grid of variances, to model unimodal distributions for mean parameters.
2.3 Estimating hyper-parameters
For K = 1 we estimate the hyperparameters (a, c) by maximizing the likelihood
| (5) |
| (6) |
where
| (7) |
| (8) |
| (9) |
We use the R command optim to numerically maximize this likelihood. The approach is similar to Smyth (2004), except that we use maximum likelihood instead of moment matching.
For K > 1, as noted above, we use K ‘large’ (e.g. 10–16), fix the values of ak to a grid of values from ‘small’ to ‘large’, and estimate the hyper-parameters by maximizing the likelihood
| (10) |
| (11) |
where is given by (8). We center the grid of ak values on the point estimate obtained for K = 1, to ensure that the grid values span a range consistent with the data (typically ak lies between 0 and 100). Moreover, if the data are consistent with K = 1 then the estimated π will be concentrated on the component with , and thus lead to similar results to limma.
To maximize the likelihood we use an iterative procedure that alternates between updating c and π, with each step increasing the likelihood. Given c, we update π using a simple EM step (Dempster et al., 1977). Given π we update c by optimizing (11) numerically using optim. We use SQUAREM (Varadhan and Roland, 2004) to accelerate convergence of the overall procedure. See Appendix for details.
2.4 Posterior calculations
Using (3) as a prior distribution for , and combining with the likelihood (1) the posterior distribution of is also a mixture of inverse-gamma distributions:
| (12) |
where
| (13) |
| (14) |
| (15) |
Following Smyth (2004) we use the posterior mean of as a point estimate for the precision :
| (16) |
Note that each can be interpreted as a shrinkage-based estimate of , since it lies between the observation and the prior mean of the kth mixture component .
When estimating variances we use the inverse of the estimated precision (16). While it may seem more natural to use the posterior mean of as a point estimate for , we found that this can be very sensitive to small changes in the estimated hyper-parameters , and so can perform poorly. And while it may also be more natural to estimate variances on a log scale, for example using the posterior mean for , the absence of closed-form expressions makes this less convenient.
2.5 Unimodal prior assumption on variance or precision
The above formulation is based on assuming a unimodal prior distribution for the variance , specifically by using a mixture of inverse-gamma distributions all with the same mode. An alternative is to assume a unimodal prior distribution for the precision , by using a mixture of gamma distributions, all with the same mode. This is equivalent to using a mixture of inverse-gamma distributions for the variance as in (3) above, but with
| (17) |
in place of (4), because the mode of a distribution is at . We present results for both approaches. In practice one can assess which of the two models provides a better fit to the data by comparing their (maximized) likelihoods (11). Note that in many (but not all) cases the fitted prior distributions under either or both approaches will end up being unimodal for both the variance and the precision. However, even in these cases, the optimal likelihood under each approach will typically differ because the family of unimodal distributions being optimized over is different.
2.6 Testing effect size
In differential expression analysis, testing if is of primary interest. Smyth (2004) suggested using the ‘moderated t-test’, which moderated the sample variance and degree of freedom by the shrunk variance estimates and its posterior degree of freedom. Here we derive an analogue of this moderated t-test in our mixture prior setting.
The distribution of given is:
| (18) |
| (19) |
| (20) |
where denotes the density of a generalized t-distribution with degree of freedom ν, location parameter μ and scale parameter σ (i.e. the density of where is a standard t distribution on ν degrees of freedom).
Hence, under the null (), follows a mixture of generalized t-distributions:
| (21) |
A p-value for testing can therefore be computed as
| (22) |
where Xj follows the mixture of generalized t-distributions in (21). In the special case where the mixture involves K = 1 components this is equivalent to the P value from Smyth’s moderated t test.
The P-value Pj measure the significance of gene j. To select significant differentially expressed genes and control the false discovery rate, these P values can be subjected to the Benjamini-Hochberg procedure (Benjamini and Hochberg, 1995), or Storey’s procedure (Storey, 2002, 2003), for example. Alternatively, the methods in Stephens (2016) can be extended to incorporate the mixture likelihood (20).
3 Results
3.1 Simulation studies
To compare and contrast our method with limma and limmaR we simulate data from the model (1)–(3), with G = 10 000, and degrees of freedom df = 3, 10, 50 (corresponding to sample sizes 4, 11 and 51 respectively) under various scenarios for the actual distribution of variances (scenarios A–D) or precisions (scenarios E–H), as summarized in Tables 1 and 2.
Table 1.
Parameters for the simulation scenarios with unimodal prior on variance
| Scenario | Description | Prior of |
|---|---|---|
| A | Single IG | InvGamma(10,11) |
| B | Single IG with outliers | 0.1InvGamma(3,4)+0.9InvGamma(10,11) |
| C | IG mixture | 0.1InvGamma(3,4) + 0.4InvGamma(5,6) + 0.5InvGamma(20,21) |
| D | Long tail log-normal mixture | 0.7logN(0.0625,0.0625) + 0.3logN(0.64,0.64) |
Table 2.
Parameters for the simulation scenarios with unimodal prior on precision
| Scenario | Description | Prior of |
|---|---|---|
| E | Single gamma | Gamma(10,9) |
| F | Single gamma with outliers | 0.1Gamma(2,1)+0.9Gamma(10,9) |
| G | Gamma mixture | 0.1Gamma(2,1) + 0.4Gamma(5,4) + 0.5Gamma(30,29) |
| H | Long tail log-normal mixture | 0.7logN(0.0625,0.0625) + 0.3logN(0.64,0.64) |
The simulation scenarios are designed to span the range from a single inverse-gamma prior as assumed by limma, to more complex distributions under which we might expect our method to outperform limma. Specifically we consider:
Single IG (or Single Gamma): single component inverse-gamma prior on variance (or gamma prior on precision), which satisfies the assumptions of limma.
Single IG (or Single Gamma) with outliers: two component inverse-gamma prior on variance (or gamma prior on precision), where one component models the majority of genes and the other component, being more spread out, attempts to capture possible outliers. The method limmaR is specifically designed to deal with the case where large variance outliers exist.
IG (Gamma) mixture: a more flexible inverse-gamma mixture prior on variance (or mixture gamma prior on precision) with multiple components.
Long tail log-normal mixture: log-normal mixture prior on variance or precision, which yields a longer tail than either the inverse-gamma or the gamma distribution.
We also assume that 90% of the genes are not differentially expressed (), while the rest of the genes are (). Here σ is held fixed at 2.
For each simulation scenario we simulate 50 datasets and apply limma, limmaR, and our proposed method (vash) to estimate (or ). We compare the relative root mean squared errors (RRMSEs) of the shrinkage estimators, which we define by
| (23) |
| (24) |
The RRMSE measures the improvement of a shrinkage estimator over simply using the sample variance or precision , with RRMSE = 1 indicating no benefit of shrinkage. (We also show the absolute RMSEs, i.e. the numerators of (23) and (24), in Supplementary Materials; Tables S1, S2.)
Figure 1 and 2 show the RRMSEs of limma, limmaR and vash for all scenarios. We summarize the main patterns as follows:
Fig. 1.
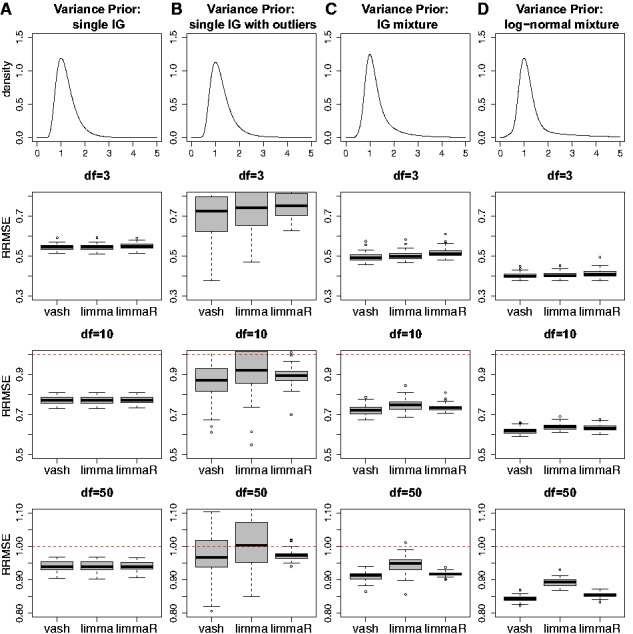
of three gene-specific variances estimators, limma, limmaR and our proposed estimator (vash) in the 4 simulation scenarios A-D with unimodal variance prior
Fig. 2.
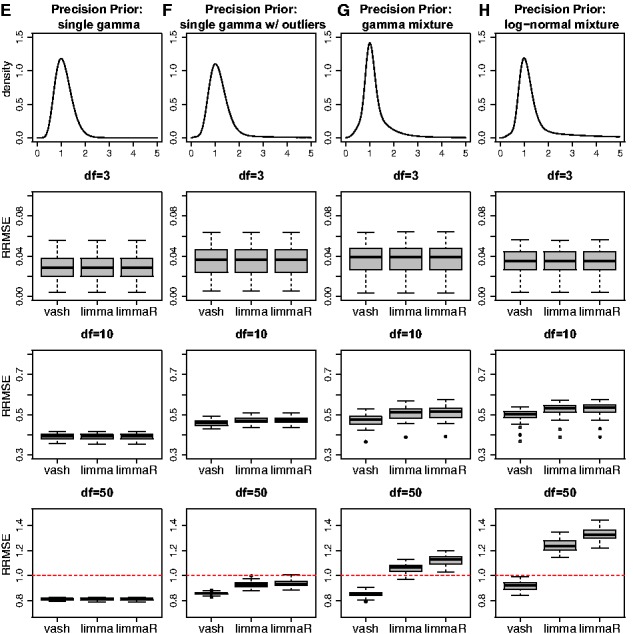
of three gene-specific variances estimators, limma, robust limmaR and our proposed estimator (vash) in the 4 simulation scenarios E-H with unimodal precision prior
Across all scenarios, the mean RRMSE of vash is consistently no worse than either limma or limmaR, and is sometimes appreciably better. In contrast, limmaR sometimes performs better than limma and sometimes worse. In this sense vash is the most robust of the three methods.
In simulations under the simplest scenario (A and E) where the assumptions of limma are met, all three methods perform similarly. In particular, the additional flexibility of vash does not come at a cost of a drop of performance in the simpler scenarios.
When sample sizes are small (df = 3) all methods perform similarly under all scenarios. This highlights the fact that the benefits of more flexible methods like vash are small if samples sizes are too small to exploit the additional flexibility. Put another way, for small sample sizes simple assumptions suffice.
When sample sizes are large (df = 50) vash can outperform the other methods, particularly under the more complex scenarios (C,D; G,H), which most strongly violate the assumptions of limma. Indeed, in these cases both limma and limmaR can have RRMSE > 1, indicating that they perform worse than the unshrunken sample estimators. That is, when sample sizes available to estimate each variance are relatively large shrinkage estimates based on oversimplified assumptions can make estimation accuracy worse rather than better. (In contrast, for small sample sizes, the benefits of shrinkage greatly outweigh any cost of oversimplified assumptions.)
We also note that in scenario B where variances are sampled from a two component inverse-gamma mixture prior (one ‘majority’ component and one ‘outlier’ component), both vash and limmaR perform similarly on average (and slightly outperform limma), but results of vash are slightly more variable than limmaR. Possibly this reflects the fact that limmaR was specifically designed to deal with such cases.
Another metric for comparing EB methods is in the accuracy of the estimated prior distribution. We measure this using , the average distance between the estimated and true cumulative distribution functions (cdfs):
| (25) |
where we take xm ranging from 0 to 10 with increment size 0.01. The results (Supplementary Fig. S1) show that, regardless of sample size, the estimated mixture prior is consistently as accurate as the single inverse-gamma prior, and noticably more accurate in scenarios C, D and G.
We also compare the final differential expression analysis results. All genes are ranked by the P-values given by limma, limmaR and vash (see Section 2.6) respectively. Supplementary Figure S2 shows the AUC (area under ROC curve) of these methods in simulation scenarios A–H. The three shrinkage methods perform very similar in all scenarios.
3.2 Assessment of variances in gene expression data
The results above demonstrate that the more flexible mixture prior implemented in vash, can in principle provide more accurate variance and precision estimates than the simple inverse-gamma prior implemented in limma. However, in practice these gains will only be realized if the actual distribution of variances differs from the single inverse-gamma model. Here we examine this issue using RNA sequencing data from the Genotype-Tissue Expression (GTEx) project (Lonsdale et al., 2013). The GTEx Project is an extensive resource which studies the relationship among genetic variation, gene expression, and other molecular phenotypes in multiple human tissues. Here we consider RNA-seq data (GTEx V6 dbGaP accession phs000424.v6.p1, release date: Oct 19, 2015, http://www.gtexportal.org/home/) on 53 human tissues from a total of 8555 samples (ranging from 6 to 430 samples per tissues).
Since in practice variance estimation is usually performed as part of a differential expression analysis (Smyth, 2004), we mimicked this set-up here: specifically we considered performing a differential expression analysis between every pair of tissues. We selected the top 20 000 most highly expressed genes, transformed their read counts into log-counts-per-million using the ‘voom’ transformation (Law et al., 2014), and used the lmFit function in the limma package to estimate the effects and de-trended variances. Since there are 53 tissues this resulted in 1378 datasets of variance estimates.
First, for each dataset, we quantified the improved fit of the mixture prior versus a single component prior by comparing the maximum log-likelihood under each prior. (For the mixture prior we fitted both the unimodal-variance and unimodal-precision priors, and took the one that provided the larger likelihood.) In principle the mixture prior log-likelihood should always be larger because it includes the single component as a special case; we observed rare and minor deviations from this in practice due to numerical issues. Across all 1378 datasets the average gain in log-likelihood of the mixture prior versus the single component prior was 34.1. The 25% quantile, median, 75% quantile, 90% quantile and maximum of the difference are given by 2.9, 15.8, 42.9, 77.4 and 705.2 respectively. A log-likelihood difference of 15.8 is already quite large: for comparison the maximum difference in log-likelihood for simulations under a single component model, Scenario A, df = 50, was 1.9. We therefore conclude that the mixture component prior fits the data appreciably better for many datasets.
To visualize the deviations from a single component prior present in these data, we examine the fitted priors in datasets where the log-likelihood differences are about 42.9 (75% quantile), 77.4 (90% quantile) and higher. Figure 3 compares the fitted single component prior and mixture prior on several typical scenarios. Generally, the mixture priors use extra components to better fit the middle portion of distribution. The single component priors can match the tails pretty well, but often fails to accurately capture the peak.
Fig. 3.
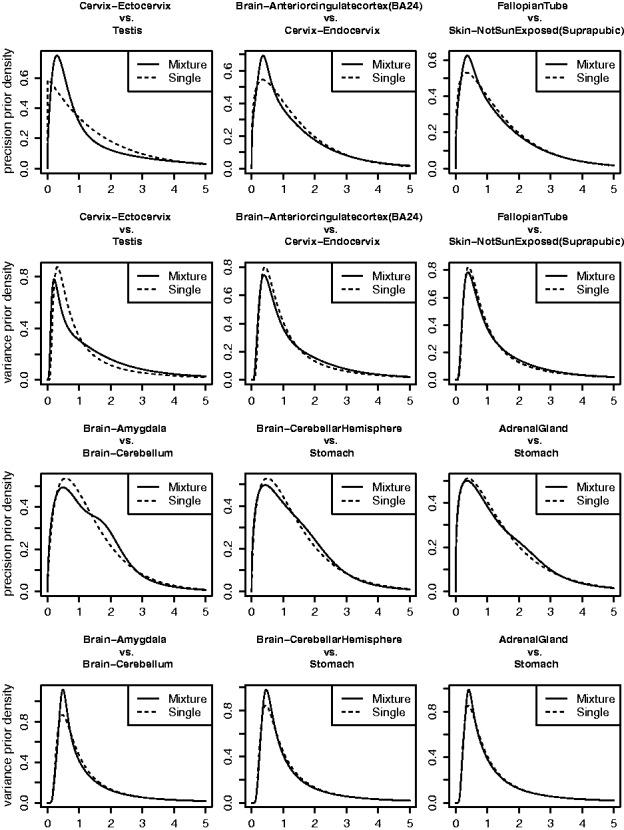
The variance priors (the 2nd and 4th row) and precision priors (the 1st and 3rd row) fitted by mixture prior model (solid line) or single component prior model (dashed line) for 6 tissue pair comparisons. The differences in the log-likelihood between the mixture prior model and the single component prior model for tissue pair comparisons ‘Cervix-Ectocervix vs Testis’, ‘Brain-Amygdala vs Brain-Cerebellum’, ‘Brain-Anteriorcingulatecortex (BA24) vs Cervix-Endocervix’, ‘Brain-CerebellarHemisphere vs Stomach’, ‘Fallopian Tube vs Skin-Not Sun Exposed (Suprapubic)’, ‘Adrenal Gland vs Stomach’ are given by 705, 166, 78, 78, 44, 44 respectively (from top-left to bottom-right)
Overall, our impression from Figure 3 is that differences between the fitted priors seem relatively minor, and might be expected to lead to relatively small differences in accuracy of shrinkage estimates, despite the large likelihood differences. To check this impression we simulated data where the variances are generated from the fitted mixture priors for four of these datasets (the four datasets on the right hand side of Fig. 3). Figure 4 compares the RRMSEs of vash, limma and limmaR in these four scenarios. In general the results confirm our impression: the three methods perform very similarly in most scenarios, although vash shows some gain in accuracy in two scenarios with df = 50.
Fig. 4.
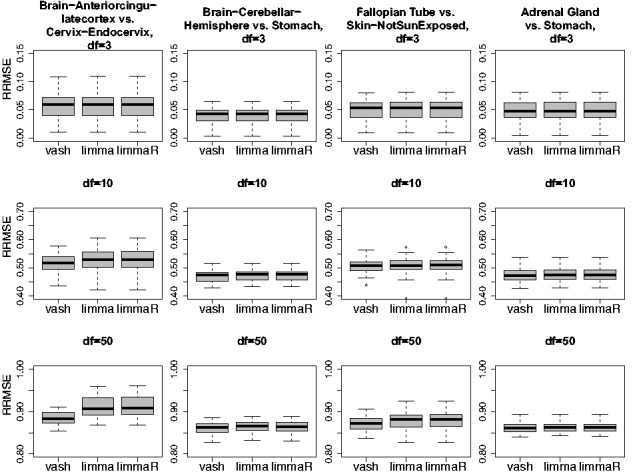
of three gene-specific variances estimators, limma, limmaR and our proposed estimator (vash) in simulation scenarios, which simulate the last four GTEx tissue pair comparisons (‘Brain-Anteriorcingulatecortex (BA24) vs Cervix-Endocervix’, ‘Brain-CerebellarHemisphere vs Stomach’, ‘Fallopian Tube vs Skin-Not Sun Exposed (Suprapubic)’ and ‘Adrenal Gland vs Stomach’) in Figure 3
4 Discussion
We have presented a flexible empirical Bayes approach (‘variance adaptive shrinkage’, or ‘vash’) to shrinkage estimation of variances. The method makes use of a mixture model to allow for a flexible family of unimodal prior distributions for either the variances or precisions, and uses an accelerated EM-based algorithm to efficiently estimate the underlying prior by maximum likelihood. Although slower than limma, vash is computationally tractable for large datasets: for example, for data with 10 000 genes, vash typically takes about 30 s (limma takes just a few seconds).
Our results demonstrate that vash provides a robust and effective approach to variance shrinkage, at least in settings where the distribution of the variances (or precisions) is unimodal. When the true variances come from a single inverse-gamma prior, vash is no less accurate than the simpler method. When the variances come from a more complex distribution vash can be more accurate than simpler methods if the sample sizes to estimate each variance are sufficiently large.
In the gene expression datasets we examined here, the gains in accuracy of vash versus limma are small, and likely not practically important. While this could be viewed as disappointing, it nonetheless seems useful to show this, since it suggests that in many gene expression contexts the simpler approaches will suffice. At the same time, it remains possible that our method could provide practically useful gains in accuracy for other datasets, and as we have shown, it comes at little cost. In addition, our work provides an example of a general approach to empirical Bayes shrinkage—use of mixture components with a common mode to model unimodal prior distributions—that could be useful more generally.
Our method is implemented in an R package vashr available from http://github.com/mengyin/vashr. Codes for reproducing analyses and figures in this paper are at https://github.com/mengyin/vash.
Supplementary Material
Acknowledgements
We thank the NIH GTEx project for providing RNA-seq datasets. We thank N. Ignatiadis, W Huber, and two anonymous referees for detailed comments on the submitted manuscript.
Funding
This work was supported by NIH grant HG002585 and by a grant from the Gordon and Betty Moore Foundation (Grant GBMF #4559).
Conflict of Interest: none declared.
References
- Baldi P., Long A.D. (2001) A Bayesian framework for the analysis of microarray expression data: regularized t-test and statistical inferences of gene changes. Bioinformatics, 17, 509–519. [DOI] [PubMed] [Google Scholar]
- Benjamini Y., Hochberg Y. (1995) Controlling the false discovery rate: a practical and powerful approach to multiple testing. J. R. Stat. Soc. Ser. B (Methodological), 57, 289–300. [Google Scholar]
- Broberg P. et al. (2003) Statistical methods for ranking differentially expressed genes. Genome Biol., 4, R41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dempster A.P. et al. (1977) Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B (Methodological), 39, 1–38. [Google Scholar]
- Efron B. (2016) Empirical Bayes deconvolution estimates. Biometrika, 103, 1–20. [Google Scholar]
- Efron B. et al. (2001) Empirical Bayes analysis of a microarray experiment. J. Am. Stat. Assoc., 96, 1151–1160. [Google Scholar]
- Law C.W. et al. (2014) Voom: precision weights unlock linear model analysis tools for RNA-seq read counts. Genome Biol., 15, R29.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lönnstedt I., Speed T. (2002) Replicated microarray data. Stat. Sin., 12, 31–46. [Google Scholar]
- Lonsdale J. et al. (2013) The genotype-tissue expression (GTEx) project. Nat. Genet., 45, 580–585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murie C. et al. (2009) Comparison of small n statistical tests of differential expression applied to microarrays. BMC Bioinformatics, 10, 1–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phipson B. et al. (2016) Robust hyperparameter estimation protects against hypervariable genes and improves power to detect differential expression. Annals of Applied Statistics, 10, 946–963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smyth G.K. (2004) Linear models and empirical Bayes methods for assessing differential expression in microarray experiments. Statistical Applications in Genetics and Molecular Biology, 3, Article 3. [DOI] [PubMed] [Google Scholar]
- Stephens M. (2016) False Discovery Rates: A New Deal. bioRxiv, p. 038216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Storey J.D. (2002) A direct approach to false discovery rates. J. R. Stat. Soc. Ser. B (Stat. Methodol.), 64, 479–498. [Google Scholar]
- Storey J.D. (2003) The positive false discovery rate: a Bayesian interpretation and the q-value. Ann. Stat., 31, 2013–2035. [Google Scholar]
- Tusher V.G. et al. (2001) Significance analysis of microarrays applied to the ionizing radiation response. Proc. Natl. Acad. Sci. U. S. A., 98, 5116–5121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varadhan R., Roland C. (2004) Squared extrapolation methods (SQUAREM): A new class of simple and efficient numerical schemes for accelerating the convergence of the em algorithm. Johns Hopkins University, Dept. of Biostatistics Working Papers. Working Paper 63.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


