Thresholds and ultrasensitivity from negative cooperativity

Abstract

Negative cooperativity is a phenomenon in which the binding of one or more molecules of a ligand to a multimeric receptor makes it more difficult for subsequent ligand molecules to bind. Negative cooperativity can make a multimeric receptor’s response more graded than it would otherwise be. We show, however, through theory and experiment, that if the ligand binds the receptor with high affinity and can be appreciably depleted by receptor binding, then negative cooperativity produces a qualitatively different type of response: a highly ultrasensitive response with a pronounced threshold. Because ultrasensitivity and thresholds are important for generating various complex systems-level behaviors, including bistability and oscillations, negative cooperativity may be an important ingredient in many types of biological response.

One Sentence Summary

Here we show that negative cooperativity can add thresholds and ultrasensitivity to a signaling system.

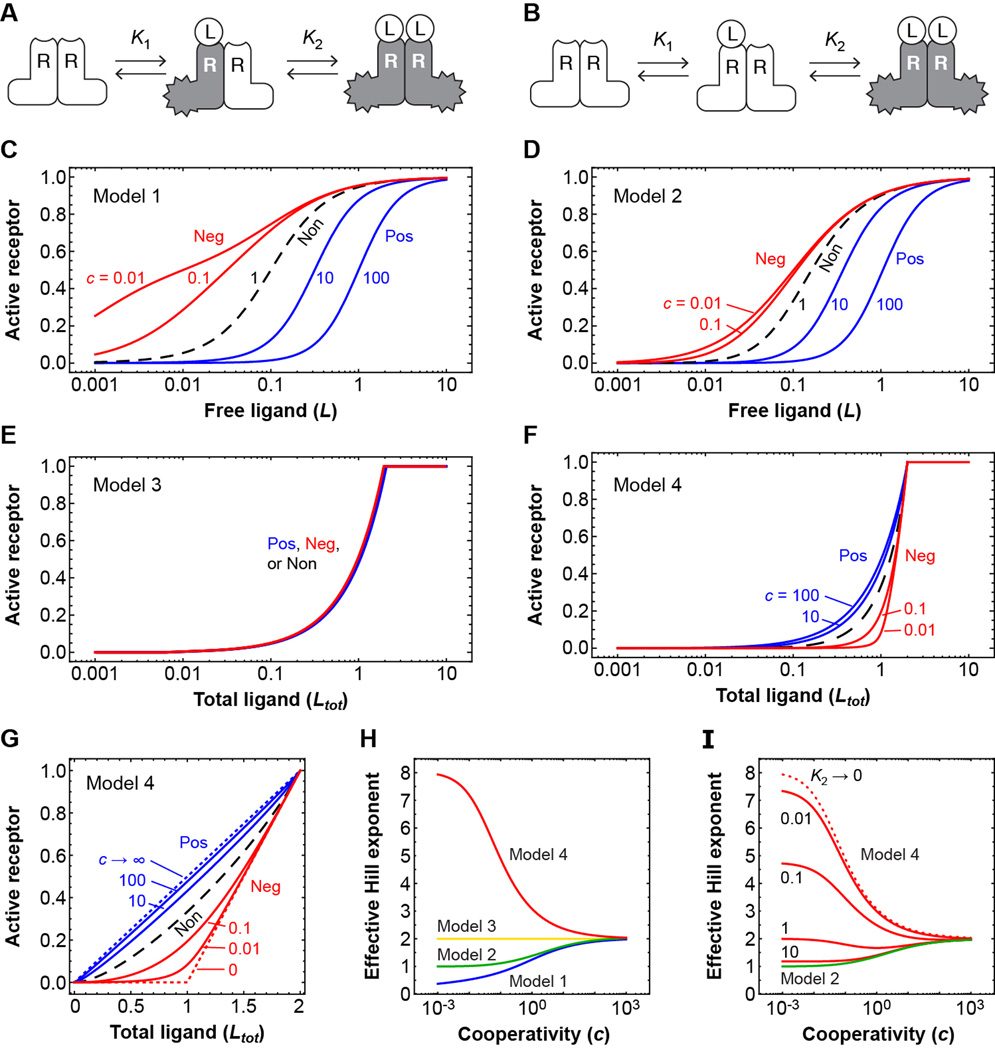
Receptors, signal transducers, and transcription factors are often present as oligomers, and so understanding the interactions of multimeric complexes with their regulators is fundamental for understanding cellular regulation. Fig. 1, A and B show two simple schemes for the sequential interaction (1, 2) of a stably dimeric receptor (R₂) with a monomeric ligand (L). If the two equilibrium constants are equal, the binding events can be viewed as independent; if the first binding is weaker than the second (K₁ > K₂), there is positive cooperativity; and if the first binding reaction is stronger than the second, there is negative cooperativity. The parameter c = K₁/K₂ can be taken as a measure of the cooperativity, with c < 1 corresponding to negative cooperativity and c > 1 to positive cooperativity.

Fig. 1. Negative cooperativity can produce a sharp threshold in the response of a dimeric receptor to a high affinity ligand.

(A and B) Schematic view of the sequential binding of a ligand to a stable dimeric receptor, assuming (A) the receptor subunits are activated independently by ligand binding, or (B) the receptor is activated only when two ligands are bound. (C to F) Receptor activity as a function of free ligand concentration [(C) and (D)] or total ligand concentration [(E) and (F)] for various assumed degrees of cooperativity. In each panel, the blue curves correspond to positive cooperativity; the dashed black curve corresponds to independent binding with c = 1; and the red curves correspond to negative cooperativity. In panels (C) and (D) it is assumed that K₂ = 0.1; higher or lower values would shift the curves to the right or left, but would not alter the shapes of the curves. In panels E and F, it is assumed that the binding affinities are very high and the equilibrium constants approach zero. (G) Linear plots of receptor activation as a function of total ligand concentration for Model 4. (H) The effective Hill exponents as a function of the cooperativity c for the four models. The Hill exponents are calculated as described by Koshland and Goldbeter (3, 24): n_H = log₁₀[81] / log₁₀[EC90 / EC10], where EC90 is the concentration of ligand that yields a 90%-maximal response, and EC10 is the concentration that yields a 10%-maximal response. (I) The effect of decreasing the ligand-receptor affinity on the effective Hill exponents for Model 4. Details of the theory can be found in the Supplementary Materials. Log-log plots of the stimulus-response curves and plots of the local response sensitivities can be found in figure S1.

If it is assumed that each receptor subunit is activated independently by ligand binding—i.e., the singly-bound receptor is half as active as the doubly-bound receptor (Model 1, Fig. 1A)—then the stimulus-response relations for various assumed degrees of cooperativity are as shown in Fig. 1C. If, instead, only the doubly-bound receptor is active (Model 2, Fig. 1B), the curves are as shown in Fig. 1D. In either case, the greater the positive cooperativity, the more switch-like or ultrasensitive the response is (Fig. 1, C and D, blue curves), and as c approaches infinity, the effective Hill exponent (n_H) for the response approaches 2. Conversely, the stronger the negative cooperativity, the more graded the response is (Fig. 1, C and D, red curves). In Model 1, high negative cooperativity makes the response subsensitive (3), with an effective Hill exponent less than 1. The system becomes less decisive, but is better able to discriminate between various high levels of stimulus than it otherwise could. In Model 2, the Hill exponent never falls below 1. However, in both models, the higher the positive cooperativity, the higher the ultrasensitivity, and the greater the negative cooperativity, the more graded the response.

Implicit in this approach is the assumption that the number of ligand molecules is much larger than the number of receptors—either the ligand concentration is higher, or the ligand is distributed through a larger volume, or both—so that receptor binding has a negligible effect on the concentration of free ligand. This is a reasonable assumption for, say, the binding of oxygen to hemoglobin, metabolites to metabolic enzymes, or circulating drugs to receptor proteins. But in some cases—notably intracellular signaling—the upstream regulator may be comparable to or even lower in concentration than the protein (or other target) it is regulating. We therefore examined how the stimulus-response curves would be affected if the ligand were not assumed to be in infinite supply.

We derived expressions for the relation between the total ligand concentration L_tot, rather than the free ligand concentration L, and the equilibrium fraction of receptor in the unbound, singly-bound, and doubly-bound states (Supplementary Materials). Because ligand depletion is most pronounced when the affinity of the ligand is high, we initially examined the response in the limit where the K values approach zero.

If it is assumed that the receptor subunits are activated independently (Fig. 1A), the stimulus-response curves are unaffected by the assumed cooperativity (Model 3, Fig. 1E). On a linear plot, the response is a simple linear increase in receptor activity with total ligand concentration, until full activation is attained (not shown). Thus the classical connection between positive cooperativity and ultrasensitivity is broken.

More strikingly, if it is assumed that two binding events are required to activate the receptor (Fig. 1B), and there is negative cooperativity in the binding, then the stimulus-response curve acquires a sharp threshold (Model 4, Fig. 1F). This can perhaps be best appreciated on a linear plot as shown in Fig. 1G. The smaller the value of c, the sharper the threshold is. The effective Hill exponent for Model 4’s response is smallest when there is a high degree of positive cooperativity in the ligand binding, and it increases as c decreases, approaching a maximum value of ~8.04 as c approaches zero. Comparing all four models (Fig. 1H), it is negative cooperativity, rather than positive cooperativity, that produces the most highly ultrasensitive responses. Similar conclusions can be drawn using a local definition of response sensitivity $(\frac{d\text{ ln}\mathit{\text{Output}}}{d\text{ ln}\mathit{\text{Input}}})$ (4) (figure S1).

So far we have assumed that the equilibrium constants for ligand binding are vanishingly small. If lower affinities are assumed, so that the receptor is less effective at depleting low concentrations of ligand, the ultrasensitivity of the response is lessened (Fig. 1I). Ultimately the binding curves and effective Hill exponents obtained from Model 4 approach those obtained with Model 2 (Fig. 1I), as expected.

An intuitive explanation of these findings is shown in Fig. 2, A and B. If there is strong negative cooperativity, then the first site acts as a stoichiometric buffer, soaking up the first increments of the depletable ligand without producing a response (5–7). Only when the concentration of ligand exceeds the capacity of this buffer can the second binding event, and the consequent receptor activation, occur.

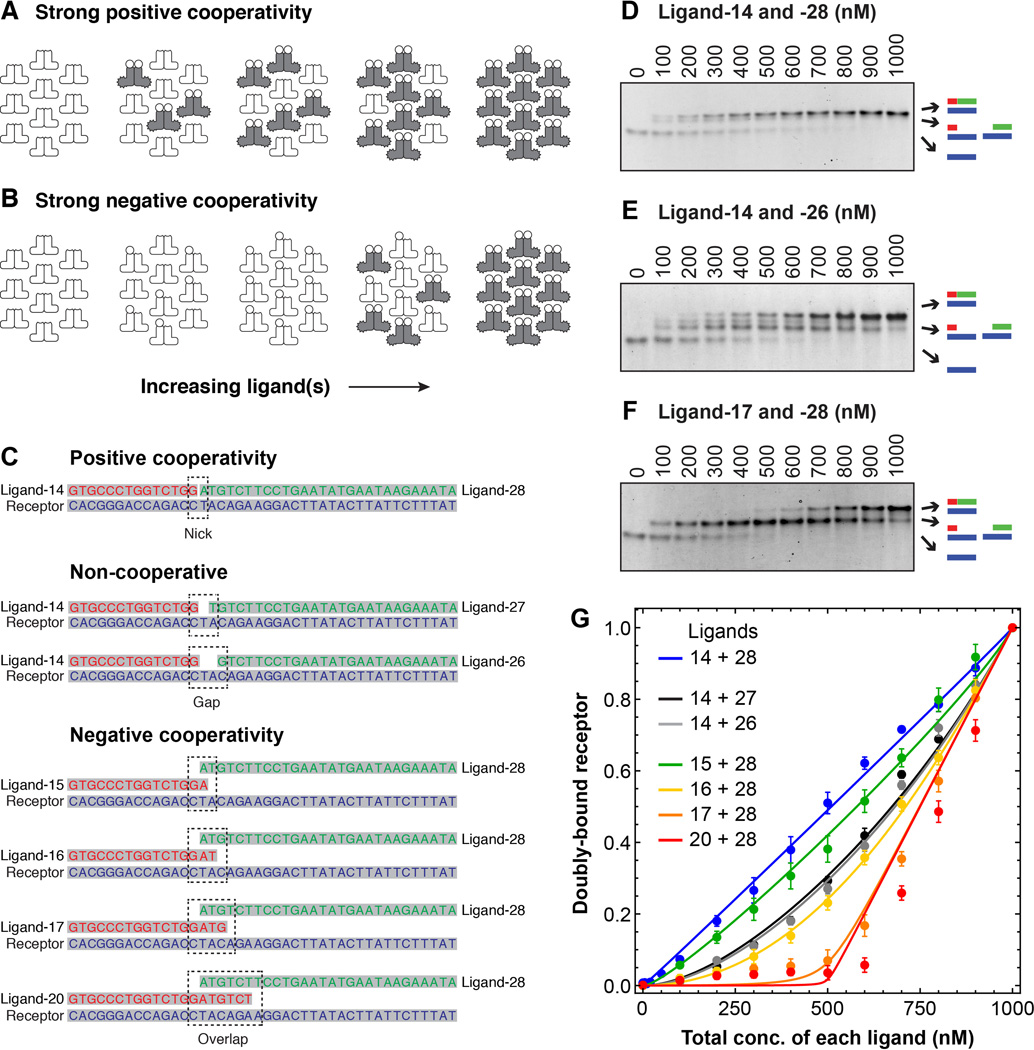
Fig. 2. The effects of positive and negative cooperativity on response thresholds in a DNA annealing model of receptor-ligand interaction.

(A and B) Schematic view of how increasing the ligand concentration at fixed receptor concentration would be expected to affect the formation of full ternary complexes in the case where binding is strongly positively cooperative (A) or strongly negatively cooperative (B). (C) Oligonucleotides used for the binding studies. The first pair was expected to exhibit positive cooperativity due to base stacking at the junction between the two ligand oligos. The next two pairs were expected to exhibit independent non-cooperative binding because of the gap between the two ligands. The four pairs labeled “negative cooperativity” were expected to exhibit either net negative cooperativity, or at least less positive cooperativity than ligands 14 + 28. See table S1 for further discussion of the expected annealing energies and cooperativities for the seven ligand pairs. (D to F) Analysis of three binding reactions by native polyacrylamide gel electrophoresis. The total receptor concentration was 1000 nM, and the two ligands were both present at the concentrations indicated. Primary binding data for the four other ligand pairs can be found in figure S2. (G) Cumulative data for all seven ligand pairs. Points represent means ± S.E. from five (all but the data for ligands 14 + 28) or ten (the ligand 14 + 28 data) experiments. The curves are fits of the data to Eq 12 from the Supplementary Materials section.

To experimentally test these theoretical findings, we engineered the high affinity binding of two ligand molecules to a receptor under conditions of independent binding, positively cooperative binding, and negatively cooperative binding, and quantitatively assessed the shapes of the binding curves. To accomplish this we turned to DNA annealing, which made it easy to obtain high affinities and to manipulate the cooperativity. The basic idea was to use one strand of DNA as the equivalent of a dimeric receptor, and then use complementary strands as ligands. To avoid the possible formation of a stable hairpin structure between a ligand molecule and both binding sites on the receptor, we used a receptor DNA strand that bound two different ligands, with similar affinities, at two adjacent binding sites (8). We made the binding positively cooperative by using ligands that would abut each other when bound, allowing for favorable base-stacking interactions (9, 10); non-cooperative by engineering a one- or two-nucleotide gap between the ligand binding sites; and negatively cooperative, or at least less positively cooperative, by having the two ligand binding sites overlap by one to six nucleotides (Fig. 2C). We then measured how the equilibrium concentration of doubly-bound receptors varied with the total ligand concentration, by native polyacrylamide gel electrophoresis, staining, and densitometry.

For the experiments shown in Fig. 2, the total concentration of the receptor oligo was held constant at 1000 nM, and the concentrations of each of the complementary ligand oligos were varied together. Pilot experiments showed that maximal complex formation was achieved at 1000 nM ligand concentration (yielding a stoichiometry of the two ligands and the receptor of 1:1:1), as expected from the theory, so we focused on a detailed dose-response relationship for ligand concentrations between 0 and 1000 nM. The theoretical binding equation (Eq 12, Supplementary Materials) was then fitted to the data, with the cooperativity c as the only adjustable parameter. Fig. 2, D to F show examples of the primary data for pairs of ligands that were expected to yield positive cooperativity (ligands 14 and 28), independent binding (ligands 14 and 26), or negative cooperativity (ligands 17 and 28). Fig. 2G shows the cumulative data for all seven ligand pairs, from five (all of the ligand pairs except 14 and 28) or ten (ligands 14 and 28) experiments.

The ligands expected to exhibit positive cooperativity (14 and 28) yielded a linear stimulus-response relationship (Fig. 2G, blue curve); those expected to bind independently (14 and 26 or 27) yielded nonlinear stimulus-response curves with c values closer to 1 (Fig. 2G, black and grey curves, and table S1); and those expected to exhibit negative (or less positive) cooperativity (15, 16, 17, or 20 plus 28) yielded a series of curves with increasingly marked thresholds and decreasing inferred values of c (Fig. 2G, green, yellow, orange, and red curves). Some of the inferred c values were higher than expected from simple energetic considerations (table S1) (11, 12). Nevertheless, the data demonstrate that negative cooperativity can, as predicted, imbue a marked threshold and a high degree of ultrasensitivity upon the formation of a ternary complex between a receptor and two high-affinity ligands.

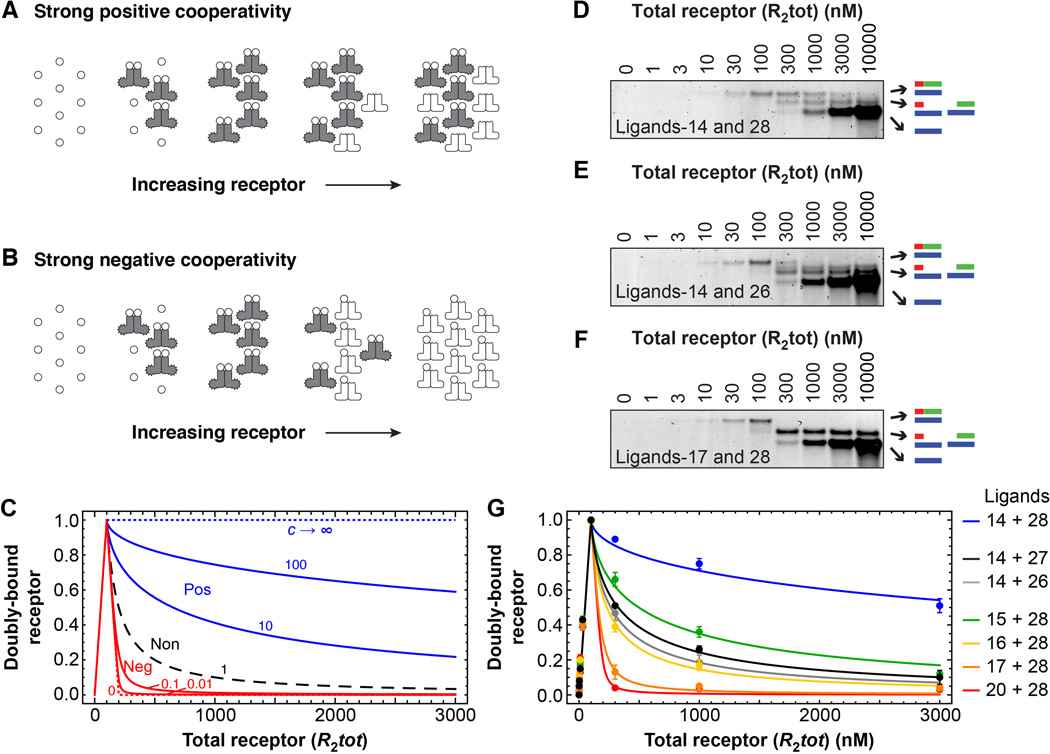
Another feature of the classical sequential models (Models 1 and 2) is that receptor activation increases linearly with the total concentration of receptor (Eqs 7 and 8). This is not true, however, for Model 4, which considers ligand depletion. In the high affinity limit, the response is predicted to be biphasic. As the receptor concentration increases, the output initially increases, peaks when the stoichiometric ratio of receptor to ligand is 1:2, and decreases thereafter (Fig. 3, A to C) (13). The narrowness of the response peak depends upon the cooperativity of the binding; positive cooperativity makes the fall-off in output at high receptor concentration occur gradually, and negative cooperativity makes the fall-off more abrupt (Fig. 3, A to C). This phenomenon is conceptually related to the prozone effect, discovered in early studies of antigen-antibody interactions (14, 15); to the phenomenon of transcriptional squelching (16–18); and to the inhibition of protein kinase signaling by overexpression of scaffold proteins (19–22). Essentially the receptor is behaving like a bivalent adaptor, and high concentrations of the receptor drive the formation of binary ligand-receptor complexes at the expense of the full ternary complex.

Fig. 3. Biphasic responses as the total receptor concentration is varied.

(A and B) Schematic view of the formation of ternary complexes as a function of receptor concentration where binding is strongly positively cooperative (A) or strongly negatively cooperative (B). (C) Theoretical binding curves based on Model 4 and Eq 12 from the Supplementary Materials. The total ligand concentration was assumed to be 200 arbitrary units. (D to F) Analysis of three binding reactions by native polyacrylamide gel electrophoresis. In each case, the concentration of each ligand was 100 nM and the total receptor concentration was varied as indicated. Primary binding data for the four other ligand pairs can be found in figure S3. (G) Cumulative binding data for all seven ligand pairs. Points represent means ± S.E. from three to eight experiments. The curves are fits of the data to Eq 12 from the Supplementary Materials section.

We therefore determined whether complex formation was a biphasic function of receptor concentration, again using the oligonucleotide ligands shown in Fig. 2C. The formation of the full ternary complex was biphasic, in good agreement with theory (Fig. 3, D to G). The ligands expected to exhibit the highest degrees of negative cooperativity produced the sharpest biphasic peaks, and, as shown in table S1, the inferred cooperativity values agreed reasonably well with those obtained from the threshold data in Fig. 2.

Our results show that for the high affinity interaction of a multimeric receptor with a depletable ligand, marked thresholds and high degrees of ultrasensitivity can arise as a result of negative cooperativity in the binding reactions. Such thresholds can allow a system to filter out small stimuli, and yet respond decisively to suprathreshold stimuli. Moreover, the thresholds and ultrasensitivity obtained through this mechanism can be critical elements for the production of more complex systems-level behaviors like bistability and oscillations (23). In addition, multimeric receptors can exhibit a biphasic response to changes in the concentration of the receptor, and this biphasic response is sharpest when strong negative cooperativity is present. These basic aspects of the regulation of multimeric proteins may be important both for understanding the behavior of natural regulatory systems and for designing synthetic ones.