Ideal charge-density-wave order in the high-field state of superconducting YBCO

Significance

Compelling evidence of various forms of nonsuperconducting electronic order in the cuprate high-temperature superconductors has fundamentally altered our understanding of the essential physics of these materials. However, it has been difficult to establish the nature of the quantum (zero-temperature) phases that compete and/or coexist with superconductivity. By studying high-quality crystals of YBCO using an X-ray laser and pulsed magnetic fields, we have established that the field induced charge-density-wave (CDW) order that arises when superconductivity is suppressed at low temperatures is incommensurate, unidirectional, and 3D-ordered. While disorder ultimately precludes true CDW long-range order, there does appear to be a sharply defined crossover field, which we associate with a transition to a nematic state with long-range orientational order.

Abstract

The existence of charge-density-wave (CDW) correlations in cuprate superconductors has now been established. However, the nature of the CDW ground state has remained uncertain because disorder and the presence of superconductivity typically limit the CDW correlation lengths to only a dozen unit cells or less. Here we explore the field-induced 3D CDW correlations in extremely pure detwinned crystals of YBa₂Cu₃O₂ (YBCO) ortho-II and ortho-VIII at magnetic fields in excess of the resistive upper critical field ($H_{\text{c}2}$) where superconductivity is heavily suppressed. We observe that the 3D CDW is unidirectional and possesses a long in-plane correlation length as well as significant correlations between neighboring CuO₂ planes. It is significant that we observe only a single sharply defined transition at a critical field proportional to $H_{\text{c}2}$, given that the field range used in this investigation overlaps with other high-field experiments including quantum oscillation measurements. The correlation volume is at least two to three orders of magnitude larger than that of the zero-field CDW. This is by far the largest CDW correlation volume observed in any cuprate crystal and so is presumably representative of the high-field ground state of an “ideal” disorder-free cuprate.

Charge-density-wave (CDW) order has been found to exist universally in the hole-doped superconducting cuprates (1–18), and the common characteristics at zero magnetic field include bidirectionality, quasi-2D and short-ranged correlations (7–17). More specifically, the CDW diffraction patterns are found in both directions of Cu–O bonds in the CuO₂ plane (Fig. 1A), and the CDW correlation lengths parallel and perpendicular to the planes (i.e., along the $a$- or $b$-axes and the $c$ axis) are less than $\sim 20$ and $\sim 1$ lattice constants, respectively (7–16), corresponding to a correlation volume of order ${10}^2$ unit cells (UCs). Thus, the properties of the quasi-2D CDW are likely strongly affected by disorder and only indirectly represent the true nature of the underlying CDW correlations. Indeed, X-ray scattering shows that the onset of the quasi-2D order is gradual without a sharp transition (7–17), consistent with the influence of quenched disorder on an incommensurate CDW (19–21). Furthermore, whereas Y-based and La-based cuprates exhibit a clear competition between CDW and superconductivity (7, 8, 12–15), such competition is not apparent in the families of Bi-based and Hg-based cuprate compounds (9–11)—a discrepancy that probably reflects different degrees of quenched disorder among cuprate families.

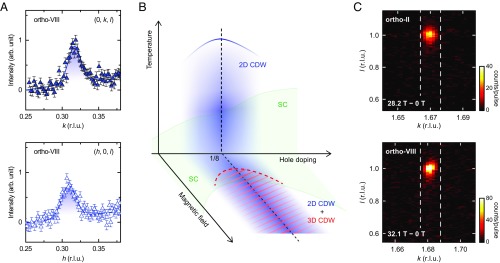
Fig. 1.

CDW orders in YBa₂Cu₃O_x (YBCO). (A) Zero-field quasi-2D CDW diffraction peak profiles (Upper and Lower) of ortho-VIII in the k- and h-directions, respectively, measured by resonant soft X-ray scattering at Cu $L_3$-edge and $T=67$ K (Materials and Methods). It is bidirectional (i.e., the diffraction peaks are found in both Cu–O bond directions in the CuO₂ plane). (B) A schematic sketch of the temperature-doping-magnetic field phase diagram of YBCO near a hole concentration $p=1/8$. The quasi-2D CDW (blue shaded area) evolves from high temperature and exists at both zero and finite magnetic fields. The 3D CDW (red-colored, hatched area) emerges only in high magnetic fields and at low temperatures but coexists with the 2D one (SI Appendix, Fig. S2B). (C) Maps of the difference between the diffraction intensities at high field and zero field in ortho-II (Upper) and ortho-VIII (Lower) (SI Appendix, Fig. S2A). The bright spots are the 3D CDW diffraction patterns located at $\text{𝐐}\sim (0,2-\text{𝑞},1)$, where q is $\sim 0.33$ in reciprocal lattice units (r.l.u.) and $\sim 0.32$ r.l.u. for ortho-II and ortho-VIII, respectively. The white dashed lines indicate the windows used to extract the projected peak profile shown in Figs. 2 and 4.

Recently, a CDW with significantly longer correlation lengths was observed in superconducting YBCO (Fig. 1B) via X-ray scattering at high magnetic fields (13, 14). This reveals the character (i.e., 3D) of the high-field charge ordering previously inferred by other measurements (3–6). At a magnetic field of $\sim 30$ T, its in- and out-of-plane correlation lengths are of the order of 100 and 10 lattice constants, respectively (13, 14), which are significantly larger than those of the zero-field 2D CDW. Thus, it arguably represents the CDW ground state of an “ideal” disorder-free cuprate superconductor. However, to date, although this 3D CDW has been reported at doping levels of $p\sim 0.12$ and $\sim 0.11$ (13, 14), limited high-field data near $H_{\text{c}2}$ are only available at $p\sim 0.12$ (13). To establish the 3D CDW phenomenology, it is important to track its doping and magnetic field dependences up to $H_{\text{c}2}$ and to elucidate its puzzling relationship with the quasi-2D CDW that coexists with the 3D one even at high field (Fig. 1B) (13, 14).

Results

To address these issues, we first investigate detwinned YBCO ortho-II ($x=6.51$) using X-ray scattering at an X-ray free electron laser (FEL) combined with a pulsed magnet (13) (Materials and Methods). With ${\mu }_{0}H=28.2$ T, we clearly observe a field-induced CDW at $\text{𝐐}=(0,2-q,1)$ with an incommensurate $q\sim 0.33$ r.l.u (Fig. 1C). Similar to the case of YBCO ortho-VIII (13), the field-induced 3D CDW exhibits the same $q$-value as that of the zero-field quasi-2D CDW but with an integer rather than a half-integer $l$-value (8, 15). Note that the quasi-2D CDW still exists at this field (SI Appendix, Fig. S2B), confirming its coexistence with the 3D CDW.

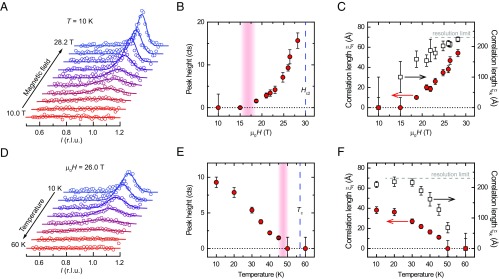
The emergence of the 3D CDW order in YBCO ortho-II as a function of magnetic field is shown in Fig. 2A. As shown in the peak intensity at $l\sim 1$ (Fig. 2B), the 3D CDW appears at ${\mu }_0{H}_{3D}\sim 18$ T. Further increase of the magnetic field not only increases the diffraction peak intensity but also narrows the peak width along both the $l$- and $k$-directions (Fig. 2C). At 28.2 T and 10 K, the ortho-II correlation lengths in the $k$- and $l$-directions are more than $230\text{Å}$ (which is limited by our instrument resolution) and $55\text{Å}$, respectively. Furthermore, the 3D CDW shows strong temperature dependence (Fig. 2D). At ${\mu }_{0}H=26.0$ T, the projected peak intensity (Fig. 2E) and correlation length (Fig. 2F) demonstrated the appearance of the 3D CDW at $T_{3\text{D}}\sim 45$ K, which is considerably lower than the onset temperature of the quasi-2D CDW ($\sim 120$ K), but just slightly lower than $T_{\text{c}}$ (57 K at 0 T). Note that the onset field and temperature agree well with the thermodynamic phase boundary deduced from sound velocity measurements (5). Altogether, the $H$- and $T$-dependences demonstrate that 3D CDW emergence is triggered by the magnetic field suppression of superconducting correlations.

Fig. 2.

Field and temperature dependences of the 3D CDW in ortho-II. (A and D) Projected peak profile along (0, 1.67, l) as a function of magnetic field at $T=10$ K ($A$) and as a function of temperature at μ₀𝐻 = 26.0 (D). The data points are obtained by integrating the field-induced signal over the range of k indicated by the dashed line in Fig. 1C. Solid lines are Gaussian fits to the data. Note that the kl difference maps in the corresponding H and T are shown in SI Appendix, Fig. S3. (B and C) Fitted 3D CDW peak heights (B) and correlation lengths (C) in the l- and k-directions as a function of magnetic field. (E and F) Fitted 3D CDW peak heights (E) and correlation lengths (F) in the l- and k-directions as a function of temperature. The red shaded area denotes the onset region of the 3D CDW. Note that the k-correlation lengths at large H and low T are resolution-limited ($\sim 230\text{Å}$, indicated by the gray dashed lines in E and F); thus, they represent lower bounds of the actual values. The displayed ${\xi }_k$ have been not corrected for an instrument resolution. All dotted lines indicate zero. The error bars denote 1 SD as obtained from the peak fitting.

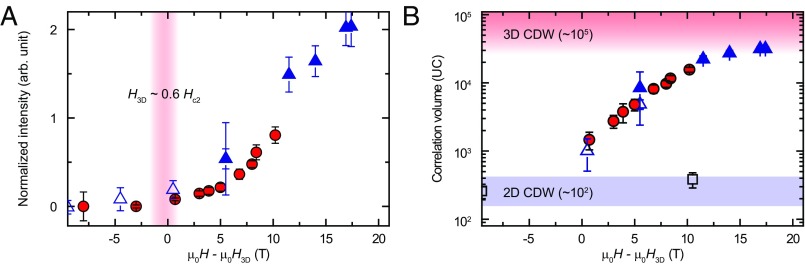
The field dependence of the 3D CDW in YBCO ortho-II is similar to that previously observed in ortho-VIII (13). As shown in Fig. 3A, if plotted as a function of shifted magnetic field (i.e., ${\mu }_{0}H-{\mu }_0{H}_{3\text{D}}$), the growth rate of the normalized 3D CDW intensity is remarkably similar in the two crystals, despite the different doping concentrations. Furthermore, both crystals exhibit a similar quantitative evolution of the 3D CDW correlation volume, which reaches $\sim {10}^5$ UCs at $H\sim H_{\text{c}2}$ (Fig. 3B)—more than two orders larger than that of the quasi-2D order. Interestingly, the ratio $H_{3\text{D}}/H_{\text{c}2}$ is ∼0.6 for both crystals, suggesting that $H_{3\text{D}}$ closely tracks $H_{\text{c}2}$, a key characteristic of the superconducting state. These findings further demonstrate the intimate relation between the 3D CDW and superconductivity, as well as supporting the attribution of the 3D CDW order as representative of the “disorder-free” situation.

Fig. 3.

Comparison of 3D CDWs in the ortho-II and ortho-VIII. (A) Fitted 3D CDW peak height of ortho-II (circles) and ortho-VIII (triangles) as a function of ${\mu }_{0}H-{\mu }_0{\text{𝐻}}_{3\text{D}}$. Here, $H_{3\text{D}}$ is 14.5 T and 18 T for the ortho-VIII (13, 14) and ortho-II crystals, respectively. The peak heights are normalized to 1 at $H_{\text{c}2}$. The values of resistive $H_{\text{c}2}$ are adapted from ref. 22: 24 T and 30 T for our ortho-VIII and ortho-II crystals, respectively. The red shaded area denotes the onset region of the 3D CDW. Data of open triangles were taken from ref. 13. (B) Estimated 3D CDW correlation volumes of ortho-II (circles) and ortho-VIII (open/closed triangles) as a function of ${\mu }_{0}H-{\mu }_0{H}_{3\text{D}}$. To estimate the correlation volume, we have assumed that the correlation length along the h-direction is the same as along the k-direction for the 3D CDW at (0, 2-q, 1). Note that the in-plane correlation length used in this estimate is resolution-limited, so the estimated volume is a lower bound. The gray shaded area denotes the 2D CDW volume in ortho-VIII; data marked by the open squares (i.e., 2D CDW volumes) were taken from ref. 13. Error bars correspond to 1 SD.

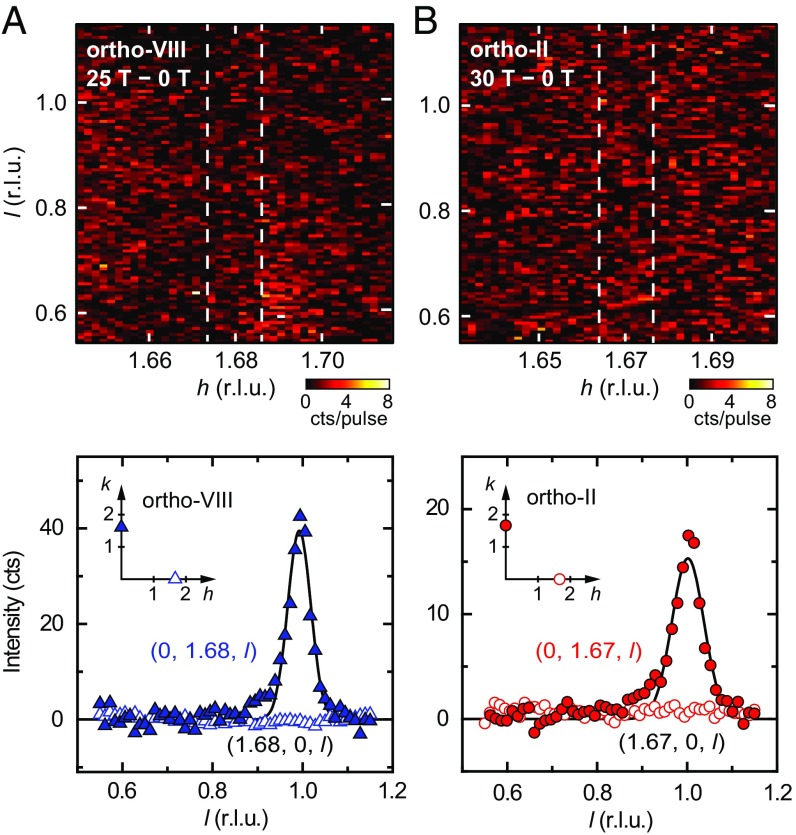
Finally, we investigate signatures of the 3D CDW at an ordering wavevector in the $h$-direction at $\sim H_{\text{c}2}$ (22). Although the zero-field 2D CDW is bidirectional (e.g., Fig. 1A) (16, 17), it was discovered in ref. 14 that the 3D CDW in ortho-VIII is unidirectional (i.e., there is no detectable 3D CDW in the $h$-direction). Since those experiments only went up to 16.9 T, which is just $\sim$2 T above $H_{3\text{D}}$, it was still unclear whether the unidirectionality is an essential feature of the 3D CDW, as the possibility of an onset of 3D CDW in the $h$-direction at a slightly higher critical field could not be discarded. In our measurement up to 25 T no sign of the CDW pattern in ortho-VIII is seen near $l=1$, as displayed in Fig. 4A, Upper. This is also evident in the featureless projected intensity along the $l$-direction (Fig. 4A, Lower) at $𝐐=(1.68,\mathrm{0,1})$, in stark contrast to that at $𝐐=(\mathrm{0,1.68},1)$. Thus, we establish that the order in ortho-VIII remains unidirectional and there is no further transition up to 25 T, in excess of $H_{\text{c}2}$ and more than 50% above $H_{3\text{D}}$. Furthermore, we have performed the same measurement on ortho-II (Fig. 4B). Similarly, we find no 3D CDW up to 30 T, which overlaps the range of field where quantum oscillations are observed (23). Altogether, we establish that 3D CDW in YBCO is robustly unidirectional; the 3D CDW is “stripe-like” with an ordering vector parallel to the Cu–O chain direction.

Fig. 4.

Unidirectional character of the 3D CDW. Zero-field-background subtracted diffraction intensity maps of ortho-VIII (A) and ortho-II (B) in high magnetic fields and in the hl-reciprocal plane (Upper). (Lower) The projected intensities along ($1.68,0,l$) (blue open triangles) and ($\mathrm{0,1.68},l$) (blue closed triangles) in ortho-VIII and ($1.67,0,l$) (red open circles) and ($\mathrm{0,1.67},l$) (red closed circles) in ortho-II. The projected intensity is obtained by integrating the signal within the window indicated by the dashed lines in A and B, Upper and Fig. 1C. Solid lines are Gaussian fits to the data.

Discussion

We now discuss the puzzling relation between the unidirectional 3D CDW and the bidirectional 2D CDW. The drastic differences in the qualitative behaviors, including their directionality (13–16), dimensionality (8, 13–15), and their $H$- and $T$-dependences (8, 13–16), suggest that the unidirectional 3D CDW is a different entity from the quasi-2D CDW (7, 8, 15, 16). However, the diffraction signals from the 2D and 3D CDWs coexist (13, 14). It seems to us that the most promising way to reconcile these observations is to assume that there are distinct domains with the two types of CDW. However, the fact that the in-plane wavevectors of the two CDWs are identical suggests that they share the same local correlations inherent in the electronic structure of YBCO. Because the 3D CDW is unidirectional, we argue that the inherent CDW correlations correspond to unidirectional charge stripes.

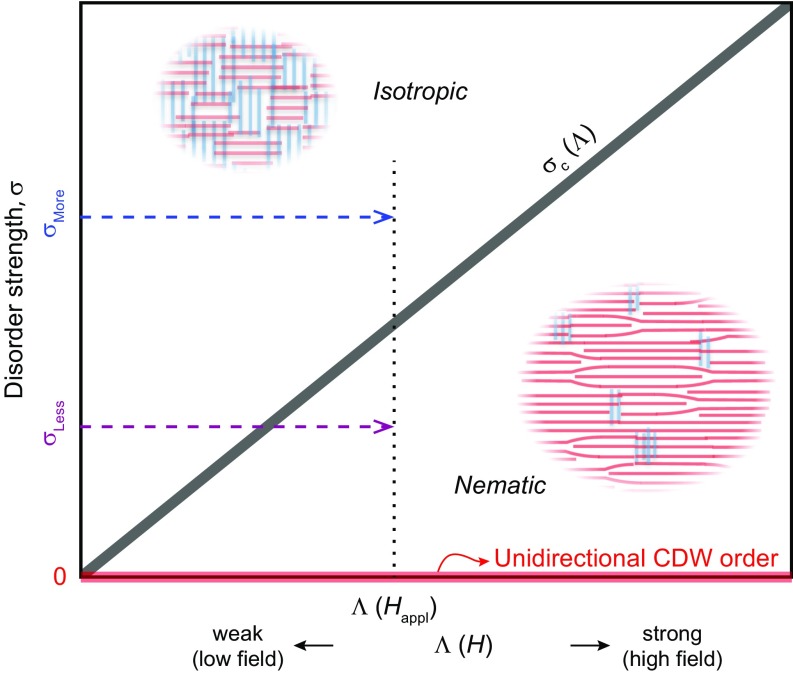
On theoretical ground (19), an incommensurate CDW phase exists as a sharply defined phase of matter (i.e., with true long-range order) only in the ideal limit of vanishing disorder. However, as shown in Fig. 5, for a unidirectional CDW in a tetragonal system, a sharply defined nematic phase, a form of “vestigial” CDW order (19) that spontaneously breaks the point-group symmetry, exists so long as the disorder strength, $\sigma$, is less than a finite critical value, ${\sigma }_c$. The phase transition at $\sigma ={\sigma }_c$ is rounded in an orthorhombic system, but so long as the symmetry breaking field is weak there remains a sharp cross-over from an approximately bidirectional phase (i.e., isotropic) for $\sigma >{\sigma }_c$ to a strongly unidirectional phase for $\sigma <{\sigma }_c$. The bidirectional phase can still be locally stripe-like (17), but with the orientation of the stripes determined by the local disorder potential rather than by the orthorhombicity. Indeed, a strong tendency to nematic order (oriented by the weak orthorhombicity of YBCO) has been inferred from various experiments (24–26). In SI Appendix we illustrate these points using an effective field theory and also address the cross over from 2D to 3D correlations at ${\sigma }_c$.

Fig. 5.

Schematic CDW phase diagram. Low-temperature phase diagram of a layered crystal as a function of disorder strength ($\sigma$) and CDW strength, $\mathrm{\Lambda }(H)$, assumed to be an increasing function of increasing H, due to the suppression of the superconductivity. It is assumed that the disorder-free state (marked by the red-colored bar on the x axis) is an incommensurate, unidirectional CDW. In a tetragonal crystal, the thick gray line marks a nematic transition, ${\sigma }_c$, whereas in a weakly orthorhombic YBCO crystal it is a cross-over. Above ${\sigma }_c$, CDW correlations are short-ranged and bidirectional. Insets show the cartoons of disorder-pinned CDW domains; approximately isotropic, bidirectional, CDW phase (top left) and sharply defined nematic, unidirectional phase (bottom right). In the context of the proposed inhomogeneity scenario, the purple and blue dashed arrows demonstrate the field-dependent CDW evolution in the less (${\sigma }_{\text{Less}}$) and more (${\sigma }_{\text{More}}$) disordered regions of the sample. At a given applied magnetic field ($H_{\text{appl}}$), the ${\sigma }_{\text{Less}}$ region transforms from the bidirectional 2D CDW into the unidirectional 3D CDW order, whereas the ${\sigma }_{\text{More}}$ region remains in the isotropic phase (see also SI Appendix and SI Appendix, Fig. S1).

This leads us to interpret our results as suggestive of a universal tendency toward unidirectional incommensurate CDW order in YBCO and a somewhat nonuniform distribution of the disorder strengths. The important theoretical point is that the existence of a critical disorder ${\sigma }_c$ implies that small variations in the values of a single parameter (i.e., disorder strength, $\sigma$) can produce the multiple qualitative differences between the 2D and 3D signals, consistent with the assumption that the local CDW order is the same everywhere. This is also illustrated in Fig. 5. Upon the application of field, the isotropic 2D CDW in the less-disordered region (${\sigma }_{\text{Less}}$) transforms into the nematic 3D CDW phase, whereas that in the more-disordered region (${\sigma }_{\text{More}}$) still remains in the isotropic phase. This conjecture is consistent with the field-induced nematicity of the CDW near vortex cores hinted in a recent scanning tunneling microscope study on the double-layer Bi-based cuprate (27), in which the influence of disorder is stronger than in YBCO.

One might expect that the integrated intensity in the 2D CDW peak would decrease above $H_{3\text{D}}$ as the CDW changes its character in a portion of the sample. However, at the same time the CDW amplitude is also reinforced by the suppression of the superconductivity (SI Appendix). Because the CDW scattering intensity is determined by two compensating factors, the CDW amplitude and its volume fraction, the integrated intensity of the 2D CDW does not necessarily decrease (13, 14).

In the context of other high-field experiments, note that quantum oscillations (QOs) have been observed (23, 28) in ortho-II crystals (with $T_{\text{c}}\sim$ 58 to 60 K) in fields above 18 to 22 T, $\sim H_{3\text{D}}$. Thus, it seems that $H_{3\text{D}}$ is always less than or equal to the lowest fields at which QOs occur, and the QOs coexist with 3D CDW order, although it is presently unclear whether the QOs arise in the portions with 2D or 3D CDW. Moreover, $H_{3\text{D}}$ agrees with the Fermi surface reconstruction field deduced from Hall coefficient measurements (29). Although the proposed inhomogeneity picture qualitatively captures our experimental observations, it is not obvious that the Cu and O lines in NMR are readily interpreted as the sum of contributions from a unidirectional and a bidirectional CDW (4, 6, 21). We tentatively suggest that this reflects the fact that the local CDW correlations—to which NMR is most sensitive—are similar in the more- and less-disordered regions, and that it is only subtle, long-distance correlations that distinguish them.

This worry aside, our results strongly suggest that the ground state competing order in “ideal” superconducting YBCO with zero disorder would be a long-range ordered, incommensurate, unidirectional CDW. Our results also lend support to the existence of nematic components in the proximate phases to the 3D CDW in the phase diagram, and to their interpretation as arising from remnant unidirectional 3D CDW correlations (19, 30).

Materials and Methods

Samples.

Detwinned single crystals of YBa₂Cu₃O_6.51 (ortho-II, $T_{\text{c}}$ = 57 K, doping concentration $p\sim$ 0.1) and YBa₂Cu₃O_6.67 (ortho-VIII, $T_{\text{c}}$ = 67 K, $p\sim$ 0.12) were studied. We note that YBCO crystals generally belong to the cleanest available cuprate among the different families (31). The single crystals were obtained from flux growth (32). For two reflection geometries (shown in SI Appendix, Fig. S4), two crystals were prepared for each doping. The longest dimensions of crystals were parallel to the crystallographic $a$ axis and $b$ axis in ($0,k,l$) and ($h,0,l$) reflection geometry, respectively, while applying the magnetic field $H$ along the $c$ axis. Note that we prepared thin crystals (less than 0.5 mm) along the $b$- and $a$-axis to avoid sample heating via eddy currents due the pulsed magnetic field.

Resonant Soft X-Ray Scattering Under Zero Magnetic Field.

The quasi-2D CDW from these crystals were characterized by resonant soft X-ray scattering (RSXS) measurements at the Cu $L_3$-edge (931 eV; maximum energy position of X-ray absorption spectroscopy) at beamline 13-3 of the Stanford Synchrotron Radiation Lightsource as shown in Fig. 1A. Note that the obtained data were from theta (sample) scans at fixed detector angle ${176}^{\circ }$. An $l$-value of $\sim 1.45$ r.l.u., that is, slightly less than the half-integer value, had to be chosen due to experimental constraints and the limited total momentum transfer at $E=931$ eV. All RSXS data backgrounds are subtracted by references that were measured at 150 K. Solid lines are Gaussian fits to the data with a linear background.

Pulsed High-Magnetic-Field X-Ray Scattering.

The experimental setup is essentially the same as that used in our previous work (13) and the scattering geometry for the X-ray scattering with a pulsed magnetic field is shown in SI Appendix, Fig. S4. The high-magnetic-field experiment was performed at the X-ray Correlation Spectroscopy instrument of the Linac Coherent Light Source at the SLAC National Accelerator Laboratory (33). We use the pink beam with an incident photon energy of 8.8 keV and a horizontally ($\sigma$) polarized X-ray, just below the Cu $K$-edge to reduce the fluorescence background from copper. The pink beam gives higher photon flux that enables single-shot-pulsed-field experiments. The momentum resolution is limited by both broad energy bandwidth ($\sim 30$ eV) of the pink beam and the beam divergence. Note that the energy bandwidth in our previous measurement (13) was $\sim 50$ eV. Femtosecond X-ray pulses were synchronized to arrive at the sample when the magnetic field pulse reached the maximum. Note that the maximum strength of magnetic field in this work is 32.1 T, which is higher than our previous work (13).

Data Acquisition.

All field-applied data were collected by synchronizing a magnetic pulse and X-ray pulse (13). To obtain the zero-field background, diffraction patterns were collected before and after the magnetic pulse. In the main text, all difference maps of diffraction patterns are produced by subtracting the zero-field data. As an example, field-applied and zero-field diffraction intensity maps of Fig. 1C are shown in SI Appendix, Fig. S2.