Abstract
To examine whether helix formation necessarily precedes chain collision, we have measured the folding of a fully helical coiled coil that has been specially engineered to have negligible intrinsic helical propensity but high overall stability. The folding rate approaches the diffusion-limited value and is much faster than possible if folding is contingent on precollision helix formation. Therefore, the collision of two unstructured chains is the initial step of the dominant kinetic pathway, whereas helicity exerts its influence only at a later step. Folding from an unstructured encounter complex may be efficient and robust, which has implications for any biological process that couples folding to binding.
Keywords: transition state, helix formation, diffusion, binding, natively unfolded
One of the most debated issues in protein folding concerns the earliest folding events leading up to the transition state (1–9). For helical proteins, the earliest productive folding steps often are postulated to involve the collision of two preformed, but not necessarily stable, helical elements, rather than collision of unstructured chains. This diffusion-collision model (D-C model) (10–12) is supported by the observation that helix formation is faster than overall folding rates (13–15). This broadly accepted view also is supported by the presence of helix in the folding transition state and an increase in kf with an increase in helical propensity (2, 4, 16–21).
However, this correlation can support an opposing model in which unstructured chains first collide, and the enhanced helicity increases the success frequency (or transmission coefficient) of each encounter (Fig. 1). In general, the highly cooperative (two-state) folding behavior of most small proteins precludes identifying the order of events leading up to the kinetic barrier. As a result, the demonstration of helical structure in the transition state cannot by itself resolve whether helix formation or chain collision occurs first.
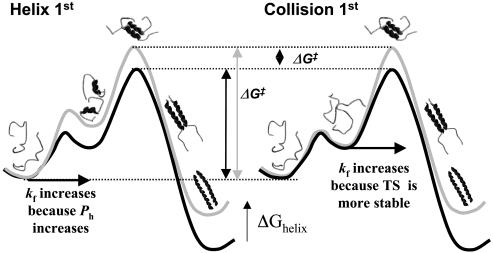
Fig. 1.
Acceleration of folding rates through helix stabilization does not identify whether helix formation comes before or after collision. The wild-type protein's free energy surface (black line) is shifted up (gray line) upon helix destabilization, ΔGhelix. For both scenarios, this destabilization slows folding identically through an increase in activation energy, 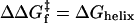 . In the D-C model, the slower folding rate is due to a reduction in the probability of helix formation before collision. The same rate reduction, ΔGhelix, is observed when helix forms after collision, because access to the transition state (TS) is thermodynamically less favorable. Hence, slower folding alone cannot distinguish the order of events leading up to the transition state. However, the use of a dimeric system with negligible intrinsic helicity, along with an analysis of folding rates, can distinguish the two models when folding is extremely fast, as for GCN4-E9G4.
. In the D-C model, the slower folding rate is due to a reduction in the probability of helix formation before collision. The same rate reduction, ΔGhelix, is observed when helix forms after collision, because access to the transition state (TS) is thermodynamically less favorable. Hence, slower folding alone cannot distinguish the order of events leading up to the transition state. However, the use of a dimeric system with negligible intrinsic helicity, along with an analysis of folding rates, can distinguish the two models when folding is extremely fast, as for GCN4-E9G4.
This obstacle can be overcome by studying a system with minimal helical propensity and composed of more than one chain, so that the rate of collision can be varied (22). These properties enable comparisons between observed folding rates and the maximum rate consistent with a model where precollision helix formation is required. Our investigation uses this strategy in conjunction with a dimeric coiled coil protein specially engineered to have negligible intrinsic helicity but high stability. This protein folds at nearly the diffusion limit and certainly at a much faster rate than would be possible if the helix must form before collision. Thus, an unstructured encounter complex can successfully initiate rapid folding, with helix formation occurring at a later step. The collision-first route sets a high basal level for the folding rate of any protein.
Materials and Methods
Peptides. GCN4-E9G4 was prepared and characterized as described in ref. 2.
Equilibrium Measurements. CD measurements were made by using a Jasco 715 spectropolarimeter (Jasco, Easton, MD), in equilibrium mode with a path length of 1 cm. All experiments were carried out in 20 mM sodium phosphate/200 mM sodium chloride, except the pH dependence of kinetics study was determined in 20 mM sodium citrate/200 mM sodium chloride.
Stopped-Flow Spectroscopy. Rapid mixing fluorescence experiments used a SFM-400 stopped-flow apparatus (Biologic, Grenoble, France) connected by a fiber optic cable to an A101 arc lamp (PTI, South Brunswick, NJ). Fluorescence spectroscopy used excitation and emission wavelengths of 280–290 nm and 300–400 nm, respectively. CD relaxation measurements were conducted at 2-nm resolution with a path length of 0.8 mm by using a Biologic SFM-4 interfaced with a CD spectropolarimeter.
Data Analysis. The diffusion constant for unfolded chains is calculated according to the Einstein–Sutherland equation, D = kT/(6 π ηRH), where η is the solvent viscosity, and RH is the hydrodynamic radius obtained from diffusion measurements of unfolded chains (23). Encounter rates are calculated according to Smoluchowski's equation, k2 = 8πNARijD, with a contact radius Rij = 10 Å. The pH dependence of stability, folding, and unfolding was fit to the following equations for a model that accommodates differential binding affinities in the unfolded, native, and transition state conformations:
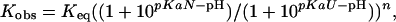 |
[1a] |
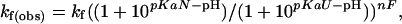 |
[1b] |
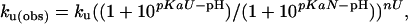 |
[1c] |
where pKaN and pKaU are the pKa values of the glutamic acid side chains in the native and unfolded states, respectively; n is the number of protons bound during folding; nF and nU are the number of protons bound before and after the transition state. The value for pKaU is fixed at the intrinsic pKa for glutamic acid (4.4), and pKaN determined by the equilibrium fit is used as a fixed-input parameter in the fit to the kinetic data.
Results and Discussion
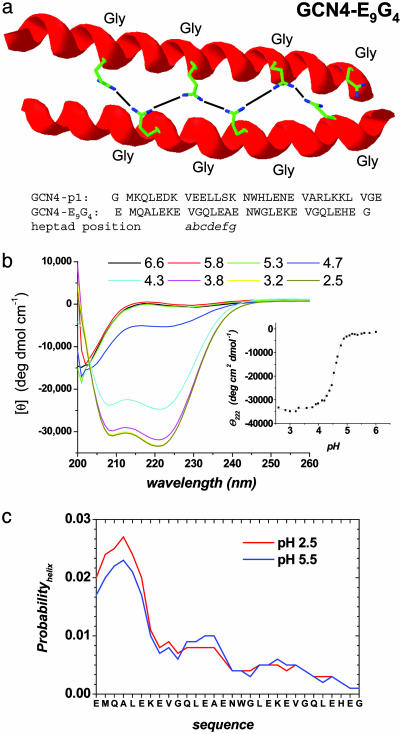
Design of a Stable Coiled Coil with Negligible Intrinsic Helicity. Dimeric coiled coils are an ideal system to test the D-C model because they are composed of only two docked helices. The coiled coil presently investigated is derived from GCN4-p1, the leucine zipper region of yeast transcription factor GCN4 (Fig. 2a). We have engineered a 30-residue version, GCN4-E9G4, which has near-zero intrinsic helicity but wild-type stability (ΔG° = 10 kcal·mol–1). To reduce helicity, four glycines are substituted at solvent-exposed positions (eight total in the dimer). As a result, the isolated chains are devoid of helical content under aqueous conditions (Fig. 2b Inset). Helix-coil calculations (24, 25) predict a maximum helicity of only 2.7% at any single position, and <1% averaged across the isolated chain at 35°C (Fig. 2c).
Fig. 2.
Design properties of stable coiled coil with negligible intrinsic helicity. (a) Coiled coils consist of heptad repeats (abcdefg)n. Hydrophobic residues are located at the interfacial positions a and d. Charged residues are often located at the e and g positions and form ionic interactions that bridge the two helices. The b, c, and f positions are the most solvent-exposed. The parent GCN4-p1 sequence was altered to include four glycines in positions b, c, or f, and nine glutamic acids in e or g positions, which form tertiary interactions to recoup the stability lost due to the insertion of the heliophobic glycines. Possible intermolecular hydrogen bonds between glutamic acid side chains are illustrated for one face of the molecule. An equivalent number on the opposite side are left out for clarity. (b) Secondary structure content of native (pH 3.2) and denatured (pH 5.3) GCN4-E9G4 are characteristic of a fully folded and a fully unfolded helical protein, respectively. (Inset) The midpoint of the pH titration is near the intrinsic pKa of glutamic acid side chains (4.4), and the steepness indicates that folding is driven by the protonation of 7 ± 1 glutamic acids. (c) Intrinsic helix propensity for isolated monomers of GCN4-E9G4, independent of tertiary interactions at 35°C (24, 25). The absence of helical structure in the monomer above pH 5.3 (blue line) is accurately reproduced by helix-coil calculations and insensitive to decreased pH. The glutamic acid side chains are too far apart to interact with each other in a helical geometry on the monomers. For GCN4-E9G4 (red line), the maximum probability for one, two, and just under four turns (the amount actually present at the transition state) is 2.4%, 0.8%, and 0.6%, respectively. For these amounts of precollisional helix formation, the D-C model predicts maximum folding rate constants of 1.6 × 106, 1.8 × 105, and 1.0 × 105 M–1·s–1 respectively, which the observed rate exceeds by 25- to 400-fold.
To offset the stability lost because of low helical propensity, nine glutamic acids are introduced in each chain at positions next to the hydrophobic interface (26). Below pH 4, the carboxylic side chains protonate and form stabilizing tertiary interactions across the dimer interface, “glutamic staples,” by either hydrogen bonds or hydrophobic interactions. The protein, which is unfolded at neutral pH, folds to a stable, fully helical structure upon acidification (Fig. 2b). The midpoint of the equilibrium pH titration is 4.5, very near the intrinsic pKa of the glutamic acid side chains.
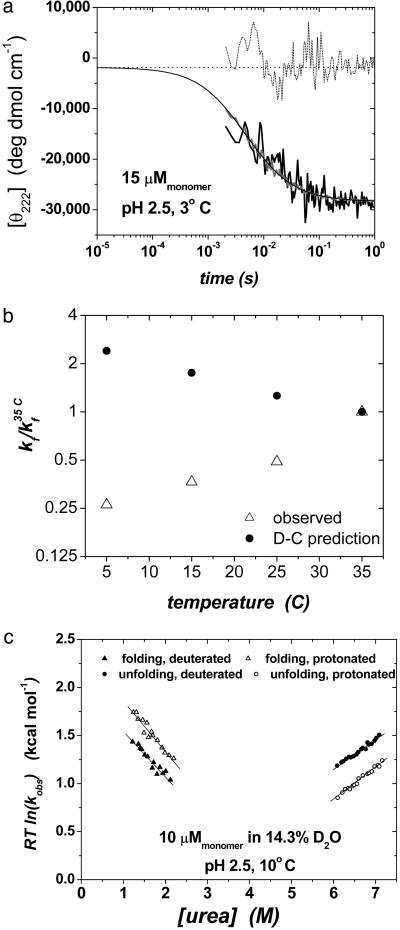
Two-State Folding Kinetics. The folding kinetics of GCN4-E9G4 are well described by a 2 (monomer) ↔ dimer bimolecular reaction (Fig. 3). The observed folding rate is proportional to protein concentration, kobs = kf ·[protein] (Fig. 5, which is published as supporting information on the PNAS web site), whereas the unfolding process is first-order and independent of protein concentration. The second-order folding rate constant is temperature-dependent, increasing from kf = 1 × 107 mol–1·s–1 at 5°C to 4 × 107 mol–1·s–1 at 35°C (Fig. 3 a and b). Rates are independent of whether folding is initiated by a decrease in pH or the dilution of denaturant. Additionally, the same rate constant is observed by a global probe sensitive to helical content (CD at 222 nm) or a local probe (total fluorescence of the sole tryptophan), consistent with the two-state nature of the reaction (Fig. 3a).
Fig. 3.
Folding behavior of the designed coiled coil GCN4-E9G4. (a) Rapidmixing folding measurements monitoring CD222 nm (dark gray) and fluorescence (black, scaled to the CD trace). The CD trace extrapolated to t = 0 s (using kfluor = 210 s–1) matches the value at its initial, unfolded CD value at pH 5.5 (dash) indicating that the unfolded monomers have negligible helical content before collision and productive folding. (b) Observed and predicted temperature dependence of folding rates. Decreasing temperature has two antagonistic effects on folding rates. The decrease in temperature from 35°Cto5°C results in a 2-fold decrease in the bimolecular collision rate but a 2-fold increase in helix propensity. As 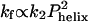 , the rate predicted by the D-C model should increase as temperatures drop. Measured rates exhibit the opposite trend, indicating that the D-C model does not correctly predict the temperature dependence. (c) The denaturant dependence of the activation energies for folding (left side) and unfolding (right side) indicates that 61 ± 6% of the net surface area is buried at the transition state [mf/mo (27)]. Similarly, the change in folding activation free energy upon backbone deuteration relative to the change in equilibrium stability,
, the rate predicted by the D-C model should increase as temperatures drop. Measured rates exhibit the opposite trend, indicating that the D-C model does not correctly predict the temperature dependence. (c) The denaturant dependence of the activation energies for folding (left side) and unfolding (right side) indicates that 61 ± 6% of the net surface area is buried at the transition state [mf/mo (27)]. Similarly, the change in folding activation free energy upon backbone deuteration relative to the change in equilibrium stability, 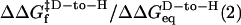 , indicates that 49 ± 2% of helical hydrogen bonds are formed in the transition state. RT, R is the gas constant and T is the temperature.
, indicates that 49 ± 2% of helical hydrogen bonds are formed in the transition state. RT, R is the gas constant and T is the temperature.
The highly cooperative, two-state folding behavior is confirmed through a “chevron analysis” with a linear dependence of the equilibrium and activation free energies for folding (f) and unfolding (u) on guanidinium chloride concentration (27) (Fig. 3c).
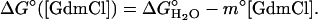 |
[2a] |
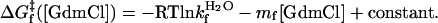 |
[2b] |
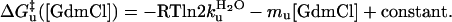 |
[2c] |
When folding is effectively two-state, the equilibrium values for the change in free energy and surface burial can be calculated from kinetic measurements according to 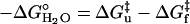 and m° = mu – mf. The equivalence of thermodynamically and kinetically determined values for
and m° = mu – mf. The equivalence of thermodynamically and kinetically determined values for 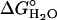 and mo demonstrates the applicability of a two-state model for GCN4-E9G4 folding. In particular, the folding arm of the chevron remains linear under all conditions. This linearity indicates that no surface is buried immediately upon transfer from high to low denaturant.
and mo demonstrates the applicability of a two-state model for GCN4-E9G4 folding. In particular, the folding arm of the chevron remains linear under all conditions. This linearity indicates that no surface is buried immediately upon transfer from high to low denaturant.
In addition, no helical structure is formed in a submillisecond “burst-phase” at temperatures as low as 3°C (Fig. 3a and Fig. 6, which is published as supporting information on the PNAS web site), and the predicted helicity at pH 2.5 is equivalent to that at pH 5.5, where the chain is seen to be devoid of helical structure (Fig. 2b). Also, the glutamic acids are too far apart to interact with each other in a helical geometry within individual monomers. Thus, multiple experimental measures all indicate that helical structure does not form to an appreciable degree before the major folding event.
Folding Is Faster than Predicted by the D-C Model. In the D-C model, the folding rate equals the product of three quantities, 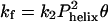 , where k2,
, where k2, 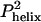 , and Θ are the second-order Smolukowski-derived bimolecular collision rate, the probability that both chains have a helix formed at the moment of collision, and the success frequency for each collision, respectively (3, 10). The D-C model predicts a maximal folding rate that is only 1/25 of the observed value at 35°C. With a collision rate of k2 = 2.8 × 109 M–1·s–1 and a 2.4% probability for the formation of a single turn of helix, the predicted folding rate constant is kf = 1.6 × 106 M–1·s–1. This calculated rate is an upper bound, because every collision is assumed to be productive (Θ = 1). The discrepancy increases to kobserved/kpredicted > 100, if either the success frequency includes the probability that the two hydrophobic faces collide in the correct orientation, or the amount of precollision helical structure is increased to two turns, the minimum we envision as necessary for a chain to be considered helical.
, and Θ are the second-order Smolukowski-derived bimolecular collision rate, the probability that both chains have a helix formed at the moment of collision, and the success frequency for each collision, respectively (3, 10). The D-C model predicts a maximal folding rate that is only 1/25 of the observed value at 35°C. With a collision rate of k2 = 2.8 × 109 M–1·s–1 and a 2.4% probability for the formation of a single turn of helix, the predicted folding rate constant is kf = 1.6 × 106 M–1·s–1. This calculated rate is an upper bound, because every collision is assumed to be productive (Θ = 1). The discrepancy increases to kobserved/kpredicted > 100, if either the success frequency includes the probability that the two hydrophobic faces collide in the correct orientation, or the amount of precollision helical structure is increased to two turns, the minimum we envision as necessary for a chain to be considered helical.
The D-C model considers the collision of two preformed helices to be rate-limiting and common throughout the ensemble of conformations comprising the folding transition state. Kinetic amide isotope measurements described below indicate that 49 ± 2% of the helical content is formed in the transition state. If this amount of helical structure must be present at the moment of collision, the observed rate is 400-fold faster than can be accommodated by the D-C model, even assuming Θ = 1.
Each chain has a net charge of +2 and no negatively charged residues. Thus, electrostatic considerations, which can enhance bimolecular rates for oppositely charged molecules [“electrostatic guidance” (28)], would only further reduce the collision rate for GCN4-E9G4. Thus, the upper bound for the D-C model is at least an order of magnitude slower than the observed folding rate, and more reasonable estimates produce a much more drastic discrepancy.
The D-C model also predicts the wrong temperature dependence for folding rates (Fig. 3b). A reduction in temperature from 35°Cto 5°C increases the helical content in isolated chains by 2-fold or a 4-fold increase in 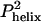 . At the frequency, same time, the second-order collision k2, is halved because of a 2-fold increase in solvent viscosity. These opposing effects combine to produce a net 2-fold increase in kf for the 30°C reduction in temperature. In fact, a 4-fold decrease is observed. Hence, folding cannot be contingent on preformed helical structure, unless the success frequency decreases by nearly an order of magnitude over the same temperature range.
. At the frequency, same time, the second-order collision k2, is halved because of a 2-fold increase in solvent viscosity. These opposing effects combine to produce a net 2-fold increase in kf for the 30°C reduction in temperature. In fact, a 4-fold decrease is observed. Hence, folding cannot be contingent on preformed helical structure, unless the success frequency decreases by nearly an order of magnitude over the same temperature range.
Finally, the folding rate of GCN4-E9G4 is about 4-fold faster than that of the wild-type sequence, despite having no more than one-tenth the intrinsic helicity across any given 4- to 10-residue stretch. Thus, the D-C model predicts, based on the decreased helicity and assuming a similar success frequency, that folding of the wild-type sequence should be 100- to 10,000-fold faster than GCN4-E9G4. This inconsistency, in conjunction with folding being too fast to be contingent on precollision helical structure, and its temperature dependence being antithetical to that predicted by the D-C model, leads us to conclude that the initial step of the dominant kinetic pathway is the collision of two unstructured chains.
GCN4-E9G4 Folding Pathway. Properties of the transition state point to a folding pathway that proceeds through a proportional buildup of secondary and tertiary structures. The denaturant dependence of kf indicates that 61 ± 6% of the total surface area is buried in the folding transition state (mf/mo) (Fig. 3b). Likewise, the pH dependence of folding rates indicates that on average 46 ± 11% of the “glutamic staples” are formed in the transition-state ensemble (Fig. 7, which is published as supporting information on the PNAS web site).
Backbone kinetic isotope effects provide a powerful method to directly monitor the helical hydrogen bond content in the transition state (20, 21, 29). When conducted under the same bulk solvent conditions, the change in folding activation free energy upon backbone deuteration relative to the change in equilibrium stability, 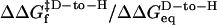 , is proportional to the fraction of hydrogen formed in the transition state. These quantities are obtained from the chevron plots for the protonated and deuterated coiled coil, conducted in a uniform 14.3% D2O solvent condition (Fig. 3c). Accordingly, we find that 49 ± 2% of helical hydrogen bonds are formed in the transition state.
, is proportional to the fraction of hydrogen formed in the transition state. These quantities are obtained from the chevron plots for the protonated and deuterated coiled coil, conducted in a uniform 14.3% D2O solvent condition (Fig. 3c). Accordingly, we find that 49 ± 2% of helical hydrogen bonds are formed in the transition state.
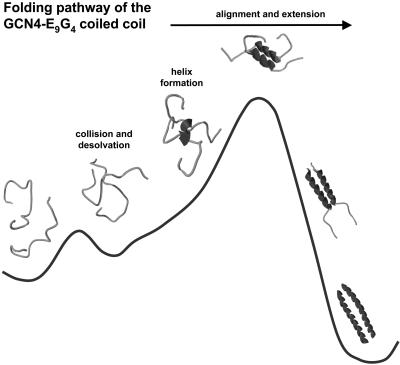
The similarity in the degree of surface burial and the fraction of staples and hydrogen bonds formed in the transition state produces the following picture for the folding pathway of GCN4-E9G4 (Fig. 4). Chain collision results in hydrophobic contacts that partially desolvate the polypeptide backbone. Exclusion of water molecules induces hydrogen bond formation and small helical regions develop at points of contact. These helical elements are then stabilized in the native register by tertiary interactions, both from hydrophobic residues at the interface and the glutamic staples. This process continues incrementally up to the transition state.
Fig. 4.
Folding pathway of a designed coiled coil. Unstructured chains collide, which results in partial desolvation of the polypeptide backbone. Intrachain hydrogen bonds form in response to the loss of solvent hydrogenbond partners, forming isolated helices at the point of contact. Tertiary contacts stabilize these helices, bring them into alignment, and further desolvate the backbone, thereby promoting the extension of helical structure incrementally up to the half-helical transition state, from which folding is energetically downhill to the native structure.
The Role of Helicity in Folding. The incompatibility of GCN4-E9G4 with the D-C model may lead to the speculation that its folding behavior is somehow unique. However, its folding properties are very similar to that of its parent (2) and most similarly sized proteins. At the transition state, the degree of surface burial is typical, both in relative and absolute terms, while the same one-to-one correspondence between surface burial and hydrogen bond formation is found for a dozen other proteins (20, 21). Thus, all the observed properties of the folding transition state of the designed coiled coil are typical of globular proteins. Calculations based on the D-C model employing a variety of input parameters, have predicted folding rates for a variety of small helical proteins (3, 30–32). This rate agreement is compatible with the present data as the agreement is for other proteins, and it does not provide proof of mechanism (2).
The collision-first route may be likened to a rudimentary mechanism that sets a basal level for the folding rate of any protein. Unexpectedly, the folding of our construct with low helical content demonstrates that this option can be very fast. It may be considered that the speed is due in part to the glutamic acids. Mutational studies of the GCN4-p1′ parent, however, have shown that folding can begin from the least helical region, contrary to the expectation of the D-C model (2), and the parent lacks these staples and even has regions of high helical propensity. Nevertheless, some proteins with very high helical propensity are likely to have regions structured at the moment of collision and could obey the D-C model (9). In general, which of the two limiting folding scenarios dominates may vary for proteins with limited amounts of residual structure.
The rapid folding of our construct indicates that an unstructured encounter complex can still be very productive, as recently proposed (33). In GCN4-E9G4, the even distribution of glutamic staples and other tertiary interactions further ensures the productivity of multiple folding routes. This mechanism may apply to a growing number of “natively unfolded” proteins (34), whose folding is coupled to binding (35).
What, then, is the required role of helicity along the pathway? Many experiments have demonstrated that enhancing intrinsic helicity accelerates folding (2, 4, 16–21). Such strengthening stabilizes all conformations containing helix, including the transition state (Fig. 1). Furthermore, kinetic isotope measurements indicate that hydrogen bond formation is intimately linked with surface burial at the transition state (20, 21). Thus, secondary structure is critical for the transition state to be thermodynamically accessible, although the amount of secondary structure present before collision may be minimal, as found for GCN4-E9G4.
Supplementary Material
Acknowledgments
We thank Profs. M. Karplus, N. Kallenbach, R. Baldwin, K. Plaxco, S. W. Englander, and members of our group for comments and discussions. We thank G. Reddy for peptide synthesis supported by a National Cancer Institute grant. This work was supported by a grant from the National Institutes of Health.
This paper was submitted directly (Track II) to the PNAS office.
Abbreviation: D-C, diffusion-collision.
References
- 1.Sosnick, T. R., Jackson, S., Wilk, R. M., Englander, S. W. & DeGrado, W. F. (1996) Proteins 24, 427–432. [DOI] [PubMed] [Google Scholar]
- 2.Moran, L. B., Schneider, J. P., Kentsis, A., Reddy, G. A. & Sosnick, T. R. (1999) Proc. Natl. Acad. Sci. USA 96, 10699–10704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Myers, J. K. & Oas, T. G. (1999) J. Mol. Biol. 289, 205–209. [DOI] [PubMed] [Google Scholar]
- 4.Zitzewitz, J. A., Ibarra-Molero, B., Fishel, D. R., Terry, K. L. & Matthews, C. R. (2000) J. Mol. Biol. 296, 1105–1116. [DOI] [PubMed] [Google Scholar]
- 5.Ibarra-Molero, B., Makhatadze, G. I. & Matthews, C. R. (2001) Biochemistry 40, 719–731. [DOI] [PubMed] [Google Scholar]
- 6.Zitzewitz, J. A., Bilsel, O., Luo, J., Jones, B. E. & Matthews, C. R. (1995) Biochemistry 34, 12812–12819. [DOI] [PubMed] [Google Scholar]
- 7.Bosshard, H. R., Durr, E., Hitz, T. & Jelesarov, I. (2001) Biochemistry 40, 3544–3552. [DOI] [PubMed] [Google Scholar]
- 8.Krantz, B. A. & Sosnick, T. R. (2001) Nat. Struct. Biol. 8, 1042–1047. [DOI] [PubMed] [Google Scholar]
- 9.Mayor, U., Guydosh, N. R., Johnson, C. M., Grossmann, J. G., Sato, S., Jas, G. S., Freund, S. M., Alonso, D. O., Daggett, V. & Fersht, A. R. (2003) Nature 421, 863–867. [DOI] [PubMed] [Google Scholar]
- 10.Karplus, M. & Weaver, D. L. (1994) Protein Sci. 3, 650–668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Karplus, M. & Weaver, D. L. (1976) Nature 260, 404–406. [DOI] [PubMed] [Google Scholar]
- 12.Myers, J. K. & Oas, T. G. (2002) Annu. Rev. Biochem. 71, 783–815. [DOI] [PubMed] [Google Scholar]
- 13.Williams, S., Causgrove, T. P., Gilmanshin, R., Fang, K. S., Callender, R. H., Woodruff, W. H. & Dyer, R. B. (1996) Biochemistry 35, 691–697. [DOI] [PubMed] [Google Scholar]
- 14.Thompson, P. A., Eaton, W. A. & Hofrichter, J. (1997) Biochemistry 36, 9200–9210. [DOI] [PubMed] [Google Scholar]
- 15.Huang, C. Y., Getahun, Z., Zhu, Y., Klemke, J. W., DeGrado, W. F. & Gai, F. (2002) Proc. Natl. Acad. Sci. USA 99, 2788–2793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Taddei, N., Chiti, F., Fiaschi, T., Bucciantini, M., Capanni, C., Stefani, M., Serrano, L., Dobson, C. M. & Ramponi, G. (2000) J. Mol. Biol. 300, 633–647. [DOI] [PubMed] [Google Scholar]
- 17.Lopez-Hernandez, E., Cronet, P., Serrano, L. & Munoz, V. (1997) J. Mol. Biol. 266, 610–620. [DOI] [PubMed] [Google Scholar]
- 18.Srivastava, A. K. & Sauer, R. T. (2000) Biochemistry 39, 8308–8314. [DOI] [PubMed] [Google Scholar]
- 19.Burton, R. E., Huang, G. S., Daugherty, M. A., Calderone, T. L. & Oas, T. G. (1997) Nat. Struct. Biol. 4, 305–310. [DOI] [PubMed] [Google Scholar]
- 20.Krantz, B. A., Srivastava, A. K., Nauli, S., Baker, D., Sauer, R. T. & Sosnick, T. R. (2002) Nat. Struct. Biol. 9, 458–463. [DOI] [PubMed] [Google Scholar]
- 21.Krantz, B. A., Moran, L. B., Kentsis, A. & Sosnick, T. R. (2000) Nat. Struct. Biol. 7, 62–71. [DOI] [PubMed] [Google Scholar]
- 22.Wagman, M. E., Dobson, C. M. & Karplus, M. (1980) FEBS Lett. 119, 265–270. [DOI] [PubMed] [Google Scholar]
- 23.Wilkins, D. K., Grimshaw, S. B., Receveur, V., Dobson, C. M., Jones, J. A. & Smith, L. J. (1999) Biochemistry 38, 16424–16431. [DOI] [PubMed] [Google Scholar]
- 24.Munoz, V. & Serrano, L. (1994) Nat. Struct. Biol. 1, 399–409. [DOI] [PubMed] [Google Scholar]
- 25.Lacroix, E., Viguera, A. R. & Serrano, L. (1998) J. Mol. Biol. 284, 173–191. [DOI] [PubMed] [Google Scholar]
- 26.Durr, E., Jelesarov, I. & Bosshard, H. R. (1999) Biochemistry 38, 870–880. [DOI] [PubMed] [Google Scholar]
- 27.Matthews, C. R. (1987) Methods Enzymol. 154, 498–511. [DOI] [PubMed] [Google Scholar]
- 28.Getzoff, E. D., Cabelli, D. E., Fisher, C. L., Parge, H. E., Viezzoli, M. S., Banci, L. & Hallewell, R. A. (1992) Nature 358, 347–351. [DOI] [PubMed] [Google Scholar]
- 29.Kentsis, A. & Sosnick, T. R. (1998) Biochemistry 37, 14613–14622. [DOI] [PubMed] [Google Scholar]
- 30.Islam, S. A., Karplus, M. & Weaver, D. L. (2002) J. Mol. Biol. 318, 199–215. [DOI] [PubMed] [Google Scholar]
- 31.Myers, J. K. & Oas, T. G. (2001) Nat. Struct. Biol. 8, 552–558. [DOI] [PubMed] [Google Scholar]
- 32.Burton, R. E., Myers, J. K. & Oas, T. G. (1998) Biochemistry 37, 5337–5343. [DOI] [PubMed] [Google Scholar]
- 33.Shoemaker, B. A., Portman, J. J. & Wolynes, P. G. (2000) Proc. Natl. Acad. Sci. USA 97, 8868–8873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Dunker, A. K., Brown, C. J., Lawson, J. D., Iakoucheva, L. M. & Obradovic, Z. (2002) Biochemistry 41, 6573–6582. [DOI] [PubMed] [Google Scholar]
- 35.Dyson, H. J. & Wright, P. E. (2002) Curr. Opin. Struct. Biol. 12, 54–60. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.