Irregularity, volatility, risk, and financial market time series

Abstract

The need to assess subtle, potentially exploitable changes in serial structure is paramount in the analysis of financial data. Herein, we demonstrate the utility of approximate entropy (ApEn), a model-independent measure of sequential irregularity, toward this goal, by several distinct applications. We consider both empirical data and models, including composite indices (Standard and Poor's 500 and Hang Seng), individual stock prices, the random-walk hypothesis, and the Black–Scholes and fractional Brownian motion models. Notably, ApEn appears to be a potentially useful marker of system stability, with rapid increases possibly foreshadowing significant changes in a financial variable.

Series of sequential data are pivotal to much of financial analysis. Enhanced capabilities of quantifying differences among such series would be extremely valuable. Although analysts typically track shifts in mean levels and in (several notions of) variability, in many instances, the persistence of certain patterns or shifts in an “ensemble amount of randomness” may provide critical information as to asset or market status. Despite this recognition, formulas to directly quantify an “extent of randomness” have not been utilized in market analyses, primarily because, even within mathematics itself, such a quantification technology was lacking until recently. Thus, except for settings in which egregious (changes in) sequential features or patterns presented themselves, subtler changes in serial structure would largely remain undetected.

Recently, a mathematical approach and formula, approximate entropy (ApEn), was introduced to quantify serial irregularity, motivated by both application needs (1) and by fundamental questions within mathematics (2, 3). ApEn grades a continuum that ranges from totally ordered to maximally irregular “completely random.” The purpose of this article is to demonstrate several applications of ApEn to the evaluation of financial data.

One property of ApEn that is of paramount importance in the present context is that its calculation is model-independent, i.e., prejudice-free. It is determined by joint-frequency distributions. For many assets and market indices, the development of a model that is sufficiently detailed to produce accurate forecasts of future price movements, especially sudden considerable jumps or drops, is typically very difficult (discussed below). The advantage of a model-independent measure is that it can distinguish classes of systems for a wide variety of data, applications, and models. In applying ApEn, we emphasize that, in many implementations, we are decidedly not testing for a particular (econometric) model form; we are attempting to distinguish data sets on the basis of regularity. Even if we cannot construct a relatively accurate model of the data, we can still quantify the irregularity of data, and changes thereto, straightforwardly. Of course, subsequent modeling remains of interest, although the point is that this task is quite distinct from the application of effective discriminatory tools. This perspective seems especially important given the empirical, nonexperimental nature of financial time series.

In addition, the widely used term volatility enters the picture as follows. Volatility, and implicitly risk, are generally equated with the magnitude of asset price fluctuations, with large swings denoted as highly volatile and, in common parlance, as highly unpredictable. However, two fundamentally distinct means exist in which series deviate from constancy: (i) they exhibit high standard deviation, and (ii) they appear highly irregular or unpredictable. These two forms are quite distinct and nonredundant, with important consequences. As we see below, standard deviation (SD) (or nonparametric variants) will remain the appropriate tool to grade the extent of deviation from centrality, whereas ApEn will prove to be the appropriate tool to grade the extent of irregularity. The point is that the extent of variation is generally not feared; rather, unpredictability is the concern. Recast, if an investor were assured that future prices would follow a precise sinusoidal pattern, even with large amplitude, this perfectly smooth roller coaster ride would not be frightening, because future prices and resultant strategies could be planned. Thus, a quantification technology to separate the concepts of classical variability and irregularity should be of interest.

The following observations are particularly germane to the discussions below.

1. ApEn applies to single sequences of both (even very short) finite and infinite length, filling voids unaddressed by axiomatic probability theory (2–5).

2. ApEn is useful not only to evaluate whether sequential data are consistent with a specified (e.g., “random”) process but, more pointedly, also to grade subtle shades of highly irregular sequences and to distinguish among them. This utility fills a critical need, because, for sequences with ApEn values ≥80% of maximal irregularity, classical statistics (e.g., spectra and correlation) oftentimes fail to clearly discriminate such sequences either from one another or from being random. This is highlighted below.

3. ApEn thus refines chartism, in that it does not require clear pattern formations to exist to detect insidious changes in serial structure.

4. Although ApEn is applicable entirely outside a model setting, it also fits naturally into a classical probability and statistics (model-based) framework. Accordingly, ApEn can be applied to evaluate and either validate or reject econometric models, e.g., random walk, Black–Scholes (B-S) diffusion, ARMA, GARCH, and fractional Brownian motion (FBM), from a perspective orthogonal to that in current practice.

5. ApEn can be applied as a marker of system stability; significantly increased ApEn values may foreshadow pronounced state (index) changes, both empirically and in model-based contexts.

ApEn. ApEn (1) assigns a nonnegative number to a sequence or time series, with larger values corresponding to greater apparent serial randomness or irregularity and smaller values corresponding to more instances of recognizable features in the data. Two input parameters, a block or run length m and a tolerance window r, must be specified to compute ApEn. In brief, ApEn measures the logarithmic frequency that runs of patterns that are close (within r) for m contiguous observations remain close (within the same tolerance width r) on the next incremental comparison. The precise formulation is given in ref. 1.

ApEn(m,r) is a family of parameters; comparisons are intended with fixed m and r. For the studies below, we calculate ApEn values for all data sets applying widely used and validated parameter values m = 1 or m = 2 and r = 20% of the SD of the specified time series. Normalizing r to each time series SD gives ApEn a translation and scale invariance (6), ensuring a complementarity of variability (SD) and irregularity (ApEn), in that ApEn remains unchanged under uniform process magnification.

ApEn is relative frequency-based and provides a finite-sequence formulation of randomness, by proximity to maximal irregularity and equidistribution (2, 3, 7). Conversely, ApEn applies to a classical probability framework by consideration of almost sure realizations of discrete time processes, with analytic expressions to evaluate ApEn given, for example, in ref. 1, equations 14 and 15.

Previous evaluations including both broad-based theoretical analysis (1, 8, 9) and numerous diverse applications (6, 10–13) demonstrate that the input parameters indicated above produce good reproducibility for ApEn for time series of the lengths considered below. In particular, the SD of ApEn is ≤0.05 for virtually all processes analyzed for the data lengths studied herein (1, 9).

In ref. 12, we provide a theoretical basis for understanding why ApEn provides a substantially more general or robust measure of feature persistence than do linear correlation and the power spectrum. Descriptively, correlation and spectral measures assess the degree of matching or recurring features (characteristic subblocks) at fixed spectral frequencies, whereas the ApEn formulation implicitly relaxes the fixed-frequency mandate in evaluating recurrent feature matching. Thus, the ApEn formalism both provides a sharper measure of equidistribution (3, 7) and also identifies many subtle yet persistent pattern recurrences in both data and models that the aforementioned alternatives fail to do.

Representative Applications. Because most financial analyses and modeling center on price increments or returns, rather than on prices, we do so below. Given a series of prices {s_i}, we consider the incremental series u_i = s_i+1 – s_i; the returns series r_i = (s_i+1/s_i) – 1; and the log-ratio series L_i = log(s_i+1/s_i). These series are prominent in evaluating “random walk”-type hypotheses. We apply these series to a variety of assets and indices to illustrate a breadth of this application mode. We note that in general theoretical and empirical settings (approximate mean stationarity), ApEn values of these series are quite similar (e.g., Fig. 1).

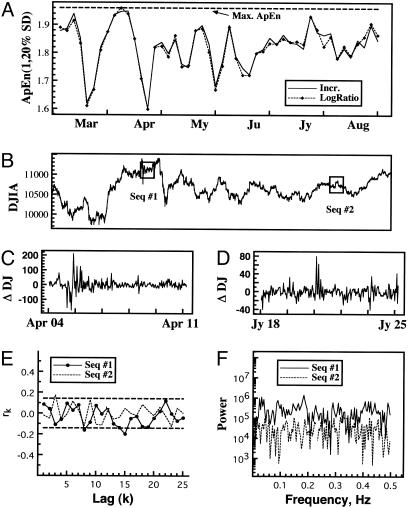
Fig. 1.

Analysis of subtle asset variation. (A) Dow Jones running ApEn(1, 20% SD, N = 200) values, applied to both incremental and “log-ratio” 10-min price series. (B) Concomitant Dow Jones Industrial Average (DJIA) index values, from February 11, 2000, to August 18, 2000. (C and D) Incremental series (Seq. #1 and #2) for periods April 4–10, ApEn = 1.600 (C) and July 18–24, ApEn = 1.778 (D). (E) Autocorrelograms (and 95% confidence intervals) for Seq. #1 and #2. (F) Power spectra for Seq. #1 and #2. Observe highly significant ApEn variation over time; also note that ApEn indicates significant differences in regularity between the time series underlying C and D, and, moreover, between each series and a maximal ApEn level of 1.949. In contrast, neither autocorrelation nor the power spectrum distinguish either segment shown in C and D from random.

Nonetheless, because ApEn can discern shifts in serial characteristics, apart from the consideration of randomness hypotheses, we expect that application of ApEn to price series {s_i} directly will prove useful in clarifying additional changes. Indeed, most empirical applications of ApEn have been to raw time series.

Subtle Asset Variation. Analysis of Dow Jones Industrial Average prices, taken at 10-min trading intervals from February 11, 2000 to August 18, 2000 (Tick Data), illustrates the ApEn quantification. Fig. 1A shows running ApEn(1, 20% SD, N = 200) values, applied to both incremental and log-ratio series. Because these two ApEn applications yield very similar results, we focus on increment analysis. We observe highly significant variation in ApEn over time from a maximal ApEn(1, 20% SD, N = 200) level of 1.949. Yet empirical ApEn values remain above 80% maximal ApEn, making it difficult to discern obvious pattern-based changes during this period.

Incremental series for two 200-point segments, denoted sequences 1 and 2, are shown in Fig. 1 C and D. ApEn(1, 20% SD) indicates significant differences in regularity between the time series underlying Fig. 1C (ApEn = 1.600) and Fig. 1D (ApEn = 1.778) and, additionally, between each time series and maximality. Notably, in contrast, neither autocorrelation nor the power spectrum (Fig. 1 E and F) distinguish either segment from “random.” Only 1 of 25 (sequence 1) and 2 of 25 (sequence 2) lagged autocorrelation coefficients exceed 95% confidence limits of approximately 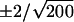for significance (14), each just outside the limits, and at arbitrary lags. Similarly, for the spectra F, neither segment had a maximal peak that differed from a white noise process at 95% significance (14).

To understand the ApEn calculation arithmetically, consider sequence 1, with r = 20% SD ≈ 7. Look at the joint relative frequency that (A) 7 < u_i < 21 and (B) –7 < u_i+1 < 7 (i.e., u_i ∈ [r,3r] and u_i+1 ∈ [–r,r]) for {u_i,u_i+1} contiguous points in sequence 1. (A) occurred 37 times and (B) occurred 51 times, with frequencies of 0.186 and 0.256 respectively. If (A) and (B) were independent, they would jointly occur with a relative frequency of ≈0.047; thus, we would expect nine pairs {u_i,u_i+1} satisfying A and B. Yet sequence 1 contains 16 such pairs (frequency = 0.080) exhibiting this modest rise followed by virtually no change. Taken alone, this single discrepancy between the product of univariate frequencies and the observed joint frequency is marginally significant. Rather, it is a steady accumulation of such modest discrepancies that in ensemble is inconsistent with a hypothesis of independent increments.

From a separate perspective, we calculated ApEn for 100 “randomly shuffled” permutations of sequence 1; each of these ApEn values was larger than the measured ApEn value of 1.600. Thus, we reject that an underlying model for sequence 1 is independent and identically distributed (i.i.d) or exchangeable with empirical significance probability P < 0.01 (8), independent of whether the one-dimensional marginal density is normal or otherwise.

B-S Model. The Black–Scholes (B-S) model of option pricing by the stochastic heat equation (15) requires special mention, given its widespread use. This model implies that security prices {s_i} obey a geometric Brownian motion with drift. Thus, for {s_i} equally spaced in time, the log-ratio series {L_i} is i.i.d. and normally distributed. ApEn of the {L_i} will then be nearly maximal for any data length; e.g., mean ApEn(1, 20% SD, N = 200){L_i} = 1.949. Asymptotically, the parameter ApEn(m,r % SD) {L_i} can be calculated by applying equation 15 from ref. 1, with f the normal distribution. Furthermore, by scale invariance, these normalized ApEn values are invariant under volatility change (σ); i.e., ApEn remains unchanged at any constant level of magnification or reduction in volatility or SD, for both data and model-based constructs. This observation reaffirms that volatility and irregularity are complementary, indeed, orthogonal notions. Importantly, substantial deviation from a nearly maximal ApEn{L_i} value, e.g., as often seen in the data analysis presented above in Subtle Asset Variation, strongly suggests that data violate the B-S model.

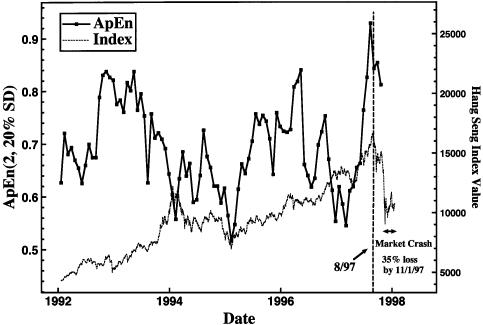
Market “Crashes.” One potential application of ApEn is to forecast dramatic market change. The relatively recent economic crises in Southeast Asia provide a good test, because many Asian economies showed extraordinary growth from 1988 to 1997, despite a lack of associated rapid growth in hard assets. In late 1997–1998, many of these nations suffered market crashes, leading to currency devaluations. We applied ApEn to a prominent Asian market, Hong Kong's Hang Seng index, from 1992 to 1998. ApEn(2, 20% SD) was applied to running 120-point incremental time series {u_i}, with {s_i} daily closing prices (Dow Jones Interactive). Fig. 2 shows the running ApEn values and concomitant index values; note the rapid increase in ApEn to its highest observed value immediately before the November 1997 crash, our primary inference.

Fig. 2.

Hang Seng (Hong Kong) running ApEn(2, 20% SD) values, applied to a 120-point incremental daily closing price series, and concomitant index values, 1992–1998. Note the rapid increase in ApEn to its highest observed value immediately before the November 1997 crash.

Furthermore, the coarseness in data sampling (daily) was made simply to accommodate ready availability. It is interesting that any inferences of qualitative economic consequence are present, given this crudeness; we anticipate that finer sampling would provide subtler inferences.

Also, ApEn was previously applied to show that the Standard and Poor's 500 (S&P 500) behaved quite differently from a log-normal random walk during 1987–1988 (16). Data were analyzed from 22 distinct 1000-point segments during this period, sampled at 10-min intervals (Tick Data); ApEn(2, 20% SD) was applied to the log-ratio series. In 21 of these 22 25-day segments, the ApEn value was at least 0.3 (i.e., 6 ApEn SDs) less than the expected ApEn value, assuming the null random-walk hypothesis, establishing consistent serial structure. Notably, the one segment where the random-walk assumption and calculated ApEn values nearly agreed was October 1, 1987, to November 5, 1987, the period covering the stock market crash.

Of course, the rejection of the log-normal random-walk hypothesis has been noted elsewhere in a variety of contexts, based on, e.g., skewness, excess kurtosis, and time-varying volatilities (17, 18). The novel points, for both the Hang Seng and S&P 500 analyses, are (i) the consistency and the degree to which ApEn remains well below maximality during economically stable epochs and (ii) the fore-shadowing of a potential crisis that a rapid rise to nearly maximal ApEn value may provide.

Finally, some caution is essential. Although we have more supporting evidence to suggest that a rapid (ApEn) rise to a very high level before a crash appears to be a broadly held pattern, we hardly expect it to be universally valid without restrictions. Ultimately, a taxonomy based on diverse contexts should clarify those settings for which this predictive capability is most consistently realized.

Persistence, and a FBM Model. If an asset value increases today, is it more likely to do so tomorrow? A direct test for this persistence, and changes to its extent, would appear to have broad utility. We indicate a straightforward technique that uses ApEn to assess this. We also illustrate its potential utility by application to a fractional Brownian motion (FBM) model, thus affirming theory from a novel perspective.

The technique is as follows. Given an asset or index time series {d_i}, define the coarse-grained binary incremental series BinInc_i:= +1, if d_i+1 – d_i > 0, –1 otherwise. Then calculate ApEn (1){BinInc_i}. [In this binary version, r < 1 is out of play (2, 3), because ApEn detects precise pattern matches.] We thus directly evaluate the proximity to equidistribution of the four {up, up}, {up, down}, {down, up}, {down, down} pairs, with “random” variation yielding ≈25% occurrence of each pair, and a nearly maximal ApEn value of approximately log 2 (ref. 2, p. 2086). Positive persistence will produce >25% occurrences of both (+1, +1) and (–1, –1), resulting in lower than maximal ApEn values. The model independence and statistical power here derive from the property that virtually all processes have extremely small ApEn error bars for BinInc, e.g., in the FBM model below, for N = 1000, SD of ApEn ≤0.002 for the Hurst index H ≈ 0.5. Most importantly, this ApEn evaluation does not assume or require that the underlying data are Markovian or indeed that we know any data or model characteristics beyond stationarity. [If the data satisfy a Markov first-order model, then ApEn (1) = ApEn (2), allowing yet further analytical inferences.]

FBM provides a prominent model of persistence (19). It dates from the 1960s, when Mandelbrot modeled phenomena that exhibited both long-range dependence, in which time series retain unusually high persistence far apart in time, and heavy-tailed distributions. It has also led to new statistical applications, e.g., of Hurst's range over SD (rescaled range, R/S statistic) (ref. 20, pp. 62–64). FBM was first applied to financial data in 1971 (21); asset data sometimes exhibit long-range dependence and, more typically, have heavy tails. Mandelbrot has pointed out serious limitations in spectral and autocorrelative methods in the analysis of such data, also discussed in refs. 20 and 22.

The FBM B_H(t), specified by 0 < H <1, is a random process with Gaussian increments that satisfies the following diffusion rule: for all t and T, (i) E[B_H(t + T) – B_H(t)] = 0 and (ii) E[B_H(t + T) – B_H(t)]² = T^2H. For H = 1/2, B_H(t) is classical Brownian motion; for H > 1/2, B_H(t) exhibits positive persistence, and, for H <1/2, it exhibits antipersistence.

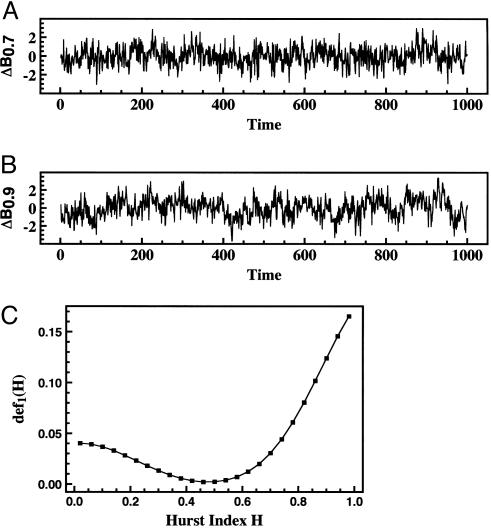
For each of 50 values of H equally spaced between 0 and 1, ApEn(1){BinInc_i}B_H(t) was estimated from 50 Monte Carlo realizations (23) of B_H(t). We illustrate the results in terms of def₁:= log 2 – ApEn(1); def₁ quantifies the extent to which ApEn(1) is not maximal (2). Series that do not exhibit persistence have a nearly maximal ApEn value, i.e., def₁ ≈ 0. In Fig. 3, we show def₁ of FBM as a function of H, for series length N = 1000 (Δt = 1), along with incremental time series for representative realizations of B_0.7(t) and B_0.9(t). In Fig. 3C, our primary observation is the monotonicity of def₁ up from 0 as H increases away from 1/2, in either direction, i.e., greater regularity with increasing H away from 0.5. (The asymmetry in def₁ about H = 1/2 is anticipated from an asymmetry of the covariance structure of B_H.)

Fig. 3.

Increments for representative realizations of fractional Brownian model (H). (A)H = 0.7. (B)H = 0.9. (C) Deficit from maximal irregularity def₁ of binary incremental time series BinInc_i of FBM(H), for series length N = 1000. Observe the monotonicity of def₁ up from 0 as H increases away from 1/2, in either direction, i.e., greater regularity with increasing H away from 0.5.

To illustrate this arithmetically, for a representative realization of B_0.7(t), BinInc =+1 occurred 517 times, and –1 occurred 482 times (nearly equal ups and downs). Yet the contiguous pair {+1, +1} occurred 324 times, whereas {+1, –1} occurred only 193 times; i.e., 63% of rises were followed by a second rise. Similarly, the pair {–1, –1} occurred 289 times, whereas {–1, +1} occurred 193 times; i.e., 60% of falls were followed by a second fall (ApEn = 0.665, def₁ = 0.027).

The B_0.9 case is even more pronounced. For a typical realization 72% of rises were followed by a second rise, and 74% of falls were followed by a second fall (ApEn = 0.579, def₁ = 0.113). ApEn characterizes the antipersistent case as well: for H = 0.1, for a typical realization, only 36% of rises were followed by a second rise, and 36% of falls were followed by a second fall; i.e., rises were more commonly followed by falls, and conversely (ApEn = 0.651, def₁ = 0.041).

Critically, once the realizations were generated, we deduced underlying structural changes without doing model-based parameter estimation. In particular, although the distribution functions of the B_H(t) realizations are readily seen as heavy-tailed, we do not need to first choose between FBM and, e.g., contrasting heavy-tailed yet short-term dependent GARCH models oftentimes favored by econometricians, or otherwise, to infer structural changes.

General “Random” Models. ApEn provides an efficient indicator of the validity of the i.i.d. assumption altogether, whether the random variables be normally distributed, log-normal, or otherwise. Assume that an underlying process is i.i.d. of unknown distribution. If the {u_i} are i.i.d. random variables, we can analytically compute the parameter ApEn(m,r). This is given by theorem 2 in ref. 1:

Theorem. For an i.i.d. process with density function f(x), with probability 1, for any m,

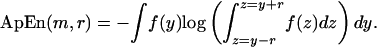[1]

In particular, note from Eq. 1 that ApEn(m,r) is independent of m for all r. Therefore, for all r, ApEn(1,r) = ApEn(2,r). So compare ApEn(1,r,N) and ApEn(2,r,N) values; if these disagree by a significant amount for some r in a statistically stable range of r, it is unlikely that the underlying process is i.i.d.

Historical Perspective: Classical Economics Approaches and Some Limitations. To better understand the utility of ApEn as applied herein, we consider the extant approaches to financial time series analysis. Historically, two primary schools of evaluating assets have existed: the “firm-foundation” and “castle-in-the-air” theories. The firm-foundation theory holds that intrinsic properties of an asset, such as price/earnings (P/E) ratios, dividend payouts, risk, and interest rates are primary determinants of a stock's value. Assessment and forecast of these properties (fundamental analysis) largely dictate financial decisions by this school. The contrasting castle-in-the-air theory holds that psychological and irrational forces and perceptual cues primarily drive the market, rather than intrinsic values. Advocates of this theory oftentimes use “technical analysis” or chartism as the essential analytical approach (24), looking for graphical trends or predictable patterns in historical records. Much has been written, won, and lost on behalf of each view; notably, castle-in-the-air advocates include Keynes (25) and Morgenstern (26), whose books and views had significant impact on policy at highest levels. However, despite numerous claims to the contrary, upon close examination, both technical and fundamental analyses have generally failed to yield benefits over the long haul, i.e., to outperform a simple “buy/hold” strategy (27). Moreover, a large fraction of significant market moves are difficult to explain on the basis of fundamental values alone (28).

Mathematical modeling and statistical analysis of price movements has become a field of its own, econometrics. The first formal mathematical model of financial asset prices was developed by Bachelier (29) in 1900 to price warrants traded on the Paris Bourse as a Brownian motion. More recently, Samuelson (30) and Arrow (31) developed highly mathematical approaches, although the resulting theory had some practical deficiencies. This was followed by the B-S model of option pricing (15), based on economic rationale and depending only on observable variables. The B-S equation and variants have become the theoretical workhorse of the financial industry and have been applied to numerous other derivatives (e.g., futures and swaps), insurance policies, and, indeed, asset prices directly. In addition to and contrasting with such structural models, the application of statistical ARMA-type models, which do not explicitly use economic theory and instead model forecast errors as simply random events, has been widespread. This application has led to a marriage of linear regression methodology and finance, with an influential history during the past 30 years. Further models incorporate long-range dependence, and more recently, dynamical systems theory and neural networks. A comprehensive treatment of econometric modeling is given in ref. 20.

However, despite all the modeling efforts, a variety of issues compromise the models' utility, in particular during periods of market instabilities, when predictive techniques are most needed. First, many models, based on retrospective studies, have lacked corroborative follow-up studies. Even for those models that persist, the accuracy of model-to-data fit often changes with evolving market conditions, undermining the effectiveness of estimated parameters to mark market evolution. Second, no a priori reason exists why future price movements need be independent of past movements for a given financial instrument; any number of violations of the random-walk hypothesis (e.g., refs. 17 and 18) suggest that one should let the data speak for themselves. Third, in fitting data to econometric models, traditional statistical assumptions generally are made based on underlying assumptions that the data were generated by experimentation. However, economic data are virtually always nonexperimental, with consequences discussed in endnote iii. Fourth, most models are real analytic, with functionals that have smoothly varying derivatives as a function of a control parameter. As a consequence, sudden dramatic changes in a market's expected value are highly unanticipated for such models. Fifth, jump process models are rarely seen, despite their apparent appropriateness in many settings when isolated political events, or discretely applied governmental or institutional constraints (e.g., interest rate changes), are primary factors. [Cox and Ross (32) provide a notable exception.] Finally, many models have several first-order practical limitations, because, to retain analytic elegance, they often ignore such aspects of financial markets as transaction costs, liquidity, and tax issues. Although corrections to these limitations have been proposed (e.g., models incorporating stochastic volatility, jump diffusions, and/or hybrid markets), in practice it appears that such corrections are either not widely implemented or that, when they are implemented, model modifications are made in an ad hoc manner, varying considerably among users, even among financial instruments.

Additionally, pollutants such as fraud and market manipulation seem nearly impossible to model, yet are real and significantly alter price movements, involving vast sums of money. The recent Enron debacle, the 2000–2001 “penny stock schemes,” and the Hunt brothers' attempts to corner the silver market in the 1980s are but three of many examples. The technical issue is that simply incorporating fraud into a random-effects component of, e.g., an ARMA model fails, because the extent of fraud is rarely chronic, but rather is much more interrupted, with ebb and flow a complicated game between judicial and legislative efforts and corruptive creativity.

A further issue is the considerable distinction between short- and long-term investment strategies. Aphorisms such as “In the long-term, earnings drive the market” abound. Yet in 1999, investors held stocks for just over 8 months on average, confirming that many investment strategies are decidedly not long-term. We thus require direct means to assess the irregularity of short sequences, without requiring a model-specification [see (iv), introduction, ref. 3]. Moreover, even if in the long run, fundamental analysis does triumph, in the short run, castle-in-the-air and perceptual issues (e.g., interpretation of cues by the Federal Reserve regarding interest rate change possibility) often appear to dominate index fluctuations. The famous Keynes (1923) quotation “In the long run we are all dead” reflects the importance of this setting—asymptotics and long-term evaluations are fine, but economists and investors should be intimately concerned as well with short- and medium-horizon dynamics.

Do these concerns matter? It appears so. The list of individuals and firms that have been badly hurt financially by inadequate “reading of the tea leaves” is daunting, including Sir Isaac Newton, and more recently, Long-Term Capital Management, an elite hedge fund based in Greenwich, CT, that lost 90% of its assets in a 6-week financial panic (1998) and needed to be bailed out by the Federal Reserve. This is to say nothing about the future of heavy investments in Internet and biotechnology stocks, whose chronic wild swings often underscore perceptual and speculative rather than asset-based valuations.

The perspective above strongly suggests that for effective, broad utility, measures of variability and irregularity should be “model-independent,” i.e., provide robust qualitative inferences across diverse model configurations. The observation that ApEn is model-independent fits squarely with this mandate. Of course, it is important to recognize that ApEn also confirms theory (establishes, e.g., monotonic parameter evolution) in instances in which models approximate reality, thus enriching and complementing extant models. However, we believe that the applicability (of ApEn) to data from complicated models of unknown form is paramount for meaningful financial data analysis and interpretation.

Independent of whether one chooses technical analysis, fundamental analysis, or model building, a technology to directly quantify subtle changes in serial structure has considerable potential real-world utility, allowing an edge to be gained. And this applies whether the market is driven by earnings or by perceptions, for both short- and long-term investments.

Endnotes.

1. The debate as to the relative importance of financial markets within economic theory is longstanding. A consensus among economists is that financial markets are a sideshow and that rational economic explanations can explain economic cycles. Without taking sides, it appears to us that, especially in evaluating short-term behavior, there is merit in treating financial market analysis and economics as distinct, albeit related endeavors. Moreover, both within economic and finance theory, there is a history of modeling toward reductionist, analytic elegance. This elegance does well in conveying central paradigms, but often it is realized at the expense of considering observed effects that muddy theory, yet critically affect outcome. We should recall that the intellectual founders of modern economic theory, including Keynes and his mentor Marshall (33), stressed its practical importance. Hence, we reinforce the need for analytic tools that prove useful both on empirical data of arbitrary lengths and unknown model formulations, yet are simultaneously useful within model-based frameworks.

2. For many mathematical models, as a control parameter evolves toward an instability boundary, not only does ApEn increase toward maximal values (1, 34), but it also changes significantly earlier in parameter space than do means and standard deviations. Thus, both empirically and in model settings, ApEn can often provide the investor with advanced warning of a first-order asset price change.

3. Some misconceptions should be clarified. Because financial time series are nonexperimental, single sequences do not necessarily satisfy “randomness” criteria given by almost sure laws of probability theory (e.g., normality) (3–5, 7). Yet many econometric models implicitly make experimental assumptions. Oftentimes, one sees as a baseline setting a linear regression model, for which the regressors have fixed values, and disturbances are presumed uncorrelated with 0 mean and constant variance. Then, presuming classical experimental assumptions, a least-squares estimator is the best linear unbiased estimator. Of course, when this model is violated, the least-squares estimator no longer has such nice properties. The form of violation (e.g., multicollinearity, specification error, serial correlation of residuals, and heteroskedasticity), and putative repairs to each type, have received much econometric attention. In the end, however, an experimental framework, with some i.i.d. model component and axiomatic inferences, is nearly always maintained, subject to the objections above. This theme, for instance, is reflected in much of the second generation of B-S and stochastic calculus-type models, and in somewhat more classical fixes such as GARCH and SARIMA models. The inadequate fit of theory to empirical data is recognized, but the fix does not satisfy the prejudice-free, nonexperimental criterion.

4. The efficient market and random-walk hypotheses are often viewed as synonymous. Although variants of the form of efficiency exist, depending on which information is available to whom and how quickly, advocates of this perspective hold that the present price of a security encompasses all presently available information, including past prices, and that future prices are impossible to predict. This has been debated ad infinitum; certainly numerous studies exist in which the data do not satisfy a random walk. However, in many violations, despite some Markovian structure, the martingale form of efficiency [interestingly, Bachelier's original position (29)] still holds; i.e., future expected gains are independent of the past.

   We have a slightly different viewpoint. The weak evidence of either technical or fundamental analysts to outperform “buy- and-hold strategies” does not necessarily imply random increments, but rather only that no one has previously quantified and exploited insidious serial structure on a consistent basis. We believe that for many markets, exploitable opportunities remain, especially in the >80% maximal irregular ApEn range, where classical chartism, correlation, and spectral methods typically disclose little.

5. Although the emphasis herein has been primarily on ApEn as a model-independent measure, it is essential to point out that ApEn has been applied in many model-based studies (1, 8, 34, 35). Thus, point 4 of the Introduction bears repeating: ApEn can be readily applied to the classical econometric modeling apparatus.

6. We propose a thematic modeling approach that may help to “explain” rapid increases in ApEn as a precursor to a significant market instability (as in Fig. 2). Consider a family of N either independent (suitably superposed) or weakly coupled oscillators. Then, it will be a generic result that as N increases, ApEn will also increase monotonically. The genericity will be robust to most forms of superposition, of oscillators or (quasi-) periodic phenomena, and of weak coupling. Thus, greater system instability can often be seen as an increasing number of primarily distinct cyclic sources, with destabilization a much greater risk in a significantly fractionized and divisive financial universe. Of course, a single abrupt catastrophe can abruptly change everything, e.g., the September 11, 2001 attack, but, whereas this type of event will remain largely unpredictable, other more insidious “structural” changes may well be detectable before a major market or asset move.

7. Superficially, ApEn has a theme common to “nonlinear” statistics such as the correlation dimension and largest Lyapunov exponent, in that it is a functional of contiguous block input. However, critical differences exist between ApEn and these methods. These latter methods are strongly prejudiced; they correctly apply primarily to deterministic dynamical systems, only one of many model forms that yield correlated output. In general, they are correctly used only in asymptotic analyses and suffer a “curse of dimensionality” when applied to typically sized data sets. Consequently, the application of such methods to most time series of moderate length and unknown model-form, e.g., financial data, yields nonreplicable results (1, 36). This reinforces the importance of the choices of parameters m and r (low-order m, relatively coarse mesh r) in the ApEn specification to ensure good replicability.

8. Cross-ApEn (2), a bivariate measure of asynchrony thematically related to ApEn, provides a measure of “correspondence” or “association” superior to linear correlation, in that its quantification matches intuition in broader settings, both theoretical mathematical and real world (12, 22). This has important implications to diversification strategies, portfolio selection, and the use of “beta” in quantifying systematic risk.