A comparative method for finding and folding RNA secondary structures within protein-coding regions

Abstract

Existing computational methods for RNA secondary-structure prediction tacitly assume RNA to only encode functional RNA structures. However, experimental studies have revealed that some RNA sequences, e.g. compact viral genomes, can simultaneously encode functional RNA structures as well as proteins, and evidence is accumulating that this phenomenon may also be found in Eukaryotes. We here present the first comparative method, called RNA-Decoder, which explicitly takes the known protein-coding context of an RNA-sequence alignment into account in order to predict evolutionarily conserved secondary-structure elements, which may span both coding and non-coding regions. RNA-Decoder employs a stochastic context-free grammar together with a set of carefully devised phylogenetic substitution-models, which can disentangle and evaluate the different kinds of overlapping evolutionary constraints which arise. We show that RNA-Decoder's parameters can be automatically trained to successfully fold known secondary structures within the HCV genome. We scan the genomes of HCV and polio virus for conserved secondary-structure elements, and analyze performance as a function of available evolutionary information. On known secondary structures, RNA-Decoder shows a sensitivity similar to the programs Mfold, Pfold and RNAalifold. When scanning the entire genomes of HCV and polio virus for structure elements, RNA-Decoder's results indicate a markedly higher specificity than Mfold, Pfold and RNAalifold.

INTRODUCTION

The last few years have shown that functional RNA molecules are much more abundant and versatile than previously expected (1). Not only have several new classes of non-coding RNA genes (2) as well as cis-acting elements in the non-translated parts of mRNAs (3) and viral genomes (4,5) been found, but, surprisingly, evidence is now accumulating for the widespread existence of functional RNA structures embedded within protein-coding regions. The majority of this evidence stems from viral genomes (6–8), but a recent study (9) has revealed strong evidence for functional RNA structures within the coding regions of Eubacteria as well as in Saccaromyces cerevisiae (baker's yeast). The function of most of these structures is still not well described. Some of the viral structures are known to be involved in genome replication (8) and in the regulation of transcription (10), whereas the structures found in Eubacteria are hypothesized to be involved in the regulation of translation (9). Additionally, exonic splice enhancers in Eukaryotes have also been suggested to involve the formation of RNA structures (11).

A range of methods has been developed for single-sequence RNA secondary-structure (RNA-ss) prediction. One of the best known being Zuker's Mfold method (12–14), which predicts the RNA-ss that minimizes the free energy of the RNA sequence. Another successful class of methods employs stochastic context-free grammars (SCFGs) (15–17). SCFGs provide a probabilistic framework for modeling long-range correlations within a sequence such as those imposed by the base-pairing nucleotides within the secondary structure of an RNA sequence. The advantage of SCFGs is that their parameters can be derived from known RNA structures and that they constitute a probabilistic framework which is capable of assigning measures of confidence to its predictions.

The alignment of several evolutionarily related RNA sequences with homologous conserved RNA-ss exhibits a characteristic pattern of compensatory mutations which maintain base pairs despite primary-sequence divergence. Comparative RNA-ss prediction methods utilize these pairs of co-varying alignment columns as evidence to predict RNA-ss (18–20). This idea can be taken one step further by explicitly modeling the entire evolutionary substitution process on a phylogenetic tree, creating the observed pattern of mutations in both the pairing and the non-pairing regions of the sequence alignment (21).

The apparent high prevalence of functional RNA structures in many genomes has created a growing interest in bioinformatics methods for RNA-ss prediction. An approach which was suggested already in 1988 by Le et al. (22), namely to search for regions with higher than expected levels of RNA-ss according to a thermodynamic criterion, has recently been applied to protein-coding regions. Evidence for the presence of RNA-ss was detected by comparing the free energies predicted by Mfold for a given coding sequence with the free energies predicted for shuffled versions of the same sequence (6,9,23). However, this type of approach has been criticized for having a low sensitivity, for its prediction resolution being limited by the window-size used, and for the results being dependent on the particularities of the shuffling algorithms (24,25).

Rivas et al. (25) compared several methods for detecting functional RNA structure within both coding and non-coding sequences. They found that their single-sequence methods could not reliably predict the known RNA-ss of these sequences. However, a comparative method, which takes as input an alignment of two evolutionarily related sequences, was later found to provide sufficient evidence for the successful prediction of regions containing functional RNA structures (26).

We here present a new method, called RNA-Decoder, which aims to specifically address the problem of finding and folding functional RNA structures within protein-coding regions. It is also capable of modeling RNA-ss in non-coding regions as well as RNA-ss spanning both coding and non-coding regions. RNA-Decoder uses a phylogeny-based stochastic model of molecular evolution for regions where the protein-coding annotation is known, but the RNA-ss is unknown. The model consists of an SCFG which is used to propose RNA-ss along the alignment, and a set of phylogenetic substitution models which evaluate the alignment columns according to the known codon position and the predicted structural category. We devised two variants of RNA-Decoder, RNA-Decoder-Extended and RNA-Decoder-Two-Step, in order to be able to predict an individual RNA-ss for each sequence in the input alignment.

SCFGs and phylogenetic models were first combined by Pfold (21,27), a comparative method for folding RNA-ss within an alignment of non-coding RNA sequences. Pfold distinguishes itself from other SCFG-based approaches by allowing any number of sequences in the input alignment and by explicitly incorporating the phylogenetic tree, which relates the sequences and defines their correlation structure (28), into the RNA structure-prediction process.

RNAalifold (20) is also a comparative method that predicts a common structure for a fixed input alignment of RNA sequences. It minimizes the overall free energy and uses information on compensatory mutations between the sequences to arrive at its predictions. Opposed to RNA-Decoder and Pfold, it does not consider the evolutionary relationship between the sequences of the input alignment, but averages energy scores and compensatory mutation scores equally over all sequences. As Pfold and RNA-Decoder, it can either be used to predict the most likely folding or to predict the pairing probabilities along the alignment.

The grammar of RNA-Decoder is capable of distinguishing regions with RNA-ss from regions without. This feature is especially important for finding RNA-ss within sequences which are a priori not expected to fold into one RNA folding. In contrast to Pfold, RNA-Decoder explicitly models the known codon positions of the alignment columns in its evolutionary analysis. This is achieved by a set of dedicated phylogenetic models, which describes the special substitution process of the different combinations of codon position and structural elements observed in regions encoding both protein and RNA-ss (29).

The development of RNA-Decoder has been challenged by a limited amount of well-curated coding RNA structures. We have trained and tested the model on genomic alignments of the hepatitis C virus, for which we know five experimentally validated RNA structures.

METHODS

RNA-Decoder takes as input both an alignment of several RNA sequences with annotated protein-encoding regions and their relating phylogenetic tree. RNA-Decoder can return two different types of predictions: either the base-pairing probability for each position in the alignment or a single folding of the alignment into RNA secondary structures together with the estimated reliability of the prediction for each alignment position. The former identifies regions containing potentially functional RNA-ss without explicitly predicting any of the RNA structures, whereas the latter predicts a single RNA folding for the input alignment.

RNA-Decoder's main source of evidence for detecting RNA structures is the evolutionary pattern within the input alignment. RNA-Decoder employs an SCFG together with several phylogenetic models in order to score each of the possible structural annotations of the input alignment, a modeling approach which has been adapted from Knudsen and Hein (21).

The stochastic context-free grammar

This section introduces SCFGs and the terminology (17), before describing our model.

SCFGs originate from the field of linguistics (30) and were developed for speech recognition (31), but have proved a convenient formalism for modeling RNA secondary structure (15,16). They can model a large variety of long-range correlations along a sequence (which, in our case, are imposed by the base pairs of RNA secondary structure), but cannot easily be extended to model the dependencies imposed by pseudo-knots (17,32).

An SCFG can be viewed as a device capable of both generating and parsing strings. We will here introduce the formalism from the parsing point of view. An SCFG takes as input a sequence of observables (in our case a sequence of alignment columns together with an annotation of protein-encoding columns) and proposes a way to derive the sequence of observables from a set of so-called production rules. These production rules together with associated probabilities completely define an SCFG. The set of production rules defines a grammar. Each production rule specifies the transition from a single non-terminal to a sequence of non-terminals and terminals. Terminals correspond to observable entities of the input sequence and non-terminals correspond to the states of the grammar. Successively applying the production rules of the grammar until all observable entities of the input sequence have been described is called parsing and defines a derivation tree. This derivation tree can then be used to assign a label to each observable entity according to the state by which it was emitted. By assigning probabilities to each production rule, each derivation tree can be assigned an overall probability, which is the product of the probabilities of each production rule used in the tree. Different predicted annotations of the input sequence can then be ranked according to the overall probability of their derivation trees.

The SCFG formalism presented here will decompose productions into two independent parts: state transitions and symbol emissions. Each state of the SCFG has an associated transition distribution and each emitting state has in addition an associated alphabet with a corresponding emission distribution. The SCFG can thus be defined by the four-tuple M = (W, t, A, e), where W is the set of states, t is the set of transition distributions, A is a set of alphabets, and e is the set of emission distributions.

If an SCFG is used to model RNA secondary structure, the production rules can be conveniently reduced to a few different types: pair (P) (W_v → x_iW_yx_j), left (L) (W_v → x_iW_y), start (S) (W_v → W_y), bifurcate (B) (W_v → W_yW_Z) and end (E) (W_v → ε), where ε is a special terminal symbol denoting the empty sequence, W_v, W_y and W_z denote different states, x denotes the input sequence of observables, and i and j positions within the input sequence.

The grammar of RNA-Decoder can be sub-divided into three sub-grammars: a high-level grammar (Figure 1) and two low-level grammars (Figure 2), one representing the structural and the other the non-structural part. A derivation tree within the high-level grammar defines a linear succession of structural and non-structural regions along the input sequence. Note that the high-level sub-grammar only allows for structural regions directly next to each other, thereby rendering it unambiguous. The structural sub-grammar defines the set of RNA-ss, which can be modeled. Each RNA-ss starts with a stem. Stems are required to have a minimum length of two base pairs and loops a minimum length of four. These constraints are enforced by the grammar architecture and by the emission distributions, respectively. Derivation trees within the non-structural sub-grammar correspond to regions with no RNA-ss, and the three emitting states model the evolutionary rate variation within protein-encoding regions.

Figure 1.

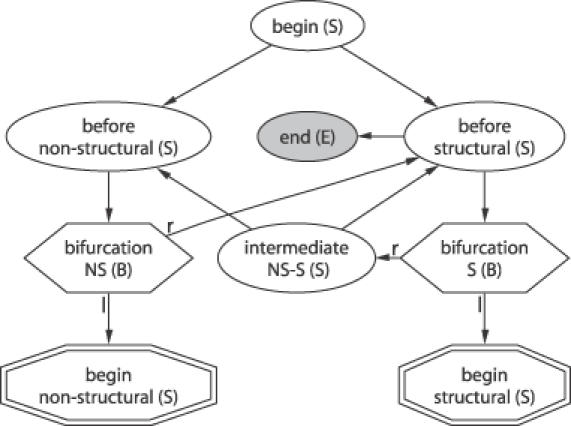
States and transitions of the high-level sub-grammar. The different state types (see abbreviation in parenthesis) are explained in the text and are indicated by the different shapes. States of type bifurcate have a bifurcating transition leading both to a left (l) and a right (r) state. Any derivation tree of the grammar has to start in the begin state. The start states of the non-structural and structural sub-grammars simultaneously act as terminals for this high-level grammar and are depicted as double-edged octagons.

Figure 2.

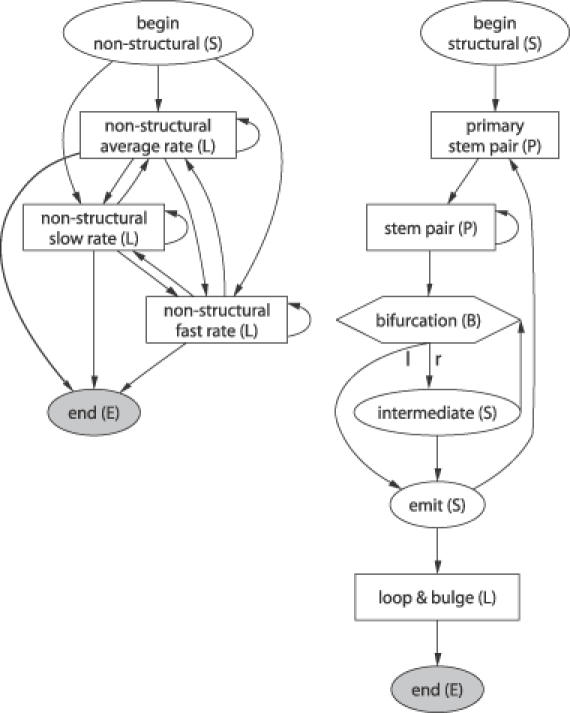
States and transitions of the non-structural (left) and the structural (right) sub-grammar. States which read terminals are depicted as squares. See Figure 1 for the high-level sub-grammar and more information.

Emission distributions

The SCFG of RNA-Decoder has six emitting states. The two pair-emitting states use the same emission distribution, and we will initially also think of the three emitting non-structural states as using a common emission distribution. This leaves us with three different emission distributions: one non-structural (ns), one stem-pairing (p), and one loop/bulge emission distribution (l).

The input sequence to RNA-Decoder is an annotated sequence of columns of a multiple sequence alignment x of n DNA sequences. The annotation of the alignment can be formally viewed as a sequence of annotation labels y^C with letters from the alphabet {1, 2, 3} which indicate the codon position of each column of the alignment. Columns of the alignment which are not protein-encoding are specified as third-codon positions. The alphabets of ns and l thus consist of the 4ⁿ possible single columns, and the alphabet of p consists of the (4 · 4)ⁿ possible column pairs. All three emission distributions are specified by a set of phylogenetic models ψ defined below.

Due to the degeneracy of the genetic code, the evolutionary constraints can vary considerably between the three codon positions. Most changes in the first or second codon positions change the encoded amino acid (non-synonymous changes), whereas most changes in the third position leave the encoded amino acid unchanged (synonymous changes). The thus resulting differences in the evolutionary substitution process can be captured by making the emission distributions dependent on the position within the codon. The single-column emission distributions (ns and l) are therefore specified by three different phylogenetic models (one for each codon position), whereas the emission distribution for pairs of columns (p) is specified by nine phylogenetic models (one for each of the nine possible pairs of codon positions).

We enumerate the phylogenetic models of the set ψ and their parameters by a function c according to the category of sites they model, e.g. ψ^c(p,1,3) denotes the model for stem-pairing first and third codon positions. The emission distribution of a single-column emitting state W_v can then be written as

where E(v) denotes the corresponding emission distribution (either ns or l). Likewise, the emission distribution of a state W_v which emits pairs of columns can be expressed as

The phylogenetic models

Phylogenetic substitution models have long been used for phylogenetic inference (33) and for the study of molecular evolution. The parameterization of the phylogenetic models used by RNA-Decoder is explained in detail in (29). Our models assume that all columns of the alignment evolve independently, except for those pairs of columns which are base-paired. The input alignment thus consists of many small fragments, each of them comprising either a single column or a pair of columns. This amounts to ignoring the dependency between nucleotides of the same codon, but has the advantage of breaking the ‘contagious’ context dependencies arising in regions that also form stem pairs, while still taking the protein-coding context of each column into account. As customary in phylogenetics, we treat gaps within the alignment as missing data.

Each of the phylogenetic models ψⁱ = φ for single columns is defined by a six-tuple φ = (Σ, Q, π,τ, β, r), where Σ is the sequence alphabet (A, C, G, U), Q is the 4 × 4 instantaneous rate matrix, π is the vector with the equilibrium frequencies, τ is the topology of the rooted binary tree with n leaves, β is the vector of branch lengths, and r is the scaling factor for the branch lengths (34). Those phylogenetic models ψⁱ that deal with pairs of columns are defined by a six-tuple, where the above Σ is replaced by (A, C, G, U) × (A, C, G, U) and the dimensions of Q and π are adjusted accordingly.

Σ, Q and π define a continuous Markov process which is used to model the substitution process along the branches of the phylogenetic tree represented by τ, and the vector of scaled branch lengths rβ. Felsenstein's peeling algorithm (35) calculates the probability of an alignment column in time O(|Σ|²n), where |Σ| denotes the size of the alphabet and n is the number of sequences in the alignment.

The rate matrix of the phylogenetic models dealing with single columns is based on the HKY-model (36), whereas the rate matrix of models dealing with pairs of columns was derived from a di-nucleotide rate matrix [which was estimated from a set of non-coding RNA-ss (21)] by modifying it to accommodate codon position-specific differences (29).

Many properties of the substitution process are common to different categories of sites. This is incorporated into the parametrization of the phylogenetic models by using coupled parameters, thereby reducing the total number of free parameters. All phylogenetic models of ψ use the same phylogenetic tree (τ and β). Differences in the substitution rates are accommodated by an individual scaling of the branch lengths by r.

The overall parametrization of phylogenetic models ψ follows the model denoted ψ₃ in (29) apart from the following differences. The models for first and second codon positions in non-structural regions have their rate matrices and equilibrium distributions coupled to the corresponding models in loop/bulge regions (Q^c(ns,1) = Q^c(l,1), π^c(ns,1) = π^c(l,1), Q^c(ns,2) = Q^c(l,2) and π^c(ns,2) = π^c(l,2)), the corresponding parameters of the third position models are treated independently.

Only modeling the codon position-dependent differences in the substitution rate of coding nucleotide sequences leaves much of the rate variation unexplained. Differences in the functional constraints imposed on the different structural regions of a protein lead to variation in the substitution rate at the amino-acid level, which can give rise to auto-correlated rate variation along the corresponding nucleotide sequence (37). We accommodate this by giving each of the three emitting states of the non-structural sub-grammar its own emission-distribution. The phylogenetic models specifying the two new distributions ns_fast and ns_slow are defined relative to those of the original (average rate) distribution ns. The only difference between the new distributions (ns_fast and ns_slow) and ns is that the substitution rate is increased in the first and second codon position models of ns_fast (r^c(ns_fast,1) = 3 · r^c(ns,1) and r^c(ns_fast,2) = 3 · r^c(ns,2)) and decreased in the corresponding models of ns_slow (r^c(ns_slow,1) = 0.2 · r^c(ns,1) and r^c(ns_slow,2) = 0.2 · r^c(ns,2)). The models of the third codon position remain unchanged, which implies that all third-position changes are assumed to be synonymous and therefore unaffected by selection at the amino acid level (37).

Each phylogenetic model is designed to fit the substitution process of a specific category of columns. For example, the phylogenetic models for base-pairing regions assign a very low probability to substitutions which involve pairs of nucleotides that cannot base pair. This implies that alignment errors or structure evolution which both increase the rate of non-pairing pairs of nucleotides are penalized so heavily that they can cause RNA-Decoder to make mispredictions. In order to allow for a low rate of mis-aligned nucleotides and some structural divergence, the phylogenetic models allow some uncertainty in the interpretation of the observed sequence symbols, thus making the predictions more robust with respect to these two potential causes of disturbance. This is done by introducing fuzzy-alphabets (27) by which 97% of the probability is assigned to the state that corresponds to the observed nucleotide, and the remaining 3% probability is distributed among the other states.

Prediction algorithms

Each derivation tree from the SCFG of RNA-Decoder assigns a sequence of labels y^S to the columns of the input alignment x. The label of each column in the alignment unambiguously indicates the state within the SCFG by which it was emitted. As the grammar of RNA-Decoder is unambiguous, every label sequence y^S corresponds to exactly one derivation tree. The prediction corresponding to the derivation tree with the highest probability

can be derived using the CYK algorithm (17).

The predicted label sequence y^S* can be mapped onto each sequence of the alignment, which assumes the RNA-ss to be the same for all, i.e. that the RNA-ss are perfectly conserved during evolution. Due to slow, but existing RNA structure evolution, this assumption need not always be fulfilled. The RNA-ss derived from y^S* thus cannot always correspond to the RNA-ss of each sequence within the alignment. In order to address this issue, we implemented two further prediction algorithms, denoted RNA-Decoder-Extended and RNA-Decoder-Two-Step, that exploit comparative information while still making individual predictions for each sequence of the alignment. These methods are explained in detail in the online supplementary material.

The posterior probability of assigning an annotation label to a position of the alignment or a pair of annotation labels to a pair of positions can be calculated by the inside–outside algorithm (17). Posterior probabilities give a measure of the reliability to each column's annotation, thus making it easy for a user to distinguish regions whose annotation is likely to be correct from those whose annotation is less certain.

Instead of using RNA-Decoder (or RNA-Decoder-Extended or RNA-Decoder-Two-Step) to predict a single RNA folding using the CYK algorithm, one can also use RNA-Decoder to predict the base-pairing probability for each position of the input alignment. This is a useful feature if the task is to identify regions which are likely to contain conserved RNA-ss within a potentially long input alignment which is a priori not expected to fold into one large conserved RNA-ss. We define the pairing probability of a given position in the alignment to be the posterior probability of it forming a stem pair with any other position. It is equal to the sum over the posterior probability of all possible base-pairing labels involving the given position. We search for RNA-ss containing regions by calculating the pairing probability along the alignment. High-scoring regions have a high likelihood of containing evolutionarily conserved RNA-ss which may therefore be functionally important. In the investigations presented here, alignments of full-length viral genomes were searched for RNA structure-containing regions by sub-dividing it into overlapping windows which were first analyzed individually, and whose non-overlapping sections were merged later. This reduces the time and memory requirements of the computational analysis considerably. As the window size determines the maximum distance between any two base-pairing positions that can be taken into account, it should be long enough to encompass the expected RNA-ss.

Parameter estimation

The free parameters of the full model are given by the set of transition distributions t and the set of emission distributions e. Both can be estimated by an expectation maximization (EM) procedure (17). The inside–outside algorithm is used to calculate the usage counts weighted by the posterior probabilities within the expectation step. The counts used in the maximization step are the estimated number of times each transition is used and the estimated column weights for each emitting state. The maximum likelihood estimate (MLE) of t given the transition counts has a simple analytical solution (17). The MLE of e given the column counts has to be found through numerical optimization (described below) since it is specified by the set of phylogenetic models ψ. This optimization strategy is similar to the method used for evolutionary hidden Markov models in Ref. (38).

The EM procedure normally takes several iterations to reach the maximum, but only a single iteration is needed when the input data is supplied with a structural annotation that defines a derivation tree within the grammar. The expectation step is then reduced to a simple counting of the state transitions and column emissions within the given derivation trees. The annotation for the training data used here only determines a derivation tree within the high-level sub-grammar and the structural sub-grammar. The derivation tree within the non-structural sub-grammar is not known since the rate category (i.e. ns_slow, ns or ns_fast) of each non-structural position is unknown. The estimation of the parameters is therefore split into the following two steps. First, all three emitting non-structural states are given the same emission distribution (ns), and their transitions are fixed. The annotation of the alignment is sufficient for estimating all free parameters of this restricted model in one iteration. Second, all non-structural transitions are allowed to vary, and the slow and fast rate emissions distributions (ns_fast and ns_slow) are introduced as described above. The EM procedure is then used to derive values for the transitions of the non-structural sub-grammar.

The estimation of the free parameters of the phylogenetic models follows the procedure defined in Ref. (29). A common phylogenetic tree is estimated from the third codon positions within the non-structural regions. Tree topologies (τ) are estimated by the sequential use of DNADIST (39) and Weighbor (40). Branch lengths (β) are estimated with BASEML (41). The MLE of the parameters specifying the rate matrices Q and the tree scaling factors r are found by numerical optimization of the combined likelihood of all the column counts using the conjugate directions search method Powell (42). The equilibrium frequencies π are estimated by the symbol-frequencies within each column category.

Implementation and computational requirements

RNA-Decoder was implemented in C++ by writing a general framework that allows the specification of the SCFG as well as the phylogenetic models by an XML input file. RNA-Decoder-Two-Step and RNA-Decoder-Extended are implemented through python scripts. The time requirement of all methods is O(nL³) and the memory requirement is O(nL²), where L is the length of the sequence alignment and n the number of aligned sequences. Scanning the entire HCV genome with RNA-Decoder using the HCV 1a set took 141 MB of memory and 103 CPU minutes spent in user mode on a 1800 MHz Mobile Intel Pentium 4 processor. Every 300 bp chunk of the genome thus took 65 CPU seconds to analyze.

RESULTS

Data sets

Our raw, unaligned data consist of 99 full-length genomic hepatitis C Virus (HCV) sequences and 26 full-length genomic polio virus sequences. We manually align these full-length sequences in several groups, before performing two different types of experiments: (i) cross-evaluations on a few structural regions in order to investigate how well and robustly RNA-Decoder can be trained; and (ii) scanning experiments, using the model that was trained on the entire HCV 1a & 1b set in order to search for structural elements along the entire alignment of the genomic sequences.

HCV data

HCV is a flavivirus of the Flaviviridae family with a positive-sense single-stranded RNA genome of about 9500 bases, which has been abundantly sequenced. The genome contains a single open reading frame encoding a poly-protein. HCV can be divided into genotypes 1–6, and each genotype can be further sub-divided into sub-types a, b, etc. Our HCV set comprises 8 HCV 1a sequences and 91 HCV 1b sequences. HCV is known to have an RNA structure in the 3′ untranslated region that initiates RNA replication (43), and one in the 5′ untranslated region that serves as an internal ribosomal entry site (44). Interestingly, RNA structure has recently been found within the 3′ part of the protein-coding region (45), where five hairpin-like RNA structures have been experimentally verified (7). These five structures constitute our structural annotation of the protein-coding part of the HCV genome.

Polio virus data

In the polio virus, a single RNA structural element has been experimentally verified within the coding region of the genome. It is termed the cis-acting replication element (CRE) and templates the uridylation of the VPg protein during viral replication (46). Full-length genomic sequences of polio virus were compiled and the structural information provided in Ref. (46) was used as structural annotation.

Alignment of the sequences, structural annotation

The alignment of the HCV 1a, the HCV 1a & 1b sequences and the polio sequences were done manually, with only very few gaps inserted. In the following, the terms ‘HCV 1a set, ‘HCV 1a & 1b set’ and ‘polio set’ will refer to the alignment of the respective set of sequences. Coding regions were aligned according to their encoded amino-acid sequence. The structural annotation of the HCV alignments was derived by projecting the experimentally verified RNA structures of the reference sequence (sequence with accession number AF271632 of the HCV 1a set) onto the alignment. We proceeded in a similar way for the polio alignment, where the reference sequence has the accession number X00925. This resulted in pairs of columns which mostly contain any of the six consensus base pairs. However, due to RNA-ss evolution, these columns may also contain pairs of nucleotides which do not pair (see Table 1).

Table 1. Cross-evaluation data sets.

Structure	Length	Pairing	Fraction not pairing
			HCV 1a set	HCV 1a & 1b set
1	99	50	0.01	0.007
2	87	50	0.02	0.163
3	62	40	0.0	0.234
4	52	28	0.0	0.06
5	42	26	0.019	0.002
All	342	194	0.01	0.101
				polio
CRE	110	42		0.075

Total sequence length in nucleotides for each structural region, number of nucleotides which are known to be base-pairing and fraction of these that do not form a consensus base pair within the alignment (the six consensus base pairs are G–C, C–G, A–U, U–A, U–G and G–U).

Training set

The training set comprises the entire coding region of the 1a & 1b alignment, apart from the first 50 sites, as these are known to contain an RNA structure that extends from the 5′ untranslated region into the protein-coding region (44). All the annotated non-consensus base pairs of the structural regions were discarded and treated as gaps in order not to influence the estimation of the evolutionary model. The HCV 1a & 1b set was chosen, as the HCV 1a set contains too few evolutionary events to reliably estimate the parameters of the evolutionary models. The entire training set was used to train the version of RNA-Decoder used for the scan experiments.

Input data for the cross-evaluation experiments

For the cross-evaluation experiments, we excised each of the five known hairpin-like structural elements within the 3′ end of the protein-coding region from the aligned HCV sequences (see Table 1). From these and from the remaining non-structural part of the training set we arrived at five HCV 1a and five HCV 1a & 1b cross-evaluation sets. The polio data set was not used for the cross-evaluation experiments, as it contains only one known structure element within the protein-coding region.

Input data for the scanning experiments

Two scan data sets were constructed from the entire HCV 1a and HCV 1a & 1b alignments, apart from their 3′UTRs, which were discarded since few of our sequences span this region. For the scanning experiments, we took the scan data sets and divided them into chunks of 300 bases' length by going along the alignments in steps of 100 bases. Each chunk of 300 bases was individually analyzed for RNA structures. The predictions for the individual chunks were then combined into one prediction for the entire alignment by combining the middle 100 bases of each chunk into one long prediction (the first 200 of the first chunk, the middle 100 bases of the intermediate chunks and bases 101 following of the last chunk).

Training of RNA-Decoder and cross-evaluation

RNA-Decoder was trained and the training evaluated in a 5-fold cross-evaluation, once evaluating on the HCV 1a set and once on the HCV 1a & 1b set of annotated RNA structures. In each of the five cross-evaluation rounds, the model's parameters were first trained on the training set, apart from one structural element, and the performance of the thus trained model was then evaluated on this remaining structural element, which had not formed part of the training set.

The quality of the predictions was measured in terms of the pair-performance as well as the single-nucleotide performance. The single-nucleotide sensitivity (sn_s) is the fraction of annotated base-pairing nucleotides which were correctly predicted to be base-pairing. The single-nucleotide specificity (sp_s) is the fraction of predicted base-pairing nucleotides which were correctly predicted to be base-pairing. The pair sensitivity (sn_p) is the fraction of annotated base pairs whose pairs were correctly predicted, and the pair specificity (sp_p) is the fraction of predicted base pairs which were correctly predicted. The pair-performance is thus by definition limited by the single-nucleotide performance.

The overall performance results for the five structures are reported in the top part of Table 2. The performance of RNA-Decoder is better on the HCV 1a set than on the larger HCV 1a & 1b set. This is probably due to the significant amount of changes in the RNA secondary structures of some sequences of the HCV 1a & 1b set (see Table 1). Comparing the single-nucleotide performance with the pair-performance shows that RNA-Decoder does better at predicting whether a site is pairing than getting the specific pair right. The online supplementary material gives the performance results for each structure as well as the performance results for RNA-Decoder-Two-Step and RNA-Decoder-Extended.

Table 2. Average cross-evaluation performance of RNA-Decoder compared to the average performance of the published and already trained versions of Pfold, RNAalifold and Mfold.

Method	sns	sps	snp	spp	Data set
RNA-Decoder	0.88	0.93	0.79	0.84	HCV 1a set
	0.73	0.85	0.61	0.71	HCV 1a & 1b set
Pfold	0.81	0.95	0.74	0.87	HCV 1a set
	0.51	0.85	0.37	0.62	HCV 1a & 1b set
RNAalifold	1.00	0.89	1.00	0.89	HCV 1a set
	0.77	0.88	0.64	0.73	HCV 1a & 1b set
Mfold	0.97	0.89	0.96	0.88	HCV reference seq.

Each method was used to separately predict each of the five known secondary structure elements in HCV. Each reported performance value corresponds to the average performance on these five structural elements. We report the performance in terms of sensitivity and specificity for pairs of base pairing nucleotides (sn_p and sp_p) as well as for single nucleotides (sn_s and sp_s). Please refer to the text for a definition of these performance measures.

Comparison of RNA-Decoder, Pfold, RNAalifold and Mfold on known RNA structures

The ability of RNA-Decoder to predict specific coding RNA-ss as revealed by the cross-evaluation experiments was compared to the prediction ability of three existing programs: Pfold (published version from 2003), RNAalifold (Vienna RNA Package version 1.5) and Mfold (version 3.1.2). Pfold (21,27) was chosen because RNA-Decoder was modeled along similar lines. RNAalifold (20) was chosen because it is a comparative method taking a multiple alignment as input. Mfold (12–14) was chosen, because it is probably the most commonly used program for RNA-ss prediction. Opposed to the other programs, Mfold takes only a single sequence and no alignment as input and predicts the RNA structure that minimizes the global minimum free energy according to a list of experimentally supported energy rules. This implies that Mfold does not make use of the information contained in co-varying pairs of alignment columns. Both RNA-Decoder and Pfold work with an underlying probabilistic model that yields explicit confidence values, which RNAalifold and Mfold cannot predict. We used both Pfold, RNAalifold and Mfold to predict the five RNA structure elements within the 3′ end of the protein-coding region. Pfold and RNAalifold were given the same input alignments as RNA-Decoder, whereas Mfold was given the corresponding segments of the reference sequence (accession number AF271632) for which the structures were experimentally found.

The bottom part of Table 2 shows the resulting performance of Pfold and Mfold. When comparing Pfold's performance to that of RNA-Decoder, it is clear that RNA-Decoder outperforms Pfold both in terms of sensitivity and specificity on the HCV 1a & 1b set. However, for the HCV 1a set this is less clear. RNA-Decoder has a slightly higher sensitivity and slightly lower specificity than Pfold. Mfold and RNAalifold generally outperform both RNA-Decoder and Pfold in sensitivity and specificity.

It should be noted that Mfold is expected to perform well on this test set: Mfold was used by Tuplin et al. (7) both to find the RNA-ss as well as to predict the folds that were later supported by enzymatic mapping. RNAalifold employs the same algorithm and energy rules as Mfold and is therefore also given an advantage on this test set.

Comparison of RNA-Decoder, Pfold, RNAalifold and Mfold in scanning experiments

A main goal was to present a method that could be used for predicting yet-unknown structural elements within both coding and non-coding regions. In order to test if and how RNA-Decoder could be used to find yet-unknown structural elements in the genomes of HCV and polio virus, we performed so-called scanning experiments with RNA-Decoder, Pfold, RNAalifold and Mfold.

All alignments were scanned by RNA-Decoder, Pfold and RNAalifold in chunks of 300 bases by walking in steps of 100 bases. Mfold was used in two different ways to analyze the respective reference sequences: (1) Mfold was used to directly fold those subsequences of the reference sequences that correspond to the 300 bp chunks of the alignments and (2) Mfold was used in Monte Carlo shuffling experiments to measure the difference between the free energy of the folded sub-sequence and the mean free energy of a set of randomized version of that sub-sequence. All predictions for the individual chunks of the alignments or the respective reference sequences were then combined into one prediction along the respective reference sequence by first merging the predictions of the individual chunks and then projecting them onto the reference sequence. Figure 3 shows the scan results for the HCV genome and Figure 4 for those of the polio virus genome.

Figure 3.

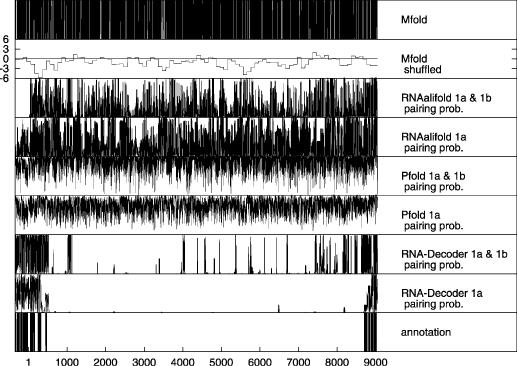
Pairing predictions along the HCV reference sequence excluding the 3′ UTR. RNA-Decoder, Pfold and RNAalifold were used on both the HCV 1a set and the HCV 1a & 1b set, and the pairing probabilities for the alignments were then projected onto the reference sequence. Mfold was directly used on the reference sequence. Please refer to the text for more information on how the scan of the HCV genome was performed. The long contiguous protein-coding region starts at position 1 and ends at position 9032 (i.e. the stop codon is at positions 9033–9035). The five known secondary structures on which RNA-Decoder was trained lie between positions 8678 and 9018. The RNA structures annotated in the coding region and the 5′UTR are from Refs. (7) and (44), respectively. A recent computational survey of RNA structures in Flaviviridae (47) predicts some new coding elements. Several of these overlap the predictions made by RNA-Decoder on the 1a & 1b set.

Figure 4.

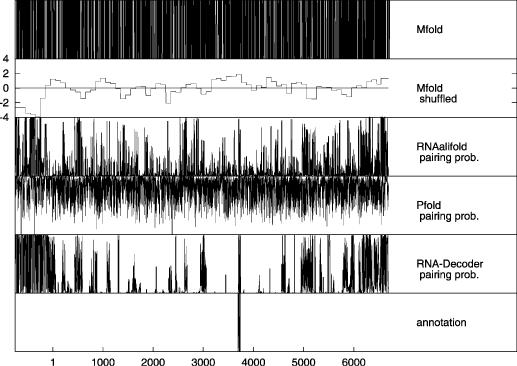
Pairing predictions along the polio reference sequence. RNA-Decoder, Pfold and RNAalifold were used on the polio alignment and the pairing probabilities for the alignment were then projected onto the reference sequence. Mfold was directly used on the reference sequence. Please refer to the text for more information on how the scan of the polio genome was performed. The protein-coding region starts at position 1 and ends at position 6639 (i.e. the stop codon is at positions 6640–6642). We have only been able to recover precise annotations of a single experimentally verified RNA structure from the literature (46). However, several elements have been inferred by homology to other vira and analysis of compensatory mutations in both the 5′UTR and the 3′UTR [(48) and references therein].

The Monte Carlo shuffling experiments performed with Mfold aim to detect regions with functional RNA structures by measuring a significant deviation between the free energy of the Mfolded sequence and the mean free energy of a set of randomized version of that sequence. For every 300 bp long sub-sequence of the reference sequence, we generate 50 randomized versions using dishuffle and dicodonshuffle (9). The deviation of the free energy of the Mfolded sub-sequence from the mean free energy of the 50 corresponding Mfolded randomized sequences is measured in units of standard deviations, i.e. a shuffled Mfold Z-score of −1 means that the free energy of the Mfolded sub-sequence is one standard deviation lower than the mean free energy of the 50 corresponding randomized sequences. The hope is that a very negative Z-score should correspond to a sub-sequence with conserved secondary structures. If we assume that the distribution of Z-scores is approximately normal (25), we can associate P-values with Z-scores, e.g. P(Z < −3.0) = 0.0023.

Figure 3 shows the results of the scanning experiments along the HCV reference sequence. Each data point in Figure 3 corresponds to exactly one nucleotide of the reference sequence. The output values of RNA-Decoder, Pfold and RNAalifold are pairing probabilities (i.e. continuous values between 0 and 1), those of Mfold either 0 (position is predicted to be unpaired) or 1 (position is predicted to be base-paired), whereas the output values of the shuffled Mfold are Z-scores that can assume any positive or negative value.

Without investigating any details, it is clear from Figure 3 that Mfold, Pfold as well as RNAalifold predict a much noisier spectrum of pairing probabilities than RNA-Decoder. The Mfold predictions are noisier than the Pfold predictions, which are in turn noisier than the RNAalifold predictions that show a visible degree of similarity between the predictions for the HCV 1a and the HCV 1a & 1b set. The shuffled Mfold predictions are constant for chunks of 100 bp, reflecting the way in which they were generated. A cut-off Z-score of −4 was used in Ref. (25) to indicate conserved secondary structure, however a cut-off of −5 was found to be required to have satisfactory specificity. The two regions with the most negative values (around −6) overlap one known structural region in the 5′ UTR and one protein-coding region for which RNA-Decoder predicts high pairing probabilities, but overall, the shuffled Mfold predictions are imprecise (chunks of 100 bp; we also tried to use 50 bp chunks with a step-size of 10 bp on the HCV reference sequence, which resulted in even noisier predictions) and noisy. Both sets of RNA-Decoder results clearly indicate potential structural and non-structural regions as there are few regions with intermediate pairing probabilities and RNA-Decoder manages to successfully predict the known structural regions. As we do not know whether or not the structural annotation of the HCV reference sequence is complete, we can only conclude that RNA-Decoder has the highest sensitivity of all tested programs on the known structures, but given its spectrum it may also have the highest specificity. This needs to be confirmed in further dedicated experiments.

The results for the polio scan, see Figure 4, are qualitatively very similar to those of the HCV scan. Mfold shows again the noisiest spectrum, followed by Pfold and then RNAalifold. Pfold and the shuffled Mfold both fail to predict the known structural region, whereas RNAalifold and especially RNA-Decoder indicate the region by predicting high pairing probabilities. RNA-Decoder again indicates potential structural and non-structural regions most clearly.

The scanning results, including a list of high scoring predictions, can be downloaded from www.stats.ox.ac.uk/~meyer/rnadecoder.

Evolutionary information and prediction performance

The performance of a comparative method such as RNA-Decoder depends on the amount of evolutionary information available in the input alignment. Large amounts of evolutionary information should lead to perfect predictions. However, the performance also depends on the amount of noise introduced by alignment errors or structural evolution. This section presents some results quantifying the performance of RNA-Decoder with regard to these factors.

In order to achieve this, we need a measure for the amount of evolutionary information present in an alignment. RNA-Decoder's performance depends on how well it can infer the type of substitution process of a column, which again depends on the amount of information available on the substitution history. We would therefore like to measure how well the alignment column entries have sampled the substitution history. There are two main components to this: the number of samples and the amount of substitution history they cover. The first is given by the number of aligned sequences, the second by the total tree length (TTL) of the phylogenetic tree spanning the sequences.

We do two types of experiments: the first effectively repeats the scanning experiments, but for a single structure, visualizing the performance given alignments of different sizes. The second experiment presents a more detailed analysis of the relationship between the performance of RNA-Decoder and the total tree length of the input alignment. The results from the second experiment can be found in the supplementary material.

Single-structure scan

The pairing probability is plotted for each position of structure 4 using different subsets of the HCV 1a data set and for the entire HCV 1a & 1b data set (see Figure 5). Structure 4 was chosen since it exhibits a relatively simple and interpretable pattern of structural evolution between the data sets. The performance on the other structures are qualitatively similar, but the pattern of structural evolution is often more complicated, leading to less clear interpretations.

Figure 5.

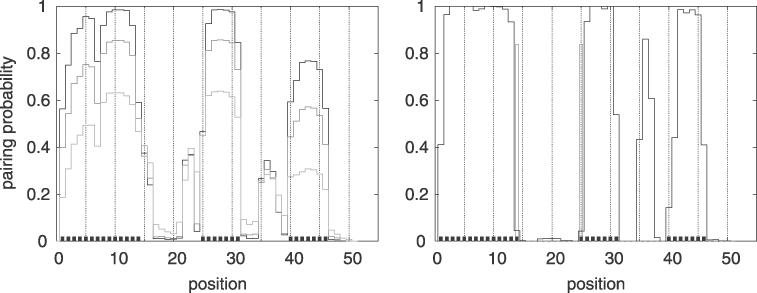
Pairing probability along structure 4 for different numbers of sequences in the input alignment. Structure 4 consists of a hairpin with a single bulge whose annotated base-pairing positions are indicated by little black boxes along the x-axis. The left figure shows the pairing probability using the reference sequence as only input (TTL = 0, light gray), using the reference sequence and two of its closest neighbor sequences as input (TTL = 0.19, medium gray) and using all eight sequences of the HCV 1a set (TTL = 0.59, black). For comparison, the right figure shows the pairing probability for structure 4 using all HCV 1a & 1b sequences (TTL = 9.84). The open boxes (pos. 14 and 25) indicate alignment columns for which a fraction of the sequences (indicated by the height of the box) do not form consensus base pairs (see caption of Table 1).

The performance on the HCV 1a set improves with the amount of evolutionary information available. The largest improvement is observed when going from no evolutionary information (a single sequence) to just a little evolutionary information (three closely related sequences). Using the entire HCV 1a set further increases the performance and results in a perfect prediction of the structure.

The performance based on the HCV 1a & 1b set shows much variation between positions. Most of the stem-pairing positions are correctly predicted with very high confidence, but a few are missed completely. Position 14 and 25 are apparently missed due to the large amount of structural evolution relative to the annotation. The reason for the high values at some of the bulge positions (pos. 35–37) is unknown, but could be due to a pseudo-knot.

DISCUSSION

RNA-Decoder is the first program to explicitly model RNA structure overlapping protein-coding regions. Despite the limited amount of data, we have shown in cross-evaluation experiments that RNA-Decoder can be trained to successfully predict a set of experimentally verified RNA structures within the protein-coding region of the HCV genome. Scanning experiments in which the trained model was used to predict the pairing probabilities along the entire HCV genome show that RNA-Decoder successfully predicts the known structural elements and that it may also have a marked higher specificity for predicting (yet unknown) conserved RNA-structure elements than the existing programs Pfold, Mfold and RNAalifold that do not explicitly model either the protein-coding context or the non-structural regions.

RNA-Decoder takes as input an alignment of evolutionarily related RNA sequences together with a phylogenetic tree and an annotation of the protein-coding regions and predicts RNA secondary structures which are evolutionarily conserved. As opposed to non-comparative methods, RNA-Decoder is capable of discriminating between functional and non-functional RNA structures by taking the evolutionary context explicitly into account.

The challenges posed by the presented folding and scanning experiments differ substantially. In the folding experiments, the programs were given short sequences known to fold almost in their entirety, whereas in the scanning experiments they were given long sequences in which to find conserved secondary structure elements. The differences in performance between all programs are best explained by comparing the aims with which they were originally designed.

Mfold was originally designed to predict the energetically most favorable conformation of a single given RNA sequence. The folding is thus based on the physical properties of the given RNA sequence. The folding experiments in which each program was presented with a short sub-sequence which each encoded one hairpin-like structure is the optimal scenario for Mfold, in which it performed very well. However, Mfold was originally also used by Tuplin et al. (7) to find these elements and to construct their structure models, which gives it an advantage over the other programs. As any RNA sequence can form some base-pairs which will lower the overall free energy of the molecule, Mfold will also predict secondary structure elements in RNA sequences that are devoid of functional secondary structure elements. Mfold can therefore not directly be used to scan for RNA structures, as is evident from its predictions as shown in the scan plots.

It has been suggested that it might be possible to use energy-minimization methods such as Mfold to find functional RNA structures by searching for regions with lower free energies than expected under Monte Carlo simulations (6,9,22,23). However, using this approach we get only coarse-grained predictions with a bad signal to noise ratio. This confirms the finding by Rivas and Eddy. (25) that specific functional RNA elements are generally not significantly more biased towards lower free folding energies than other regions. We have not investigated the power of the Monte Carlo shuffling approach to detect the overall presence or absence of functional RNA structures in larger regions, which is the primary application in e.g. Katz and Burge (9).

RNAalifold is a comparative method that predicts a common structure for an alignment using minimal energy scores as well as information on compensatory mutations between the sequences. As opposed to RNA-Decoder and Pfold, it does not consider the evolutionary relationship between the sequences of the input alignment, but simply averages energy scores and compensatory mutation scores equally over all sequences. With unbalanced trees, as in our HCV 1a & 1b set, the overall scores can become misleading, a pitfall that RNA-Decoder and Pfold naturally avoid. RNAalifold employs the same RNA structure model as Mfold and therefore does not model non-structural regions explicitly. If the sequences of the alignment are highly conserved, RNAalifold defaults to the method behind Mfold. These are probably the main reasons for the apparent high degree of over-prediction made by RNAalifold in the scanning experiments.

Pfold and RNA-Decoder share the same modelling approach. A main difierence is that Pfold does not model the coding context. Protein conservation can lead to highly conserved first and second codon positions, which can be misinterpreted as conservation of functional RNA structures. RNA-Decoder explicitly models the evolutionary pattern of each codon position and requires an additional level of conservation before predicting an RNA structure. This difference becomes most pronounced when strong evolutionary signals are present, as is the case in the large HCV 1a & 1b set, explaining the poor performance of Pfold on this set.

Another major difference is that Pfold, like Mfold and RNAalifold, does not explicitly model the non-structured regions in between the regions of conserved structural elements. Pfold therefore models the evolutionary process within loop regions in the same way as within non-structural regions, whereas these two types of regions have been found to evolve significantly differently (29). RNA-Decoder explicitly uses this difference in order to discriminate between structural and non-structural regions and to improve the performance of scanning experiments.

We found that introducing rate variation into RNA-Decoder's model of non-structural coding regions (i.e. explicitly modelling the highly conserved coding regions) can improve the scan performance significantly by yielding more distinct predictions of the known structures (results not shown). This emphasizes the importance of modelling the conserved parts of coding regions when scanning for coding RNA structures.

RNA-Decoder only predicts a single RNA structure common to all sequences of the input alignment. However, due to structural evolution, the individual sequences may differ in parts of their secondary structures (see e.g. Table 1). RNA-Decoder will only predict stem pairs with low confidence when a subset of the sequences are not stem-pairing, since the pattern of compensatory mutations will be broken. This means that RNA-Decoder, as any existing program which takes as input a fixed alignment, will have problems predicting any complete structure when the structures have evolved. However, it is reasonable to assume that the functional constraints will conserve some core parts of a structure throughout the alignment. In the folding experiments, we found that restricting the predictions of RNA-Decoder to include only high-confidence stem pairs resulted in a very high specificity (see the Supplementary Material). RNA-Decoder can therefore be used to predict the structurally most conserved regions, which are likely to be also the functionally most important. If the complete structure is of interest, the set of conserved stem pairs can be used to reduce the remaining folding problem for each individual sequence, as we have done in the RNA-Decoder-Two-Step procedure (see the Supplementary Material).

The fact that RNA-Decoder only predicts a single common structure for a fixed input alignment makes it very vulnerable to alignment errors. Alignment errors give rise to similar structural variation between the sequences as structural evolution does, resulting in a decreased sensitivity for predicting base-pairs. We significantly reduce the risk of alignment errors in coding regions by aligning the sequences according to their encoded amino acids. Second, we argue that the rate of insertions and deletions in information-rich sequences is very low. This is certainly the case in the HCV and polio virus alignments, which were readily aligned and contained only very few gaps (0.3% gaps in the large 1a & 1b set).

There are several ways in which RNA-Decoder could be improved. As the current training set of only five hairpin-like structural elements within the protein-coding regions of the HCV genome is neither large nor diverse, a new training set is likely to improve the current estimates of the model's parameters and might also be used to train a more sophisticated phylogenetic model with more parameters.

One potential improvement to the model could be to allow for non-geometric length distributions by explicitly modeling the state duration of some states within the SCFG similarly to states within hidden Markov models (49). Another way to improve the predictions and remedy the fact that the underlying SCFG cannot model pseudo-knots, might be to model the rate variation in loop/bulge regions in order to capture a rate reduction due to the presence of overlapping pseudo-knots and to thus avoid erroneous stem predictions.

We hope that RNA-Decoder will help to detect functionally important RNA structures in or near protein-coding genomic regions, and that it will find use both in studies on vira and cellular organisms.

A Linux executable of RNA-Decoder as well as the training set and the predictions of the scanning experiments can be downloaded from www.stats.ox.ac.uk/~meyer/rnadecoder

SUPPLEMENTARY MATERIAL

Supplementary Material is available at NAR Online.