Abstract
Matrix completion has attracted significant recent attention in many fields including statistics, applied mathematics and electrical engineering. Current literature on matrix completion focuses primarily on independent sampling models under which the individual observed entries are sampled independently. Motivated by applications in genomic data integration, we propose a new framework of structured matrix completion (SMC) to treat structured missingness by design. Specifically, our proposed method aims at efficient matrix recovery when a subset of the rows and columns of an approximately low-rank matrix are observed. We provide theoretical justification for the proposed SMC method and derive lower bound for the estimation errors, which together establish the optimal rate of recovery over certain classes of approximately low-rank matrices. Simulation studies show that the method performs well in finite sample under a variety of configurations. The method is applied to integrate several ovarian cancer genomic studies with different extent of genomic measurements, which enables us to construct more accurate prediction rules for ovarian cancer survival.
Keywords: Constrained minimization, genomic data integration, low-rank matrix, matrix completion, singular value decomposition, structured matrix completion
1 Introduction
Motivated by an array of applications, matrix completion has attracted significant recent attention in different fields including statistics, applied mathematics and electrical engineering. The central goal of matrix completion is to recover a high-dimensional low-rank matrix based on a subset of its entries. Applications include recommender systems (Koren et al., 2009), genomics (Chi et al., 2013), multi-task learning (Argyriou et al., 2008), sensor localization (Biswas et al., 2006; Singer and Cucuringu, 2010), and computer vision (Chen and Suter, 2004; Tomasi and Kanade, 1992), among many others.
Matrix completion has been well studied under the uniform sampling model, where observed entries are assumed to be sampled uniformly at random. The best known approach is perhaps the constrained nuclear norm minimization (NNM), which has been shown to yield near-optimal results when the sampling distribution of the observed entries is uniform (Candés and Recht, 2009; Candés and Tao, 2010; Gross, 2011; Recht, 2011; Candes and Plan, 2011). For estimating approximately low-rank matrices from uniformly sampled noisy observations, several penalized or constrained NNM estimators, which are based on the same principle as the well-known Lasso and Dantzig selector for sparse signal recovery, were proposed and analyzed (Keshavan et al., 2010; Mazumder et al., 2010; Koltchinskii, 2011; Koltchinskii et al., 2011; Rohde et al., 2011). In many applications, the entries are sampled independently but not uniformly. In such a setting, Salakhutdinov and Srebro (2010) showed that the standard NNM methods do not perform well, and proposed a weighted NNM method, which depends on the true sampling distribution. In the case of unknown sampling distribution, Foygel et al. (2011) introduced an empirically-weighted NNM method. Cai and Zhou (2013) studied a max-norm constrained minimization method for the recovery of a low-rank matrix based on the noisy observations under the non-uniform sampling model. It was shown that the max-norm constrained least squares estimator is rate-optimal under the Frobenius norm loss and yields a more stable approximate recovery guarantee with respect to the sampling distributions.
The focus of matrix completion has so far been on the recovery of a low-rank matrix based on independently sampled entries. Motivated by applications in genomic data integration, we introduce in this paper a new framework of matrix completion called structured matrix completion (SMC), where a subset of the rows and a subset of the columns of an approximately low-rank matrix are observed and the goal is to reconstruct the whole matrix based on the observed rows and columns. We first discuss the genomic data integration problem before introducing the SMC model.
1.1 Genomic Data Integration
When analyzing genome-wide studies (GWS) of association, expression profiling or methylation, ensuring adequate power of the analysis is one of the most crucial goals due to the high dimensionality of the genomic markers under consideration. Because of cost constraints, GWS typically have small to moderate sample sizes and hence limited power. One approach to increase the power is to integrate information from multiple GWS of the same phenotype. However, some practical complications may hamper the feasibility of such integrative analysis. Different GWS often involve different platforms with distinct genomic coverage. For example, whole genome next generation sequencing (NGS) studies would provide mutation information on all loci while older technologies for genome-wide association studies (GWAS) would only provide information on a small subset of loci. In some settings, certain studies may provide a wider range of genomic data than others. For example, one study may provide extensive genomic measurements including gene expression, miRNA and DNA methylation while other studies may only measure gene expression.
To perform integrative analysis of studies with different extent of genomic measurements, the naive complete observation only approach may suffer from low power. For the GWAS setting with a small fraction of loci missing, many imputation methods have been proposed in recent years to improve the power of the studies. Examples of useful methods include haplotype reconstruction, k-nearest neighbor, regression and singular value decomposition methods (Scheet and Stephens, 2006; Li and Abecasis, 2006; Browning and Browning, 2009; Troyanskaya et al., 2001; Kim et al., 2005; Wang et al., 2006). Many of the haplotype phasing methods are considered to be highly effective in recovering missing genotype information (Yu and Schaid, 2007). These methods, while useful, are often computationally intensive. In addition, when one study has a much denser coverage than the other, the fraction of missingness could be high and an exceedingly large number of observation would need to be imputed. It is unclear whether it is statistically or computationally feasible to extend these methods to such settings. Moreover, haplotype based methods cannot be extended to incorporate other types of genomic data such as gene expression and miRNA data.
When integrating multiple studies with different extent of genomic measurements, the observed data can be viewed as complete rows and columns of a large matrix A and the missing components can be arranged as a submatrix of A. As such, the missingness in A is structured by design. In this paper, we propose a novel SMC method for imputing the missing submatrix of A. As shown in Section 5, by imputing the missing miRNA measurements and constructing prediction rules based on the imputed data, it is possible to significantly improve the prediction performance.
1.2 Structured Matrix Completion Model
Motivated by the applications mentioned above, this paper considers SMC where a subset of rows and columns are observed. Specifically, we observe m1 < p1 rows and m2 < p2 columns of a matrix A ∈ ℝp1×p2 and the goal is to recover the whole matrix. Since the singular values are invariant under row/column permutations, it can be assumed without loss of generality that we observe the first m1 rows and m2 columns of A which can be written in a block form:
| (1) |
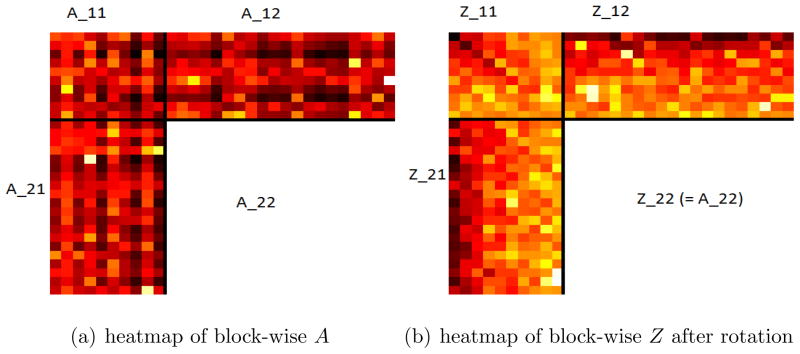
where A11, A12, and A21 are observed and the goal is to recover the missing block A22. See Figure 1(a) in Section 2 for a graphical display of the data. Clearly there is no way to recover A22 if A is an arbitrary matrix. However, in many applications such as genomic data integration discussed earlier, A is approximately low-rank, which makes it possible to recover A22 with accuracy. In this paper, we introduce a method based on the singular value decomposition (SVD) for the recovery of A22 when A is approximately low-rank.
Figure 1.
Illustrative example with A ∈ ℝ30×30, m1 = m2 = 10. (A darker block corresponds to larger magnitude.)
It is important to note that the observations here are much more “structured” comparing to the previous settings of matrix completion. As the observed entries are in full rows or full columns, the existing methods based on NNM are not suitable. As mentioned earlier, constrained NNM methods have been widely used in matrix completion problems based on independently observed entries. However, for the problem considered in the present paper, these methods do not utilize the structure of the observations and do not guarantee precise recovery even for exactly low-rank matrix A (See Remark 1 in Section 2). Numerical results in Section 4 show that NNM methods do not perform well in SMC.
In this paper we propose a new SMC method that can be easily implemented by a fast algorithm which only involves basic matrix operations and the SVD. The main idea of our recovery procedure is based on the Schur Complement. In the ideal case when A is exactly low rank, the Schur complement of the missing block, , is zero and thus can be used to recover A22 exactly. When A is approximately low rank, cannot be used directly to estimate A22. For this case, we transform the observed blocks using SVD; remove some unimportant rows and columns based on thresholding rules; and subsequently apply a similar procedure to recover A22.
Both its theoretical and numerical properties are studied. It is shown that the estimator recovers low-rank matrices accurately and is robust against small perturbations. A lower bound result shows that the estimator is rate optimal for a class of approximately low-rank matrices. Although it is required for the theoretical analysis that there is a significant gap between the singular values of the true low-rank matrix and those of the perturbation, simulation results indicate that this gap is not really necessary in practice and the estimator recovers A accurately whenever the singular values of A decay sufficiently fast.
1.3 Organization of the Paper
The rest of the paper is organized as follows. In Section 2, we introduce in detail the proposed SMC methods when A is exactly or approximately low-rank. The theoretical properties of the estimators are analyzed in Section 3. Both upper and lower bounds for the recovery accuracy under the Schatten-q norm loss are established. Simulation results are shown in Section 4 to investigate the numerical performance of the proposed methods. A real data application to genomic data integration is given in Section 5. Section 6 discusses a few practical issues related to real data applications. For reasons of space, the proofs of the main results and additional simulation results are given in the supplement (Cai et al., 2014). Some key technical tools used in the proofs of the main theorems are also developed and proved in the supplement.
2 Structured Matrix Completion: Methodology
In this section, we propose procedures to recover the submatrix A22 based on the observed blocks A11, A12, and A21. We begin with basic notation and definitions that will be used in the rest of the paper.
For a matrix U, we use U[Ω1,Ω2] to represent its sub-matrix with row indices Ω1 and column indices Ω2. We also use the Matlab syntax to represent index sets. Specifically for integers a ≤ b, “a: b” represents {a, a + 1, ···, b}; and “:” alone represents the entire index set. Therefore, U[:,1:r] stands for the first r columns of U while U[(m1+1):p1,:] stands for the {m1 + 1, …, p1}th rows of U. For the matrix A given in (1), we use the notation A•1 and A1• to denote and [A11, A12], respectively. For a matrix B ∈ ℝm×n, let be the SVD, where Σ = diag{σ1(B), σ2(B), …} with σ1(B) ≥ σ2(B) ≥ ··· ≥ 0 being the singular values of B in decreasing order. The smallest singular value σmin(m,n), which will be denoted by σmin(B), plays an important role in our analysis. We also define and . For 1 ≤ q ≤ ∞, the Schatten-q norm ||B||q is defined to be the vector q-norm of the singular values of B, i.e. . Three special cases are of particular interest: when q = 1, ||B||1 = Σi σi (B) is the nuclear (or trace) norm of B and will be denoted as ||B||*; when q = 2, is the Frobenius norm of B and will be denoted as ||B||F; when q = ∞, ||B||∞ = σ1(B) is the spectral norm of B that we simply denote as ||B||. For any matrix U ∈ ℝp×n, we use PU ≡ U (U⊤U)† U⊤ ∈ ℝp×p to denote the projection operator onto the column space of U. Throughout, we assume that A is approximately rank r in that for some integer 0 < r ≤ min(m1, m2), there is a significant gap between σr(A) and σr+1(A) and the tail is small. The gap assumption enables us to provide a theoretical upper bound on the accuracy of the estimator, while it is not necessary in practice (see Section 4 for more details).
2.1 Exact Low-rank Matrix Recovery
We begin with the relatively easy case where A is exactly of rank r. In this case, a simple analysis indicates that A can be perfectly recovered as shown in the following proposition.
Proposition 1
Suppose A is of rank r, the SVD of A11 is A11 = UΣV⊤, where U ∈ ℝp1×r, Σ ∈ ℝr×r, and V ∈ ℝp2×r. If
then rank(A11) = r and A22 is exactly given by
| (2) |
Remark 1
Under the same conditions as Proposition 1, the NNM
| (3) |
fails to guarantee the exact recovery of A22. Consider the case where A is a p1 × p2 matrix with all entries being 1. Suppose we observe arbitrary m1 rows and m2 columns, the NNM would yield Â22 ∈ ℝ (p1−m1)×(p2−m2) with all entries being (See Lemma 4 in the Supplement). Hence when m1m2 < (p1 − m1)(p2 − m2), i.e., when the size of the observed blocks are much smaller than that of A, the NNM fails to recover exactly the missing block A22. See also the numerical comparison in Section 4. The NNM (3) also fails to recover A22 with high probability in a random matrix setting where with B1 ∈ ℝp1×r and B2 ∈ ℝp2×r being i.i.d. standard Gaussian matrices. See Lemma 3 in the Supplement for further details. In addition to (3), other variations of NNM have been proposed in the literature, including penalized NNM (Toh and Yun, 2010; Mazumder et al., 2010),
| (4) |
and constrained NNM with relaxation (Cai et al., 2010),
| (5) |
where Ω = {(ik, jk): Aik,jk observed, 1 ≤ ik ≤ p1, 1 ≤ jk ≤ p2} and t is the tunning parameter. However, these NNM methods may not be suitable for SMC especially when only a small number of rows and columns are observed. In particular, when m1 ≪ p1, m2 ≪ p2, A is well spread in each block A11, A12, A21, A22, we have ||[A11 A12]||* ≪ ||A||*, [A12]* ≪ ||A||*. Thus,
In the other words, imputing A22 with all zero yields a much smaller nuclear norm than imputing with the true A22 and hence NNM methods would generally fail to recover A22 under such settings.
Proposition 1 shows that, when A is exactly low-rank, A22 can be recovered precisely by A21(A11)† A12. Unfortunately, this result heavily relies on the exactly low-rank assumption that cannot be directly used for approximately low-rank matrices. In fact, even with a small perturbation to A, the inverse of A11 makes the formula A21(A11)† A12 unstable, which may lead to the failure of recovery. In practice, A is often not exactly low rank but approximately low rank. Thus for the rest of the paper, we focus on the latter setting.
2.2 Approximate Low-rank Matrix Recovery
Let A = UΣV⊤ be the SVD of an approximately low rank matrix A and partition U ∈ ℝp1×p1, V ∈ ℝp2×p2 and Σ ∈ ℝp1×p2 into blocks as
| (6) |
Then A can be decomposed as A = Amax(r) + A−max(r) where Amax(r) is of rank r with the largest r singular values of A and A−max(r) is general but with small singular values. Then
| (7) |
Here and in the sequel, we use the notation U•k and Uk• to denote and [Uk1, Uk2], respectively. Thus, Amax(r) can be viewed as a rank-r approximation to A and obviously
We will use the observed A11, A12 and A21 to obtain estimates of U•1, V•1 and Σ1 and subsequently recover A22 using an estimated .
When r is known, i.e., we know where the gap is located in the singular values of A, a simple procedure can be implemented to estimate A22 as described in Algorithm 1 below by estimating U•1 and V•1 using the principal components of A•1 and A1•.
Algorithm 1.
Algorithm for Structured Matrix Completion with a given r
|
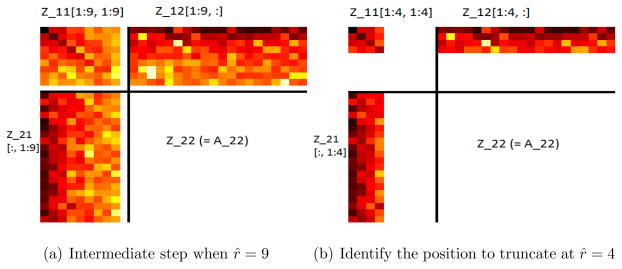
However, Algorithm 1 has several major limitations. First, it relies on a given r which is typically unknown in practice. Second, the algorithm need to calculate the matrix divisions, which may cause serious precision issues when the matrix is near-singular or the rank r is mis-specified. To overcome these difficulties, we propose another Algorithm which essentially first estimates r with r̂ and then apply Algorithm 1 to recover A22. Before introducing the algorithm of recovery without knowing r, it is helpful to illustrate the idea with heat maps in Figures 1 and 2.
Figure 2.
Searching for the appropriate position to truncate from r̂ = 10 to 1.
Our procedure has three steps.
-
First, we move the significant factors of A•1 and A1• to the front by rotating the columns of A•1 and the rows of A1• based on the SVD,After the transformation, we have Z11, Z12, Z21,
Clearly A and Z have the same singular values since the transformation is orthogonal. As shown in Figure 1(b), the amplitudes of the columns of and the rows of Z1• = [Z11, Z12] are decaying.
-
When A is exactly of rank r, the {r + 1, ···, m1}th rows and {r + 1, ···, m2}th columns of Z are zero. Due to the small perturbation term A−max(r), the back columns of Z•1 and rows of Z1• are small but non-zero. In order to recover Amax(r), the best rank r approximation to A, a natural idea is to first delete these back rows of Z1• and columns of Z•1, i.e. the {r + 1, ···, m1}th rows and {r + 1, ···, m2}th columns of Z.
However, since r is unknown, it is unclear how many back rows and columns should be removed. It will be helpful to have an estimate for r, r̂, and then use Z21,[:,1:r̂], Z11,[1:r̂,1:r̂] and Z12[1:r̂,:] to recover A22. It will be shown that a good choice of r̂ would satisfy that Z11,[1:r̂,1:r̂] is non-singular and , where TR is some constant to be specified later. Our final estimator for r would be the largest r̂ that satisfies this condition, which can be identified recursively from min(m1, m2) to 1 (See Figure 2).
-
Finally, similar to (2),A22 can be estimated by
(9) The method we propose can be summarized as the following algorithm.
Algorithm 2.
Algorithm of Structured Matrix Completion with unknown r- Input: A11 ∈ ℝm1×m2, . Thresholding level: TR, (or TC).
- Calculate the SVD A•1 = U(1)Σ(1)V(1)⊤, A1• = U(2)Σ(2)V(2)⊤.
- Calculate Z11 ∈ ℝm1×m2, Z12 ∈ ℝm1×(p2−m2), Z21 ∈ ℝ(p1−m1)×m2
- for s = min(m1, m2): −1: 1 do (Use iteration to find r̂)
- Calculate DR,s ∈ ℝ(p1−m1)×s (or DC,s ∈ ℝs×(p2−m2)) by solving linear equation system,
- if Z11,[1:s,1:s] is not singular and ||DR,s|| ≤ TR (or ||DC,s|| ≤ TC) then
- r̂ = s; break from the loop;
- end if
- end for
- if (r̂ is not valued) then r̂ = 0.
- end if
- Finally we calculate the estimate as
It can also be seen from Algorithm 2 that the estimator r̂ is constructed based on either the row thresholding rule ||DR,s|| ≤ TR or the column thresholding rule ||DC,s|| ≤ TC. Discussions on the choice between DR,s and DC,s are given in the next section. Let us focus for now on the row thresholding based on . It is important to note that Z21[:,1:r] and Z11,[1:r,1:r] approximate U21Σ1 and Σ1, respectively. The idea behind the proposed r̂ is that when s > r, Z21[:,1:s] and Z11,[1:s,1:s] are nearly singular and hence DR,s may either be deemed singular or with unbounded norm. When s = r, Z11,[1:s,1:s] is non-singular with ||DR,s|| bounded by some constant, as we show in Theorem 2. Thus, we estimate r̂ as the largest r such that Z11,[1:s,1:s] is non-singular with ||DR,s|| < TR.
3 Theoretical Analysis
In this section, we investigate the theoretical properties of the algorithms introduced in Section 2. Upper bounds for the estimation errors of Algorithms 1 and 2 are presented in Theorems 1 and 2, respectively, and the lower-bound results are given in Theorem 3. These bounds together establish the optimal rate of recovery over certain classes of approximately low-rank matrices. The choices of tuning parameters TR and TC are discussed in Corollaries 1 and 2.
Theorem 1
Suppose  is given by the procedure of Algorithm 1. Assume
| (10) |
Then for any 1 ≤ q ≤ ∞,
| (11) |
Remark 2
It is helpful to explain intuitively why Condition (10) is needed. When A is approximately low-rank, the dominant low-rank component of A, Amax(r), serves as a good approximation to A, while the residual A−max(r) is “small”. The goal is to recover Amax(r) well. Among the three observed blocks, A11 is the most important and it is necessary to have Amax(r) dominating A−max(r) in A11. Note that A11 = Amax(r),[1:m1,1:m2] + A−max(r),[1:m1,1:m2],
We thus require Condition (10) in Theorem 1 for the theoretical analysis.
Theorem 1 gives an upper bound for the estimation accuracy of Algorithm 1 under the assumption that there is a significant gap between σr(A) and σr+1(A) for some known r. It is noteworthy that there are possibly multiple values of r that satisfy Condition (10). In such a case, the bound (11) applies to all such r and the largest r yields the strongest result.
We now turn to Algorithm 2, where the knowledge of r is not assumed. Theorem 2 below shows that for properly chosen TR or TC, Algorithm 2 can lead to accurate recovery of A22.
Theorem 2
Assume that there exists r ∈ [1, min(m1, m2)] such that
| (12) |
Let TR and TC be two constants satisfying
Then for 1 ≤ q ≤ ∞, Â22 given by Algorithm 2 satisfies
| (13) |
when r̂ is estimated based on the thresholding rule ||DR,s|| ≤ TR or ||DC,s|| ≤ TC, respectively.
Besides σr(A)
and
σr+1(A),
Theorems 1 and 2 involve
σmin(U11)
and
σmin(V11),
two important quantities that reflect how much the low-rank matrix is concentrated on the first
m1 rows and m2
columns. We should note that
σmin(U11)
and
σmin(V11)
depend on the singular vectors of A and
σr(A) and
σr+1(A)
are the singular values of A. The lower bound in Theorem 3
below indicates that
σmin(U11),
σmin(V11),
and the singular values of A together quantify the
difficulty of the problem: recovery of A22 gets
harder as
σmin(U11)
and
σmin(V11)
become smaller or the {r + 1,
···, min(p1,
p2)}th
singular values become larger. Define the class of approximately
rank-r matrices 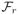 (M1,
M2) by
(M1,
M2) by
| (14) |
Theorem 3 (Lower Bound)
Suppose r ≤ min(m1, m2, p1 − m1, p2 − m2) and 0 < M1, M2 < 1, then for all 1 ≤ q ≤ ∞,
| (15) |
Remark 3
Theorems 1, 2 and 3 together immediately yield the optimal rate of
recovery over the class 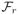 (M1M2),
(M1M2),
| (16) |
Since U11 and V11 are determined by the SVD of A and σmin(U11) and σmin(V11) are unknown based only on A11, A12, and A21, it is thus not straightforward to choose the tuning parameters TR and TC in a principled way. Theorem 2 also does not provide information on the choice between row and column thresholding. Such a choice generally depends on the problem setting. We consider below two settings where either the row/columns of A are randomly sampled or A is itself a random low-rank matrix. In such settings, when A is approximately rank r and at least O(r log r) number of rows and columns are observed, Algorithm 2 gives accurate recovery of A with fully specified tuning parameter. We first consider in Corollary 1 a fixed matrix A with the observed m1 rows and m2 columns selected uniformly randomly.
Corollary 1 (Random Rows/Columns)
Let A = UΣV⊤ be the SVD of A ∈ ℝp1×p2. Set
| (17) |
Let Ω1 ⊂ {1, ···, p1} and Ω2 ⊂ {1, ···, p2} be respectively the index set of the observed m1 rows and m2 columns. Then A can be decomposed as
| (18) |
-
Let Ω1 and Ω2 be independently and uniformly selected from {1, ···, p1} and {1, ···, p2} with or without replacement, respectively. Suppose there exists r ≤ min(m1, m2) such thatand the number of rows and number of columns we observed satisfyAlgorithm 2 with either column thresholding with the break condition ||DR,s|| ≤ TR where or row thresholding with the break condition ||DC,s|| ≤ TC where satisfies, for all 1 ≤ q ≤ ∞,
-
If Ω1 is uniformly randomly selected from {1, ···, p1} with or without replacement (Ω2 is not necessarily random), and there exists r ≤ m2 such thatand the number of observed rows satisfies
(19) then Algorithm 2 with the break condition ||DR,s|| ≤ TR where satisfies, for all 1 ≤ q ≤ ∞, -
Similarly, if Ω2 is uniformly randomly selected from {1, ···, p2} with or without replacement (Ω1 is not necessarily random) and there exists r ≤ m2 such thatand the number of observed columns satisfies
(20) then Algorithm 2 with the break condition ||DC,s|| ≤ TC where satisfies, for all 1 ≤ q ≤ ∞,
Remark 4
The quantities and in Corollary 1 measure the variation of amplitude of each row or each column of Amax(r). When and become larger, a small number of rows and columns in Amax(r) would have larger amplitude than others, while these rows and columns would be missed with large probability in the sampling of Ω, which means the problem would become harder. Hence, more observations for the matrix with larger and are needed as shown in (19).
We now consider the case where A is a random matrix.
Corollary 2 (Random Matrix)
Suppose A ∈ ℝp1×p2 is a random matrix generated by A = UΣV⊤, where the singular values Σ and singular space V are fixed, and U has orthonormal columns that are randomly sampled based on the Haar measure. Suppose we observe the first m1 rows and first m2 columns of A. Assume there exists such that
Then there exist uniform constants c, δ > 0 such that if m1 ≥ cr, Â22 is given by Algorithm 2 with the break condition ||DR,s|| ≤ TR, where , we have for all 1 ≤ q ≤ ∞,
Parallel results hold for the case when U is fixed and V has orthonormal columns that are randomly sampled based on the Haar measure, and we observe the first m1 rows and first m2 columns of A. Assume there exists such that
Then there exist unifrom constants c, δ > 0 such that if m2 ≥ cr, Â22 is given by Algorithm 2 with column thresholding with the break condition ||DC,s|| ≤ TC, where , we have for all 1 ≤ q ≤ ∞,
4 Simulation
In this section, we show results from extensive simulation studies that examine the numerical performance of Algorithm 2 on randomly generated matrices for various values of p1, p2, m1 and m2. We first consider settings where a gap between some adjacent singular values exists, as required by our theoretical analysis. Then we investigate settings where the singular values decay smoothly with no significant gap between adjacent singular values. The results show that the proposed procedure performs well even when there is no significant gap, as long as the singular values decay at a reasonable rate.
We also examine how sensitive the proposed estimators are to the choice of the threshold and the choice between row and column thresholding. In addition, we compare the performance of the SMC method with that of the NNM method. Finally, we consider a setting similar to the real data application discussed in the next section. Results shown below are based on 200–500 replications for each configuration. Additional simulation results on the effect of m1, m2 and ratio p1/m1 are provided in the supplement. Throughout, we generate the random matrix A from A = UΣV, where the singular values of the diagonal matrix Σ are chosen accordingly for different settings. The singular spaces U and V are drawn randomly from the Haar measure. Specifically, we generate i.i.d. standard Gaussian matrix Ũ ∈ ℝp1×min(p1,p2) and Ṽ ∈ ℝp2×min(p1,p2), then apply the QR decomposition to Ũ and Ṽ and assign U and V with the Q part of the result.
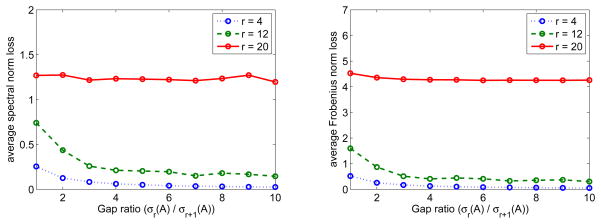
We first consider the performance of Algorithm 2 when a significant gap between the rth and (r + 1)th singular values of A. We fixed p1 = p2 = 1000, m1 = m2 = 50 and choose the singular values as
| (21) |
Here r is the rank of the major low-rank part Amax(r), is the gap ratio between the rth and (r + 1)th singular values of A. The average loss of Â22 from Algorithm 2 with the row thresholding and under both the spectral norm and Frobenius norm losses are given in Figure 3. The results suggest that our algorithm performs better when r gets smaller and gap ratio g = σr(A)/σr+1(A) gets larger. Moreover, even when g = 1, namely there is no significant gap between any adjacent singular values, our algorithm still works well for small r. As will be seen in the following simulation studies, this is generally the case as long as the singular values of A decay sufficiently fast.
Figure 3.
Spectral norm loss (left panel) and Frobenius norm loss (right panel) when there is a gap between σr(A) and σr+1(A). The singular value values of A are given by (21), p1 = p2 = 1000, and m1 = m2 = 50.
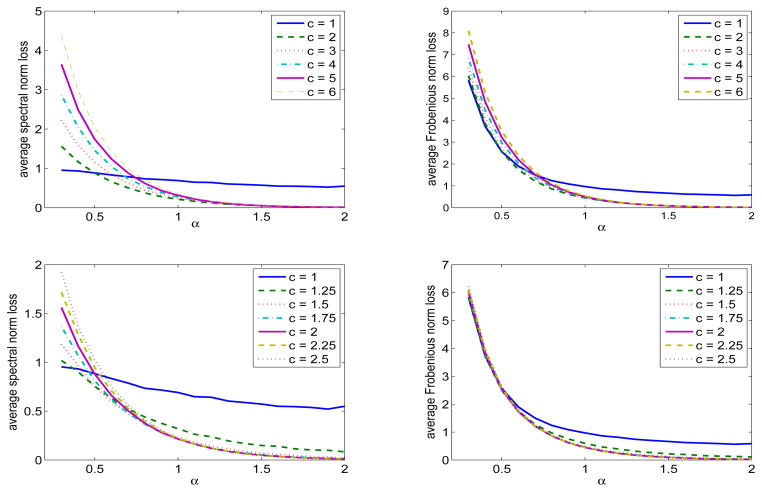
We now turn to the settings with the singular values being {j−α, j = 1, 2, …, min(p1, p2)}and various choices of α, p1 and p2. Hence, no significant gap between adjacent singular values exists under these settings and we aim to demonstrate that our method continues to work well. We first consider p1 = p2 = 1000, m1 = m2 = 50 and let α range from 0.3 to 2. Under this setting, we also study how the choice of thresholds affect the performance of our algorithm. For simplicity, we report results only for row thresholding as results for column thresholding are similar. The average loss of Â22 from Algorithm 2 with under both the spectral norm and Frobenius norm are given in Figure 4. In general, the algorithm performs well provided that α is not too small and as expected, the average loss decreases with a higher decay rate in the singular values. This indicates that the existence of a significant gap between adjacent singular values is not necessary in practice, provided that the singular values decay sufficiently fast. When comparing the results across different choices of the threshold, c = 2 as suggested in our theoretical analysis is indeed the optimal choice. Thus, in all subsequent numerical analysis, we fix c = 2.
Figure 4.
Spectral norm loss (left panel) and Frobenius norm loss (right panel) as the thresholding constant c varies. The singular values of A are {j−α, j = 1, 2, …} with α varying from 0.3 to 2, p1 = p2 = 1000, and m1 = m2 = 50.
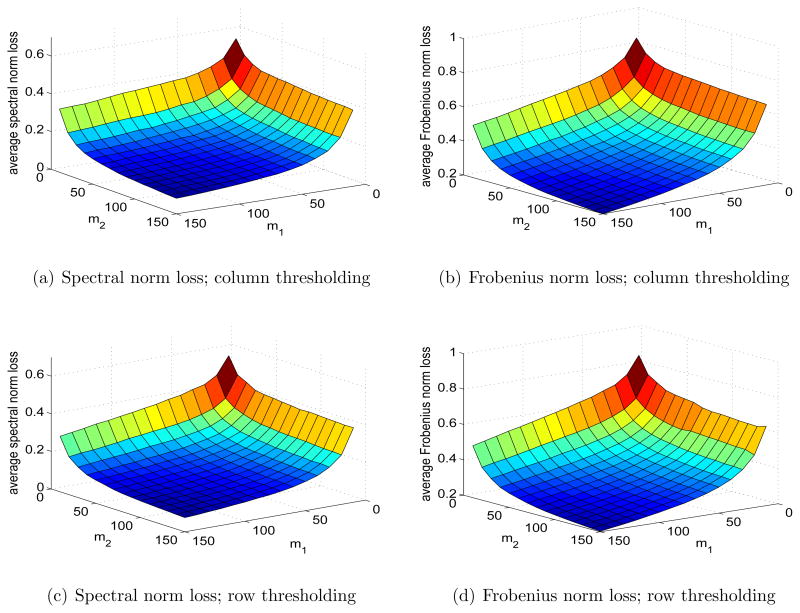
To investigate the impact of row versus column thresholding, we let the singular value decay rate be α = 1, p1 = 300, p2 = 3000, and m1 and m2 varying from 10 to 150. The original matrix A is generated the same way as before. We apply row and column thresholding with and . It can be seen from Figure 5 that when the observed rows and columns are selected randomly, the results are not sensitive to the choice between row and column thresholding.
Figure 5.
Spectral and Frobenius norm losses with column/row thresholding. The singular values of A are {j−1, j = 1, 2, …}, p1 = 300, p2 = 3000, and m1, m2 = 10, …, 150.
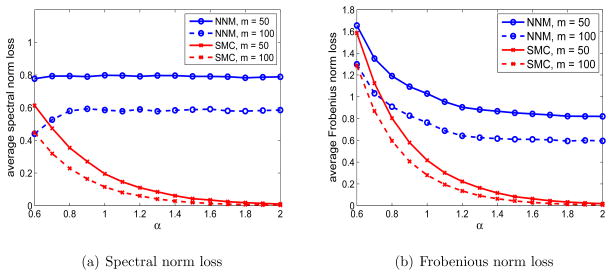
We next turn to the comparison between our proposed SMC algorithm and the penalized NNM method which recovers A by (4). The solution to (4) can be solved by the spectral regularization algorithm by Mazumder et al. (2010) or the accelerated proximal gradient algorithm by Toh and Yun (2010), where these two methods provide similar results. We use 5-fold cross-validation to select the tuning parameter t. Details on the implementation can be found in the Supplement.
We consider the setting where p1 = p2 = 500, m1 = m2 = 50, 100 and the singular value decay rate α ranges from 0.6 to 2. As shown in Figure 6, the proposed SMC method substantially outperform the penalized NNM method with respect to both the spectral and Frobenius norm loss, especially as α increases.
Figure 6.
Comparison of the proposed SMC method with the NNM method with 5-cross-validation for the settings with singular values of A being {j−α, j = 1, 2, …} for α ranging from 0.6 to 2, p1 = p2 = 500, and m1 = m2 = 50 or 100.
Finally, we consider a simulation setting that mimics the ovarian cancer data application considered in the next section, where p1 = 1148, p2 = 1225, m1 = 230, m2 = 426 and the singular values of A decay at a polynomial rate α. Although the singular values of the full matrix are unknown, we estimate the decay rate based on the singular values of the fully observed 552 rows of the matrix from the TCGA study, denoted by {σj, j = 1, …, 522}. A simple linear regression of {log(σj), j = 1, …, 522} on {log(j), j = 1, …, 522} estimates α as 0.8777. In the simulation, we randomly generate A ∈ ℝp1×p2 such that the singular values are fixed as {j−.8777, j = 1, 2, ···}. For comparison, we also obtained results for α = 1 as well as those based on the penalized NNM method with 5-cross-validation. As shown in Table 1, the relative spectral norm loss and relative Frobenius norm loss of the proposed method are reasonably small and substantially smaller than those from the penalized NNM method.
Table 1.
Relative spectral norm loss (||Â22 – A22||/||A22||) and Frobenius norm loss (||Â22 – A22||F/||A22||F) for p1 = 1148, p2 = 1225, m1 = 230, m2 = 426 and singular values of A being {j−α: j = 1, 2, ···}.
| Relative spectral norm loss
|
Relative Frobenius norm loss
|
|||
|---|---|---|---|---|
| SMC | NNM | SMC | NNM | |
| α = 0.8777 | 0.1253 | 0.4614 | 0.2879 | 0.6122 |
| α = 1 | 0.0732 | 0.4543 | 0.1794 | 0.5671 |
5 Application in Genomic Data Integration
In this section, we apply our proposed procedures to integrate multiple
genomic studies of ovarian cancer (OC). OC is the fifth leading cause of cancer
mortality among women, attributing to 14,000 deaths annually (Siegel et al., 2013). OC is a relatively heterogeneous
disease with 5-year survival rate varying substantially among different subgroups.
The overall 5-year survival rate is near 90% for stage I cancer. But the
majority of the OC patients are diagnosed as stage III/IV diseases and tend to
develop resistance to chemotherapy, resulting a 5-year survival rate only about
30% (Holschneider and Berek, 2000).
On the other hand, a small minority of advanced cancers are sensitive to
chemotherapy and do not replapse after treatment completion. Such a heterogeneity in
disease progression is likely to be in part attributable to variations in underlying
biological characteristics of OC (Berchuck et al.,
2005). This heterogeneity and the lack of successful treatment strategies
motivated multiple genomic studies of OC to identify molecular signatures that can
distinguish OC subtypes, and in turn help to optimize and personalize treatment. For
example, the Cancer Genome Atlas (TCGA) comprehensively measured genomic and
epigenetic abnormalities on high grade OC samples (Cancer Genome Atlas Research Network, 2011). A gene expression risk
score based on 193 genes, 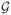 , was trained
on 230 training samples, denoted by
TCGA(t), and shown as highly
predictive of OC survival when validated on the TCGA independent validation set of
size 322, denoted by TCGA(v), as
well as on several independent OC gene expression studies including those from Bonome et al. (2005) (BONO), Dressman et al. (2007) (DRES) and Tothill et al. (2008) (TOTH).
, was trained
on 230 training samples, denoted by
TCGA(t), and shown as highly
predictive of OC survival when validated on the TCGA independent validation set of
size 322, denoted by TCGA(v), as
well as on several independent OC gene expression studies including those from Bonome et al. (2005) (BONO), Dressman et al. (2007) (DRES) and Tothill et al. (2008) (TOTH).
The TCGA study also showed that clustering of miRNA levels overlaps with
gene-expression based clusters and is predictive of survival. It would be
interesting to examine whether combining miRNA with 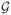 could improve survival prediction when compared to
could improve survival prediction when compared to
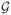 alone. One may use
TCGA(v) to evaluate the added
value of miRNA. However, TCGA(v)
is of limited sample size. Furthermore, since miRNA was only measured for the TCGA
study, its utility in prediction cannot be directly validated using these
independent studies. Here, we apply our proposed SMC method to impute the missing
miRNA values and subsequently construct prediction rules based on both
alone. One may use
TCGA(v) to evaluate the added
value of miRNA. However, TCGA(v)
is of limited sample size. Furthermore, since miRNA was only measured for the TCGA
study, its utility in prediction cannot be directly validated using these
independent studies. Here, we apply our proposed SMC method to impute the missing
miRNA values and subsequently construct prediction rules based on both
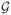 and the imputed miRNA, denoted by for these independent validation sets. To
facilitate the comparison with the analysis based on
TCGA(v) alone where miRNA
measurements are observed, we only used the miRNA from
TCGA(t) for imputation and
reserved the miRNA data from
TCGA(v) for validation
purposes. To improve the imputation, we also included additional 300 genes that were
previously used in a prognostic gene expression signature for predicting ovarian
cancer survival (Denkert et al., 2009). This
results in a total of m1 = 426 unique gene
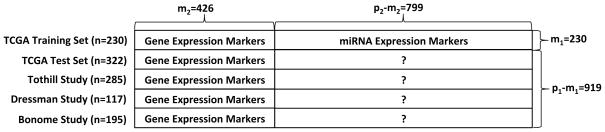
expression variables available for imputation. Detailed information on the data used
for imputation is shown in Figure 7. Prior to
imputation, all gene expression and miRNA levels are log transformed and centered to
have mean zero within each study to remove potential platform or batch effects.
Since the observable rows (indexing subjects) can be viewed as random whereas the
observable columns (indexing genes and miRNAs) are not random, we used row
thresholding with threshold as suggested in the theoretical and simulation
results. For comparison, we also imputed data using the penalized NNM method with
tuning parameter t selected via 5-fold cross-validation.
and the imputed miRNA, denoted by for these independent validation sets. To
facilitate the comparison with the analysis based on
TCGA(v) alone where miRNA
measurements are observed, we only used the miRNA from
TCGA(t) for imputation and
reserved the miRNA data from
TCGA(v) for validation
purposes. To improve the imputation, we also included additional 300 genes that were
previously used in a prognostic gene expression signature for predicting ovarian
cancer survival (Denkert et al., 2009). This
results in a total of m1 = 426 unique gene
expression variables available for imputation. Detailed information on the data used
for imputation is shown in Figure 7. Prior to
imputation, all gene expression and miRNA levels are log transformed and centered to
have mean zero within each study to remove potential platform or batch effects.
Since the observable rows (indexing subjects) can be viewed as random whereas the
observable columns (indexing genes and miRNAs) are not random, we used row
thresholding with threshold as suggested in the theoretical and simulation
results. For comparison, we also imputed data using the penalized NNM method with
tuning parameter t selected via 5-fold cross-validation.
Figure 7.
Imputation scheme for integrating multiple OC genomic studies.
We first compared to the observed miRNA on TCGA(v). Our imputation yielded a rank 2 matrix for and the correlations between the two right and left singular vectors to that of the observed miRNA variables are .90, .71, .34, .14, substantially higher than that of those from the NNM method, with the corresponding values 0.45, 0.06, 0.10, 0.05. This suggests that the SMC imputation does a good job in recovering the leading projections of the miRNA measurements and outperforms the NNM method.
To evaluate the utility of for predicting OC survival, we used the
TCGA(t) to select 117 miRNA
markers that are marginally associated with survival with a nominal
p-value threshold of .05. We use the two leading principal
components (PCs) of the 117 miRNA markers, , as predictors for the survival outcome in addition
to G. The imputation enables us to integrate information from 4 studies including
TCGA(t), which could
substantially improve efficiency and prediction performance. We first assessed the
association between {miRNAPC, 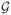 } and OC survival by fitting a stratified
Cox model (Kalbfleisch and Prentice, 2011) to
the integrated data that combines
TCGA(v) and the three
additional studies via either the SMC or NNM methods. In addition, we fit the Cox
model to (i) TCGA(v) set alone
with miRNAPC obtained from the observed miRNA; and (ii) each individual
study separately with imputed miRNAPC. As shown in Table 2(a), the log hazard ratio (logHR) estimates for
miRNAPC from the integrated analysis, based on both SMC and NNM
methods, are similar in magnitude to those obtained based on the observed miRNA
values with TCGA(v). However, the
integrated analysis has substantially smaller standard error (SE) estimates due the
increased sample sizes. The estimated logHRs are also reasonably consistent across
studies when separate models were fit to individual studies.
} and OC survival by fitting a stratified
Cox model (Kalbfleisch and Prentice, 2011) to
the integrated data that combines
TCGA(v) and the three
additional studies via either the SMC or NNM methods. In addition, we fit the Cox
model to (i) TCGA(v) set alone
with miRNAPC obtained from the observed miRNA; and (ii) each individual
study separately with imputed miRNAPC. As shown in Table 2(a), the log hazard ratio (logHR) estimates for
miRNAPC from the integrated analysis, based on both SMC and NNM
methods, are similar in magnitude to those obtained based on the observed miRNA
values with TCGA(v). However, the
integrated analysis has substantially smaller standard error (SE) estimates due the
increased sample sizes. The estimated logHRs are also reasonably consistent across
studies when separate models were fit to individual studies.
Table 2.
Shown in (a) are the estimates of the log hazard ratio (logHR) along with their corresponding standard errors (SE) and p-values by fitting stratified Cox model integrating information from 4 independent studies with imputed miRNA based on the SMC method and the nuclear norm minimization (NNM); and Cox model to the TCGA test data with original observed miRNA (Ori.). Shown also are the estimates for each individual studies by fitting separate Cox models with imputed miRNA.
| (a) Integrated Analysis with
Imputed miRNA vs Single study with observed miRNA | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| logHR | SE | p-value | ||||||||
| Ori. | SMC | NNM | Ori. | SMC | NNM | Ori. | SMC | NNM | ||
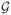
|
.067 | .143 | .168 | .041 | .034 | .028 | .104 | .000 | .000 | |
|
|
−.012 | −.019 | −.013 | .009 | .006 | .012 | .218 | .001 | .283 | |
|
|
.023 | .018 | −.005 | .014 | .009 | .014 | .092 | .039 | .725 | |
| (b) Estimates for Individual
Studies with Imputed miRNA from the SMC method | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| logHR | SE | p-value | |||||||||||
| TCGA | TOTH | DRES | BONO | TCGA | TOTH | DRES | BONO | TCGA | TOTH | DRES | BONO | ||
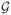
|
.051 | .377 | .174 | .311 | .048 | .069 | .132 | .117 | .286 | .000 | .187 | .008 | |
|
|
−.014 | −.021 | −.031 | −.010 | .011 | .012 | .014 | .014 | .207 | .082 | .030 | .484 | |
|
|
.014 | .045 | −.021 | .036 | .016 | .018 | .022 | .019 | .391 | .009 | .336 | .054 | |
| (c) Estimates for Individual
Studies with Imputed miRNA from the NNM method | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| logHR | SE | p-value | |||||||||||
| TCGA | TOTH | DRES | BONO | TCGA | TOTH | DRES | BONO | TCGA | TOTH | DRES | BONO | ||
|
.082 | .405 | .361 | .258 | .037 | .066 | .114 | .088 | .028 | .000 | .002 | .003 | |
|
|
−.045 | .016 | .055 | −.008 | .021 | .026 | .031 | .023 | .034 | .544 | .076 | .721 | |
|
|
.008 | −.086 | −.043 | .019 | .026 | .027 | .034 | .029 | .758 | .002 | .201 | .496 | |
We also compared the prediction performance of the model based on
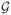 alone to the model that includes
both
alone to the model that includes
both 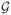 and the imputed
miRNAPC. Combining information from all 4 studies via standard meta
analysis, the average improvement in C-statistic was 0.032 (SE = 0.013) for
the SMC method and 0.001 (SE = 0.009) for the NNM method, suggesting that
the imputed miRNAPC from the SMC method has much higher predictive value
compared to those obtained from the NNM method.
and the imputed
miRNAPC. Combining information from all 4 studies via standard meta
analysis, the average improvement in C-statistic was 0.032 (SE = 0.013) for
the SMC method and 0.001 (SE = 0.009) for the NNM method, suggesting that
the imputed miRNAPC from the SMC method has much higher predictive value
compared to those obtained from the NNM method.
In summary, the results shown above suggest that our SMC procedure accurately recovers the leading PCs of the miRNA variables. In addition, adding miRNAPC obtained from imputation using the proposed SMC method could significantly improve the prediction performance, which confirms the value of our method for integrative genomic analysis. When comparing to the NNM method, the proposed SMC method produces summaries of miRNA that is more correlated with the truth and yields leading PCs that are more predictive of OC survival.
6 Discussions
The present paper introduced a new framework of SMC where a subset of the rows and columns of an approximately low-rank matrix are observed. We proposed an SMC method for the recovery of the whole matrix with theoretical guarantees. The proposed procedure significantly outperforms the conventional NNM method for matrix completion, which does not take into account the special structure of the observations. As shown by our theoretical and numerical analyses, the widely adopted NNM methods for matrix completion are not suitable for the SMC setting. These NNM methods perform particularly poorly when a small number of rows and columns are observed.
The key assumption in matrix completion is the matrix being approximately low rank. This is reasonable in the ovarian cancer application since as indicated in the results from the TCGA study (Cancer Genome Atlas Research Network, 2011), the patterns observed in the miRNA signature are highly correlated with the patterns observed in the gene expression signature. This suggests the high correlation among the selected gene expression and miRNA variables. Results from the imputation based on the approximate low rank assumption given in Section 5 are also encouraging with promising correlations with true signals and good prediction performance from the imputed miRNA signatures. We expect that this imputation method will also work well in genotyping and sequencing applications, particularly for regions with reasonably high linkage disequilibrium.
Another main assumption that is needed in the theoretical analysis is that there is a significant gap between the rth and (r + 1)th singular values of A. This assumption may not be valid in real practice. In particular, the singular values of the ovarian dataset analyzed in Section 5 is decreasing smoothly without a significant gap. However, it has been shown in the simulation studies presented in Section 4 that, although there is no significant gap between any adjacent singular values of the matrix to be recovered, the proposed SMC method works well as long as the singular values decay sufficiently fast. Theoretical analysis for the proposed SMC method under more general patterns of singular value decay warrants future research.
To implement the proposed Algorithm 2, major decisions include the choice of threshold values and choosing between column thresholding and row thresholding. Based on both the-oretical and numerical studies, optimal threshold values can be set as for column thresholding and for row thresholding. Simulation results in Section 4 show that when both rows and columns are randomly chosen, the results are very similar. In the real data applications, the choice between row thresholding and column thresholding depends on whether the rows or columns are more \homogeneous”, or closer to being randomly sampled. For example, in the ovarian cancer dataset analyzed in Section 5, the rows correspond to the patients and the columns correspond to the gene expression levels and miRNA levels. Thus the rows are closer to random sample than the columns, consequently it is more natural to use the row thresholding in this case.
We have shown both theoretically and numerically in Sections 3 and 4 that Algorithm 2 provides a good recovery of A22. However, the naive implementation of this algorithm requires min(m1, m2) matrix inversions and multiplication operations in the for loop that calculates ||DR,s|| (or ||DC,s||), s ∈ {r̂, r̂ + 1, ···, min(m1, m2)}. Taking into account the relationship among DR,s (or DC,s) for different s’s, it is possible to simultaneously calculate all ||DR,s|| (or ||DC,s||) and accelerate the computations. For reasons of space, we leave optimal implementation of Algorithm 2 as future work.
Supplementary Material
Acknowledgments
We thank the Editor, Associate Editor and referee for their detailed and constructive comments which have helped to improve the presentation of the paper.
Footnotes
The research of Tianxi Cai was supported in part by NIH Grants R01 GM079330 and U54 H6007963; the research of Tony Cai and Anru Zhang was supported in part by NSF Grants DMS-1208982 and DMS-1403708, and NIH Grant R01 CA127334.
Contributor Information
Tianxi Cai, Professor of Biostatistics, Department of Biostatistics, Harvard University, Boston, MA.
T. Tony Cai, Dorothy Silberberg Professor of Statistics, Department of Statistics, The Wharton School, University of Pennsylvania, Philadelphia, PA.
Anru Zhang, Student, Department of Statistics, The Wharton School, University of Pennsylvania, Philadelphia, PA
References
- Argyriou A, Evgeniou T, Pontil M. Convex multi-task feature learning. Machine Learning. 2008;73(3):243–272. [Google Scholar]
- Berchuck A, Iversen ES, Lancaster JM, Pittman J, Luo J, Lee P, Murphy S, Dressman HK, Febbo PG, West M, et al. Patterns of gene expression that characterize long-term survival in advanced stage serous ovarian cancers. Clinical Cancer Research. 2005;11(10):3686–3696. doi: 10.1158/1078-0432.CCR-04-2398. [DOI] [PubMed] [Google Scholar]
- Biswas P, Lian TC, Wang TC, Ye Y. Semidefinite programming based algorithms for sensor network localization. ACM Transactions on Sensor Networks (TOSN) 2006;2(2):188–220. [Google Scholar]
- Bonome T, Lee JY, Park DC, Radonovich M, Pise-Masison C, Brady J, Gardner GJ, Hao K, Wong WH, Barrett JC, et al. Expression profiling of serous low malignant potential, low-grade, and high-grade tumors of the ovary. Cancer Research. 2005;65(22):10602–10612. doi: 10.1158/0008-5472.CAN-05-2240. [DOI] [PubMed] [Google Scholar]
- Browning BL, Browning SR. A unified approach to genotype imputation and haplotype-phase inference for large data sets of trios and unrelated individuals. The American Journal of Human Genetics. 2009;84(2):210–223. doi: 10.1016/j.ajhg.2009.01.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cai JF, Candès E, Shen Z. A singular value thresholding algorithm for matrix completion. SIAM J Optim. 2010;20(4):1956–1982. [Google Scholar]
- Cai T, Cai TT, Zhang A. Supplement to \structured matrix completion with applications to genomic data integration”. Technical Report. 2014 doi: 10.1080/01621459.2015.1021005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cai TT, Zhang A. Perturbation bound on unilateral singular vectors. Technical report 2014 [Google Scholar]
- Cai TT, Zhou W. Matrix completion via max-norm constrained optimization. 2013 arXiv preprint arXiv:1303.0341. [Google Scholar]
- Cancer Genome Atlas Research Network. Integrated genomic analyses of ovarian carcinoma. Nature. 2011;474(7353):609–615. doi: 10.1038/nature10166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Candes EJ, Plan Y. Tight oracle inequalities for low-rank matrix recovery from a minimal number of noisy random measurements. Information Theory, IEEE Transactions on. 2011;57(4):2342–2359. [Google Scholar]
- Candès EJ, Recht B. Exact matrix completion via convex optimization. Foundations of Computational Mathematics. 2009;9(6):717–772. [Google Scholar]
- Candès EJ, Tao T. The power of convex relaxation: Near-optimal matrix completion. Information Theory, IEEE Transactions on. 2010;56(5):2053–2080. [Google Scholar]
- Chen P, Suter D. Recovering the missing components in a large noisy low-rank matrix: Application to sfm. Pattern Analysis and Machine Intelligence, IEEE Transactions on. 2004;26(8):1051–1063. doi: 10.1109/TPAMI.2004.52. [DOI] [PubMed] [Google Scholar]
- Chi EC, Zhou H, Chen GK, Del Vecchyo DO, Lange K. Genotype imputation via matrix completion. Genome Research. 2013;23(3):509–518. doi: 10.1101/gr.145821.112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Denkert C, Budczies J, Darb-Esfahani S, Györffy B, Sehouli J, Könsgen D, Zeillinger R, Weichert W, Noske A, Buckendahl AC, et al. A prognostic gene expression index in ovarian cancervalidation across different independent data sets. The Journal of pathology. 2009;218(2):273–280. doi: 10.1002/path.2547. [DOI] [PubMed] [Google Scholar]
- Dressman HK, Berchuck A, Chan G, Zhai J, Bild A, Sayer R, Cragun J, Clarke J, Whitaker RS, Li L, et al. An integrated genomic-based approach to individualized treatment of patients with advanced-stage ovarian cancer. Journal of Clinical Oncology. 2007;25(5):517–525. doi: 10.1200/JCO.2006.06.3743. [DOI] [PubMed] [Google Scholar]
- Foygel R, Salakhutdinov R, Shamir O, Srebro N. Learning with the weighted trace-norm under arbitrary sampling distributions. NIPS. 2011:2133–2141. [Google Scholar]
- Gross D. Recovering low-rank matrices from few coefficients in any basis. Information Theory, IEEE Transactions on. 2011;57(3):1548–1566. [Google Scholar]
- Gross D, Nesme V. Note on sampling without replacing from a finite collection of matrices. 2010 arXiv preprint, arXiv:1001.2738. [Google Scholar]
- Holschneider CH, Berek JS. Seminars in surgical oncology. Vol. 19. Wiley Online Library; 2000. Ovarian cancer: epidemiology, biology, and prognostic factors; pp. 3–10. [DOI] [PubMed] [Google Scholar]
- Kalbeisch JD, Prentice RL. The statistical analysis of failure time data. Vol. 360. John Wiley & Sons; 2011. [Google Scholar]
- Keshavan RH, Montanari A, Oh S. Matrix completion from noisy entries. J Mach Learn Res. 2010;11(1):2057–2078. [Google Scholar]
- Kim H, Golub GH, Park H. Missing value estimation for dna microarray gene expression data: local least squares imputation. Bioinformatics. 2005;21(2):187–198. doi: 10.1093/bioinformatics/bth499. [DOI] [PubMed] [Google Scholar]
- Koltchinskii V. Von neumann entropy penalization and low-rank matrix estimation. Ann Statist. 2011;39(6):2936–2973. [Google Scholar]
- Koltchinskii V, Lounici K, Tsybakov AB, et al. Nuclear-norm penalization and optimal rates for noisy low-rank matrix completion. Ann Statist. 2011;39(5):2302–2329. [Google Scholar]
- Koren Y, Bell R, Volinsky C. Matrix factorization techniques for recommender systems. Computer. 2009;42(8):30–37. [Google Scholar]
- Laurent B, Massart P. Adaptive estimation of a quadratic functional by model selection. Ann Statist. 2000;28:1302–1338. [Google Scholar]
- Li Y, Abecasis GR. Mach 1.0: rapid haplotype reconstruction and missing genotype inference. Am J Hum Genet S. 2006;79(3):2290. [Google Scholar]
- Mazumder R, Hastie T, Tibshirani R. Spectral regularization algorithms for learning large incomplete matrices. Journal of Machine Learning Research. 2010;11:2287–2322. [PMC free article] [PubMed] [Google Scholar]
- Recht B. A simpler approach to matrix completion. J Mach Learn Res. 2011;12:3413–3430. [Google Scholar]
- Rohde A, Tsybakov AB, et al. Estimation of high-dimensional low-rank matrices. Ann Statist. 2011;39(2):887–930. [Google Scholar]
- Salakhutdinov R, Srebro N. Collaborative filtering in a non-uniform world: Learning with the weighted trace norm. 2010 arXiv preprint arXiv:1002.2780. [Google Scholar]
- Scheet P, Stephens M. A fast and exible statistical model for large-scale population genotype data: applications to inferring missing genotypes and haplotypic phase. The American Journal of Human Genetics. 2006;78(4):629–644. doi: 10.1086/502802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siegel R, Naishadham D, Jemal A. Cancer statistics, 2013. CA: a cancer journal for clinicians. 2013;63(1):11–30. doi: 10.3322/caac.21166. [DOI] [PubMed] [Google Scholar]
- Singer A, Cucuringu M. Uniqueness of low-rank matrix completion by rigidity theory. SIAM Journal on Matrix Analysis and Applications. 2010;31(4):1621–1641. [Google Scholar]
- Toh KC, Yun S. An accelerated proximal gradient algorithm for nuclear norm regularized least squares problems. Pacific J Optimization. 2010;6:615–640. [Google Scholar]
- Tomasi C, Kanade T. Shape and motion from image streams: a factorization method parts 2810 full report on the orthographic case. 1992 doi: 10.1073/pnas.90.21.9795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tothill RW, Tinker AV, George J, Brown R, Fox SB, Lade S, Johnson DS, Trivett MK, Etemadmoghadam D, Locandro B, et al. Novel molecular subtypes of serous and endometrioid ovarian cancer linked to clinical outcome. Clinical Cancer Research. 2008;14(16):5198–5208. doi: 10.1158/1078-0432.CCR-08-0196. [DOI] [PubMed] [Google Scholar]
- Troyanskaya O, Cantor M, Sherlock G, Brown P, Hastie T, Tibshirani R, Botstein D, Altman RB. Missing value estimation methods for dna microarrays. Bioinformatics. 2001;17(6):520–525. doi: 10.1093/bioinformatics/17.6.520. [DOI] [PubMed] [Google Scholar]
- Vershynin R. Introduction to the non-asymptotic analysis of random matrices. Cambridge Univ. Press; Cambridge: 2010. [Google Scholar]
- Vershynin R. Spectral norm of products of random and deterministic matrices. Probab Theory Relat Fields. 2013;150:471–509. [Google Scholar]
- Wang X, Li A, Jiang Z, Feng H. Missing value estimation for DNA microarray gene expression data by support vector regression imputation and orthogonal coding scheme. BMC Bioinformatics. 2006;7(1):32. doi: 10.1186/1471-2105-7-32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu Z, Schaid DJ. Methods to impute missing genotypes for population data. Human Genetics. 2007;122(5):495–504. doi: 10.1007/s00439-007-0427-y. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.