General expressions for R_1ρ relaxation for N-site chemical exchange and the special case of linear chains

Abstract

Exploration of dynamic processes in proteins and nucleic acids by spin-locking NMR experiments has been facilitated by the development of theoretical expressions for the R_1ρ relaxation rate constant covering a variety of kinetic situations. Herein, we present a generalized approximation to the chemical exchange, R_ex, component of R_1ρ for arbitrary kinetic schemes, assuming the presence of a dominant major site population, derived from the negative reciprocal trace of the inverse Bloch-McConnell evolution matrix. This approximation is equivalent to first-order truncation of the characteristic polynomial derived from the Bloch-McConnell evolution matrix. For three- and four-site chemical exchange, the first-order approximations are sufficient to distinguish different kinetic schemes. We also introduce an approach to calculate R_1ρ for linear N-site schemes, using the matrix determinant lemma to reduce the corresponding 3N × 3N Bloch-McConnell evolution matrix to a 3 × 3 matrix. The first- and second order-expansions of the determinant of this 3 × 3 matrix are closely related to previously derived equations for two-site exchange. The second-order approximations for linear N-site schemes can be used to obtain more accurate approximations for non-linear N-site schemes, such as triangular three-site or star four-site topologies. The expressions presented herein provide powerful means for the estimation of R_ex contributions for both low (CEST-limit) and high (R_1ρ-limit) radiofrequency field strengths, provided that the population of one state is dominant. The general nature of the new expressions allows for consideration of complex kinetic situations in the analysis of NMR spin relaxation data.

Graphical abstract

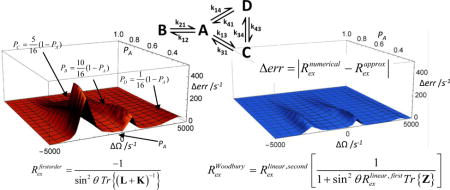
Introduction

Dynamic processes in proteins and nucleic acids can be studied using various techniques in nuclear magnetic resonance (NMR) spectroscopy [1]. Nuclear spin relaxation in the presence of a radiofrequency (rf) field is characterized by the rotating-frame R_1ρ and R_2ρ relaxation rate constants. Rotating-frame relaxation measurements can be used to study conformational and chemical processes that range from slow to fast on the chemical shift time scale [2]. In particular, spontaneous inter-conversion between different protein structures, ligand-binding events, chemical reaction kinetics, and protein folding processes that occur with rate constants between 10 and 10⁵ s⁻¹ can be probed by R_1ρ experiments with rf field strengths ranging from Hz (CEST-limit) to kHz (R_1ρ-limit) [2, 3]. Most analyses of experimental data have assumed two-state exchange kinetics, but examples featuring three-site [4, 5], four-site [6, 7] and other [8] topologies illustrate the need to provide theoretical insight into more complex kinetic schemes.

Exact numerical solutions for R_1ρ can be obtained by numerical integration of the Bloch-McConnell differential equation or by calculation of the largest (least negative) real eigenvalue of the Bloch-McConnell evolution matrix and elegant fast numerical algorithms have been described [9]. However, analytic expressions for R_1ρ facilitate understanding of the relationship between model parameters and the phenomenological relaxation rate constant and can lead to new methodological advances. For example, first-order expressions show the importance of the minor state resonance frequency when exchange is not fast [10] and the effect of differential relaxation (from processes other than chemical exchange) of the major and minor states [2, 11]. As another example, the perturbation treatment of N-site exchange mechanisms provides insight into the reduction of complex exchange schemes to simpler ones if exchange within subgroups of states is fast compared to exchange between subgroups [12]. In addition, analytic solutions allow straightforward symbolic differentiation with respect to model parameters. The obtained derivatives can be used in gradient-based minimization procedures, such as the Levenberg-Marquardt algorithm, to find optimal parameters more efficiently than possible with either numerically estimated derivatives, or non-gradient-based methods, such as grid-search or simplex routines.

Analytical solutions for R_1ρ for two-state exchange outside the fast-exchange limit were obtained previously by finding the least negative (smallest magnitude) real root of the characteristic sixth-order polynomial derived from the Bloch-McConnell evolution matrix. An approximation retaining only the two lowest-order terms (first order in the eigenvalue) is valid for highly skewed site populations [10, 11]. The Laguerre approximation to a second-order truncation of the sixth-order characteristic polynomial is more accurate than the first-order treatment for site populations that are less skewed [13]. In an alternative approach, the relevant 6 × 6 Bloch-McConnell matrix for the two exchanging magnetization vectors is reduced to a 3 × 3 matrix describing evolution of the average magnetization. The average magnetization approach yields expressions of similar accuracy as the Laguerre approximation, but somewhat increased algebraic complexity [14]. The average-magnetization approach also yields analytical, although complex, expressions for R_1ρ for a general N-site exchange mechanism (vide infra). Compact analytical solutions for N-site schemes can be obtained by perturbation theory applied to the 3N × 3N Bloch-McConnell evolution matrix [12]. The general solution obtained from this approach is valid only if one of the N populations is highly dominant. While most treatments of R_1ρ have assumed a constant-amplitude rf field, the theoretical and experimental results have been extended to time-varying adiabatic sweeps of the rf field [9, 15–18].

Herein, we present a general approach to obtain first-order approximations for R_1ρ, which are valid for any kinetic scheme in which one site is sufficiently highly populated. Furthermore, we introduce an approach to reduce the 3N × 3N Bloch-McConnell matrix for any linear exchange scheme to a 3 × 3 matrix by repetitive use of the matrix determinant lemma.

Theory

The Bloch-McConnell equation is

$$\frac{d\mathbf{M}(t)}{dt}=\left(\mathbf{L}+\mathbf{R}+\mathbf{K}\right)\mathbf{M}(t)$$ (1)

in which M(t) = [M₁(t), …, M_N(t)]^T, M_j(t) = [M_xj(t), M_yj(t), M_zj(t)]^T, and N is the number of exchanging states. The evolution matrix has the form:

$$\mathbf{L}+\mathbf{R}+\mathbf{K}=\left[\begin{array}{ccc}{\mathbf{L}}_A& \dots & \mathbf{0}\\ ⋮& \ddots & ⋮\\ \mathbf{0}& \dots & {\mathbf{L}}_N\end{array}\right]+\left[\begin{array}{ccc}{\mathbf{R}}_A& \dots & \mathbf{0}\\ ⋮& \ddots & ⋮\\ \mathbf{0}& \dots & {\mathbf{R}}_N\end{array}\right]+\mathbf{k}\otimes \mathbf{I}$$ (2)

in which,

$${\mathbf{L}}_j=\left[\begin{array}{ccc}0& -{\delta }_j& 0\\ {\delta }_j& 0& -{\omega }_1\\ 0& {\omega }_1& 0\end{array}\right]$$ (3)

$$\begin{array}{l}{\mathbf{R}}_j=\left[\begin{array}{ccc}-R_{2j}& 0& 0\\ 0& -R_{2j}& 0\\ 0& 0& -R_{1j}\end{array}\right]=-{\overline{R}}_2\mathbf{I}+\left[\begin{array}{ccc}{\overline{R}}_2-R_{2j}& 0& 0\\ 0& {\overline{R}}_2-R_{2j}& 0\\ 0& 0& \left({\overline{R}}_2-{\overline{R}}_1\right)\end{array}\right]\\ =-{\overline{R}}_2\mathbf{I}+\mathrm{\Delta }{\mathbf{R}}_j\end{array}$$ (4)

0 and I are the zero and identity matrices, respectively, with dimensions set by context (3 × 3 in Eq. 2); δ_j = _j− ω_rf is the resonance offset frequency, _j is the resonance frequency, and R_1j and R_2j are the longitudinal and transverse relaxation rate constants in the absence of exchange, respectively, for spins in the j^th site; ω_rf and ω₁ are the frequency and amplitude (measured in frequency units; termed the Rabi frequency) of the rf spin-lock field; ${\overline{R}}_{1j}$ and ${\overline{R}}_{2j}$ are the population-averaged longitudinal and transverse relaxation rate constants in the absence of exchange; and $R_{1j}-{\overline{R}}_1\approx 0$ is assumed. The elements of the N × N kinetic rate matrix k are k_jn, the (pseudo) first-order rate constant for transitions from state j to state n (j • n) and

$$k_{jj}=-{\displaystyle \sum _{\begin{array}{l}n=1\\ n\ne j\end{array}}^N{k}_{\mathit{jn}}}$$ (5)

The formal solution to the Bloch-McConnell equation is given by:

$$\begin{array}{l}\mathbf{M}(t)=\exp \left\{\left(\mathbf{L}+\mathbf{R}+\mathbf{K}\right)t\right\}\mathbf{M}(0)\\ ={\displaystyle \sum _{i=1}^N|{\mathbf{u}}_i\rangle }\langle {\mathbf{u}}_i^{-1}|\mathbf{M}(0)e^{{\lambda }_{i}t}\end{array}$$ (6)

in which |u_i〉 and λ_i are the right eigenvectors and eigenvalues of the Bloch-McConnell evolution matrix.

In a typical measurement of R_1ρ, initial magnetization is aligned along a tilted rotating frame of reference, yielding M_j(0) ∝ p_jv, in which p_j is the equilibrium population of the j^th state, v = [sinθ, 0, cosθ]^T, tan θ = ω₁/ΔΩ, and $\mathrm{\Delta }\mathrm{\Omega }={\displaystyle {\sum }_j{p}_j{\delta }_j}$ is the population-average resonance offset frequency. In turn, the spin-locked z-magnetization in the tilted frame of reference following the relaxation period is M′_z(t) = dM(t) in which d = [v, …, v] is a 1 × 3N row vector. If p₁ → 1, perturbation theory shows that |u₁> → [v, 0, …, 0]^T; consequently, the decay of the spin-locked magnetization is highly monoexponential with damping constant λ₁ (which will be simply called λ in the following) [12]. If |u₁> diverges from [v, 0, …, 0]^T, then contributions from other eigenvalues contribute to the magnetization decay. In such cases, the magnetization decay contains oscillatory components, arising from complex eigenvalues, but inhomogeneity of the B₁ field suppresses these contributions, particularly for long relaxation times (such as those used in CEST experiments). The ideal result that |u₁> → [v, 0, …, 0]^T, i.e. yielding negligible contributions from other eigenvalues, also is approached for larger values of the exchange rate constants, the resonance offset, and the spin-lock field (vide infra). The effects of dispersion of the eigenbase relative to the tilted frame are reduced if the site magnetizations are aligned with their own tilted frames, defined by tanθ_j = ω₁/ΔΩ_j, as would be obtained by an adiabatic sweep shorter than the jump time between states. Broadly speaking, the assumption that the R_1ρ relaxation can be described by a monoexponential decay is more accurate with off-resonance irradiation, larger exchange kinetic rate constants, larger ω₁ and with relatively larger population of the dominant chemical state.

The R_1ρ relaxation rate constant therefore can be defined to be the negative of the largest (least negative) real eigenvalue of the evolution matrix, i.e. R_1ρ = −λ. The eigenvalues are given by the zeros of the characteristic polynomial:

$$\begin{array}{l}0=\left|\mathbf{L}+\mathbf{R}+\mathbf{K}-\lambda \mathbf{I}\right|\\ =\left|\mathbf{L}+\mathbf{R}+\mathbf{K}\right|\left|\mathbf{I}-\lambda {\left(\mathbf{L}+\mathbf{R}+\mathbf{K}\right)}^{-1}\right|\\ =\left|\mathbf{I}-\lambda {\left(\mathbf{L}+\mathbf{R}+\mathbf{K}\right)}^{-1}\right|\\ \approx 1-\lambda \mathit{Tr}\left\{{\left(\mathbf{L}+\mathbf{R}+\mathbf{K}\right)}^{-1}\right\}\end{array}$$ (7)

in which |A| is the determinant and Tr[A] is the trace of the matrix A, respectively. The last line is obtained assuming that the magnitude of the desired eigenvalue is small. With the aforementioned definition of R_1ρ we then obtain

$$R_{1\rho }=-\lambda =-1/\mathit{Tr}\left\{{\left(\mathbf{L}+\mathbf{R}+\mathbf{K}\right)}^{-1}\right\}$$ (8)

When values of R_2j are small, the above expression can be simplified to first-order in R by the following:

$$\begin{array}{l}0=\left|\mathbf{L}+\mathbf{R}+\mathbf{K}-\lambda \mathbf{I}\right|\\ =\left|\mathbf{L}+\mathbf{K}\right|\left|\mathbf{I}-\lambda {\left(\mathbf{L}+\mathbf{K}\right)}^{-1}+{\left(\mathbf{L}+\mathbf{K}\right)}^{-1}\mathbf{R}\right|\\ =\left|\mathbf{I}-\lambda {\left(\mathbf{L}+\mathbf{K}\right)}^{-1}+{\left(\mathbf{L}+\mathbf{K}\right)}^{-1}\mathbf{R}\right|\\ \approx 1-\lambda \mathit{Tr}\left\{{\left(\mathbf{L}+\mathbf{K}\right)}^{-1}\right\}+\mathit{Tr}\left\{{\left(\mathbf{L}+\mathbf{K}\right)}^{-1}\mathbf{R}\right\}\end{array}$$ (9)

Solving this equation for λ and using Eq 4 gives,

$$\begin{array}{l}{R}_{1\rho }={\overline{R}}_2-\frac{\mathit{Tr}\left\{{\left(\mathbf{L}+\mathbf{K}\right)}^{-1}\mathrm{\Delta }\mathbf{R}\right\}}{\mathit{Tr}\left\{{\left(\mathbf{L}+\mathbf{K}\right)}^{-1}\right\}}-\frac{1}{\mathit{Tr}\left\{{\left(\mathbf{L}+\mathbf{K}\right)}^{-1}\right\}}\\ =R_{\mathit{eff}}+{\sin }^2\theta R_{\mathit{ex}}\end{array}$$ (10)

in which

$$R_{\mathit{ex}}=\frac{-1}{{\sin }^2\theta \mathit{Tr}\left\{{\left(\mathbf{L}+\mathbf{K}\right)}^{-1}\right\}}=\frac{-\lambda }{{\sin }^2\theta }$$ (11)

$$R_{\mathit{eff}}={\overline{R}}_2-\frac{\mathit{Tr}\left\{{\left(\mathbf{L}+\mathbf{K}\right)}^{-1}\mathrm{\Delta }\mathbf{R}\right\}}{\mathit{Tr}\left\{{\left(\mathbf{L}+\mathbf{K}\right)}^{-1}\right\}}$$ (12)

and is the largest negative real eigenvalue of L + K in Eq. 11. For two-state exchange, Eq. 10 is identical to Eq. 5 of Baldwin and Kay [11]. If $R_{2j}={\overline{R}}_2$ for all j, Eq. 10 reduces to Eq. 11 in Trott and Palmer [10] and Eq. 9 in Baldwin and Kay [11]. In addition, if the population of the dominant site is large, then Eq. 12 simplifies to

$$R_{\mathit{eff}}={\overline{R}}_1{\cos }^2\theta +{\overline{R}}_2{\sin }^2\theta$$ (13)

so that

$$\begin{array}{l}{R}_{1\rho }={\overline{R}}_1{\cos }^2\theta +{\overline{R}}_2{\sin }^2\theta -\frac{1}{\mathit{Tr}\left\{{\left(\mathbf{L}+\mathbf{K}\right)}^{-1}\right\}}\\ ={\overline{R}}_1{\cos }^2\theta +{\overline{R}}_2{\sin }^2\theta +{\sin }^2\theta R_{\mathit{ex}}\end{array}$$ (14)

Equations 10–14 are the major results of this work. The approximations leading to these equations are accurate if 1/λ dominates the sum of the inverses of the other eigenvalues for L + K and L + R + K because for a matrix A, $\mathit{Tr}\left\{{\mathbf{A}}^{-1}\right\}={\displaystyle \sum _j{\lambda }_j^{-1}}$. As discussed elsewhere [19], the conditions for which this approximation holds depends in general on all the parameters in Eq. 1, but usually is met if one of the sites is sufficiently more highly populated than the other N − 1 sites. Expressions obtained from Eqs. 10–14 for N-site exchange (N > 2) are more complex than those obtained using the perturbation approach of Trott and Palmer [12], but are accurate for a larger range of site populations. Crucially, the matrix traces and inverses in these expressions do not need to be expanded algebraically for analysis of experimental data because the necessary derivatives with respect to model parameters can be obtained symbolically, as shown in Supplementary Material III (S16–S23).

The above first-order approach can be extended in accuracy by considering the evolution of the average magnetization, rather than the N individual magnetization vectors. As shown by Trott and coworkers [14], the evolution equation for the average magnetization <M>(t) under the steady-state approximation is:

$$\frac{d\langle \mathbf{M}\rangle (t)}{dt}=\left\{\langle {\mathbf{L}}_k\rangle -{\mathbf{F}}_2{\mathbf{F}}_4^{-1}{\mathbf{F}}_3\right\}\langle \mathbf{M}\rangle (t)$$ (15)

in which 〈L_k〉 is the 3 × 3 population average of the N individual site matrices

$$\begin{array}{l}\mathbf{F}=\mathbf{UL}{\mathbf{U}}^{-1}+\mathbf{Uk}{\mathbf{U}}^{-1}\otimes \mathbf{I}=\left[\begin{array}{cc}<{\mathbf{L}}_k>& {\mathbf{F}}_2\\ {\mathbf{F}}_3& {\mathbf{F}}_4\end{array}\right]\hfill \\ \mathbf{U}|p_1,p_2,\rightleftharpoons ,p_N\rangle =|1,0,\rightleftharpoons ,0\rangle \hfill \end{array}$$ (16)

and rows 2, …, N of U are orthogonal. The blocks F₂, F₃, and F₄ have dimensions 3 × 3(N −1), 3(N −1) × 3, and 3(N − 1) × 3(N − 1), respectively. Using the above ansatz,

$$\begin{array}{l}0=\left|\langle {\mathbf{L}}_k\rangle -{\mathbf{F}}_2{\mathbf{F}}_4^{-1}{\mathbf{F}}_3-\lambda \mathbf{I}\right|\\ =\left|\mathrm{I}-\lambda {\left(\langle {\mathbf{L}}_k\rangle -{\mathbf{F}}_2{\mathbf{F}}_4^{-1}{\mathbf{F}}_3\right)}^{-1}\right|\\ =1-\lambda \mathit{Tr}\left\{{\left(\langle {\mathbf{L}}_k\rangle -{\mathbf{F}}_2{\mathbf{F}}_4^{-1}{\mathbf{F}}_3\right)}^{-1}\right\}\end{array}$$ (17)

leading to:

$$\lambda =-R_{\mathit{ex}}{\sin }^2\theta =\frac{1}{\mathit{Tr}\left\{{\left(\langle {\mathbf{L}}_k+{\mathbf{R}}_k\rangle -{\mathbf{F}}_2{\mathbf{F}}_4^{-1}{\mathbf{F}}_3\right)}^{-1}\right\}}$$ (18)

from which R_1ρ can be obtained using Eqs. 10 or 14.

Two-site chemical exchange

For two-site exchange between sites A and B, Eq. 10 yields the expression of Baldwin and Kay [11] and Eq. 11 yields the original expression (Eq. 24) of Trott and Palmer [10]:

$$R_{\mathit{ex}}=\frac{p_A{p}_B\mathrm{\Delta }{\omega }^2{k}_{\mathit{ex}}}{{\omega }_A^2{\omega }_B^2/{\omega }_e^2+k_{\mathit{ex}}^2}$$ (19)

in which Δω = Ω_B − Ω_A, ${\omega }_j^2={\delta }_j^2+{\omega }_1^2$, ${\omega }_e^2=\mathrm{\Delta }{\mathrm{\Omega }}^2+{\omega }_1^2$, and k_ex = k₁₂ + k₂₁. The average magnetization approach (Eq. 18) gives

$$R_{\mathit{ex}}=\frac{p_A{p}_B\mathrm{\Delta }{\omega }^2{k}_{\mathit{ex}}}{{\omega }_A^2{\omega }_B^2/{\omega }_e^2+k_{\mathit{ex}}^2-2{\sin }^2\theta p_A{p}_B\mathrm{\Delta }{\omega }^2}$$ (20)

which is identical to Eq. 74 of Trott et al. [14]. Equation 20 approaches Eq. 19 as p_B → 0.

Recently, we showed that the R_1ρ relaxation rate constant for two-site exchange could be reduced to the reciprocal of the trace of a 3 × 3 matrix [20]. This derivation is reproduced below, in slightly more compact form to motivate the subsequent treatment of chemical exchange in linear chains with three or more sites. The exchange matrix K is rank-deficient and can be factored as:

$$\mathbf{K}=\left[\begin{array}{cc}-k_{12}& k_{21}\\ k_{12}& -k_{21}\end{array}\right]\otimes \mathbf{I}=\left[\begin{array}{c}\mathbf{I}\\ -\mathbf{I}\end{array}\right]\left[-k_{12}\mathbf{I}{k}_{21}\mathbf{I}\right]=\mathbf{U}{\mathbf{V}}^T$$ (21)

As before, the eigenvalues of L + K are determined by equating the characteristic polynomial to 0:

$$\begin{array}{l}0=\left|\mathbf{L}+\mathbf{K}-\lambda \mathbf{I}\right|\\ =\left|\mathbf{L}-\lambda \mathbf{I}+\mathbf{U}{\mathbf{V}}^T\right|\\ =\left|\mathbf{L}-\lambda \mathbf{I}\right|\left|\mathbf{I}+{\mathbf{V}}^T{\left(\mathbf{L}-\lambda \mathbf{I}\right)}^{-1}\mathbf{U}\right|\end{array}$$ (22)

in which the last line is obtained using the matrix determinant lemma. A series of manipulations that utilize the block structure of L yields:

$$\begin{array}{l}0=\left|\mathbf{L}-\lambda \mathbf{I}\right|\left|\mathbf{I}+{\mathbf{V}}^T{\left(\mathbf{L}-\lambda \mathbf{I}\right)}^{-1}\mathbf{U}\right|\\ =\left|{\mathbf{L}}_A-\lambda \mathbf{I}\right|\left|{\mathbf{L}}_B-\lambda \mathbf{I}\right|\left|\mathbf{I}+{\mathbf{V}}^T{\left(\mathbf{L}-\lambda \mathbf{I}\right)}^{-1}\mathbf{U}\right|\\ =\left|{\mathbf{L}}_A-\lambda \mathbf{I}\right|\left|\mathbf{I}-k_{12}{\left({\mathbf{L}}_A-\lambda \mathbf{I}\right)}^{-1}-k_{21}{\left({\mathbf{L}}_B-\lambda \mathbf{I}\right)}^{-1}\right|\left|{\mathbf{L}}_B-\lambda \mathbf{I}\right|\\ =\left|\left({\mathbf{L}}_A-\lambda \mathbf{I}\right)\left({\mathbf{L}}_B-\lambda \mathbf{I}\right)-k_{12}\left({\mathbf{L}}_B-\lambda \mathbf{I}\right)-k_{21}\left({\mathbf{L}}_A-\lambda \mathbf{I}\right)\right|\\ =\left|\left({\mathbf{L}}_A^{\prime }-\lambda \mathbf{I}\right)\left({\mathbf{L}}_B^{\prime }-\lambda \mathbf{I}\right)-k_{12}{k}_{21}\mathbf{I}\right|\\ =\left|\left({\mathbf{L}}_A^{\prime }{\mathbf{L}}_B^{\prime }-k_{12}{k}_{21}\mathbf{I}\right)-\lambda \left({\mathbf{L}}_A^{\prime }+{\mathbf{L}}_B^{\prime }\right)+{\lambda }^2\mathbf{I}\right|\\ =\left|\mathbf{I}-\lambda {\left({\mathbf{L}}_A^{\prime }{\mathbf{L}}_B^{\prime }-k_{12}{k}_{21}\mathbf{I}\right)}^{-1}\left({\mathbf{L}}_A^{\prime }+{\mathbf{L}}_B^{\prime }\right)+{\lambda }^2{\left({\mathbf{L}}_A^{\prime }{\mathbf{L}}_B^{\prime }-k_{12}{k}_{21}\mathbf{I}\right)}^{-1}\right|\\ =\left|\mathbf{I}-\lambda {\mathbf{Z}}^{-1}\mathbf{X}+{\lambda }^2{\mathbf{Z}}^{-1}\mathbf{Y}\right|\end{array}$$ (23)

in which

$${\mathbf{L}}_j^{\prime }={\mathbf{L}}_j-k_{jj}\mathbf{I}$$ (24)

$$\begin{array}{l}\mathbf{X}={\mathbf{L}}_A^{\prime }+{\mathbf{L}}_B^{\prime }\\ \mathbf{Y}=\mathbf{I}\\ \mathbf{Z}={\mathbf{L}}_A^{\prime }{\mathbf{L}}_B^{\prime }-k_{12}{k}_{21}\mathbf{I}\end{array}$$ (25)

The right-hand side of the last line of Eq. 23 now is the determinant of a matrix with dimension 3 × 3, rather than 6 × 6 as in the starting expression. As above, when λ is small in magnitude, the determinant can be expanded to first order in λ and solved to yield

$$R_{\mathit{ex}}=\frac{-\lambda }{{\sin }^2\theta }=\frac{-1}{{\sin }^2\theta \mathit{Tr}\left\{{\mathbf{Z}}^{-1}\mathbf{X}\right\}}$$ (26)

Substituting Eq. 25 into Eq. 26 yields:

$$R_{\mathit{ex}}=\frac{-\lambda }{{\sin }^2\theta }=\frac{-1}{{\sin }^2\theta \mathit{Tr}\left\{{\left({\mathbf{L}}_A^{\prime }{\mathbf{L}}_B^{\prime }-k_{12}{k}_{21}\mathbf{I}\right)}^{-1}\left({\mathbf{L}}_A^{\prime }+{\mathbf{L}}_B^{\prime }\right)\right\}}$$ (27)

as a first-order approximation and yields a result identical to that obtained from Eq. 11 and shown in Eq. 19.

Unlike Eq. 11, the determinant of the last line of Eq. 23 can be expanded to second order in λ to give

$$\begin{array}{l}0=\left|\mathbf{I}-\lambda {\mathbf{Z}}^{-1}\mathbf{X}+{\lambda }^2{\mathbf{Z}}^{-1}\mathbf{Y}\right|\\ =1-\lambda \mathit{Tr}\left\{{\mathbf{Z}}^{-1}\mathbf{X}\right\}+{\lambda }^2\mathit{Tr}\left\{{\mathbf{Z}}^{-1}\mathbf{Y}+{\mathbf{M}}_1\left({\mathbf{Z}}^{-1}\mathbf{X}\right)\right\}\end{array}$$ (28)

in which M₁(A) is the first minor of the matrix A. The Laguerre approximation of the root of Eq. 28 gives:

$$R_{\mathit{ex}}=\frac{-\lambda }{{\sin }^2\theta }=\frac{-1}{{\sin }^2\theta \left(\mathit{Tr}\left\{{\mathbf{Z}}^{-1}\mathbf{X}\right\}-\mathit{Tr}\left\{{\mathbf{Z}}^{-1}\mathbf{Y}+{\mathbf{M}}_1\left({\mathbf{Z}}^{-1}\mathbf{X}\right)\right\}/\mathit{Tr}\left\{{\mathbf{Z}}^{-1}\mathbf{X}\right\}\right)}$$ (29)

For two-site exchange schemes, X, Y and Z from Eq (25) are substituted into Eq. 29. This result can be expanded to show that this is an expression for two-site exchange identical to the second-order approximation of Miloushev and Palmer and is more accurate than Eqs. 8 or 11:

$$R_{\mathit{ex}}=\frac{p_A{p}_B\mathrm{\Delta }{\omega }^2{k}_{\mathit{ex}}}{{\omega }_A^2{\omega }_B^2/{\omega }_e^2+k_{\mathit{ex}}^2-{\sin }^2\theta p_A{p}_B\mathrm{\Delta }{\omega }^2\left\{1+\frac{2k_{\mathit{ex}}^2\left(p_A{\omega }_A^2+p_B{\omega }_B^2\right)}{{\omega }_A^2{\omega }_B^2+{\omega }_e^2{k}_{\mathit{ex}}^2}\right\}}$$ (30)

R_1ρ can be obtained by substituting R_ex from Eq. 30 into Eqs. 10 or 14. For a significantly large R_1ρ contribution at = 0 (for example, for large ω₁ or ${\mathrm{\Omega }}_A\approx \overline{\mathrm{\Omega }}$), Eq. 14 is preferred.

Three-site chemical exchange

We next consider the linear three-site exchange mechanism:

$$B\underset{k_{12}}{\overset{k_{21}}{\rightleftarrows }}A\underset{k_{31}}{\overset{k_{13}}{\rightleftarrows }}C$$ (31)

in which the evolution matrix has the form:

$$\mathbf{L}+\mathbf{K}=\left[\begin{array}{ccc}{\mathbf{L}}_A& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& {\mathbf{L}}_B& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& {\mathbf{L}}_C\end{array}\right]+\left[\begin{array}{ccc}-k_{12}-k_{13}& k_{21}& k_{31}\\ k_{12}& -k_{21}& 0\\ k_{13}& 0& -k_{31}\end{array}\right]\otimes \mathbf{I}$$ (32)

If p_A >> p_B and p_A >> p_C, then the N-site perturbation formalism of Trott and Palmer [12] yields the compact expression:

$$R_{1\rho }={\overline{R}}_1{\cos }^2\theta +{\overline{R}}_2{\sin }^2\theta +{\sin }^2\theta \left\{\frac{k_{12}{\left({\mathrm{\Omega }}_B-{\mathrm{\Omega }}_A\right)}^2}{k_{21}^2+{\omega }_B^2}+\frac{k_{13}{\left({\mathrm{\Omega }}_C-{\mathrm{\Omega }}_A\right)}^2}{k_{31}^2+{\omega }_C^2}\right\}$$ (33)

The first-order expressions for R_ex and R_1ρ are obtained by substituting Eq. 32 into Eqs. 10–14. For completeness, the average magnetization approach defines the matrix U for a three-site scheme as:

$$\mathbf{U}=\left[\begin{array}{ccc}1& 1& 1\\ p_2& -1+p_2& p_2\\ -p_2^2-p_1{p}_3-p_3^2& p_2(p_1-p_3)& p_1^2+p_2^2+p_1{p}_3\end{array}\right]$$ (34)

from which the average magnetization expression for R_1ρ is obtained from Eqs. 15–18. The resulting expanded first-order and average magnetization expressions are lengthy and not reproduced here.

In light of the above derivation for two-site exchange, the exchange matrix in Eq. 32 can be factored as:

$$\mathbf{K}=\left[\begin{array}{cc}\mathbf{I}& -\mathbf{I}\\ -\mathbf{I}& 0\\ 0& \mathbf{I}\end{array}\right]\left[\begin{array}{ccc}-k_{12}\mathbf{I}& k_{21}\mathbf{I}& \mathbf{0}\\ k_{13}\mathbf{I}& 0& -k_{31}\mathbf{I}\end{array}\right]=\mathbf{U}{\mathbf{V}}^T$$ (35)

By use of the matrix determinant lemma,

$$\begin{array}{l}0=\left|\mathbf{L}+\mathbf{K}-\lambda \mathbf{I}\right|=\left|{\mathbf{L}}_A-\lambda \mathbf{I}\right|\left|{\mathbf{L}}_B-\lambda \mathbf{I}\right|\left|{\mathbf{L}}_C-\lambda \mathbf{I}\right|\left|\mathbf{I}+{\mathbf{V}}^T\left({\left(\mathbf{L}-\lambda \mathbf{I}\right)}^{-1}\right)\mathbf{U}\right|\\ =\left|{\mathbf{L}}_A-\lambda \mathbf{I}\right|\left|{\mathbf{L}}_B-\lambda \mathbf{I}\right|\left|{\mathbf{L}}_C-\lambda \mathbf{I}\right|\\ \times \left|\left[\begin{array}{cc}\mathbf{I}-k_{21}{\left({\mathbf{L}}_B-\lambda \mathbf{I}\right)}^{-1}& \mathbf{0}\\ \mathbf{0}& \mathbf{I}-k_{31}{\left({\mathbf{L}}_C-\lambda \mathbf{I}\right)}^{-1}\end{array}\right]+\left[\begin{array}{cc}-k_{12}{\left({\mathbf{L}}_A-\lambda \mathbf{I}\right)}^{-1}& k_{12}{\left({\mathbf{L}}_A-\lambda \mathbf{I}\right)}^{-1}\\ k_{13}{\left({\mathbf{L}}_A-\lambda \mathbf{I}\right)}^{-1}& -k_{13}{\left({\mathbf{L}}_A-\lambda \mathbf{I}\right)}^{-1}\end{array}\right]\right|\end{array}$$ (36)

The second matrix on the last line of Eq. 36 can be factored as

$$\left[\begin{array}{cc}-k_{12}{\left({\mathbf{L}}_A-\lambda \mathbf{I}\right)}^{-1}& k_{12}{\left({\mathbf{L}}_A-\lambda \mathbf{I}\right)}^{-1}\\ k_{13}{\left({\mathbf{L}}_A-\lambda \mathbf{I}\right)}^{-1}& -k_{13}{\left({\mathbf{L}}_A-\lambda \mathbf{I}\right)}^{-1}\end{array}\right]=\left[\begin{array}{c}-k_{12}\mathbf{I}\\ k_{13}\mathbf{I}\end{array}\right]\left[\begin{array}{cc}{\left({\mathbf{L}}_A-\lambda \mathbf{I}\right)}^{-1}& -{\left({\mathbf{L}}_A-\lambda \mathbf{I}\right)}^{-1}\end{array}\right]$$ (37)

so that a second application of the matrix determinant lemma gives:

$$\begin{array}{l}0=\left|{\mathbf{L}}_A-\lambda \mathbf{I}\right|\left|{\mathbf{L}}_B-\lambda \mathbf{I}\right|\left|{\mathbf{L}}_C-\lambda \mathbf{I}\right|\left|\mathbf{I}-k_{21}{\left({\mathbf{L}}_B-\lambda \mathbf{I}\right)}^{-1}\right|\left|\mathbf{I}-k_{31}{\left({\mathbf{L}}_C-\lambda \mathbf{I}\right)}^{-1}\right|\\ \times \left|\mathbf{I}+\left[{\left({\mathbf{L}}_A-\lambda \mathbf{I}\right)}^{-1}-{\left({\mathbf{L}}_A-\lambda \mathbf{I}\right)}^{-1}\right]\left[\begin{array}{cc}{\left\{\mathbf{I}-k_{21}{\left({\mathbf{L}}_B-\lambda \mathbf{I}\right)}^{-1}\right\}}^{-1}& \mathbf{0}\\ \mathbf{0}& {\left\{\mathbf{I}-k_{31}{\left({\mathbf{L}}_C-\lambda \mathbf{I}\right)}^{-1}\right\}}^{-1}\end{array}\right]\right|\left[\begin{array}{c}-k_{12}\mathbf{I}\\ k_{13}\mathbf{I}\end{array}\right]\\ =\left|{\mathbf{L}}_B-\lambda \mathbf{I}\right|\left|{\mathbf{L}}_C-\lambda \mathbf{I}\right|\left|\mathbf{I}-k_{21}{({\mathbf{L}}_B-\lambda \mathbf{I})}^{-1}\right|\left|\mathbf{I}-k_{31}{({\mathbf{L}}_C-\lambda \mathbf{I})}^{-1}\right|\\ \times \left|\left({\mathbf{L}}_A-\lambda \mathbf{I}\right)-k_{12}{\left\{\mathbf{I}-k_{21}{({\mathbf{L}}_B-\lambda \mathbf{I})}^{-1}\right\}}^{-1}-k_{13}{\left\{\mathbf{I}-k_{31}{\left({\mathbf{L}}_C-\lambda \mathbf{I}\right)}^{-1}\right\}}^{-1}\right|\\ =|({\mathbf{L}}_B-\lambda \mathbf{I}-k_{21}\mathbf{I})({\mathbf{L}}_A-\lambda \mathbf{I})({\mathbf{L}}_C-\lambda \mathbf{I}-k_{31}\mathbf{I})\\ -k_{12}({\mathbf{L}}_B-\lambda \mathbf{I})({\mathbf{L}}_C-\lambda \mathbf{I}-k_{31}\mathbf{I})-k_{13}({\mathbf{L}}_B-\lambda \mathbf{I}-k_{21}\mathbf{I})({\mathbf{L}}_C-\lambda \mathbf{I})|\end{array}$$ (38)

The determinant of the 9 × 9 original Bloch-McConnell matrix has now been reduced to the determinant of a 3 × 3 matrix, once again. The products are expanded to obtain a polynomial in λ:

$$\begin{array}{l}0=|{\mathbf{L}}_B^{\prime }{\mathbf{L}}_A^{\prime }{\mathbf{L}}_C^{\prime }-k_{13}{k}_{31}{\mathbf{L}}_B^{\prime }-k_{12}{k}_{21}{\mathbf{L}}_C^{\prime }\\ -\lambda \left({\mathbf{L}}_B^{\prime }{\mathbf{L}}_A^{\prime }+{\mathbf{L}}_A^{\prime }{\mathbf{L}}_C^{\prime }+{\mathbf{L}}_B^{\prime }{\mathbf{L}}_C^{\prime }-\left\{k_{12}{k}_{21}+k_{13}{k}_{31}\right\}\right)\\ +{\lambda }^2\left({\mathbf{L}}_B^{\prime }+{\mathbf{L}}_A^{\prime }+{\mathbf{L}}_C^{\prime }\right)-{\lambda }^3\mathbf{I}|\end{array}$$ (39)

Keeping only the two lowest-order terms, we immediately obtain first- and second-order approximations by substituting X, Y and Z into Eqs. 26 and 29:

$$\begin{array}{l}\mathbf{X}=\left({\mathbf{L}}_B^{\prime }{\mathbf{L}}_A^{\prime }+{\mathbf{L}}_A^{\prime }{\mathbf{L}}_C^{\prime }+{\mathbf{L}}_B^{\prime }{\mathbf{L}}_C^{\prime }-\{k_{12}{k}_{21}+k_{13}{k}_{31}\}\right)\\ \mathbf{Y}=\left({\mathbf{L}}_B^{\prime }+{\mathbf{L}}_A^{\prime }+{\mathbf{L}}_C^{\prime }\right)\\ \mathbf{Z}=\left(|{\mathbf{L}}_B^{\prime }{\mathbf{L}}_A^{\prime }{\mathbf{L}}_C^{\prime }-k_{13}{k}_{31}{\mathbf{L}}_B^{\prime }-k_{12}{k}_{21}{\mathbf{L}}_C^{\prime }\right)\end{array}$$ (40)

The first-order approximation is identical to that obtained from Eq. 11.

Four-site chemical exchange

The four-site linear kinetic scheme is

$$B\underset{k_{12}}{\overset{k_{21}}{\rightleftarrows }}A\underset{k_{31}}{\overset{k_{13}}{\rightleftarrows }}C\underset{k_{43}}{\overset{k_{34}}{\rightleftarrows }}D$$ (41)

The exchange matrix again is factorizable:

$$\begin{array}{l}\mathbf{K}=\left[\begin{array}{cccc}-k_{12}-k_{13}& k_{21}& k_{31}& 0\\ k_{12}& -k_{21}& 0& 0\\ k_{13}& 0& -k_{31}-k_{34}& k_{43}\\ 0& 0& k_{34}& -k_{43}\end{array}\right]\otimes \mathbf{I}\\ =\left[\begin{array}{ccc}\mathbf{I}& -\mathbf{I}& 0\\ -\mathbf{I}& 0& 0\\ 0& \mathbf{I}& -\mathbf{I}\\ 0& 0& \mathbf{I}\end{array}\right]\left[\begin{array}{cccc}-k_{12}\mathbf{I}& k_{21}\mathbf{I}& 0& 0\\ k_{13}\mathbf{I}& 0& -k_{31}\mathbf{I}& 0\\ 0& 0& k_{34}\mathbf{I}& -k_{43}\mathbf{I}\end{array}\right]=\mathbf{U}{\mathbf{V}}^T\end{array}$$ (42)

As shown in Supplemental Material I (Eqs. S1–S5), three successive applications of the matrix determinant lemma again reduces the 12 × 12 dimensional problem to the determinant of a 3 × 3 matrix, yielding:

$$\begin{array}{l}\mathbf{X}={\mathbf{L}}_B^{\prime }{\mathbf{L}}_A^{\prime }{\mathbf{L}}_C^{\prime }+{\mathbf{L}}_B^{\prime }{\mathbf{L}}_A^{\prime }{\mathbf{L}}_D^{\prime }+{\mathbf{L}}_B^{\prime }{\mathbf{L}}_C^{\prime }{\mathbf{L}}_D^{\prime }+{\mathbf{L}}_A^{\prime }{\mathbf{L}}_C^{\prime }{\mathbf{L}}_D^{\prime }\\ -(k_{13}{k}_{31}+k_{34}{k}_{43}){\mathbf{L}}_B^{\prime }-k_{34}{k}_{43}{\mathbf{L}}_A^{\prime }-k_{12}{k}_{21}{\mathbf{L}}_C^{\prime }-(k_{12}{k}_{21}+k_{13}{k}_{31}){\mathbf{L}}_D^{\prime }\\ \mathbf{Y}={\displaystyle \sum _{\underset{j>i}{i,j}}{\mathbf{L}}_i^{\prime }{\mathbf{L}}_j^{\prime }-k_{12}{k}_{21}-k_{13}{k}_{31}}-k_{34}{k}_{43}\\ \mathbf{Z}={\mathbf{L}}_B^{\prime }{\mathbf{L}}_A^{\prime }{\mathbf{L}}_C^{\prime }{\mathbf{L}}_D^{\prime }-k_{34}{k}_{43}{\mathbf{L}}_B^{\prime }{\mathbf{L}}_A^{\prime }-k_{13}{k}_{31}{\mathbf{L}}_B^{\prime }{\mathbf{L}}_D^{\prime }-k_{12}{k}_{21}{\mathbf{L}}_C^{\prime }{\mathbf{L}}_D^{\prime }+k_{12}{k}_{21}{k}_{34}{k}_{43}\end{array}$$ (43)

which can be substituted into Eqs. 26 and 29 to give the first- and second-order expressions for λ.

Triangular and more complex kinetic schemes

The triangular (all-with-all) three-site kinetic scheme has the kinetic matrix:

$$\begin{array}{l}\mathbf{K}=\left[\begin{array}{ccc}-k_{12}-k_{13}& k_{21}& k_{31}\\ k_{12}& -k_{21}-k_{23}& k_{32}\\ k_{13}& k_{23}& -k_{31}-k_{32}\end{array}\right]\otimes \mathbf{I}\\ =\left[\begin{array}{ccc}-k_{12}-k_{13}& k_{21}& k_{31}\\ k_{12}& -k_{21}& 0\\ k_{13}& 0& -k_{31}\end{array}\right]\otimes \mathbf{I}+\left[\begin{array}{ccc}0& 0& 0\\ 0& -k_{23}& k_{32}\\ 0& k_{23}& -k_{32}\end{array}\right]\otimes \mathbf{I}\\ ={\mathbf{K}}_0+\left[\begin{array}{c}\mathbf{0}\\ \mathbf{I}\\ -\mathbf{I}\end{array}\right]\left[\begin{array}{ccc}\mathbf{0}& -k_{23}\mathbf{I}& k_{32}\mathbf{I}\end{array}\right]={\mathbf{K}}_0+\mathbf{U}{\mathbf{V}}^T\end{array}$$ (44)

in which K₀ is the kinetic rate matrix for the linear system. The first-order approximation of the eigenvalue according to Eq. 11 is then:

$$-\lambda ={\sin }^2\theta R_{\mathit{ex}}=-1/\mathit{Tr}\left\{{\left(\mathbf{L}+\mathbf{K}\right)}^{-1}\right\}=-1/\mathit{Tr}\left\{{\left(\mathbf{L}+{\mathbf{K}}_0+\mathbf{U}{\mathbf{V}}^T\right)}^{-1}\right\}$$ (45)

Additional insight is obtained by using the factorization of the matrix K. The Woodbury formula for the matrix inverse gives the result:

$$\begin{array}{l}-\lambda ={\sin }^2\theta R_{\mathit{ex}}=-1/\mathit{Tr}\left\{{\left(\mathbf{L}+{\mathbf{K}}_0\right)}^{-1}-\mathbf{Z}\right\}=-1/\left[\mathit{Tr}\left\{{\left(\mathbf{L}+{\mathbf{K}}_0\right)}^{-1}\right\}-\mathit{Tr}\left\{\mathbf{Z}\right\}\right]\\ =\frac{1}{\mathit{Tr}\left\{{\left(\mathbf{L}+{\mathbf{K}}_0\right)}^{-1}\right\}}\left[\frac{1}{1-\mathit{Tr}\left\{\mathbf{Z}\right\}/\mathit{Tr}\left\{{\left(\mathbf{L}+{\mathbf{K}}_0\right)}^{-1}\right\}}\right]\end{array}$$ (46)

in which

$$\mathbf{Z}={\left(\mathbf{L}+{\mathbf{K}}_0\right)}^{-1}\mathbf{U}{\left(\mathbf{I}+{\mathbf{V}}^T{\left(\mathbf{L}+{\mathbf{K}}_0\right)}^{-1}\mathbf{U}\right)}^{-1}{\mathbf{V}}^T{\left(\mathbf{L}+{\mathbf{K}}_0\right)}^{-1}$$ (47)

Therefore, the first-order approximation for the triangular state is:

$$R_{\mathit{ex}}^{\mathit{triang},\mathit{first}}=R_{\mathit{ex}}^{\mathit{linear},\mathit{first}}\left[\frac{1}{1+{\sin }^2\theta R_{\mathit{ex}}^{\mathit{linear},\mathit{first}}\mathit{Tr}\left\{\mathbf{Z}\right\}}\right]$$ (48)

using only the first-order approximation of R_ex for the linear system. If exchange between sites B and C (not part of the linear fragment) is slow, compared to exchange with site A, then the simplification

$$\mathit{Tr}\left\{\mathbf{Z}\right\}=\mathit{Tr}\left\{{\mathbf{V}}^T{\left(\mathbf{L}+{\mathbf{K}}_0\right)}^{-2}\mathbf{U}\right\}$$ (49)

is obtained; this is the “weak minor site exchange” limit [12].

As shown in Supplemental Material II (Eqs. S6–S15), the modified expression:

$$R_{\mathit{ex}}^{\mathit{triang},\mathit{Woodbury}}=R_{\mathit{ex}}^{\mathit{linear},\mathit{second}}\left[\frac{1}{1+{\sin }^2\theta R_{\mathit{ex}}^{\mathit{linear},\mathit{first}}\mathit{Tr}\left\{\mathbf{Z}\right\}}\right]$$ (50)

which is called Woodbury approximation herein, leads to increased accuracy if the boundary condition

$$2\frac{R_{\mathit{ex}}^{\mathit{triang},\mathit{first}}}{R_{\mathit{ex}}^{\mathit{triang},\mathit{exact}}}\le \frac{R_{\mathit{ex}}^{\mathit{linear},\mathit{first}}}{R_{\mathit{ex}}^{\mathit{linear},\mathit{second}}}+1$$ (51)

is satisfied. However, replacing both first-order approximation terms for the linear system with second-order approximations is not as accurate. The boundary condition implies that high accuracy of the linear approximations relative to that of the triangular first-order approximation yields a more accurate Woodbury approximation.

More complex kinetic schemes are also accessible using this approach because the Woodbury formula can be use in a nested manner:

$$\begin{array}{l}{\sin }^2\theta R_{\mathit{ex}}=-1/\mathit{Tr}\left\{{\left(\mathbf{L}+{\mathbf{K}}_0+{\mathbf{U}}_1{\mathbf{V}}_1^T+{\mathbf{U}}_2{\mathbf{V}}_2^T\right)}^{-1}\right\}\\ =-1/\left[\mathit{Tr}\left\{{\left(\mathbf{L}+{\mathbf{K}}_0\right)}^{-1}\right\}-\mathit{Tr}\left\{{\mathbf{Z}}_1\right\}-\mathit{Tr}\left\{{\mathbf{Z}}_2\right\}\right]\\ =\frac{-1}{\mathit{Tr}\left\{{\left(\mathbf{L}+{\mathbf{K}}_0\right)}^{-1}\right\}}\left[\frac{1}{1-\mathit{Tr}\left\{{\mathbf{Z}}_1+{\mathbf{Z}}_2\right\}/\mathit{Tr}\left\{{\left(\mathbf{L}+{\mathbf{K}}_0\right)}^{-1}\right\}}\right]\\ {\mathbf{Z}}_1={\left(\mathbf{L}+{\mathbf{K}}_0\right)}^{-1}{\mathbf{U}}_1{\left(\mathbf{I}+{\mathbf{V}}_1^T{\left(\mathbf{L}+{\mathbf{K}}_0\right)}^{-1}{\mathbf{U}}_1\right)}^{-1}{\mathbf{V}}_1^T{\left(\mathbf{L}+{\mathbf{K}}_0\right)}^{-1}\\ {\mathbf{Z}}_2=\left[{\left(\mathbf{L}+{\mathbf{K}}_0\right)}^{-1}+{\mathbf{Z}}_1\right]{\mathbf{U}}_2{\left(\mathbf{I}+{\mathbf{V}}_2^T\left[{\left(\mathbf{L}+{\mathbf{K}}_0\right)}^{-1}+{\mathbf{Z}}_1\right]{\mathbf{U}}_2\right)}^{-1}{\mathbf{V}}_2^T\left[{\left(\mathbf{L}+{\mathbf{K}}_0\right)}^{-1}+{\mathbf{Z}}_1\right]\end{array}$$ (52)

Therefore, the Woodbury approximation for complex kinetic schemes is

$$R_{\mathit{ex}}^{\mathit{Woodbury}}=R_{\mathit{ex}}^{\mathit{linear},\mathit{second}}\left[\frac{1}{1+{\sin }^2\theta R_{\mathit{ex}}^{\mathit{linear},\mathit{first}}\mathit{Tr}\{{\mathbf{Z}}_1+{\mathbf{Z}}_2\}}\right]$$ (53)

The same boundary condition as above applies. In using the Woodbury approximation, K can only be replaced by K₀ + UV^T if the number of sites in K₀ and K are identical. An example for a scheme where this is not immediately possible would be the star four-site scheme (three minor sites in exchange with one central major site). However, minimally occupied pseudo-sites that rapidly exchange with a site with an identical offset can be introduced as necessary (vide infra).

Results

The accuracy of the above theoretical expressions for the R_1ρ relaxation rate constant was tested for selected values of the model parameters for two-, three-, and four-site kinetic schemes. Illustrative results are presented in Figures 1–3, respectively and additional figures are given in Supplemental Information.

Figure 1.

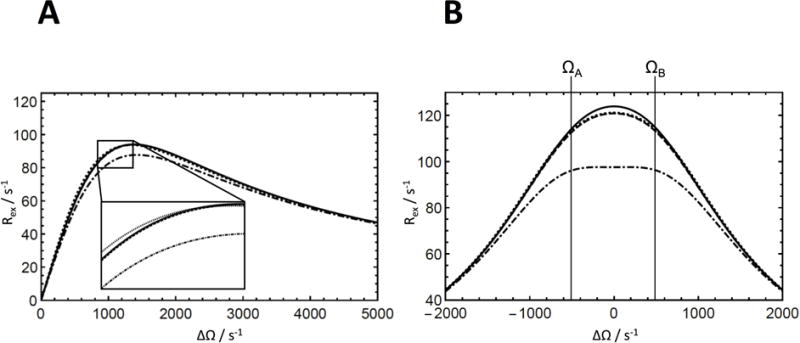
Approximations to the R_ex contribution to R_1ρ for two-site chemical exchange. (Solid) Numerical calculation of R_ex = −λ/sin²θ from the least negative real eigenvalue of the 6 × 6 evolution matrix, (dashed) calculation from the second-order approximation from Eqs. 25 and 29, (dotted) calculation from the average magnetization approximation from Eq. 30, (dashed-dotted) calculation from the first-order approximation from Eq. 11, which is equivalent to Eq. 19. The inset exemplifies regions in which the results of the calculations differ. (a) Exchange rate, k_ex = k₁₂+k₂₁, dependence of the R_ex contribution to R_1ρ. Parameters used for the calculation were p_A = 0.5, p_B = 0.5, ω₁ = 1000 s⁻¹, Ω_B − Ω_A = 1000 s⁻¹, and Ω = 1000 s⁻¹. (b) Offset dependence of the R_ex contribution to R_1ρ. Parameters used for the calculations were p_A = 0.5, p_B = 0.5, ω₁ = 1000 s⁻¹, Ω_B − Ω_A = 1000 s⁻¹, and k_ex = k₁₂ + k₂₁ = 1000 s⁻¹.

Figure 3.

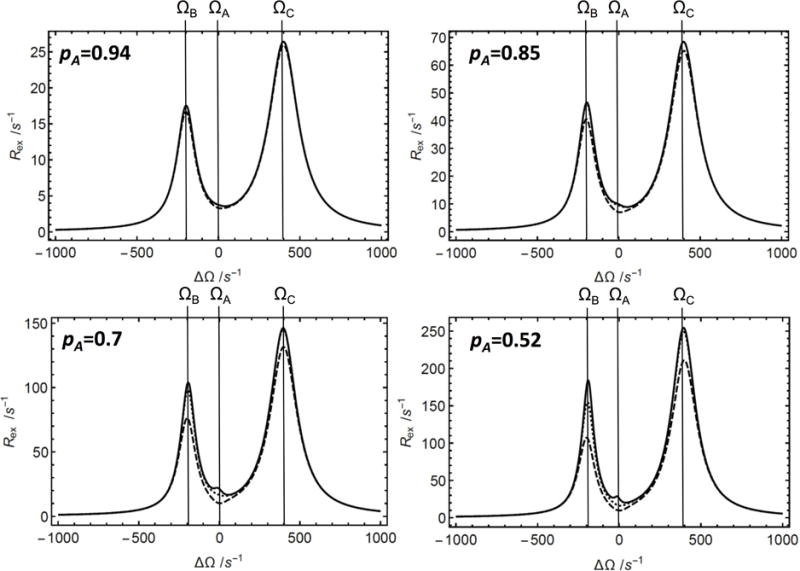
Offset dependence of the R_ex contribution to R_1ρ for linear three-site exchange for varying major populations in the weak field limit (p_A = 0.94, p_A = 0.85, p_A = 0.7 and p_A = 0.52, as indicated). (Solid) Numerical calculation of R_ex = −λ/sin² θ from the least negative real eigenvalue of the 9 × 9 evolution matrix, (dashed) calculation from the first-order approximation from Eq. 11, and (dotted) calculation from the second-order approximation from Eqs. 29 and 40. The inset exemplifies a region in which the results of the calculations differ. To center the graph, parameters were chosen so that δ_A = ΔΩ. Parameters used for the calculations were p_B = 2(1− p_A)/3, p_C = (1−p_A)/3, k₁₂+k₂₁ = 50 s⁻¹, k₁₃ +k₃₁ = 100 s⁻¹, ω₁ = 50 s⁻¹, Ω_B − Ω_A = 200 s⁻¹, and Ω_C − Ω_A = −400 s⁻¹.

The dependence of the R_ex contribution to R_1ρ on the chemical exchange rate constant k_ex = k₁₂ + k₂₁ and on the rf frequency offset for two-site exchange is illustrated in Figure 1 for the extreme case with p_A = p_B = 0.5. The accuracy of the expressions increases from the first-order result (Eqs. 11 or 19), to the average magnetization result (Eq. 20), and to the second-order Laguerre result (Eqs. 29 or 30). These results are consistent with those obtained in the original publications describing these theoretical expressions [10, 13, 14].

For the example presented in Fig. 1, the largest negative eigenvalue dominates the inverses of the other eigenvalues, as illustrated in Figure S1. However, the first-order approximations given in Eqs. 8, 10 and 14 differ in the treatment of relaxation by mechanisms other than chemical exchange. If the values of R_2j vary substantially between sites, Eqs. 8 or 10 are more accurate than Eq. 14. Equation 14 is more accurate than Eqs. 8 or 10 if $R_{2j}\approx {\overline{R}}_2$ or for a significantly large R_1ρ contribution at = 0 (for example, for large ω₁ or ${\mathrm{\Omega }}_A\approx \overline{\mathrm{\Omega }}$). Furthermore, as shown in the example in Figure 2, the higher powers of R that contribute to Eq. 8 reduce accuracy slightly compared to the truncated first-order expression of Eq. 10. Thus, Eqs. 10 or 14 are the preferred first-order approximations for practical use.

Figure 2.

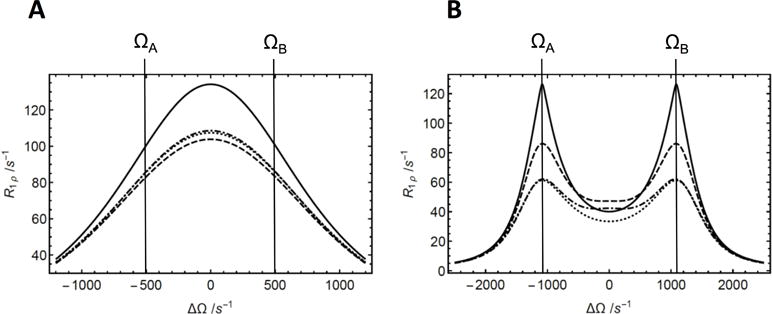
Approximations of R_1ρ for two-site chemical exchange. (a) (Solid) Numerical calculation of the least negative real eigenvalue of the 6 × 6 evolution matrix, (dashed) calculation from the first-order (in) approximation, based on L + K + R (Eq. 8); (dotted) calculation from the first-order (in) approximation, based on L + K + R, and truncated to first order in R (Eq. 10), as also previously provided by Trott and Palmer [10] and Baldwin and Kay [11]; (dashed-dotted) calculation from the first-order approximation, based on L + K (Eq. 14). Parameters used for the calculations were R₁ = 1.5 s⁻¹, R₂ = 11 s⁻¹, p_A = 0.5, p_B = 0.5, ω₁ = 1000 s⁻¹, Ω_B − Ω_A = 1000 s⁻¹, and k_ex = k₁₂ + k₂₁ = 1000 s⁻¹. (b) (solid) Numerical calculation of the least negative real eigenvalue of the 6 × 6 evolution matrix; (dashed) calculation from the second-order approximation from Eqs. 14, 25 and 29; (dotted) calculation from the first-order (in) approximation, based on L + K + R (Eq. 8); (dashed-dotted) calculation from the first-order approximation, based on L + K (Eq. 14). Parameters used for the calculations were R₁ = 1.5 s⁻¹, R₂ = 11 s⁻¹, p_A = 0.5, p_B = 0.5, ω₁ = 500 s⁻¹, Ω_B − Ω_A = 2400 s⁻¹, and k_ex = k₁₂ + k₂₁ = 250 s⁻¹.

The dependence on the rf frequency offset of the R_ex contribution to R_1ρ is shown in Figure 3 and Supplemental Information Figures S2 – S4 for a linear three-site kinetic scheme. Results are shown for values of ω₁ between 50 s⁻¹, which corresponds to values that would be used in CEST experiments, to 1250 s⁻¹, which corresponds to values that would be used in relaxation dispersion experiments. As shown previously using the N-site perturbation approach [12], local maxima in R_ex (which would correspond to local minima in CEST experiments) are obtained when the rf frequency is resonant with the frequencies of the sparsely populated states. The widths of the profiles around the local maxima depend on the kinetic rate constants and the strength of the ω₁ field [12]. Consequently, in the fast-exchange limit, discrimination between sites becomes increasingly difficult; in this limit, R_ex depends only on the offset relative to the average chemical shift (Figure S2). Congruent with the results for two-site exchange, the second-order results are more accurate than the first-order ones. However, as shown in Figures 3 and S3, for skewed populations, the main region of difference between results for first- and second-order approximations is near resonance with the major species. Both first- and second-order expressions for R_ex become less accurate as the site populations become less highly skewed (Fig. 2). The second-order approximation for R_ex is also accurate when the time scales of the two exchange regimes in the three-site linear kinetic scheme are distinct (k₁₂+k₂₁ = 200 s⁻¹, k₁₃+k₃₁ = 5000 s⁻¹, Figure S3).

Not only for first-order approximations, but also for the other approximations introduced herein, R_1ρ is in practice best obtained from R_ex by adding R_eff (from Eqs. 12 or 13) to sin²θ R_ex. Figure S4 compares various second-order approximations for R_1ρ, exemplified for the linear three-state kinetic scheme. R_ex is obtained from Eqs. 29 and 40, and then substituted into either Eq. 10 or Eq. 14. In order to include terms that are of higher order in R, a second order approximation based on L + R + K, rather than L + R, was also used by replacing ${\mathbf{L}}_k^{\prime }$ with ${\mathbf{L}}_k^{\prime }+\mathbf{R}$ in Eq. 40. Eq. 14 is more accurate if the values of R_2k do not vary substantially between sites and if the R_1ρ contribution at = 0 is large. Such large R_1ρ is obtained for higher amplitude ω₁ fields, much higher population of the dominant site, or $\overline{\mathrm{\Omega }}\approx {\mathrm{\Omega }}_A$. Eq. 10 is more accurate in most other cases. Using an untruncated second-order approximation based on L + R + K, which does not use R_eff and includes higher-order R terms, usually is not more accurate than the second-order R_1ρ approximations from Eqs. 10, 29 and 40. The second-order approximation from Eqs. 11, 29 and 40 is accurate even if no major population is present (Fig. S4, p_A = p_B = p_C = 0.33); however, accuracy is lower than that obtained if one population is dominant. The assumption that R_1ρ is identical to the largest negative eigenvalue will obtain only with the appropriate combination of other parameters, as discussed above. In the given example, the contribution of the largest negative eigenvalue to the magnetization decay t = 0 s and = 0 s⁻¹ is only 83%, mostly due the presence of negative complex eigenvalues (using Eq. 6, similar to Fig. S1).

The dependence of the R_ex contribution to R_1ρ on the rf frequency offset is shown in Figure 4 for a linear four-site kinetic scheme, a four-site star-like scheme, and a four-site kite-like scheme with one dominant site population p_A = 0.90 in all cases. As above, results are shown for values of ω₁ between 50 s⁻¹ and 1250 s⁻¹. The values of R_ex are very sensitive to the presence or absence of kinetic exchange between two minor sites, as illustrated in Figure 4 by comparing the star-like and kite-like topologies. In addition, as previously noted [12], fast averaging within a subset of sites can lead to a R_ex profile with an apparent reduction in the number of discernable “effective sites”. This phenomenon is frequently of practical importance in reducing N-site kinetic schemes to simpler apparent topologies. For example, in studies of protein folding, fast averaging amongst conformations in the unfolded ensemble allows a two-state-like description of exchange between a folded and a “random-coil-like” effective unfolded state [21]. As another example, fast averaging amongst side chain rotameric states with different populations (a 2M-site model in which M is the number of rotamers) results in an effective two-state-like model termed population-shuffling [8].

Figure 4.

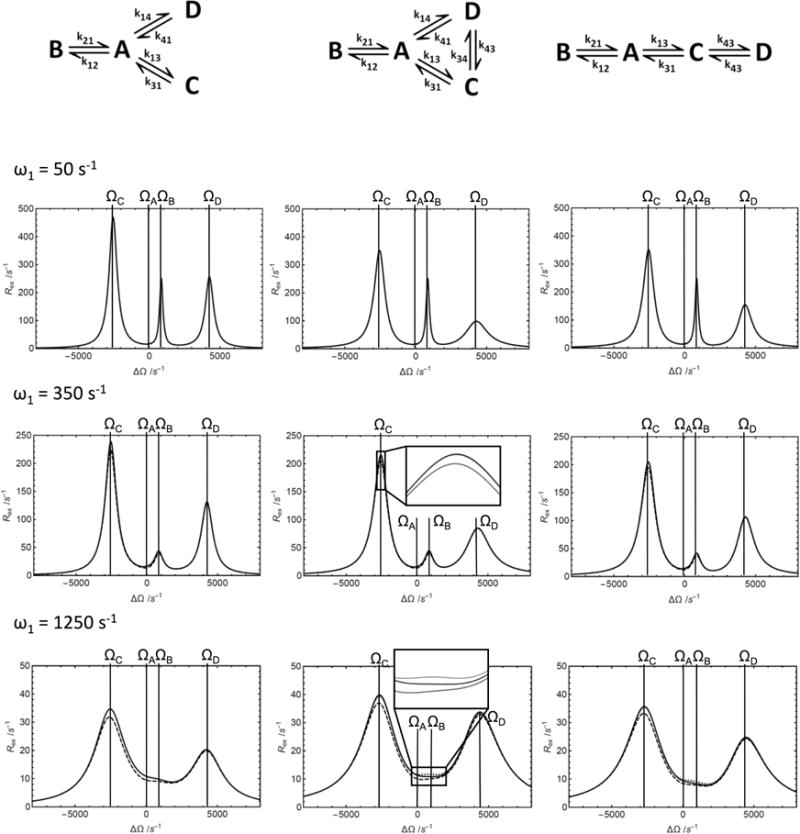
Approximations of the R_ex contribution to R_1ρ for 4-state chemical exchange schemes. Three different kinetic situations (illustrations at the top of the columns) have been analyzed, star-like four-state scheme (left column), kite-like four-state scheme (middle column), linear four-state scheme (right column). The calculations have been performed at the different irradiating fields, ω₁ = 50 s⁻¹ (top row), ω₁ = 500 s⁻¹ (middle row), ω₁ = 1250 s⁻¹ (bottom row). (Solid) Numerical calculation of R_ex = −λ/sin²θ from the least negative real eigenvalue of the 12 × 12 evolution matrix, (dashed) calculation from the first order approximation from Eq. 11, (dotted, linear scheme) calculation from the second-order approximation from Eqs. 29 and 40, (dotted, kite scheme) calculation from the Woodbury approximation from Eq. 50. The insets exemplify regions in which the results of the calculations differ. To center the graph, parameters were chosen so that δ_A = ΔΩ. Parameters used for all calculations were p_A = 0.95, p_B = 0.05, p_C = 0.025, p_D = 0.005, k₁₂+k₂₁ = 140 s⁻¹, k₁₃+k₃₁ = 350 s⁻¹, Ω_B − Ω_A = −850 s⁻¹, Ω_C − Ω_A = 2550 s⁻¹, and Ω_D − Ω_A = −4250 s⁻¹. Additional parameters used depending on exchange scheme: k₃₄+k₄₃ = 700 s⁻¹ and k₁₄+k₄₁ = 350 s⁻¹.

The Woodbury approximation can be used to obtain improved estimates of R_ex for complex N-site schemes by combining second- and first-order linear N-site approximations with coupling factors for the nonlinear interchanges between sites. The Woodbury approximation is often, but not always more accurate than the first-order expression, which is exemplified by R_ex profiles for the triangular three-state scheme (Figure S5). The values of the kinetic rate constants for the non-linear part of the scheme changes the relative accuracy of the two approximations. The accuracy of the Woodbury approximation also depends on which components of the kinetic scheme are chosen as the linear fragment, as demonstrated for the triangular three-state scheme (Figure 5). Excluding the slowest exchange process in the scheme from the linear fragment leads to the highest accuracy of the Woodbury approximation. If this exchange process is much slower than the processes in the linear fragment, the Woodbury approximation can be reduced further using Eq. 49. In the example given for the kite-like four-state scheme (Figure 4), the Woodbury approximation from Eq. 50 is more accurate than the first-order approximation. The Woodbury approximation also is accurate when the populations are not skewed (Figure S6). The possibility to substitute any N-site linear scheme by an (N+1)-site scheme is illustrated for the triangular scheme in Figure S7. This gives access to Woodbury approximations for N-site schemes from which a N-site linear sub-scheme cannot be readily extracted.

Figure 5.

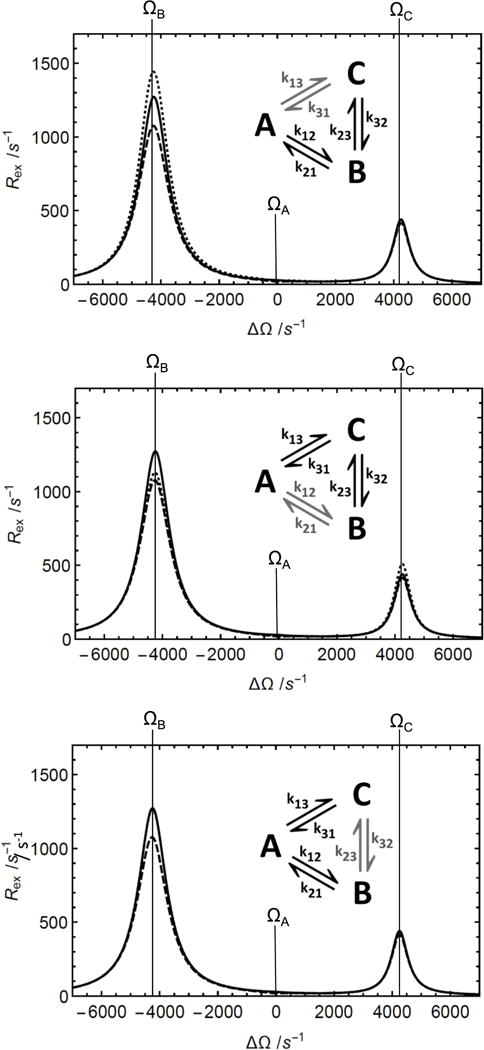
The Woodbury approximation of the R_ex contribution to R_1ρ in the triangular three-state chemical exchange situation depends on how the linear fragment for the approximation is chosen. (Solid) Numerical solution of R_ex = −λ/sin²θ from the least negative real eigenvalue of the 9 × 9 evolution matrix, (dashed) first-order approximation (Eq. 11) and (dotted) Woodbury approximation (Eq. 50). To center the graph, parameters were chosen so that δ_A = ΔΩ. Parameters used for all calculations were p_A = 0.9, p_B = 0.05, p_C = 0.05, k₁₂ +k₂₁ = 500 s⁻¹, k₁₃+k₃₁ = 50 s⁻¹, k₂₃+k₃₂ = 20 s⁻¹, ω₁= 350 s⁻¹, Ω_B − Ω_A = 4250 s⁻¹, and Ω_C − Ω_A = −4250 s⁻¹. The kinetic scheme is shown in each panel (black: linear fragment; grey: non-linear fragment). Linear fragments are (top) A-B-C, (middle) A-C-B, (bottom) C-A-B. The Woodbury approximation fits best when the slowest exchange process is chosen as the nonlinear fragment.

Discussion and Conclusion

The perturbation approach of Trott and Palmer [12] provides simple closed-form approximations for R_1ρ when the population of one site is much greater than the populations of the others (typically p_A > 0.90, depending on other parameters). The main result obtained herein is a first-order approximation of R_1ρ for any kinetic scheme. For linear kinetic schemes, the matrix determinant lemma can be used to reduce the determinant of the 3N × 3N Bloch-McConnell matrix to the determinant of a 3 × 3 matrix polynomial. This latter approach leads to both first- and second-order approximations of R_1ρ. The first-order expressions of Eqs. 8, and 10 and the second-order expressions of Eq. 29 for linear chains are more accurate than the expressions obtained from the perturbation approach when the population of the major state is less dominant. The first-order approximation of the eigenvalue of the evolution matrix for the average magnetization (Eq. 18) yields expressions for R_1ρ that have accuracies between the first- and second-order expressions. For these and other N-site kinetic schemes, the first-order analysis described above in Eq. 10 frequently provides analytical solutions that are accurate enough to differentiate between different kinetic scenarios provided that the site populations are skewed. Expansion of matrix trace expressions or inverse operations in these equations is not required for use in fitting procedures, as illustrated in Supplemental Material III (Eqs. S16–S23).

The above procedure based on the matrix determinant lemma can be extended to even longer N-site linear chains; however, the resulting second order expressions are increasingly complex and little insight is gained over the first-order expression of Eq. 10. The theoretical approach presented for determining a second-order approximation for R_1ρ from a reduced 3 × 3 matrix yields convenient results only for linear chains. The triangular three-site exchange mechanism and the four-site kite mechanism (Figure 4) have exchange matrices that do not permit factorization to a useful form for application of the matrix determinant lemma. The four-site star mechanism (Figure 4) has an exchange matrix with a simple factorization, but commutation properties of the matrices (L_j − λ) prevent needed simplifications as obtained for linear chains.

A combination of first- and second-order R_1ρ approximations for linear schemes can be used to approximate R_1ρ for non-linear schemes. This approximation is obtained by the Woodbury decomposition of the inverse of the matrix L + K and can in principle be obtained for (almost) any kinetic scheme. However, the accuracy of the Woodbury approximation depends on the particular decomposition of the kinetic scheme and on the relative contributions of the various components that contribute to R_ex. The best Woodbury approximation is obtained if the slowest exchange processes are not included in the linear fragment; the accuracy of the Woodbury approximation is comparably high also for unskewed populations.

In conclusion, a remarkably simple first-order analytic approximation to the R_1ρ relaxation rate constant is obtained from the trace of the inverse of the Bloch-McConnell evolution matrix for N-site chemical exchange with arbitrary topology. For linear chains, second-order approximations of higher accuracy also are derived by application of the matrix determinant lemma. Second-order solutions for linear schemes can be used in many circumstances to increase the accuracy of expressions for R_1ρ in related non-linear kinetic schemes. The present results extend existing results for two-state chemical exchange to complex kinetic schemes and will be powerful in interpretation of numerous spin-locking NMR experiments.

Highlights.

• Analytical expressions for the R_1ρ relaxation rate for arbitrary kinetic schemes

• Expressions for R_1ρ with increased accuracy for linear N-site kinetic schemes

• Examples for linear, triangular three-site, kite- and star-like kinetic mechanisms