CHARMM36m: An Improved Force Field for Folded and Intrinsically Disordered Proteins

Abstract

The all-atom additive CHARMM36 protein force field is widely used in molecular modeling and simulations. We present its refinement, CHARMM36m (http://mackerell.umaryland.edu/charmm_ff.shtml), with improved accuracy in generating polypeptide backbone conformational ensembles for intrinsically disordered peptides and proteins.

There is increasing interest in intrinsically disordered peptides and proteins (IDPs) due to their abundance and functional importance in eukaryotes, as well as their association with various human disorders ranging from cancer to neurodegenerative diseases. Rather than folding into a single, well-defined three-dimensional structure, an IDP fluctuates between an ensemble of interconverting conformational states, which allows some IDPs to interact with several different binding partners, thereby functioning in protein-protein interaction networks.¹ Experimental characterization of conformational ensembles of IDPs is challenging; assistance from computer simulations is often needed, as the number of degrees of freedom of an IDP far exceed the number of available experimental observables.² Recent advances in hardware and software allow molecular simulations to reach relevant timescales for sampling IDP conformations, but a major limiting factor lies in the accuracy of their underlying models, typically empirical force fields (FFs).³ Protein FFs were mostly developed targeting folded proteins and their accuracy in modeling IDPs needs to be scrutinized and improved.^4-6

In a recent benchmark study on the structural ensembles of a disordered arginine/serine (RS) peptide obtained with different force fields, the CHARMM36 (C36) protein FF⁷ was found to generate a high population of left-handed α-helix (α_L), inconsistent with nuclear magnetic resonance (NMR) and small-angle X-ray scattering (SAXS) experimental measurements. We now present an improved C36 FF based on a refined backbone CMAP potential⁸ derived from reweighting calculation (Online Methods) and a better description of specific salt bridge interactions (Online Methods). We validate the modified FF, CHARMM36m (C36m), using a comprehensive set of 15 peptides and 20 proteins with a cumulative simulation time of more than 500 μs (Supplementary Table 1).

The sampling of α_L helical conformations in IDP ensembles generated with the C36m FF is significantly reduced compared to C36, as we demonstrated for four IDPs including the RS peptide, the FG-nucleoporin (FG) peptide, a hen egg white lysozyme N-terminal fragment (HEWL19) and the N-terminal domain of HIV-1 integrase (IN) (Table 1). The average α_L propensity of non-Gly, non-Pro residues for these four IDPs changes from 20.0% to 5.7%, much closer to the value of 5.1% from protein coil libraries.⁹ With the bias towards α_L sampling removed, the C36m FF generates molecular dynamics (MD) ensembles that improve the prediction of experimental observables, for example the NMR scalar couplings for the central alanine residues in the HEWL19 peptide (Supplementary Table 2). The ensemble obtained with C36m for the RS peptide is in significantly better agreement with NMR data (J couplings, chemical shifts, and hydrodynamic radius) compared to the RS peptide ensemble obtained with C36 (Supplementary Table 3 and 4). In addition, the predicted SAXS profile from the C36m ensemble of the RS peptide agrees within error with the experimental SAXS curve (Figure 1), indicating good agreement between computed and measured chain dimensions.

Table 1.

α_L conformational sampling in four IDP systems in MD simulations with the C36 and the C36m FFs. The α_L probability is computed as the fraction of the ensemble containing left-handed α-helix, and the α_L propensity as the probability for non-Gly, non-Pro residues to sample the α_L region. The maximum length of the α_L helices observed in the simulations is also listed.

system	simulation	αL probability	αL propensity	max. αL length
FG peptide	C36	32% ± 6%	22% ± 2%	14 aa
	C36m	1.1% ± 0.3%	6.2% ± 0.2%	5 aa
RS peptide	C36	80% ± 2%	41% ± 1%	17 aa
	C36m	1.8% ± 0.5%	5.5% ± 0.2%	5 aa
IN	C36	64% ± 18%	14% ± 2%	7 aa
	C36m	3% ± 2%	5.6% ± 0.5%	4 aa
HEWL19 peptide	C36	11% ± 7%	12% ± 2%	8 aa
	C36m	0.5% ± 0.4%	6.1% ± 0.7%	3 aa

Figure 1.

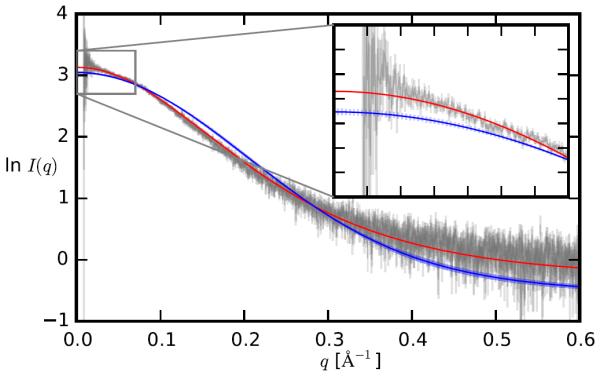
SAXS profiles of the RS peptide. Ensemble-averaged scattering curves from the C36 simulation (blue) and the C36m simulation (red) are plotted, with the experimental curve⁴ shown with error in gray. The nonweighted error function χ² as defined in Ref. ²⁰ was 0.63 using C36, and 0.12 using C36m. The error bars represent the standard deviation computed by dividing the conformational ensembles in two, and computing the average SAXS profile for each half separately. For the C36m ensemble, the error bars are smaller than the line width.

We tested secondary structure sampling for a number of model peptides. The fraction of right-handed α helices in the Ac-(AAQAA)₃-NH₂ peptide simulated with the C36m FF equals 17%, which is larger than the C36 result of 13% and closer to the NMR estimate of ~19% and ~21% at 300 K (Supplementary Fig. 1 and Supplementary Table 5). We carried out folding simulations of four β-hairpins (GB1, chignolin, CLN025 and Nrf2); starting from unfolded, fully extended conformations, native-like β-hairpin structures were sampled for all four peptides (Supplementary Fig. 2, 3, 4 and 5). For the GB1 β-hairpin, the MD ensembles generated by the C36m and C36 FFs were found to be very similar (Supplementary Fig. 2 and 3) and consistent with NMR estimate of the folded state population.¹⁰ However, the folded state populations of chignolin and CLN025 are significantly lower than the NMR estimates (Supplementary Table 6), indicating that the C36m FF may underestimate the stability of some β-hairpins.

To directly compare to previous C36 results,¹¹ we tested C36m by simulating polyglutamine (polyQ) peptide, an IDP with relatively compact collapsed states due to the hydrogen bonding interactions between polar side chains. Similar to the C36 results, the 30-residue polyQ peptide (Q₃₀) was disordered during 98% of the simulation time. On average, 7% of φ/ψ torsion angles were in the α_L region with C36m. A broad conformational ensemble was sampled with the most favorable states being relatively compact (first major minimum at the end-to-end distance of 25 Å) (Supplementary Fig. 6). Extrapolation of fluorescence resonance energy transfer (FRET) measurements of shorter polyglutamine peptides¹² to a length of 30 residues leads to an estimate of end-to-end distance of 25 Å, which compares favorably with the C36m simulation results.

We also tested C36m in modeling the kinetics of protein dynamics with the disordered Ac-C(AGQ)_nW-NH₂ peptides. The C-terminal tryptophan of C(AGQ)_nW peptides can be optically excited into the triplet state, with the rate of quenching of that state due to contact formation with the N-terminal cysteine corresponding to the rate of loop closure.^{13, 14} The decay of triplet survival probabilities calculated from MD simulations compares favorably with experiments for four C(AGQ)_nW peptides with n = 1-4 at 293 K (Supplementary Fig. 7). The computed loop closure rates, and both their diffusion-limited parts and reaction-limited parts, agree with experiments for shorter peptides (n=1-2) (Supplementary Table 7).¹⁴ The calculated diffusionlimited rates for longer peptides (n=3-4) are higher than experimental estimations, indicating the simulation ensembles being too collapsed.

We also validated C36m using 15 different folded proteins. All were stable during the 1 μs simulation time (Supplementary Fig. 8), and the distribution of backbone φ, ψ dihedral angles from these simulations closely resembles the Ramachandran plot of the “top500” protein structures¹⁵ (Supplementary Fig. 9), indicating the high quality of the C36m FF in treating the backbone conformational properties of folded proteins. NMR observables of ubiquitin computed from microsecond MD simulations with the C36m FF correlate well with both the C36 results and experimental data (Supplementary Table 8-12).

We additionally performed a folding free energy calculation of villin head piece HP36 (Supplementary Table 13 and Supplementary Fig. 10), conformational sampling of a N-terminal fragment of HP36, HP21 (Supplementary Fig. 11-14), and MD simulations of designed protein GA95 and GB95 with 95% sequence identity but different folds (Supplementary Fig. 15). The HP21 peptide folds to the correct folded state (Supplementary Fig. 11), consistent with the fact that the peptide is partially folded and has a preference for native structure.¹⁶ The most predominant secondary structure is alpha helix (Supplementary Fig. 12), as expected based on NMR studies¹⁶ and a recent simulation study of this peptide.¹⁷ The helical state is slightly destabilized (by approximately ~ 1 kT) compared to the population based on the chemical shifts and secondary structure propensity (Supplementary Fig. 13 and Supplementary Tables 14, 15). For the HP36 protein, we find that C36m gives improved agreement in the folding free energy compared to C36 (Supplementary Table 13).

Finally, we comment on the general problem of overly-compact IDP ensembles, a problem that is encountered with most physics-based atomistic models.^{5, 6, 18} While the C36m FF, based on the CHARMM modified TIP3P water model, leads to good agreement between computed and experimental chain dimensions for the RS peptide, the ensemble averaged radii of gyration (R_g) of IN and the Cold-shock protein from Thermotoga maritima (CspTm) with the C36m FF are 13.8 ± 0.2 Å and 12.8 ± 0.2 Å. These dimensions are much smaller than the experimental estimates of 24 Å and 15 Ź⁹ (Supplementary Table 16), respectively, which are inferred from FRET measurements assuming a Gaussian chain model. An approach to correct for this bias is to increase the dispersion interactions between the protein and water. One study applied a general scaling factor to scale up the total protein-water van der Waals (VdW) interactions,⁵ while another proposed a reparametrized water model with the oxygen Lennard-Jones (LJ) well depth ε_O increased by 50%.⁶ Motivated by the difference between the CHARMM modified and the original TIP3P water model, we propose here an alternative water model in which the LJ well depth parameter ε_H of the water hydrogen atoms is increased (from −0.046 kcal/mol in CHARMM TIP3P) while the oxygen LJ parameters and the water-water interactions are maintained. This approach specifically makes the dispersion part of protein-water interactions more favorable with minimal perturbation on the repulsive part versus the larger impact of altering the oxygen LJ parameters (Online Methods).

In simulations using a water model in which the ε_H value was set to −0.10 kcal/mol good agreement with the experimentally estimated R_g is obtained for CspTm, (Supplementary Table 16 and 17). In contrast, computed ensemble averaged <R_g>’s were found to be larger than the experimental value for the RS peptide and smaller than the experimental value for the IN protein (Supplementary Fig. 16 and Supplementary Table 16). These results suggest that no universal ε_H can be found to be applicable to all IDP systems and that IDP specific water models may be of utility; further studies are required to address this issue.

Online Methods

The origin of left-handed α helices in the C36 protein FF

Left-handed helices are very rare in peptides and proteins due to the steric clash between amino acid side-chains and the bulkier CO groups than the NH group in the case of common, right-handed helices. Though present in both models (Supplementary Fig. 17), such steric effect is weaker in the C36 FF compared to the C22/CMAP FF, because of the inclusion of refined Lennard-Jones (LJ) parameters for aliphatic carbon atoms in the C36 FF that give improved condensed phase properties of alkanes.²¹ Specifically, the van der Waals (vdW) radius of alanine Cβ atoms changed from 2.06 Å in C22/CMAP to 2.04 Å in C36, for the Cβ atoms in Ile, Thr and Val from 2.275 Å to 2.0 Å, and for the Cβ atoms in the remaining non-Gly, non-Pro amino acids from 2.175 Å to 2.01 Å. Notably, these changes also represent improved treatment in the FF of intramolecular interactions, as the CMAP corrections to the original C22 FF contains large negative values in the α_L region to take into account that the steric clash disfavoring α_L was overestimated due to the larger vdW radii. As improved LJ parameters were adopted in the C36 FF, a decrease in the contribution of the CMAP correction that favors α_L was needed. However, as the original C36 CMAP (Supplementary Fig. 17) has the same CMAP potential in the α_L region as C22/CMAP, oversampling of the α_L region occurs, requiring the present additional refinement and subsequent validation of the model.

Optimization of the CMAP potential

Central to any optimization problem is its target function. While left-handed α-helices are very rare, there is little qualitative experimental information on the probability or the average length of left-handed helices, or how often an amino acid populates the α_L conformation. Protein coil libraries^{22, 23} estimate an average α_L propensity of 6.4% for all amino acids and 5.1% for non-Gly, non-Pro residues. It is anticipated that α_L propensity in different IDPs will depend on their primary sequence,^{24, 25} and arguments on the amount of α_L sampled in specific peptides dates back to earlier days of molecular mechanics force fields.^26-28 As experimental target data on the correct amount of α_L population is lacking, we instead attempted to answer a related and more general question: what is the minimal perturbation of the current CMAP potential energy, E, that reduces α_L sampling to an approximate target value? This corresponds to minimizing the following target function:

$$E=\mathit{kT}\ln P+w{\mathrm{RMS}}_{\mathrm{CMAP}}$$ (1)

, where P represents the probability of conformations in a structural ensemble containing a left-handed α-helix (α_L probability), w is an adjustable weighting factor, and RMS_CMAP is the root mean square difference between the two CMAPs:

$${\text{RMS}}_{\text{CMAP}}=\sqrt{\frac{1}{\mathit{mn}}{\Sigma }_{i=1}^m{\Sigma }_{j=1}^n{\left({\text{CMAP}}_{i,j}^{\text{new}}-{\text{CMAP}}_{i,j}^{\text{orig}}\right)}^2}$$ (2)

, where m=n=24 are the two dimensions of the tabulated CMAP potentials.

Reweighting has emerged as a powerful tool in force field parametrization.^29-31 Given a well-converged conformational ensemble generated by a force field parameter set λ, the ensemble average of a certain property A under a new force field parameter set λ+Δλ is given by

$$\langle A_{\lambda +\Delta \lambda }\rangle =\langle A_{\lambda }{e}^{-\beta (E_{\lambda +\Delta \lambda }-E_{\lambda })}\rangle ∕\langle e^{-\beta (E_{\lambda +\Delta \lambda }-E_{\lambda })}\rangle$$ (3)

, where E_λ and E_λ+Δλ are the potential energies with FF parameters λ and λ+Δλ for each sampled conformation, and β is the reciprocal of the thermodynamic temperature. In the context of left-handed helices, α_L probability P associated with a certain CMAP modification can be computed as

$$P=\frac{{\Sigma }_{i=1}^n{h}_i{e}^{-\beta \Delta E_i^{\text{CMAP}}}}{{\Sigma }_{i=1}^n{e}^{-\beta \Delta E_i^{\text{CMAP}}}}$$ (4)

, where n is the number of frames, h_i is a binary that equals 1 if the i-th conformation contains a left helix and 0 if not, and $\Delta E_i^{\text{CMAP}}$ is the potential energy change associated with the CMAP modification at the i-th conformation. The reweighted α_L probability was determined based on $\Delta E_i^{\text{CMAP}}$, as this was the only energy term adjusted in the FF that directly impacts backbone conformational sampling, which allows efficient evaluation of the target function.

A Monte Carlo simulated annealing (MCSA) simulation is combined with the reweighting equation (Eq. 4) to derive the optimized CMAP potential for the target function (Supplementary Fig. 18). 10⁵ MCSA steps were carried out with a starting MCSA temperature of 10 K, and random CMAP revisions between −0.01 kcal/mol and 0.01 kcal/mol were added to individual grid points in a broadly defined α_L region (Supplementary Fig. 18) in each MC step. The full set of φ, ψ values of the FG peptide from the MD ensemble generated with the C36 FF at 298K³² was used as the input data, and MCSA optimizations were run with different weighting factor w (Supplementary Table 18). Smaller w values lead to more pronounced reduction of α_L probability, indicating w balances between the amount of α_L and the magnitude of the CMAP modification. The predicted α_L probability reduced to 1.1% with w=2kT, and further decreases of w brings little improvement in α_L reduction (Supplementary Table 18). The CMAP resulting from a 10⁵ step MCSA run with w=2kT is determined to be used as the CMAP for non-Gly and non-Pro residues in the C36m FF. The revision to the original C36 CMAP is localized to the α_L region around φ, ψ =60°, 45° and much smaller than with the full region allowed to optimize as indicated by the black lines in Supplementary Fig. 18. The final number of parameters (ie. CMAP grid points) being modified is much less than the number of parameters allowed to freely change during fitting, which is a good indication that overfitting has been avoided. The penalty term (RMS_CMAP) in the optimization target function helps maintain minimal revision to the CMAP potential while maximally reducing the α_L probability.

Improved modeling of the guanidinium and carboxylate salt bridge

Another refinement in the C36m FF concerns improved description of salt bridge interactions involving guanidinium and carboxylate functional groups with a pair-specific non-bonded LJ parameter (NBFIX term in CHARMM) between the guanidinium nitrogen in arginine and the carboxylate oxygen in glutamate, aspartate as well as the C terminus. This salt bridge interaction was found to be too favorable in the CHARMM protein force fields as indicated by the overestimation of the equilibrium association constant of a guanidinium-acetate solution ,^{33, 34} as well as the underestimation of its osmotic pressure (personal communication, Benoit Roux). The added NBFIX term increases the R_min from the 3.55 Å based on the Lorentz-Berthelot rule to a larger value of 3.637 Å (Shen and Roux, personal communication), which we subsequently showed to improve the agreement with the experimental osmotic pressure of guanidinium acetate solutions (Supplementary Figure 19). We noted that the NBFIX approach employed here differs from Piana et al’s work²⁷ where the CHARMM22 charges of the Arg, Asp and Glu side chains were reduced in magnitude, with both approaches leading to weaker and more realistic salt-bridge interactions. The NBFIX term makes sure only the specific interaction between Arg and Asp/Glu is modified, while the interaction of these residues with other amino acids, water, or ions are kept the same as in the C36 FF. Again, our aim is to improve the C36 FF with minimal changes in the model.

Molecular dynamics simulations

The C36m FF was validated using a variety of systems including peptides, IDPs, unfolded states of proteins, and globular proteins. The CHARMM-modified TIP3P model³⁵ was used in all simulations, unless noted. All the systems studied here are in high dilution such that the systems did not test the force fields with respect to aggregation. A summary of the validation simulations is given in the Supplementary Table 1, and detailed information of setup and analysis for each simulation system is given in the Supplementary Note. Briefly, temperature replica exchange (T-REX) simulations were carried out with GROMACS³⁶ for the RS peptide (0.63 μs * 34 replica), the GB1 hairpin (0.8 μs * 32 replica), the Nrf2 hairpin (1 μs * 28 replica), Chignolin (6 μs * 29 replica) and CLN025 (6 μs * 29 replica). Hamiltonian replica exchange (HREX) simulation was carried out with CHARMM³⁷ for polyQ using the end-to-end distance as the biasing reaction coordinate. Harmonic umbrella potentials with a force constant of 0.2 kcal/mol/Ų were applied to target end-to-end distances ranging from 5 to 75 Å spaced at 5 Å intervals. Similar H-REX protocol using distance as the biasing reaction coordinate was applied to study the folding free energy of HP21. Conformations were also sampled using single, long MD trajectories with OpenMM,³⁸ including 5 μs simulations for the HEWL19 peptide, IN and CspTm, 10 μs simulations for the (AGQ)_n peptides, and 16 μs simulations for (AAQAA)₃. A 1.2 μs simulation of ubiquitin was carried out with NAMD to compare with previous results using the C36 FF.³⁹ Alternative water models were tested with the RS peptide using T-REX simulations (0.63 μs * 34 replica) and with IN and CspTm using 5 μs MD simulations.

Analysis of MD trajectories was carried out using GROMACS³⁶ or CHARMM.³⁷ A left-handed α-helix is defined as having at least three consecutive residues with φ, ψ~falling in the α_L region (30°<φ<100° and 7°<ψ< 67°, Supplementary Fig. 20). The α_L probability is computed as the fraction of the ensemble containing left α-helix as in Ref.³² We also compute the α_L fraction as the probability for residues to be in a left-handed α-helix, and the α_L propensity as the probability for residues’ φ, ψ to be in the α_L region, as additional measurement of α-left helix sampling.

Statistics

Observables were computed as the ensemble average of ~10⁴ to 10⁶ frames in MD trajectories. Unless noted, uncertainties were estimated with block analysis by partitioning MD trajectories into five blocks (n = 5).

Sampling extended states of IDPs with alternative water model

A promising way to obtain larger <R_g> is to introduce stronger dispersion interactions between the protein and water. We first test the approach suggested by Best et al⁴⁰ which employs a general scaling factor for the VdW interaction between protein and water. A scaling factor of 1.05 is tested with the C36m FF, and it is confirmed that scaling up protein-water VdW interaction leads to more extended conformational states for the RS peptide, the IN proteins and the CspTm proteins (Supplementary Fig. 16 and Supplementary Table 16).

We propose an alternative water model with specific modification of water hydrogen LJ parameters. This is inspired by the difference in conformational sampling with the CHARMM modified TIP3P model and with the original TIP3P model. The CHARMM modified TIP3P contains additional LJ parameters on the hydrogen atoms (ε_H~= −0.046 kcal/mol and R_min/2 = 0.2245 Å), so it has more favorable dispersion interactions which stabilize extended conformations leading to less structured conformational ensembles as compared to the original TIP3P water model.^{32, 41} By further increasing the ε_H value while maintaining the LJ parameters of the water oxygen atom and resetting the water-water interaction to be same as the CHARMM modified TIP3P water with NBFIX terms, one can specifically make the dispersion part of the VdW interactions between protein and water more favorable while not perturbing the water properties. The advantage of altering the ε_H value is due to the LJ potential containing both repulsion (r⁻¹²) and dispersion (r⁻⁶) terms. Therefore, alteration of the water oxygen atom LJ parameters will affect its effective size based on the repulsive term such that, for example, the change would alter the balance between the attractive and repulsive interactions of water-protein interactions. In contrast, the water hydrogen atom has a very small LJ radius so that its repulsive wall remains inside the repulsive wall of the oxygen atom in such a way that its LJ term only contributes favorable dispersion interactions. Thus, by only modifying the hydrogen LJ ε_H parameter, we ensure minimal perturbation of the Hamiltonian, i.e. only the dispersion interaction of the protein with water in the simulation systems is changed. As our goal in the present study was to verify that such an approach would lead to improved sampling of IDPs we approximately doubled the ε_H value from −0.046 to −0.1 kcal/mol.

Code availability

The computer code used to perform optimization of the CMAP potentials via reweighting is deposited at https://github.com/jing-huang/CMAPoptimizer.

Data Availability

The C36m FF is available along with the remainder of the CHARMM force fields at http://mackerell.umaryland.edu/charmm_ff.shtml. More specifically, the parameter file (par_all36_prot_mod.prm) is provided in the toppar_c36_jul16.tgz file. The C36m FF is also included in the CHARMM program (version c41 and onward). In addition, the FF may be used in a number of open source molecular simulation programs including NAMD, GROMACS and OpenMM.