Data-driven models of foot-and-mouth disease dynamics: a review

Summary

Foot-and-mouth disease virus (FMDV) threatens animal health and leads to considerable economic losses worldwide. Progress towards minimizing both veterinary and financial impact of the disease will be made with targeted disease control policies. In order to move towards targeted control, specific targets and detailed control strategies must be defined. One approach for identifying targets is to use mathematical and simulation models quantified with accurate and fine-scale data to design and evaluate alternative control policies. Nevertheless, published models of FMDV vary in modeling techniques and resolution of data incorporated. In order to determine which models and data sources contain enough detail to represent realistic control policy alternatives, we performed a systematic literature review of all FMDV dynamical models that use host data, disease data, or both data types. For the purpose of evaluating modeling methodology, we classified models by control strategy represented, resolution of models and data, and location modeled. We found that modeling methodology has been well developed to the point where multiple methods are available to represent detailed and contact-specific transmission and targeted control. However, detailed host and disease data needed to quantify these models are only available from a few outbreaks. To address existing challenges in data collection, novel data sources should be considered and integrated into models of FMDV transmission and control. We suggest modeling multiple endemic areas to advance local control, global control, and better understand FMDV transmission dynamics. With incorporation of additional data, models can assist with both the design of targeted control and identification of transmission drivers across geographic boundaries.

Introduction

Foot-and-mouth disease (FMD) is a perennial plague of livestock caused by a highly contagious apthovirus that infects cloven-hoofed animals worldwide (Rweyemamu et al., 2008b). Animals infected with the foot and mouth disease virus (FMDV) show characteristic signs of fever and blisters on the hooves and around the mouth (Grubman and Baxt, 2004); nevertheless, signs are often mild and most animals recover. More severe consequences stem from wide-ranging economic impacts attributable to infection, such as elevated juvenile mortality, fertility problems, decreased production, decreased draught power, economic embargos, and disease control programs (Thompson et al., 2002, Yang et al., 1999, Knight-Jones and Rushton, 2013). Across all endemic areas, direct and indirect costs are jointly estimated between US$ 6.5 and 21 billion per year (Knight-Jones and Rushton, 2013), while costs of control for the 2001 FMDV outbreak in the United Kingdom (UK) amounted to over £4 billion and over 6 million animals culled (Tildesley et al., 2008, Anderson, 2002, Thompson et al., 2002). To reduce both high disease incidence and high economic costs, the Food and Agriculture Organization of the United Nations (FAO), the European Commission for the Control of Foot and Mouth Disease (EuFMD), and the World Organization for Animal Health (OIE) have called for a more targeted control strategy in the Progressive Control Pathway for FMD (Rweyemamu et al., 2008a, Paton et al., 2009, Jamal and Belsham, 2013). However, specific targets for control still need to be defined. One approach to design and evaluate alternative control strategies is to use mathematical models and simulations.

Models of infectious disease dynamics have a rich history of advancing the study of pathogen transmission and control. The first models, presented in 1760, address the use of vaccinations to control smallpox (Dietz and Heesterbeek, 2002, Bernoulli, 1760) and later models established general theory of outbreaks (Kermack and McKendrick, 1927, Ross, 1916, Klepac et al., 2013). By the mid 20^th century, models of FMDV transmission and control appeared in the literature (Hughjones, 1976, Klaring and Timischl, 1979). Generally, transmission models categorize individuals by disease status; for FMDV transmission, the SEIR model denotes animals as susceptible (S) to FMDV, exposed (E) or infected but not yet infectious, infected (I) and infectious, and recovered or removed (R) from chains of transmission (Anderson and May, 1991, Keeling and Rohani, 2008). Transmission between infected and susceptible individuals is a function of both population and disease factors: contact rates are population-dependent and may vary with time, while the probability of transmission over a contact depends on the pathogen (Begon et al., 2002). The transmission model can be coupled with a control model; for FMD control, traditional strategies include movement restrictions, culling, or vaccination (Ferguson et al., 2001a, Ferguson et al., 2001b, Keeling et al., 2003, Keeling et al., 2001). The efficacy of alternative control policies can be quantified by comparing the number of secondary cases produced by each infectious case (R_t), where t represents time, under scenarios where the control measure is absent versus scenarios where the control measure is present. When the count of secondary cases is below unity (R_t<1), infected individuals transmit the pathogen at rates below replacement, and the outbreak will fade out (Anderson and May, 1991, Keeling and Rohani, 2008). Other metrics compared when evaluating alternative control policies include total counts of herds infected and depopulated. Regardless of metrics used to evaluate control policies, all models that help design targeted control should realistically describe specific populations under the threat of FMDV infection, which requires the incorporation of accurate data (Keeling, 2005).

Both host and disease data are used to quantify models. Host data provide information for abundance and spatial distribution of individual farms or animals, direct contacts, and indirect contacts. Disease data provide counts of infected animals over time, which can be used to estimate parameters that quantify the transmission model (Ferguson et al., 2001a, Ferguson et al., 2001b, Keeling et al., 2003, Keeling et al., 2001). Once accurately quantified, models can be used to predict future disease impact or to design targeted control strategies. Targeted control implies that individual farms can be identified, which requires that models represent transmission and control at a very fine spatial resolution. To accurately quantify these models, both host and disease data are needed at the same fine scale. However, currently published models differ widely in modeling approaches and resolution of data used to quantify the model. Given the vast and disparate literature on FMDV dynamical models, it is unclear which modeling techniques and data sources are resolved enough to help design targeted FMD control.

Therefore, we investigated if published dynamical models and the data that parameterize them contain enough detail to help design and assess targeted control. We performed a systematic literature search to find all articles that included dynamical models of FMDV transmission and control, provided that they represent a physical host system using host data, disease data, or both. First, we classified models by control strategy to see if all three approaches used or proposed in large-scale outbreak control – movement restrictions, vaccination, and culling – were represented in the models. Second, we classified models by methods used to represent transmission to determine if infectious contacts were represented with enough detail to identify individual farms or areas for targeted control. Third, we classified models by data incorporated to determine if host and disease data were detailed enough to quantify models of targeted control. Finally, we described best practices for making models more applicable to investigations of targeted control. By synthesizing the collective group of FMDV dynamical models with respect to applicability for designing targeted control, we aim to provide knowledge that could help improve efficiency of veterinary intervention across geographic boundaries.

Materials and Methods

Literature Search

In order to find all published articles that used dynamical models of FMDV transmission, we performed a literature search using Web of Science on March 22, 2015. We searched over all years for the phrase “foot and mouth disease” and at least one of fourteen terms we chose to designate dynamical models (see supplementary material for additional details). The initial search yielded 3724 publications. By individual analysis of titles and abstracts, we excluded models that did not specifically represent foot and mouth disease virus (FMDV) dynamics. We also excluded conference proceedings, published comments, and articles written in languages other than English so that a set of 272 articles remained. We omitted 166 articles that did not include dynamical models or data after reading the papers. Our final set consisted of 106 articles.

Categorizing the models by structure and methodology

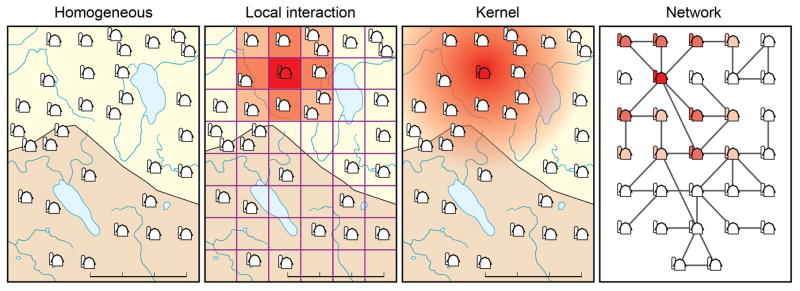
We categorized models in our final set of articles based on three criteria related to model structure and methodology. One paper could have fallen into any combination of these groups. First, we categorized models on methods used to represent control, which included both implicit and explicit representation of movement restrictions, culling, or vaccination. These strategies were modeled either explicitly – incorporating control into the model structure – or implicitly, by making inference using incidence data collected while control was enacted. We also categorized models on metrics used to measure the impact of modeled control, which included reduction in FMD cases, reduction in FMD carriers, and explicit economic costs. Second, we categorized models by methods used to represent transmission among diverse host species, which included ignoring species diversity or representing multiple livestock species, single wildlife species, or multiple wildlife species. Finally, we categorized models by methods used to represent contacts that drive transmission, including homogeneous mixing, local interactions, kernel-based methods, and network models (Figure 1). Homogeneously mixing models assume that each farm has an equally likely chance of mixing with any other farm over the entire study area. Local interaction models permit homogeneous mixing only within a defined geographic range. Distance-based kernels inversely scale transmission with distance from an infected farm. Network or movement models provide an alternative representation of connectivity between farms that is not strictly distance based. Additional information and categorizations are documented in the Supplementary Material.

Figure 1. Spatial representation of FMDV transmission.

Multiple methods have been used to capture FMDV transmission among farms. Some models assume homogeneous mixing, implying high rates of mixing in the host population (Ap Dewi et al., 2004, Bouma et al., 2003, Garner and Lack, 1995a, Haydon et al., 1997, Kobayashi et al., 2007a, Tsutsui et al., 2003). Other models assume local interactions (Doran and Laffan, 2005, Highfield et al., 2010, Ward et al., 2009) or kernel weighted spread (Chis Ster and Ferguson, 2007, Keeling et al., 2001), indicating that transmission is based on the distance between susceptible and infectious farms. Finally, network models provide an alternative representation, in which the contact structure is based on multiple factors (Green et al., 2006, Kao et al., 2007, Kiss et al., 2006).

Categorizing the models by data usage

We categorized models in our final set of 106 articles based on two criteria related to use of data. First, we classified models by the presence or absence of disease data. If disease data were present, we further classified the models by the type of disease data incorporated: epidemic time-series data, endemic case reports, or endemic serology data. Second, we classified models by the presence or absence of host data. If host data were present, we further classified models by the source of host data incorporated: national registry, national census, investigator-directed survey, land cover data obtained from geographical information systems (GIS), or other methods. National registries, often organized by a governmental agency, provided the most complete data. National censuses are also organized by a governmental agency but often provided data that were less detailed in temporal resolution, spatial resolution, or both.

Determining the geographic distribution of FMD cases relative to locations modeled

We classified models by the geographic location represented, determined by the location at which the disease and/or host data were collected. We compared these locations to the worldwide distribution of FMD cases using data from the World Organization for Animal Health (OIE). Data from OIE’s World Animal Health Information Database (WAHID) interface of Animal Health Information provide disease status timelines for all countries and territories listed by OIE from 2005 to 2013 (http://web.oie.int/wahis/public.php?page=disease_timelines). The status used in our analyses is the most recent status listed in the timeline as of February 18, 2013 and the data obtained from WAHID are provided as a supplementary file.

Results

We created a database, which details the categorization of the 106 articles, provided in the supplementary material (Tables S1 and S2). We explored five aspects of the database, which highlighted factors that should be considered when selecting or developing a model for FMD control. We first summarized methods used to model control. We then categorized transmission among multiple species and transmission using detailed contacts. We also summarized data used to quantify models of control and models of transmission. Finally, we surveyed locations modeled to determine where detailed models and data were available.

Modeling control

To determine if published models represent the various strategies implemented during outbreak control, we categorized articles into three groups: those that represented movement restrictions, culling, or vaccination (Tables S1 and S2). The majority of articles incorporated movement control implicitly (35/106) or explicitly (21/106). Articles also explored the effects of culling (implicitly: 12/106; explicitly: 56/106) and vaccination (implicitly: 3/106; explicitly: 40/106; Figure S4). Therefore, methodology has been developed to the point where current disease containment policies and realistic alternative scenarios were incorporated into FMD models.

To determine how models measured the efficacy of implemented control, we categorized models by metrics used to quantify impact. All articles (106/106) used reduction in FMD cases as the primary measure to quantify the effect of modeled control. One article (1/106) used reduction in FMD carries as a secondary metric; some articles also modeled explicit economic costs (14/106). Therefore, most FMD models used epidemiological metrics instead of economic costs as the metric for measuring control efficacy.

Modeling host species diversity

To determine if published models represent transmission at a detailed resolution such that individual host species can be identified and targeted, we categorized articles by methods used to represent species diversity (Table S2; Figure S2) (Bajardi et al., 2012, Boender et al., 2010, Bouma et al., 2003, Durand and Mahul, 1999). The majority of articles (51/106) did not consider species diversity; instead, they represented hosts homogeneously. The articles also considered species diversity in one of three other ways. Some articles (47/106) represented hosts as mixed species farms, while other articles represented hosts as a single wildlife species (10/106) or as mixed wildlife species (2/106). Therefore, even though models of FMDV dynamics can represent species diversity, only about one-half of publications used this technique. Predictive models based on wildlife abundance also indicate species-specificity in transmission potential. In wildlife systems, the differential dynamics may be species-specific (Ward et al., 2009) but have also been shown to correlate with host density (Garner and Lack, 1995a, Highfield et al., 2009), which may vary seasonally (Doran and Laffan, 2005). Nevertheless, these simulation models were not validated by disease data collected in wildlife hosts, and showed the extent to which wildlife might contribute to an outbreak instead of implicating them as transmission vectors.

Modeling detailed contacts in transmission

To determine if published models represent transmission at a detailed resolution such that individuals can be identified and targeted, we categorized articles by methods used to represent contacts among farms (Table S2; Figure S3, Figure 1). Homogeneously mixing models were used to represent some populations (18/106). Local interaction models were less common (8/106). Models incorporating distance-based kernels were the most common representation (35/106). Network or movement models were also used (31/106). Therefore, local interaction models, kernel-based methods, and network models have been developed and used to represent spatial connectivity and transmission among farms at scales detailed enough to help design and evaluate targeted control.

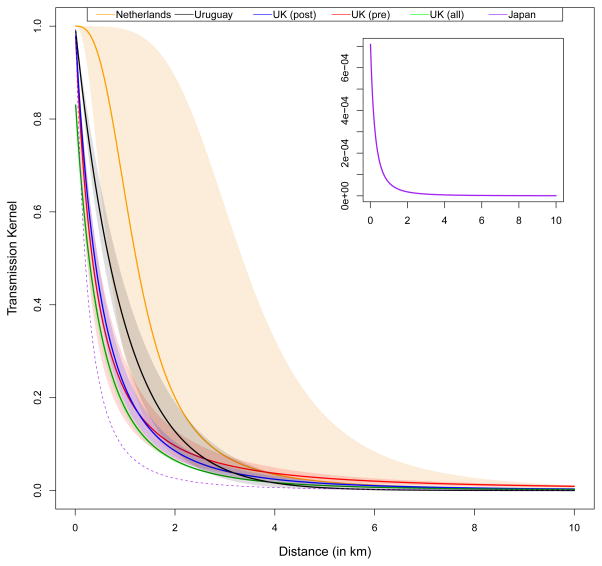
Previously, detailed models combined with high-resolution disease data have been used to describe FMDV transmission. Transmission kernels, which estimated the probability of transmission based on the distance from an infected farm, have been estimated from spatial incidence data from outbreaks that occurred in 2001 in the Netherlands (Boender et al., 2010), UK (Chis Ster et al., 2012, Chis Ster and Ferguson, 2007, Chis Ster et al., 2009), and Uruguay (Chowell et al., 2006) and in 2010 in Japan (Hayama et al., 2013) (Figure 2). The widest kernel represented transmission in the Dutch outbreak (Boender et al., 2010) and the narrowest kernel represented transmission in the Japanese outbreak (Hayama et al., 2013). All three kernels that represented the UK outbreak are similar and demonstrate widths intermediate between the Dutch and Japanese kernels. The UK kernels – with overlapping 95% credible intervals – surprisingly suggested little difference before and after a movement ban (Chis Ster et al., 2012, Chis Ster and Ferguson, 2007, Chis Ster et al., 2009). The last kernel, which represents transmission in Uruguay (Chowell et al., 2006), showed a width intermediate between the kernels for the UK and the Netherlands. The location-specific kernel width highlighted the need to estimate kernels at multiple locations and with multiple FMDV strains. The relevance of these differences in transmission kernels to targeting of control measures has not been evaluated and will be informed by a better understanding of the variability in transmission kernels. Estimation of this variability can only occur with detailed host and disease data across a wide variety of host-mobility systems and viral strains.

Figure 2. Transmission kernels.

The function that scales transmission with distance was estimated for the Dutch 2001 Panasia O outbreak (orange) (Boender et al., 2010), the Uruguayan 2001 type A outbreak (black) (Chowell et al., 2006), the UK 2001 Panasia O outbreak (red, blue, and green) (Chis Ster et al., 2012, Chis Ster and Ferguson, 2007, Chis Ster et al., 2009), and the Japanese 2010 outbreak (Hayama et al., 2013). The kernels for the UK outbreak were estimated for before the Feb 23^rd movement ban (“pre”), after the Feb 23^rd movement ban (“post”) or for the entire epidemic (“all”). The shaded regions represent 95% confidence intervals for the Dutch and Uruguayan kernels and 95% credible intervals for the three UK kernels. The Japanese kernel is represented in the upper right panel with a different scale on the y-axis. For comparison with kernels estimated from other locations, the Japanese kernel has been scaled-up and represented by the dotted purple line in the main pane.

Host data

To determine if data on host abundance are available and detailed enough such that individuals and the contacts between them can be accurately quantified for use in models of targeted control, we categorized articles based on types of host data incorporated (Table S2; Figure S5). Most articles (83/106) incorporated host data from a national registry or census. Data from national registries were used most frequently in FMD models located in the UK (39), Denmark (5), Australia (3), Netherlands (3), and Sweden (2). Data from national censuses were used most frequently in FMD models located in the United States (13), France (2), and Germany (2). When nationally organized data were unavailable, the models were supplemented with data from investigator-directed surveys (13/106) or GIS land cover data (8/106), primarily in the US. Other sources of data were also used (13/106) (Table S2). Therefore, the majority of models used previously collected data available at the national level at a resolution suitable for modeling detailed control; however, these data were only present in a few locations and may have restricted the locations that models could represent.

Disease data

To determine if disease data were available and detailed enough to use in targeted models of FMD control, we categorized articles based on the presence or absence of disease data. Only approximately one-third of the articles (32/106) directly incorporated disease data (Table S2; Figure S5). All but one article used time-series incidence data; the other article used case reports and serological data from an endemic setting (Vergne et al., 2012). Models that quantified transmission using disease data incorporate data on FMD cases from twelve different epidemics; however, over half (17) used case reports from the 2001 UK epidemic (Table 1). Numerous articles (49/106) did not use disease data in any manner, often because they were unavailable at the location modeled (Table S2). Thus, disease data – especially from outbreaks other than the one that occurred in the UK in 2001 – were generally unavailable at a resolution suitable for detailed modeling or not used in this manner.

Table 1. FMDV outbreaks represented in the dynamical modeling literature.

The set of articles reviewed was obtained using Web of Science, searching over all years, on March 22, 2015.

Location and dates of foot-and-mouth disease cases	Citations
United Kingdom, 1967–68	Gerbier et al. (2002) Haydon et al. (1997) Howard and Donnelly (2000)
Austria, 1973	Klaring and Timischl (1979)
Saudi Arabia, 1988–93	Woolhouse et al. (1996) Woolhouse et al. (1997)
Turkey, 1990–2002	Gilbert et al. (2005)
Taiwan, 1997	Howard and Donnelly (2000)
United Kingdom, 2001	Chis Ster and Ferguson (2007) Chis Ster et al. (2009) Chis Ster et al. (2012) Deardon et al. (2010) Deardon et al. (2012) Diggle (2006) Ferguson et al. (2001a) Ferguson et al. (2001b) Hosseinkashi et al. (2012) Jewell et al. (2009) Kao (2003) Keeling et al. (2001) Lawson et al. (2011) Savill et al. (2007) Tildesley et al. (2008a) van den Broek et al. (2007) Xiang and Neal (2014)
Netherlands, 2001	Bouma et al. (2003) Boender et al. (2010)
Uruguay, 2001	Chowell et al. (2006) Rivas et al. (2003)
Japan, 2003	Tsutsui et al. (2003)
Peru, 2004	Estrada et al. (2008)
Cambodia, 2009	Vergne et al. (2012)
Japan, 2010	Hayama et al. (2013)

Location

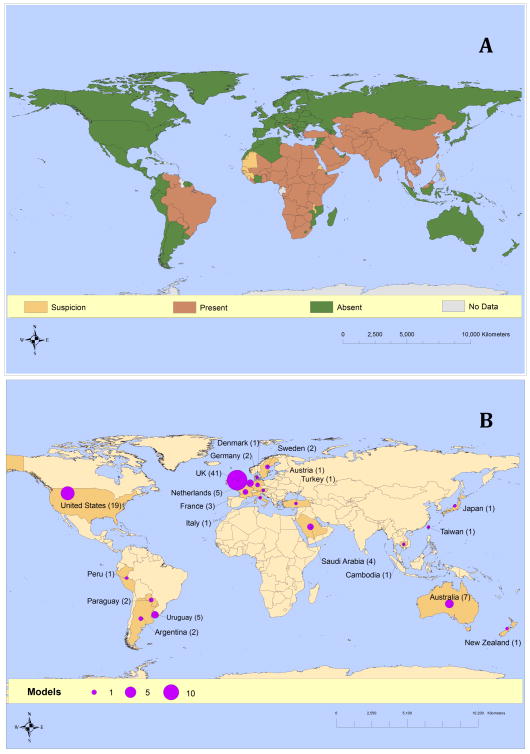
To determine the availability and accessibility of data worldwide, we compared the locations represented by FMDV dynamical models with the geographic distribution of FMD incidence, we determined the location represented by the model in each article and compared it to worldwide distribution of FMD cases as provided by OIE’s World Animal Health Information Database (WAHID). Locations represented by FMDV dynamical models were heavily concentrated in Europe, with a particular emphasis on the United Kingdom. Other locations strongly represented in the FMDV modeling literature included the United States and Australia (Figure 3A). In contrast, confirmed infections or infection zones were reported in Ecuador and in multiple countries throughout Africa and Asia (Figure 3B). This discrepancy partially reflects the periodicity of FMDV infections: in Europe, FMD incidence shows epidemic behavior whereas in Africa and Asia, FMD incidence often shows endemic or seasonally epidemic behavior (Pomeroy et al., 2015). Nevertheless, locations with the most frequent FMD incidence were underrepresented in the modeling literature.

Figure 3. Locations of FMDV incidence contrasted with locations of FMDV models.

(A) Counts of FMD models published in the English language in peer-reviewed journals by geographical location. Data for this map are provided as a supplementary file.

(B) Data from OIE’s WAHID interface of Animal Health Information provide disease status timelines for all countries and territories listed by OIE from 2005 to 2013 (http://web.oie.int/wahis/public.php?page=disease_timelines). The status shown in the map is the most recent status listed in the timeline as of February 18, 2013.

Discussion

Mathematical and simulation models of FMD can be used to help design targeted control and evaluate alternative strategies. After reviewing published models, we found that a wide range of modeling methodology has been well developed: techniques are available to describe movement restrictions, animal culls, and vaccination (Table S2). Heterogeneities in transmission are also well described, with models representing differential transmission and susceptibility that vary by host species (Keeling et al., 2001, Tildesley et al., 2008). Models can also represent detailed contacts among farms using local interaction, kernel-based, or network methods (Table S2). These detailed models are necessary to design targeted control, in that they identify individual farms, regions, or host production types at which control can be applied. Some models are quantified with host data at a resolution appropriate for modeling targeted control; however, locations using host data are largely limited to Australia (Dexter, 2003, Doran and Laffan, 2005, Garner and Lack, 1995a, Garner and Lack, 1995b, Pech and Hone, 1988), Europe (Ap Dewi et al., 2004, Haydon et al., 1997, Kao et al., 2007, Keeling et al., 2001, Tildesley et al., 2006, Ferguson et al., 2001a, Ferguson et al., 2001b, Kao, 2003), and the United States (Bates et al., 2003a, Bates et al., 2003b, Carpenter et al., 2007, Carpenter et al., 2011, Highfield et al., 2010, Tildesley et al., 2012, Ward et al., 2007, Ward et al., 2009). Only a subset of models directly incorporates disease data (Boender et al., 2010, Bouma et al., 2003, Chis Ster et al., 2012, Chis Ster and Ferguson, 2007, Chis Ster et al., 2009, Chowell et al., 2006, Deardon et al., 2010, Deardon et al., 2012, Diggle, 2006, Estrada et al., 2008, Ferguson et al., 2001a, Ferguson et al., 2001b, Gerbier et al., 2002, Gilbert et al., 2005, Haydon et al., 1997, Hosseinkashi et al., 2012, Howard and Donnelly, 2000, Jewell et al., 2009, Keeling et al., 2001, Klaring and Timischl, 1979, Lawson et al., 2011, Rivas et al., 2003, Savill et al., 2007, Tildesley et al., 2008, Tsutsui et al., 2003, van den Broek and Heesterbeek, 2007, Vergne et al., 2012, Woolhouse et al., 1997, Woolhouse et al., 1996); of this subset, the UK 2001 outbreak is overrepresented. Overall, models appropriate for targeted control represent areas where current infections with FMDV are not observed and locations with high FMD incidence are not represented in the modeling literature.

When using a model to help design targeted control, best practices center on representation and quantification of FMDV transmission and all alterative control options at a fine-scale resolution. First, the model must be flexible enough to incorporate vaccination and culling at the level of an individual, region, or production type, while also allowing for localized movement restrictions. Second, the model must incorporate both species-specific transmission parameters and detailed contacts in transmission using a local interaction, kernel-based, or network transmission model. Third, timely host and disease data are needed at the same detailed resolution to accurately quantify the model. Finally, we propose an expansion of locations modeled – which were previously focused on the UK and other locations with intermittent incidence – to include endemic areas.

Endemic systems warrant study and model development to advance both local and global control and fundamental knowledge about FMDV dynamics. First, many areas with endemic FMD participate in some sort of disease control. Modeling these locations with high resolution can assist local government or veterinary agencies in designing targeted policies for more efficient local control. Second, management of FMD in endemic areas is crucial for management of global FMD dynamics. Endemic areas likely seed new outbreaks; furthermore, as the global veterinary community is beginning to call for eradication of FMD, most of this work will be done in endemic settings experiencing outbreaks of the disease. Third, studying endemic systems advances understanding of FMD dynamics and modeling methodology because they provide an opportunity to validate models in the presence and absence of control. The accuracy of predictive models is uncertain (Kitching, 2004) and rests on a set of assumptions; modeling and parameterizing multiple outbreaks will help evaluate the accuracy and generalizability of assumptions made in predictive models and help determine drivers of FMDV outbreaks.

When employed, detailed models combined with detailed disease data have confirmed insights into patterns and processes that drive FMDV transmission among multiple host species that were first identified by animal experiments (Alexandersen and Mowat, 2005, Alexandersen et al., 2003). Specifically, models of the 2001 UK outbreak quantified relative transmissibility and susceptibility of different livestock species, and confirmed that cattle are both more infectious and more susceptible than sheep (Chis Ster and Ferguson, 2007, Chis Ster et al., 2009, Keeling et al., 2001). Furthermore, models suggest a correlation between incidence and cattle abundance, while proposing no such relationship for sheep after a low abundance is reached (Chis Ster et al., 2009, Deardon et al., 2010). Also, when considering dynamics within farms, it is believed that transmission is greater in cattle farms than in sheep farms (Chis Ster et al., 2012). Finally, simulations suggest that animal movement alone can produce a large epidemic, but network models of the 2003–2004 UK animal census and movement data propose this occurs only when the movement is comprised mostly of cattle (Green et al., 2006). In this way, it is thought that cattle contributed more to the 2001 UK outbreak than sheep; however, these findings are suggested only by modeling data from one outbreak. More extensive data from endemic situations in Asia that seem to relate more to pigs (Yang et al., 1999) and sheep (Barnett and Cox, 1999, Perez et al., 2006) would help to determine whether this finding is specific to the host population or to the pathogen.

Policies predicted to control disease have been evaluated by both efficiency in case reduction and explicit calculation of cost-effectiveness. Recommendations for control are not universal; in contrast, they vary by location modeled, initial epidemic characteristics, and metrics used to determine success. For example, simulations in California indicate that vaccination is the optimal choice for FMD control (Kobayashi et al., 2007b), but in analysis of outbreaks occurring in the UK and the Netherlands, combined strategies of culling and vaccination were deemed most effective (Tildesley and Keeling, 2008, Traulsen et al., 2011, Keeling et al., 2003). Since the ramifications of FMD are largely due to the combination of animal health and economic implications, it is important to consider economic factors explicitly. The number of cases may not be directly proportional to the cost because many trade implications relate to the speed of FMD control and the spatial extent of infection. Therefore, design of targeted control policies will require site-specific models and data that represent control and transmission and costs with detailed resolution.

The lack of available or accessible high-resolution data presents a serious challenge to progress in using models to help design targeted control strategies. Lack of host data hinders the design of targeted control, while lack of disease data inhibits characterization of pathogen behavior and identification of transmission drivers. To address these challenges, more complete data should be collected. Yet, data collection is not an easy or trivial task. Collection of disease data during an outbreak in a traditionally disease-free area is often inhibited by priorities understandably placed on veterinary practice and disease containment, and by confusion that occurs during an emergency. Even in locations where disease occurrence is more regular, lack of disease reporting and data analysis may be attributed to a lack of veterinary infrastructure, competing priorities for limited resources, and few perceived benefits to reporting. Similarly, collection of host data is hindered by privacy concerns, global livestock mobility for rearing and trade, and lack of reporting infrastructures. The lack of data currently used to quantify models underscores the challenge in collecting such data. In cases where host data are not available, additional modeling of host presence and connectivity could supplement existing low-resolution sources without the need for livestock tracking and data repositories (Buhnerkempe et al., 2014, Moritz et al., 2015).

Another approach to solving the problem of data insufficiency is for models to be flexible about data types that can be incorporated or used to quantify parameters. For example, multiple studies have presented serological data, phylogenetic data, and retrospective reports of disease from animal herders or farmers to reconstruct population-level disease patterns (Ludi et al., 2014, Ehizibolo et al., 2014, Tekleghiorghis et al., 2014b). Models of other host-pathogen systems have made great progress in developing modeling frameworks that can incorporate these data sources: the catalytic model is applicable to seroprevalence data (Griffiths, 1974, Hens et al., 2010) and phylogenetic data can be used to infer epidemiological dynamics (Grad and Lipsitch, 2014, Rasmussen et al., 2014, Popinga et al., 2014, Pomeroy et al., 2008). Collection of data from novel sources and model development to accommodate such data can be used not only for the design of targeted control, but they can also address many outstanding questions in the understanding of FMDV transmission.

Multiple challenges remain in understanding FMDV transmission and associated drivers (Tekleghiorghis et al., 2014a, Arzt et al., 2011) for which detailed models could prove useful in overcoming. For example, multiple host species, including wildlife, have been implicated in transmission, but their role remains largely unresolved. Similarly, the role of animal movement has been proposed as a transmission driver in both outbreak and endemic regions, but quantification and understanding of this driver remains elusive. Identification of transmission drivers will present new avenues for targeted control with applications to both outbreak and endemic areas.

In conclusion, models of FMDV transmission and control have been developed to represent targeted control strategies and transmission among detailed contacts. Designing targeted control will require additional data availability and accessibility. Novel data sources should be considered for quantification of FMDV transmission models. In the future, model use can be expanded from identification of control targets to also include identification of transmission drivers, in an effort to help inform broader understanding of FMDV transmission and control.